Real-time Ultrasound Thermography and Thermometry

This article describes the basic principles of ultrasound thermography (UST) and its real-time implementation using GPU-enabled software architecture. In medicine, the term thermography is mostly associated with heat-sensing infrared cameras for recording surface temperature changes. In this article, we use this term to describe the qualitative noninvasive imaging of tissue temperature change using any imaging modality. Examples of these modalities include microwave radiometry, magnetic resonance imaging (MRI), ultrasound imaging and photoacoustic tomography (PAT). Of these imaging methods, ultrasound and MR are the most widely investigated. Table I lists some ultrasound and MR based methods for tissue thermography reported in recent literature.

TABLE I.

Example MR and Ultrasound Methods for Thermography and Thermometry.

Modality	Method	Temperature Dependence	Tissue Dependence	Sensitivity	Spatial Res	Temporal Res
MR	Proton Resonance Frequency	ω(θ) = γx0(1 − σ(θ))	Low	~0.01 ppm/°C	$\mathcal{O}\left(\text{mm}\right)$	$\mathcal{O}\left(1\mathrm{s}\right)$
MR	Spin-lattice Relaxation	$T_1~e^{-\frac{E_a(T_1)}{k\theta }}$	High	1-2%/°C	$\mathcal{O}\left(\text{mm}\right)$	$\mathcal{O}\left(1\mathrm{s}\right)$
MR	Water Diffusion Coefficient	$D~e^{-\frac{E_a(D)}{k\theta }}$	Medium	~2%/°C	$\mathcal{O}\left(\text{mm}\right)$	$\mathcal{O}\left(1\mathrm{s}\right)$
US	Mean Scatterer Resonance	$f(\theta )=\frac{c(\theta )}{2d_s(\theta )}$	High	~0.05%/°C	$\mathcal{O}\left(\text{mm}\right)$	$\mathcal{O}\left(\text{ms}\right)$
US	Echo Shift	Equation 5	High	~0.05%/°C	$\mathcal{O}\left(\text{mm}\right)$	$\mathcal{O}\left(\text{ms}\right)$
US	Backscatter Energy	Equation 4	High	0.3 dB/°C	$\mathcal{O}\left(1\text{cm}\right)$	$\mathcal{O}\left(1\mathrm{s}\right)$

Parameters: γ (gyromagnetic ratio), B₀ (static magnetic field), σ (shielding constant), E_a (activation energy), k (Boltzmann constant); c (speed of sound), d_s (mean scatterer spacing)

The methods listed in Table I have been validated experimentally in various media, including in vivo [1], [3], [5]. As indicated in the table, all these methods exhibit some level of tissue dependence. In order to measure quantitative thermometry data, the changes in the measured temperature-sensitive parameter need to be adjusted for tissue type such as muscle, fat, liver, etc. This can be challenging in some tissues such as cirrhotic liver or breast.

Image guidance offers the promise of revolutionizing surgery in the 21st century. For example, focused ultrasound (FUS) has been shown to produce localized thermal therapy in deep tissue targets without the need for resection. However, while the principle of this surgery was well demonstrated in the early 1950s, it never gained clinical acceptance until after the successful demonstration of MR-guided FUS (MRgFUS) surgery. In particular, the implementation of MR thermometry [1] was the key enabling image guidance technology for MRgFUS to gain clinical approval from the US Food and Drug Administration (FDA). Given ultrasound’s high accessibility, cost effectiveness and clinical utility in initial diagnosis, robust implementation of UST on real-time scanners could significantly impact the use of image-guided FUS (IgFUS) worldwide, with or without MRI.

Noninvasive thermometry remains a sought after goal in medical imaging with numerous applications. In the context of image guidance, quantitative thermometry will provide the tools for delivering and evaluating the treatment as a prescription in addition to the monitoring and guidance provided by real-time UST (rtUST). More significantly, noninvasive thermometry will open the door for applications such as imaging inflammation and metabolic rate. These applications require high sensitivity and specificity due to the need to detect very small changes in temperature at the inflammation site, possibly in the presence of large tissue motion and deformation.

The feasibility of 2D temperature imaging using diagnostic pulse-echo ultrasound was demonstrated almost two decades ago [2]. The approach that received the most attention is based on the detection and estimation of minute temperature-induced echo shifts, which could be processed to generate the desired 2D maps of temperature change. The principle of measurement has been confirmed by a number of groups in tissue-mimicking phantoms, ex vivo models and recently in vivo small animal models [3]. Furthermore, GPU-enabled rtUST systems have been developed and demonstrated in pre-clinical settings.

The advent of rtUST, together with validation studies by numerous groups worldwide, has improved the odds of its clinical acceptance, but important challenges remain. One challenge is the reliable echo shift estimation in the presence of large tissue deformations in organs such as the liver and the heart. Tissue deformations result in echo decorrelation, which increases the variance of the estimation error. This is partially mitigated by the development of rtUST software architectures capable of supporting hundreds of frames per second thus minimizing frame-to-frame echo decorrelations. Another challenge is the distortion of the ultrasound imaging beams as they traverse regions undergoing temperature change. This introduces errors in the echo shift estimation distal to the heated region, i.e. spatially correlated estimation errors. All of these remaining challenges are in the realm of signal processing, requiring solutions ranging from spatio-temporal model-based filters to iterative reconstructive imaging. Once overcome, rtUST could lead to quantitative thermometry with high sensitivity and specificity with potential applications in noninvasive, nonionizing imaging inflammation, a grand challenge in medical imaging.

Ultrasound Temperature Sensitivity

The temperature dependence of the speed of sound is well known and has been extensively studied for decades. More recently, based on a careful examination of the literature, Miller et al [4] proposed a model for the speed of sound in tissue given by

$$\frac{1}{c(\theta )}=\frac{1}{c_w(\theta )}+\frac{1}{c_f(\theta )}+\frac{1}{c_r(\theta )},$$ (1)

where θ is the temperature, c is the speed of sound and the subscripts w, f, & r refer to water, fat and residual tissue (protein, etc), respectively. Empirical formulas for the three components were also given

$$c_w(\theta )={\displaystyle \sum _{i=0}^5{k}_w^i{\theta }^k},c_f(\theta )=k_f^0-k_f^1\theta ,c_r(\theta )=k_r^0-k_r^1\theta .$$ (2)

Based on (1) and specific values of parameters in (2), in most aqueous tissues, the temperature dependence can be described as an inverted quadratic curve, which peaks in the 45 - 55°C range.

In addition to the speed of sound, the change in backscatter energy (CBE) was also proposed as a method for the estimation of temperature change using pulse-echo ultrasound [5]. The backscatter coefficient from a random distribution of sub-wavelength scatterers is given by:

$$\eta (\theta )=\frac{{\left({\rho }_m{c}_m\left(\theta \right)-{\rho }_s{c}_s\left(\theta \right)\right)}^2}{{\left({\rho }_s{c}_s\left(\theta \right)\right)}^2}+\frac{1}{3}{\left(\frac{3{\rho }_s-3{\rho }_m}{2{\rho }_s+{\rho }_m}\right)}^2,$$ (3)

where ρ_m, ρ_m (ρ_s, c_s) are the density and the speed of sound for the medium (scatterer), respectively. For a plane wave propagating in the z direction, the backscatter energy is given by

$$E(\theta )=\frac{\eta (\theta )}{\overline{\alpha }(\theta )}\left(1-e^{-2\overline{\alpha }(\theta )z}\right),$$ (4)

where $\overline{\alpha }(\theta )$ is the attenuation coefficient of the medium. In [5], a temperature imaging relation was proposed based on the ratio E(θ)/E(θ₀) for some reference temperature, θ₀. The basis for this approach is the empirical result showing that the ratio in dB is increases or decreases monotonically in the 37 - 45°C range [5] for fat and aqueous tissues.

The Echo-Shift Model and Imaging Equations

A survey of the literature reveals that the echo-shift model is the most widely used in the medical ultrasound imaging community. Temperature change in tissue induces changes in the speed of sound as well as thermal expansion of the affected tissue. The former produces apparent echo shifts due to the change in the acoustical path length. The latter produces physical shifts due to the actual change in the location of the scattering elements within the heated volume. The details of the derivation can be found in [2] for what is now called the infinitesimal echo-strain filter δ-ESF. More recently, [3] introduced a modified version that resulted in a recursive echo-strain filter (RESF), which includes the δ-ESF as a special case.

To derive the RESF, assume a simple model of pulse-echo response from a single point scatterer at a distance z from the transducer face. Assume further that the medium is homogeneous at a constant baseline temperature, θ₀. An emitted pulse, p(t), will reach the scatterer after a delay of z/c₀ and the scattered echo will be detected by the transducer after an additional delay of z/c₀ for a total delay of 2z/c₀. For the inhomogeneous case, c(z, θ) and assuming infinitesimal temperature change, θ(z) = θ₀ + δθ(z), |δθ| ≪ θ₀, we can express the echo shift from two transmissions at T₀ and T₁:

$$\begin{gathered} \delta \tau (z)=\tau (z)-{\tau }_0(z) \\ \approx 2{\displaystyle {\int }_0^{z(\theta )(1-\alpha \delta \theta )}\left[\frac{1+\alpha (\xi )\delta \theta (\xi )}{c(\xi ,\theta (\xi ))}-\frac{1}{c(\xi ,{\theta }_0)}\right]d}\xi , \end{gathered}$$ (5)

where α is the linear coefficient of thermal expansion. The second term in the integrand accounts for the propagation delay at time T₀.

The Recursive Echo Strain Filter

Since |δθ| ≪ θ₀, one may assume c(z; θ(z)) = c₀(z)[1 + β(z)δθ(z)], which is justifiable near normal physiological temperatures. Substituting and differentiating (5) with respect to z, we get:

$$-\alpha z\frac{\partial \delta \theta }{\partial z}+(\alpha -\beta )\delta \theta =\frac{c(z,\theta )}{2}\frac{\partial \delta \tau (z)}{\partial z}.$$ (6)

This is a differential equation with spatially-varying coefficients, which can be solved numerically using a variety of methods. However, we seek a filtering approach for real-time implementation on a variety of platforms, including FPGAs. A considerable insight can be obtained by treating the coefficients as space invariant, including the coefficient of $\frac{\partial \delta \theta }{\partial z}$. Setting z = z_m and assuming α, β, & c are constants, we transform (6) into a constant-coefficient differential equation. Using τ = 2z/c ⟹ ∂τ = 2∂z/c allows us to discretize the equation on the uniform RF sampling grid ${\left\{{\tau }_i=i{T}_s\right\}}_{i=1}^{N_s}$ to arrive at the recursive equation [3]:

$$\delta \theta ({\tau }_i)=a\cdot \delta \theta ({\tau }_{i-1})+b\cdot (\delta \tau ({\tau }_i)-\delta \tau ({\tau }_{i-1})),$$ (7)

with the filter coefficients given by:

$$a=\frac{\alpha {\tau }_m}{\alpha {\tau }_m-T_s(\alpha -\beta )},\mathit{and}b=-\frac{1}{\alpha {\tau }_m-T_s(\alpha -\beta )}$$

where τ_m = 2z_m/c₀. The higher the value of z_m the narrower the bandwidth of the lowpass filter defined by the recursive term. The recursive term determines the extent of spatial memory, which is controlled by z_m.

It should be noted that (6) is an approximation of an integro-differential equation with higher order spatial derivatives of δθ and even nonlinear terms. The low order approximation is shown here due to the insight provided by the coefficients a&b in Equation 7. These coefficients produce well calibrated temperature estimates in terms of the computed echo strain differentials, (δτ(τ_i) − δτ(τ_i−1)).

The Infinitesimal Echo Strain Filter

Setting z_m = 0 reduces (7) to the discrete-space differentiator originally proposed in [2] or the δ-ESF. The echo strain equation described in [4] was derived under the same assumptions used to derive the δ-ESF while ignoring the thermal expansion term. Several other authors have used this model, including [6], [7], to demonstrate temperature imaging (thermography) in tissue-mimicking phantoms and tissue media. It was shown to be valid when the range of δθ is such that θ₀+δθ < 50°C when appropriate values of α, β, & c are used.

Parameter Sensitivity

Based on the δ-ESF model, it is easy to see that Δδτ_i = δτ(τ_i − δτ(τ_i−1) = T_s(β − α)δθ(τ_i). In muscle tissue, for example, β ~ 6.5 × 10⁻⁴ and α ~ 1.23 × 10⁻⁴ in the normal physiological body temperature range. Therefore, the infinitesimal echo strain is ~ 5 × 10⁻⁴/°C or 0.05%/°C.

Signal Processing Considerations

Speckle Tracking for Echo-shift Estimation

The coherent nature of pulse-echo ultrasound gives rise to speckle phenomenon which gives B-mode images their grainy appearance. In imaging, speckle reduces the soft-tissue contrast and is normally considered a undesirable. For tissue displacement estimation, however, speckle signal components provide an opportunity to estimate tissue motion and deformation with very high resolution [8]. The displacement estimation is typically achieved by performing localized cross correlation of RF echo signals from consecutive frames, s(x, z, T), s(x, z, T_i+1). The echo shift is simply obtained by determining the peak of the cross correlation.

The temperature imaging filters operate on the echo shifts induced by temperature change as well as other tissue motions and deformations. Depending on the frame rate, the frame-to-frame temperature-induced echo shifts are in the range nanoseconds to low microseconds. These shifts represent minute to small fractions of the sample times for a typical diagnostic ultrasound system (RF echo sampling in the range of 20 - 40 MHz.) Robust estimation of echo-shift profiles is the key to the success of ultrasound thermography and thermometry.

Several implementations of cross-correlation techniques for time delay estimation have been described in the literature. In [2], [3], [7], a complex cross correlation with zero-phase projection was used. This has the advantage of determining the true peak of the cross correlation with sub-sample accuracy without the need for interpolation. This is due to the fact that, in the absence of pulse distortion, the phase of the cross correlation is linear and makes a zero crossing at the true peak of the cross correlation function (See [9] and references thereof for the 2D case.)

Model Limitations, Imaging Artifacts and Mitigations

The echo shift models and the corresponding temperature imaging equations ignored tissue inhomogeneities and assumed linear dependence of the speed of sound on temperature. For example, 2D temperature estimates obtained based on the δ-ESF model exhibited thermal lensing artifacts [2] due to the distortion of the imaging beam as traversed the heated region. Briefly, since the speed of sound changes with temperature, the heated region behaves like a lens, which distorts the imaging beam. The distortion can be especially severe where the imaging beam traverses regions with sharp temperature gradients. This distortion produces axial and lateral oscillations in the echo shifts distal to the heated region, which are accentuated by the axial gradient ∂δτ/δz in (6). In [6], spatial compounding was shown to be effective in reducing thermal lensing artifacts.

Another source of artifacts is tissue heterogeneity (e.g. variation in fat content), which leads to variation in the values of α, β, & c as well as their temperature dependencies. These artifacts are inherent to pulse-echo ultrasound imaging, where beamforming is performed assuming a constant speed of sound, i.e. ignoring tissue inhomogeneity. However, modern scanners provide research mode with access to raw channel data. These software defined ultrasound systems allow users to investigate reconstructive imaging accounting for tissue inhomogeneity. If successful, reconstructive imaging could provide a basis for quantitative UST or ultrasound thermometry. In addition, the effects of temperature dependencies could be addressed by iterative reconstructive imaging solutions to the temperature estimation problem. At a minimum, one could implement a post-processing algorithm that enforces some of the known constrains about temperature fields:

1. Non negativity; for example, in a heating experiment, the temperature field cannot have values below the steady state baseline temperature.

2. Spatiotemporal evolution; temperature fields in tissue media is governed by the bioheat-transfer equation (BHTE), which is a modified version of the parabolic heat conduction equation. The Green’s function of the BHTE is a time-varying spatial Gaussian kernel [9].

3. Boundary conditions; skin temperature or core temperature away from the heated region.

These constraints can be combined to regularize the 2D temperature field using projection onto convex sets (POCS) algorithm described by Youla in [10]:

$${\theta }_{k+1}(x,z,T_i)=\mathcal{G}(T_i)\mathcal{P}(T_i)\mathcal{B}(T_i){\theta }_k(x,z,T_i),$$ (8)

where T_i is the ith frame (wall clock) time, $\mathcal{G}(T_i)$, $\mathcal{P}(T_i)$, and $\mathcal{B}(T_i)$ are (convex) projection operators corresponding to the Gaussian spatial bandwidth, positivity and boundary condition constraints.

From Thermography to Thermometry

UST as described above is more like echography due to the assumption of homogeneous medium in deriving the imaging equations. Nonetheless, UST has been shown to be useful in guiding therapy [2] and even quantitative tissue property measurements based on temperature transients [7]. The ultimate goal is to perform thermometry by developing quantitative measurements based on truly localized analysis of echo data. For this purpose, spectral analysis of the echo data could provide the answer [11]. Amini et al compared the infinitesimal echo shift model with a frequency shift model given by:

$$\delta f_m\approx f_m({\theta }_0)\left[\beta ({\theta }_0)-\alpha ({\theta }_0)\right]\delta \theta ,$$ (9)

where f_m is the mth harmonic of the resonance frequency associated with mean scatterer spacing in the region of interest and α, β, & θ are as in the RESF model above. The frequency shift leads to a more localized temperature change measurement. To improve the spatial resolution of this measurement, high resolution spectral estimation methods were employed (See [11] and references thereof.) We note that Equation (9) gives a sensitivity factor of ~0.05%/° (percent shift in resonance.)

Real-time Implementation of Ultrasound Thermography

The rtUST algorithm implementation is illustrated with the help of Figure 1, which shows a GPU/CUDA-enabled multi-stream architecture (a). This system is representative of the state-of-the-art in rtUST in that it supports parallel tasks on sequences of RF frames to meet the real-time constraints. For example, in each stream processor there are three threads that handle inter-process messaging and data processing, respectively. A stream processor can be assigned to any GPU in the system and is fully reconfigurable on the fly using shared memory. Any application which supports calling C functions (e.g. MATLAB, Octave or NumPy) can interact with the pipeline and act as an external engine.

Fig. 1.

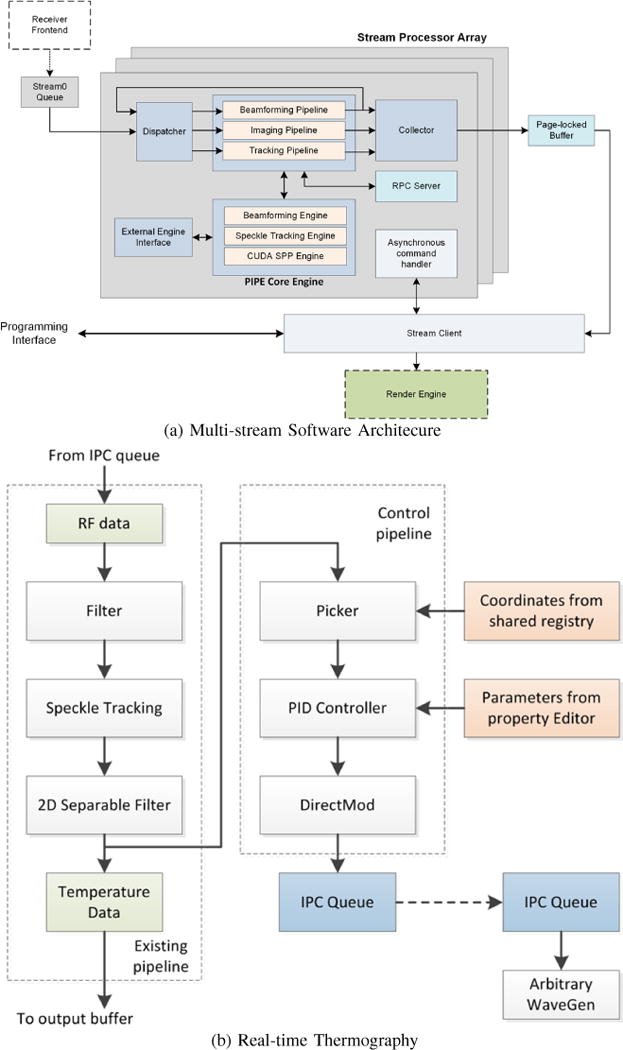
A state-of-the-art GPU-enabled software architecture for rtUST: (a) Multi-stream architecture with asynchronous beamforming, imaging and tracking pipelines running in parallel. The architecture allows for seamless interface with External Engines (e.g. MATLAB, Octave, etc.) through shared registry and a high performance IPC Queue. (b) Real-time Thermometry as currently implemented using the Tracking Pipeline, which supports a Control Pipeline for closed-loop control based on rtUST temperature feedback.

Figure 1b shows the tracking pipeline which operates on the RF echo data (from an imaging scanner or the External Engine). The RF data is optionally pre-filtered before speckle tracking is performed, followed by 2D separable FIR filtering to generate thermography imaging frames (Temperature Data). The tracking pipeline optionally connects to a real-time closed-loop temperature control at relatively high frame rates. The current system supports 1000 frames per second (fps). The benefits of high frame rates are twofold: 1) minimize frame-to-frame echo decorrelation and maintain the quality of the echo shift estimates, and 2) capture the tissue motion and deformation components together with the temperature-induced component at high rate to allow signal separation algorithms.

Experimental Validation in Tissue Media

Tissue-mimicking Phantom Results

Numerous reports on ultrasound thermography and temperature imaging used tissue mimicking phantoms to provide initial validation of the algorithms used [2]–[7]. Tissue-mimicking phantoms can be made homogeneous to provide validation of the imaging equations in a controlled, well characterized environment. They can also be made with different levels of contrast for certain acoustic and thermal parameters to answer basic questions regarding robustness of the estimation algorithms. In [2], [4], carefully planned and executed experiments using tissue-mimicking phantoms provided clear validation for the δ-ESF approach for small temperature changes and identified its limitations. Similar validation results from the RESF were shown in [3].

UST in Inhomogeneous Tissue Media

While ultrasound is currently the leading image guidance modality of RFA, it is primarily used to provide echographic B-mode images for visualization purposes. Several groups have proposed the use of UST and other semi-quantitative methods such as elastography. Example results from controlled RF heating experiments are presented here to illustrate the promise of rsUST in this important medical application. They also illustrate the current challenges facing UST when the target tissue is inhomogeneous and the size of the heated region is relatively large.

Figure 2 illustrates the basic setup (left) with a helical coil used as a heating source. The active segment of the coil is colored in red while the blue is insulated. The beamformed RF frames were acquired from a plane orthogonal to the coil axis approximately at the center of the active segment. A thermocouple was used to provide temperature feedback for closed loop control at the center of the target volume. The controlled heating procedure was as follows:

• Data collection was started at 0s acquiring 1 frame every 2s, i.e. 0.5 fps. Each frame was composed of N_L = 128 image lines (38 mm laterally) with N_s = 1900 samples of echo data from (3.85 - 76.96 mm axially).

• Heating began at 20s; just after Frame 10. Baseline temperature was 18.7°C.

• Closed loop control engaged at 80s with a set point of 40°C.

• Heating was completed at 320s; just after Frame 160.

• Ultrasound data collection stopped at 400s; just after Frame 200.

• RF frames were saved in MATLAB format for off-line processing

Frame-to-frame displacements were computed using the GPU-enabled speckle tracking algorithms described in [7]. A GTX770 (NVIDIA) was used to process the 1900 × 128 × 201 data set to produce a displacement data set of size 1900 × 128 × 200, i.e. a displacement field sampled at the same level as the RF data. MATLAB served as the External Engine calling the Speckle Tracking Engine in Figure 1a to produce the displacement fields with average execution time of 0.8684s or ≈ 230 fps. The RESF was applied to the data in MATLAB followed by 5 iterations of the POCS algorithm (8) for each frame (typically converged in 3 iterations). Two-dimensional temperature profiles at time Tj were computed as θ(x,z,T_i) = θ(x,z,T_i−1) + δθ(x, z, T_i) and overlayed on the grayscale B-mode image (acquired at T_i). Example B-mode image and corresponding 2D temperature map are shown in Figure 2 (middle two panels). The “+” marker just above a visible segment of the helical coil in B-mode. The estimated temporal temperature profile at marker location is shown in the top right panel. It reflects the dynamics of the controlled heating experiment, i.e. start of heating, start of control and cessation of heating. Furthermore, the estimated δT at the set point was close to the true ΔT for this experiment.

Fig. 2.

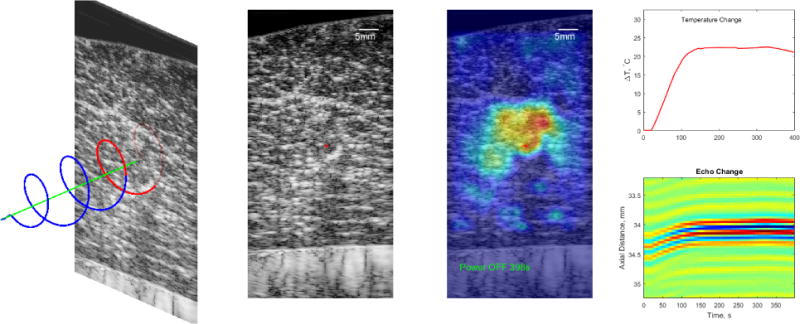
UST Monitoring of RF Heating in Bovine Muscle Ex Vivo. Left: Experiment setup showing the helical heating device and the position of the ultrasound imaging plane. Middle Left: A B-mode image of the target showing the inhomogeneous nature of the tissue. The “+” marker indicates the center of the heated region. Middle Right: The estimated 2D temperature profile overlaid on the B-mode image. Right: A temporal profile of the temperature change (top) at the “+” marker and a spatio-temporal representation of the echoes from 200 frames at the “+” marker.

The lower right panel of Figure 2 illustrates the echo shift phenomenon that was utilized in estimating the temperature change. It shows a 2-mm segment of the echo data centered axially at the “+” marker in the B-mode image. At this location, the echo gradually shifts towards the transducer by approximately 250 μm in about 114 seconds. The frame-to-frame correlation between the echo segments at this location remained high throughout the experiment despite the relatively low frame rate. In general, however, the echo locations as well as the echogenicity change significantly over the course of the experiment.

Figure 3 illustrates the advantages and limitations of the UST algorithm described above. Each panel shows a montage of 10 frames of estimated 2D temperature before, during, and after the controlled RF heating. The top panel shows the 2D temperature estimates obtained using the RESF without any additional post processing. The temperature profiles show the heating was maximum in crescent-shaped region, which correspond to a segment of the helix closest to the imaging slice. This pattern is nonexistent at time T = 0, faint at T = 40s, almost constant for 160s < T < 320s and shows some decay at T = 360s. These are consistent with the dynamics of the heating protocol. On the other hand, the temperature patterns exhibit spatial discontinuities inconsistent with the smooth nature of heat conduction in tissue media. Furthermore, the patterns exhibit artifacts at numerous locations distal to the heated region, e.g. pixel-size hot spots distal to the heated region in increasing numbers with time.

Fig. 3.

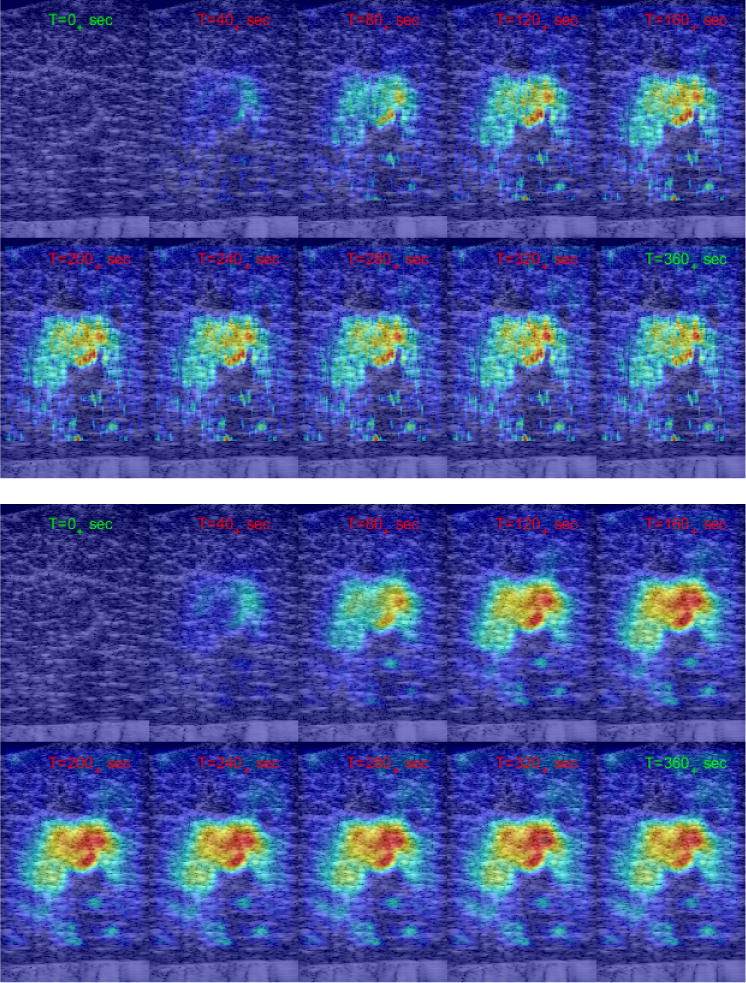
Montage of temperature profiles at selected frames before, during and after controlled RF heating using helical coil. Top: Resulting from RESF without post processing. Bottom: RESF and three iterations of POCS (8).

The lower panel in Figure 3 shows the same set of frames obtained using RESF followed by 5 iterations of the POCS algorithm (8). The temperature profiles are considerably smoother and are free from pixel-size hot spots seen in the RESF-only case. This is achieved without excessive smoothing. For example, the crescent-shaped heating region can still be seen and is consistent with the temporal dynamics of the heating experiment and the appearance of the coil segment in B-mode. In fact, the crescent appears to be more pronounced in the post-processed frames compared to the RESF-only temperature estimates.

While it produced significant improvements, POCS did not remove all artifacts, including tail-like patterns on both sides of the heated region. These are reminiscent of the thermoacoustic lens artifact reported in [2], [6]. In addition to the thermoacoustic lens effect, one can also see regions of localize apparent heating below the heated region. Some of these artifacts are due to reverberations in the RF echo data, especially in regions where the SNR is low.

In summary, the results demonstrate the high sensitivity of UST in detecting and spatially mapping temperature change from minute frame-to-frame echo shifts in heterogeneous tissue medium. In numerous similar experiments and other settings described in the literature, rtUST was shown to capture the dynamics of temperature change accurately. However, the specificity of UST is compromised due to echo-shift estimation errors resulting from imaging beam distortion due to thermal lensing and echo reverberations in low SNR regions.

Concluding Remarks and Future Outlook

We now have a wealth of data supporting the models for temperature imaging using pulse-echo ultrasound. These models need to be refined and validated in the context of quantitative estimation of temperature change. One possible approach is the use of extended Kalman filtering based on the spatio-temporal integro-differential equation derived in [3]. The Kalman filter approach was used to regularize the temperature fields in MR thermometry [12].

Spatio-temporal Kalman filtering and similar statistical signal processing tools are also necessary for the estimation and separation of large tissue deformation effects in organs like the heart and liver. The range of motion and deformation in these organs provides significant challenge, but the advent of high frame rate ultrasound technology (2D and 3D) could be the key to addressing this challenge. The multistream architecture described above supports speckle tracking at frame rates up to of 1000 fps, which helps to capture the tissue deformation more accurately by minimizing signal decorrelation effects [8]. The design of the KF as well as the required statistics could be informed by rtUST.

In addition to the illustrative results shown in this article, rtUST has been demonstrated in vivo [3] in the presence of tissue motion and deformation. Adaptive spatial filtering was successfully used for motion compensation albeit in a small animal model. These results provide further validation of the applicability of the models, especially the RESF, to realistic in vivo conditions. However, important challenges remain and the answers to these are firmly in the realm of advanced real-time signal processing. The most significant challenge to UST is the lack of specificity due to the thermal lensing effect, especially when the extent of the heated region is large. Advanced dereverberation methods could be used as part of the prefiltering block shown in Figure 1 (b). More importantly, pre-and post-beamforming methods to compensate for the distortion in the imaging beam by thermal lensing are needed. This may require tomographic reconstruction from pulse-echo data, which may or may not materialize. A statistical framework for the errors in echo shift estimation could improve the performance of post-processing algorithms such as POCS.

In this article, we emphasized the echo-shift methods because they led to imaging equations well suited for rtUST using FPGA and GPU platforms. However, it was also shown that temperature change can be measured through frequency shift estimation [11] based on (9) or the CBE [5]. A direct comparison between the echo and frequency shift methods revealed that the two models produce different artifacts, which resulted in improved temperature estimation by compounding. Multi-parameter estimation methods would be needed to improve the robustness of temperature estimation. The multi-stream architecture shown in Figure 1 was designed with this in mind.

Addressing the large tissue deformation challenge and removing or reducing displacement estimation errors will increase the value of UST in the guidance and monitoring of thermal therapy procedures. This opens the door to challenging, high impact applications such as the monitoring of the metabolic rate and imaging inflammation using thermometry. These are grand challenges in medical imaging.

Real-time Thermography in Medicine

The best known example of thermography in medicine is infrared imaging of the breast. This method was proposed in the 1950s and gained FDA approval in 1982. However, it has not been accepted either as a screening tool in the detection of breast cancer or as an adjunctive diagnostic tool. While this method reliably measures surface temperature, reconstructing the internal 3D temperature fields remains a major challenge. Microwave radiometry is another method that has a great appeal due to the fundamental nature of thermal noise, but has not gained acceptance in clinical applications due to poor spatial and temporal resolutions. Modern diagnostic imaging modalities such as MR and ultrasound offer the promise of thermographic solutions with higher specificity than infrared imaging and microwave radiometry. Today, MR thermography (MRT) and ultrasound thermography (UST) are the most widely investigated modalities. Even within each modality, several methods have been proposed, each exploiting the temperature sensitivity of one or more imaging parameters. For example, in MRI, the proton resonance frequency (PRF) is a temperature-sensitive parameter due to the temperature dependence of the shielding constant σ(θ). Furthermore, σ(θ) ∞ θ, which produces a linear temperature imaging equation Δθ = (Φ (θ) − Φ (θ_ref))/(k_p·f_ref·TE), where the PRF shift (f (θ) − f_ref) is interpreted as a phase shift. The values of σ for fat and water are ~ 1.3 × 10⁻⁶ and ~ 4.5 × 10⁻⁶, respectively. The temperature dependence of the water proton resonance is ~ 0.01 ppm/°C while the PRFs of lipid hydrogens are largely independent of temperature. Therefore, tissues with significant fat content present a challenge for this method. In the absence of fat, this parameter is largely tissue independent with the small dependency related to ion concentration. The spatial and temporal resolutions reported in the table for the PRF method were obtained with a standard deviation of < 1°C in immobile tissues. For all the other methods in the table, the temperature imaging equations are nonlinear and exhibit higher levels of tissue dependence.

MRT vs UST

The PRF method stands out being largely tissue independent, which is a key advantage. Furthermore, as with most MR parameters, the dependence is related to the molecular composition, which could lead to higher specificity. On the other hand, all ultrasound-based methods exhibit high tissue dependence, which limits their range to temperatures below 50°C. Fortunately, this still covers the majority of envisioned medical applications, including imaging inflammation. The spatial resolution is comparable for both methods with UST holding a slight advantage. UST holds a clear advantage in terms temporal resolution, especially with the advent of high frame rate ultrasound. Finally, MR continues to be expensive and requires MR compatibility (e.g. when using MRT for monitoring interventions). These provide clear advantages for UST, which is inexpensive and can be easily integrated with other medical devices.