PCA in High Dimensions: An orientation

Abstract

When the data are high dimensional, widely used multivariate statistical methods such as principal component analysis can behave in unexpected ways. In settings where the dimension of the observations is comparable to the sample size, upward bias in sample eigenvalues and inconsistency of sample eigenvectors are among the most notable phenomena that appear. These phenomena, and the limiting behavior of the rescaled extreme sample eigenvalues, have recently been investigated in detail under the spiked covariance model. The behavior of the bulk of the sample eigenvalues under weak distributional assumptions on the observations has been described. These results have been exploited to develop new estimation and hypothesis testing methods for the population covariance matrix. Furthermore, partly in response to these phenomena, alternative classes of estimation procedures have been developed by exploiting sparsity of the eigenvectors or the covariance matrix. This paper gives an orientation to these areas.

I. Introduction

Principal Component Analysis (PCA) is used throughout science and engineering to help summarize, represent and display data measured on many variables in terms of a smaller number of derived variables. The method originated with Karl Pearson in 1901 [1] and Harold Hotelling in 1933 [2]; further historical discussion appears in the book by Joliffe [3]. Its routine use in analysis of data required—and boomed with—the advent of electronic computers: an early classic in meteorology is the use by Lorenz [4] of the Whirlwind general purpose computer at MIT in the early 1950s to summarize air pressure data from p = 64 stations across the U.S.

The scale of data collection has exploded in recent decades, and it is no longer uncommon that the number of variables or features collected, p, may be on the order of, or larger than, the number of cases (or sample size), n. In this “high-dimensional” setting, under certain assumptions on the covariance structure of the data, the statistical properties of PCA exhibit phenomena that are perhaps unexpected when viewed from the historically standard perspective of many samples and a fixed number of variables.

This paper seeks to give an orientation to some of these high dimensional phenomena, which we label eigenvalue spreading, Section III, eigenvalue bias, Section IV and eigenvector inconsistency, Section V. The discussion is couched in terms of a particular assumed form for the covariance structure, the “spiked covariance model”, and focuses on a proportional asymptotic growth model in which p/n → γ ∈ (0, ∞) While certainly somewhat special, it allows clear statements of the phenomena which occur more widely. The results are introduced first in the setting of Gaussian observations, then Section VI reviews some of the many results now available beyond the Gaussian assumption.

Section VII looks at consequences of these high-dimensional phenomena in two estimation settings: covariance matrix estimation in a simple spiked model, and the exploitation of sparsity to estimate leading eigenvectors. Section VIII considers inferential questions in spiked models from the point of view of hypothesis tests.

Section IX departs from the proportional growth asymptotic model to review some non-asymptotic results and bounds, valid for p and n fixed. Finally Section X contains some concluding discussion, including some directions for extension of spiked models both for PCA, and for a variety of other multivariate models.

A. Basics of PCA

We start with observed data $X_1,\dots ,X_n\in {ℝ}^p,$, always using n for the number of observations on each of p variables, dimensions, or features. In this paper the observations will be assumed independent, though frequently they are correlated, as in time series. The data for us is real-valued, but everything goes over to the complex valued data that arises in signal processing, and indeed results are sometimes easier to prove for complex valued data.

The p × p sample covariance matrix is

$$S_n=n^{-1}{\displaystyle \sum }_{i=1}^n\left(X_i-\overline{X}\right){\left(X_i-\overline{X}\right)}^{\prime }$$

Mean correction by $\overline{X}$ is important in practice, but here for simplicity we assume that $\mathbb{E}{X}_i=0,$ and work instead with

$$S_n=n^{-1}{\displaystyle \sum }_{i=1}^n{X}_i{X}_i^{\prime }=n^{-1}X{X}^{\prime }\text{,}$$

where the p × n data matrix X has as its ith column the observation X_i. In the traditional formulation of large sample theory, p is taken as fixed and n is large, and it is then well known that we can estimate the population covariance matrix ∑ consistently. For example if the X_i are assumed independent and identically distributed (i.i.d.) with $\mathbb{E}{X}_i{X^{\prime }}_i=\Sigma ,$ then $S_n\stackrel{\text{a.s.}}{\to }\Sigma \text{ as }n\to \infty .$

Our main focus is1the eigenstructure of covariance matrices. Linguists and information theorists note that the most basic concepts typically have short representations in many languages. So it is with the eigenvalue-eigenvector decomposition of a sample covariance matrix, which has been given acronyms in many fields, curiously always with three letters, for example: PCA: Principal Component Analysis, KLT: Karhunen Loeve Transform, EOF: Empirical Orthogonal Functions, and POD: Proper Orthogonal Decomposition. It is also closely related to the SVD: Singular Value Decomposition of the data matrix X.

It is important to distinguish the population and the sample versions of the eigendecomposition. For the population covariance matrix, we write the eigenvalue-eigenvector decomposition as

$$\Sigma ={\ell }_1{u}_1{u^{\prime }}_1+\dots +{\ell }_p{u}_p{u^{\prime }}_p=UL{U}^{\prime },$$

where U is a p × p orthogonal matrix whose columns are the eigenvectors u_i and L is a diagonal matrix, with entries ${\ell }_i$ being the eigenvalues of ∑, by convention arranged in decreasing order, and assumed here to be distinct. The sample covariance eigendecomposition is

$$S_n={\lambda }_1{v}_1{v^{\prime }}_1+\dots +{\text{λ}}_p{v}_p{v^{\prime }}_p=V\Lambda V^{\prime },$$

where now the orthogonal matrix V has columns which are the sample eigenvectors v_i and diagonal $\Lambda$ has entries being the sample eigenvalues λ_i, again in decreasing order. Even with distinct eigenvalues, the sign of the eigenvectors is not identified—this is usually handled by specifying a convention for choice of sign. Again, in the traditional setting of p fixed, and large i.i.d. samples n, the sample eigen-quantities converge to their population targets: as n → ∞, we have ${\lambda }_k\stackrel{\text{a.s.}}{\to }{\ell }_k$ and $v_k\stackrel{\text{a.s.}}{\to }{u}_k,$ for each k = 1,..., p. Comprehensive references for this setting include classic texts such as [3], [5], [6].

p and n and all that. We noted that the traditional setting has p much smaller than n. Conversely, there are now many applications in which p is much larger than n - for example in genomics, in which there may be hundreds of patients n but millions of SNPs. For definiteness, this paper, and much theory, considers the important “boundary” case, where p is of the same order of magnitude as n, so that it makes sense to do asymptotic approximations in which p and n grow proportionately: γ_n = p/n → γ ∈ (0, ∞).

B. A low rank “spiked” covariance model

We focus on an idealized model for the population eigende-composition, consisting of a known ‘base’ covariance matrix ∑₀ and a low rank perturbation:

$$\Sigma ={\Sigma }_0+{\displaystyle \sum }_{k=1}^K{h}_k{u}_k{u^{\prime }}_k,$$ (1)

The signal strengths, or “spikes” h_k, as well as the orthonormal eigenvectors u_k are taken as unknown. The rank K is small, (and stays fixed in asymptotic models as p and n grow). In the simplest form of this “spiked” model, ∑₀ is assumed equal to the identity matrix, or to a (possibly unknown) scalar multiple ∑₀ = σ²I, [7]. The term generalized spike model is used when ∑₀ is not necessarily a multiple of the identity [8], [9].

Our study of statistical properties will be primarily asymptotic, and we remark that an essential feature of high dimensionality captured in the (generalized) spiked model is that as p grows, the empirical distribution (defined in Section III) of the population eigenvalues of ∑ is approximated by a nontrivial limiting probability distribution—or by a sequence of distributions, one for each p, in the case of approximation by deterministic equivalents, e.g. [10, Ch. 6]) on [0, ∞). We contrast this with, for example, the important domain1of “functional data analysis” and functional PCA, in which the observation vectors X_i have some intrinsic temporal or spatial smoothness, and the eigenvalues of ∑ decay at some rapid rate, e.g. [11], [12].

Returning to model (1), regarding the eigenvectors u₁,..., u_K, we want to contrast two situations. The first makes no assumptions about them, while in the second, we assume that they are sparse in some known orthonormal basis.

For simplicity, we mostly assume distinct population eigenvalues so that eigenvectors are identified. Many of the papers cited in fact include cases when population eigenvalues coalesce (i.e., are degenerate), and some consider estimation of the resulting eigensubspaces, i.e., the linear subspaces spanned by the eigenvectors corresponding to distinct population eigenvalues.

1). Some examples:

A (generalized) spike model may be an attractive and plausible idealization for data arising in many domains in science and engineering. An early example [13], [14] is provided by electrocardiogram (ECG) traces, Figure 1. The signal measured in the ith beat might be modeled as

$$X_i=\mu +{\displaystyle \sum }_{k=1}^K\sqrt{h_k}{s}_{ki}{u}_k+\sigma Z_i.$$ (2)

The periodic beats vary about the mean beat according to a small number of modes uk with random Gaussian amplitudes, the kth mode having variance hk. Independent Gaussian measurement noise is added. The corresponding covariance matrix Cov(Xi) has the finite rank perturbation form (1) with ∑₀ = σ²I.

Fig. 1.

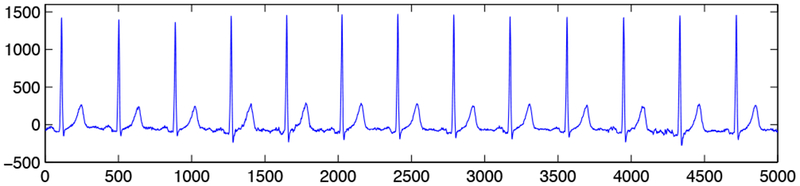
sample from an ECG trace sampled at 500 Hz, via Jeffrey Froning and Victor Froelicher, then at cardiology group at Palo Alto Veterans Affairs Hospital.

Some other examples, described superficially, might include

• Microarrays: X_i might represent the levels of expression of p genes in the ith individual. The eigenvector u_i may be sparse as only a small number of genes may be involved in a given pathway.

• Satellite images: X_i may be suitable sub-images. After a discrete cosine transform, the u_i may be sparse, [15].

• Medical shapes: X_i may be vectors derived from landmarks of body organs. Eigenvectors u_i may be sparse due to localized variation, [16].

• Climate: X_i might be measurements from a global sensor network at time i, the EOFs u_i are often localized.

• Signal detection: X_i are observations at sensors, u_i columns of the steering matrix, with signals s_ki (compare model (2)).

• Finance: X_i is a vector of returns of p assets at time i, u_i are factor loadings, often not sparse, $f_{ki}=\sqrt{h_k}{s}_{ki}$ are factors and Z_i idiosyncratic terms.

In summary, the many examples suggest that the spiked model is worthy of theoretical study, especially because it is relatively easy to manage.

II. Statistical framework : Distribution of eigenvalues of the sample covariance matrix

For explicit calculations and proofs it is often helpful to assume that the observations X_i are Gaussian and we will do so in Sections II– V unless stated otherwise. The results often remain true if the vectors X_i are not Gaussian, though still independent, satisfying some structure and moment conditions – these will be discussed in Section VI.

The Wishart Distribution.

Suppose then that the column vectors X_i are independently distributed as N_p(μ, ∑), a p- variate multivariate normal distribution with population mean vector μ and covariance matrix ∑. With mean μ = 0, the unnormalized sample covariance H = XX^′ is said to have the Wishart W_p(n, ∑) distribution with p variables and sample size, or degrees of freedom n. In what follows, the “null” case will have ∑ = I, though one could put in an unknown scale parameter. If p ≤ n, which we suppose for the rest of this section, then H is non-singular with probability one. For p > n, the singular Wishart distribution is defined in [17].

For completeness, we briefly describe the joint density function of H and its eigenvalues, although they will not be needed in the sequel. Already in 1928, Wishart showed [18] that the density function of H ~ W_p(n, ∑) is

$$c_{pn}{\left(\det \Sigma \right)}^{-n/2}{\left(\det H\right)}^{\left(n-p-1\right)/2}\exp \left\{-\frac{1}{2}\text{tr}\left({\Sigma }^{-1}H\right)\right\}.$$

For details, including the normalization constant c_pn, see e.g. [6, pp. 85, 62]. The joint density of the sample eigenvalues λ₁ > λ₂ > ⋯ > λ_p of S = n⁻¹H was obtained by James [19], and has the form

$$c_{pn}^{\prime }{\left(\det \Sigma \right)}^{-n/2}{\displaystyle \prod _{i=1}^p{\lambda }_i^{{}^{\left(n-p-1\right)/2}}{\displaystyle \prod _{i<j}^p{\left({\lambda }_i-{\lambda }_j\right)}_0{F}_0^{(p)}\left(-\frac{n}{2}\Lambda ,{\Sigma }^{-1}\right)}}$$

where the normalizing constant c^′_pn is given in [6, p. 388], ${}_{\text{0}}{}^{}F{}_0^{\left(p\right)}\left(X,Y\right)$ is a hypergeometric function with two symmetric p × p matrix arguments X and Y , defined in [6, p. 259], and $\Lambda =\text{diag}\left({\lambda }_1,\dots ,{\lambda }_p\right).$

These density functions, although explicit, are sufficiently elaborate in form that it is desirable to develop approximations. When dimensionality p and sample size n are large, such approximations may be derived from random matrix theory, as will be reviewed in succeeding sections.

III. High-dimensional phenomena I: Spreading of eigenvalues

Our first high dimensional phenomenon relates to the general fact, perhaps emphasized first by Charles Stein, [20], [21], that the sample eigenvalues are more spread out, or dispersed, than the population eigenvalues.

When p is proportional to n, the effect is very strong. Figure 2 illustrates this: in the left panel, all population eigenvalues equal 1, but the p = 100 sample eigenvalues have a histogram (over repeated sampling) that spreads over an order of magnitude! In the right panel, the population eigenvalues are equally spaced between 5 and 25, and the sample eigenvalues spread over a range from less than 1 to over 50. We see that the effect depends both on the population matrix ∑ and also very strongly on the ratio γ_n = p/n, becoming more pronounced as γ_n increases.

Fig. 2.

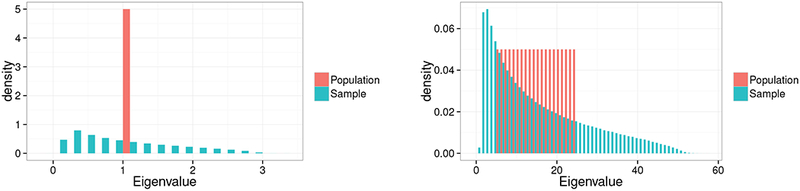
Eigenvalue spreading, for p = 100, n = 200. Population eigenvalues shown as histograms in red: left all at 1, ∑ = I, right equally spaced on [5, 25]: ∑ = diag(25,..., 5). Corresponding histograms of sample eigenvalues shown in blue. Figure credit: Brett Naul.

The Quarter Circle Law.

The importance of the spreading phenomenon, and the complexity of the exact joint distributions for fixed n and p makes it natural to look for approximations and limits. Marchenko and Pastur [22], see also [23], [24], gave a celebrated functional equation for the limiting distribution as p/n → γ for general ∑. The special case of ∑ = I, that is, the ‘null’ or ‘white’ case, has a simple and important form that we show here. Suppose that H ~ W_p(n, I). The empirical distribution function for the p sample eigenvalues of S_n = H/n is given by $F_p\left(x\right)=p^{-1}\#\left\{{\lambda }_j\le x\right\}.$

If p/n → γ ≤ 1, then the empirical distribution converges F_p(x) → F (x), with the limit distribution F having a density function of the celebrated quarter-circle form

$$f^{MP}\left(x\right)=\frac{1}{2\pi \gamma x}\sqrt{\left(b_{+}-x\right)\left(x-b_{-}\right)},$$ (3)

for x within the interval defined by the upper and lower edges $b_{\pm }={\left(1\pm \sqrt{\gamma }\right)}^2.$ The larger the ratio p/n, and hence γ, the larger the interval, in other words, the larger is the spreading of sample eigenvalues. If p is small relative to n then the distribution concentrates at 1, as occurs for p fixed, and as is to be expected when the data asymptotically allows perfect estimation. Figure 3 shows the examples p = n/4 in blue, and the extreme case p = n in green.

Fig. 3.

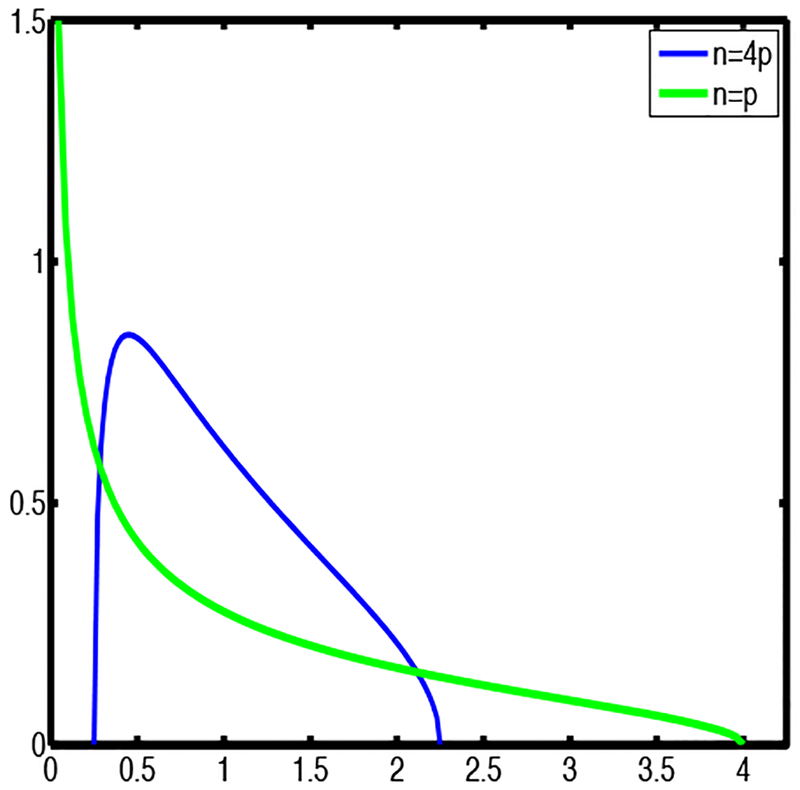
Two instances of the Marchenko-Pastur quarter circle law f^MP (x) from (3): blue for γ = p/n = 1/4, green for γ = 1.

If p > n, the sample covariance S_n has only n positive eigenvalues (with probability 1), and the remaining p – n eigenvalues equal 0. If p/n → γ > 1, the limit distribution F may be written in differential form as

$$F\left(dx\right)=\left(1-1/\gamma \right){\delta }_0\left(dx\right)+f^{MP}\left(x\right)dx,$$

with δ₀ representing a unit point mass at 0, and f^MP as above, supported on the interval $b_{\pm }={\left(\sqrt{\gamma }\pm 1\right)}^2.$

The name quarter-circle law also recalls the related, and celebrated Wigner semicircle law [25] which describes the limiting eigenvalue distribution for symmetric square matrices with i.i.d. entries¹.

IV. High-dimensional phenomena II: Eigenvalue bias

The second important phenomenon to emerge when p is proportional to n is that of bias in the top eigenvalues, combined with a phase transition in behavior that depends on the strength of the spike(s). Known as the Baik-Ben Arous-Péché (BBP) phase transition, it was first established for complex valued data in [27]. We first give an informal description of the bias and limiting distribution of the top sample eigenvalue(s) in the spiked model, and then a fuller set of references to the now large literature.

Consider a single spike, K = 1, and suppose that a basis has been chosen so that the population covariance matrix is diagonal: $\Sigma =\text{diag}\left({\ell }_1,1,\dots ,1\right).$ If p = γn, the sample eigenvalues are approximately spread out according to the Marchenko-Pastur distribution, with upper end point of the bulk at $b_{+}={\left(1+\sqrt{\gamma }\right)}^2,$ compare Figure 4.

Fig. 4.

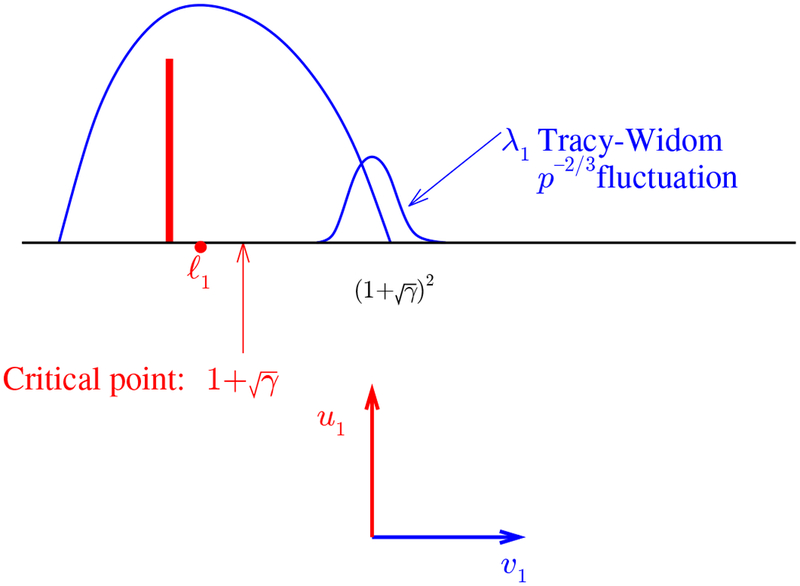
Below phase transition: Population quantities are in red, sample ones in blue. All population eigenvalues equal 1 except perhaps for the top one, ${\ell }_1$. Below the critical value $1+\sqrt{\text{γ},}$, the value of ${\ell }_1$ has no effect on the limiting distribution of λ₁, the Tracy-Widom distribution as in (5).

In a “null hypothesis” case, we have also ${\ell }_1=1.$ In that case, the largest sample eigenvalue is located near the upper edge b₊ and fluctuates on the (small) scale n^−2/3 approximately according to the real-valued Tracy Widom distribution: λ₁ ≈ μ(γ) + n^−2/3σ(γ)TW₁, where

$$\begin{array}{cc}\mu \left(\gamma \right)=b_{+}={\left(1+\sqrt{\gamma }\right)}^2,& \sigma \left(\gamma \right)={\left(1+\sqrt{\gamma }\right)}^{4/3}{\gamma }^{-1/6}\end{array}.$$ (4)

For fixed γ ∈ (0, ∞), this was established for complex-valued data (with limit distribution TW₂) in [28] and for real-valued data in [7]. An extension for p/n → 0 or ∞ (so long as min{p, n} → ∞) was given by [29].

In the non-null cases, with ${\ell }_1>1,$ the limiting bulk distribution of all sample eigenvalues is unchanged, essentially since it is unaffected by a single value. More surprisingly however, for ${\ell }_1\le 1,+\sqrt{\gamma },$ the largest sample eigenvalue has the same limiting Tracy-Widom distribution – the (small) spike in the top population eigenvalue has no limiting effect on the distribution of the sample top eigenvalue. Put another way, asymptotically the largest sample eigenvalue is of no use in detecting a subcritical spike in the largest population eigenvalue.

A phase transition occurs at $1+\sqrt{\gamma }$: for larger values of ${\ell }_1,$ the largest sample eigenvalue λ₁ now has a limiting Gaussian distribution, with scale on the usual order of n^−1/2, compare Figure 5. The mean of this Gaussian distribution shows a significant upward bias, being significantly larger than the true value of ${\ell }_1.$ It is perhaps noteworthy that the phase transition point $1+\sqrt{\gamma }$ for ℓ lies buried within the bulk.

Fig. 5.

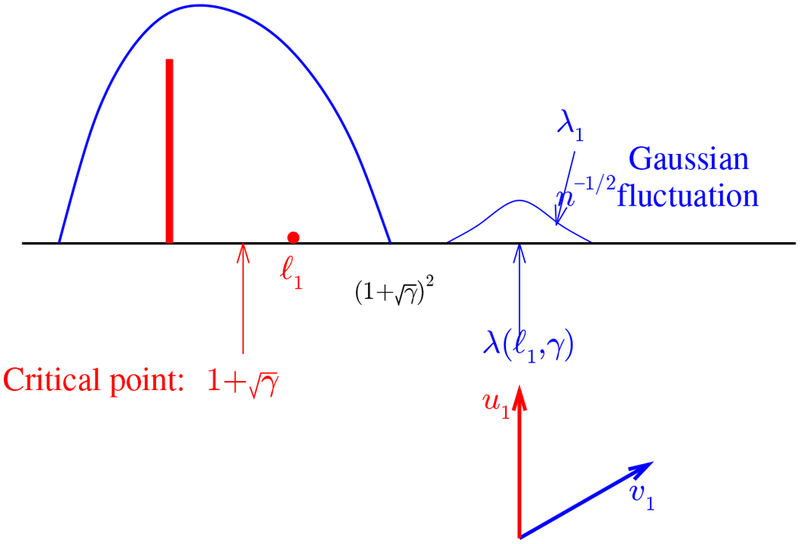
Above the phase transition: for ${\ell }_1>1+\sqrt{\text{γ},}$ the limiting distribution of λ₁ is now Gaussian, as in (6).

Appendix A gives a heuristic derivation and explanation for the inconsistency and the bias formula above the phase transition.

To summarize, for $1\le \ell <1+\sqrt{\gamma },\text{ if }p/n=\gamma +o\left(n^{-2/3}\right),$

$$n^{2/3}\left[\frac{{\lambda }_1-\mu \left(\gamma \right)}{\sigma \left(\gamma \right)}\right]\stackrel{\mathcal{D}}{\Rightarrow }T{W}_{\beta },$$ (5)

where μ(γ), σ(γ) in (4) do not depend on $\ell .$ The limiting Tracy-Widom distribution TW_β is more dispersed for real valued data (β = 1, [30]) than complex data (β = 2, [31]), but the centering and scaling constants are unaffected. The complex data result is established in [27] via analysis of Fredholm determinants, and the real case in [32] using a triadiagonal representation of XX^′.

On the other hand, above the phase transition, $\ell >1+\sqrt{\gamma },$

$$n^{1/2}\left[\frac{{\lambda }_1-\lambda \left(\ell ,\gamma \right)}{{\tau }_{\beta }\left(\ell ,\gamma \right)}\right]\stackrel{\mathcal{D}}{\Rightarrow }N\left(0,1\right).$$ (6)

There is a simple formula for the limiting upward bias in λ₁,

$$\lambda \left(\ell ,\gamma \right)-\ell =\gamma \frac{\ell }{\ell -1},$$ (7)

which does not vanish as ℓ increases; on the contrary it decreases to the limiting value $\gamma \text{ as }\ell \to \infty .$ See Figure 6. The bias formula (as an almost sure limit) was established in [33]. The asymptotic variance is

$${\tau }_1^2\left(\ell ,\gamma \right)=2{\ell }^2\left(1-\frac{\gamma }{{\left(\ell -1\right)}^2}\right).$$

in the real case, the convergence (6) being established by [34] by a perturbative method. An O(n^−1/2) Edgeworth correction term is given by [35]. In the complex case, ${\tau }_2^2={\tau }_1^2/2,$ as shown in the orignal BBP paper [27], via a Fredholm determinant analysis.

Fig. 6.

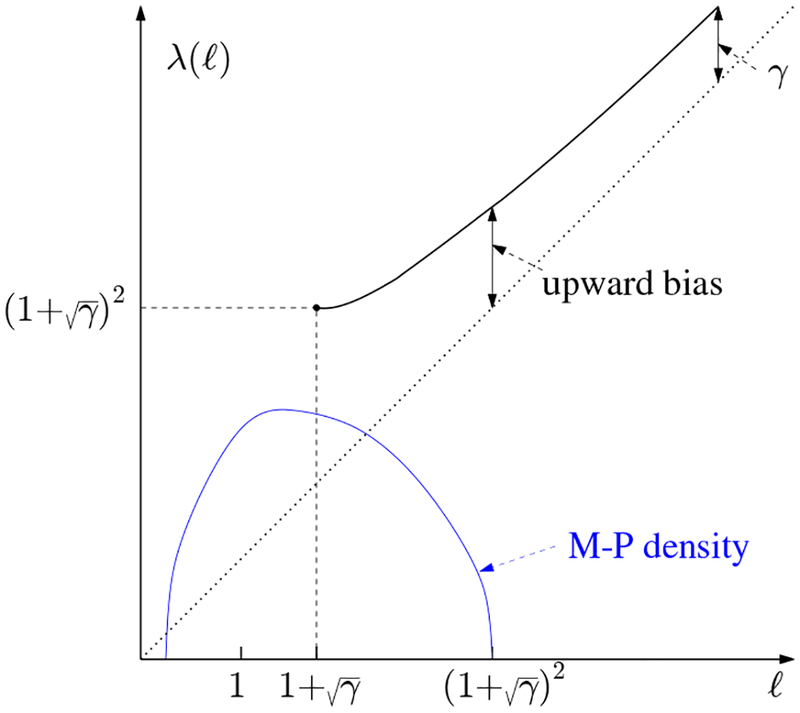
Upward bias of (asymptotic) mean of λ₁, denoted by $\text{λ}(\ell )=\text{λ}\left(\ell ,\gamma \right)$ in (7) above, for $\ell >1+\sqrt{\text{γ.}}$ Marchenko-Pastur density shown for reference in blue – the phase transition point is well inside the bulk.

If $\ell -1-\sqrt{\gamma }~w{n}^{-1/3},$ corresponding to the critical regime, then the limit distribution for λ₁, still on scale n^−2/3, is given by a modification of TW that depends on w, [27],[32].

In the domain of factor models in economics, [36] shows how these formulas exactly explain formerly puzzling phenomena observed in an influential empirical study [37] of properties of PCA applied to factor models published nearly 20 years earlier.

V. High-dimensional phenomena III: Eigenvector inconsistency

The third new phenomenon of the proportional sample size regime is perhaps the least recognized: namely that the leading eigenvectors in high dimensional PCA can be inconsistent.

Continuing the informal description in Figures 4 and 5, note that even when the population eigenvalue ${\ell }_1$ is well above the phase transition, there is a non-trivial angle between the sample eigenvector v₁ and its population counterpart u₁. As the signal strength of the eigenvalue ${\ell }_1$ decreases, the angle between v₁ and u₁ increases, indeed, when ${\ell }_1$ falls below the phase transition $1+\sqrt{\gamma },$ v₁ is asymptotically orthogonal to u₁, and gives no information about u₁. More explicitly, if p/n → γ > 0,

$${\langle v_1,u_1\rangle }^2\to \{\begin{array}{ll}\frac{1-\gamma /{\left({\ell }_1-1\right)}^2}{1+\gamma /\left({\ell }_1-1\right)}\hfill & {\ell }_1>1+\sqrt{\gamma }\hfill \\ 0\hfill & {\ell }_1\in \left[1,1+\sqrt{\gamma }\right],\hfill \end{array}$$ (8)

Appendix B gives a heuristic derivation of this formula, continuing the arrowhead matrix method set out in Appendix A.

Inconsistency of the largest sample eigenvector in this setting was first established by Lu [38], [39]. The formula (8) appears in various settings in the physics literature [40], [41], and rigorous discussions in high dimensional PCA under various model assumptions have appeared in many articles, including [34], [42]–[46].

Figure 7 depicts the sample PC v₁ as approximately uniformly distributed on a spherical cap at a non-zero angle to the population PC u₁ More precisely, the angle ${\langle v_1,u_1\rangle }^2$ concentrates near the limiting value given in (8). However, if $v^{\perp }=v_1-\langle v_1,u_1\rangle u_1$ is the component of v₁ orthogonal to u₁, then $v^{\perp }/\Vert v^{\perp }\Vert$ is uniformly distributed on a unit sphere S^p−1. This picture is exactly correct when the data X_i are i.i.d. Gaussian [34, Theorem 6], and asymptotically accurate more generally – the “delocalization” property to be discussed in Section VI-B below.

Fig. 7.

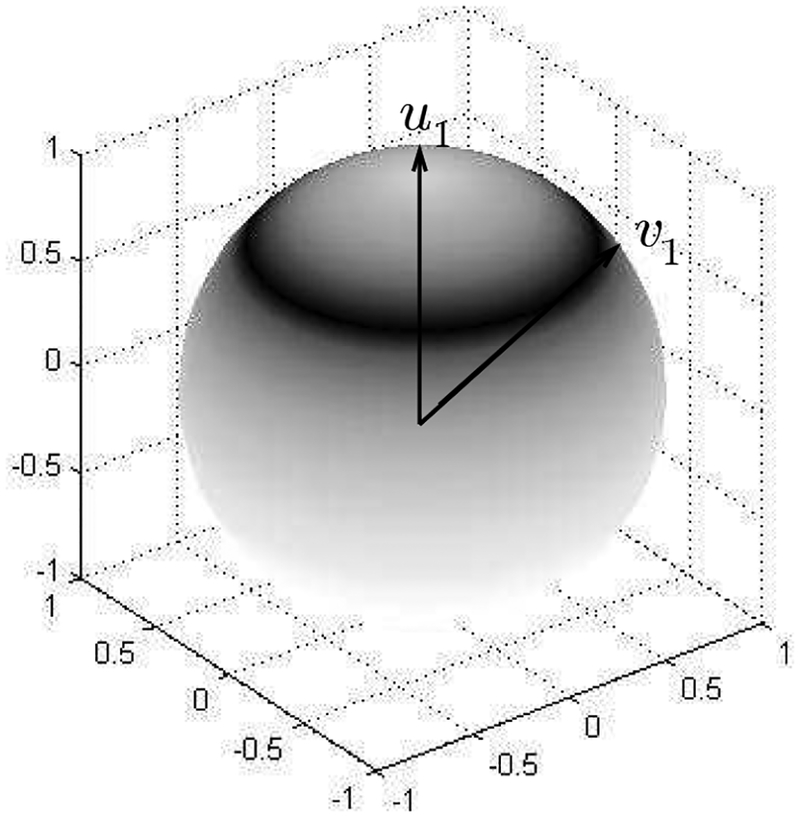
Inconsistency of the top sample eigenvector v₁ for estimating the top population eigenvector u₁ in the spiked covariance model when p ∝ n. See (8).

The discussion here focuses on the proportional regime p/n → γ ∈ (0, ∞). The behavior of PCA in settings when dimensionality p is much larger than n has been studied for example in [47]–[50]. Broadly speaking, if the spike eigenvalues remain fixed as p grows, the inconsistency properties can only get worse, but if the spike eigenvalues grow sufficiently fast with p and n, then consistent estimation of eigenvalues and vectors can still be possible.

VI. Universality phenomena

As we have seen, in the context of spectral analysis of the sample covariance matrix, the boundary case, namely when p/n → γ ∈ (0, ∞), yields many fascinating phenomena associated with the spectral elements of the Wishart matrix S = n⁻¹XX^′ with far reaching implications for statistical inference and signal processing in high-dimensional problems. However, many of the asymptotic results, especially those related to the behavior of extreme sample eigenvalues, and the sample eigenvectors under a spiked covariance model, were initially derived under the assumption of Gaussianity. In spite of providing valuable insights, these results by themselves are therefore still limited in their scope for practical data analysis. However, during the last decade, a large body of literature has been developed, primarily by analysts and probabilists, under the banner of “universality”, that has greatly extended the scope of these results, and therefore enhanced the scope of statistical inference.

Universality in the context of random matrix theory (RMT) typically refers to the phenomenon that the limiting behavior of certain eigenvalue/eigenvector statistics does not depend on the distribution of the entries of the random matrix. One of the major threads of contemporary research in RMT has been to establish that the asymptotic behavior of eigenvalues both at the bulk and and at the edges essentially remains invariant as long as the first few moments of the distribution of entries match with those of a Gaussian data matrix.

A. Universality of eigenvalue statistics

At the level of convergence of the empirical spectral distribution, the bulk behavior of the eigenvalues of the sample covariance matrix is universal, as long as the entries of that data matrix X are standardized independent random variables satisfying a Lindeberg-type condition [51]. The limiting distribution of normalized extreme (or edge) eigenvalues started receiving increased attention with the works of Soshnikov [52] who proved the Tracy-Widom limit of the normalized largest eigenvalues a Wishart matrix. This result, and its extension by[53] required the existence of all moments (in particular, sub-Gaussian tails) and symmetry of the distribution of entries of X. Phase transition phenomena for the leading eigenvalues of a sample covariance matrix were established by [54] assuming only the existence of fourth moments of the observations. Bai and Yao ([55]) extended these results and the Gaussian limits for the leading sample eigenvalues when their population counterparts are above the phase transition point. In [56], they extended these results further to the setting of a generalized spiked model where the non-leading eigenvalues are slowly varying as opposed to a constant.

Over last few years, radical progress on establishing the universality phenomena have been made by Erdös, Yau and co-authors ([57]–[60]), and Tao and Vu ([61]–[63]) who used analytical techniques to study the question of both bulk and edge universality under much more relaxed assumptions on the entries. The “Four Moments Theorems” of Tao and Vu assert effectively that the limiting behavior of the local eigenvalue statistics of a matrix of the form XX^′ is the same as when the entries of the data matrix X are i.i.d. standard Gaussian, provided the first four moments of the entries of X match with those of the standard Gaussian. A prototypical instance of such results is the following.

Theorem ([63]): Let X = ((X_ij)) and $\tilde{X}=\left(\left({\tilde{X}}_{ij}\right)\right)$ be p×n matrices with p, n → ∞ such that p/n → y ∈ (0, 1]. The entries X_ij (respectively, ${\tilde{X}}_{ij}$) are independently distributed, have mean zero and variance 1, and obey the moment condition ${\sup }_{i,j}\mathbb{E}\left[{\left|X_{i,j}\right|}^{C_{\text{0}}}\right]<C$ for a sufficiently large constant C₀ ≥ 2 and some C independent of p, n. Moreover, all the moments of order up to 4 are identical for X_ij and ${\tilde{X}}_{ij}.$. Let S and $\tilde{S}$ denote the associated covariance matrices. Then the following holds for sufficiently small c₀ and for every ε ∈ (0, 1) and for every k ≥ 1:

Let $G:{ℝ}^k\to ℝ$ be a smooth function obeying the derivative bound

$$\Vert {\nabla }^{j}G\left(x\right){\Vert }_{\infty }\le n^{C_{\text{0}}}$$

(where $\Vert \cdot {\Vert }_{\infty }$ denotes the largest element) for all 0 ≤ j ≤ 5 and $x\in {ℝ}^k.$ Then for any εp ≤ i₁ < i₂ < ⋯ < i_k ≤ (1−ε)p, and for sufficiently large n on depending ε, k, c₀, we have

$$\left|\mathbb{E}\left[G\left(n{\lambda }_{i_1}\left(S\right),\dots ,n{\lambda }_{i_k}\left(S\right)\right)\right]-\mathbb{E}\left[G\left(n{\lambda }_{i_1}\left(\tilde{S}\right),\dots ,n{\lambda }_{i_k}\left(\tilde{S}\right)\right)\right]\right|\le n^{-c_{\text{0}}},$$

where λ_j denotes the j-th largest eigenvalue.

[64] extended the domain of validity of the bulk and edge universality results even further by only requiring that the first two moments of the entries of X match that of a standard Gaussian, subject to a sub-exponential tail behavior. Key steps in the derivation of these results are: (i) to derive a strong local Marchenko-Pastur law, which gives a precise estimate of the local eigenvalue density; (ii) to embed the covariance matrix into a stochastic flow of matrices so that the eigenvalues evolve according to a coupled system of stochastic differential equations, called the Dyson Brownian motion; (iii) to implement a Green function comparison method that establishes closeness between the eigenvalue statistics of the Dyson Browian motion at time t = O(n⁻¹) with that of the original matrix, corresponding to flow at time t = 0. As a corollary, one obtains that the limiting distribution of the normalized largest eigenvalue of S is the Tracy-Widom distribution. The use of Dyson Brownian motion in the work of [64], can be broadly seen as a stochastic interpolation technique that builds a bridge between the data matrix X and a matrix of the same dimension with i.i.d. Gaussian entries with identical first two moments.

Above universality results are for the null Wishart case. For the more general setting, when X = ∑^1/2Z, where ∑^1/2 is a symmetric p × p matrix and Z is a p × n matrix with i.i.d., zero mean, unit variance entries, universality of extreme eigenvalues of S = n⁻¹XX^′ has been an object of intense study more recently. For a spiked covariance model, universality of extreme eigenvalues was established by [65] under the assumption that ∑ is diagonal with all but a finite number of diagonal entries equal to 1, and the entries of Z have vanishing odd moments. The latter assumption was relaxed by [66], who also established large deviation bounds on the spiked eigenvalues of S. Edge universality, and in particular the phase transition phenomena and Tracy-Widom limit for renormalized spiked sample eigenvalues in the sub-critical regime, for a general non-identity diagonal matrix ∑, has been established by [67] and [68]. They have used techniques closely related to those utilized by [64].

B. Universality of sample eigenvectors

Study of the behavior of the eigenvectors of a sample covariance matrix arises in the context of PCA. When X has i.i.d. zero mean Gaussian entries, distributional invariance under multiplication of X by orthogonal matrices implies that the matrix of eigenvectors of the sample covariance matrix S is Haar distributed, that is, the distribution is uniform on the space of orthogonal matrices. In particular, this means that the individual eigenvectors of S are uniformly distributed on the unit sphere in ${ℝ}^p.$ Several results have been derived to describe analogous behavior of the matrix of eigenvectors even when X is not Gaussian. A first result of this kind was proved by [69] who showed that if the first four moments of the entries of the data matrix match those of the standard Gaussian, then the matrix of eigenvectors is asymptotically Haar distributed as p/n → γ ∈ (0,∞).

One of the qualitative features of these results is the observation that entries of individual sample eigenvectors are of similar magnitude, a phenomenon often referred to as a delocalization property of eigenvectors. Such delocalization results are typical byproducts, and indeed important ingredients, in the contemporary investigations on universality of sample eigenvalues ([63], [64]).

Eigenvectors associated with the spiked eigenvalues of S under a spiked covariance model are of obvious interest. The eigenvector phase transition result (8) suggests that when a population spike is below the phase transition limit $1+\sqrt{\gamma },$ the corresponding sample eigenvector is orthogonal to the population eigenvector and therefore does not contain any information about the latter. As a generalization, [66] established the large deviation properties of linear functionals of the sample eigenvectors under a spiked population model, with a diagonal population covariance matrix ∑ that is a fixed rank perturbation of the identity, and with distributions of observations having subexponential tails. They showed that, when a population spike eigenvalue ${\ell }_j$ is above the phase transition limit $1+\sqrt{\gamma },$ the corresponding sample eigenvector v_j concentrates on the intersection of the unit sphere and a cone around the true population eigenvector, as in the Gaussian case (Figure 7). Moreover, the eigenvector v_j is completely delocalized in any direction orthogonal to the corresponding population eigenvector u_j, while for spikes below and strictly away from the phase transition limit, the corresponding sample eigenvectors are completely delocalized. A surprising finding of [66] is that, when a spiked eigenvalue ${\ell }_j$, say, is in close proximity to the phase transition point, so that, $\left|{\ell }_j-\left(1+\sqrt{\gamma }\right)\right|\ll 1,$ the complete delocalization of the sample eigenvector v_j in the direction of the corresponding population eigenvector u_j breaks down.

VII. Estimation in spiked models

Spiked covariance model has a natural interpretation in terms of factor models that are commonly used in econometrics and various branches of sciences. Partly because of this, and partly owing to the well-understood characterization of the asymptotic behavior of the sample eigenvectors and eigenvalues, the spiked covariance model has gained popularity in high-dimensional statistical estimation theory and inference. Investigations have focused on two related problems, one primarily dealing with estimation of the leading eigenvectors of a spiked covariance matrix, and the other focusing on the estimation of the covariance matrix itself.

A. Estimation of leading eigenvectors under sparsity

One branch of this estimation theory assumes some form of sparsity of the eigenvectors associated with the spiked eigenvalues. Specifically, the covariance matrix ∑ is assumed to be of the form $\Sigma ={\displaystyle \sum }_{k=1}^K{\tilde{\ell }}_k{u}_k{u}_k^T+{\sigma }^2{I}_p,$ where ${\tilde{\ell }}_1\ge \cdots \ge {\tilde{\ell }}_K>0,$ with the orthonormal eigenvectors u₁,..., u_K having only a few coordinates significantly different from zero. Under this framework, various nonlinear estimation strategies have been proposed for estimating the eigenvectors of ∑. This line of research started with [14] who established consistency of an eigenvector estimator that is obtained by a two-stage procedure. In this method, the first stage involves selection of coordinates based on thresholding the sample variances, which is then followed by a PCA of the selected submatrix of the sample covariance matrix. Improved coordinate selection schemes, together with detailed analyses of the minimax optimality of the proposed estimators have been studied by [70] and [71], while alternative estimation strategies and their asymptotic properties have been investigated by [72] and [73], among others. Under the assumed model, the eigenvector estimators can also be utilized to obtain consistent estimates of ∑ or ∑⁻¹ (e.g. [74]).

B. Estimation of the covariance matrix

While the assumption of sparsity of the eigenvectors allows one to solve the problem of covariance estimation in dimensions much larger than the sample size, in the absence of such structural assumptions, there is little hope of obtaining meaningful estimates in the p ≫ n setting. However, interesting covariance estimation procedures have been developed by making use of the eigenvalue and eigenvector phase transition phenomena in the “boundary case” p/n → γ ∈ (0, ∞) under the spiked covariance model. There are alternative estimation strategies (notably, by [75] and [76]) that do not rely on a spiked covariance formulation, but rather restrict attention to rotation-equivariant estimators. These estimators of ∑ are of the form $V_{\eta }(\Lambda )V^{\prime },$ where $V\Lambda V^{\prime }$ denotes the spectral decomposition of the sample covariance matrix S, and η(.) denotes an appropriate nonlinear shrinkage applied to the·sample eigenvalues (diagonal of Λ).

To keep the discussion well-connected with the remainder of this paper, below we focus on an estimation strategy [77] specifically designed for a spiked covariance model. It also shows clearly the consequences for estimation of each of the three high-dimensional phenomena discussed in Sections III, IV and V.

The strategy is inspired by early work of Stein, reported in the 1975 IMS Rietz Lecture, partly published in [78]. Suppose that $X_i\stackrel{i.i.d.}{~}{N}_p\left(0,{\Sigma }_p\right),$ for i = 1,...,n, with ∑_p having a spiked covariance structure, namely, the eigenvalues of ∑ are ${\ell }_1\ge \cdots \ge {\ell }_r>1=\cdots =1$ for some fixed r ≥ 1. Because of the eigenvalue spreading phenomenon, we want to shrink the sample eigenvalues. Here we propose using a single univariate function η to do the shrinking. With no prior information about the population eigenvectors, we leave the sample eigenvectors alone. This leads to an orthogonally invariant estimator of the form

$${\widehat{\Sigma }}_{\eta }\left(S_n\right)=\eta \left({\lambda }_1\right)v_1{v^{\prime }}_1+\dots +\eta \left({\lambda }_p\right)v_p{v^{\prime }}_p$$

While this is a more special form than the general rotation invariant estimator $V\eta \Lambda V^{\prime }$ mentioned earlier, it turns out that in the present setting, nothing is lost asymptotically by the restriction to scalar shrinkers [77, Sec. 8].

In view of the eigenvalue bias phenomenon, and the explicit upward bias function (7) for the top sample eigenvalue, it is natural to think that one could just undo the bias by choosing the shrinkage function η to be the inverse of $\lambda (\ell )$:

$$\ell (\lambda )=\{\begin{array}{ll}\frac{\lambda +1-\gamma +\sqrt{{\left(\lambda +1-\gamma \right)}^2-4\lambda }}{2}\hfill & \lambda >{\lambda }_{+}\left(\gamma \right)\hfill \\ 1\hfill & \lambda \le {\lambda }_{+}\left(\gamma \right).\hfill \end{array}$$ (9)

Note that the inversion is to be applied only to sample eigenvalues above the phase transition ${\lambda }_{+}\left(\gamma \right)={\left(1+\sqrt{\gamma }\right)}^2.$

However, this idea is complicated by the eigenvector inconsistency phenomenon. In view of (8), the top population and sample eigenvectors u₁ and v₁ span a plane, shown in Figure 8. Inversion of λ₁ to $\ell \left({\lambda }_1\right)$ still makes an error because the error of v₁ in tracking u₁. Depending on how we measure the error, it seems clear that some other shrinkage value η(λ₁) might lead to smaller error than simply undoing the bias.

Fig. 8.

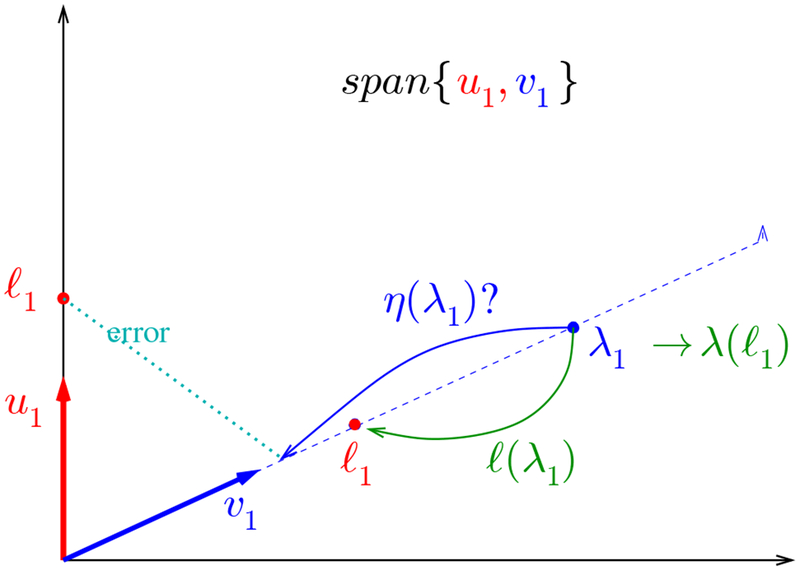
Schematic to motivate dependence of optimal shrinkage on the error measure. The observed sample eigenvalue λ₁ is shrunk by η(λ₁) along sample eigenvector v₁. Since v₁ is necessarily mis-aligned with the truth u₁, the error incurred depends on the metric used.

Indeed, Table I shows some many commonly used orthogonally invariant loss functions, such as the Operator loss, Frobenius loss, Entropy loss, Stein’s loss and Fréchet loss, and the optimal shrinkage function, available in closed form, that minimizes the limiting loss

$$L_{\infty }\left(\eta |{\ell }_1,\dots ,{\ell }_r\right)=\underset{n,p\to \infty }{\lim }{L}_p\left({\Sigma }_p,{\widehat{\Sigma }}_{\eta }\left(S_n\right)\right),$$ (10)

in the asymptotic framework p/n → γ ∈ (0, 1] as p, n → ∞. Indeed, for operator norm, it is best to invert the bias function, but for the other loss functions, a notably larger amount of shrinkage is done, especially for Stein’s loss. The key point is that the choice of loss function critically affects which estimator is optimal, and this follows directly from the high dimensional phenomena outlined earlier.

TABLE I.

Optimal shrinkage functions η^∗(λ; γ) for a selelection of loss functions under a spiked covariance model [77]. We set $c=c(\ell )=\sqrt{(1-\text{γ}/{(\ell -1)}^2)/(1+\text{γ}/(\ell -1))}$ and $s=\sqrt{1-c^2.}$. Here $\ell =\ell (\lambda ),c=c(\ell (\text{λ)})$ and $s=s(\ell (\text{λ)})$ depend on λ through (9) and implicitly also on γ. Values shown are shrinkers for λ > λ₊(γ); all shrinkers satisfy η^∗(λ) = 1 for λ ≤ λ₊(γ).

Loss function	Form of Lp(A,B)	Optimal shrinker η∗(λ; γ)
Operator loss	${\Vert A-B\Vert }_{op}$	ℓ
Frobenius loss	${\Vert A-B\Vert }_F^2$	$\ell c^2+s^2$
Entropy loss	$\frac{1}{2}(\text{trace}(B^{-1}A-I)-\log (\left|A\right|/\left|B\right|))$	$\ell c^2+s^2$
Frobenius loss on precision	${\Vert A^{-1}-B^{-1}\Vert }_F^2$	$\ell /(c^2+\ell s^2)$
Stein loss	$\frac{1}{2}(\text{trace}(A^{-1}B-I)-\log (\left|B\right|/\left|A\right|))$	$\ell /(c^2+\ell s^2)$
Fréchet loss	$\text{trace}(A+B)-2(\sqrt{A}\sqrt{B})$	${(s^2+\sqrt{\ell c^2})}^2$

VIII. Inferential questions under the spiked model framework

One of the earliest uses of the distribution of the largest eigenvalue of the sample covariance matrix is in testing the hypothesis H₀ : ∑ = I_p when i.i.d. samples are drawn from a N(μ, ∑) distribution. This testing problem, typically referred to as testing the hypothesis of sphericity, has a long history. Mauchly [79] first derived the likelihood ratio test for sphericity under the classical fixed p and Gaussian observations regime. The (Gaussian) locally most powerful invariant (under shift, scale and orthogonal transformations) test was obtained by John ([80], [81]) and by [82]. [83] proposed extensions (for the unknown and known scale problems) of John’s test, while [84] proposed corrections to Mauchly’s likelihood ratio test for the p/n → γ ∈ (0, ∞) regime. Taking a different approach, Pillai ([85], [86], [87]) utilized the asymptotic behavior of the largest sample eigenvalue to develop tests for sphericity under the fixed p (Gaussian) regime.

The Tracy-Widom law for the largest sample eigenvalue under the null Wishart case, i.e., when the population covariance matrix ∑ = I_p, allows a precise determination of the cut-off value for the largest root test. With a careful calibration of the centering and normalizing sequences, this cut-off value is very accurate in terms of having the correct level of significance even for relatively small p and n ([7], [88], [89]). In addition, the Tracy-Widom law for the largest eigenvalue has been extensively used for signal detection ([90], [91], [92], [93]). Many of these approaches use a sequential hypothesis testing framework whereby the Tracy-Widom law is used to determine the null distribution for testing the presence of an additional signal direction.

In view of various contrasting approaches, a detailed analysis of the behavior of the power function for tests of sphericity requires formulating suitable alternative models. The spiked covariance model provides such a convenient model that has easy interpretability, and at the same time has enabled researchers to carry out precise power analysis. The asymptotic power of various tests for sphericity has been thoroughly investigated by Onatski, Johnstone and coauthors ([94], [95], [96]). We provide here a brief overview of these works.

Onatski et al. [94] studied the asymptotic power of tests of sphericity against perturbations in a single unknown direction as both p and n go to infinity. They established the convergence, under the null hypothesis and contiguous alternatives, of the log ratio of the joint densities of the eigenvalues of the sample covariance under the alternative and the null, to a Gaussian process indexed by the norm of the perturbation. They showed that when the norm of the perturbation is below the phase transition threshold, the limiting log-likelihood ratio process is nondegenerate, and the joint eigenvalue densities under the null and alternative hypotheses are mutually contiguous. Importantly, consistent with formula (5) above, under the contiguous alternative regime, the asymptotic power of the Tracy-Widom-type tests is trivial (i.e., equals the asymptotic size), whereas that of the eigenvalue-based likelihood ratio test is always larger than the size and increases to one as $\ell \nearrow 1+\sqrt{\gamma }.$

IX. Finite sample behavior of principal components

While most of the work within the framework of high-dimensional PCA is asymptotic in nature, with both p, n → ∞ together, there have been notable recent developments in terms of providing finite sample bounds on the discrepancy between the population eigenvalues and eigenvectors and their sample counterparts. One of the first works of this kind is by Nadler [42], who considered a Gaussian observation model with a single spike for the covariance matrix, and established probabilistic bounds for fluctuations of the largest eigenvalue of the sample covariance matrix for arbitrary p and n. He also established a finite sample probabilistic bound for the sine of the angle between the leading sample eigenvector and the corresponding population eigenvector. A feature of the work by Nadler [42] is the use of “small-noise-asymptotics”, whereby for fixed p and n, the noise variance (which equals the value of the non-spiked eigenvalues) is allowed to converge to zero. He provided analytic expansions of the leading sample eigenvalue under this asymptotic regime. [97] extends this small-noise approach to other spiked multivariate models.

Understanding the behavior of eigenprojections – orthogonal projection operators onto the eigensubspaces – of the sample covariance matrix, not necessarily under the spiked covariance model, has received attention from multiple communities. Vaswani and coauthors [98], [99] studied signal recovery through PCA in a framework that allows both nonisotropic noise and noise that are correlated with the signal. Specifically, they considered the observation model

$$Y_t=Q{a}_t+M_{t}Q{a}_t+v_t,$$ (11)

where Q is a p × m matrix with m ≪ p, with Qa_t denoting the random signal, while the uncorrelated noise component v_t satisfies $\mathbb{E}\left(Q{a}_t{v}_t^T\right)=0.$ For unknown p × p matrices M_t, the component M_tQa_t represents the component of noise that is correlated with the data. They discussed various engineering and signal processing applications, including PCA based on missing data. In each case, an estimate of Q is formed by the matrix consisting of the first r eigenvectors of the sample covariance matrix of {Y₁,..., Y_n}. Assuming sub-Gaussian signal and noise, [99] established finite sample probabilistic bound for subspace recovery error, defined as sine of principal angle between the column spaces of Q and $\widehat{Q}.$ Under the spiked covariance model, their results are analogous to those by [42].

In related works, Koltchinskii and Lounici [100], [101] studied the behavior of $\Vert {\widehat{P}}_r-{\text{P}}_r{\Vert }_2^2,$ where P_r denotes the eigenprojection corresponding to the r-th largest distinct eigenvalue of the population covariance ∑, and ${\widehat{P}}_r$ is the corresponding sample eigenprojection based on i.i.d. observations from the population, while the norm is the Hilbert-Schmidt norm. They established the uniform convergence of the standardized version of this quantity to a standard normal distribution. While their work is not within the context of the p/n → c > 0 setting, they showed that the accuracy of the normal approximation is characterized by the so called “effective rank” $r(\Sigma ):=\text{trace}(\Sigma )/\Vert \Sigma \Vert$ where $\Vert \Sigma \Vert$ denotes the operator norm of ∑. They also established finite sample concentration bounds for ${\Vert {\widehat{P}}_r-P_r\Vert }_2^2$ and nonasymptotic bounds its expectation and variance.

The framework adopted by [100] is closely linked with the functional principal component analysis framework studied by many researchers. Without delving into the huge literature associated with this topic, we just mention a few works that are most relevant. [102] established nonasymptotic bounds on the L² risk of estimating the eigenfunctions of a covariance operator under different regimes, including polynomial and exponential decay of the eigenvalues of the population covariance operator. [103] established nonasymptotic bounds on the expected excess empirical risk associated with the projection of the observed data onto the eigensubspaces associated with the leading eigenvalues. The bounds show that the excess risk differs considerably from the subspace distances between the population and sample eigenprojections.

X. Concluding Discussion

We have provided a broad overview of the key phenomena associated with high-dimensional PCA. In this section, we summarize some of the recent trends, and discuss some unresolved questions, in theoretical analyses of PCA and allied methodologies. Strikingly, this literature is characterized by increasingly sophisticated utilization of tools from random matrix theory. The research directions we outline here are broadly categorized into three sub-categories: (i) extensions around high-dimensional PCA in different domains, including time-dependent data, variance components modeling, and hypothesis testing involving the covariance matrix; (ii) exploration of spike phenomena in other multivariate models; and (iii) resampling based inference for principal components.

A. Some extensions (around PCA)

Time dependent data:

While traditional multivariate statistical analysis focuses on independently observed samples, much of the data in real world are intrinsically time-dependent. It is notable that PCA is routinely applied for dimension reduction and signal detection in data that can best be characterized as a time series. There is a voluminous econometric literature focusing on static factor models with time-dependent factor loadings when p/n → 0. There is also a growing literature on dynamic factor models (DFM) [104]. Until recently, there were little theoretical investigations on statistical properties of estimators under these models when p/n → c ∈ (0, ∞). Motivated by the question of determination of the number of dynamic factors in a DFM, Jin et al. [105] established the existence of a limiting spectral distribution of the ESD of symmetrized sample autocovariance matrices based on the “null model”, i.e., when the observations are assumed to be i.i.d. and isotropic. Liu et al. [106] extended these results to a class of linear processes with simultaneously diagonalizable coefficient matrices. A further relaxation on the structure of the linear process was achieved by [107]. These results raise the prospect of extending analyses already carried out for i.i.d. observation, such as establishment of phase transition phenomena, characterization of limiting distribution of extreme eigenvalues, establishment of CLT for linear spectral statistics, estimation of spectra of population covariance, to the setting of time-dependent data. Significant progress related to phase transition phenomena for singular values of sample autocovariances has been made in [108] and [109]. A method for estimating the joint spectrum of coefficient matrices of a class of ARMA processes has been developed in [110]. A different kind of phase transition phenomenon for the largest sample eigenvalues and associate eigenvectors, when the coefficient matrix of an AR(1) process has low rank, has been described in [111]. These results point to the possibility of a rich exploration of phenomena associated with eigen-analysis in the context of high-dimensional time series.

Multivariate variance components:

We have been concerned with spectral properties of data relating to a single high-dimensional covariance matrix. In a multivariate variance components model, more than one covariance matrix appears:

$$X=U_1{\alpha }_1+\cdots +U_k{\alpha }_k.$$

Here U_r are fixed n × I_r design matrices, while the I_r rows of α_r are independently distributed as N_p(0, ∑_r). High dimensional settings in which p, n and each I_r grow proportionately are of interest, for example, in quantitative genetics. Spectral properties of quadratic estimators ${\widehat{\Sigma }}_r=X^{\prime }{B}_{r}X$ of the variance components ∑_r can be investigated: [112] and [113] describe results for the bulk and edge eigenvalues of ${\widehat{\Sigma }}_r.$ Work in progress by the same authors studies analogs of the results of Sections IV and V for spiked models for each ∑_r.

Tests of sphericity beyond the spiked alternative:

In a recent work, Dobriban [114] dealt with the question of detection of directionality in high-dimensional data by going beyond the spiked alternatives formulation. His approach addresses the question whether it is possible to detect weak PCs under the general covariance matrix models of [22]. He formulated the hypothesis testing problem within the framework of a non-parametric, non-Gaussian generalization of the spiked model. Specifically, denoting E_p to be the empirical distribution of the eigenvalues of ∑, this formulation boils down to testing

$$H_{\text{0},p}:E_p\left(1-h/p\right)E+\left(h/p\right)G_0$$

against

$$H_{\text{1},p}:E_p\left(1-h/p\right)E+\left(h/p\right)G_1$$

where E, G₀ and G₁ are pre-specified probability distributions supported on ${ℝ}^{+},$ and 0 < h < p is a specified constant. Clearly, by taking E = G₀ = δ₁ (degenerate at 1), the test becomes that of testing sphericity, while at the same time, taking h to be a fixed integer and $G_1=h^{-1}{\displaystyle \sum }_{j=1}^h{\delta }_{1+c_j}$ for positive c_j’s leads to a spiked alternative. [114] developed new tests based on asymptotic Gaussianity of linear functionals of eigenvalues of the sample covariance matrix to detect weak PCs under this model. A related approach to test of sphericity, involving a correction for the likelihood ratio statistic to compensate for the dimensionality, is discussed in [115].

B. Other multivariate models

PCA is only one of a whole arsenal of methods of multivariate statistics which are based on eigenvalues and eigenvectors of one or two sample covariance matrices. Examples include signal detection, MANOVA and multiple response regression, canonical correlations, discriminant analysis and so on—these form much of the content of textbooks on multivariate statistical analysis such as [5]. James ([116]) organized all these problems into a hierarchy of five different classes (indexed by the classical hypergeometric functions _pF_q).

The high dimensional phenomena discussed in earlier sections extend to the James hierarchy. For example [95] and [96] consider the spike testing problem. Each of James’ five testing problems is related to the eigenvalues of E⁻¹H where H and E are independent and proportional to high-dimensional Wishart matrices. Under the null hypothesis, both Wisharts are central with identity covariance. Under the alternative, the non-centrality or the covariance parameter of H has a single eigenvalue, or a spike, that stands alone. When the spike is larger than a case-specific phase transition threshold, one of the eigenvalues of E⁻¹H separates from the bulk. This makes the alternative easily detectable, so that reasonable statistical tests are consistent, in the sense that their power converges to 1 and a local asymptotic normality theory can be built [96]. In contrast, when the spike lies below the threshold, none of the eigenvalues separates from the bulk, which makes the testing problem more challenging. [95] shows that, the measures corresponding to the joint distributions of the eigenvalues under the alternative and the null hypotheses are mutually contiguous when the magnitude of the spikes are below the phase transition threshold. Furthermore, the log-likelihood ratio processes parametrized by the values of the spikes are asymptotically Gaussian, with logarithmic mean and autocovariance functions. These findings allow computation of the asymptotic power envelopes for the tests for the presence of spikes in the different multivariate models.

C. Bootstrapping high-dimensional PCA

Resampling methods have been very popular in statistics and machine learning due to their distribution-free characteristics and easy applicability. In finite-dimensional problems, under mild regularity conditions, bootstrap techniques provide a useful alternative to (nearly always) asymptotic inference procedures that typically involve quantities requiring costly estimation procedures. However, application of bootstrap techniques to high-dimensional inference, especially in the context of PCA, has had limited success. A succinct explanation of the failure of standard non-parametric bootstrap methods in the p/n → c ∈ (0, ∞) setting has recently been given by El Karoui and Purdom [117]. They also showed that, in the case where the population covariance matrix is well-approximated by a finite rank matrix, which corresponds to a spiked model with much larger spiked eigenvalues compared to the noise eigenvalues, the bootstrap performs as well as it does in the finite-dimensional setting. In a complementary study, Lopes et al. [118] developed a consistent method for bootstrapping linear spectral statistics of sample covariance matrices by appropriately modifying the usual parametric bootstrap procedure. This method has the salient feature that it allows the user to circumvent the difficulties of complex asymptotic formulas involved in the description of CLT for linear spectral statistics. Development of provably consistent resampling strategies constitutes an exciting new frontier for high-dimensional PCA and related techniques such as MANOVA and CCA.

Biographies

Iain Johnstone received the B.Sc. (Hons) degree in Pure Mathematics and Statistics and M.Sc. degree in Statistics from the Australian National University in 1977 and 1978 respectively, and the Ph.D. degree in Statistics from Cornell University in 1981. Since 1981 he has been Assistant, Associate and then Full Professor in the Department of Statistics at Stanford University. Since 1989, he has also held a 50% time appointment in Biostatistics in the Stanford University School of Medicine. His research in theoretical statistics has used ideas from harmonic analysis, such as wavelets, to understand noise-reduction methods in signal and image processing. More recently, he has applied random matrix theory to the study of high-dimensional multivariate statistical methods, such as principal components and canonical correlation analysis. In biostatistics, he has collaborated with investigators in cardiology and prostate cancer. He is a member of the U.S. National Academy of Sciences and the American Academy of Arts and Sciences and a former president of the Institute of Mathematical Statistics.

Debashis Paul finished his B.Stat. and M.Stat. from Indian Statistical Institute, Kolkata, in 1997 and 1999, respectively, and received his Ph.D. degree in Statistics from Stanford University in 2005 under the supervision of Professor Iain Johnstone. In 2005, he joined the Department of Statistics at the University of California, Davis as Assistant Professor. One of his main research interests is in high-dimensional inference and random matrix theory. He has served on the editorial boards of several journals including Annals of Statistics, Bernoulli and Statistica Sinica.

Appendix A. Heuristic derivation for bias

We work in the simplest setting, with a single spike. We follow, with modifications, the approach of Nadler [42]. Assume that the observations are Gaussian, and that population covariance matrix is diagonal, with a single signal dimension with variance ${\ell }_1>1,$ so that $\Sigma =\text{diag}\left({\ell }_1,1,\dots ,1\right).$ In the spiked model, we can achieve this if necessary by a population-level rotation of the variables.

The data matrix X, by assumption, has n independent columns, each with mean zero and covariance ∑. Now partition

$$X=\left[\begin{array}{c}{X^{\prime }}_1\\ {X^{\prime }}_2\end{array}\right]$$

with the first 1 × n row containing the “signal” observations with elevated variance ${\ell }_1,$ and an (p − 1) × n matrix ${X^{\prime }}_2$ containing the noise variables.

Create modified data

$$\tilde{X}=\left[\begin{array}{c}{X^{\prime }}_1\\ {V^{\prime }}_2{X^{\prime }}_2\end{array}\right]$$

by rotating the noise variables by an orthogonal matrix V₂ obtained from the eigendecomposition

$$\begin{array}{ll}{n}^{-1}{X^{\prime }}_2{X}_2=V_2\Lambda {V^{\prime }}_2,\hfill & \Lambda =\text{diag}\left({\lambda }_2,\dots ,{\lambda }_p\right)\hfill \end{array}$$

The first row ${X^{\prime }}_1$ is left alone. Note that the rotation V₂ = V₂(X₂) is data dependent.

In this new basis, the sample covariance has the form of an arrowhead matrix. Indeed, with

$$\tilde{X}{\tilde{X}}^{\prime }=\left[\begin{array}{c}{X^{\prime }}_1\\ {V^{\prime }}_2{X^{\prime }}_2\end{array}\right]\left[\begin{array}{ll}{X}_1\hfill & X_2{V}_2\hfill \end{array}\right],$$

we obtain, on defining the scalar $s=n^{-1}{X^{\prime }}_1{X}_1$ and vector $b={\left(b_2,\dots ,b_p\right)}^{\prime }:=n^{-1}{V^{\prime }}_2{X^{\prime }}_2{X}_1\in {ℝ}^{p-1},$

$$\tilde{S}=n^{-1}\tilde{X}{\tilde{X}}^{\prime }=\left[\begin{array}{ll}s\hfill & b^{\prime }\hfill \\ b\hfill & \Lambda \hfill \end{array}\right]=\left[\begin{array}{llll}s\hfill & b_2\hfill & \cdots \hfill & b_p\hfill \\ b_2\hfill & {\lambda }_2\hfill & \hfill & \hfill \\ ⋮\hfill & \hfill & \ddots \hfill & \hfill \\ b_p\hfill & \hfill & \hfill & {\lambda }_p\hfill \end{array}\right]$$

The shaft of the arrow consists of the sample noise eigenvalues, which are of order 1 because we have normalized the sample covariance matrix.

The border entries b_i (the “head” of the arrow) are much smaller, as we now show. Since ∑ is diagonal and the data Gaussian, the first row ${X^{\prime }}_1$ is independent of the noise matrix ${X^{\prime }}_2$ The entries of X₁ are i.i.d. $N\left(0,\ell \right),$ so we calculate

$$\begin{array}{lll}E\left[b|X_2\right]\hfill & =\hfill & 0\hfill \\ E\left[b{b}^{\prime }|X_2\right]\hfill & =\hfill & n^{-2}{\tilde{X}}_2^{\prime }E\left[X_1{X^{\prime }}_1\right]{\tilde{X}}_2\hfill \\ \hfill & =\hfill & n^{-2}\ell {\tilde{X}}_2^{\prime }{\tilde{X}}_2=n^{-1}\ell \Lambda \hfill \end{array}$$

Thus, conditional on X₂, each b_j has mean 0 and variance $n^{-1}\ell {\lambda }_j$ and so is O_p(n^−1/2).

Spectrum of arrowhead matrices For an arrowhead matrix, we can solve more or less directly for the eigenvalues and vectors. Indeed, the equation $\tilde{X}v=xv$ can be written (if we normalize v by setting v₁ = 1) as

$$\begin{array}{r}\hfill s+b_2{v}_2+\cdots b_p{v}_p=x\\ \hfill b_2+{\lambda }_2{v}_2=x{v}_2\\ \hfill b_3+{\lambda }_3{v}_3=x{v}_3\\ \hfill ⋮\\ \hfill b_p+{\lambda }_p{v}_p=x{v}_p\end{array}$$

From the last p − 1 equations, it is immediate that

$$v\propto \left(1,\frac{b_2}{x-{\lambda }_2},\dots ,\frac{b_p}{x-{\lambda }_p}\right),$$ (12)

while the first equation reduces to the secular or characteristic equation²

$$f\left(x\right)=x-s-{\displaystyle \sum }_{j=2}^p\frac{b_j^2}{x-{\lambda }_j}=0.$$ (13)

Since the noise eigenvalues λ_j are distinct with probability one, a graph of f(x) against x shows that the sample covariance eigenvalues x_i interleave the λ_j:

$${\lambda }_p<x_p<{\lambda }_{p-1}<\cdots <{\lambda }_3<x_2<{\lambda }_2<x_1.$$

We can now read off the behavior of the top sample eigenvalue from the eigenvalue equation, rewritten in the form

$$x_1=s+{\displaystyle \sum }_{j=2}^p\frac{b_j^2}{x_1-{\lambda }_j}$$ (14)

²Here is another route to the eigenvalue equation. We can write $\tilde{S}-xI$ as a rank two perturbation of the diagonal matrix of the diagonal matrix D = diag(s − x, λ₂ − x,..., λ_p − x):

$$\tilde{S}-xI=D+\left[\begin{array}{ll}{e}_1\hfill & b\hfill \end{array}\right]\left[\begin{array}{l}{b}^{\prime }\hfill \\ {e^{\prime }}_1\hfill \end{array}\right]$$

where, with slight abuse of earlier notation, now b^′ = (0 b₂ … b_p) and ${\text{e}}_1^{\prime }=\left(10\dots 0\right).$ Apply the matrix determinant lemma $\left|D+U{V}^{\prime }\right|=\left|D\right|\left|I+V^{\prime }{D}^{-1}U\right|:$ the diagonal entries of $V^{\prime }{D}^{-1}U$ vanish because of the zero pattern in b and e₁, hence

$$\left|I+V^{\prime }{D}^{-1}U\right|=\left|\begin{array}{cc}1& b^{\prime }{D}^{-1}\text{b}\\ {\text{e}}_1^{\prime }{D}^{-1}{\text{e}}_1& 1\end{array}\right|=1-\frac{1}{s-x}{\displaystyle \sum }_{j=2}^p\frac{b_j^2}{{\lambda }_j-x}.$$

Equivalently the eigenvalues x_i solve the secular equation (13). together with the fact that $s={\ell }_1+O_p\left(n^{-1/2}\right)$ and the b_j have expected square of order 1/n.

If p is fixed, the contribution of the sum is negligible and the leading eigenvalue converges to ℓ and so is consistent:

$$x_1={\ell }_1+O_p\left(n^{-1/2}\right)+O_p\left(n^{-1}\right)$$

However everything changes if p/n → γ > 0. Recalling the behavior when we condition on the noise variables X₂, we have

$$\begin{array}{ll}E\left(s|X_2\right)=\ell \hfill & E\left(b_j^2|X_2\right)=\frac{\ell }{n}{\lambda }_j\hfill \end{array}$$

Proceeding heuristically, the sum on j in (14) now looks like an empirical average of a function of the noise eigenvalues λ_i:

$$x_1\approx E\left[x_1|X_2\right]=\ell +\ell \frac{p}{n}\cdot \frac{1}{p}{\displaystyle \sum }_{j=2}^p\frac{{\lambda }_j}{x_1-{\lambda }_j}$$

Since the empirical distribution of the sample λ_j converges to Marchenko-Pastur, it is plausible and can be shown that as p/n → γ, the largest eigenvalue x₁ converges to a limit $\lambda (\ell )$ which satisfies the equation

$$\lambda (\ell )=\ell +\ell \gamma {\displaystyle \int \frac{\lambda }{\lambda (\ell )-\lambda }}d{F}_{\gamma }^{MP}(\lambda )$$ (15)

While the integral can certainly be evaluated directly, it is instructive to consider an alternative indirect approach. The Stieltjes transform of a probability measure, in this case the Marchenko-Pastur law, is defined by

$$m(z)={\displaystyle \int \frac{d{F}_{\text{γ}}^{MP}(\lambda )}{\lambda -z}},z\in {ℂ}^{+},$$

and is known [51] to satsify the quadratic equation

$$\text{γ}z{m}^2(z)+(z+\text{γ}-1)m(z)+1=0.$$ (16)

Equation (15) above can be rewritten using the Stieltjes transform as

$$\ell \text{γλ}m(\lambda )=\ell -\ell \text{γ}-\lambda ,$$ (17)

where we abbreviate $\text{λ=λ}(\ell ).$ Evidently, we may substitute the latter equation into the former, evaluated at $z=\text{λ}(\ell ).$ When the resulting equation is viewed as a (quadratic) polynomial in λ, it turns out that the constant term vanishes, and so one arrives at the evaluation

$$\lambda (\ell )=\ell +\frac{\ell \text{γ}}{\ell -1}.$$ (18)

Thus, above the phase transition at $1+\sqrt{\text{γ},}$ the bias is given by $\text{γ}\ell /(\ell -1).$ So the bias is always at least γ, no matter how large the top population eigenvalue is.

Appendix B. Heuristic derivation for eigenvector inconsistency

Recall that by assumption the top population eigenvectur u₁ = e₁. Using the explicit form found in (12), one easily calculates the cosine between population and sample as

$${\cos }^2\alpha =\frac{{\langle {\text{v,e}}_{\text{1}}\rangle }^2}{{\Vert \text{v}\Vert }^2}=\frac{1}{1+T^2},T^2={\displaystyle \sum _{j=2}^p\frac{b_j^2}{{(x_1-{\lambda }_j)}^2}}$$ (19)

When p is fixed there are a finite number of terms each of order 1/n, so cos² α → 1 and the sample eigenvector is consistent.

However, when p is large and proportional to γn, then T² converges to a positive constant:

$$\begin{array}{ll}{T}^2\to \ell \gamma {\displaystyle \int \frac{\text{λ}}{{\left[\text{λ}(\ell )-\text{λ}\right]}^2}}d{F}_{\gamma }\left(\text{λ}\right)\hfill & >0\hfill \end{array}$$

An easy way to evaluate this integral is to observe from (15) and (18) that

$${\displaystyle \int \frac{\text{λ}}{\left[\text{λ}(\ell )-\text{λ}\right]}}d{F}_{\gamma }\left(t\right)=\frac{1}{\ell -1}.$$

Differentiating w.r.t. ℓ, we obtain

$${\lambda }^{\prime }(\ell ){\displaystyle \int \frac{\text{λ}}{{\left[\text{λ}(\ell )-\text{λ}\right]}^2}}d{F}_{\gamma }\left(\text{λ}\right)=\frac{1}{{\left(\ell -1\right)}^2}.$$

From (18), $\lambda \prime \text{(}\ell \text{)}=1-\text{γ}/{(\ell -1)}^2$.Substituting into (19), we find that

$$\begin{array}{ll}{\cos }^2\alpha \to \{\begin{array}{l}\frac{1-\text{γ}/{(\ell -1)}^2}{1+\text{γ}/(\ell -1)}\\ 0\end{array}\hfill & \ell >1+\sqrt{\text{γ}}\hfill \\ \hfill & \ell \le 1+\sqrt{\text{γ}}.\hfill \end{array}$$