Abstract
The tree-based scan statistic is a statistical data mining tool that has been used for signal detection with a self-controlled design in vaccine safety studies. This disproportionality statistic adjusts for multiple testing in evaluation of thousands of potential adverse events. However, many drug safety questions are not well suited for self-controlled analysis. We propose a method that combines tree-based scan statistics with propensity score matched analysis of new initiator cohorts, a robust design for investigations of drug safety. We conducted plasmode simulations to evaluate performance. In multiple realistic scenarios, tree-based scan statistics in cohorts that were propensity score matched to adjust for confounding outperformed tree-based scan statistics in unmatched cohorts. In scenarios where confounding moved point estimates away from the null, adjusted analyses recovered the pre-specified type 1 error while unadjusted analyses inflated type 1 error. In scenarios where confounding moved point estimates toward the null, adjusted analyses preserved power whereas unadjusted analyses greatly reduced power. Although complete adjustment of true confounders had the best performance, matching on a moderately mis-specified propensity score substantially improved type 1 error and power compared to no adjustment. When there was true elevation in risk of an adverse event, there were often co-occurring signals for clinically related concepts. TreeScan with propensity score matching shows promise as a method for screening and prioritization of potential adverse events. It should be followed by clinical review and safety studies specifically designed to quantify the magnitude of effect, with confounding control targeted to the outcome of interest.
Keywords: TreeScan, Active Surveillance, Methods, Simulation, Screening, Scanning, Propensity Score, Database study, Cohort
INTRODUCTION
Identification of potential adverse events related to drugs or other marketed medical products can come from many sources, including experiences during early trials, spontaneous reporting by members of the public (doctors, patients, other stakeholders), post-marketing studies, as well as active surveillance activities.1,2 The United States Food and Drug Administration’s has built a large distributed network that includes 17 Data Partners and over 175 million covered lives as part of the Sentinel Initiative for prospective, post-market safety surveillance. Specific adverse events are investigated in post-market safety evaluations because someone has hypothesized a credible link between use of a particular drug and the occurrence of a particular adverse event. Data mining is one method to inform these hypotheses and can be applied in administrative and clinical healthcare databases, such as the ones participating in the Sentinel Initiative.3–8
Tree-based scan statistics are a data mining approach implemented by TreeScan™ software (www.treescan.org). The statistics were developed for application in longitudinal data and are compatible with a variety of epidemiology study designs and analytic approaches.9,10 Three features set tree-based scan statistics apart from most other disproportionality methods11–14; 1) they are built on scan statistical theory, 2) they use a hierarchical diagnosis tree to simultaneously evaluate outcomes at different levels of granularity (including specific diagnoses and groups of related diagnoses), and 3) they use a frequentist method to formally adjust for the multiple testing inherent in evaluation of thousands of potential adverse events.15
TreeScan has previously been used in self-controlled analyses of vaccine safety; however, self-controlled designs are not well suited for many drug safety questions due to the complexity of confounding related to timing of initiation, duration of exposure of interest and reference exposure.16–20 In contrast, propensity score propensity score matched active-comparator analyses in new initiators are a flexible and commonly used design for investigations of drug safety.21–23 Tree-based scan statistics have never been used for screening potential adverse outcomes with a propensity score matched new initiator, active-comparator cohort design. Our objective was to conduct a plasmode simulation24 to evaluate the performance of the unconditional Bernoulli TreeScan statistic when scanning across outcomes for a propensity score matched new initiator cohort design with active comparators.
METHODS
Proposed Method for Signal Detection
The Tree
The “tree” in tree-based scan statistics refers to a hierarchical classification system for clinical concepts. These concepts may be drug products, procedures or diagnoses. When scanning across outcomes for a given exposure, one hierarchical classification of diagnoses that could be used is the multi-level Clinical Classifications Software produced by the Healthcare Cost and Utilization Project (HCUP) sponsored by the Agency for Healthcare Research and Quality.25
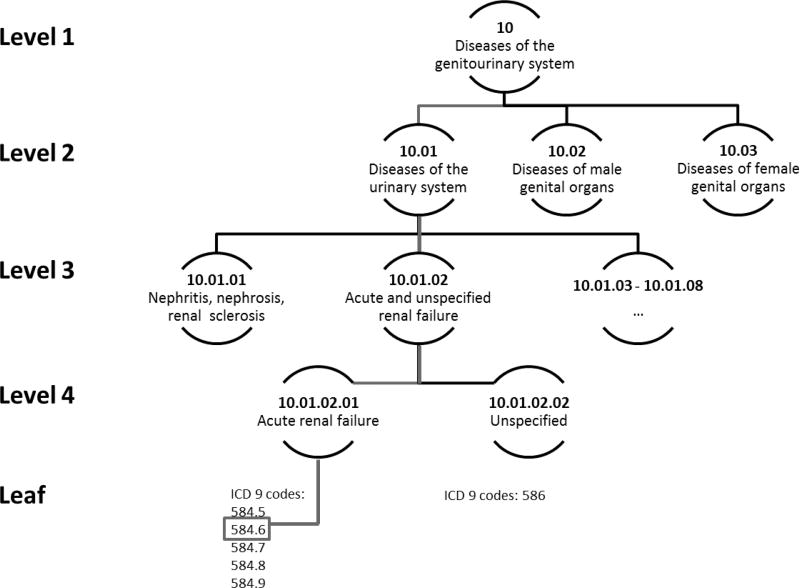
Our multi-level Clinical Classifications Software tree included International Classification of Diseases (ICD) 9th revision diagnosis codes grouped into four hierarchical levels representing increasingly specific clinical concepts. At the top level, there are 18 categories, most of which represent different body systems. At each level of the hierarchical tree, there are mutually exclusive nodes that contain increasingly specific classification of ICD-9 codes. The increasing specificity of hierarchical levels and tree-structure is depicted in Figure 1, eAppendix 1. The tree we used was curated to remove conditions that were unlikely to be caused by drugs or had long induction times relative to exposure (details in eAppendix 2).
Figure 1. Example of a multi-level Clinical Classification tree.
At level 1, there are 18 categories that largely represent different body systems. In this example, the category specifies only that the person has a disease of the genitourinary system. There are several potential sub-classifications of the genitourinary system. By moving to level 2, one could discern whether the patient has a disease of the urinary system or a disease of a genital organ. At level 3, the finer classification can identify that a disease of the urinary system is acute and unspecified renal failure. At level 4, the type of renal failure is further specified as acute renal failure. Finally, each node in the leaf node of the hierarchy is based on specific ICD-9 codes. In this figure, the specific diagnosis code for the patient was 584.6 “acute kidney failure with lesion of renal cortical necrosis”. In this figure, the level 3 node “Acute and unspecified renal failure” has 1 parent, “Diseases of the urinary system” and is the parent of two level 4 children, “Acute renal failure” and “Unspecified”. Children of children down to and including the leaf nodes are considered descendants. Thus the diagnosis code 584.6 is a descendant of the level 3 node “Acute and unspecified renal failure” but is not a descendant of the level 3 node “Nephritis, nephrosis, renal sclerosis”.
The Tree-based Scan Statistic
An unconditional Bernoulli tree-based scan statistic is appropriate for propensity score-matched cohort analyses comparing two treatments. This statistic assumes that the follow up window is the same for the exposed and comparator patients in a matched pair and tests the null hypothesis of no difference in incidence rate for adverse events in any node against a one-sided alternative that there is at least one node where the rate of adverse events is higher in the exposed group than the comparator.
The distribution of the test statistic T is unknown so we derive p-values non-parametrically using Monte Carlo hypothesis testing where permutations of the data are generated under the null hypothesis. For these random datasets, nodes contain the same number of events as observed in the original data; however, the events are assigned to exposure based on a binomial draw with the expected proportion based on the null hypothesis. In a 1:1 matched setting, the expected probability of being in the exposure group is 0.5. Formulas and additional details regarding tree-based scan statistic methodology are available in eAppendix 3.
Plasmode simulation
To evaluate the performance of tree-based scan statistic with propensity score matching on screening for potential adverse events, we chose to use a plasmode simulation24 rather than generate entirely synthetic data. These simulations retain the complexity of relationships among 1) baseline covariates, 2) covariates and exposure, and 3) clustering of co-occurring outcomes within patients observed within the real dataset used as the basis for the simulation. The complex relationships between diagnosed outcomes are particularly important to maintain when investigating a method that scans across thousands of outcomes in a hierarchical tree. The complexity of the correlation across outcomes would be difficult to generate with conditional probability models. We permuted the data to simulate a true increase of risk for the exposure of interest by assigning a higher proportion of outcomes in selected nodes to initiators of the exposure than initiators of the comparator. However, outcomes in selected nodes do not occur independently from outcomes in other nodes. Therefore, when permuting the data, outcomes across all nodes were clustered at the patient-level and assigned together to either exposure or comparator.
We constructed simulation scenarios that varied the number of outcome nodes affected by confounding, whether confounding moved the crude estimate closer to or farther from the null, and the magnitude of the true effect. For each set of simulated data, we performed varying degrees of confounding adjustment by including random subsets of true confounders.
The plasmode simulation process that we implemented expands upon a previous plasmode simulation24 framework. In brief, the steps we took were:
Extract a cohort of incident users of an exposure drug and comparator drug of interest and their baseline covariates from Optum Clinformatics, a large administrative healthcare database.
Extract incident outcomes across the multi-level Clinical Classifications Software tree for the cohort of incident users
For each scenario, generate 1,000 simulated datasets by permuting relationships between baseline covariates, exposure, and outcome at the patient level.
Run the tree-based scan statistic with 1:1 propensity score matching in simulated data and evaluate its performance
Additional details on the simulation process are available in eAppendix 4.
Step 1. Extract cohort of incident users and baseline covariates
We used a publicly available SAS macro based tool from the Sentinel routine analytic framework, the Cohort Identification and Descriptive Analysis + propensity score matching tool (CIDA version 3.3.0)26, to extract the underlying cohort for our simulations. The cohort was created from Optum Clinformatics data converted to the Sentinel Common Data Model (version 5.0)27. We extracted a cohort consisting of new users of DPP4-inhibitors (exposure of interest) or sulfonylureas (comparator) based on a protocol used in a prior Sentinel analysis.28 We selected this protocol because the evaluated products have an established safety profile and adequate uptake in the data source. The study period was 1 January 2007 and 31 December 2010. The index date was the first dispensing date for a study drug after 1) at least 183 days without a dispensing for either study drug, and 2) continuous drug and medical coverage (30 day gaps allowed). Twenty-six baseline covariates were defined, but no outcome was specified. More details on cohort parameters are available eAppendix 5. This project made secondary use of de-identified data. Human subject review was not required.
Step 2. Extract incident outcomes across multi-level Clinical Classifications Software tree
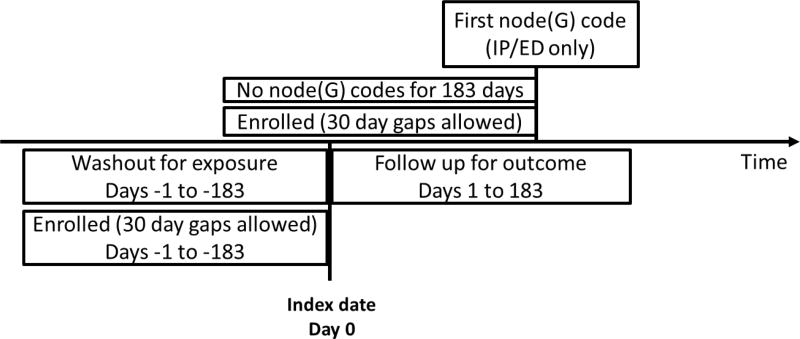
We defined incidence at level 3 of the multi-level Clinical Classifications Software tree. Incident outcomes were defined by the date of the first emergency department or inpatient diagnosis in the node after at least 183 days of medical and drug enrollment with no diagnosis codes from the node recorded in any care setting (Figure 2). Incident outcomes were included if they occurred within 183 days following the index date for initiation of a study drug. Hypothesis testing occurred at levels 3, 4, and the leaf level (individual ICD-9 codes).
Figure 2. Incident outcome criteria.
Note that there was a fixed follow up window of 183 days for incident outcomes.
Step 3. Generate cohorts with known truth for 11 simulation scenarios
For our simulation, we chose three level 3 outcome nodes to insert true elevation in risk and/or confounding. The three outcome nodes were: (1) hemorrhage from gastrointestinal ulcer; (2) acute cerebrovascular disease; (3) acute and unspecified renal failure. These nodes were selected to span a range in frequency of incident outcomes observed in the extracted cohort.
We permuted the observed data in order to inject known truths and confounding while maintaining as much of the complexity of the observed data as possible. The permutation strategy retained the observed baseline characteristics and exposure for patients as well as the collection of co-occurring outcomes observed within patients. However, the permutation randomly assigned which baseline characteristics and exposure were assigned to which set of outcomes. Because of the permutation strategies we implemented, unknown effects of exposure that existed in the original observed data were eliminated. We were also able to simulate the desired “true” magnitude of effect and confounding in selected nodes. For this simulation, we chose to use the 26 predefined covariates as true confounders.
We simulated data under 11 scenarios (Table 1). Scenario 1 had no confounding and no true elevation in risk from exposure in any node. Scenario 2 had positive confounding that moved estimates away from the null in the three selected nodes, but no true effect of exposure in any node. Scenarios 3, 4, and 5 had no confounding, but true elevation in relative risk for three selected nodes of magnitude 1.5, 2.0 and 4.0. Scenarios 6–8 had positive confounding that biased effect estimates away from the null, but after adjusting for confounders in a perfectly specified outcome model, the true relative risks were 1.5, 2.0, and 4.0. Scenarios 9–11 had negative confounding, where bias moved the unadjusted estimate closer to the null, but after adjusting for confounding in a perfectly specified outcome model, the true relative risks were 1.5, 2.0, and 4.0.
Table 1.
Simulation scenarios
| Scenario | Confounding? | Direction of confounding | True Relative Risk | # Nodes with true effect |
|---|---|---|---|---|
| 1 | No | n/a | 1.0 | 0 |
| 2 | Yes | Positive (away from the null) | ||
|
|
||||
| 3 | No | n/a | 1.5 | 3 |
| 4 | 2.0 | |||
| 5 | 4.0 | |||
|
|
||||
| 6 | Yes | Positive (away from the null) | 1.5 | |
| 7 | 2.0 | |||
| 8 | 4.0 | |||
|
|
||||
| 9 | Yes | Negative (toward the null) | 1.5 | |
| 10 | 2.0 | |||
| 11 | 4.0 | |||
Step 4. Run TreeScan with propensity score matching and evaluate performance
For the simulation scenarios with no true confounding (Table 1 scenarios 1, 3, 6, 9) we randomly 1:1 matched initiators of the exposure of interest to initiators of the comparator drug because there was no need for confounding adjustment. For simulation scenarios that included positive or negative confounding, we varied the degree of confounding adjustment in the analyses. For 0% adjustment of confounding, we 1:1 matched initiators of the exposure of interest and comparator drug randomly. For partial adjustment, we used nearest-neighbor matching on a propensity score derived from a logistic regression model that included a subset of true confounders, where the subset included a random 11 (40%), 13 (50%), 18 (60%), or 21 (80%) of the full set of true confounders. For full adjustment, we used nearest-neighbor matching on a propensity score with 100% of true confounders.
In all scenarios, the propensity score matching caliper was 0.025 on the probability scale. We arbitrarily chose to set the threshold for alerting to p <0.01. For each dataset in each scenario, we ran TreeScanTM to identify signals. For each scenario, we then calculated the proportion of datasets with signals in each of the three selected nodes, their descendant nodes, and non-descendant nodes to evaluate power and type 1 error. For scenarios where there is a true increase in risk for the exposure of interest over the comparator in a selected node, power was defined as the proportion of the 1,000 simulated datasets for which there is a signal in the selected node.
RESULTS
The base cohort extracted from a large healthcare database included 25,849 initiators of DPP4-inhibitors and 88,312 initiators of sulfonylureas. There were some imbalances between the exposure groups (Table 2).
Table 2.
Distribution of covariates by exposure
| Baseline Covariates | DPP4 inhibitor | Sulfonylurea | ||
|---|---|---|---|---|
| n = 25,849 | n = 88,312 | |||
| Mean | (SD) | Mean | (SD) | |
| Age | 56 | (11.0) | 54 | (12.6) |
| Count | (%) | Count | (%) | |
| Gender (F) | 12,185 | (47.1) | 40,510 | (45.9) |
| Chronic Kidney Disease | 1,419 | (5.5) | 4,053 | (4.6) |
| Hypoglycemia | 757 | (2.9) | 2,435 | (2.8) |
| Diabetic Nephropathy | 935 | (3.6) | 2,300 | (2.6) |
| Diabetic Neuropathy | 1,594 | (6.2) | 4,401 | (5.0) |
| Diabetic Retinopathy | 1,025 | (4.0) | 2,726 | (3.1) |
| Diabetic Peripheral Circulatory Disorder | 510 | (2.0) | 1,497 | (1.7) |
| Erectile Dysfunction | 689 | (2.7) | 2,098 | (2.4) |
| Skin Infections | 341 | (1.3) | 1,199 | (1.4) |
| Diabetic Unspecified Complications | 842 | (3.3) | 2,514 | (2.8) |
| Alphaglucosidase | 104 | (0.4) | 198 | (0.2) |
| Glitazones | 8,188 | (31.7) | 16,184 | (18.3) |
| GLP1RA | 1,326 | (5.1) | 3,097 | (3.5) |
| Insulin | 2,844 | (11.0) | 6,079 | (6.9) |
| Meglitinides | 945 | (3.7) | 934 | (1.1) |
| Metformin | 13,662 | (52.9) | 47,816 | (54.1) |
| Mean | (SD) | Mean | (SD) | |
| Number of ambulatory visits | 8.5 | 9.1 | 7.8 | 9.4 |
| Number of emergency department visits | 0.2 | 1.5 | 0.2 | 1.5 |
| Number of inpatient visits | 0.1 | 0.4 | 0.2 | 0.5 |
| Number of institutional stays | 0.1 | 0.8 | 0.1 | 1.1 |
| Number of outpatient visits | 0.4 | 1.7 | 0.4 | 1.8 |
| Number of classes of medication | 7.4 | 4.5 | 6.5 | 4.2 |
| Number of generic medications | 8.4 | 4.8 | 7.4 | 4.5 |
| Number of dispensations | 20.1 | 15.6 | 15.6 | 14.0 |
Age defined at the index date, all other characteristics defined using data within the 183 days prior to the index date. SD indicates standard deviation.
The three selected nodes in which we inserted confounding and/or true effect of exposure, had incidence in the unmatched cohort of DPP4-inhibitor and sulfonylurea initiators ranging from 0.0005 to 0.0069 (Table 3) over 183 days of follow up. The number of outcomes that were included in matched datasets varied with direction of confounding and true effect size. The simulation results for each scenario are presented in eAppendix 6 and are discussed below.
Table 3.
Observed frequency of outcomes in selected nodes
| MLCCS Level 3 node |
Concept | Count | Incidence |
|---|---|---|---|
| 09.10.01 | Hemorrhage from gastrointestinal ulcer | 53 | 0.0005 |
| 07.03.01 | Acute cerebrovascular disease | 217 | 0.0018 |
| 10.01.02 | Acute and unspecified renal failure | 792 | 0.0069 |
Multi-level clinical classification software (MLCCS)
Scenario 1 had no confounding and no true elevation in risk from exposure in any node. With a pre-specified threshold of p<0.01, 9 out of 1,000 (0.009) simulated datasets had a node that signaled, while 991 datasets did not have a single node that signaled. Thus, the observed type 1 error was close to the expected.
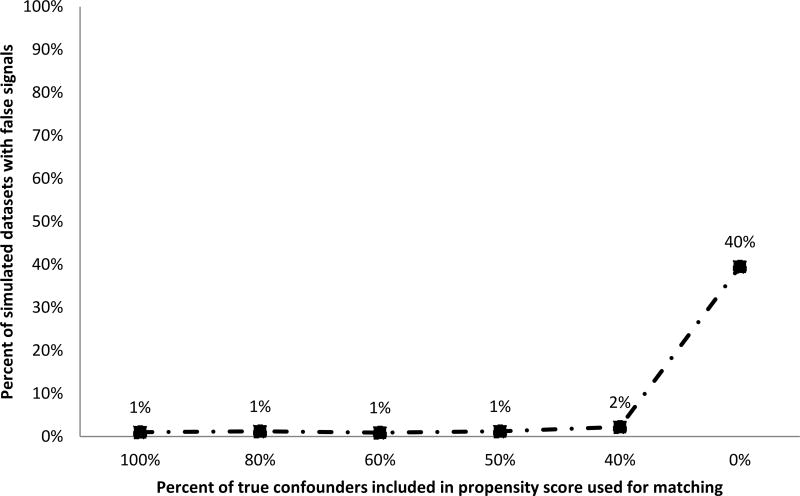
Scenario 2 had confounding that moved estimates away from the null in the selected nodes, but no true effect of exposure in any node. Nearly 40% of simulated datasets had a false positive signal when there was no confounding adjustment (Figure 3). With propensity score adjustment, the rate of false positive alerts was close to the nominal type 1 error rate if at least 50% of true confounders were included in the propensity score model. Propensity score models that included larger subsets of true confounders had better performance in terms of type 1 error.
Figure 3. Percent of simulated datasets with false signals when there is confounding but no true effect of exposure.
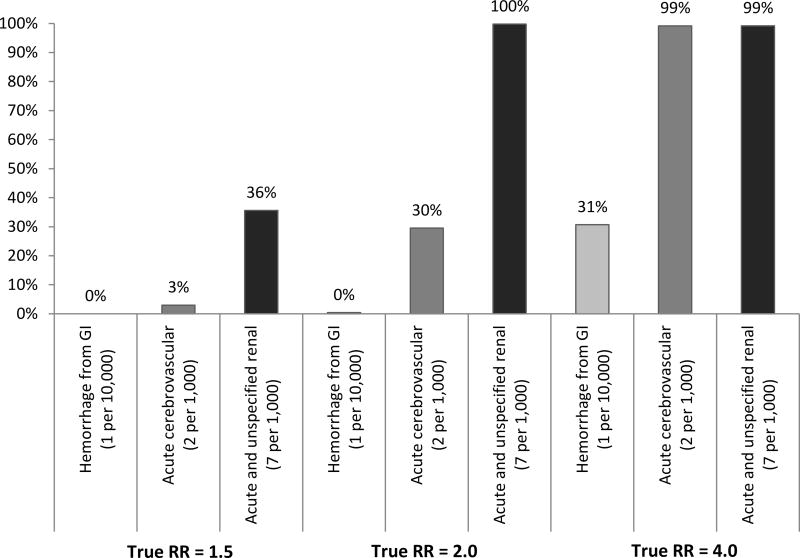
Scenarios 3–5 had true elevation in relative risk for selected nodes of magnitude 1.5, 2.0 and 4.0 and no confounding. Unsurprisingly, the power to detect true elevation in risk increased both with the magnitude of the true effect and the prevalence of the outcome (Figure 4). Because the threshold for TreeScan signaling is designed to maintain an overall type 1 error level when scanning across thousands of outcomes, the power to detect true signals was lower than it would have been had only a single node been evaluated. The power to detect a relative risk of 2.0 with alpha at 0.01 in a one-sided test of difference in proportions would have been 25% for “hemorrhage from gastrointestinal [tract]” 82% for “acute cerebrovascular disease,” and 100% for “acute and unspecified renal disease”. When the true relative risk was 2.0 and alpha set to 0.01, for the same nodes, TreeScan signaled 0%, 30%, and 100% of the time (eAppendix 6). There were more signals in nodes that were not descendants of the nodes where true effects were inserted than would have been expected based on the pre-specified threshold of 0.01. When the true relative risk for the three selected nodes was set as 4.0, over half of the permuted datasets included signals in non-descendant nodes. We speculate that these non-descendant nodes signaled because they were associated with the nodes where true signals were inserted. Non-descendant nodes that signaled when there was true elevation in risk for selected nodes were not randomly dispersed throughout the multi-level Clinical Classifications Software tree. Nodes covering concepts such as “respiratory failure”, “hyposmolality” and “hemiplegia” signaled repeatedly (Table 4). These non-descendant nodes represent co-occurring conditions that are clinically related to the selected nodes where we had simulated true elevation in risk. Our simulations retained the observed co-occurrence of diagnoses within patients. In the observed data, patients with incident “acute and unspecified renal failure” were over 10 times as likely to also have incident “acute cerebrovascular disease” than those without the renal outcome (2.5% vs. 0.2%). Patients with incident outcomes in either of these selected nodes where true effects were simulated were more likely to have co-occurring signals in non-descendant but clinically related nodes such as “respiratory failure,” “hyposmolality” and “hemiplegia” (p <0.001). As an example, patients with incident “acute cerebrovascular disease” were nearly 1,000 times as likely as those without to have a co-occurring “hemiplegia” (19% vs. 0%, p <0.001).
Figure 4. Power to detect true signal in the absence of confounding.
Table 4.
Percent of simulated datasets in scenarios with true effect = 4.0 and no confounding where non-descendant nodes that signaled at alpha = 0.01
| Node | Percent | MLCCS level 3 |
|---|---|---|
| 08.06.01 | 32.6 | Respiratory failure |
| 03.08.01 | 18.6 | Hyposmolality |
| 06.03.01 | 17.7 | Hemiplegia |
| 07.01.02 | 17.5 | Hypertension with complications |
| 03.08.05 | 13.7 | Other fluid and electrolyte disorders |
| 17.01.05 | 11.0 | Shock |
| 10.01.03 | 10.4 | Chronic kidney disease |
| 10.01.04 | 8.2 | Urinary tract infections |
| 07.02.11 | 6.7 | Congestive heart failure; nonhypertensive |
| 03.08.03 | 4.2 | Hyperpotassemia |
Signals that occurred at level 4 and leaf level were rolled up to level 3 to calculate percents.
Multi-level clinical classification software (MLCCS)
Scenarios 6–8 had confounding that moved estimates away from null, true relative effect ranging from 1.5 to 4.0 and varying degree of confounding adjustment. The power to detect signals increased with outcome prevalence and true effect size, but some of the “signals” were due to residual confounding. As the number of true confounders included in the propensity score decreased, residual confounding increased and the proportion of simulated datasets with signals at alpha 0.01 increased (eAppendix 6, 7). This reflected a mix of signals arising due to the true effect and signals due to confounding. The pattern of signals in descendant nodes (children of the 3 selected nodes) paralleled the pattern in the three selected nodes. The proportion of datasets that signaled in non-descendant nodes increased as residual confounding increased. When the true effect size was a relative risk of 4.0, 75% of simulated datasets included signals in non-descendant nodes after matching on a propensity score that included all true confounders. These signals reflected co-occurring diagnoses for conditions clinically related to the selected nodes.
Scenarios 9–11 had confounding that moved estimates toward the null, true relative effect ranging in magnitude from 1.5 to 4.0, and varying degrees of confounding adjustment. Unadjusted analyses had low power to detect true elevation in risk when the magnitude of the effect was smaller and the prevalence of the outcome lower (eAppendix 6, 7). With increased confounding adjustment, power to detect true signals was recovered. For example, when the true relative risk for acute and unspecified renal disease was 2.0, the power to detect the signal was around 8% in unadjusted analyses but around 90% if at least 80% of true confounders were included in propensity score adjustment. When there was greater power to detect true signals, there was also an increase in signals for co-occurring diagnoses of conditions clinically related to the selected nodes.
DISCUSSION
Lack of confounding control will lead to alerts for spurious findings as well as decreased ability to detect true associations.29 We conducted simulations to evaluate the ability of the tree-based scan statistic to screen for unknown adverse events when used with a new initiator cohort design and propensity score matching to adjust for confounding. Use of a plasmode simulation allowed us to evaluate the performance of TreeScan in a setting with known truth while also retaining the observed complexity in relationships between baseline characteristics and observed clustering of outcomes within patients in a cohort created from a large healthcare database.
In multiple realistic scenarios, tree-based scan statistics in cohorts that were propensity score matched to adjust for confounding outperformed tree-based scan statistics in unmatched cohorts. In scenarios with confounding that moved point estimates away from the null, adjusted analyses recovered the pre-specified type 1 error while unadjusted analyses had inflated type 1 error. In scenarios with confounding that moved point estimates toward the null, adjusted analyses preserved power while unadjusted analyses had greatly reduced power. Although complete adjustment of true confounders had the best performance, matching on a moderately mis-specified propensity score substantially improved type 1 error and power compared to no adjustment. Our plasmode simulation was based on a real dataset and preserved the observed correlation of baseline characteristics. Because of this correlation between true confounders, even when some true confounders were left out of the propensity score model, their confounding effect could be partially adjusted by inclusion of correlated confounders (e.g. proxy adjustment30).
When we simulated true elevation in risk in selected nodes, there was an increase in signals from non-descendant nodes. Many of these were clinically related diagnoses that co-occur with the selected nodes for which we simulated true signals. It would be possible to reduce signals from co-occurring diagnoses by 1) only considering the signal from the most extreme node in the observed data or 2) restricting outcomes to inpatient diagnoses in the primary position, rather than any inpatient or emergency room visit. However, signals in co-occurring non-descendant nodes could help paint a more complete picture of the underlying clinical issue related to exposure. Relationships between nodes that signal at the pre-specified alpha level could be evaluated holistically via a clinical lens as well as statistically by examining correlation matrices between relevant nodes.
There are several limitations of our evaluation of the performance of the tree-based scan statistic with propensity score matching. First, the plasmode simulation was based on the correlation structure between exposure, covariates, exposure, and outcomes from a single cohort of commercially insured patients. In other cohorts, the prevalence of outcomes may differ as well as the degree of correlation between covariates and their association with exposure.
Second, we used 1:1 matching with a fixed follow up of 183 days but did not address considerations of how to choose an appropriate risk window. It is unlikely that any single risk window will be the correct and best choice across all potential adverse events in an outcome tree. Development of tree-based scan statistics compatible with variable ratio matching and variable follow up (time-to-event) is underway.
Third, the hierarchical multi-level Clinical Classifications Software classification system we used is primarily organ-based, and the diagnostic codes and their classification into different nodes are not based on validated algorithms for specific outcomes. In contrast, the observed data from a large administrative claims data source reflect patterns of coding for multi-system diseases that may span in multiple branches of the multi-level Clinical Classifications Software tree. Our results highlight the necessity of combining data mining techniques with clinical review and other screening of potential signals.
Fourth, our evaluation did not address how to select covariates for a propensity score to simultaneously address confounding for potential adverse events across an outcome tree. Tree-based scan statistics consider thousands of outcomes, making it difficult to choose risk factors for inclusion in the propensity score model used for adjustment. However, the variable reduction property of propensity score analyses allow adjustment for many covariates, making it more likely that risk factors (or their proxies) for a range of outcomes will be balanced for compared exposure groups. In our simulations, we varied the degree of propensity score misspecification. Given our findings that partial adjustment could perform nearly as well in terms of type 1 error and power as full adjustment, we expect that a general propensity score that includes numerous measures of general comorbidity31 or frailty32 would provide broad confounding coverage. A set of empirically identified baseline covariates selected30 based on the strength of their relationships with exposure could also provide balance on a wide spectrum of baseline characteristics. However, the relative performance of confounder selection strategies in the context of scanning across outcomes should be evaluated further.
Finally, Bayesian approaches are another option to support decisionmaking and prioritization of potential safety signals. These approaches can capitalize on the availability of other information to generate prior distributions.33–35 However, when screening for unanticipated safety signals, decision-makers must decide which estimates merit further investigation when there is no informative prior. The tree-based scan statistic produces p-values that are adjusted for multiple testing. Traditional frequentist methods for adjusting p-values for multiple comparisons are too conservative for scan statistics, where the multiple testing adjustment needs to account for correlation between similar tests of related hypotheses. This means that when there is no elevation in risk of potential adverse events with exposure relative to a comparator (and negligible confounding), with a threshold for alerting at p = 0.01, TreeScan has a 99% probability of not generating any alerts at all.
Adjusting for multiplicity will decrease power compared to analyzing a single pre-specified hypothesis, so the tree-based scan statistic should only be used in surveillance for unanticipated outcomes, where there is no prior hypothesis. As such, tree-based scan statistics can fill an important gap, complementing the FDA Adverse Event Reporting System, a system that has been helpful in detecting rare events but is less sensitive at detecting modest differences for relatively higher prevalence outcomes. Furthermore, as with other disproportionality measures in signal detection, statistical significance is only one dimension to evaluate. Because p-values conflate sample size with effect size, they can be a useful metric for prioritizing associations for further investigation to avoid excessive false alarms. Possible signals should also be prioritized based on metrics such as relative risk, attributable risk, disease severity or other clinical criteria.
Tree-based scan statistics with propensity score matching shows promise as a method for screening and prioritization of potential drug adverse event signals to pursue with deeper investigation. This method could be particularly useful in the context of newly marketed drugs, where there is little experience and few hypotheses regarding the safety profile. However, the method is not limited to application with drug or vaccine safety. For example, it could be applied to screen for adverse health effects of exposures studied in ‘omics’ research (e.g. metabolomics, exposome, biomarkers). Screening should be followed by efforts to better understand the clinical context around potential signals as well as studies specifically designed to quantify the magnitude of effect, with confounding control tailored to the outcome under investigation.
Supplementary Material
eAppendix 1. Specifications For Cohort Extraction Using CIDA + Propensity Score Matching
eAppendix 2. Curation of the multi-level Clinical Classifications Software Tree
eAppendix 3. Tree-Based Scan Statistics
eAppendix 4. Data Generation Process
eAppendix 5. Example excerpt from a hierarchical diagnosis tree
eAppendix 6. Average number of outcomes and signals in 1,000 simulated datasets per scenario
eAppendix 7.Signals in each simulation scenario
Acknowledgments
Source of funding:
The Sentinel task order was funded by the FDA through the Department of Health and Human Services (HHS) Contract number HHSF22301010T-0004.
Conflict of interest: At the time that this work was conducted, Dr. Wang was principal investigator on other grants from: Agency for Healthcare Research Quality (AHRQ), Food and Drug Administration (FDA) Sentinel Program, and an investigator initiated grant from Novartis for unrelated research. Dr. Wang is a consultant to Aetion, Inc., a software company. Dr. Gagne has received salary support from grants from Novartis Pharmaceuticals Corporation and Eli Lilly and company to Brigham and Women’s Hospital and is a consultant to Aetion, Inc. and to Optum, Inc., all for unrelated work. James Rogers is a consultant to Aetion, Inc. Dr. Schneeweiss is consultant to WHISCON, LLC and to Aetion, Inc., a software manufacturer of which he also owns equity. He is principal investigator of investigator-initiated grants to the Brigham and Women’s Hospital from Bayer, Genentech and Boehringer Ingelheim for unrelated research.
Footnotes
Data and computer code: The data underlying the simulation was licensed from Optum Clinformatics and our data.
References
- 1.Ralph Edwards I. Spontaneous reporting—of what? Clinical concerns about drugs. [03/01/received 04/20/accepted];British journal of clinical pharmacology. 1999 48(2):138–141. doi: 10.1046/j.1365-2125.1999.00000.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Gagne JJ, Han X, Hennessy S, et al. Successful Comparison of US Food and Drug Administration Sentinel Analysis Tools to Traditional Approaches in Quantifying a Known Drug-Adverse Event Association. Clinical pharmacology and therapeutics. 2016 Nov;100(5):558–564. doi: 10.1002/cpt.429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Huang L, Zalkikar J, Tiwari RC. A Likelihood Ratio Test Based Method for Signal Detection With Application to FDA’s Drug Safety Data. [2011/12/01];Journal of the American Statistical Association. 2011 106(496):1230–1241. [Google Scholar]
- 4.Schuemie MJ, Coloma PM, Straatman H, et al. Using Electronic Health Care Records for Drug Safety Signal Detection: A Comparative Evaluation of Statistical Methods. Medical care. 2012;50(10):890–897. doi: 10.1097/MLR.0b013e31825f63bf. [DOI] [PubMed] [Google Scholar]
- 5.Brown J, Petronis K, Bate A, et al. Drug Adverse Event Detection in Health Plan Data Using the Gamma Poisson Shrinker and Comparison to the Tree-based Scan Statistic. Pharmaceutics. 2013;5(1):179. doi: 10.3390/pharmaceutics5010179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Huang L, Zalkikar J, Tiwari R. Likelihood ratio based tests for longitudinal drug safety data. Statistics in Medicine. 2014;33(14):2408–2424. doi: 10.1002/sim.6103. [DOI] [PubMed] [Google Scholar]
- 7.Cederholm S, Hill G, Asiimwe A, et al. Structured Assessment for Prospective Identification of Safety Signals in Electronic Medical Records: Evaluation in the Health Improvement Network. Drug safety. 2015;38:87–100. doi: 10.1007/s40264-014-0251-y. 12/25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.VanderWeele TJ. Outcome-wide Epidemiology. Epidemiology. 2017 May;28(3):399–402. doi: 10.1097/EDE.0000000000000641. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Group. TPW. Taxonomy for monitoring methods within a medical product safety surveillance system: Report of the Mini-Sentinel Taxonomy Project Work Group. 2010 [Google Scholar]
- 10.Workgroup. P. Taxonomy for monitoring methods within a medical product safety surveillance system: year two report of the Mini-Sentinel Taxonomy Project Workgroup. 2012 http://www.mini-sentinel.org/work_products/Statistical_Methods/Mini-Sentinel_Methods_Taxonomy-Year-2-Report.pdf.
- 11.van Puijenbroek EP, Bate A, Leufkens HGM, Lindquist M, Orre R, Egberts ACG. A comparison of measures of disproportionality for signal detection in spontaneous reporting systems for adverse drug reactions. Pharmacoepidemiology and drug safety. 2002;11(1):3–10. doi: 10.1002/pds.668. [DOI] [PubMed] [Google Scholar]
- 12.Ang PS, Chen Z, Chan CL, Tai BC. Data mining spontaneous adverse drug event reports for safety signals in Singapore – a comparison of three different disproportionality measures. [2016/05/03];Expert opinion on drug safety. 2016 15(5):583–590. doi: 10.1517/14740338.2016.1167184. [DOI] [PubMed] [Google Scholar]
- 13.Bate A, Lindquist M, Edwards IR, Orre R. A Data Mining Approach for Signal Detection and Analysis. Drug safety. 2002 May 01;25(6):393–397. doi: 10.2165/00002018-200225060-00002. [DOI] [PubMed] [Google Scholar]
- 14.Harpaz R, DuMouchel W, Shah NH, Madigan D, Ryan P, Friedman C. Novel Data-Mining Methodologies for Adverse Drug Event Discovery and Analysis. Clinical Pharmacology & Therapeutics. 2012;91(6):1010–1021. doi: 10.1038/clpt.2012.50. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Kulldorff M, Dashevsky I, Avery TR, et al. Drug safety data mining with a tree-based scan statistic. Pharmacoepidemiology and drug safety. 2013 May;22(5):517–523. doi: 10.1002/pds.3423. [DOI] [PubMed] [Google Scholar]
- 16.Yih KMJ, Dashevsky I, Anderson S, Baker M, Mba-Jones A, Russek-Cohen E, Shoaibi A, Yan L, Kulldorff M. Evaluation of HPV9 (Gardasil 9) Vaccine Safety Surveillance Using the TreeScan Data Mining Method. 2016 [Google Scholar]
- 17.Yih KNM, Maro JS, Baker M, Balsbaugh C, Brown J, Cole D, Dashevsky I, Kulldorff M. Pilot of Self-Controlled Tree-Temporal Scan Analysis for Gardasil Vaccine. 2015 [Google Scholar]
- 18.Wang S, Linkletter C, Maclure M, et al. Future cases as present controls to adjust for exposure trend bias in case-only studies. Epidemiology. 2011 Jul;22(4):568–574. doi: 10.1097/EDE.0b013e31821d09cd. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Wang SV, Gagne JJ, Glynn RJ, Schneeweiss S. Case-crossover studies of therapeutics: design approaches to addressing time-varying prognosis in elderly populations. Epidemiology. 2013 May;24(3):375–378. doi: 10.1097/EDE.0b013e31828ac9cb. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Wang SV, Schneeweiss S, Maclure M, Gagne JJ. "First-wave" bias when conducting active safety monitoring of newly marketed medications with outcome-indexed self-controlled designs. American journal of epidemiology. 2014 Sep 15;180(6):636–644. doi: 10.1093/aje/kwu162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Schneeweiss S. Developments in post-marketing comparative effectiveness research. Clinical pharmacology and therapeutics. 2007 Aug;82(2):143–156. doi: 10.1038/sj.clpt.6100249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Schneeweiss S. On Guidelines for Comparative Effectiveness Research Using Nonrandomized Studies in Secondary Data Sources. Value in Health. 2009;12(8):1041–1041. doi: 10.1111/j.1524-4733.2009.00607.x. [DOI] [PubMed] [Google Scholar]
- 23.Schneeweiss S, Gagne JJ, Glynn RJ, Ruhl M, Rassen JA. Assessing the comparative effectiveness of newly marketed medications: methodological challenges and implications for drug development. Clinical pharmacology and therapeutics. 2011 Dec;90(6):777–790. doi: 10.1038/clpt.2011.235. [DOI] [PubMed] [Google Scholar]
- 24.Franklin JM, Schneeweiss S, Polinski JM, Rassen JA. Plasmode simulation for the evaluation of pharmacoepidemiologic methods in complex healthcare databases. Computational statistics & data analysis. 2014 Apr;72:219–226. doi: 10.1016/j.csda.2013.10.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Clinical Classifications Software (CCS) 2015 https://www.hcup-us.ahrq.gov/toolssoftware/ccs/CCSUsersGuide.pdf.
- 26.Center M-SC. [Accessed June 12, 2017];Routine Querying Tools (Modular Programs) 2014 http://mini-sentinel.org/data_activities/modular_programs/details.aspx?ID=166.
- 27.Mini-Sentinel I. Mini-Sentinel: Overview and Description of the Common Data Model v5.0.1. http://www.mini-sentinel.org/work_products/Data_Activities/Mini-Sentinel_Common-Data-Model.pdf. Accessed 2016.
- 28.Zhou M, Wang SV, Leonard CE, et al. Sentinel Modular Program for Propensity Score-Matched Cohort Analyses: Application to Glyburide, Glipizide, and Serious Hypoglycemia. Epidemiology. 2017 Nov;28(6):838–846. doi: 10.1097/EDE.0000000000000709. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Avorn J, Schneeweiss S. Managing drug-risk information--what to do with all those new numbers. The New England journal of medicine. 2009 Aug 13;361(7):647–649. doi: 10.1056/NEJMp0905466. [DOI] [PubMed] [Google Scholar]
- 30.Schneeweiss S, Rassen JA, Glynn RJ, Avorn J, Mogun H, Brookhart MA. High-dimensional propensity score adjustment in studies of treatment effects using health care claims data. Epidemiology. 2009 Jul;20(4):512–522. doi: 10.1097/EDE.0b013e3181a663cc. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Gagne JJ, Glynn RJ, Avorn J, Levin R, Schneeweiss S. A combined comorbidity score predicted mortality in elderly patients better than existing scores. Journal of clinical epidemiology. 2011 Jul;64(7):749–759. doi: 10.1016/j.jclinepi.2010.10.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Kim DH, Schneeweiss S. Measuring frailty using claims data for pharmacoepidemiologic studies of mortality in older adults: evidence and recommendations. Pharmacoepidemiology and drug safety. 2014 Sep;23(9):891–901. doi: 10.1002/pds.3674. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Poole C. Multiple comparisons? No problem! Epidemiology. 1991 Jul;2(4):241–243. [PubMed] [Google Scholar]
- 34.Greenland S, Robins JM. Empirical-Bayes adjustments for multiple comparisons are sometimes useful. Epidemiology. 1991 Jul;2(4):244–251. doi: 10.1097/00001648-199107000-00002. [DOI] [PubMed] [Google Scholar]
- 35.Rothman KJ. No adjustments are needed for multiple comparisons. Epidemiology. 1990 Jan;1(1):43–46. [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
eAppendix 1. Specifications For Cohort Extraction Using CIDA + Propensity Score Matching
eAppendix 2. Curation of the multi-level Clinical Classifications Software Tree
eAppendix 3. Tree-Based Scan Statistics
eAppendix 4. Data Generation Process
eAppendix 5. Example excerpt from a hierarchical diagnosis tree
eAppendix 6. Average number of outcomes and signals in 1,000 simulated datasets per scenario
eAppendix 7.Signals in each simulation scenario