A Conversation between Theory, Methods, and Data

Abstract

The ten year anniversary of the COGITO Study provides an opportunity to revisit the ideas behind the Cattell data box. Three dimensions of the persons × variables × time data box are discussed in the context of three categories of researchers each wanting to answer their own categorically different question. The example of the well-known speed-accuracy tradeoff is used to illustrate why these are three different categories of statistical question. The 200 persons by 100 variables by 100 occasions of measurement COGITO data cube presents a challenge to integrate theories and methods across the dimensions of the data box. A conceptual model is presented for the speed-accuracy tradeoff example that could account for cross-sectional between persons effects, short term dynamics, and long term learning effects. Thus, two fundamental differences between the time axis and the other two axes of the data box include ordering and time scaling. In addition, nonstationarity in human systems is a pervasive problem along the time dimension of the data box. To illustrate, the difference in nonstationarity between dancing and conversation is discussed in the context of the interaction between theory, methods, and data. An information theoretic argument is presented that the theory-methods-data interaction is better understood when viewed as a conversation than as a dance. Entropy changes in the development of a theory-methods-data conversation provide one metric for evaluating scientific progress.

Introduction

Ten years ago the COGITO Study was undertaken at the Max Planck Institute for Human Development in Berlin (Schmiedek, L¨ovd´en, & Lindenberger, 2010). This study incorporated what, at the time, was a radical idea in research design: 100 individuals in each of two age groups were measured on 100 variables repeating over 100 days—the so-called COGITO Cube. The design explicitly embodied the idea of Cattell’s data box (Cattell, 1966) which posits that data can be organized into a three dimensional persons × variables × time array. One might then take slices from the data box that are time-specific persons × variables matrices, person-specific variables × time matrices, or 1variable-specific persons × time matrices. These three types of matrices are respectively the data organizations underlying cross-sectional, person-specific, and time series analyses.

Research designs generally pick one type of slice through the data box to test hypotheses and answer questions that are in turn constrained by which slice was chosen to sample (Baltes, 1968; Bereiter, 1963; Fiske & Rice, 1955). The COGITO data cube presents a methodological and theoretic challenge: How can we best integrate all three dimensions of the data box and what new questions can be asked that do not arise in two dimensional designs? The current article uses the opportunity provided by the 10 year anniversary of the COGITO Study to step back from the specifics of analyses in order to reflect on how theory and methods and data may mutually influence one another (see e.g., Wohlwill, 1991). Nesselroade (2006) wrote of this interplay as a dance between theory and method where first one is in the lead and then the other, while still there is coordination and cooperation between the two dance partners: Sometimes theory is driven by new development in methods and sometimes methods are driven by new developments in theory.

A Roadmap

This article ranges across a broad landscape of ideas. With this in mind, we will first present a short roadmap to the journey to help prepare the reader for some of the twists and turns ahead. There are three main parts to this article. The first part is a concrete example that develops a conceptual dynamical model and points to the need to consider the time dimension of the data box as being fundamentally different than the other two dimensions. The second part uses the ideas from the first part to discuss how human adaptability to changing contexts impacts the way we as scientists adapt and change our theories and methods. The third part uses the ideas developed in the first two parts along with a discussion of information theory to discuss how we might evaluate the interplay between theory, methods, and data.

We begin the first section with three types of questions that can be asked about a concrete example of the tradeoff between speed and accuracy in order to ground the issues that arise when discussing the three dimensions of Cattell’s data box. Our first point is that there are fundamental differences in the kinds of questions that can be answered when sampling different slices of the data box and that misunderstandings can arise when the category of question is not matched with the appropriate slice. The second point of this section is that when we create models that attempt to unify the three dimensions of the data box, we must take into account humans’ adaptable goals and long term learning and plasticity. This leads us to conclude that the time dimension of the data cube has both organization and instability that cannot be treated in the same way as the other two dimensions of the data box. The problem of unstable within-person time dependency motivates the discussion in the second section.

The second section uses two examples to illustrate the contrast between stable and unstable within-person time dependency. Dance is an example of relatively stable time dependency. In contrast, conversation has an inherently unstable time dynamic and is characterized by short periods of synchronization partitioned by desynchronizing events. The complexity of adaptable goals in conversational interaction is illustrated by a short hypothetical conversation between three people.

The third section proposes a metaphor that theory, method, and data comprise three partners in a conversation. This metaphor is designed to highlight two important concepts. First, conversation is self-organizing and embodies elements of both synchronization and spontaneous desynchronization. Synchronization and desynchronization between theory, methods, and data are important elements of progress in science. Second, a three partner interaction is inherently more complex than a two partner interaction and the complexity of the interactions between theory, methods, and data need to be addressed. In conclusion, it is hoped that the conversation metaphor will encourage readers to reconsider how the inherently multi-modal, multidimensional, and multivariate nature of data in the real world can productively be incorporated into a conversation between theory and methods.

Three Types of Questions from Three Types of Questioners

What can data tell us about health and behavior? Before we can answer that question, we must consider that there are several different categories of answers. Which of these categories are appropriate depends on who is asking the question. A policy maker may want to understand something very different than does a clinician. An educator may want to know the answer to a question that is qualitatively different than either the policy maker or the clinician.

If the person asking the question is a policy maker, she is likely to be interested in answers that have to do with the population of her nation or of the world at large. A government official might be interested in knowing the overall incidence of dementia in the nation’s population. Has there been a trend up or down in the incidence of dementia over the past two decades? This helps in planning for national needs for long term health care facilities. Or in another example, a public health policy maker who is attempting to design policies to reduce the incidence of smoking in her nation will want to know the effectiveness of past policy changes. Critical information includes the incidence of smoking before and after previous policy changes and a wide range of covariates in order to isolate the effect of the intervention. A randomized clinical trial might then be designed to assign different public information interventions in order to test which is the most effective prior to a nation-wide rollout.

The policy makers’ questions are answered by a persons × variables slice through the data box. The analyses and research designs in which the policy maker has interest are those that allow generalization to the population with a minimum cost of the research. But an analysis that generalizes to a population does not necessarily give information about any specific individual. And so a clinician will likely be unsatisfied with the answers from the policy maker’s research and analyses because the clinician actually wants to answer a different category of question.

If the person asking the question is a clinician, he is likely to be interested in answers that help him understand and treat the client who just walked in the door of the clinic. This involves the health and behavior of a specific individual. When a randomized clinical trial is analyzed with traditional hypothesis testing, there is an assumption of an uninformative prior after accounting for covariates. But the clinician does not want to know the risk of dementia for an average person in the population after accounting for age. He wants to know the risk for this person with this history at this particular moment in time. For a variety of reasons, a prediction for an individual cannot be inferred from population statistics (Molenaar, 2004). Optimal answers to the clinicians’ questions require a variables × time slice through the data box for that particular client. That is to say, the clinician needs to know that particular person’s history on a variety of variables in order to make a diagnosis.

If the person asking the question is an educator, she is likely to want to know if a particular training program is effective in producing learning and retention in the population. The questions of interest to educators are addressed by persons × time slices through the data box. By randomly assigning participants to training conditions and then repeatedly testing, the educator intends to understand how to produce an ideal training program that produces maximum learning for the average participant and simultaneously maximizes retention over the long term. Neither the policy maker’s answer nor the clinician’s answer satisfies the educator.

The developmental scientists who designed the COGITO study are interested in all three types of questions. They want to know if intensive cognitive training over a wide range of domains generalizes within the individual and to the population. The integration of all of the dimensions of the data box has long been a topic of interest (see Lamiell, 1998). We next provide an example in order to make these distinctions more concrete.

Speed and Accuracy

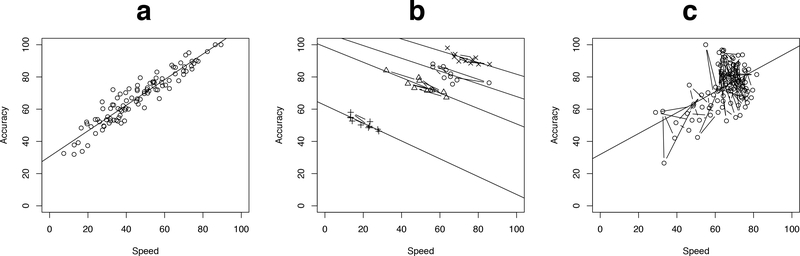
Why is there such a difference between generalizing to the population, making predictions about individual behavior, and maximizing long term adaptation? Consider the example of typing speed and accuracy. Speed and accuracy in movements and in decisions have long been known to be related (Wickelgren, 1977; Woodworth, 1899). In Figure 1, we present simulated results that illustrate relevant features of these classic and often replicated findings (e.g., Fitts, 1954; MacKenzie, 1992; Schmidt, Zelaznik, Hawkins, Frank, & Quinn Jr, 1979; Todorov, 2004).

Figure 1.

Three views of a simulated relationship between typing speed and accuracy. (a) When each of 100 typists is measured once, faster typists tend to also be more accurate. (b) When four typists (plotted using plus, cross, triangle, and circle) are each measured 10 times within a single day, a speed-accuracy tradeoff is observed: the faster one types, the more mistakes are made. (c) A single typist is given training and observed over 100 days. The typist’s speed and accuracy both improve over the course of training.

Suppose the policy maker needs to know whether typing speed and accuracy are related in the population of her country. She asks a scientist to test this theory. The scientist carefully selects a representative sample of 100 participants and asks them to each type a passage of text on a high quality keyboard on which the backspace key has been disabled. The scientist measures how long it takes each participant to complete the task and also counts the number of errors that were made while typing the prescribed passage. Each participants’ words per minute and percent correctly typed words are plotted in Figure 1-a. The scientist reports that there is a significant positive relation between speed and accuracy in the population. The policy maker’s question has been answered: Faster typists tend to be more accurate typists.

The clinician reads the policy maker’s report about typing speed and accuracy, and applies it as a theory about clients’ speed and accuracy. He asks the scientist, “If I ask a client to focus on typing faster, will that lead to greater accuracy?” The scientist selects a sample of four individuals and performs the same investigation as previously described, but repeating the investigation 10 times on within a single day for each individual. The results for the four individuals are plotted in Figure 1-b. Each person has some variation in how quickly they type and how many mistakes they make. The scientist reports back to the clinician that there is a significant negative relation between speed and accuracy within individual. The clinician’s question is answered: The faster a person types, the less accurately he or she types.

An educator reads the clinician’s report and the policy maker’s report with confusion. The educator formulates a theory about learning and neural plasticity and then asks the scientist, “Is it true that one cannot train a person to simultaneously type faster and more accurately?” The scientist conducts an intensive typing training regime of 100 sessions with 20 participants and the results for one participant are plotted in 1-c. The scientist reports back that the average participant significantly improved both accuracy and speed over the course of the 100 sessions, but any 10 consecutive sessions still show a within-person speed-accuracy tradeoff. Whereas average speed and average accuracy both improved, the speed-accuracy tradeoff was not trained away — the short term dynamics (speed-accuracy tradeoff) and long term dynamics (training to criterion) of typing have different relationships with respect to time. So, there are two answers to the educator’s question since it depends on whether one is making short time interval comparisons or long time interval comparisons.

The policy maker, the clinician, and the educator are each asking categorically different questions. One must be careful that the data and the method are appropriate to the theory that one wishes to test. Others have cautioned that one must assume that the dimensions of the data box are not interchangeable using the notion of ergodicity (Molenaar, 2004, 2008; Ram, Brose, & Molenaar, 2014). But this does not mean that we cannot simultaneously provide answers to each category of question. The COGITO Study is attempting to provide answers to the three categories of questions and challenges us to provide methods that allow integration across the three dimensions of the data box and theories that unify the three categories of questions. We next present a candidate model that might help integrate the example problem across the three questions.

Intrinsic Capacity and Functional Ability

A recent WHO Working Group on Metrics and Research Standards for Healthy Ageing (World Health Organization Department of Ageing and Life Course, 2017) proposed a research focus on two concepts relevant to the current discussion: intrinsic capacity and functional ability. Intrinsic capacity was proposed as a measure of physical and cognitive capacities that are internal to a person and which can be drawn upon to perform relevant functions and actions. Functional ability was framed as the observable outcomes of an interaction between intrinsic capacity and the environmental context, i.e., the challenges and/or supports presently available in the context of a person’s life (see, e.g., Baltes & Baltes, 1990; Magnusson, 1995). We next expand on these concepts of intrinsic capacity and functional ability in order to further explore the speed-accuracy tradeoff example and to illustrate one way that the three categories of questions discussed above might be integrated. Differentiating between the capacities and functioning of persons can help organize thinking about within-person results, between-person results, and results of short and long time-scale dynamics.

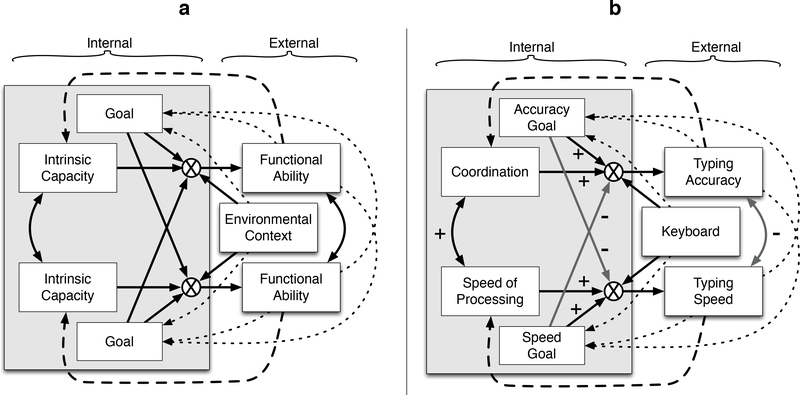
Simultaneously considering the WHO proposal and the COGITO Cube leads us to propose the conceptual model shown in Figure 2-a. In this conceptual diagram, intrinsic capacities and goals are internal to the person whereas functional abilities and environmental context are external and thus can be observed. All of the arrows in this conceptual diagram are intended to represent within-person relationships and thus are intended to be indicators of the dynamics inherent within an individual over time. The solid black single-headed arrows represent how functional abilities are an outcome of a three way interaction between intrinsic capacities, personal goals, and the environmental context in which an individual is embedded. The solid black double-headed arrows represent that there is some correlation between intrinsic capacities and also some correlation between functional abilities. The single-headed arrows with dotted lines represent perceptual feedback over short time scales. This feedback may affect a person’s goals, but do not directly affect intrinsic capacities. That is to say, what one perceives about one’s environmental context and functional abilities may change one’s goals but not necessarily change one’s intrinsic capacities. Finally, the dashed single-headed arrows represent long term effects of plasticity. Thus, repeated use or neglect of one’s functional abilities can have long term effects on one’s intrinsic capacities.

Figure 2.

Relationships between intrinsic capacities and goals internal to the person and environmental context and functional abilities external to the person. Dotted lines represent short-term perceptual feedback and dashed lines represent long term feedback effects of plasticity. (a) Goals, intrinsic capacities, and environmental context are combined in a 3-way interaction (represented by an × within a circle) to produce observable functional abilities. In short time scales a person’s observation of her or his own functional abilities may alter goals. (b) Application to the typing speed and accuracy example. Solid black lines represent positive effects and grey lines represent negative effects. A short term goal of increased accuracy produces reduced typing speed, resulting in an observed short time scale within-person negative correlation between speed and accuracy. Due to positive correlation between intrinsic coordination and speed of processing, between-person analyses result in a positive observed correlation between speed and accuracy. Training that improves both coordination and speed of processing as applied to typing also produce long time scale positive correlation between typing speed and accuracy.

Typing Speed and Accuracy

In Figure 2-b, the typing speed and accuracy example from the previous section is operationalized into the conceptual model. The measured functional abilities are typing speed and typing accuracy. The environmental context is the keyboard used for the investigation. Intrinsic capacities are labeled as coordination and speed of processing. The observed within-person short term negative correlation between typing speed and accuracy is shown as a solid gray double-headed arrow with a minus sign. The often-reported between-person positive correlation between cognitive abilities leads us to posit that coordination and speed of processing have a positive between-person correlation. Given that relationship, it is not unreasonable that a positive within-person correlation between intrinsic capacities for coordination and speed of processing exists as shown by the solid black double-headed arrow with a plus sign in the figure. The hypothesis of a within-person positive correlation between intrinsic capacities implies either mutual influence or a common antecedent such that development, training, daily variation, or injury would be expected to result in within-person change with the same sign for both intrinsic capacities.

It seems reasonable to assume that there is a positive relation between coordination and observed accuracy, and likewise a positive relation between accuracy goal and observed accuracy as shown by the dark single-headed arrows with plus signs beside them. Given the observed negative correlation between speed and accuracy, there is likely to be a negative relation between accuracy goal and typing speed such that when one attempts to improve one’s accuracy, one tends to slow down. This is represented by the solid gray single-headed arrow with the minus sign beside it. Similarly, in this conceptual model, when one attempts to type faster than one’s normal speed, one tends to reduce attention to accuracy.

In this model, the short term perceptual feedback, represented by dotted-line single-headed arrows, can produce a system dynamic that self-regulates. For instance, if one speeds up but notices that one’s accuracy has not suffered, one may attempt to speed up even more. Conversely, if one speeds up but it becomes obvious that one is making a large number of errors, one might slow down until the accuracy is acceptable. Environment can also produce self-regulation by perceptual feedback. If, for instance, a participant is given a keyboard with one key that tends to stick, accuracy and speed goals can be adjusted to account for the changes in the environmental context. This dynamical self-regulation increases the complexity of our conceptual model, but also allows representation of self-regulatory phenomena that are often observed.

Long term practice effects are represented by solid black dashed-line single-headed arrows. Long term plasticity in intrinsic capacities can be measured through investigations that engage in long term practice such as the COGITO study. In our model we do not draw a dashed arrow indicating transfer of repeated practice for accuracy to the intrinsic capacity of speed of processing. Transfer effects of long term practice have often been tested, but only rarely have been reported to be successful.

Now, consider how the model in Figure 2-b would produce data that correspond to the questions asked by the policy maker, the clinician, and the educator. When a cross-sectional study is run in order to answer the policy maker’s questions, the positive within-person correlation between the intrinsic capacities shows up as the between-persons main effect whereas the negative within-person speed-accuracy correlation shows up as test-retest unreliability in the measures of speed and accuracy. When a short time scale repeated measures study is performed to answer the clinician’s questions, the negative within-person correlation between speed and accuracy dominates whereas the between-person differences show up as a random intercept term. When a single subject long term learning study is run to answer the educator’s questions, the within-person learning effect dominates, but there is reduced power to distinguish the separate intrinsic capacities so obvious in the cross-sectional study. By setting the model up in this way, we have simultaneously accounted for the between-persons positive correlation between speed and accuracy, the short term within-person negative correlation between speed and accuracy, and the long term training improvement in speed and accuracy without changing the speed accuracy tradeoff through training. In addition, we are beginning to account for the kind of goal selection on the part of participants that can produce complicated short and long time-scale dynamics when a study is taken out of the lab and into a real-world context.

The adaptations inherent in this model are examples of nonstationarity in that the parameters of the system are changing over time and even the way that the parameters change may itself be time varying. We next define nonstationarity and present an argument that it plays a nontrivial part in the time dimension of the data box. From this we conclude that the time dimension of the data box cannot be treated in the same manner as are the other two dimesions. The assertion is made that nonstationarity is commonly observed in human systems and is illustrated using examples of dance movements and nonverbal communicative movements made in conversation. The choice of dance and conversation as metaphors are intended to illustrate the notion of nonstationarity while also serving to set up the ensuing argument that the interaction between theory, methods, and data is more similar to conversation than it is to a dance.

Nonstationarity and Information Transfer

What is nonstationarity? Formally, when equal–N contiguous subsamples of a time–series give time dependent estimates of the statistical properties of the full time–series, this time-series is said to be nonstationary (see Hendry & Juselius, 2000; Shao & Chen, 1987). One may consider this to be a problem of non-representative sampling. In a nonstationary system, a sample of consecutive observations starting at time t₁ may have different characteristics than a second sample of consecutive observations starting at time t₂. Not only means, variances and autocorrelations may be different, but the deterministic dynamics may be qualitatively different. By deterministic dynamics we mean the processes that lead to the predictable evolution of a system over time. A nonstationary system may qualitatively change the way it evolves. Most methods for estimating parameters of models for time series assume that one can average over many samples of time (e.g., Box, Jenkins, Reinsel, & Ljung, 2015; Cook, Dintzer, & Mark, 1980). But for non-stationary systems, this time averaging can attenuate or obscure relevant short term dynamics (Boker, Xu, Rotondo, & King, 2002). This is especially true of systems that exchange information (Schreiber, 2000). Systems that exchange information are ones where information contained in one variable (or individual) is transferred to another variable (or individual). The deterministic dynamics of such systems are defined both within and between variables (or in the case of conversation, between individuals).

At this point, some readers may be asking themselves, “Why is this a discussion about nonstationarity and not about non-ergodicity?” Ergodic systems are those in which time and space are interchangeable (Birkhoff, 1931). In reference to the data box, both nonstationarity and non-ergodicity imply that the dimensions of the data box cannot be substituted for one another (Molenaar, 2004). However, nonstationarity also has the specific implication that time is not homoscedastic. Thus when a system is nonstationary, parameters of deterministic dynamics cannot be assumed to be time-independent and there is even the potential that the structure of the model for the deterministic dynamics is not time-independent.

In the simulated investigations in the previous sections, we did not allow the short term dynamics to be changed by the long term training. However, there is no reason that short term dynamics need be invulnerable to training effects (Woodrow, 1964). In fact, some training programs may be targeted at improving short time scale regulation. In principle, any process occurring within an individual may exhibit plasticity. Thus, the conceptual model presented in Figure 2 remains impoverished by not explicitly representing how short term dynamics might change and adapt to training and to lifespan development and aging. When the short term dynamics of a system are themselves time-varying, the system has the property of being nonstationary. We next present an argument that human systems can be expected to exhibit nonstationarity.

Consider two people engaging in conversation. First, person A, (e.g., Ann) is the speaker, then she is the listener, and then the speaker again. In a turn-taking dyadic conversation, person B (e.g., Bob) might start as the listener, then he would be the speaker, and next the listener again. If Ann and Bob can perfectly predict what each other is going to say at each turn then according to a Shannon entropy calculation (Shannon & Weaver, 1949), no information is being transmitted between the conversation partners (Schreiber, 2000). It is only when speaker Ann and Bob surprise each other that information can be exchanged. But, Ann and Bob may wish to show that they understand one another. Acknowledgment is a backchannel communication that is, by definition, redundant (Dittmann & Llewellyn, 1968). Synchronizing nonverbal conversational movements or providing backchannel verbal expressions of acknowledgment increase redundancy in conversation (Laskowski, Wolfel, Heldner, & Edlund, 2008; Redlich, 1993). Thus, both surprise and redundancy are essential to conversation; a fundamental human ocial behavior.

According to information theory, only to the extent that predictive models fail is information exchanged. Although information theory (Shannon & Weaver, 1949) is commonly used in physics, it may be unfamiliar to many in the social and behavioral sciences. We next offer a very brief outline of the concepts behind information theory in order to ground our arguments that rely on the close relationship between information, entropy, and surprise.

Information and Surprise

How much do we know about a continuously valued variable given two measurements of that variable? One way to estimate this is by estimating how much imprecision is inherent in the two measurements (for an expanded version of this paragraph see Resnikoff, 1989). Suppose there is a variable with a true value m and two measurements v₁ and w₁ as shown in Figure 3-a. The imprecision in measurement of m can be estimated as a function of the spread of the measurements, in this case the interval w₁ − v₁. We might wish to say that our estimate of m has n significant digits since n expresses something about the size of m relative to the imprecision estimated by w₁ − v₁. Often, this imprecision is estimated using binary numbers and the number of significant digits is written as log₂(w₁ − v₁). Now suppose a new, more precise instrument is discovered which results in the measurements w₂ and v₂ as shown in Figure 3-b. The improvement in significant digits, p, of our measurement can now be written as

$$\begin{gathered} I_2={\log }_2\left(w_1-v_1\right)-{\log }_2\left(w_2-v_2\right) \\ ={\log }_2\left(\frac{w_1-v_1}{w_2-v_2}\right), \end{gathered}$$ (1)

where log₂ is the logarithm in base 2 and so the scale of I₂ is expressed in bits, i.e., number of significant digits expressed in binary. The gain by using the more precise instrument is I₂ bits of information. In general, if we wish our estimate of information to not depend on the units we choose or where we place zero for our variable scaling, the information function needs to take on the form

$$I_2=c{\log }_2(b),$$ (2)

where c is a constant and b is an estimate of imprecision.

Figure 3.

Change in precision of a measurement. (a) Two measurements v₁ and w₁ give us some estimate of the imprecision (w₁ − v₁) in the estimated value of m. (b) A more precise instrument gives two additional measurements v₂ and w₂ which reduced estimated imprecision (w₂ − v₂) in the estimated value of m

This logic can be applied to joint probabilities (Pompe, 1993). The gain in precision by knowledge of the joint probability of two variables x and y after accounting for the precision of x and y being independent can be calculated as

$$\begin{gathered} I_2={\log }_2(\text{p}(xy))-{\log }_2(\text{p}(x)\text{p}(y)) \\ ={\log }_2\left(\frac{\text{p}(xy)}{\text{p}(x)\text{p}(y)}\right). \end{gathered}$$ (3)

This ratio has more than a passing similarity to the formula for a Pearson product moment correlation coefficient. Take a moment to think about the ratio of the joint probability of x and y over the product of the independent probabilities:$\frac{\text{p}(xy)}{\text{p}(x)\text{p}(y)}$_. When x and y are independent, then the joint probability is equal to the product of the independent probabilities and so the ratio is equal to 1. The log of 1 (in binary or any other base) is 0 and so the gain in information by knowing the joint probability of x and y is zero. As the joint probability becomes larger than the product of independent probabilities, the ratio is greater than one and so the information gained in bits is a positive number.

When x and y are measurements taken from two time series X and Y, then the mutual information (Abarbanel, Masuda, Rabinovich, & Tumer, 2001; Fraser & Swinney, 1986) between the two time series is a generalization of Equation 3,. Time delay, τ, between the two time series must be incorporated and since there are many observations in each time series a mean of the mutual information can be calculated and written as

$$I_{XY}(\tau )=\frac{1}{T}{\displaystyle \sum }_{t=1}^{T}p\left(x_t,y_{t+\tau }\right){\log }_2\left[\frac{p\left(x_t,y_{t+\tau }\right)}{p\left(x_t\right)p\left(y_{t+\tau }\right)}\right]$$ (4)

The quantity I_XY (τ) is typically called the average mutual information between the two time series X and Y for a specified time delay τ.

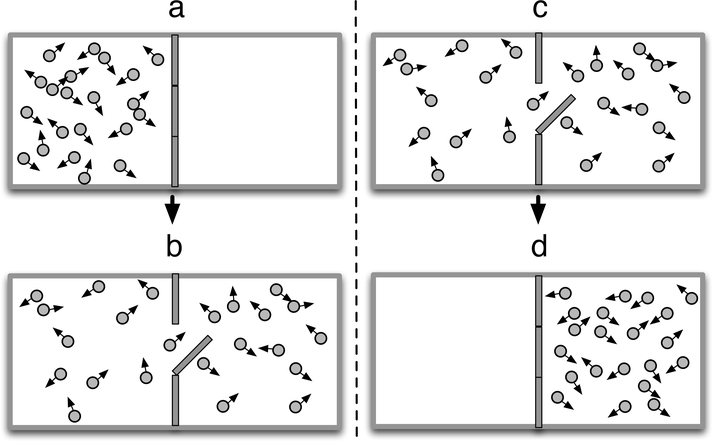
To complete this short tutorial on information, we will briefly discuss the relationship between information and entropy. The physicist Leo Szilard (1972) elegantly demonstrated the equivalence of information and entropy using a Gedanken experiment called “Maxwell’s Demon” which was originally proposed by the 19th century physicist James Clerk Maxwell (Thomson, 1879), and is here illustrated in Figure 4. Suppose that there is a double chambered tank with the left chamber filled with a gas and the right chamber in a vacuum as shown in Figure 4-a. We know which chamber each molecule of the gas is in: the left chamber. Thus each molecule of gas has associated with it 1 bit of information about its position in the double chambered vessel. In Figure 4-b we open a door between the chambers. The second law of thermodynamics takes over and increases the entropy of the system so that after a short period of time we cannot tell which chamber any particular molecule might be in. Thus, each molecule has lost 1 bit of information. If we start with the door open as in Figure 4-c, the process can be run in reverse. Maxwell’s Demon sits at the door and keeps the door closed except when a molecule is about to pass through the door from left to right. At that moment the Demon opens the door for an instant and allows that molecule to pass through then quickly closes the door again. After some amount of time, all of the molecules are in the right chamber. But this means entropy decreases! How does this happen? The demon needs the information that a molecule is approaching the door in order to know when to open it. Thus 1 bit of information is added back to each molecule. In this way, Szilard argued that entropy and information are exactly exchangeable quantities but opposite in sign. And in fact the form of their respective equations is exactly the same, but opposite in sign.

Figure 4.

Diagram of Maxwell’s Gedanken experiment. (a) Gas molecules are in the left chamber. For every molecule, you have one bit of information about which chamber it is in. (b) The door between the chambers is opened and the gas equalizes pressure: the second law of thermodynamics says entropy increases. For each molecule you now have zero bits of information about which chamber it is in. (c) Gas molecules start in both chambers with zero bits of information about which chamber they are in. (d) Maxwell proposed a “demon” who sits at the door between chambers and only briefly opens the door any time a molecule is about to go through the door from the left chamber to the right chamber. After some time, you again have one bit of information for each molecule. But entropy has decreased in violation of the second law of thermodynamics!

If information is to be passed from one person to another in a conversation, surprising events must occur. Let us examine how surprise and information transfer in a conversation are related by extending the example of Maxwell’s demon to mutual information. If Ann has information that is unknown to Bob, then Bob will not be able to predict what Ann is about to communicate. From Bob’s perspective, this is like panel c of Figure 4, in other words he has little information available about Ann’s thoughts. As Ann communicates, she is acting like Maxwell’s demon, adding information to each particle until in panel d they are all on one side. From Bob’s perspective, Ann’s communication has increased his ability to predict Ann’s thoughts. Now, their mutual information has increased. How does Ann add information? By surprising Bob—communicating something that he could not already predict. By this logic, the mutual information between their time series must start low and not be more predictable from past events in order to transfer information. For information transfer to repeatedly occur during a conversation, surprise must occur often. Referring back to Equation 4, the mutual information of Ann and Bob’s behaviors at any tau must be small relative to the product of their independent probabilities at all tau. This kind of unpredictability in a time series is a defining quality of nonstationarity. Thus information transfer and nonstationarity in conversation must be related. From these first principles we conclude that conversation must be nonstationary (unpredictable even accounting for time lag) in order to incorporate information transfer between conversational partners. The next section reviews some empirical evidence in accord with this conclusion.

Nonstationarity in Conversation and Dance

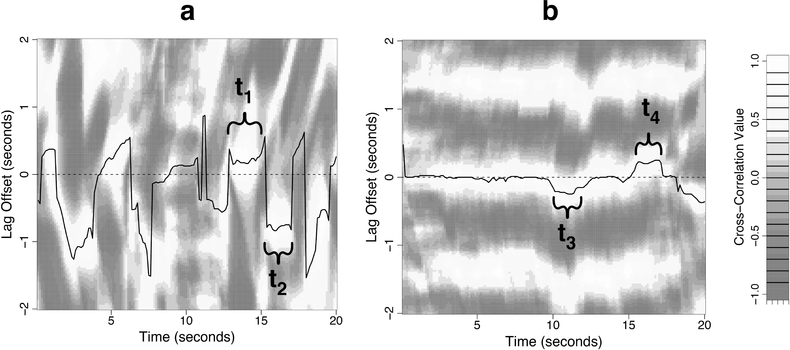
Nonstationarity can be observed by motion-tracking head movements during conversation and dance. Figure 5-a plots windowed cross correlation (Boker et al., 2002) of head velocities tracked during 20 seconds of dyadic conversation between two participants in a “get to know you” experiment (Ashenfelter, Boker, Waddell, & Vitanov, 2009). High positive correlations are white and high negative correlations are grey. Each vertical column of pixels through the density plot is displaying a cross-correlation function between the head velocities of the two participants for a window of ±2 seconds around the elapsed time for that column as given in seconds on the × axis. The undulating solid line tracks the peak correlation that is closest to a lag of zero — an indicator of the phase lag between the two participants’ head velocities. When the peak correlation has a positive lag (e.g., during interval t₁), Ann’s head movements are predicting Bob’s movements a short time later. When the peak correlation has a negative lag (e.g., during interval t₂), Bob’s movements are predicting Ann’s.

Figure 5.

Density plots of Windowed Cross Correlation (WCC) from 20 seconds of (a) motion-tracked head velocities during a dyadic “get to know you” conversation, (b) motion-tracked body velocities during a dyadic dance to a rhythm that repeated every 1.4 seconds.

The intervals t₁ and t₂ are particularly interesting because within each short interval the peak correlation line is nearly horizontal, indicating a short interval of stationarity. These intervals of stationarity can also be thought of as being intervals displaying high degrees of symmetry between the conversational partners, that is to say they are mirroring each others’ movements. This symmetry also indicates redundancy, since the conversational partners’ movements can be predicted from one another. But note that there is an abrupt change between interval t₁ and t₂. These sudden transitions between two intervals of symmetry have been called symmetry breaking events (Boker & Rotondo, 2002) and they are signatures of moments of high entropy (i.e., surprise) in a conversation.

Coordinated movements exhibited by the two dance partners plotted in Figure 5-b show a very different pattern than that shown in conversation. During this 20 second interval of windowed cross correlations between dance partners, a high degree of stationarity is observed (Brick & Boker, 2011). The two dancers can see each other and are both listening to a repeating cowbell rhythm with an inter-repetition interval of 1.4 seconds. For the first 10 seconds, the dancers’ movements are highly correlated with each other at a lag close to zero as plotted by the peak correlation tracking line. Note also that the repetition interval of the auditory stimulus can be observed as the horizontal light colored stripe at ±1.4 seconds lag. When the dancers synchronize to a stationary (unvarying and repeating) auditory pattern, then their coordinated movements also tends to become stationary. At interval t₃, the dancers lose their low latency synchronization and dancer B is in the lead by about .2 seconds. They soon re-establish symmetry with a lag of close to zero. A few seconds later, the pair again change their near zero lag synchronization to one in which dancer A is in the lead by about .2 seconds during interval t₄. Note that both the loss and re-establishment of low lag symmetry before and after interval t₃ and t₄ do not involve the sudden transition that characterizes symmetry breaking in the conversation plotted in Figure 5-a.

Of Dances, Conversations, and Science

We next apply the ideas of nonstationarity and information transfer to develop a metaphor for the interplay between theory, methods, and data. We explore two potential metaphors — dance and conversation — and come to the conclusion that conversation is more apt.

Dances and conversations are similar in that they involve two or more participants engaged in socially coordinated action. In both dance and conversation, there may be shifting lead and lag relationships as illustrated in Figure 5. But there are two fundamental differences between dance and conversation.

The first difference has to do with intention. The intention of dance is the coordinated action. Thus, when we speak of a beautiful dance, we are evaluating the dance on variables such as the degree, the smoothness, the symmetry, and the complexity of the coordination of the partners with each other and with the music.

Intentions underlying conversation are more complicated. Coordinated action is certainly part of the story. But other intentions may include information transfer between individuals — information that might include facts, opinions, emotions, goals, or desires. Another intention might be to persuade or come to consensus; to transform a dyad or multi-party group that had been far apart in informational terms into one that has a much smaller entropy difference. This transformation of a disparate group into a group displaying consensus is of particular interest for advancing the metaphor of a theory-methods-data conversation. When speaking of a conversation with intent to form consensus, variables come into play such as how far apart the parties were to begin with, how close they were at the end of the conversation, how smoothly they came together, how much each party contributed to the consensus, or even surprise at the eventual result given the initial conditions and temporal sequence of the conversation.

The second fundamental difference between dance and conversation is that in dance there is music to which the dancers coordinate. Music is an external stimulus that provides synchronizing input available to both dancers. To the extent the music exhibits stationarity the dancers can be expected to also exhibit stationarity. Conversation may have no externally provided organizing influence. Conversation is self-organizing and the structure of synchronization between conversational partners exhibits a high degree of nonstationarity. But as noted in the previous paragraph, the value of a conversation might be due to its surprising events.

A Theory-Methods Dance

Consider the metaphor of the interaction between theory and methods as being a dance. First theory may be in the lead and then methods. Imagine these two partners dancing a beautiful dance; the movements smooth, symmetric, and coordinated. Changes in lead are neither abrupt nor surprising. Most of the time the lag between the two partners is close to zero and their correlation is high, so they predict each other very well. How does this kind of coordination come about in a real dance? If the music has a predictable pattern, then the dancers can each predict the music as well as each other’s movements.

But in a dance between theory and methods, what provides the music? Are theory and methods dancing to data? Data tend to be gathered in order to test theories and the structure of data is dictated by the research design which in turn is the product of methods. So it would stretch the metaphor to suggest that data are calling the tune when they must be somehow part and parcel of the dance itself.

When Le Sacre du Printemps was first performed in 1913, the audience was angry and upset. By some contemporary reports, fights broke out and as many as 40 people were arrested. Stravinsky’s score and Nijinsky’s choreography for Le Sacre du Printemps included what were, at the time, many surprising, dissonant musical changes and abrupt, jerky dance movements — what the music critic Taruskin (2012) called “ugly earthbound lurching and stomping”. Shortly after the performance, Stravinsky was quoted (New York Times, 1913) as saying, “No doubt it will be understood one day that I sprang a surprise on Paris, and Paris was disconcerted.” As time has gone on, we are not so surprised by Le Sacre du Printemps and many now consider it to be beautiful. But when it was first performed it was widely considered ugly.

The metaphor of dance misses what we believe to be a critical component of science: when a scientific result is highly surprising and then replicable, it tends to be highly valued. In contrast, when a dance is highly surprising it may be perceived as ugly. Let us next consider the metaphor of a conversation between theory, methods, and data.

A Theory-Methods-Data Conversation

Imagine a three-way conversation in which one person, Ann is the speaker and the other two, Bob and Carla, are listeners. Perhaps Ann is saying something that contains new information from the standpoint of Bob and Carla. To the extent that Bob and Carla are surprised—that is to say to the extent to which they were unable to predict the speaker’s message—information has been transmitted. This information might be easily accepted by Bob and Carla, in which case, one would expect some sort of acknowledgment such as mutually synchronized head nods between Ann, Bob and Carla. The acknowledgment of agreement is a form of symmetry and thus implies mutual predictability between the speaker and the listeners. Next, either the speaker-listener roles will change or perhaps the current speaker, Ann, will again present novel information.

However, if the novel information is difficult for Bob and/or Carla to accept, then there might result a discussion back and forth until some agreement is reached. This process of consensus formation might involve each person presenting new, but less surprising information until there is agreement. Or it might involve a process of logic to determine where and why each person’s world view differs from the others. Once consensus is reached or the group agrees to continue the discussion later, a new topic can be undertaken.

After agreement, if Ann perseveres in speaking redundantly, Bob and Carla are likely to become bored, resulting in one of them taking on the role of speaker. Whereas it might seem counterintuitive, boredom is a central force for ensuring that novelty continues to occur in a conversation.

How would theory, methods, and data have this kind of three way conversation? Suppose theory is in the speaker role. A surprising theory is one that, in some sense, is unpredictable from current methods and/or data and thus presents a challenge and opportunity to them both. In order for the conversation to proceed, new methods and/or new data must be obtained in order to see if the theory is still surprising given the new methods and/or data. When the combination of methods and data are somehow greatly simplified within the novel theoretic context, one might say that the novel information provided by the new theory has had a large effect. In this case, the total entropy of the conversation has been reduced by the introduction of the new theory. We consider such a reduction in entropy, that is to say, the reduction in the total complexity of the conversation between theory, methods, and data to be a candidate signature for being a valuable theory.

Suppose methods are in the speaker role. A method that provides novel information to data and theory is one that again, in some sense, is unpredictable from current data and theory. Such a method provides both challenge and opportunity to collect data in new ways or use existing data in new ways. It also presents a challenge to develop new theories that might have been untestable prior to the existence of the new method. The methods, data, and theory will then need to come to some consensus. New methods can be profoundly transformative to data and theory; opening up new avenues of inquiry, new ways of collecting data, or new ways to organize thinking. New methods can open up flood gates of conversation between theory, data, and methods. We consider a large increase in the flow of this three-way conversation to be a candidate signature for a valuable method.

Finally it may be that data are in the speaker role. If new data are not predicted given current theory and methods, then the new data are providing new information. Data being in the speaker role is the most well-understood of the three conversational partners since most of statistics, whether Bayesian or frequentist, are predicated on determining the likelihood of data. However, it is worth considering how methods and theory might respond to unlikely data — new information in the conversation provided by data as the speaker. The most likely response is that theory is challenged to change to accommodate the surprising data. Existing theory does not predict the occurrence of surprising data, but perhaps a better theory might. Old methods might be inadequate to correctly calculate the likelihood of the data. When data produces change in theory and/or methods that either simplify them or make them more comprehensive, then these data would have a candidate signature for valuable data.

What is the role of the scientist in a conversation between theory, methods, and data? Ultimately, scientists play many roles. We are facilitators of the conversation by bringing together the three conversational partners and ensuring the challenges are met and opportunities fulfilled. We play the part of adjudicator between the conversational partners, deciding when where there is disagreement and when there is sufficient agreement in order to move on to the next topic.

An Entropic Waterfall

Finally, we wish to ask readers to consider how they would characterize the value of a conversation between theory, methods, and data. Thinking about how symmetry forms and breaks in cross-correlations between participants’ head movements during conversation, we have been led to consider a few possibilities for evaluating a scientific 1 conversation.

When all partners agree all the time, a conversation is redundant, predictable, and boring. But when all partners are always surprising, a conversation is chaotic. In order for the conversation between theory, methods, and data to have value, it must have some balance of surprise and redundancy. By definition, surprise and redundancy cannot co-exist, so in order to construct that balance, there must be moments of surprise alternating with periods of redundancy.

How the conversation leads from one partner introducing surprise to all partners being in agreement is a candidate for evaluating the quality of a conversation. For instance, suppose a conversation starts with a high degree of redundancy—all partners being in a predictable and quiescent state. Then surprise is introduced by one partner and suddenly there is a great deal of activity, readjustment, and flow of information between the partners. Finally, all partners come to a new agreement where the new state is at a much lower entropy than it was previously. Thus, the process of the conversation has created a more ordered organization than previously existed. Just as a waterfall starts with quiet water at a height and then falls chaotically down a cliff face to quiet water down below, a conversational process composed of quiescence at a high level of entropy, active reduction of entropy with high information flow, and a new agreement at a lower entropy might be viewed as being an entropic waterfall and a beautiful conversation between theory, methods, and data. That “Aha!” moment of epiphany is the feeling of dropping off the entropic waterfall’s edge.

Conclusions

The challenge of integrating the three dimensions of Cattell’s data box was presented and illustrated through an example model for the speed-accuracy tradeoff. This model simultaneously wrestles with the problems of between-person cross-sectional findings, within-person short term dynamics, and long term plasticity and learning. The model also points to how personal goals and environmental context can play an important role in determining what we may observe in behavior. Whereas this model of intrinsic capacity, functional ability, personal goals, and the environment is conceptual, we hope that it has spurred thought about how different categories of questions might be unified in order to simplify understanding.

The speed-accuracy tradeoff example led to a conclusion that the time dimension of data box is fundamentally different than the other two dimensions and must be treated separately. The properties of sequential ordering and multiple time-scale dynamics are not present in the other two dimensions. This led to a discussion of nonstationarity: when ordered samples on the time dimension may not be representative. In order to deal with this problem we provided short outline reviews of the concepts of mutual information and entropy in order to measure surprise as unpredictability.

Empirical evidence was reviewed suggesting that nonstationarity is a component of conversations and an argument was presented that this is due to the need for surprise to be present in order for information transfer to occur between conversational partners. Finally, an argument was made that the interplay between theory, methods, and data may better be considered as a conversation than as a dance. The argument rested on properties displayed in the correlated movements of dyadic dancers versus head movements recorded in conversations. A metaphoric three-way conversation was expanded in order to think in detail about why some scientific advances might be perceived to be more appealing than others.

In sum, this article was itself designed to foster conversation among readers. We ask: “What is a beautiful conversation between theory, methods, and data?” How can these three foundations of science better work together to advance understanding?