A Robust Regression Methodology via M-estimation

Abstract

A robust regression methodology is proposed via M-estimation. The approach adapts to the tail behavior and skewness of the distribution of the random error terms, providing for a reliable analysis under a broad class of distributions. This is accomplished by allowing the objective function, used to determine the regression parameter estimates, to be selected in a data driven manner. The asymptotic properties of the proposed estimator are established and a numerical algorithm is provided to implement the methodology. The finite sample performance of the proposed approach is exhibited through simulation and the approach was used to analyze two motivating datasets.

1. Introduction

Regression is the most common and useful statistical tool which can be used to quantify the relationship between a response variable (y) and explanatory variables (x). To this end, the seminal works of both Legendre in 1805 and Gauss in 1809 proposed the method of least squares (LS), which has arguably become the most popular approach to conducting a regression analysis. This popularity is likely attributable to the fact that the LS estimator can be expressed in closed form and can be shown to achieve minimum variance among all unbiased estimators, when the underlying error distribution is normal; e.g., see Rao (1945). However, this approach does not provide an optimal estimator for non-normal settings and is very sensitive to outlying observations (Koenker and Bassett, 1978). Further, experience has shown that LS regression may not be appropriate when the response variable differs from the regression function in an asymmetric manner, which is commonly encountered in medical data, among other venues. In lieu of these deficiencies, herein a general regression methodology is proposed which allows for the possibility of non-normal tail behavior and asymmetry in the conditional distribution of y given x, but will still perform well for symmetric and/or normally distributed data.

One way to improve parameter estimates for non-normal data and to guard against the influence of outlying observations is to replace the LS loss function (i.e., the squared error loss) by a loss function which can accommodate asymmetry in the error distribution and is less susceptible to the magnitude of the residuals. For example, in 1793 Laplace proposed least absolute deviations (LAD), or L₁-norm regression as an alternative to LS. This regression technique is less sensitive to outlying observations and is more appropriate, when compared to LS, for error distributions whose tails are heavier than that of the normal. More generally one can replace the LAD estimator, with an L_p norm estimator; for further discussion see Zeckhauser and Thompson (1970), Mineo (1989) and Agrò (1992). Quantile regression estimates are found by minimizing the quantile (check) loss function, and since they estimate quantiles of the conditional distribution of y given x, they are appropriate for asymmetric and heavy tailed distributions (Koenker and Bassett, 1978).

Each of the aforementioned loss functions have corresponding conditional distributions of y given x for which the maximum likelihood estimator (MLE) is equivalent to the estimator which minimizes the corresponding loss: the LS estimator corresponds to the MLE when the error distribution is normal; the LAD estimator is equivalent to the MLE under Laplace errors, the L_p norm estimator corresponds to the MLE when the error terms obey the generalized error distribution (GED) (Subbotin, 1923); and the quantile regression estimator is equivalent to the MLE when the errors follow an asymmetric Laplace distribution (ALPD). Moreover, in these very specific settings the regression estimators are asymptotically most efficient. More generally, the aforementioned loss functions do provide consistent estimators, under standard regularity conditions, but the efficiency of the resulting estimator is inherently tied to the chosen loss and underlying error distribution. That is, there does not exist a universally most efficient approach to conducting a regression analysis. Although, provided a priori knowledge of the error distribution, which is typically not available, a regression methodology could be selected with efficiency in mind. For example, in a location scale regression framework, the efficiency of the quantile regression estimator depends on the quantile of interest. Moreover, under asymmetric Laplace errors the asymptotic variance of the quantile regression estimator is minimized when the analysis proceeds to use the true skewness parameter as the quantile of interest. More generally, the quantile that corresponds to minimizing the asymptotic variance of the estimator depends on the underlying error distribution, which is unknown. The salient point is that to perform a regression analysis an analyst must select a particular methodology, which, in some sense, is equivalent to specifying either the error distribution or loss function under which the regression coefficients are estimated. This work provides a more general approach which allows the loss function to be selected in a data adaptive fashion, thus resulting in a more efficient and robust estimator.

In order to develop a robust regression procedure one could consider two competing approaches; i.e., perform the regression analysis with respect to multiple loss functions or allow the characteristics of the data to dictate the selection of the loss function. In order to improve the efficiency of quantile regression, Zou and Yuan (2008) introduced composite quantile regression (CQR), which optimizes over a sum of multiple quantile loss functions. As a robust regression procedure, CQR combines the strength of multiple quantile regressions to estimate the same “slope” coefficients across different quantiles. Kai et al. (2010) adapted CQR to the local polynomial framework and established that for many common non-normal errors this extension provided for gains in estimation efficiency when compared to its local LS counterpart. Regretfully, when implementing CQR it is still unclear how many quantiles should be used and simply increasing the number of quantiles does not necessarily improve the efficiency of the estimator; for further discussion see Kai et al. (2010). Alternately, one could consider a convex combination of loss functions; e.g., Zheng et al. (2013) extended CQR by embedding the usage of an empirically weighted average of quantile loss functions and the LS loss function, so that the LS loss tends to be weighted heavier for normally distributed data. Rather than using several quantiles, another tact would be to let the data select the quantile of interest in quantile regression. Bera et al. (2016) proposed a Z-estimator which could be used to simultaneously obtain the quantile regression estimator and the quantile of interest in a data driven fashion, and is hereafter referred to as ZQR. In particular, this estimator is obtained by minimizing an objective function which is inspired by the maximum likelihood score function under the ALPD. Proceeding in this fashion results in a penalized quantile regression framework where the penalty depends on the quantile of interest.

Motivated by the work of Bera et al. (2016), the regression methodology presented herein is developed in the same vein. In particular, a robust loss function is constructed so that the proposed estimator corresponds to the MLE when the error terms obey the asymmetric exponential power distribution (AEPD). The AEPD class of distributions was first proposed by Fernandez et al. (1995), and was further studied in Theodossiou (2000), Ayebo and Kozubowski (2003), and Komunjer (2007). This flexible class of distributions holds the normal, skewed normal, Laplace, ALPD, and GED as special cases, among many others. Developing the proposed regression methodology under the AEPD has several definitive advantages. First, and foremost, the proposed method selects the best loss function (e.g., LS, LAD, L_p, quantile, etc.) from a broad class in a data driven fashion. For this reason, one could view this proposal as a method which unifies and bridges the gaps between LS, LAD, L_p norm, and quantile regression. Secondly, the proposed technique can effectively capture the tail decay and/or asymmetry of the error distribution, thus maintaining a high level of estimation efficiency in venues where other competing procedures do not. Lastly, as the AEPD holds many common distributions as special cases (e.g., normal, skewed normal, ALPD, GED, etc.), one may use model selection criteria, such as AIC or BIC, to identify the “best” model (e.g., LS fit, specific quantile regression fits, etc.), as is demonstrated in subsequent sections.

The remainder of this article is organized as follows. Section 2 presents the modeling assumptions, develops the proposed loss function based on the AEPD, and provides a stable numerical algorithm which can be used to obtain the regression parameter estimates. The consistency and asymptotic normality of the proposed estimator are established in Section 3. The results of an extensive Monte Carlo simulation study designed to assess the finite sample performance of the proposed procedure is provided in Section 4. The results of the motivating data analyses are provided in Section 5. Section 6 concludes with a summary discussion, and the regularity conditions under which the theoretical results can be established are provided in the appendix.

2. Methodology

2.1. Model assumption

Consider a linear regression model

$$y={\mathit{x}}^{\prime }\beta +ϵ,$$ (1)

where y denotes the response variable, x is a (p + 1)-dimensional vector of covariates, β is the corresponding vector of regression coefficients, and is the error term. Throughout the remainder of this article it is assumed that the error term is independent of the covariates (i.e., x ⊥ ϵ, where ⊥ denotes statistical independence) and that the probability density function of has a unique mode at zero. Under these assumptions, the linear predictor x’β = β₀ + x₁β₁ + ··· + x_pβ_p represents the unique mode of the conditional distribution of y given x. Note, this model becomes a mean regression model when the distribution of is symmetric and has a finite first moment. The primary focus of this work is aimed at estimating the “slope” parameters, β^∗ = (β₁,...,β_p)’, since the intercept, β₀, provides solely for a shift between different regression functions of interest; i.e., regression functions such as the mean and median for (1) have identical unknown slope parameters.

For ease of exposition, assume that the error term in (1) follows an AEPD, this assumption is later relaxed in subsequent sections. A random variable is said to follow an AEPD if there exist parameters α > 0, μ ∈ ℝ, σ > 0 and 0 < τ < 1 such that the probability density function of has the form

$$f(ϵ)=\frac{\alpha \tau (1-\tau )}{\mathrm{\Gamma }\left(\frac{1}{\alpha }\right)\sigma }\exp \left\{-\frac{|ϵ-\mu {|}^{\alpha }}{{\sigma }^{\alpha }}\left[I(ϵ\ge \mu ){\tau }^{\alpha }+I(ϵ<\mu ){(1-\tau )}^{\alpha }\right]\right\},$$ (2)

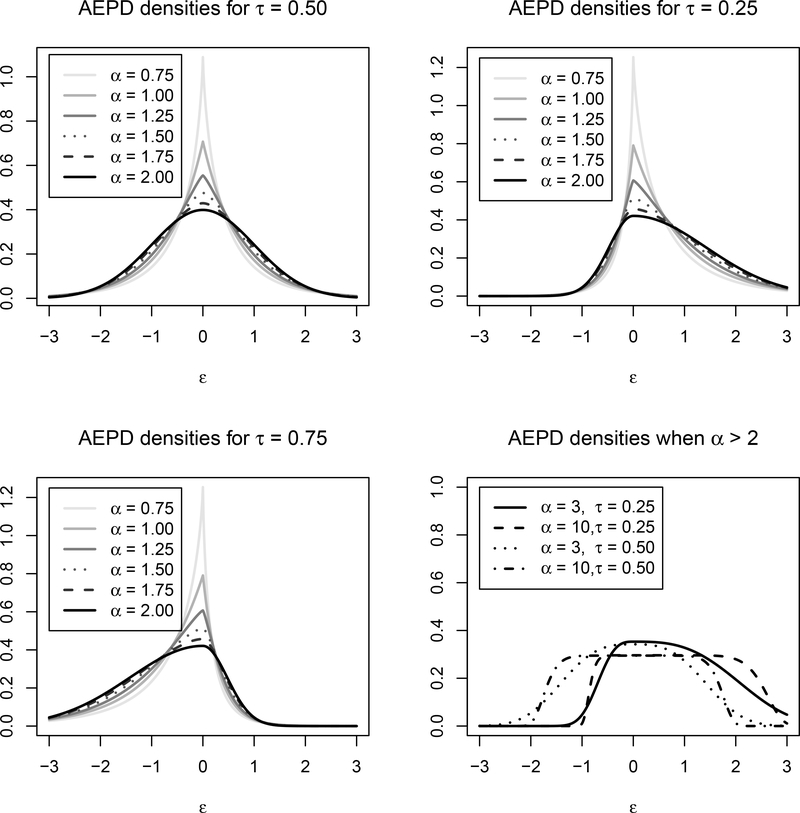
where μ is the location (mode) parameter, σ is the scale parameter, τ controls the skewness and α is the shape (tail decay) parameter. For notational brevity, this relationship is denoted ϵ ~ AEPD(μ,α,σ,τ). The AEPD class of distributions hold many common distributions as special cases; e.g., the epsilon-skew-normal distribution, studied by Mudholkar and Hutson (2000), is obtained when α = 2, which holds the normal distribution as a special case when τ = 0.5; Specifying α = 1 results in the ALPD which holds the Laplace distribution as a special case when τ = 0.5; And the GED results from specifying τ = 0.5. Moreover, as α approaches ∞, the AEPD approaches a uniform distribution with parameter (μ − σ/(1 − τ), μ + σ/τ). To illustrate the broad spectrum of shapes for which the AEPD density can take, Figure 1 depicts several AEPD densities for different combinations of α and τ, where μ = 0 and σ is specified such that the variance is unity.

Figure 1:

The AEPD densities for different parameter configurations.

Under the aforementioned assumptions, the response variable conditionally, given the covariates, follows an AEPD; i.e., y|x ∼ AEPD(x’β, α, σ, τ). Thus, the log-likelihood of the observed data $\left\{\left(y_i,{\mathit{x}}_i^{\prime }\right),i=1,\dots ,n\right\}$ is given by

$$\begin{gathered} \rho (\mathit{\theta })=\frac{1}{n}{\displaystyle \sum _{i=1}^n\ln }f\left(y_i|{\mathit{x}}_i;\mathit{\theta }\right)=\ln \left[\frac{\alpha }{\mathrm{\Gamma }(1/\alpha )}\right]+\ln [\tau (1-\tau )]-\ln (\sigma ) \\ -\frac{1}{n{\sigma }^{\alpha }}{\displaystyle \sum _{j=1}^n{\left|y_i-{\mathit{x}}_i^{\prime }\beta \right|}^{\alpha }}\left[I\left(y_i\ge {\mathit{x}}_i^{\prime }\beta \right){\tau }^{\alpha }+I\left(y_i<{\mathit{x}}_i^{\prime }\beta \right){(1-\tau )}^{\alpha }\right], \end{gathered}$$ (3)

where θ = (β’, α, σ, τ) denotes the collection of model parameters and ${\mathit{\theta }}_0=\left({\beta }_0^{\prime },{\alpha }_0,{\sigma }_0,{\tau }_0\right)$ represents the true unknown value of θ. More generally, in the case in which the error distribution does not belong to the AEPD class, (3) can be viewed as a loss function, which still can be used to efficiently estimate the regression coefficients, as is demonstrated in Sections 4 and 5. In either case, let $\widehat{\mathit{\theta }}=({\widehat{\beta }}^{\prime },\widehat{\alpha },\widehat{\sigma },\widehat{\tau })$ denote the value of θ which maximizes (3); i.e., $\widehat{\mathit{\theta }}$ is the proposed estimator of θ₀.

To illustrate how the proposed approach is data adaptive, it is first noted that the process of estimating θ₀ via maximizing (3), can be viewed as a two-step process. First, for fixed values of α, σ and τ an estimate of β₀ is obtained by minimizing the following loss function

$${\displaystyle \sum _{i=1}^n{\left|y_i-{\mathit{x}}_i^{\prime }\beta \right|}^{\alpha }}\left[I\left(y_i\ge {\mathit{x}}_i^{\prime }\beta \right){\tau }^{\alpha }+I\left(y_i<{\mathit{x}}_i^{\prime }\beta \right){(1-\tau )}^{\alpha }\right],$$ (4)

This estimator is denoted as $\widehat{\beta }(\alpha ,\tau )$. The second step estimates the remaining parameters by maximizing (3) after replacing β by $\widehat{\beta }(\alpha ,\tau )$. The key feature of this approach is that every combination of α and τ corresponds to a different loss function specification in (4), and consequently results in obtaining a different estimate of β₀. For example, if α = 2 and τ = 0.5, the proposed approach and LS obtain the same estimate; when α = 1 and τ = τ^∗, the resulting estimate is identical to the quantile regression estimate with the quantile of interest being τ^∗. The salient point: by estimating α₀ and τ₀ the proposed procedure allows the data to determine the shape and skewness of the underlying distribution and as consequence selects the form of the loss function which is used to estimate the regression coefficients.

2.2. A general error distribution and the Kullback Leibler divergence

In the setting in which the error distribution does not belong to the AEPD class, one could view the model for the conditional distribution of y, given x, as being misspecified. Denote the true probability density function for y, given x, by f^∗(y|x), the assumed parametric density by f(y|x; θ), and the density of x as h(x). Further, define the joint density of y and x as ɡ^∗(y, x) = f^∗(y|x)h(x) and ɡ_θ(y, x) = f(y|x; θ)h(x) under the true and assumed model, respectively. Subsequently, the Kullback-Leibler divergence is defined by

$$D_{KL}\left(g^{*}\Vert g_{\mathit{\theta }}\right)=-E\left[\ln \frac{g_{\mathit{\theta }}(y,\mathit{x})}{g^{*}(y,\mathit{x})}\right]=-E\left[\ln \frac{f(y|\mathit{x};\mathit{\theta })}{f^{*}(y|\mathit{x})}\right],$$ (5)

where the expectation is taken with respect to the true distribution ɡ^∗. Minimizing (5) with respect to θ, or equivalently maximizing (3), results in identifying the AEPD density closest to f^∗(y|x), i.e., $f(y|\mathit{x};\widehat{\mathit{\theta }})$ is the “projection” of f^∗(y|x) onto the AEPD class. More specifically, obtaining $\widehat{\mathit{\theta }}$ as the maximizer of (3) is equivalent to finding the AEPD density closest to the true probability density with respect to the observed empirical distribution. This feature allows the proposed approach to be robust to the structure of the underlying error distribution and to maintain a high level of estimation efficiency, by permitting the loss function (i.e., the assumed AEPD density) to adapt to the true underlying structure of the data.

2.3. Numerical algorithm

In order to develop a numerical algorithm for obtaining $\widehat{\mathit{\theta }}$, the dimension of the loss function presented in (3) is reduced. In particular, for fixed values of β and α, the values of σ and τ which maximize (3) can be expressed as

$$\sigma (\beta ,\alpha )={\left(\frac{\alpha }{n}\left\{e^{+}(\beta ,\alpha )\tau {(\beta ,\alpha )}^{\alpha }+e^{-}(\beta ,\alpha ){[1-\tau (\beta ,\alpha )]}^{\alpha }\right\}\right)}^{1/\alpha },$$

$$\tau (\beta ,\alpha )={\left\{1+{\left[e^{+}(\beta ,\alpha )/e^{-}(\beta ,\alpha )\right]}^{1/(\alpha +1)}\right\}}^{-1},$$

respectively, where $e^{+}(\beta ,\alpha )={\sum }_{i=1}^n{\left|y_i-{\mathit{x}}_i^{\prime }\beta \right|}^{\alpha }I\left(y_i\ge {\mathit{x}}_i^{\prime }\beta \right)$ and $e^{-}(\beta ,\alpha )={\sum }_{i=1}^n{\left|y_i-{\mathit{x}}_i^{\prime }\beta \right|}^{\alpha }I(y_i<{\mathit{x}}_i^{\prime }\beta )$. Replacing σ and τ in (3) by σ (β, α) and τ (β, α), respectively, leads to the following loss function

$$Q(\beta ,\alpha )=\ln \left[\frac{\alpha }{\mathrm{\Gamma }(1/\alpha )}\right]-\frac{1}{\alpha }\ln \left(\frac{\alpha }{n}\right)-\frac{1}{\alpha }-\frac{1+\alpha }{\alpha }\ln \left[e^{+}{(\beta ,\alpha )}^{1/(\alpha +1)}+e^{-}{(\beta ,\alpha )}^{1/(\alpha +1)}\right].$$ (6)

In order to maximize (6) with respect to β and α, an iterative algorithm is employed with a well specified initial value. The proposed algorithm proceeds as follows:

1. Set j = 1 and initialize θ⁽⁰⁾ = [β⁽⁰⁾, α⁽⁰⁾, σ⁽⁰⁾, τ⁽⁰⁾] as β(0) = β(τ⁽⁰⁾), α⁽⁰⁾ = 1,

$${\sigma }^{(0)}=n^{-1}{\displaystyle \sum _{i=1}^n{\rho }_{{\tau }^{(0)}}}\left(y_i-{\mathit{x}}_i^{\prime }{\beta }^{(0)}\right),$$

$${\tau }^{(0)}=\underset{\tau }{\arg \min }{\displaystyle \sum _{i=1}^n{\rho }_{\tau }}\left[y_i-{\mathit{x}}_i^{\prime }\beta (\tau )\right]/[\tau (1-\tau )],$$

where ρ_τ(·) is the usual quantile check loss function and $\beta (\tau )=\arg {\min }_{\beta }{\sum }_{i=1}^n{\rho }_{\tau }\left(y_i-{\mathit{x}}_i^{\prime }\beta \right)$.

• 2.Compute β^(j) = argmax_β Q(β,α^(j−1)) and α^(j) = argmax_α Q(β^(j), α), respectively, and set j = j + 1.
• 3.Repeat step 2 until convergence.

At the point of convergence the proposed estimator $\widehat{\mathit{\theta }}=({\widehat{\beta }}^{\prime },\widehat{\alpha },\widehat{\sigma },\widehat{\tau })$ is determined as $\widehat{\beta }={\beta }^{(j)}$, $\widehat{\alpha }={\alpha }^{(j)}$, $\widehat{\sigma }=\sigma ({\beta }^{(j)},{\alpha }^{(j)})$, and $\widehat{\tau }=\tau ({\beta }^{(j)},{\alpha }^{(j)})$. Note, the more complex initialization step provides the numerical algorithm with a well posed initial value and results in gains in computational efficiency. Further, the necessary optimization steps throughout the algorithm can easily be completed using standard numerical software; e.g., quantreg, optim, and optimize in R.

3. Asymptotic properties

The proposed methodology falls under the general class of M-estimators introduced by Huber (1964), and as such, standard regularity conditions ensure consistency and asymptotic normality of the resulting estimators. The specific technical conditions required are given in the appendix, along with a brief discussion.

Theorem 1. (Consistency). Under regularity condition (A1)-(A6), provided in the appendix, $\widehat{\mathit{\theta }}$ is a consistent estimator of θ₀; i.e. $\widehat{\mathit{\theta }}\stackrel{p}{\to }{\mathit{\theta }}_0$.

Theorem 2. (Asymptotic Normality). Under regularity condition (A1)-(A7), provided in the appendix, and for α₀ > 1. The M-estimator $\widehat{\mathit{\theta }}$ of θ₀ is asymptotically normal; i.e.,

$$\sqrt{n}\left(\widehat{\mathit{\theta }}-{\mathit{\theta }}_0\right)\stackrel{d}{\to }N\left(0,{\mathit{V}}_{2{\mathit{\theta }}_0}^{-1}{\mathit{V}}_{1{\mathit{\theta }}_0}{\mathit{V}}_{2{\mathit{\theta }}_0}^{-1}\right),$$

where ${\mathit{V}}_{1{\mathit{\theta }}_0}=E[\psi \left(y,x,{\mathit{\theta }}_0\right)\psi {\left(y,x,{\mathit{\theta }}_0\right)}^{\prime }]$, ${\mathit{V}}_{2{\mathit{\theta }}_0}={\left\{\partial E[\psi (y,\mathit{x},\mathit{\theta })]/\partial {\mathit{\theta }}^{\prime }\right\}|}_{\mathit{\theta }={\mathit{\theta }}_0}$, and ψ(y, x, θ) = ∂ ln[f(y|x;θ)]/∂θ.

Note, the proofs of Theorems 1 and 2 are standard, and simply involve verifying the conditions outlined by Huber (2009); for further discussion see the appendix. To establish these conditions, it is sufficient to assume that α₀ > 1. This assumption ensures the differentiability of the loss function depicted in (3), and though sufficient this assumption may not be necessary. It is worthwhile to note that the computation of the asymptotic covariance matrix in Theorem 2 depends on the unknown distribution of the errors, thus making a direct appeal to asymptotic based inference challenging; i.e., an additional step has to be undertaken in order to estimate the error distribution. This same challenge is commonly encountered in other existing techniques; e.g., quantile regression. Further, based on simulation studies (results not shown), it was ascertained that standard asymptotic based inference based on the result established in Theorem 2 may not be appropriate for relatively small sample sizes; e.g., when n = 200. Thus, it is suggested that bootstrapping be adopted for the purposes of conducting finite sample inference.

In what follows, the bootstrapping procedure implemented throughout the remainder of this article is briefly described. To begin, for a given data set (i.e., $\left(y_i,{\mathit{x}}_i^{\prime }\right)$, i = 1,…,n) the numerical algorithm described in Section 2.3 is used to obtain an estimate of the regression parameters. Using the regression coefficient estimates, one then computes the residuals $e_i=y_i-{\mathit{x}}_i^{\prime }\widehat{\beta }$, for i = 1,...,n. A random sample of size n is then drawn from the set of residuals, with replacement, providing the bootstrapped residuals $e_i^{*}$, for i = 1,...,n. The bootstrapped response is subsequently obtained via $y_i^{*}={\mathit{x}}_i^{\prime }\widehat{\beta }+e_i^{*}$, and the proposed approach is used to model this data (i.e., $\left(y_i^{*},{\mathit{x}}_i^{\prime }\right)$, i = 1,...,n) resulting in the bootstrapped estimate θ^∗. This process is repeated B times yielding B bootstrap replicates of the regression coefficients. The bootstrap replicates can then be used to construct standard error estimates in the usual fashion (Efron, 1982), and (1 − α)100% bootstrap confidence intervals using the empirical (α/2)100%th and (1−α/2)100%th percentiles of the bootstrap distribution.

4. Simulation study

In order to examine the finite sample performance of the proposed approach, the following Monte Carlo simulation study was conducted. This study considers a model of the form

$$y_i={\beta }_0+{\beta }_1{x}_i+{ϵ}_i,\text{for}i=1,\dots ,n,$$ (7)

where β₀ = 1, β₁ = 0.1, and x_i ∼ N(0,1). In order to illustrate the robustness property of the proposed estimator, several distributions of the error term _i are considered, both within and outside of the AEPD class. In particular, the investigations discussed herein consider the settings in which the error terms are distributed AEPD(0,2,σ,0.5), AEPD(0,1,σ,0.5), and AEPD(0,1.5,σ,0.25), with the two former specifications providing for standard normal and Laplacian errors, respectively, where the σ parameters were selected so that the variance of the error term is 1. For error distributions outside of the AEPD class, this study considers Student’s t-distribution with 3 degrees of freedom; a skewed normal distribution with a slant parameter of 4 (Azzalini, 1985); a skewed tdistribution with 3 degrees of freedom and a skewing parameter of 0.5 (Fernandez and Steel, 1998); a Chi-square distribution with 3 degrees of freedom; and a log-normal distribution with location and scale parameters being set to be 0 and 0.5, respectively. These choices provide for a broad spectrum of characteristics of the error distribution which are commonly encountered in practical applications; to include symmetry, heavy tails, and positive skewness. For each of the above error distributions, m = 500 independent data sets were generated, each consisting of n = 200 observations.

The proposed methodology denoted by AME (adaptive M-estimator) was implemented to analyze each of the simulated data sets, using the techniques outlined in Section 2 and 3. In order to provide a comparison between the proposed methodology and existing techniques, several competing procedures were also implemented. In particular, each data set was analyzed using LS, LAD, and ZQR. The two former techniques are staples among standard data analysis methods, while the latter can be viewed as a generalization of quantile regression which estimates the quantile of interest along with the rest of the model parameters, thus allowing the approach to “adapt” to the data. In order to estimate standard errors and to construct confidence intervals the standard techniques were used for LS, while bootstrapping techniques with B = 1000 were used for the proposed approach, LAD, and ZQR. It is worthwhile to point out that all of the aforementioned methods attempt to estimate the same slope coefficient (i.e., β₁) in the data generating model above; i.e., β₁ is the slope coefficient for the mean and all quantile functions. Thus, this study focuses solely on the results that were obtained from the proposed approach and the three competing techniques for the slope parameter.

Table 1 provides a summary of the estimators resulting from the proposed procedure, across all considered error distributions. In particular, this summary includes the empirical bias, the relative efficiency of the estimator (i.e., the average estimated standard error of the estimator divided by the average estimated standard error of the proposed estimator), empirical coverage probabilities associated with 95% confidence intervals, and average confidence interval length. From these results, one will notice that the proposed method performs very well; i.e., our estimator exhibits little if any evidence of bias and the empirical coverage probabilities appear to attain their nominal level.

Table 1:

Simulation results summarizing the estimates of the “slope” coefficient obtained by AME, LS, LAD, and ZQR, for both the AEPD and non-AEPD error distributions. This summary includes the average estimate minus the true value (Bias), relative efficiency (Eff), estimated coverage probability (Cov) associated with 95% confidence intervals, and averaged confidence interval length (AL). Here t₃ denotes Student’s t-distribution with 3 degrees of freedom; ${\chi }_3^2$ denotes a Chi-square distribution with 3 degrees of freedom; SN(4) denotes a skewed normal distribution with a slant parameter of 4; ST(3,0.5) for skewed t-distribution with 3 degrees of freedom and a skewing parameter of 0.5.

	N(0,1)				t3
	Bias	Eff	Cov	AL	Bias	Eff	Cov	AL
LS	0.0051	0.9741	0.960	0.2796	−0.0064	1.2331	0.954	0.4677
LAD	0.0037	1.2626	0.958	0.3598	−0.0036	1.0238	0.953	0.4042
ZQR	0.0037	1.2064	0.976	0.3765	−0.0028	1.0023	0.955	0.4174
AME	0.0053	1.0000	0.974	0.3104	−0.0023	1.0000	0.961	0.4238
	${\chi }_3^2$				Log-normal
LS	0.0053	2.3995	0.943	0.6811	−0.0017	1.4453	0.929	0.1665
LAD	−0.0016	2.5165	0.959	0.7644	−0.0028	1.4602	0.965	0.1814
ZQR	−0.0043	1.1525	0.977	0.4027	−0.0049	1.1287	0.963	0.1429
AME	−0.0030	1.0000	0.969	0.3426	−0.0032	1.0000	0.965	0.1276
	SN (4)				ST (3,0.5)
LS	−0.0014	1.0958	0.952	0.1768	−0.0224	2.0737	0.947	0.7030
LAD	−0.0020	1.4075	0.966	0.2276	−0.0081	1.4816	0.971	0.5871
ZQR	0.0004	1.2190	0.958	0.1988	−0.0066	1.0047	0.977	0.4375
AME	−0.0012	1.0000	0.942	0.1659	−0.0075	1.0000	0.979	0.4375
	Laplace				AEPD(0, 1.5, σ, 0.25)
LS	−0.0016	1.2904	0.942	0.2781	0.0037	1.3014	0.957	0.2780
LAD	−0.0028	0.9875	0.964	0.2347	0.0030	1.5021	0.979	0.3390
ZQR	−0.0042	0.9971	0.968	0.2434	0.0012	1.1321	0.973	0.2733
AME	−0.0044	1.0000	0.972	0.2562	0.0001	1.0000	0.965	0.2510

Table 1 also provides the same summary for the other three competing regression techniques. Unsurprisingly, the same conclusions discussed above can also be drawn for LS, LAD, and ZQR, but differences in performance are apparent. First, under normal (Laplacian) errors the most efficient procedure is LS (LAD), which can be ascertained by examining both the relative efficiency and the average confidence interval length. Note, this finding was expected since LS and LAD result in the MLE under normal and Laplacian errors, respectively. With that being said, one will also note that the estimators resulting from the proposed approach are almost as efficient as the most efficient estimator under normal and Laplacian errors, even though the proposed method is tasked to estimate two additional parameters in these settings. Second, for all other considered error distributions the proposed method provided for the most efficient estimator, with the exception of the setting in which the errors obey a Student’s t-distribution. In some cases the efficiency gains are substantial; e.g., under Chi-square errors the proposed estimator is twice as efficient when compared to the the LS and LAD estimators. In general, the proposed approach performed better in terms of estimation efficiency than LS, LAD, and ZQR when the error distribution was asymmetric. Moreover, the proposed approach surprisingly outperformed ZQR, which is the most comparable existing technique, in all considered settings. In summary, this simulation study illustrates that the proposed methodology provides reliable estimates across a broad spectrum of potential error distributions, and can provide for more efficient estimates when compared to existing regression methods. Moreover, these gains in estimation efficiency are more dramatic for asymmetric errordistributions.

4.1. Power of the hypothesis test

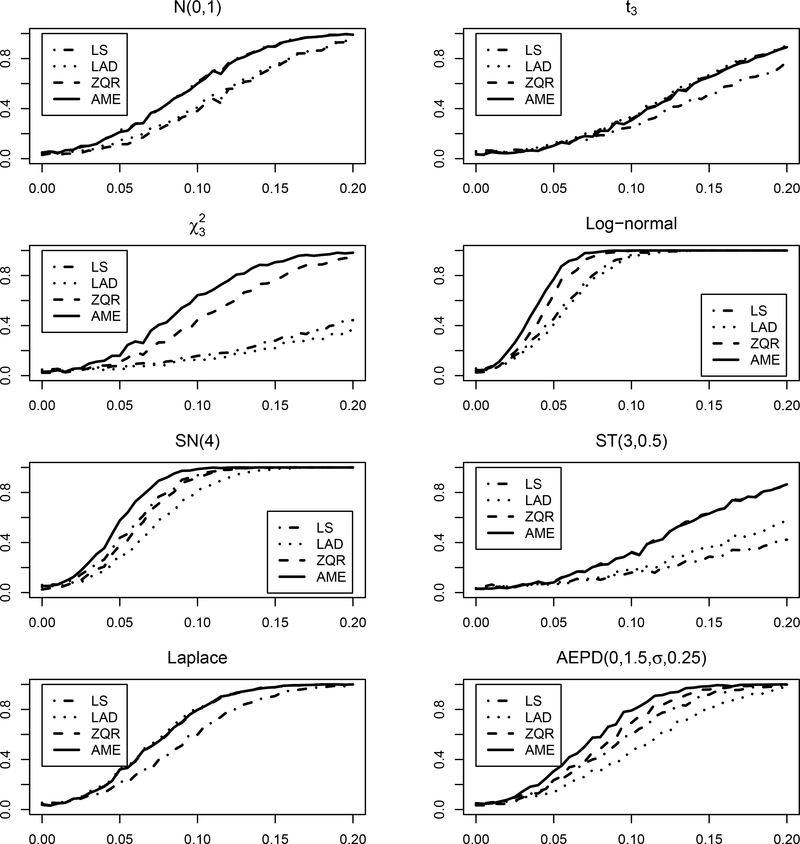
In order to investigate other inferential characteristics of the proposed approach, a power analysis was conducted to assess the performance of the proposed methodology when utilized to test H₀ : β₁ = 0 versus H₁ : β₁ ≠ 0, at the α = 0.05 significance level. Data for this study was generated in the exact same fashion as was described above with a few minor exceptions; i.e., here the slope coefficient is taken to be β₁ ∈ {0,0.005,...,0.2}, then for each error distribution and value of β₁, m = 1000 independent data sets are generated each consisting of n = 500 observations. Our approach along with LS, LAD, and ZQR were applied to each of the data sets and the results from these analyses were used to create 95% confidence intervals, as was described in the previous section. Decisions between the null and alternative hypothesis were made based on the confidence intervals in the usual fashion. These results were then used to construct power curves for each of the regression techniques, under each of the considered error distributions.

Figure 2 provides the empirical power curves for all four regression techniques across all considered error distributions. Again, as one should expect, in the case of Gaussian and Laplacian errors the methods with the most power are LS and LAD, respectively, but the power curve for the proposed approach is practically identical. In contrast, when the error distribution is not normal or Laplace, LS and LAD can suffer from a dramatic loss in power (e.g., Chi-square or skewed t errors) a feature which the proposed approach does not possess. In fact, for skewed distributions one will note that the proposed approach has the most power to detect departures from the null, under all considered configurations. In summary, the findings from this study reinforce the main findings discussed above; i.e., the proposed methodology provides for efficient estimation and reliable inference across a broad spectrum of error distributions.

Figure 2:

Empirical power curves obtained under AME, LS, LAD, and ZQR. Here t₃ denotes Student’s t-distribution with 3 degrees of freedom; ${\chi }_3^2$ denotes a Chi-square distribution with 3 degrees of freedom; SN(4) denotes a skewed normal distribution with a slant parameter of 4; ST(3,0.5) for skewed t-distribution with 3 degrees of freedom and a skewing parameter of 0.5.

5. Data applications

In this section the proposed M-estimator is used to analyze two data sets. These applications further illustrate the useful properties of the proposed regression methodology.

5.1. Blood pressure data

The National Health and Nutrition Examination Survey (NHANES) is a Center for Disease Control and Prevention program which was initiated to assess the general health of the populous in the United States. As a part of this study, data is collected from participants via questionnaires and various physical exams, to include laboratory testing. This information is subsequently made publicly available so that researchers may address/explore future medical, environmental, and public health issues that the United States, and more generally the world, may face. One such issue involves the significant number of adults who are affected by high blood pressure. In fact, the World Health Organization (World Health Organization; 2016) estimates that 22% of adults overs the age of 18 have abnormally high blood pressure, equating to approximately 1.2 billion afflicted individuals world wide. Individuals with chronic high blood pressure may develop further sequelae to include aneurysms, coronary artery disease, heart failure, strokes, dementia, kidney failure, etc. (Chobanian et al., 2003). Thus, developing a sound understanding of the relationship that exists between blood pressure and other risk factors is essential to public health.

To this end, the analysis considered herein examines blood pressure data collected on the participants of the NHANES study during the years of 2009–2010, and attempts to relate this response (diastolic blood pressure) to several different risk factors. In particular, the risk factors selected for this study include a binary variable (Food) indicating whether the participant had eaten within the last 30 minutes (with 1 indicating that they had, and 0 otherwise), the average number of cigarettes smoked per day during the past 30 days (Cigarette), the average number of alcoholic drinks consumed per day during the past 12 months (Alcohol), and the participants age (Age). This analysis assumes that a first order linear model is appropriate, and uses the proposed approach as well as LS, LAD, and ZQR to complete model fitting. These techniques were implemented in the exact same fashion as was described in Section 4. Table 2 reports the estimated regression coefficients as well as the corresponding standard errors obtained from this analysis.

Table 2:

Blood pressure data analysis: Estimated regression coefficients, their estimated standard errors in parenthesis, and the values of the model selection criteria AIC and BIC, resulting from AME, LS, LAD, and ZQR.

Estimate(SE)
Method	Food	Alcohol	Cigarette	Age	(AIC,BIC)
LS	−0.481(1.279)	0.452(0.157)	−0.001(0.069)	0.473(0.041)	(7066.61, 7095.06)
LAD	0.170(1.251)	0.430(0.170)	−0.024(0.057)	0.385(0.044)	(7028.93, 7057.37)
ZQR	1.429(1.451)	0.429(0.182)	0.000(0.051)	0.286(0.051)	(6985.03, 7018.22)
AME	0.675(1.170)	0.405(0.160)	0.004(0.047)	0.316(0.039)	(6962.68, 7000.61)

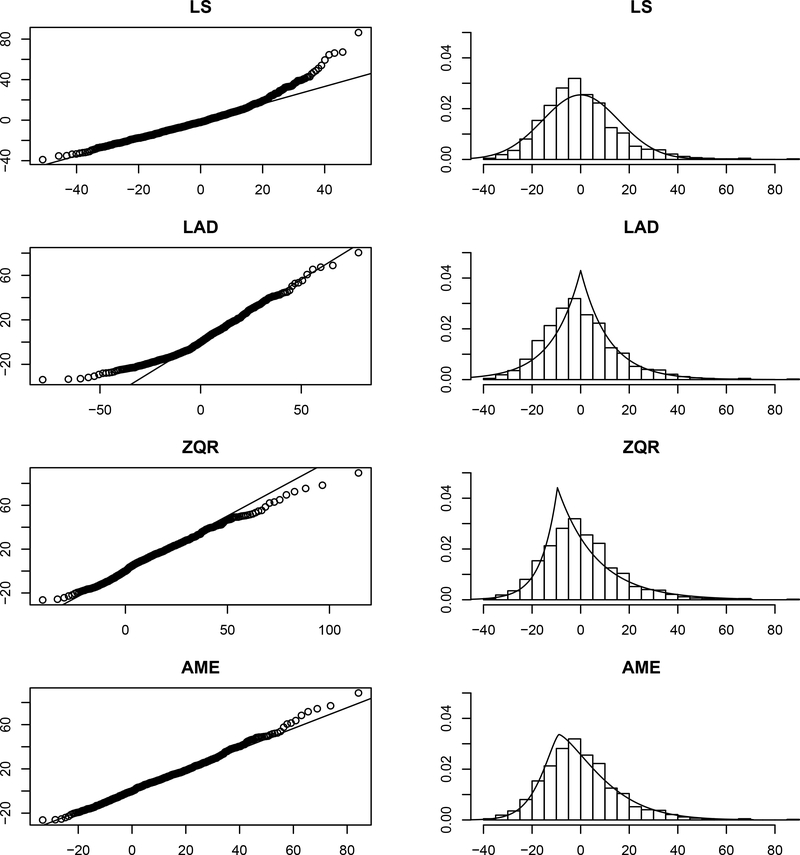
From the results presented in Table 2, one will note that the findings between the four regression methodologies are similar, but differences are apparent. In particular, this analysis finds that age and alcohol are significantly (positively) related to diastolic blood pressure, with the other two covariates being insignificant. The effect estimate associated with alcohol consumption is in agreement across all of the techniques, but the same cannot be said for the age effect. In particular, the proposed method actually renders an age effect estimate that is statistically different (or essentially) than the effect estimate which was obtained by LS. In contrast, the age effect estimates obtained by the proposed approach and ZQR are generally in agreement, this is likely attributable to the fact that both of these techniques are designed to adapt to the asymmetry of the data, which is present in this analysis; e.g., the proposed approach estimated the shape parameter to be $\widehat{\alpha }$ ≈ 1.4 and the skewness parameter to be $\widehat{\tau }$ ≈ 0.3, indicating that the error distribution has heavy tails and is right skewed. To further investigate this, Figure 3 provides QQ-plots and histograms of the residuals obtained under the four regression methodologies. From Figure 3 one would note that LS, LAD, and likely even ZQR would fail basic diagnostic checks. Further, when comparing the standard error estimates of the age effect one will also note that the proposed approach renders a smaller value when compared to LS, LAD and ZQR, which is not surprising given the results discussed in Section 4. Ultimately, in terms of choosing a “best” model fit in this scenario one could make use of the Akaike Information Criterion (AIC) or the Bayesian Information Criterion (BIC) to select between model fits, noting that the proposed approach holds the other 3 as special cases. Table 2 provides the values of these model selection criteria for all of the regression techniques, and one will note that both techniques unanimously select the model fit via the proposed approach. In summary, whether based on standard diagnostic procedures, estimator efficiency, or model selection criteria, the proposed approach appears to be the favorable technique for this application.

Figure 3:

QQ-plots and histogram of the residuals under AME, LS, LAD, and ZQR for the blood pressure dataset.

5.2. Miscarriage data

The Collaborative Perinatal Project (CPP) was a longitudinal study, conducted from 1957 to 1974, which was aimed at assessing multiple aspects of maternal and child health (Hardy, 2003). Even though this study was conducted half a century ago, the information collected still constitutes an important resource for biomedical research in many areas of perinatology and pediatrics. For example, in 2007 a nested case-control study which examined whether circulating levels of chemokines were related to miscarriage risk was conducted using (n = 745) stored serum samples collected as a part of the original CPP study, for further details see Whitcomb et al. (2007). In particular, this study focused on monocyte chemotactic protein-1 (MCP1), which is a cytokine that is located on chromosome 17 in the human genome and is believed to have a pregnancy regulatory function, for further details see Wood (1997). The cases (controls) in the study were participants who had (not) experienced a spontaneous miscarriage, and cases were matched with controls based on gestational age. In addition to the measured MCP1 levels, several other variables were collected on each participant; i.e., age, race (with 1 denoting Africa American, and 0 otherwise)), smoke (with 1 denoting that the participant had smoked before and 0 otherwise) and miscarriage status (with 1 denoting that miscarriage had been experienced, and 0 otherwise).

In this analysis, the measured MCP1 level is considered to be the response variable and all other variables are treated as covariates. A full linear model consisting of all first order terms, as well as all pairwise interactions, is assumed and best subset model selection is implemented using BIC as the criteria. The proposed approach was used to fit all possible models, including models where (α,τ) were set to be (2,0.5), (1,0.5), and (1,τ), which are equivalent to implementing LS, LAD, and ZQR, respectively. Model fitting was conducted in the exact same fashion as was described in Section 4. This process identified an intercept only model for LS, a model consisting of race as the only covariate for ZQR, and a first order model consisting of both age and race as covariates for LAD and AME, with BIC values of 431.28, −395.51, −822.02, and −937.55 for LS, LAD, ZQR, and AME, respectively. From these results, one will note that important relationships will potentially be missed when the appropriate regression methodology is not used. In particular, this study illustrates that the best model chosen under these existing procedures may differ from the best model chosen under the proposed approach. When one considers the model selection process described above, it would be natural to place more faith in the results that were obtained under the proposed approach. This assertion is based on two primary facts. First, the proposed procedure holds the other competing procedures as special cases, thus the analysis described above should be viewed as a much more in depth model selection process which evaluates whether it is more reasonable to view α and τ as being fixed (with known value) or as unknown parameters. Second, of the considered techniques the proposed procedure has the ability to more aptly adapt to the underlying error structure, and is therefore able to render a more reliable analysis.

6. Conclusions

This work has developed a general robust regression methodology, which was inspired by the asymmetric exponential power distribution. In particular, the proposed methodology is robust with respect to the underlying error structure, thus rendering reliable estimation and inference across a broad spectrum of error distributions, even in the case of heavy tails and/or asymmetry. This is made possible by the fact that the loss function is chosen in a data adaptive fashion, during the estimation process, thus capturing the shape and skewness of the underlying distribution of the errors. The asymptotic properties of the proposed estimator are established. Through an extensive Monte Carlo simulation study, the proposed approach was shown to perform as well if not better than several existing techniques. In particular, these studies show that the proposed method generally performs better than these existing techniques when the error distribution is heavy-tailed and/or skewed. The strengths of the proposed method were further exhibited through the analysis of two motivating data sets. To further disseminate this work, code (written in R) which implements the proposed methodology has been prepared and is available upon request.

A direction for future research, pointed out by an anonymous referee, could explore the development of a more general loss function, which could account for even more asymmetry in the error distribution. Similar to the proposed approach, this could be developed based on a very broad class of distributions, such as the extended AEPD distribution (Zhu and Zinde-Walsh, 2009). Although, initial investigations into this generalization showed little promise at providing more efficient estimation and was far more computationally complex when compared to the proposed approach.

Appendix

The regularity conditions under which consistency and asymptotic normality of the proposed Mestimator can be established are provided below.

A1: [(x_i, y_i),i = 1,...,n] is an i.i.d. sequence of random variables.

A2: The conditional cumulative distribution function of y|x is absolutely continuous and has a positive density denoted by f^∗(·|·).

A3: The parameter space Θ ⊂ Ξ ≡ {θ|α > 0,σ > 0,τ ∈ (0, 1),β_i ∈ ℝ,∀i} and is a compact set.

A4: There exists a unique θ₀ ∈ Θ such that E[ln f(y|x, θ)] is maximized and has nonsingular second derivative at θ₀.

A5: There exists a unique interior $\widehat{\mathit{\theta }}\in \mathrm{\Theta }$ such that ρ(θ) is differentiable at $\widehat{\mathit{\theta }}$ and $\Vert n^{-1}{\sum }_{i=1}^n\psi (y_i,{\mathit{x}}_i,\widehat{\mathit{\theta }})\Vert =o_p(n^{-1/2})$.

A6: There exists a δ such that $0<\delta <\underset{\_}{\alpha }-1,E\left(|ϵ{|}^{2\overline{\alpha }+4\delta }\right)<\infty$, and $E\left({\left|x_j\right|}^{2\overline{\alpha }+4\delta }\right)<\infty$, for j = 1,...,p, where $\underset{\_}{\alpha }$ and $\overline{\alpha }$ denote the infimum and supremum of the set of all α in Θ, respectively.

A7: ${\mathit{V}}_{1{\mathit{\theta }}_0}$ and ${\mathit{V}}_{2{\mathit{\theta }}_0}$ exist and are finite, ${\mathit{V}}_{1{\mathit{\theta }}_0}$ is positive definite, and ${\mathit{V}}_{2{\mathit{\theta }}_0}$ is invertible.

Conditions A1-A5 and A7 are common in the literature, see Huber (1967), Huber and Ronchetti (2009), Koenker (2005), and Bera et al. (2016). Condition A2 restricts the conditional distribution of the dependent variable and Condition A7 is assumed so that the asymptotic variance of the estimator exists and is finite. Condition A4 ensures identifiability and existence of a unique solution. Condition A5 is used to ensure that the derivative of the loss function evaluated at $\widehat{\mathit{\theta }}$ is “nearly zero”. Condition A6 restricts the absolute moments on the conditional distribution of y|x and each covariate x_j in order to ensure the asymptotic behavior of the proposed estimator.

The consistency and asymptotic normality of the proposed estimator are established by verifying the conditions in Huber and Ronchetti (2009) (page 127 for consistency and Theorem 6.6 as well as its corollary for normality). The arguments to verify these assumptions are similar to those in Zhu and Zinde-Walsh (2009) and Bera et al. (2016), and the details of these arguments are available from the corresponding author.