A continuous fiber distribution material model for human cervical tissue

Abstract

The uterine cervix during pregnancy is the vital mechanical barrier which resists compressive and tensile loads generated from a growing fetus. Premature cervical remodeling and softening is hypothesized to result in the shortening of the cervix, which is known to increase a woman’s risk of preterm birth. To understand the role of cervical material properties in preventing preterm birth, we derive a cervical material model based on previous mechanical, biochemical and histological experiments conducted on nonpregnant and pregnant human hysterectomy cervical tissue samples. In this study we present a three-dimensional fiber composite model that captures the equilibrium material behavior of the tissue in tension and compression. Cervical tissue is modeled as a fibrous composite material, where a single family of preferentially aligned and continuously distributed collagen fibers are embedded in a compressible neo-Hookean ground substance. The total stress in the collagen solid network is calculated by integrating the fiber stresses. The shape of the fiber distribution is described by an ellipsoid where semi-principal axis lengths are fit to optical coherence tomography measurements. The composite material model is fit to averaged mechanical testing data from uni-axial compression and tension experiments, and averaged material parameters are reported for nonpregnant and term pregnant human cervical tissue. The model is then evaluated by investigating the stress and strain state of a uniform thick-walled cylinder under a compressive stress with collagen fibers preferentially aligned in the circumferential direction. This material modeling framework for the equilibrium behavior of human cervical tissue serves as a basis to determine the role of preferentially-aligned cervical collagen fibers in preventing cervical deformation during pregnancy.

1. Introduction

During pregnancy, a closed firm cervix is required to maintain the developing fetus in utero. Towards the end of gestation, a normal cervix significantly deforms, dilates and shortens in preparation for delivery. An early onset of cervical shortening, hypothesized to be caused by premature cervical remodeling, is known to put pregnant patients at risk for preterm birth (PTB) (Iams et al., 2011). The true causes of preterm birth remain to be determined, but the mechanical failure of the cervix is a final common pathway for multiple etiologies (Gravett et al., 2010; Solomon and Iams, 2014). The overall research goal of our work is to quantify the mechanical environment of pregnancy and to determine how the cervix functions as a resistive barrier to prevent PTB. The objectives of this study are to present an equilibrium constitutive material model that captures the tension/compression nonlinearity of previously published uni-axial data of human cervical tissue samples (Myers et al., 2008, 2010) and to describe how to incorporate directionality and dispersion parameters measured by optical coherence tomography (OCT) (Gan et al., 2014) into this material model. The purpose of this paper is to report fiber composite material properties for human cervical tissue and initiate a starting point for a 3-dimensional material model that can capture the salient nonlinear features of the cervical material behavior while accounting for its collagen fiber directionality.

The in vivo 3-dimensional (3D) deformation and stress state of the cervix during pregnancy is complex due to patient-specific pelvic geometry, pelvic tissue material properties, passive and active external loading, and the contact and boundary conditions between organs (House et al., 2009, 2012, 2013; Mahmoud et al., 2013; Fernandez et al., 2015). The stress state of the cervix has been studied using CAD-based (House et al., 2012; Mahmoud et al., 2013) and patient-specific MRI-based (Fernandez et al., 2015) finite element models of the pregnant pelvis. Simulation results reveal that under a constant intrauterine pressure the stress state of the cervix is a combination of tension and compression (Fig. 1), where the magnitude and directionality of the principal stress and strain highly depend on the placement of the cervix within the pelvis, material characteristics of the cervix, and the interactions between the amniotic sac, the lower uterine segment, and the internal os (e.g. the opening of the cervix into the uterus) (House et al., 2012; Fernandez et al., 2015). Generally, there is a principal compressive stress in the longitudinal axis of the cervix, parallel to the inner canal, caused by the amniotic sac pushing on the internal os. This compressive stress translates into prominent tensile principal strains in the circumferential and radial directions. Taken together these forces cause the cervix to expand radially and shorten, similar to a thick-walled cylinder resisting a compressive axial stress.

Fig. 1.

Representative principal strain and stress directions depicted for a pregnant patient at 22 weeks of gestation. The intrauterine pressure of 8.6 kPa was applied to the inner surface of the fetal membranes, which are adhered to the lower uterine segment (Fernandez et al., 2015). The mechanical deformation state of the human cervix is a mix of tension and compression. Depending on the placement of the cervix within the pelvis, regions of the cervix experience a longitudinal compressive stress.

The collagen ultrastructure of the cervix plays a crucial role to withstand the circumferential, radial, and longitudinal stresses throughout the tissue. A traditional view of the preferred directionality of the collagen was elucidated by X-ray diffraction techniques by Aspden from an average of eight nonpregnant human cervices (Aspden, 1988). This view details three seamless zones of aligned collagen with an inner and outer zone of longitudinal fibers and a middle zone of circumferential fibers. Additionally, this study reports a level of dispersion around the main fiber direction. More recently, second harmonic generation (SHG) (Feltovich et al., 2012) and OCT data (Gan et al., 2014, 2015) of human cervical tissue specimens reveal a large band of circumferential fibers that extend to the outer radial edges of the cervix (Fig. 2A). From these ultrastructure studies, it is clear that the dense core of the cervix contains bands of collagen fibers circling the inner canal preventing circumferential dilation of the cervix. The width of this band of circumferential collagen and also the amount of dispersion for both nonpregnant and pregnant tissue are still under investigation. As we continue to elucidate these possible regions of preferentially-aligned collagen fibers, we develop here a material model that directly incorporates collagen fiber directionality and dispersion from OCT data (Gan et al., 2014).

Fig. 2.

Optical coherence tomography (OCT) fiber orientation maps and measurement locations for an axial slice of (A) a nonpregnant and (B) a pregnant human cervix (Gan et al., 2014). (C) A typical shape of the fiber distribution for a 1 mm 1 mm zone. (D) A planar ellipse fit to the fiber distribution shown in C. (E) An extrapolation and normalization (Eq. (7)) of the planar ellipse into a 3D ellipsoid where it is assumed that the minor radii are equal. (F) Thick-walled cylinder loading condition, with sliding boundary conditions on the bottom and stress-free conditions on the outer walls and inner canal.

A critical element to evaluating the mechanical loading pattern on the cervix during pregnancy is a micro-structurally inspired constitutive material model for cervical tissue that captures its material response to physiologically-relevant loading patterns. Previous mechanical testing data has found that the material response of human cervical tissue to loading is nonlinear, anisotropic, and time-dependent, where the overall material response for pregnant tissue is orders of magnitude less than nonpregnant tissue (Myers et al., 2008, 2010; Badir et al., 2013; Parra-Saavedra et al., 2011; Fernandez et al., 2013; Yao et al., 2014; Hee et al., 2014; Liao et al., 2014). In both the instantaneous and equilibrium response, one of the most important features of cervical material behavior is the non-linearity between the tension and compression stress response. Cervical tissue is much softer in compression than tension. This asymmetry is due in part to the collagen fiber network, where collagen fibers support loads when they are engaged in a tensile strain.

The goal of this modeling study is to determine the simplest form of a material constitutive equation that describes the salient tension/compression feature of the cervical tissue’s equilibrium stress response, after the transient visco- and poro-elastic effects have subsided. Additionally, the derivation considers the dominant features of the cervical extracellular matrix that are hypothesized to remodel and cause cervical softening during pregnancy, mainly the collagen fiber stiffness, directionality, and dispersion (Gan et al., 2014, 2015; Danforth, 1947, 1983; Read et al., 2007; Akins et al., 2010; Myers et al., 2009; Feltovich et al., 2010; Myers and Ateshian, 2014; Yoshida et al., 2014). We model cervical tissue as a fiber composite material where the stress in the tissue is balanced by a continuously-distributed collagen fiber network embedded in an isotropic compressible neo-Hookean ground substance (Lanir, 1983). The model contains a single family of preferentially oriented fibers, where the fibers are dispersed about the main direction described by an ellipsoidal orientation density function (Ateshian et al., 2009; Myers and Ateshian, 2014). Both directionality and dispersion are informed by OCT collagen fiber measurements of an axial slice of a nonpregnant and pregnant human cervical sample (Gan et al., 2014). We present the tension and compression uni-axial model fits to previously published data (Myers et al., 2008, 2010). We illustrate how the cervical collagen ultrastructure plays a role in preventing cervical deformation by investigating the compression of a thick-walled cylinder with circumferentially aligned fibers, which serves as a simplistic toy model for the stress state of the cervix experienced in vivo.

2. Methods

2.1. Equilibrium material model for human cervical tissue

A tissue material element of the cervix is modeled as a composite of a preferentially-aligned collagen network embedded within an isotropic, compressible neo-Hookean ground substance. Here we assume isothermal and equilibrium conditions, where the transient effects of the interstitial fluid pressurization and the intrinsic viscoelasticity of the collagen network have subsided. Additionally, in the initial form of this model we assume that the tissue does not actively contract and that the fixed charge density of the entangled glycosaminoglycans is sufficiently low that it does not contribute to the compressive material response of the tissue. The collagen fiber network has a single family of aligned fibers, where the directionality and dispersion are informed by a measure of the ultrastructure of collagen fibers (Gan et al., 2014). The collagen fibers are extensible, deform affinely with the ground substance, and in the current form of the model they do not interact with each other.

The total Cauchy stress σ^TOT for this equilibrium cervical material model is given by

$${\mathbf{\sigma }}^{\text{TOT}}=\frac{1}{J}\frac{\partial {\Psi }^{\text{TOT}}\left(\mathbf{F},{\widehat{\mathbf{a}}}_{\mathbf{o}},\frac{b}{a}\right)}{\partial \mathbf{F}}{(\mathbf{F})}^T,$$ (1)

where Ψ^TOT is the total Helmholtz free energy density of the continuously distributed collagen fiber composite, defined per unit reference volume. F is the deformation gradient given by a standard definition derived from the motion of the material from the reference to the deformed configuration, J = detF is the Jacobian, and â_o and b/a are the preferred direction of a single family of collagen fibers and a measure of the fiber dispersion (per Eq. (6)) in the reference configuration, respectively. This hyperelastic relation is derived from thermodynamic restrictions imposed by the axiom of entropy inequality (Holzapfel, 2000).

The total Helmholtz free energy density Ψ^TOT is the additive contribution from the fibrous collagen network Ψ^COL and the neo-Hookean ground substance Ψ^GS of non-collagenous ECM components, such as elastin, glycosaminoglycans, and other matricellular proteins, given by

$${\Psi }^{\text{TOT}}\left(\mathbf{F},{\widehat{\mathbf{a}}}_{\mathbf{o}},\frac{b}{a}\right)={\Psi }^{\text{GS}}(\mathbf{F})+{\Psi }^{\text{COL}}\left(\mathbf{F},{\widehat{\mathbf{a}}}_{\mathbf{o}},\frac{b}{a}\right).$$ (2)

The free energy density of the ground substance Ψ^GS is given by a standard isotropic, compressible neo-Hookean relation:

$${\Psi }^{GS}=\frac{\mu }{2}(I_1-3)-\mu \ln J+\frac{\lambda }{2}{(\ln J)}^2,$$ (3)

where I₁ = trC is the first invariant of the right Cauchy–Green tensor C = (F)^TF and μ and λ are the standard lamé constants. These lamé constants combine to form Young’s modulus and Poisson’s ratio of the ground substance E^GS = μ(3 + 2μ/λ)/(1 + μ/λ) and ν^GS = 1/2(1 + μ/λ), respectively.

The free energy density of the solid collagen network Ψ^COL is an orientation average of the free energy density of a single collagen fiber ${\Psi }_{\mathrm{n}}^{\text{COL}}(I_{\mathrm{n}})$ (Eq. (5)) weighted by an ellipsoidal distribution $D\left({\mathbf{n}}_o.\frac{b}{a}\right)$ (Eq. (6)) and is given by

$${\Psi }^{\text{COL}}\left(\mathbf{F},{\widehat{\mathbf{a}}}_{\mathbf{o}},\frac{b}{a}\right)={\displaystyle {\int }_0^{2\pi }{\displaystyle {\int }_0^{\pi }H(I_n-1){\Psi }_n^{\text{COL}}(I_n)D\left({\mathbf{n}}_{\mathbf{o}},\frac{b}{a}\right)\sin \varphi d\varphi d\theta ,}}$$ (4)

where n_o = cos θ sin ϕe₁ + sin θ sin ϕe₂ + cos ϕe₃ in a local Cartesian basis {e₁, e₂, e₃} with spherical coordinates θ, and ϕ and â_o defines the preferred directionality. I_n = n_o ·C ·n_o is the square of the fiber stretch, and H is the unit step function that enforces collagen fibers sustain only tension. The free energy density of a single fiber bundle ${\Psi }_n^{\text{COL}}$ (i.e. collection of crosslinked collagen fibrils) is constitutively prescribed to be

$${\Psi }_n^{\text{COL}}=\xi {(I_n-1)}^{\beta },$$ (5)

where ξ and β represent material properties of the collagen fiber bundle. ξ is the elastic modulus of the collagen fiber, with units of stress, and β is a unitless stiffening parameter giving the shape of tensile nonlinearity of the fiber. (An odd value of β is invalid if the unit step function H is not employed in Eq. (4).)

The distribution of the single family of preferentially aligned collagen fibers is described by an ellipsoidal fiber distribution (Fig. 2E), expressed in a local material element basis {e_i} using spherical coordinates:

$$D\left({\mathbf{n}}_{\mathbf{o}},\frac{b}{a}\right)={\left(\frac{{\cos }^2\theta {\sin }^2\varphi }{a^2}+\frac{{\sin }^2\theta {\sin }^2\varphi }{b^2}+\frac{{\cos }^2\varphi }{b^2}\right)}^{-1/2},$$ (6)

where [a, b] are the semi-axes of a planar ellipse fit (Fig. 2D) to the collagen fiber orientation distribution (Fig. 2C) normalized by

$$1={\displaystyle {\int }_0^{2\pi }{\displaystyle {\int }_0^{\pi }D\left({\mathbf{n}}_{\mathbf{o}},\frac{b}{a}\right)\sin }\varphi d\varphi d\theta .}$$ (7)

For the case of the cervix as a thick-walled cylinder, and based on our initial OCT fiber-tracking maps (Fig. 2A&B), ${\widehat{\mathbf{a}}}_{\mathbf{o}}$ aligns with the circumferential direction represented by the local coordinate e₁ (Fig. 2F). Considering, the OCT dispersion measurements are taken on the cervical plane perpendicular to the inner canal, we need to make an assumption regarding dispersion in the orthogonal plane. Therefore, we assume that the dispersion is equal in both orthogonal directions of the main fiber direction. In the case of the circumferential fibers the dispersion is in the longitudinal and radial directions, where the ratio b/a gives the amount of dispersion. When b/a is equal to 1 the fibers are evenly spread around a unit sphere, representing a case with no preferential direction in the reference configuration. When b/a tends towards 0, the fibers are highly aligned, representing a limiting case with no dispersion.

2.2. Collagen fiber ultrastructure characterization

We recently established a collagen fiber tracking protocol for human cervical tissue using optical coherence tomography (OCT) (Gan et al., 2014). In that work, we describe a methodology to numerically assemble multiple volume sets of OCT data to produce collagen fiber maps of axial cervical slices, and we demonstrate the methodology on specimens from one nonpregnant (age 40) and one pregnant (age 29, 36 weeks of gestation) patient who underwent a hysterectomy. Both samples were taken within 5 mm of the internal os. The OCT signal was conditioned based on a previously published algorithm for heart tissue (Fleming et al., 2008; Gan and Fleming, 2013) and optimized for cervical collagen (Gan et al., 2014).

In this paper, fiber orientation distributions (Fig. 2C) were extracted from the OCT data within 12 different 1 mm × 1 mm regions: 3 different radial zones in the anterior, posterior, left, and right of the axial slice (measurement locations indicated in Fig. 2A and B). Within each measurement location the prominent direction â_o was identified and the planar fiber dispersion was described by an ellipse (Eq. (6)), with ϕ = π/2 and θ representing the angle from the preferred direction. The ellipse parameters [a, b] were optimized using a nonlinear least squares optimization routine in Matlab (v 2013b) such that the equation described OCT dispersion data (Fig. 2D). To extrapolate to a 3D ellipsoid, both the minor axes of the ellipsoid were set equal to [b]. Lastly, the major [a] and minor [b] semi-principal axes were normalized under the condition in Eq. (7) (Fig. 2E).

2.3. Model fits to uni-axial mechanical testing data

To obtain averaged material parameters [E_GS. ν_GS. ξ, β] the proposed material model was fit to equilibrium compression and tension data of nonpregnant and pregnant human cervical tissue reported in two previously published studies (Myers et al., 2008, 2010). The detailed mechanical testing protocols were published in those reports. Briefly, tissue samples were acquired from nonpregnant and term pregnant hysterectomy patients of various obstetric backgrounds and ages. Uni-axial tension and compression samples were taken from axial slices that were cut perpendicular to the inner canal at various locations throughout the cervix. Tensile strips (~ 10 mm by 5 mm) (Myers et al., 2010) and compression cylindrical biopsies (~ Ø8 mm by 5 mm) (Myers et al., 2008) were cut exclusively from the dense mid-stromal region. All samples were tested in a hydrated environment in a series of ramp-hold tests. Equilibrium data were averaged here for all nonpregnant and pregnant samples after the transient material response has dissipated. The averaged data along with the range in the stress response are reported in Fig. 4. Because it was challenging to obtain whole cervices during pregnancy, there was only a single set of pregnant tensile data reported, and therefore a range of tensile behavior is not reported.

Fig. 4.

(A) Averaged tension and (B) compression equilibrium stress in response to uni-axial loading for nonpregnant tissue. (C) Averaged tension and (D) compression equilibrium stress in response to uni-axial loading for nonpregnant tissue. Material model fits are presented for the averaged data and the range when possible, and material parameters are reported in Table 1. The uni-axial tension and compression mechanical data are from Myers et al. (2008, 2010).

Best-fit material parameters for these data were found by informing the material model with the collagen directionality [â_o] and averaged dispersion [b/a] measured from our initial OCT results (Fig. 2 and Table 1). We assumed that the preliminary OCT data was representative of typical nonpregnant and pregnant collagen fiber orientation and dispersion. (This assumption will be tested as we collect more OCT data, and the limitations of this assumption are discussed below.) Therefore, since tension samples were mechanically tested with the loading axis aligned with the circumferential direction and compression samples were tested with the loading axis aligned with the longitudinal axis (i.e. the inner canal axis), models fits were done such that ${\widehat{\mathbf{a}}}_{\mathbf{o}}$ aligned accordingly. To get a first approximation of the material properties for the ground substance [E_GS. ν_GS], an analytical form of the material model with no fiber dispersion was fit to the tension and compression stress response data using a nonlinear least squares optimization routine in Matlab (v 2013b). Once these parameters were obtained from the simplified model, the full form of the model with the collagen dispersion was fit to the data using FEBio (v2.0, http://febio.org/), where the ellipsoidal fiber distribution model is numerically implemented and documented (Ateshian et al., 2009). In this last step of the fitting, the collagen fiber parameters [ξ, β] were optimized by inspection such that the model calculations matched the experimental data.

Table 1.

Material model fit parameters. [â_o and b/a] are measured from the OCT analysis of a nonpregnant (NP) and a pregnant (PG) cervical axial slice (Gan et al., 2014), where the average and range are reported for the 12 1 mm × 1 mm zones depicted in Fig. 2A and B. [E_GS. ν_GS. ξ, β] are the best-fit material model parameters, informed by the preliminary OCT data, and fit to uni-axial tension and compression mechanical data reported in Myers et al. (2008, 2010). The range reported for the material parameters ξ for the nonpregnant data represents the fits to the highest and lowest tensile stress response reported for the tissue. The range reported for the material parameters E_GS for the pregnant data represents the fits to the highest and lowest compression stress response reported for the tissue.

NP/PG	EGS [kPa]	νGS	ξ [kPa]	β	âo	$\frac{b}{a}$
NP	2	0.3	190 (40–460)	3	circum	0.77 (0.58–0.90)
PG	0.65 (0.50–0.80)	0.3	0.7	2	circum	0.84 (0.64–0.98)

2.4. Thick-walled cylinder investigation

The deformation patterns of a thick-walled cylinder under compressive loading were investigated to understand how changes in the material parameters, particularly the fiber ultrastructure, affect the ability of the structure to carry a load. This simplistic boundary value problem attempts to explore the contribution of material characteristics as opposed to the complex geometric factors present during pregnancy. The in vivo loading conditions of the cervix depend on many interacting geometric and material factors, including anatomical shape, tissue material properties, and contact between the organs. A review of these variables and the current state of pregnancy biomechanics is presented in a companion paper in this special issue (Myers et al., 2015).

A thick-walled cylinder was constructed within FEBio using dimensions measured from MRI data of a pregnant patient at 22 weeks of gestation as reported in Fernandez et al. (2015). The inner canal radius was 8 mm, the outer radius of the cervix was 28 mm, and the length was 38 mm. The model was meshed using 3510 8-node hexahedral elements, where each element was assigned the proposed ellipsoidal dispersion material model. The preferential direction of the collagen fibers [â_o] was aligned with the circumferential direction of the cylinder, with equal amounts of dispersion in the radial and longitudinal directions (Fig. 2F). A longitudinal 1 kPa compressive stress was applied to the top of the cylinder, with sliding boundary conditions on the bottom and stress-free conditions on the outer walls and inner canal (Fig. 2F). These boundary conditions attempt to mimic the stress pattern seen in the posterior part of the cervix in mid-pregnancy (Fig. 1). The longitudinal, radial, and circumferential strains within the cylinder were investigated as a function of cylinder fiber modulus ξ and fiber dispersion b/a, where the baseline material parameters for comparison were set equal to the averaged nonpregnant values reported in Table 1.

3. Results

3.1. Cervical collagen ultrastructure by OCT: directionality and dispersion

The detailed OCT methodology and analysis of cervical collagen directionality and dispersion are reported in Gan et al. (2014), and the preliminary results are used here to demonstrate how to incorporate the OCT data into the continuous fiber distribution material model. OCT fiber maps of axial slices of human cervix indicate a large band of circumferential collagens in nonpregnant (Fig. 2A) and pregnant (Fig. 2B) cervix, where the circumferential fibers exist as far as the outer radial edges of the cervix. Similar to the X-ray data, the collagen fibers are dispersed about the main fiber direction in both the nonpregnant and pregnant tissue (Fig. 3). Averaging the dispersion (b/a) data for 12 OCT measurement locations for each of the cervical slices from the internal os, the collagen fiber dispersion is higher in the pregnant tissue slice when compared to the nonpregnant tissue slice (Fig. 3 and Table 1). This result was not statistically significant, and there was also no statistically significant difference between collagen dispersion measured in the different radial zones (Student’s t-test, p > 0.05; two-tailed power=0.025 with p=0.05; Fig. 3). An increase in sample size is needed to conclude if collagen fiber dispersion changes throughout pregnancy and if there are distinct zones of fiber families in the human cervix.

Fig. 3.

Fiber dispersion b/a in the outer, middle, and inner zones for the nonpregnant and pregnant tissue axial slice. There is in an increase in dispersion for the pregnant tissue slice compared to the nonpregnant slice. There was no statistically significant difference in fiber dispersion between the zones for each slice.

3.2. Fiber composite model fit to uni-axial data

The proposed fiber composite material model, informed by the averaged OCT directionality and dispersion (Fig. 3), captured the uni-axial tension and compression equilibrium stress behavior of the cervical tissue (Fig. 4). The best-fit material properties for the averaged set of nonpregnant and pregnant data are given in Table 1. With a single set of material parameters, one each for the nonpregnant and the pregnant case, the material model describes the averaged tension and compression uni-axial stress response (Fig. 4). The total sums of the squared differences between model calculations and data (calculated in kPa) are 212 and 0.120 for the nonpregnant and the pregnant fit, respectively.

The range in the collagen fiber modulus ξ reported in Table 1 for the nonpregnant case captures the highest and lowest tensile stress response reported (Fig. 4A), while all other material parameters are kept to their averaged value. Changing ξ alone, however, does not sufficiently capture the highest compressive stress response for the nonpregnant tissue (Fig. 4B). The range in the material parameter E_GS reported in Table 1 for the pregnant case captures the highest and lowest compressive stress response (Fig. 4D), while all other material parameters are kept to their averaged value.

3.3. Compression of a thick-walled cylinder with circumferential fibers

For a thick-walled cylinder under a 1 kPa compressive longitudinal load, where â_o is aligned circumferentially, and with material properties as listed for nonpregnant tissue in, Table 1 the magnitude of radial strain (Fig. 5A) is larger than the circumferential strain (Fig. 5B). The collagen fiber modulus ξ influences the magnitude of the radial and circumferential strain experienced within the cylinder, but it does not influence the pattern of strain. The radial strain is mostly uniform throughout the thickness (< 3% change throughout thickness), whereas the circumferential strain is nonuniform. The radial strain ranges between 0.027 and 0.067, for the highest and lowest measured values of the collagen fiber modulus ξ, respectively. The corresponding circumferential strain is smallest at the inner canal (0.022–0.053) and is largest at the outer edge (0.025–0.060). As the fiber modulus ξ increases, and the overall behavior of the tissue gets stiffer, there is a protective effect of the collagen fibers to maintain the radius and thickness of the thick-walled structure under a constant load. Incremental improvements to this protective effect decreases as ξ continues to increase because of the nonlinear stiffening of the material behavior.

Fig. 5.

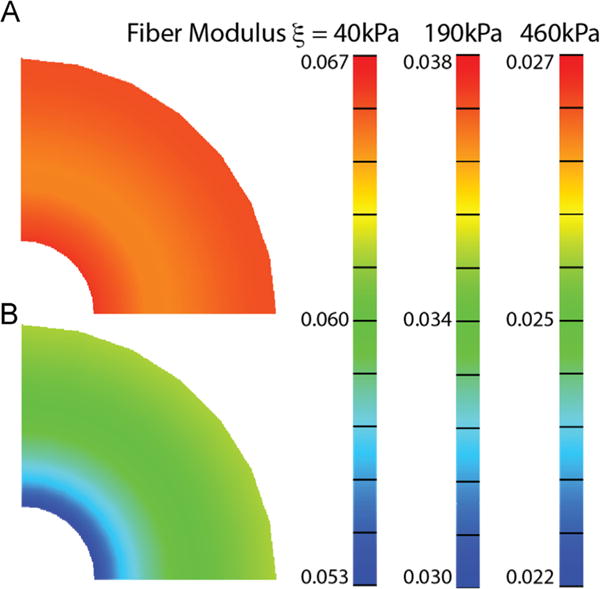
Effect of collagen fiber modulus ξ. An increase in ξ decreases the amount of radial and circumferential strain in a thick-walled cylinder that maintains a compressive stress of 1 kPa. The material properties used for this simulation are listed for the nonpregnant tissue in Table 1, where the range represents the material model fit to the highest and lowest tensile stress response measured for nonpregnant human cervical tissue (Myers et al., 2010).

Preferentially-aligned fibers in the circumferential direction help maintain the radius of a thick-walled cylinder under a constant compressive load (Fig. 6). Decreasing the dispersion such that the collagen fibers become more circumferentially aligned causes a reduction to the circumferential strain and an increase in the radial strain. In other words, the pattern of circumferential strain evolves with decreasing fiber dispersion, where an increase in anisotropy creates regions of reduced strain closer to the inner canal. There is an approximately 30% reduction in circumferential strain at the inner canal if all of the collagen fibers within the cylinder have the lowest measured dispersion in the nonpregnant tissue (b/a=0.58) as compared to a cylinder with the randomly distributed fibers (b/a = 1). The level of radial strain, which tends to change the cylinder thickness, only increases by 3% for this level of alignment (b/a=0.58).

Fig. 6.

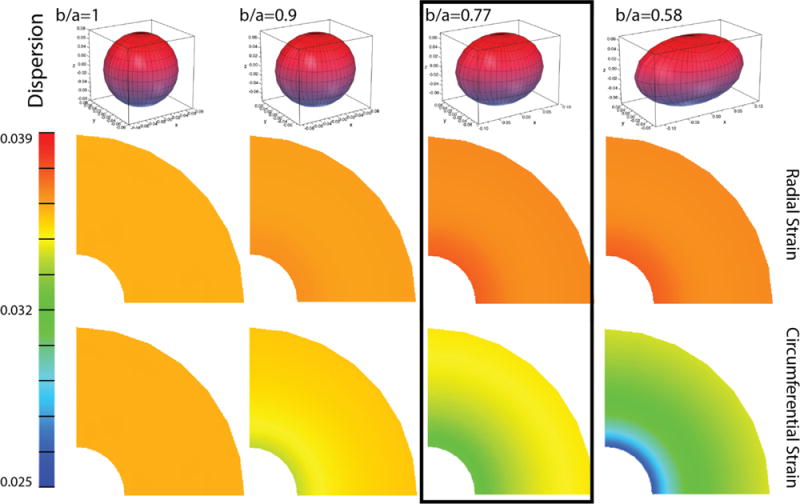
Effect of collagen fiber dispersion b/a. A decrease in collagen fiber dispersion, corresponding to an increase in circumferential fiber alignment, increases the amount of radial strain and decreases the amount of circumferential strain in a thick-walled cylinder that maintains a compressive stress of 1 kPa. The material properties used for this simulation are listed for the nonpregnant tissue in Table 1, where the range in dispersion represents the range in dispersion measured for a nonpregnant sample (Gan et al., 2014). The results indicated in the box represent the average material characteristics for nonpregnant tissue.

4. Discussion

Collagen fiber ultrastructure is a key component to the mechanical function of the human cervix during pregnancy. As such, we present a 3D constitutive material model for human cervical tissue that captures its material response to physiologically-relevant loading patterns and is equipped with ultrastructural parameters that describe cervical softening during pregnancy. Experimental uni-axial compression and tension tests reveal that the stress response of the tissue in tension is much higher than in compression and that pregnant tissue is considerably softer than nonpregnant tissue (Myers et al., 2008, 2010), and imaging data of the cervical stroma reveal zones of preferentially-aligned collagen fibers with a level of dispersion (Gan et al., 2014, 2015; Aspden, 1988). To describe these known material characteristics of the cervical tissue, we develop here a fiber composite material model with a continuously distributed fiber network, where changes to the collagen fiber stiffness capture the drastic softening that occurs during pregnancy (Fig. 4).

During pregnancy there is a drastic softening that must occur within the cervical tissue to accommodate the delivery of the baby (see cervical mechanics review in this special issue Myers et al., 2015). This softening is accomplished through a complex biochemical cascade of events that remodel the ECM components of the tissue (Read et al., 2007; Word et al., 2007; Holt et al., 2011). Our initial evidence from collagen ultrastructure imaging suggests that the overall preferential direction of the collagen fibers remains in the circumferential direction, but the level of dispersion increases (Gan et al., 2014). This increase in dispersion alone cannot capture the substantial softening that occurs during pregnancy. To capture the difference in the nonpregnant and pregnant material stress response the collagen fiber ξ modulus must be reduced by approximately two orders of magnitude (from an average of 190 to 0.7 kPa). Therefore, we hypothesize that this reduction for the individual fiber component indicates that along with changes to the collagen ultrastructure, the collagen must intrinsically remodel to accommodate such a level of cervical softening. Evidence of this collagen remodeling has been found in human and mouse tissue. Previous studies by our group have shown that the amount of collagen content does not significantly change in pregnancy, in both human (Myers et al., 2009) and mouse tissue (Yoshida et al., 2014). Instead tissue solubility increases in human pregnant tissue, indicating a reduction in collagen crosslinking (Myers et al., 2009). In mouse tissue we found evidence of a drastic decline in the total mature crosslink density (moles of pyridinoline and deoxypyridinoline normalized by moles of collagen) in day 15 pregnant tissue compared to day 6 pregnant tissue, of a 19 day mouse gestational period (Yoshida et al., 2014). To prove our hypothesis, we are currently measuring the collagen crosslinking density in nonpregnant (Zork et al., 2014) and pregnant human cervical tissue.

The nonlinearity in the tension/compression stress response is typical for soft hydrated tissues with a collagen fiber network, where collagen fibers provide resistance to tension and any preferential alignment will give added deformation resistance. In the case of the cervix, the collagen fibers have a preferred circumferential orientation with a level of dispersion, as viewed by X-ray diffraction (Aspden, 1988) and OCT (Gan et al., 2014, 2015) investigations. This collagen ultrastructure plays a key role in maintaining the mechanical function of the cervix during pregnancy. In the first form of the model, we ignore the transient material response of the tissue to investigate the contribution of fiber stiffness, fiber directionality, and dispersion. We demonstrate this mechanical function here using a thick-walled cylinder under a compressive load and in patient-specific finite element models presented in Fernandez et al. (2015).

For the case of the thick-walled cylinder, the circumferential collagen fibers reduce the amount of circumferential strain, where decreasing levels of dispersion increase this resistance to changes in the radius. We hypothesize that this added resistance to the circumferential strain is a protective feature of the cervix preventing dilation and over-stretching of interspersed cells that may control cervical remodeling. Additionally, the level of fiber distribution and dispersion aids in deformation resistance in directions that are not aligned with the main fiber family. This dispersion plays an important role in resisting deformation for the non-uniform and asymmetric loading found in the physiologic-loading scenario, where the geometry of the anatomy and the placement of the cervix within the pelvis drives patient-specific patterns of cervical stress and strain (Fernandez et al., 2015). A previous study, by Liao et al., details a three-fiber family model (with no dispersion) to describe the cervical collagen ultrastructure (Liao et al., 2014), using a modeling method common in arterial wall mechanics (Gasser et al., 2006). This material model does a good job of capturing the mechanical response of the cervical tissue to inflation of the inner canal (Liao et al., 2014). However, it is unknown if this type of three-fiber family model can capture the tension/compression behavior seen in the in-vivo loading scenario. A full comparison of all cervical material models is given in a cervical mechanics review presented this special issue (Myers et al., 2015).

Obtaining and testing human cervical tissue is a challenge, especially for pregnant tissue specimens. In this modeling study we made simplifying assumptions based on the available data sets for human cervical tissue to establish a framework to study the cervical collagen ultrastructure. These assumptions create limitations, where components of our model need to be validated and extended. First, the OCT, tensile, and compression data were not conducted on the same cervical tissue. Here, we use initial imaging data results coupled with a database of averaged stress responses from previous studies. Second, previous mechanical tests reveal that the material response of human cervical tissue is time-dependent, with stress-relaxation and hysteresis measured during ramp-hold and load-unload tests (Myers et al., 2008, 2010; Yao et al., 2014). The next iteration of our model will account for this viscoelastic, and possible poroelastic behavior (Fernandez et al., 2013), by extending a previously explored one-dimensional nonlinear viscoelastic model (Myers et al., 2010) to 3D. Third, we have not mechanically tested human cervical tissue in tension in multiple anatomical directions and we have not taken compression tests to high levels of strain in which fiber directionality influences the results. We are currently conducting additional mechanical tests to validate if this fiber dispersion model can predict tissue behavior in multiple anatomical directions. Lastly, the thick-walled cylinder is modeled as being homogeneous with even levels of dispersion and directionality throughout the radius. Here we do not account for the possibility of additional families of fibers directed longitudinally. The heterogeneity of tissue characteristics and its effect on how the cervix maintain a mechanical load will be a topic of another study.

5. Conclusion

Here we present a necessary framework for a 3D equilibrium material model that accounts for the collagen fiber ultrastructure of the tissue. Equipping the material model with features of the collagen network allows us to explore the influence of individual collagen fiber properties and network organization to the overall mechanical response of the tissue. As we continue to collect and mechanically test cervical tissue specimens, we will add deformation mechanisms to the constitutive model as needed to describe the deformation as a result of physiologically-relevant loading scenarios and to describe the remodeling process of the cervix in pregnancy. In this study, we show that a continuously-distributed fiber network embedded in a compressible ground substance can represent the stress response of the tissue to uni-axial loading, and we demonstrate that the collagen directionality and dispersion play a role in resisting physiological relevant deformation during pregnancy.