Abstract
We introduce a modeling approach for characterizing heterogeneity in healthcare utilization using massive medical claims data. We first translate the medical claims observed for a large study population and across five years into individual-level discrete events of care called utilization sequences. We model the utilization sequences using an exponential proportional hazards mixture model to capture heterogeneous behaviors in patients’ healthcare utilization. The objective is to cluster patients according to their longitudinal utilization behaviors and to determine the main drivers of variation in healthcare utilization while controlling for the demographic, geographic, and health characteristics of the patients. Due to the computational infeasibility of fitting a parametric proportional hazards model for high-dimensional, large sample size data we use an iterative one-step procedure to estimate the model parameters and impute the cluster membership. The approach is used to draw inferences on utilization behaviors of children in the Medicaid system with persistent asthma across six states. We conclude with policy implications for targeted interventions to improve adherence to recommended care practices for pediatric asthma.
Keywords: Healthcare Utilization, Latent Variable Model, Pediatric Asthma, Proportional Hazards Model, Survival Analysis, Medicaid system
1. Introduction
Appropriate utilization of the healthcare system is a positive tenet in preempting severe health outcomes and is the basis for more effective healthcare practices (Chang et al. 2014; McGrady and Hommel 2013; Piecoro et al. 2001). A well-managed health condition and adherence to recommended care practices typically result in reduced use of the emergency room (ER) and hospitalizations, thus leading to better health outcomes and less costly care for patients with chronic diseases (McGrady and Hommel 2013). Characterizing utilization behaviors and studying the drivers of variations in healthcare utilization can suggest targeted interventions for improving chronic disease management.
Understanding and managing healthcare utilization is now possible with the advent of individual-detailed health records and claims data, available from healthcare providers, and public or private insurers. The largest insurer in the United States, the Centers for Medicare and Medicaid Services (CMS), has provided a platform for acquiring such data in a standardized format across all states. Typically, CMS claims data include not only healthcare services information such as the type and place of care, services provided, diagnosis and procedure codes but also individual-specific information such as demographics for more than 100 million patients.
The CMS Medicaid claims data are only available as identifiable patient health information divided into multiple files depending on the healthcare services provided, by year and by state. The patient identification is unique across all files allowing researchers to trace patients longitudinally. Thus, in order to characterize longitudinal healthcare utilization at the individual level, the Medicaid claims data need to be mapped into longitudinal sequences of care events, referring to visits to different provider types including physician office, emergency department and hospitalization, and to (re) filling medication prescriptions. After this initial translational process, statistical modeling can be applied to make inference on the heterogeneity in healthcare utilization.
In this study, we seek to make inferences on healthcare utilization for Medicaid-enrolled children diagnosed with persistent asthma across six states, including five southeast states, Georgia, Louisiana, Mississippi, North Carolina and Tennessee with comparison to Minnesota. Medicaid-eligible children typically belong to disadvantaged socioeconomic groups and are, therefore, more likely to utilize the healthcare system disparately (Pylypchuk and Sarpong 2013). We focus on asthma as it is the most prevalent respiratory chronic condition for children (Department of Health and Human Services, Centers for Disease Prevention and Control 2012). The study population includes more than 400,000 children with approximately 6 million asthma events. The utilization sequences are complemented by child characteristics including demographics, enrollment characteristics, urbanization environment of their residence, spatial access to primary care (Gentili et al. 2015) and clinical risk group (CRG) derived using the 3M Clinical Risk Grouping Software among others. Substantive computational challenges arise in deriving inferences from such highdimensional, massive datasets within a restrictive data environment in place for identifiable protected health information (PHI).
Healthcare utilization has been a topic of interest for many healthcare studies, where most studies explain the frequency of utilization with respect to patient characteristics and other determinants of utilization for various conditions, typically relying on statistical methods such as regression or general linear models, see Bahler et al. 2015; Grosse et al. 2013; Huber et al. 2013; Roebuck et al. 2011; Ross et al. 2010 among many others.
The motivating application has several challenging characteristics. Utilization data derived from medical claims are subject to data censoring, referring to missed events when a patient may not be eligible for Medicaid benefits or events occurring outside the study time period. The second limitation is the presence of the effects of event types on the prevalence of other event types. Moreover, each patient potentially has re-current events over the time period of interest. Thus, we have a competing-risks, repeated-events framework. A third limitation involves incorporating demographic and health-related covariates into the model.
To address these limitations, we will combine techniques from survival analysis and statistical clustering analysis to measure the rate at which patients in the study population receive treatment for asthma from various types of care. A central theme in survival analysis is that of handling censored data. Cox’s proportional hazards model allows for the inclusion of possibly censored survival times in the likelihood function while also incorporating knowledge on characteristics of the patient. In this study, we will fit a parametric proportional hazards model to find the rate at which pediatric asthma patients visit different provider types given variables such as access to care, their current overall health condition, demographic variables, differences in state-based Medicaid programs, and history of healthcare utilization. We assume a mixture of proportional hazard models to capture heterogeneity in utilization behaviors. Using this model, we will derive three primary outputs from which we aim to determine the main contributors to variations in healthcare utilization: the posterior probabilities that a patient belongs to a specific cluster of patients given a set of control variables and utilization history, estimated effects of control covariates on the event hazard rates, and parameter estimates for the explanatory variables used to evaluate the impact of potential interventions on the rate of healthcare visits.
This method was inspired by the complexity of the healthcare data set that we study and has roots in the survival analysis literature, particularly an adaptation of the Cox model to parametric counting process data (Borgan 1984) and models for heterogeneity in discrete choice models and survival analysis (Blossfeld and Hamerle 1992; Browning and Carro 2010; Dunn et al. 1987; Greene and Hensher 2003; Heckman and Borjas 1980; Heckman 1981; Reader 1993; Vaupel and Yashin 1985). Two areas that are closely related to the proposed methodology are those of determining ‘long-term’ survivors in a cohort (Farewell 1982; Kuk and Chen 1992; McLachlan and McGiffin 1994; Sy and Taylor 2000) as well as the use of the multivariate Weibull mixture model to capture heterogeneity in duration data (Bucar et al. 2004; Farcomeni and Nardi 2010; Mair and Hudec 2009; Mosler 2003; Mosler and Scheicher 2008; Mosler and Seidel 2001; Nagode and Fajdiga 2000). We look to extend the contributions of these authors by generalizing the proportional hazards cure model to allow for different rates for multiple (more than two) subpopulations. Furthermore, while mixture modelling is prevalent in the literature, few authors incorporate explanatory and/or controlling factors, see Bucar et al. 2004; Mair and Hudec 2009; Nagode and Fajdiga 2000. By bringing the computational feasibility of the estimation algorithm to bear, we can analyze massive, high-dimensional datasets. This is a promising contribution in light of the exponential growth of healthcare data (EMC Corporation 2014) and demonstrates the ability to apply these methods to high-dimensional counting process data.
The remaining structure of the paper is as follows: in Section 2 we further summarize the target population and the covariates we include in this study, in Section 3 we present the model and model estimation techniques, in Section 4 we present results from our application to pediatric asthma, and we conclude with a discussion in Section 5. We provide additional derivations and details on the results for the motivating case study in the Supplemental Materials.
2. Data
We begin by translating the Medicaid Analytic Extract (MAX) claims data into individual- level utilization data. Our study population consists of all Medicaid-enrolled children ages 4–18 with persistent asthma (Wakefield and Cloutier 2006) from Georgia (GA), Louisiana (LA), Mississippi (MS), Minnesota (MN), North Carolina (NC), and Tennessee (TN) between 2005 and 2009. Children age 0–3 are not included in the study due to inconsistency in asthma diagnosis at this age. We only include children with persistent asthma, that is, children that have at least one emergency room visit or hospitalization with a diagnosis of asthma, at least three outpatient visits with a diagnosis of asthma, or a prescription fill for asthma controller medications. In total we have 426,400 patients, approximately 4 million healthcare events. Tables 1–3 in Supplemental Material A provide summary statistics.
To specify the provider type, we use a combination of Place of Service Code and Type of Service Code from the MAX data files. We abbreviate the provider types in the following manner: clinic visits (CL), emergency room and outpatient hospitalizations (ER), inpatient hospitalizations (HO), physician’s office visits (PO), and nurse practitioner care in a physician’s office (NP). In addition, we model a claim where a patient visits the pharmacy to fill a prescription for asthma controller medication (RX) as a unique event type.
We also extract demographic, zip code, and health-related information such as age, Medicaid eligibility status and health condition or clinical risk group (CRG) derived using the 3M Core Grouping Software (version 2014.3.2 with the Clinical Risk Groups version 1.12) from the MAX data. Using the zip code of the child, we include additional variables such as the state of residence, urbanization level of a child’s residence zip code derived using the RUCA categorization (Morrill et al. 2005) and travel distance to pediatric primary care derived using optimization models (Gentili et al. 2015). We only consider access to primary care since it is the most prevalent non-emergency care type for Medicaid-insured children diagnosed with asthma.
We divide the covariates into two groups: control and explanatory. The control variables are patient-specific information used to account for the bias in the individual-level healthcare utilization. We include such variables to adjust for their confounding effect on the relationship between utilization patterns and explanatory variables. More specifically, the control variables in this study are: age group (4–5, 6–14, 15–17), race (white, black, and other), overall health condition of the child (healthy: CRG 1, minor chronic: CRG 2–4, chronic: CRG 5–7, and severe: CRG 8–9, determined by the 3M software), reason for Medicaid eligibility (disabled, foster care and income-based) and the last event type to account for the child’s healthcare history.
The explanatory variables are those that are assumed to be association with healthcare utilization patterns. The explanatory variables in this study include the state of residence of the child, urbanicity categorized as urban (RUCA 1–3), suburban (RUCA 4–6) and rural (RUCA 7–10) and travel distance to pediatric primary care.
A summary of the observed vectors of data is given below. Throughout this paper bold typeface will be used for vectors and matrices.
Hr(t) = {hr1 (t), . . . , hrS(t)} the count of visits for each child r to providers of type s ϵ {1, . . . , S} over the time t. In our study, we consider S = 6 event types (CL, ER, HO, PO, NP, and RX). H contains all counting processes for all children.
• dr and er are row vectors of observed covariates corresponding to the control and explanatory variables, respectively. D and E contain all covariates for all children.
3. The Proportional Hazards Mixture Model
In this section we first motivate the use of survival analysis for this particular problem. We then introduce the mixture model formulation and demonstrate the use of the expectation- maximization (EM) algorithm to estimate the model parameters. Finally, we present a computationally efficient, iterative algorithm to estimate the proportional hazard and utilization-choice model parameters, which applies to high-dimensional, large sample size data.
3.1. The Proportional Hazards Model
Consider a counting process N(t) counting the number of events up to time t. Then Aalen (1978) and Andersen and Gill (1982) show that N(t) has a random hazard process λ(t) defined as
| (1) |
where T is a random variable for the time of the event. Let f(t) be the probability density function for an event at time t and S(t) be the survival function up to time t. Then we can relate the three functions with the following formula: f (t) = λ(t)S(t).
The Cox regression model (Cox 1992) specifies the hazard rate given a set of time varying covariates x(t) via the equation
| (2) |
where λ0 is a fixed underlying baseline hazard function. This model is typically referred to as the ‘proportional-hazards’ model due to the fact that the hazard rate of an event at time t for different subpopulations are proportional to each other.
Our model of the hazard rate for an event of type s can be written as
| (3) |
where βs = [β0s, β1s, . . . , βPs]. Thus, the baseline hazard function is λ0 = exp(β0). Furthermore, the vector dr may vary with time because it includes dummy variables for the last event type as well as the health status of the patient which may change annually. It is important to note that this differs from a competing risk model in that the time to event of type r is reset to 0 only when an event of type r occurs. The effect of other events are captured by a dummy variable for the last event type in the full model specification.
| (4) |
| (5) |
Generally, the model provides probabilistic insights on the gap time (called interarrival time) between events, under the assumption that the hazard rates are allowed to depend on previous event types in a Markov manner. Specifically, the clock for an event type does not reset until that particular event occurs again, and an event gap may span multiple years. The dependence on previous events is not only on individual event type, but also on other event types.
A Word on the Time Domain: In this paper we are interested in the time-to-event data and the effect of historical and demographic information on the times between events of the same type. We will denote the standard time domain with t and the time since the last event or re-enrollment time as τ. Changes from enrolled to unenrolled are considered to be censored lifetimes. See Supplemental Material B for an example.
3.1.1. Choice of Baseline Hazard Function
In the field of survival analysis there are two primary choices for the baseline hazard model: a nonparametric baseline hazard function and a parametric baseline hazard function such as the exponential, Weibull or log-logistic, for instance. We choose a parametric baseline because we must force the baseline hazard function to be unimodal, otherwise heterogeneous subpopulations may be incorrectly grouped together. We chose the exponential for the interarrival times distribution because of the analytic properties of the exponential survival model, resulting in computational efficiency and and simple computation on interarrival rates for different control variable combinations. This model assumption also holds for the motivating application (see Supplemental Materials H). Extensions to other distributions such as the Weibull distribution will not benefit from this computational efficiency hence other computational approaches, such as distributed computing, could be considered in the context of high-dimensional, large sample data.
3.2. The Mixture Model
The problem we are trying to solve is that of clustering similar patients based on their utilization patterns, estimating the coefficients corresponding to the control variables, and determining the factors that explain the variations in longitudinal utilization behaviors. Let zr be a multinomial random variable denoting the latent cluster membership of patient r taking values 0 and 1, where zrk = 1 if patient r belongs to cluster k. Given that zrk = 1 the likelihood contributed by each patient history is
| (6) |
where Tlr is the lth interarrival time between consecutive events, censoring, or re-enrollment times for patient r, and δs(τ) is an indicator function taking value 1 if patient r visits provider type s at time τ and 0 otherwise.
Following the cure model of Farewell (1982), Kuk and Chen (1992), McLachlan and McGiffin (1994), and Sy and Taylor (2000), we want to model the probability that patient r belongs to cluster k given the explanatory variables er. (For the purposes of the study we assume patients do not move.) Let zrk|er be a multinomial random variable denoting the latent cluster membership of patient r with explanatory variables er. We assume that the probability that zrk|er = 1 follows a multinomial logistic regression model:
| (7) |
and
| (8) |
Combining Equations 6 and 7, we can derive the likelihood function for b and β as
| (9) |
This model controls for the effects of the control covariates, dr, and allows the cluster- specific baseline hazard of an event to vary while explaining the causes of variations due to the explanatory variables er.
The optimal number of clusters can be selected based on the resulting likelihood, AIC or BIC derived from the estimated model. Specifically, the mixture model is estimated for different number of clusters and we select the model with the highest likelihood/AIC/BIC. The selected model using this classic approach can be complemented by additional user input on re-clustering based on insights on whether there is redundancy or overlap among the identified clusters.
3.3. The EM Algorithm
Together [Z, H, D, E], where Z = [z1,..., zR], form the complete information on a patient’s utilization history. However, Z is unknown and must be inferred from [H, D, E]. We will use the EM algorithm (Dempster et al. 1977) to estimate the probability that patient r belongs to cluster k, Pr(Zrk = 1), for all r, k.
Under the framework of complete information we can revise Equation 9 to get the complete likelihood function:
| (10) |
| (11) |
Due to the fact that the complete likelihood function can be split between a likelihood for b and β we can divide the model estimation procedures into three parts: estimating the probability that patient r belongs to cluster k (E-step), and estimating separately the proportional hazards coefficients and the multinomial logistic coefficients (M-step).
3.3.1. The E-Step
In the E-step we find the expected values of the missing values Z with respect to the distribution given the current estimates for the model parameters, b(m) and β(m):
| (12) |
| (13) |
After performing the E-step we take the current estimates, Z(m+1), and use them to calculate the next step estimates for the parameters in the proportional hazards and multinomial logistic regression model.
3.3.2. The M-Step
Assuming that the probability distribution of events follows an exponential distribution we have that where Then the total likelihood function for all patients, LC(β), can be written as
| (14) |
| (15) |
where the equality holds in the second line because for zr only one entry is equal to one and all others are zero. Now, set where Recall that βs are common across all clusters k ϵ {1, . . . , K}. Then the complete log likelihood function can be written as:
| (16) |
Before moving onto the iterative procedure for estimating β and b we must perform some derivations first on the complete likelihood function for b, following the arguments of (Czepiel 2002):
| (17) |
| (18) |
| (19) |
Therefore the log likelihood function is
| (20) |
3.3.3. An Iterative Solution to the Likelihood Equations
Now we employ the iterative procedure of Genkin et al. (2007), Meng and Rubin (1993), Mittal et al. (2013), and Zhang and Oles (2001) to estimate the parameters b and β. The main idea of the algorithm is to split the large, computationally extensive task of estimating β and b into many single estimation steps. Therefore, in order to find the next step estimate for βρs, p ϵ {1,..., P} given the current estimates β(m) and Z(m+1), we take the derivative of ℓC (β) with respect to a single βρs:
| (21) |
| (22) |
| (23) |
Likewise, the second derivative is:
| (24) |
| (25) |
Using Taylor’s expansion, we have that the one-step update for βps is
Following similar arguments for β0ks we have that
| (26) |
| (27) |
| (28) |
and
| (29) |
As in Genkin et al. (2007), Mittal et al. (2013), and Zhang and Oles (2001), we perform a complete sweep over all parameters in β multiple times instead of performing multiple iterations of a single parameter and moving onto the next.
Following the arguments of Czepiel (2002) one can show that the first and second derivatives of Equation 20 with respect to a single bjk is
| (30) |
and
| (31) |
The one-step update for bjk is
As with the proportional hazards coefficients we perform multiple sweeps over all model parameters instead of multiple iterations for a single parameter.
When performing these one-step estimation algorithms it is important that a single step does not go too far. This can occur when the log-likelihood function is not locally quadratic and can lead to ill-fitting results. Therefore, we employ the trust region algorithm of Genkin et al. (2007) and Zhang and Oles (2001). Furthermore, we only perform a maximum of five sweeps for the proportional hazards model coefficients in the M-Step, as the likelihood function will still sufficiently increase. The pseudocode is provided in Algorithm 1.
Algorithm 1.

M Step for PH and MN Coefficients
4. Case Study
In this section we present the results of our study on uncovering utilization patterns among the asthma diagnosed children in the Medicaid system.
4.1. Model Implementation and Evaluation
An important assumption in the implementation of the model is the independence across the states. Medicaid programs are run at the state level and thus each state Medicaid program will have its own public health policies and system characteristics, hence the assumption of independence.
The model selected using the approach in the Supplemental Material C presents five clusters of patients according to their utilization behavior. The model selection approach selects the model with the largest likelihood; the BIC or AIC penalty is small compared to the likelihood function and thus our approach is equivalent to identifying the number of clusters using such approaches. The estimated model parameters for a model with five clusters are in the Supplemental Material D.
Statistical significance of the covariate effects and multinomial logistic parameters is investigated using the Fisher information in the Supplemental Material E. The uncertainty associated with the model estimation is further studied using a multiple stratified sampling approach presented in the Supplement Material G. Based on this approach, we find that the resulting model parameters are identifiable and approximately unbiased. (See Supplemental Material H for details.)
The algorithm for the model estimation is computationally attractive, allowing for complete model estimation in 2–3 hours for a set of more than 420,000 patients and 6 million interarrival times. The computation scales approximately linear in time with varying problem sizes as discusses in Supplemental Material J.
We provide the estimated model along with a practical interpretation and various visualizations of the results in Supplemental Material D.
4.2. Proportional Hazards Model
4.2.1. Baseline Rates
We first present the baseline rate of events per year for each provider type. To derive the baseline rates and their multipliers, we simply take exp(β), where β is the coefficient value.
The baseline group represents the population of children who are white, chronically ill, aged 4–5, have not visited a healthcare provider yet in our study and are not eligible for Medicaid for reasons including blindness, disability or foster care. The baseline rates are in Figure 1. The proportion of children belonging to each cluster are 55.74% (Cluster 1), 16.10% (Cluster 2), 15.09% (Cluster 3), 10.32% (Cluster 4), and 2.75% (Cluster 5).
Figure 1:
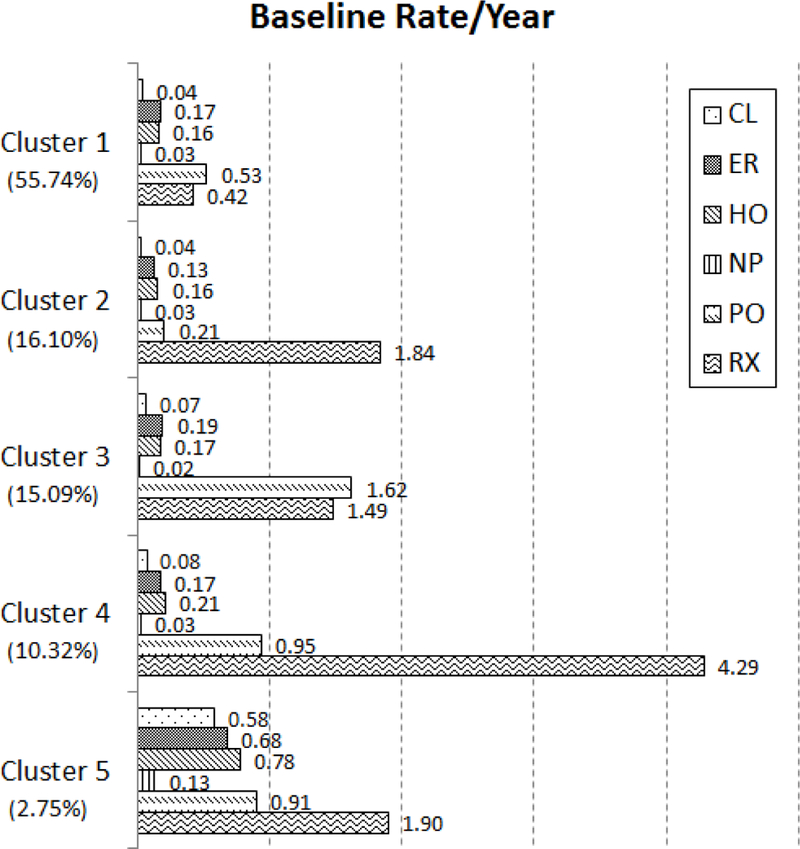
Baseline rate of events per year for white, chronically ill patients, aged 4–5, who are not eligible for Medicaid for blindness/disability or foster care, and without a prior observed event.
The baseline rate changes for each subpopulation within a cluster, and thus, should not be interpreted solely on their absolute value but on their relative values across clusters also. For instance, patients in Cluster 4 are more than twice as likely to fill a prescription than patients in any other cluster. Likewise, patients in Cluster 5 are more than six times as likely to visit a healthcare clinic than other patients. Because the effects of the control variables are the same regardless of cluster membership, these statements will hold regardless of age, demographics, or health status.
Cluster 1, with the greatest proportion of the population, has the least number of RX visits per year, less than one third of the cluster with the next lowest RX rate. Patients in Cluster 2 rely almost solely on RX visits, with low rates of visits to all other provider types. Cluster 3 patients have the highest rate of PO visits but the second lowest number of RX visits. Patients belonging to Cluster 4 have the greatest number of RX visits per year, but also have the second highest rate of HO visits. Finally, Cluster 5, with the fewest patients, has the greatest number of CL, ER and HO visits, with the third highest rate of PO visits and second highest rate of RX visits.
4.2.2. Covariate Effects
Now we describe the effects of the control covariates on the baseline visitation rates. In Figure 2 we provide the rate multipliers for the different covariate values. The rates of visits for different subpopulations can be found by multiplying the baseline rate by the rate multipliers from this chart. For instance, to find the rates for a black, age 16 child one would multiply the baseline rate from Figure 1 by the rate multipliers from the black and age 15–17 covariates in Figure 2. It is important to remember that the effects of these covariates are the same across all clusters. That is, a severely ill patient will have 6.79 times more hospitalizations regardless of whether they belong to Cluster 1 or Cluster 5.
Figure 2:
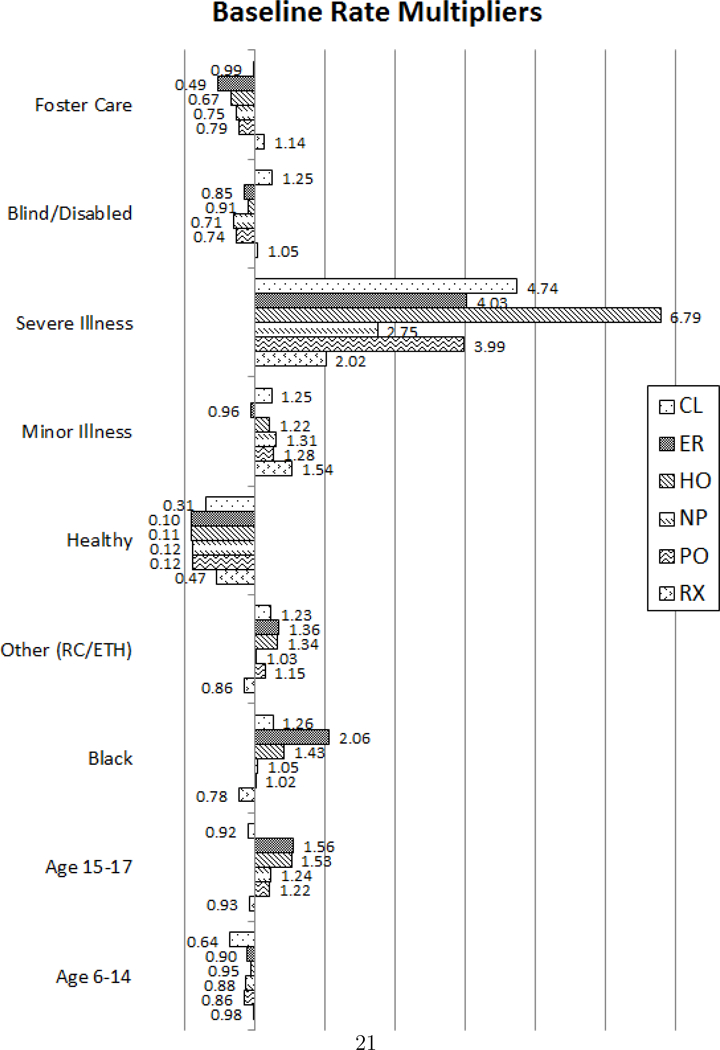
Baseline rate multipliers for each subpopulation
We find that the effects of health status or clinical risk group (healthy, minor or severely ill) have the greatest practically significant effect on the baseline rate. While the clinical risk group is an overall evaluation of the health condition, it can also reflect the severity of asthma. For example, a patient categorized as healthy will have mild asthma. A severely ill patient has a higher rate for all provider types but the rate of hospitalizations is 6.79 times higher than a chronically ill patient. Children with a minor chronic illness have little relative change, while healthy children have drastically less events of all types. Other findings include higher utilization of the CL, ER, and HO and lower utilization of RX for patients that are non-white, while patients who are eligible for Medicaid due to being blind or disabled or in foster care have overall lower rates of visits. Finally, the effects of age seem to have little practical difference for children in age group 6–14, while children age 15–17 have higher rates of visits to all provider types except CL and RX.
4.2.3. Provider Networks
Now we demonstrate how our model outputs can be used to visualize the provider transition networks for patients in different subpopulations and/or clusters. In this example, we compare the effects of the patient’s clinical risk group on healthcare utilization for the baseline group of patients. We chose this example for illustration purposes because of the drastic multiplicative effects of health status on the baseline visit rates as shown in Figure 2.
In Figure 3, we compare the network plots of healthy, chronically ill, and severely ill patients, leaving out those with a minor illness due to the small change from those that are chronically ill. The transition probability labeled on the edge is the probability for a patient to go to next event given patient’s last event type. The middle column of networks in Figure 3 pertains to chronically ill patients and the rate parameters are λ0ks = exp(β0ks), where β0ks are the baseline proportional hazard coefficients for cluster k and event s.
Figure 3:
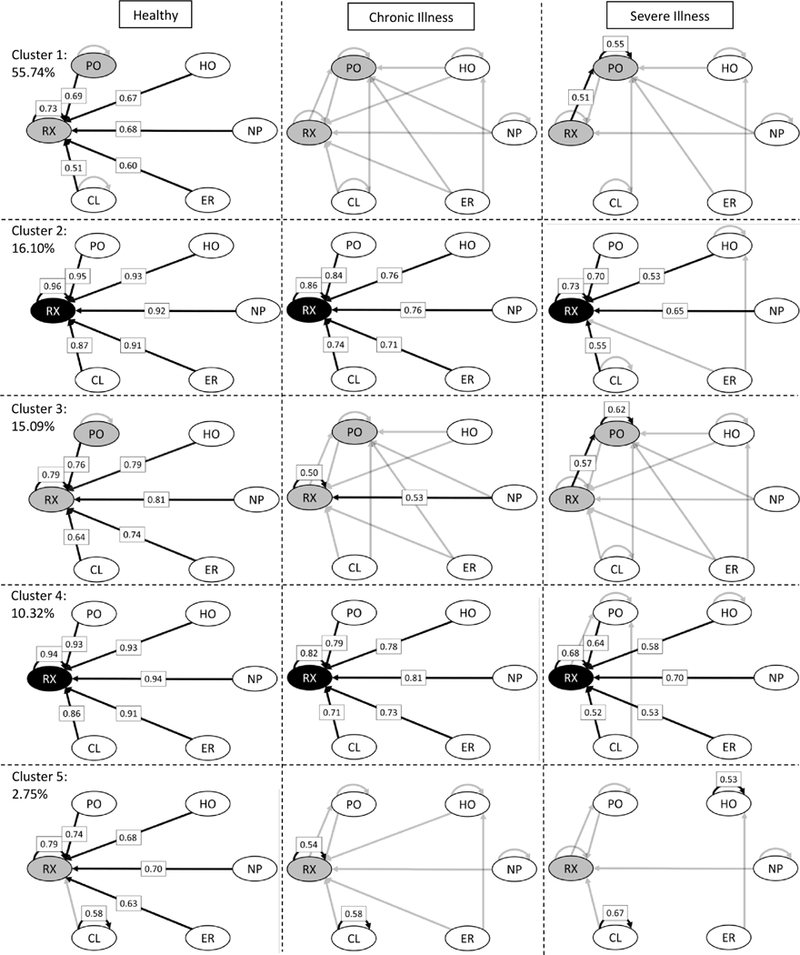
Provider networks inferred from the proportional hazards coefficients. The following rules were used in setting the grayscale of the coefficients and nodes: < 0.2 → not shown/white, [0.2, 0.5) →gray, and ≥ 0.5 → black.
Let βHealthy,s and βSevere,s be the coefficients for the healthy and severely ill patients, respectively. Then the event rates for these two groups are exp(β0ks × βHealthy,s) and exp(β0ks × βSevere,s). Furthermore, we can determine the rates for, say, a healthy patient with a last visit of CL by calculating exp(β0ks × βHealthy,s × βCL,s). Now we employ the following result on exponential random variables.
Let T1, . . . , T|S| be exponentially distributed random variables for the interarrival times for events 1,..., |S| with parameters λ1,..., λ|S|. Then it can be easily shown that the probability that Ts is the smallest of T1,..., T|S| is
These probabilities are the transition probabilities depicted in the provider networks.
Clusters 2, 3, and 4 networks have strong connections from all nodes leading to RX visits. However, as a child’s health condition becomes more severe, utilization becomes more variational, with a greater number of connections between different provider types for the chronic and severe illness columns. Patients in Cluster 1 have high probability transitions into PO and RX provider types, with a higher probability of readmission into HO for chronically and severely ill children. Clusters 2 and 4 are similar for healthy and chronically ill patients, except more transitions into HO in Cluster 2 and PO in Cluster 4. Cluster 3 healthy patients have similar networks as Cluster 2 and 4 healthy patients but with much greater variation for those with a chronic or severe illness. Patients in cluster 2 route into RX regardless of overall health condition. Chronic and Severe patients in Clusters 1 and 3 have high probability transitions into PO from all nodes, while severe patients in Cluster 4 have some transitions from CL to PO. Cluster 5, with the smallest percentage of patients, consists of those who more frequently utilize ER and HO with significant transitions into HO for both chronically ill and severely ill patients, while severely ill patients having more than 50% chance of readmission into HO. Across all clusters, NP is insignificant and primarily routes patients back to NP or into PO or RX visits.
4.3. Latent Variable Model
Next we provide visualizations for the effects of the explanatory variables on cluster membership. The parameter outputs from the model chosen are in Supplemental Material D.
In Figure 4 we plot the proportion of children from each state by urbanicity category and by cluster. That is, for a given state and urbanicity level, the sum of the values in the chart across clusters will be one. The black dashed lines indicate the overall proportion of children belonging to a given cluster regardless of state and urbanicity.
Figure 4:
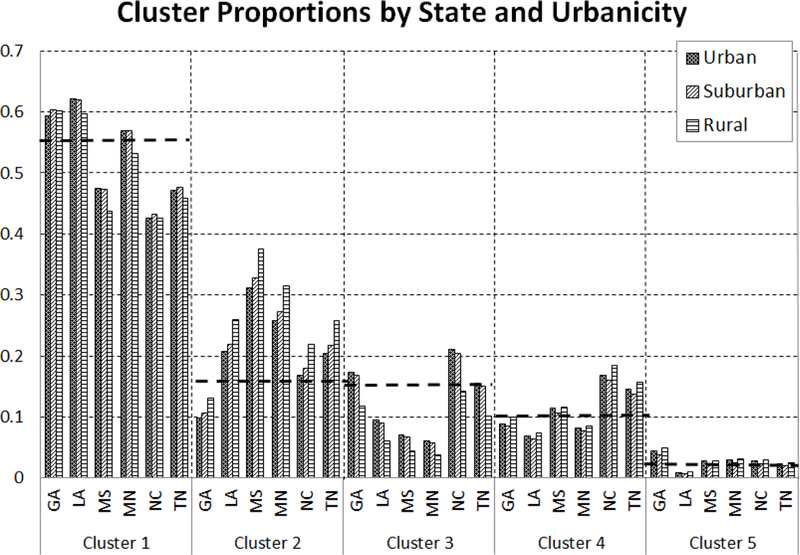
Proportions of patients belonging to each cluster stratified by state and urbanicity
While the urbanicity level of the child’s residence does affect cluster membership, it is the child’s residence state that is the main driver of variation in utilization behaviors. Furthermore, it appears that within each state, urban and suburban patients act similarly while rural patients behave differently. Clusters 1 and 3 have a higher proportion of urban and suburban patients relative to rural patients while Clusters 2 and 4 have the opposite. Cluster 5 appears to be evenly divided among the three urbanicity measures.
GA and MS behave differently than the other states while LA and MN, and NC and TN behave similarly. Recall that Cluster 1 patients rely on PO and RX visits, Clusters 2 and 4 rely almost solely on RX for healthy and chronically ill patients, Cluster 3 has a high rate of PO visits and some RX visits, and Cluster 5 utilizes more ER and HO visits than the others. From Figure 4, it becomes clear that GA patients are overall more variational, relying less on RX visits than the overall average and more on other provider types, having the greatest proportion of patients in Cluster 5. MS has the highest proportion of patients belonging to clusters dominated by RX visits, namely Clusters 2 and 4, with MN, NC, and TN patients also having relatively high proportions in those clusters. LA has the highest proportion of patients belonging to Cluster 1 and the lowest belonging to Cluster 5.
The third explanatory variable in our study is a measure of travel distance to primary care, which is the main source of care for asthma for the Medicaid-insured children. Interpreting the effects of travel distance on cluster membership is more difficult because the variable is numerical instead of categorical. However, we provide an example of the effects of increased travel time on cluster membership, assuming that the baseline probability of belonging to Clusters 1–5 are equal (this is not always the case as state and urbanicity also factor in). In Figure 5, we demonstrate the change in probability for this hypothetical example for patients in Clusters 1–5 with travel distances ranging from 0–25 miles.
Figure 5:
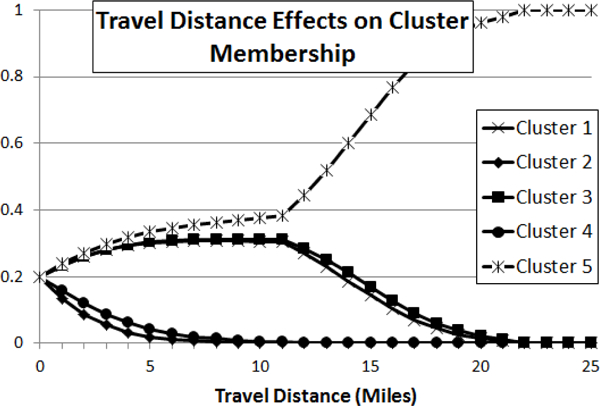
Plot of the change in probability for Clusters 1–5 with travel time ranging from 0–10.
This graph should be interpreted by the relative change in probability across clusters. We find that higher travel distances increase the probability of membership in Clusters 1, 3, and 5, with 5 being the greatest, while probabilities decrease for Clusters 2 and 4 as travel distance increases. Incidentally, Clusters 1, 3, and 5 tend to be more variational when compared to Clusters 2 and 4, which primarily rely on RX utilization.
5. Discussion
In this paper we introduce a model-based clustering analysis via a parametric proportional hazards model that allows for derivation of model parameters, cluster membership probabilities and visualizations. We also demonstrate the applicability of the methodology to policy-making on healthcare utilization. By studying pediatric asthma patients from six states, we are able to determine the drivers of inter-cluster variation while controlling for the effects of controlling covariates such as age, race and ethnicity, and overall health status.
The primary outputs from our model consists of the rate of visits by event type for patients belonging to the baseline group; the effects of the control covariates on the baseline rates in the form of rate multipliers indicating the variations of utilization that cannot be impacted by interventions; and the effects of the last visit type on future utilization choice. We show how these effects can be used to determine a one-step provider network. We finish with visualizations of the effects of the explanatory variables on cluster membership.
The baseline rate per year shows that the majority of patients, those belonging to Cluster 1 (55%), utilize asthma controller medications the least but also have few emergency room visits or hospitalizations. The provider networks across health conditions show that as the patient’s condition worsens, patients tend to utilize the physician’s office more, indicating that the majority of asthma patients are well-managed and require minimal, routine care to control asthmatic conditions. Cluster 3 (15%) is similar to Cluster 1 just with more visits to the physician’s office and prescription fills for asthma controller medication and relatively few emergency room visits or hospitalizations, also indicating patients who require minimal care. Higher travel distances increase the probability of membership within these two clusters. From Figure 4 we see that GA and LA have above average representation in Cluster 1, with MS, NC, and TN having well below average. Cluster 3 has above average representation of NC patients while LA, MS, and MN are well below average.
Cluster 2, with 16% of the population consists of those patients who rely heavily on medication and little else, thus representing those patients with the least utilization of the system of care, hence with a well controlled asthma. The effects of health status on the provider networks are minimal with slightly more admission into hospitalizations for patients with a severe health condition. Despite the fact that lower travel distances increase the probability of membership in this cluster, these patients rarely utilize the physician’s office. GA has well below average representation in this cluster while MS has the greatest.
Cluster 4 (10%) patients are the highest utilizers of medication with relatively high rates of visits physician office visits but also relatively low baseline rates of ER and HO visits, hence another cluster of patients with well controlled asthma. This cluster has the least variation when comparing across health status with the severely ill patients having high transition rates to the physician’s office. NC and TN have above average representation in this cluster. Lower travel distances increase membership probability in this cluster which could explain the high baseline rate of visits to physician office. While NC has average representation in Cluster 2, it has the highest proportion of patients in Cluster 4.
Finally, Cluster 5 (3%) consists of those patients who have the highest utilization of the emergency department and hospitalizations, and are likely to be those patients with the most severe asthmatic conditions requiring high-end care. Both chronically and severely ill patients have higher rates of emergency department visits and hospitalizations as indicated by the provider networks. GA has the most patients in this cluster and LA the least. These patients also tend to have the highest travel times to a physician’s office.
Supplementary Material
Some important findings drawn from this study are:
The most influential factor on the differences between children at the baseline or entry point in the system is the overall health condition.
Older children are higher utilizers of the system, particularly of both emergency departments and hospitalizations. One explanation is that asthma in older children can interfere with sleep, school, sports and social activities.
Children in foster care are lower utilizers of the system with a lower rate of both emergency departments and hospitalizations. This is expected because such visits require the presence of a social worker and possibly a member of the foster care agency if one is involved. This additional requirements may discourage utilization of emergency services.
The black population has twice the rate of emergency department visits. Prior research has not found a statistically significant association of the percentage of non-white population to geographic access while controlling for income in Georgia (Nobles et al. 2014).
Patients who are categorized as severely ill using the clinical risk group classification have the highest utilization across all provider types and of being prescribed medication. This is not unexpected because other comorbidities could lead to more severe outcomes for asthma. Moreover, these patients are most challenging to control because of the preexistence of other conditions that could more severely affect a patient than asthma.
The clustering of the patients reflects different utilization behaviors. While the majority of the patients utilize the system disparately (Cluster 1), others have a high rate of medication uptake with little interaction with the system (Cluster 2), with some utilization of the physician office (Cluster 3) or with high utilization of the physician’s office and high rate of medication uptake (Cluster 4). There is also a small percentage of patients (3%) who are higher utilizers of the system, not necessarily with a high medication uptake, that visit the emergency department or hospital at a higher rate with a 0.2–0.5 probability of being followed by a hospitalization for most subpopulations.
The probability of follow-up visits once a patient visits the emergency department or has a hospitalization is lower than 0.2 for most subpopulations that are not severely ill across all clusters except for some subpopulations in Clusters 1 and 5. Additionally, except for healthy patients, the probability of filling a prescription for an asthma controller medication after an emergency department visit or hospitalization is lower than 0.5 except for Clusters 2 and 4.
Most of all visits to a healthcare provider, including a hospital, a clinic or physician, result in a medication prescription being filled, with a high probability of a refill.
There are some variations across different urbanicity levels although the variations are higher between states. GA, LA and MN have a larger percentage of patients who utilize the system disparately (Cluster 1) while NC and TN have a higher percentage of patients who are high utilizers of medication (Cluster 4).
Acknowledgments
* This research has been supported by National Science Foundation (CMMI-0954283) and by National Institutes of Health (R56HL126761). The authors are thankful to Matt Sanders and Richard Starr in assisting with data safeguards and the information technology infrastructure. The authors are thankful to Dr. Julie Swann for the leadership in the protocol submission of the use of the MAX Medicaid claims data to the Centers of Medicare and Medicaid and in the Internal Review Board (IRB) approval process. The IRB approval was obtained under the protocol number H11287.
References
- Aalen O (1978). Nonparametric inference for a family of counting processes. The Annals of Statistics, 701–726. [Google Scholar]
- Andersen PK and Gill RD (1982). Cox’s regression model for counting processes: a large sample study. The Annals of Statistics, 1100–1120. [Google Scholar]
- Bähler C, Huber CA, Brüngger B, and Reich O (2015). Multimorbidity, health care utilization and costs in an elderly community-dwelling population: a claims data based observational study. BMC Health Services Research 15(1), 23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blossfeld H-P and Hamerle A (1992). Unobserved heterogeneity in event history models. Quality & Quantity 26 (2), 157–168. [Google Scholar]
- Borgan Ø (1984). Maximum likelihood estimation in parametric counting process models, with applications to censored failure time data. Scandinavian Journal of Statistics, 1–16. [Google Scholar]
- Browning M and Carro JM (2010). Heterogeneity in dynamic discrete choice models. The Econometrics Journal 13(1), 1–39. [Google Scholar]
- Bučar T, Nagode M, and Fajdiga M (2004). Reliability approximation using finite weibull mixture distributions. Reliability Engineering & System Safety 84 (3), 241–251. [Google Scholar]
- Chang J, Freed GL, Prosser LA, Patel I, Erickson SR, Bagozzi RP, and Balkrishnan R (2014). Comparisons of health care utilization outcomes in children with asthma enrolled in private insurance plans versus medicaid. Journal of Pediatric Health Care 28 (1), 71–79. [DOI] [PubMed] [Google Scholar]
- Cox DR (1992). Regression models and life-tables. Springer. [Google Scholar]
- Czepiel, S. A. (2002). Maximum likelihood estimation of logistic regression models: theory and implementation. Technical report. [Available at czep.net/stat/mlelr.pdf].
- Dempster AP, Laird NM, and Rubin DB (1977). Maximum likelihood from incomplete data via the em algorithm. Journal of the royal statistical society. Series B (methodological), 1–38. [Google Scholar]
- Department of Health and Human Services, Centers for Disease Prevention and Control (2012). National Health Interview Survey (NHIS) data: 2011 lifetime and current asthma.
- Dunn R, Reader S, and Wrigley N (1987). A nonparametric approach to the incorporation of heterogeneity into repeated polytomous choice models of urban shopping behaviour. Transportation Research Part A: General 21 (4–5), 327–343. [Google Scholar]
- EMC Corporation (2014). Vertical industry brief: digital universe driving data growth in health care. Technical report. [Online accessed 27-April-2017].
- Farcomeni A and Nardi A (2010). A two-component weibull mixture to model early and late mortality in a bayesian framework. Computational statistics & data analysis 54 (2), 416–428. [Google Scholar]
- Farewell VT (1982). The use of mixture models for the analysis of survival data with long-term survivors. Biometrics, 1041–1046. [PubMed] [Google Scholar]
- Genkin A, Lewis DD, and Madigan D (2007). Large-scale bayesian logistic regression for text categorization. Technometrics 49(3), 291–304. [Google Scholar]
- Gentili M, Serban N, O’Conor J, and Swann J (2015). Quantifying disparities in accessibility and availability of pediatric primary care with implication for policy. Health Services Research, in press, DOI: 10.1111/1475-6773.12722. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greene WH and Hensher DA (2003). A latent class model for discrete choice analysis: contrasts with mixed logit. Transportation Research Part B: Methodological 37(8), 681–698. [Google Scholar]
- Grosse SD, Boulet SL, Grant AM, Hulihan MM, and Faughnan ME (2013). The use of us health insurance data for surveillance of rare disorders: hereditary hemorrhagic telangiectasia. Genetics in Medicine 16(1), 33–39. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heckman JJ (1981). Heterogeneity and state dependence, pp. 91–140. University of Chicago Press. [Google Scholar]
- Heckman JJ and Borjas GJ (1980). Does unemployment cause future unemployment? definitions, questions and answers from a continuous time model of heterogeneity and state dependence. Economica 47(187), 247–283. [Google Scholar]
- Huber CA, Schneeweiss S, Signorell A, and Reich O (2013). Improved prediction of medical expenditures and health care utilization using an updated chronic disease score and claims data. Journal of clinical epidemiology 66(10), 1118–1127. [DOI] [PubMed] [Google Scholar]
- Kuk AY and Chen C-H (1992). A mixture model combining logistic regression with proportional hazards regression. Biometrika, 531–541. [Google Scholar]
- Mair P and Hudec M (2009). Multivariate weibull mixtures with proportional hazard restrictions for dwell-time-based session clustering with incomplete data. Journal of the Royal Statistical Society: Series C (Applied Statistics) 58(5), 619–639. [Google Scholar]
- McGrady ME and Hommel KA (2013). Medication adherence and health care utilization in pediatric chronic illness: a systematic review. Pediatrics 132(4), 730–740. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McLachlan G and McGiffin D (1994). On the role of finite mixture models in survival analysis. Statistical methods in medical research 3(3), 211–226. [DOI] [PubMed] [Google Scholar]
- Meng X-L and Rubin DB (1993). Maximum likelihood estimation via the ecm algorithm: A general framework. Biometrika 80 (2), 267–278. [Google Scholar]
- Mittal S, Madigan D, Cheng JQ, and Burd RS (2013). Large-scale parametric survival analysis. Statistics in medicine 32 (23), 3955–3971. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morrill R, Cromartie J, and Hart G (2005). Rural-urban communting area. http://depts.washington.edu/uwruca/ruca-maps.php/.RuralHealthResearchCenter.
- Mosler K (2003). Mixture models in econometric duration analysis. Applied Stochastic Models in Business and Industry 19 (2), 91–104. [Google Scholar]
- Mosler K and Scheicher C (2008). Homogeneity testing in a weibull mixture model. Statistical Papers 49(2), 315–332. [Google Scholar]
- Mosler K and Seidel W (2001). Theory & methods: Testing for homogeneity in an exponential mixture model. Australian & New Zealand Journal of Statistics 43(2), 231–247. [Google Scholar]
- Nagode M and Fajdiga M (2000). An improved algorithm for parameter estimation suitable for mixed weibull distributions. International Journal of Fatigue 22(1), 75–80. [Google Scholar]
- Nobles M, Serban N, Swann J, et al. (2014). Spatial accessibility of pediatric primary healthcare: Measurement and inference. The Annals of Applied Statistics 8 (4), 1922–1946. [Google Scholar]
- Piecoro LT, Potoski M, Talbert JC, and Doherty DE (2001). Asthma prevalence, cost, and adherence with expert guidelines on the utilization of health care services and costs in a state medicaid population. Health Services Research 36 (2), 357. [PMC free article] [PubMed] [Google Scholar]
- Pylypchuk Y and Sarpong EM (2013). Comparison of health care utilization: United states versus canada. Health Services Research 48(2pt1), 560–581. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reader S (1993). Unobserved heterogeneity in dynamic discrete choice models. Environment and Planning A 25 (4), 495–519. [Google Scholar]
- Roebuck MC, Liberman JN, Gemmill-Toyama M, and Brennan TA (2011). Medication adherence leads to lower health care use and costs despite increased drug spending. Health Affairs 30 (1), 91–99. [DOI] [PubMed] [Google Scholar]
- Ross JS, Maynard C, Krumholz HM, Sun H, Rumsfeld JS, Normand S-LT, Wang Y, and Fihn SD (2010). Use of administrative claims models to assess 30-day mortality among veterans health administration hospitals. Medical care 48(7), 652. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sy JP and Taylor JM (2000). Estimation in a cox proportional hazards cure model. Biometrics 56 (1), 227–236. [DOI] [PubMed] [Google Scholar]
- Vaupel JW and Yashin AI (1985). Heterogeneity’s ruses: some surprising effects of selection on population dynamics. The American Statistician 39(3), 176–185. [PubMed] [Google Scholar]
- Wakefield DB and Cloutier MM (2006). Modifications to hedis and cste algorithms improve case recognition of pediatric asthma. Pediatric Pulmonology 41 (10), 962–971. [DOI] [PubMed] [Google Scholar]
- Zhang T and Oles FJ (2001). Text categorization based on regularized linear classification methods. Information retrieval 4 (1), 5–3F [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


