Cine Cardiac MRI Slice Misalignment Correction Towards Full 3D Left Ventricle Segmentation

Abstract

Accurate segmentation of the left ventricle (LV) blood-pool and myocardium is required to compute cardiac function assessment parameters or generate personalized cardiac models for pre-operative planning of minimally invasive therapy. Cardiac Cine Magnetic Resonance Imaging (MRI) is the preferred modality for high resolution cardiac imaging thanks to its capability of imaging the heart throughout the cardiac cycle, while providing tissue contrast superior to other imaging modalities without ionizing radiation. However, there exists an inevitable misalignment between the slices in cine MRI due to the 2D + time acquisition, rendering 3D segmentation methods ineffective. A large part of published work on cardiac MR image segmentation focuses on 2D segmentation methods that yield good results in mid-slices, however with less accurate results for the apical and basal slices. Here, we propose an algorithm to correct for the slice misalignment using a Convolutional Neural Network (CNN)-based regression method, and then perform a 3D graph-cut based segmentation of the LV using atlas shape prior. Our algorithm is able to reduce the median slice misalignment error from 3.13 to 2.07 pixels, and obtain the blood-pool segmentation with an accuracy characterized by a 0.904 mean dice overlap and 0.56 mm mean surface distance with respect to the gold-standard blood-pool segmentation for 9 test cine MR datasets.

1. INTRODUCTION AND OBJECTIVES

Magnetic Resonance Imaging (MRI) is the preferred imaging modality for cardiac diagnosis, as well as planning and guidance of cardiac interventions in light of its good soft tissue contrast, high image quality, and lack of exposure to ionizing radiation. Cardiac cine MRI produces anatomical images of the heart with high temporal and spatial resolution that are used to measure clinically relevant Left Ventricular (LV) parameters such as mass, volume, and ejection fraction, as well as reconstruct high quality LV models depicting full cardiac morphology. These models can be used to precisely localize pathologies during an image guided intervention. For these applications, an accurate and robust segmentation of the LV is crucial. Manual delineation is the standard approach which is both time consuming as well as prone to inter- and intra- user variability, suggesting a need for semi-/fully-automatic methods for LV segmentation.

A comprehensive review of segmentation techniques applied to short axis cardiac MR images can be found in [1]. Generally speaking, thresholding, edge-based and region-based approaches or pixel-based classification approaches depend solely on image content (with weak or no priors) and are computationally efficient, but cannot produce accurate segmentation results in image regions with ill-defined boundaries. On the other hand, methods that employ strong priors such as deformation models, active shape and appearance models, and atlas based approaches, can overcome segmentation challenges imposed by ill-defined regions, but at the expense of computation time and manual construction of training data.

A characteristic of cine MRI is the inherent misalignment between the slices as the acquisition is performed one slice at a time throughout the cardiac cycle (2D + time acquisition) during a single breath-hold, generating a stack of slices that covers the entire heart. Several methods for slice misalignment correction have been previously proposed. Elen et al. [2] optimized the intensity similarity between the 2D long axis (LA) and short axis (SA) slices along the line of intersection. Similarly, Slomka et al. [3] performed 3D registration of LA and SA slices by minimizing the cost function derived from plane intersections for all cine phases. Although helpful, these algorithms feature limited robustness, as they rely on a limited amount of information available at the plane intersections. Therefore, since the alignment of acquired 2D cine MR slices into a full, cohesive 3D volume is challenging and prone to error, most of the segmentation algorithms rely on 2D processing, compromising the segmentation results in the apical and basal regions.

Deep learning techniques [4] have been demonstrated highly successful in high level computer vision tasks, speech recognition, and many other domains in recent years. Specifically, Convolutional Neural Networks-based (CNNs) supervised learning techniques have significantly improved image classification performance [5]. The unique capability of CNNs to learn problem specific hierarchical features in an end-to-end manner have established them as a powerful general purpose supervised machine learning tool that can be deployed for various computer vision problems yielding state-of-the-art performance. This performance motivated the use of CNNs in medical image analysis. However, the limited availability of medical imaging data and associated costly manual annotation posed real challenges in their adaptation in the field. Various techniques including patch-based training, data augmentation, and transfer learning have been used to overcome these challenges. A comprehensive review of deep learning techniques in medical image analysis can be found in [6].

In the context of image segmentation, Long et al. [7] proposed a fully convolutional network for semantic image segmentation adapting the contemporary classification networks fine-tuned for the segmentation task obtaining state-of-the-art performance. Since then, various architectures and post-processing schemes have been proposed as summarized in [8]. Specifically, the U-Net [9] architecture with data augmentation has been very successful in medical image segmentation.

Here we propose a novel CNN architecture that uses multi-resolution features to accurately regress the center of the LV blood-pool from cine MR images. Subsequently, we correct for the slice misalignment to generate a full 3D volume. Finally, we leverage the 3D information to segment the LV blood-pool and myocardium using a 3D extension of the atlas and graph-cut based segmentation technique described in [10].

2. METHODOLOGY

2.1. Cardiac MRI Data

This study employed 97 de-identified cardiac MRI image datasets from patients suffering from myocardial infraction and impaired LV contraction available as a part of the STACOM Cardiac Atlas Segmentation Challenge project [11, 12] database^*. Cine-MRI images in short-axis and long-axis views are available for each case. The images were acquired using the Steady-State Free Precession (SSFP) MR imaging protocol with the following settings: typical thickness ≤ 10mm, gap ≤ 2mm, TR 30 − 50ms, TE 1.6ms, flip angle 60⁰, FOV 360mm and 256 × 256mm image matrix using multiple scanners from various manufacturers.

We divided the 97 available dataset into 80% training, 10% validation (to avoid over-fitting during training), and 10% test set, and perform our evaluation on the test set.

2.1.1. LV blood-pool ground-truth generation

Ground truth myocardium segmentation generated from expert analyzed 3D surface finite element model is available for all 97 cases. As the slice segmentations are obtained from the intersection of images slices with the 3D model, partial myocardium can be observed in some basal slices. To obtain the corresponding blood-pool segmentation, each slice of the provided myocardium segmentation is inverted and a morphological opening operation is performed. If the connected component analysis results in two connected components, the smaller connected region is selected as the blood-pool. Hence, the slices with partial myocardium do not yield any blood-pool region. This has a significant effect in the segmentation evaluation of basal slices.

2.2. Data Preparation and Augmentation

The physical pixel spacing in SA images ranged from 0.7031 to 2.0833 mm. We used SimpleITK [13] to resample all images to the most common spacing of 1.5625 mm along both x- and y-axis. The resampled images were center cropped or zero padded to a common resolution of 192 × 192 pixels. To simulate the real-world scenario, the images were transformed using combinations of 9 translations (±10%) along x- and y- axis, 7 rotations (±10⁰,±20⁰,±30⁰), and 3 scaling (±10%). The resulting 189 different combinations were used to train the CNN. The ground truth LV center was computed as the centroid of the LV blood pool obtained from the inner contour of the provided ground truth myocardium segmentation. The LV center from closest mid-slice was propagated to the apical/basal slices with partial/no ground truth myocardium segmentation.

2.3. CNN Architecture for LV Center Regression

We propose a novel CNN architecture to predict the LV blood-pool center from SA cine MR images. The proposed approach requires minimal pre-processing (i.e. resampling and crop/pad to fixed resolution) and minimal user input to generate a training set, as the expert needs to select a single LV center point per image.

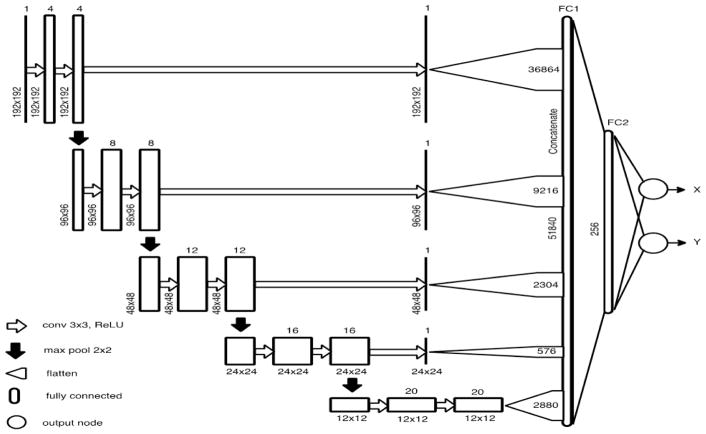
The CNN network architecture is shown in Fig. 1. The input image is passed through several convolutional layers followed by Rectified Linear Unit (ReLU) non-linearity and four max-pooling layers spread across the network. The global image information obtained in the final convolutional layers are flattened into a single vector to form a fully connected layer. In addition, we generate a single feature map from each resolution and feed it directly to the fully connected layer. These skip connections enable the network to use multi-resolution features to yield a more accurate prediction of the LV center, while maintaining the number of tractable network parameters. The output of the network consists of two values representing the x- and y- coordinates of the LV center.

Figure 1.

CNN Architecture for regression of LV center from each short axis slice.

2.4. Slice-misalignment Correction

Assuming there is only translational misalignment between the slices, we translate the predicted LV centers so that they are collinear, resulting in a corrected 3D volume. Fig. 2 shows the 3D volume reconstructed from the ground-truth LV myocardium segmentation before and after misalignment correction. This step helps restore the 3D connectivity structure of the LV improving the subsequent graph-cut segmentation.

Figure 2.

Reconstructed 3D models generated from the ground-truth LV myocardium segmentation before and after slice misalignment correction.

2.5. LV Blood-pool Segmentation

We extend the atlas prior based graph-cut segmentation method presented in [10] to 3D for the segmentation of LV blood-pool from the slice-misalignment corrected 3D volume.

2.5.1. Atlas Generation

We select a patient volume with an average LV size as a reference. All other training patient volumes are registered to this reference utilizing the ITKv4 registration framework [14] via the SimpleITK interface [13]. We use an affine transformation, with the mutual information similarity metric and the Nelder-Meade optimizer. The registration initialization uses the ground-truth myocardium bounding boxes to obtain initial scaling. The optimum transformation parameters are applied to the corresponding blood-pool segmentations. The registered patient volumes and blood-pool segmentations are averaged to obtain the average intensity atlas and blood-pool probability map, respectively.

2.5.2. Blood-pool Label Transfer

Robust registration of the average intensity atlas to a new test patient volume is crucial for the subsequent graph-cut segmentation. However, due to large variability in LV sizes in the dataset, and the tendency of optimizers to converge to a local minimum, registration results using a single starting point in parameter space are unreliable. We therefore perform the registration from multiple starting points that are selected using an exhaustive search strategy on the scale parameters along each axis and on the translation along the long axis, z direction, of the affine transformation. We evaluate the value of the normalized cross-correlation (NCC) between the atlas and the test volume using multiple scale factors. The parameters corresponding to the top k=5 similarity metric values are used as initial values for the subsequent registrations. Finally, the optimum transformation resulting in the best NCC metric is applied to the blood-pool probability map to transfer the label to the test volume as shown in Fig. 3a. The test patient image is cropped based on the blood-pool probability map to reduce the computational complexity for subsequent graph-cut segmentation.

Figure 3.

Example of left ventricle blood-pool segmentation using the proposed approach: a) Blood-pool probability map transferred to the test volume via registration; b) Initial Graph-cut segmentation (first Iteration); c) Segmentation result after refinement based on Intersection-over-Union, small over-segmented region in aorta similar in intensity with blood-pool has been removed; d) Segmentation result after iterative refinement (converged on third iteration); e) Final blood-pool segmentation after refinement using Stocastic Outlier Selection, over-segmented basal slice with distinct shape statistics compared to other slices has been removed.

Algorithm 1.

Blood-pool Label Transfer

2.5.3. Graph-cut Segmentation

We represent the cropped test volume as a 3D graph with 6-neighbor connectivity. Two special terminal nodes representing two classes — the source background (BG), and the sink blood pool (BP) — are added to the graph. The segmentation is formulated as an energy minimization problem over the space of optimum labelings f:

$$E(f)=\sum _{p\in \mathcal{P}}{D}_p(f_p)+\sum _{\{p,q\}\in \mathcal{N}}{V}_{p,q}(f_p,f_q),$$ (1)

where the first term represents the data energy that reduces the disagreement between the labeling f_p given the observed data at every pixel p ∈ P, and the second term represents the smoothness energy that forces pixels p and q defined by a set of interacting pair 𝒩 (in our case, the neighboring pixels) towards the same label.

The data energy term encoded as terminal link (t-link) between each node to source (or sink) is assigned as the weighted sum of the log-likelihood computed from the Gaussian Mixture Model (GMM) of intensity distributions, blood-pool probability map, and signed distance map obtained from the thresholded blood-pool probability map:

$$D_p(f_p)=-w_1\mathit{lnPr}(I_p\mid f_p)+\frac{w_2}{1+e^{-\mathit{itr}}}P(f_p)+\frac{w_3}{1+e^{-\mathit{itr}}}Dm(f_p)$$ (2)

where,

• Pr(I_p|f_p) is the likelihood of observing the intensity I_p given that pixel p belongs to class f_p. The log-likelihood for BP and BG are obtained by fitting intensity values within the convex-hull of most recent BP segmentation and outside the BP probability map thresholded at Th_BG to 1- and 2-Gaussian GMM models, respectively.

• P(f_p) is the probability of pixel p being class f_p. The probabilities for BP and BG are the BP-probability map and its inverse, respectively.

• Dm(f_p) is the likelihood of pixel p being class f_p computed from a signed distance map obtained via BP-probability map thresholded at Th_BP, with the inside regions being positive and outside regions being negative. This strongly encourages pixels inside and outside the thresholded BP-probability map to be assigned as BP and BG, respectively.

• itr is the iteration number. The weights are assigned such that the contribution of BP probability map increases with increasing iteration number, reflecting its increasing reliability as the iteration proceeds.

The smoothness energy term is computed over the links between neighboring nodes (n-links) and is assigned as a weighted sum of intensity similarity between the pixels and average probability of the pixels belonging to BP based on the BP probability map:

$$V_{p,q}(f_p,f_q)=\{\begin{array}{ll}{w}_4\ast \mathit{exp}\left(-\frac{\mid I_p-I_q\mid }{\sigma }\right)+w_5\ast \mathit{exp}\left(\frac{P(p)+P(q)}{2}\right)\hfill & \text{if}{f}_p\ne f_q\hfill \\ 0\hfill & \text{if}{f}_p=f_q\hfill \end{array}$$ (3)

where,

• w₄ and w₅ are weights for the intensity similarity term and atlas prior term, respectively, and P(.) is the probability of a pixel belonging to BP obtained from the BP probability map.

After assigning appropriate unary and pairwise potentials to the graph, the minimum cut is identified using the α-expansion algorithm [15]. The obtained labeling minimizes the global energy of the graph and corresponds to the optimal BP/BG segmentation as shown in Fig. 3b.

2.5.4. Segmentation Refinement using Intersection-over-Union

Due to the intensity similarity between blood-pool and some background regions, the raw graph-cut segmentation is sometimes noisy and requires additional processing. We perform slice-wise refinement via connected-component analysis, such that a single connected region per slice is retained which maximizes the Intersection-over-Union (IoU) metric to the BP of closest mid-slice and to the BP probability map thresholded at Th_BP. The refinement starts at mid-slice and then proceeds to the apical/basal slices. To accommodate for small blood-pool regions in apical slices, the IoU value is set to 1.0 if one object is completely inside the other. Further, we only retain the slice segmentations with IoU greater than a predefined threshold Th_Iou to filter out small implausible segmentation regions. The BP segmentation result after IoU based refinement is shown in Fig. 3c.

Algorithm 2.

Refining Graph-cut Segmentation Result using IoU

2.5.5. Iterative Segmentation Refinement

The initial global registration of the average intensity atlas to a test patient volume might not be accurate, hence producing sub-optimal graph-cut segmentation result. To address this limitation, Otsu thresholding [16] of the region inside the registered BP probability map thresholded at Th_BP yields the approximate BP segmentation for the first iteration, which is further refined iteratively.

We compute a slice-wise convex-hull for the recently obtained refined graph-cut segmentation. A 3D thresholded distance map, $D{m}_{Th}^S$, is computed from the convex-hull with the regions inside the segmentation assigned a constant value of 0. Similarly, a 3D thresholded distance map, $D{m}_{Th}^{P_{T{h}_{BP}}}$, is computed from the BP probability map thresholded at Th_BP, P_ThBP. The distance map $D{m}_{Th}^{P_{T{h}_{BP}}}$ is registered to $D{m}_{Th}^S$ using gradient descent optimizer with mean squared difference (MSD) as the similarity metric within a mask defined in the apical regions up until the basal slice with non-zero P_ThBP. We exclude the basal regions during the registration as they could contain over-segmented aortic valve with intensity similar to the BP, adversely affecting the segmentation refinement. The obtained optimum 3D affine transformation is applied to the BP probability map and hence used to update the graph energy in (2) and (3).

The intensity values within the convex-hull of the latest refined graph-cut segmentation is used to update the 1-Gaussian GMM model for BP. Similarly, the intensity values outside the transformed BP probability map thresholded at Th_BG are used to update the 2-Gaussian GMM model for the BG. The intensity likelihoods obtained from updated BP and BG GMM models are used to update the Pr(I_p|f_p) term of graph energy in (2).

The optimal binary labeling of the graph is obtained via minimum-cut using the α-expansion algorithm. The obtained noisy graph-cut segmentation is “cleaned” using the method described in Algorithm 2 and hence used to update the BP probability map and the graph energy for the next iteration. This iterative process is repeated until the IoU of BP segmentations between consecutive iterations is below some threshold, Th_stop, or maximum number of iterations, itr_max, has been reached. Fig. 3d shows the BP segmentation result obtained after the iterative refinement process converges in three iterations.

Algorithm 3.

Segmentation Refinement using Stocastic Outlier Selection

2.5.6. Segmentation Refinement using Stochastic Outlier Selection

The segmentation result obtained after iterative refinement might contain over-segmented regions of the aorta or incorrectly segmented apical slices. Hence, we analyze the shape statistics of the segmented region for all the slices and remove outlier apical/basal slices.

We extract four shape statistics from the segmented region in each slice:

1. Thinness ratio: $\frac{4\pi \times \mathit{Area}}{{\mathit{Perimeter}}^2}$, measures circularity of the segmented region

2. Eccentricity: Ratio of focal distance over the major axis length of least square fitted ellipse

3. Solidity: Ratio of pixels in the region to pixels in its convex hull

4. Extent: Ratio of pixels in the region to pixels in the total bounding box

The Stochastic Outlier Selection (SOS) algorithm [17] computes the probability of each slice being an outlier based on the affinity matrix obtained from the shape features. The variance of a data point depends on the density of the neighborhood, which is set such that each data point has the same number of neighbors. This number is controlled via the only parameter of SOS, called perplexity (k_SOS).

If the slice with maximum probability of being an outlier has a higher probability than a pre-defined probability threshold, Th_SOS, and belongs to apical/basal region (determined by the thresholded BP probability map), slices above/below this slice have a high probability of being an over-segmented aorta/apex region, and hence are removed to obtain the final BP segmentation, as described in Algorithm 3. As observed in Fig. 3e, over-segmented aorta in the basal region has been removed after the SOS refinement to obtain the final BP segmentation.

3. IMPLEMENTATION DETAILS

The CNN model was implemented in Python using the Keras application programming interface (API) [18] running on top of TensorFlow [19]. The programming environment was setup as a docker^† container for portability and reproducibility. The system comprised of Intel(R) Xeon(R) CPU X5650 @ 2.67GHz with 12 cores, 96 GB of system memory, and two 12 GB Nvidia Titan Xp GPUs.

The 4D dataset with 189 different augmentations were saved as 189 shuffled files (2.8 GB), with each shuffled file containing a randomly augmented volume from all 97 datasets. During training, the files were read ahead and pushed to a queue such that the data generator could generate a random batch of training data without significant IO delay. The network weights were initialized using the Xavier uniform initializer, from a uniform distribution within [−L,+L] with $L=\sqrt{\frac{6}{{\mathit{fan}}_{in}+{\mathit{fan}}_{\mathit{out}}}}$, where fan_in and fan_out are the number of input and output units in the weight tensor, respectively.

The 97 datasets were randomly split into 79 training, 9 validation, and 9 test sets. The network was trained for 100 epochs with each epoch comprising of 100 random shuffled files and requiring 46 minutes on average. The sum of squared difference error between predicted and ground truth LV center was used as the loss function. The model yielding the lowest validation loss at the end of an epoch was saved and used to evaluate the results on the test set. The model requires 1.23 seconds on average to predict the LV centers for 9 test datasets (2670 SA slices).

The parameters for LV blood-pool segmentation were empirically tuned based on the validation dataset. For the exhaustive search based image registration, the number of scaling factors, s, per dimension is set to 5, and the number of z-translations, t, is set to 3, such that the NCC similarity measure for 5³ ×3 = 425 different scale and translation combinations have to be computed between the test and transformed average intensity image. We select k = 5 best initial transforms for subsequent registration and use the transformation producing best NCC similarity to transfer the BP probability map to a test dataset. The BP and BG thresholds for the BP probability map are set to Th_BP = 0.5 and Th_BG = 0.0, respectively. The weights for data energy term in (2) are set to w₁ = 10.0, w₂ = 2.0, w₃ = 15.0, and the weights for the smoothness energy term in (3) are set to w₄ = 50.0 and w₅ = 50.0. Similarly, the intensity spread parameter in the smoothness term (3) is set to σ = 0.1, as we rescale the image intensities to a range of 0.0 to 1.0. The threshold for IoU based BP refinement as defined in Algorithm 2 is set to Th_IOU = 0.6. The iterative segmentation refinement is stopped when the IoU between two consecutive segmentations is greater than Th_stop = 0.95 or maximum number of iterations itr_max = 10 has been reached. Finally, for the segmentation refinement using SOS, the outlier probability threshold Th_SOS is set to 0.6, and the perplexity parameter, k_SOS, is set to number of slices with BP segmentation subtracted by 2, allowing only few slices to be considered as an outlier.

4. RESULTS

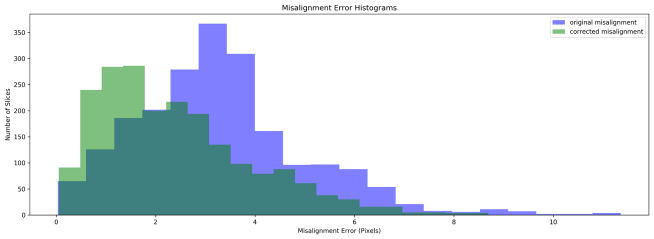
We computed the mean of the LV center across all the slices in the 3D test volume. Assuming the slices need to be translated to the mean center point for slice misalignment correction, we computed the distance of each true LV center point to the mean and designated it as the initial slice misalignment in the test data. Similarly, the Euclidean distance between the predicted and true LV center points yielded the residual slice misalignment after the proposed correction. Table 1 shows the misalignment statistics, Fig. 2 shows significant reduction of stair-step artifact on the 3D reconstructed LV myocardium, Fig. 4 shows the histogram of misalignment errors, and Fig. 5 shows the box plot for errors, before and after the misalignment correction. Further, the Kolmogorov-Smirnov statistics on the errors before and after misalignment correction was able to reject the null hypothesis that the two error samples come from the same distributions with a p-value of 1.617e⁻⁷⁶. Hence, the proposed CNN regression architecture was successful in reducing the slice misalignment error statistically significantly from median error of 3.13 to 2.07 pixels.

Table 1.

Mean, Standard Deviation, and Median slice misalignment in pixels before and after the correction.

Method	Before Correction (pixels)	After Correction (pixels)
Mean ± Std	3.30 ± 1.71	2.40 ± 1.54
Median	3.13	2.07

Figure 4.

Histogram for misalignment errors before and after the correction.

Figure 5.

Boxplot for misalignment errors before and after the correction. Median (orange line), Interquartile range (box), and outliers (points outside the whiskers) can be observed in the plot. The median misalignment error is reduced from 3.20 to 2.14 pixels.

On average, the proposed algorithm converges in 3 iterative refinement steps and requires ~ 2.2 mins to segment a 3D test volume. The obtained segmentation results were validated against the blood-pool segmentation extracted from the provided ground-truth myocardium segmentation as shown in Fig. 6. We computed the Jaccard and Dice similarity measures along with the mean surface distance and Hausdorff distance for both the validation and the test datasets as shown in Table 2. Although the parameters for the algorithm are tuned using the validation dataset, the proposed method generalizes well in the test dataset with similar results.

Figure 6.

Blood-pool segmentation result obtained from the proposed method compared against: a) Ground-truth myocardium segmentation; b) Blood-pool segmentation extracted from the myocardium. The ground-truth, obtained segmentation result, and the intersection regions are shown in red, blue, and white, respectively. Due to the difficulty of obtaining blood-pool segmentation from the partial myocardium slices, these slices are assumed to not contain blood-pool, hence significantly affecting the blood-pool segmentation evaluation.

Table 2.

Evaluation of the End Diastole blood-pool segmentation results against the ground truth blood-pool segmentation using Jaccard, Dice, Hausdorff Distance and Mean Surface Distance measures for the Validation and Test datasets.

Dataset	Jaccard	Dice	Hausdorff Distance (mm)	Mean Surface Distance (mm)
Test Set	0.829 ± 0.077	0.904 ± 0.048	9.446 ± 4.936	0.560 ± 0.566
Validation Set	0.825 ± 0.074	0.902 ± 0.045	9.290 ± 2.088	0.371 ± 0.213

5. DISCUSSION, CONCLUSION, AND FUTURE WORK

We presented a CNN based regression architecture to predict the LV blood-pool center from the SA cine MR slices. The predicted LV center points for all slices were translated to image center to reduce the median slice-misalignment from 3.13 to 2.07 pixels. As our algorithm in its current form requires minimal pre-processing, specifically resampling the SA images to a spacing of 1.5625 × 1.5625 mm and center cropping/zero-padding to a common resolution of 192×192 pixels, we obtain a large number of network parameters at the fully connected layers, requiring a large training dataset. We plan to crop an ROI from the original SA images using the Fourier first harmonics information obtained from the image sequence throughout the cardiac cycle, such that the CNN network parameters would be reduced and possibly yield better LV alignment. Furthermore, we will be exploring a segmentation-based approach, where we obtain a rough LV blood-pool segmentation and compute its centroid as LV center for misalignment correction.

After obtaining a coherent 3D volume from the slice-misalignment correction, we performed a full 3D segmentation of the LV blood-pool by exploiting the 3D context information using the LV atlas. The 6-neighborhood graph structure ensured smoothness between slice segmentations. Since image registration is highly dependent on a good initialization, we perform an exhaustive search and refinement to obtain the best possible registration result between the average intensity atlas and the test patient volume. Any initial misalignments are further corrected by a graph-cut based iterative refinement process. In addition, due to the intensity similarity of the aortic region in basal slices to the blood-pool region, basal slices could be over-segmented, and are removed if their segmented shape is significantly different from that of the other slices using the Stochastic Outlier Selection algorithm.

Despite the difficulty of obtaining the gold-standard blood-pool segmentation from the provided ground-truth myocardium segmentation in the partial myocardium regions, our segmentation algorithm is able to obtain a mean dice similarity metric of over 90%, with mean surface distance of ~ 0.5 mm, and Hausdorff distance of ~ 9.4 mm. As there would be no gold-standard blood-pool in the partial myocardium slices, it significantly affects the similarity metrics and surface distance measurements. Furthermore, although the current algorithm parameters are tuned empirically using a validation dataset, we plan to do an extensive study of their impact in the final segmentation result. We also plan to extend our work for myocardium segmentation throughout the cardiac cycle.