Abstract
The catalytic mechanisms underlying Escherichia coli alkaline phosphatase’s (AP) remarkable rate enhancement have been probed extensively. Past work indicated that whereas the serine nucleophile (Ser102) electrostatically repels the product phosphate, another oxyanion, tungstate, binds more strongly in the presence of Ser102. These results predict a covalent bond between the serine nucleophile and tungstate, a model that we test herein. The crystal structure of tungstate-bound alkaline phosphatase provides evidence for a covalent adduct model and further shows that the ligand adopts trigonal bipyramidal geometry, which is infrequently observed for tungstate in small molecules and other active sites but mirrors the geometry of the presumed phosphoryl transfer transition state. The AP active site is known to stabilize another oxyanion, vanadate, in trigonal bipyramidal geometry, but the extent to which binding of either ligand reproduces the energetics of the transition state cannot be deduced from structural inspection alone. To test for transition state analog behavior, we determined the relationship between catalytic activity and affinity for tungstate and vanadate for a series of 20 AP variants. Affinity and activity were highly correlated for tungstate (r2 = 0.89) but not vanadate (r2 = 0.23), indicating that the tungstate•AP complex may better mimic this enzyme’s transition state properties. The results herein suggest that tungstate will be a valuable tool for further dissecting AP catalysis and may prove helpful in mechanistic studies of other phosphoryl transfer enzymes.
Keywords: enzymes, phosphoryl transfer, transition state
Introduction
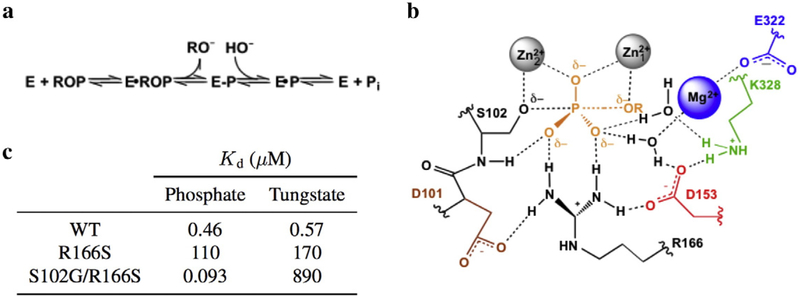
Escherichia coli alkaline phosphatase (AP) is a powerful model system for studying general mechanisms by which enzymes accelerate chemical reactions [1,2]. As a nonspecific phosphatase, AP faces the challenge of hydrolyzing diverse phosphate monoesters by interacting exclusively with the transferred phosphoryl group and the leaving group oxygen atom but no other atoms of the leaving group during catalysis (Fig. 1a and b). Despite this, the rate enhancement conferred by AP is up to 1027-fold, one of the largest recorded for enzymes [2]. The AP active site consists of a bimetallic Zn2+ core that activates the proximal Ser102 nucleophile and stabilizes charge that develops on the leaving group oxygen atom. Additional stabilization of the phosphoryl transfer transition state is thought to be provided by Arg166 and active site water molecules coordinated to the Mg2+ ion and hydrogen bonded to Lys328 (Fig. 1b) [3–5]. The tetrahedral geometry of the substrate is thought to achieve trigonal bipyramidal geometry in the phosphoryl transfer transition state [1].
Fig. 1.
Summary of the AP active site. (a) Reaction scheme for the phosphomonoester hydrolysis catalyzed by AP. ROP and E-P represent the phosphate monoester substrate and covalent seryl-phosphate intermediate, respectively. (b) Schematic of the AP active site drawn with partial bonds as in the presumed phosphoryl-transfer transition state. (c) Inhibition constants were calculated for the AP•HPO and AP•WO complexes for select AP mutants at pH 8. From Andrews et al. [6].
Prior mechanistic work that probed AP’s affinity for differentially protonated phosphate species used tungstate as a control since these anions have different pKa values. An intriguing observation from this study was that the binding affinity of the two ligands changes distinctly with mutation: specifically, while ablation of active site Arg166 reduces affinity for both anions at pH 8, additional removal of the Ser102 nucleophile increases phosphate affinity by 1200-fold, while it reduces tungstate affinity by 5-fold (Fig. 1c) [6]. Stronger tungstate binding in the presence of Ser102 could arise from the formation of a covalent adduct between the serine nucleophile and tungstate, a model that we test herein. Because tungstate in other active sites most frequently adopts tetrahedral [7–14] and more rarely trigonal bipyramidal [7,15] or octahedral geometries [16,17] (Table S1), detailed structural inspection of AP in complex with tungstate would additionally provide insight into the extent to which the AP active site stabilizes tungstate in a geometry that matches the presumed trigonal bipyramidal geometry of the transition state during phosphomonoester hydrolysis (Fig. 1b). Nevertheless, structural mimicry of the presumed transition state geometry does not guarantee that a ligand reproduces the energetics of transition state binding. We have therefore investigated both the structural and energetic properties of tungstate binding to the AP active site and compared tungstate binding to that of vanadate, a putative transition state analog, and phosphate, a known ground state mimic.
Results and Discussion
To test the model that Ser102 forms a covalent adduct with tungstate, we obtained a crystal structure of tungstate-bound AP at 2.0 Å resolution (Table 1). AP is a dimer, and the presence of a ligand in the active site of each monomer was evident from positive density in the difference map that appeared when the structure was modeled as the apo enzyme. We took advantage of density peaks in an anomalous scattering map generated from the same dataset to confirm that the ligand was not phosphate (Fig. S1a), which does not have an absorption edge near the wave length used for data collection. The anomalous scattering map also confirmed that the Mg2+ site was occupied by a Zn2+ ion, as residual density in the difference map suggested (Fig. S1a and b). Whereas prior work has demonstrated that the metal content of AP in solution is two Zn2+ ions and one Mg2+ ion and per active site [4,18], substitution at the Mg2+ site has previously been observed crystallographically [19]. The comparison of two previously obtained sub-2 Å resolution structures of phosphate-bound AP, one with full Mg2+ occupancy (3TG0 from Ref. [20]) and the other with partial Zn2+ occupancy at the third metal site (1ED8 from Ref. [20]), suggests that Zn2+ substitution does not perturb the positions, within the coordinate error of the models, of the water molecules coordinated by the metal ion at this site. Thus, this substitution at the third metal site is not expected to affect the interpretation of the structural data presented herein.
Table 1.
X-ray crystallographic data collection and refinement statistics
| Data Collection | |
|---|---|
| Space group | P6322 |
| Unit cell axes | |
| a, b, c (Å) | 161.3, 161.3, 139.4 |
| α, β, γ (°) | 90.0,90.0, 120.0 |
| Wavelength (Å) | .9795 |
| Resolution range (Å) | 52.74–2.03 (2.08–2.03)a |
| Rmerge | 0.059 (0.276)b |
| Rpim | 0.028 (0.129) |
| <l>/<σl> | 14.1 (3.9) |
| Completeness (%) | 93.6 (93.4) [82.3 (83.9)c |
| Multiplicity | 5.6 (5.7) [2.8 (3.2)] |
| CC1/2 | 0.823 (0.964) |
| Refinement | |
| Resolution range (Å) | 52.74–2.03 |
| No. of unique reflections | 64069 (6309) |
| No. of atoms | 6731 |
| Average B factors (Å2) | |
| protein | 40.1 |
| solvent | 33.4 |
| ligands | 34.4 |
| RMSD from standard geometry | |
| bond lengths (Å) | 0.02 |
| bond angles (°) | 1.9 |
| Ramachandran statistics | |
| favored regions | 98.1 |
| allowed regions | 1.9 |
| outliers (%) | 0 |
| PDB code | 5C66 |
Values in parenthesis are for the highest resolution shell.
Rmerge= Σ| Iobs - Iavg |/ΣIobs.
Values in brackets are for anomalous reflections.
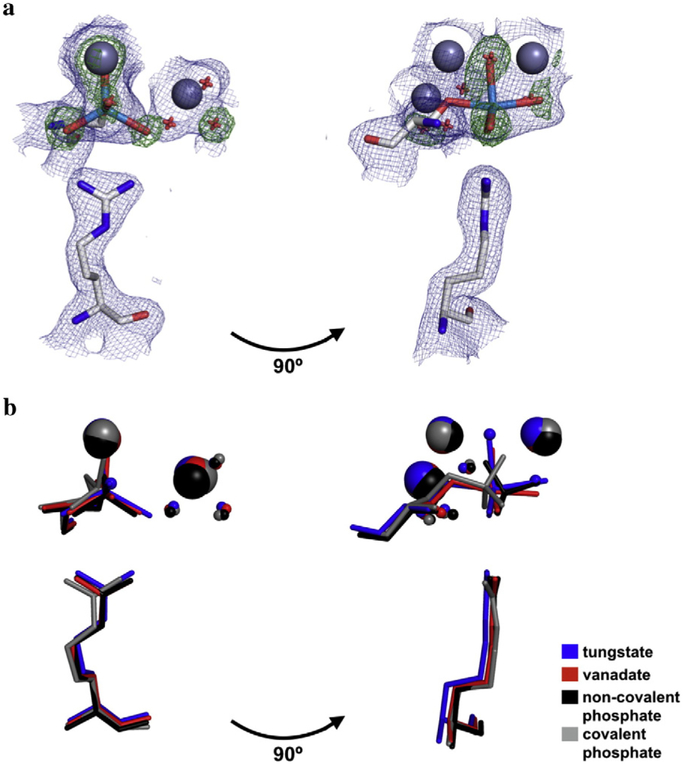
The tungstate molecule of our new structure was modeled in stages to most precisely position the tungstate atoms and avoid model bias. The anomalous scattering map was used to locate the tungsten atom relative to the adjacent Zn2+ ions (Fig. S1b). Refining the model with a tungsten atom in the active site left residual density peaks in the difference map that corresponded to the oxygen atoms of the tungstate (Fig. S1c); three of these peaks were roughly coplanar with the tungsten atom, and another peak was approximately colinear with the tungsten atom and Ser102 oxygen atom, consistent with trigonal bipyramidal geometry. These difference map peaks were absent in the final model that contained a partially occupied tungstate molecule covalently bound to Ser102 and in a trigonal bipyramidal configuration (Fig. S1d). As a further test of this geometry, a simulated annealing omit map was calculated in which the ligand oxygen atoms were omitted. Again, three density peaks coplanar with and spaced ~120° around the tungsten atom and a fourth peak colinear with the tungsten and Ser102 oxygen atom were observed, consistent with the modeled ligand geometry (Fig. 2a).
Fig. 2.
Structure of the tungstate-bound AP active site and in comparison to other bound anionic ligands. (a) Overlay of maps of the 2Fo-Fc electron density (contoured at 1σ) of the final model (blue) and the Fo-Fc map electron density (contoured at 4σ) from the simulated annealing omit map in which the oxygen atoms of the tungstate ion were omitted (green). Zn2+ ions are colored dark gray; tungstate, light blue; Ser102 and Arg166, light gray; waters, red. For clarity, only one active site is shown. (b) Crystal structures of AP bound to tungstate, vanadate, and phosphate (both covalently and non-covalently) were overlaid to compare the positions of ligands with respect to Ser102, Arg166, the active site Zn2+ and Mg2+ ions, and the Mg2+-coordinated water molecules. In the tungstate structure, the ligand was modeled in at partial occupancy, with partially occupied water molecules at sites that presumably coordinate the Zn2+ ions in the fraction of enzyme without bound tungstate. The PDB codes for vanadate, non-covalently bound phosphate, and covalently bound phosphate are 1B8J, 3TG0, and 1HJK, respectively.
The structure of tungstate-bound AP supports the prediction that tungstate forms a covalent adduct with the serine nucleophile. The W–Onuc distance is 2.2 Å, similar to the average distance of 2.1 Å between the non-nucleophile oxygen atoms and tungsten atom. (The coordinate error for this structure is 0.16 Å; see Materials and Methods). The sum of the ionic radii of tungsten and oxygen yields an expected distance of 1.86 Å for a covalent W–O bond [21]; however, this neglects partial double bond character and assumes that the tungsten atom is in its maximal and preferred +6 oxidation state. These effects are expected to reduce and increase the covalent W–O bond distance, respectively, and this distance may be further perturbed by ligand geometry and additional bonds to the oxygen ligands [21,22]. Indeed, W–O bond lengths span 1.66 to 2.18 Å in small-molecule crystal structures of pentacoordinate tungstate (WO5), with mean distances of 1.70 and 1.90 Å when the oxygen atom has no other covalent bond or is esterified, respectively (Table S2, Fig. S2). The W–O bonds observed in the tungstate•AP crystal structure are uniformly longer than these mean values. This difference may arise because longer W–O bonds optimize interactions between tungstate and the active site, or because differences in the properties, such as unit cell compactness and elemental composition, between small molecule and protein crystals bias the distributions of W–O bonds observed. The observation of a covalent bond between Ser102 and tungstate accounts for the favorable contribution of the serine nucleophile to tungstate affinity observed by Andrews et al. [6].
In addition to testing the model of a covalent bond with Ser102, the structure of tungstate-bound AP revealed that the AP active site stabilizes tungstate in the trigonal bipyramidal configuration of the presumed transition state. This geometry is similar to the ligand geometry observed in the 1.9 Å resolution crystal structure of vanadate-bound AP (PDB 1B8J [23]), although tungstate may be slightly more distorted from pure trigonal bipyramidal as indicated by the greater deviation from colinearity in the O–W–O angle for the apical oxygen atoms (164° for tungstate compared to 170° for vanadate) (Fig. 2b, Table S3; see Fig. S3 for separate depictions of the phosphate-bound structures and the vanadate- and tungstate-bound structures). Similar to vanadate and non-covalently bound phosphate, tungstate appears to form two hydrogen bonds to the well-positioned side chain of Arg166 (Fig. 2b, Table S4) [20,23]. However, the distortion of the apical oxygen atoms from colinearity combined with the longer W–O bonds appears to enable tungstate to provide superior coordination of the Zn2+ ions. All four of its Zn2 +–O distances fall in the expected range of 1.95–2.14 Å [24], whereas one of these bonds is considerably longer for vanadate, non-covalent phosphate, and covalently bound phosphate (2.4, 2.7, and 2.6 Å, respectively), and another is absent from covalently bound phosphate (Fig. 2b, Table S5) [20,23,25].
Unlike phosphate, tungstate and vanadate can undergo valency expansion to accommodate trigonal bipyramidal geometry. However, pentacoordinate tungstate infrequently adopts this geometry in small--molecule compounds and the active sites of other phosphatases (Tables S1 and S2), so the observation of trigonal bipyramidal geometry in the AP active site would not be expected based solely on structural precedent [26]. A survey of tungsten-containing small molecules in the Cambridge Structural Database [27] reveals that tungsten coordinated exclusively by oxygen atoms is most commonly hexacoordinate with octahedral geometry (Table S2). Pentacoordi-nate tungsten favors square pyramidal geometry, and there are no observed instances of trigonal bipyramidal geometry with five oxygen ligands. When structures of pentacoordinate tungsten containing one non-oxygen ligand are considered, only one example of trigonal bipyramidal geometry is found, with the majority of the 41 WO4X compounds favoring square pyramidal geometry (Table S2). A survey of active sites containing tungstate in the Protein Data Bank reveals a mix of tetrahedral, trigonal bipyramidal, and (in the case of histidine nucleophiles) octahedral geometries. However, with the exception of hexose phosphate phosphatase, cases that exhibit a trigonal bipyramidal configuration consistently deviate from the ideal geometry (in which the equatorial oxygen atoms are coplanar and spaced 120° apart) and, unlike AP, appear to be tetra- rather than pentacoordinate due to the distance between the tungsten atom and the enzyme’s nucleophile (Table S1).
The observation that wild-type (WT) AP stabilizes both tungstate and vanadate in the trigonal bipyramidal geometry of the presumed transition state prompted us to assess both oxyanions as transition state analogs. Strong binding affinity of a ligand—greater than that for substrates and products—is often considered an indication that a ligand is a transition state analog [28,29]. However, high binding affinity can also arise from fortuitous interactions that do not mimic transition state binding [30]. Conversely, weak binding affinity does not necessarily indicate a complete absence of transition state character in the ligand’s interaction with the active site. A more stringent criterion for a transition state analog is a linear log–log relationship between affinity and catalysis with a slope of one across a series of systematic perturbations to the enzyme (or ligand) [29,31]. High correlation in this relationship indicates that the energetics of ligand binding and transition state stabilization are sensitive to the same perturbations, and a slope of one suggests that these energetic effects are of the same magnitude for a given perturbation [29].
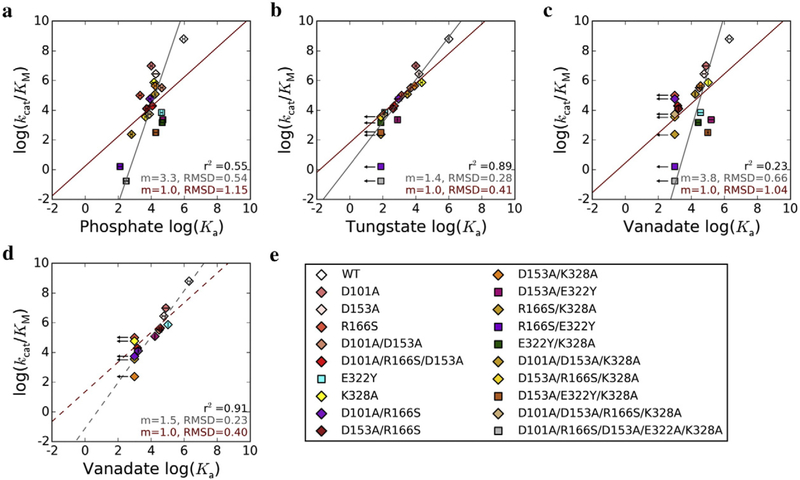
We therefore determined the relationship between ligand association constants, Ka, and kcat/KM for 20 AP variants that collectively span nine orders of magnitude in reaction rate (Table 2). Binding affinities for phosphate, a ground state mimic, span only four orders of magnitude, so despite some correlation (r2 = 0.55), the correlation line’s slope is substantially greater than one (m = 3.3, RMSD = 0.54; Fig. 3a, Table 3). By contrast, the logarithms of tungstate association constants and kcat/KM for the same set of mutants are highly linearly correlated (r2 = 0.89) with a slope close to one (m = 1.4, RMSD = 0.28; Fig. 3b, Table 3). This behavior supports tungstate as a good transition state analog, and the slope of 1.4 rather than 1 suggests that there are differences between tungstate binding and transition state stabilization that remain to be understood. Surprisingly, the log–log relationship of vanadate binding affinities and catalytic efficiencies does not show a similar linear correlation, with a slope of 3.8 and a coefficient of determination of only 0.23 (Fig. 3c, Table 3). Intriguingly, if the E322Y mutants that lack the Mg2+ ion are excluded from the fit, a strong correlation with a slope closer to one emerges (Fig. 3d, Table 3; r2 = 0.91, m = 1.5, RMSD = 0.23). The same trends are observed when a linear model with the slope constrained to 1 is fit to each dataset (Fig. 3, red lines): phosphate and vanadate behaviors are poorly fit by this model (RMSD of 1.15 and 1.04, respectively; Fig. 3a and c, Table 3), whereas the tungstate data fit well (RMSD = 0.41, Fig. 3b, Table 3) and the vanadate data fit well but only after the E322Y-containing mutants are excluded (RMSD = 0.40, Fig. 3d, Table 3).
Table 2.
Inhibition constants and catalytic efficiencies for AP mutants
| Kia(μM) | kcat/KMb (M−1S−1) |
|||
|---|---|---|---|---|
| Phosphate | Tungstate | Vanadate | ||
| WT | 1.1 (0.2)c | 1.0 (0.1)d | 0.50e | 6.3×108 |
| D101A | 100 (14) | 99 (12) | 13 (5) | 9.9×106 |
| D153A | 53 (19) | 64 (6) | 17 (0) | 2.8×106 |
| R166S | 4.8 (0.8)×102,f | 7.4 (0.1)×102 | ≥1×103 | 1.0×105 |
| D101A/D153A | 23 (4) | 2.0 (0)×102 | 32 (12) | 3.3×105 |
| D101A/R166S/D153A | 85 (30) | 2.0 (0.4)×103 | 6.7 (2.8)×102 | 2.0×104 |
| E322Y | 24 (4) | 7.7 (0.8)×103 | 28 (12) | 7.2×103 |
| K328A | 68 (20) | 44 (6) | 9.4 (0.2) | 7.5×105 |
| D101A/R166S | 1.2 (0.2)×102 | 1.1 (0.5)×103 |
≥1×103 | 5.8×104 |
| D153A/R166S | 1.9 (0.3)×102 | 2.4 (0.6)×103 | 5.9(0.3)×102 | 1.3×104 |
| D153A/K328A | 57 (10) | 1.2 (0.3)×102 | 28 (6) | 4.4×105 |
| D153A/E322Y | 20 (6) | 1.3 (0.1)×103 | 6.3 (3.0) | 2.3×103 |
| D153A/E322Ag | 12 (5) | 1.8×103 | 47 (0) | - |
| R166S/K328A | 1.6 (0.2)×103 | ≥1.3×104 | ≥1×103 | 2.4×102 |
| R166S/E322Y | 7.8 (2.3)×103 | ≥1.3×104 | ≥1×103 | 1.6 |
| E322Y/K328A | 22 (6) | ≥1.3×104 | 39 (11) | 1.5×103 |
| D101A/D153A/K328A | 58 (5) | 3.3 (0.6)×102 | 59 (3) | 1.2×105 |
| D153A/R166S/K328A | 2.2 (0.3)×102 | ≥1.3×104 | ≥1×103 | 3.6×103 |
| D153A/E322Y/K328A | 53 (14) | ≥1.3×104 | 10 (1) | 3.2 ×102 |
| D101A/D153A/R166S/K328A | 1.3 (0.3)×102 | 8.9 (1.0)×103 | ≥1×103 | 5.5×103 |
| D101A/R166S/D153A/E322A/K328A | 3.3 (1.0)×103 | ≥1.3×104 | ≥1×103 | 0.17 |
The listed values correspond to the observed pH-dependent Ki in contrast to the species-specific Ki listed in Fig. 1c. Errors are noted in parenthesis and correspond to the standard deviations from 2–3 independent experiments.
Values are reproduced from Sunden et al. [18], in which rates were measured by monitoring the hydrolysis of p-nitrophenol phosphate (pNPP) for all AP variants except WT, because the chemical step is not rate-limiting for WT AP with this substrate [3]. The chemical step is, however, rate-limiting for WT hydrolysis of the less reactive substrate methyl phosphate [3], so the WT kcat/KM value listed is the kcat/KM,obs value measured for methyl phosphate multiplied by the ratio of the kcat/KM values observed for pNPP and methyl phosphate for AP mutants for which the chemical step is rate-limiting. This ratio of 20 is constant across several mutants, supporting its use as a correction factor to estimate the expected kcat/KM value [18].
Value is reproduced from O’Brien et al. [3].
L. D. Andrews and D. Herschlag, unpublished result.
A similar value of 4.6 × 102 μM has been reported for this mutant [5].
Inhibition constants for the D153A/E322A mutant were measured to test whether the differential responses of tungstate and vanadate to ablation of the Mg2+ ion arise from interactions with the Tyr introduced at this position. The D153A/E322Y and D153A/E322A mutants have similar inhibition constants for phosphate and tungstate, but vanadate binds 7.5-fold stronger when E322 is replaced with Tyr rather than Ala. A favorable interaction between vanadate and E322Y is the simplest model for this difference and would weaken the correlation between vanadate affinity and enzymatic activity. To assess the consequences of this effect, we adjusted vanadate inhibition constants for mutants containing E322Y by a factor of 7.5-fold, assuming a constant Tyr effect, and recalculated the linear fit. Even with this adjustment, the vanadate correlation is worse than that observed for tungstate, with a slope of m = 2.4 (RMSD = 0.43) for the total least squares regression linear fit and a coefficient of determination of r2 = 0.67, whereas the corresponding values for the tungstate correlation are m = 1.4 (RMSD = 0.28) and r2 = 0.89. When the linear regression is recalculated with the slope constrained to m = 1, the RMSD of the fit for the vanadate data with this correction factor is 0.79, compared to an RMSD of 0.41 for the tungstate data.
Fig. 3.
Transition state analog behavior of phosphate, tungstate, and vanadate. Correlations between the log of kcat/KM and log of association constant, Ka, for (a) phosphate, (b) tungstate, and (c) vanadate. The linear fit from total least squares regression is shown by the gray lines, and the slope (m) and RMSD are given in gray at the bottom right of each plot. The red lines show linear regressions with the slope constrained to 1, and the m and RMSD values are given in red. The value for the coefficient of determination, r2, is given for each dataset in black. For vanadate, the linear fit was also calculated excluding mutants with the Mg2+ site ablated (d). The AP variants used are listed in (e); mutants with an intact Mg2+ site are represented by diamonds, and those deficient in Mg2+ binding due to the presence of the E322Y mutation are indicated by squares. Arrows denote mutants for which only an upper limit for Ka could be determined; these mutants were not included in the linear fits. Error bars correspond to standard deviations from 2–3 independent experiments.
Table 3.
Transition state analog behavior for phosphate, tungstate, and vanadate
| Phosphate | Tungstate | Vanadate | |
|---|---|---|---|
| Coefficient of | 0.55 | 0.89 | 0.23 [0.91]a |
| determination, r2 | |||
| mbest fitb | 3.3 | 1.4 | 3.8 [1.5] |
| RMSDbest fitc | 0.54 | 0.28 | 0.66 [0.23] |
| RMSDm=1d | 1.15 | 0.41 | 1.04 [0.40] |
Brackets denote values calculated after excluding mutants with an ablated Mg2+ site.
Slope of the best fit line was determined from orthogonal distance regression; see Materials and Methods.
RMSD was calculated from the orthogonal residual between data points and the noted linear model.
RMSD was calculated between data points and the best fit linear model with slope constrained to 1.
These observations raise the following questions: why is tungstate a superior transition state analog compared to vanadate?, and why is vanadate binding affinity insensitive to loss of the Mg2+ ion? Prior work dissecting the AP active site has shown that apart from the Ser102 nucleophile and bimetallic Zn2+ core, the Mg2+ ion and Arg166 are the active site moieties that have the largest effects on catalysis (Table 2) [4,5]. However, the Mg2+ ion and its associated water network provide significantly more transition state-specific stabilization compared to Arg166, which stabilizes both the transition and ground states (Fig. 1b) [4,5,18]. The relative contributions of the Mg2+ ion to binding affinity versus rate enhancement would thus be expected to probe how well a ligand mimics the energetics specific to AP’s transition state, so the insensitivity of vanadate but not tungstate binding affinity to loss of the Mg2+ ion is particularly striking in the context of transition state analog behavior (Fig. 3, Tables 2 and 3).
Inherent differences in the charge distribution, protonation states, and/or favored bond lengths and geometries of vanadate and tungstate oxyanions may account for the distinct energetic contributions of the Mg2+ ion to their stabilities in the AP active site. However, our functional data suggest that the first two models do not account for the observed Mg2+ effect. Specifically, a model that attributes vanadate’s and tungstate’s distinct energetic properties to their different charge distributions would not predict the ligands’ similar responses to ablation of Arg166 and its electrostatic interactions (Fig. 3, Table 2). Likewise, the same trends and correlations are observed across pH, providing evidence against complications from differential protonation states of the ligands (see Materials and Methods). In contrast, comparison of the AP•tungstate and AP•vanadate structures suggests that energetic differences may arise from distinct interactions between the ligand oxygen atoms and the Zn2+ core due to the longer W–O than V–O bond. Specifically, both ligands appear to interact with the Mg2+-associated water network (Fig. S4), but tungstate coordinates the Zn2+(1) ion that presumably stabilizes the leaving group oxygen of the transition state whereas vanadate does not (Fig. 2b, Table 2). It is possible, given vanadate’s bond lengths, that interactions with the Mg2 +–water network and Zn2+(1) cannot be simultaneously optimized. If this were the case, loss of the Mg2 +–water network interactions might be energetically compensated by the formation of a Zn2+(1)–oxygen interaction in the vanadate complex. This interaction is already present in the WT AP•tungstate complex (Fig. 2b, Table S5), so this complex would not experience compensation for the energetic cost of Mg2+ ion removal and could thus mimic transition state energetics. It is also possible that loss of the Mg2+ ion increases the conformational mobility of the tungstate oxygen atom that interacts with the Mg2+-associated water molecule, and this in turn destabilizes the Zn2+(1)–oxygen interaction that is present in tungstate but not in vanadate. These models make distinct predictions for the properties of mutant AP complexes with tungstate and vanadate.
The finding that tungstate is covalently bound to Ser102 resolves the question of why, in contrast to phosphate, the presence of the serine nucleophile contributes favorably to tungstate affinity (Fig. 1c) [6]. The observation that the AP active site stabilizes tungstate in trigonal bipyramidal geometry is striking given how infrequently tungstate adopts this geometry in other enzyme active sites and small-molecule compounds. We cannot experimentally measure the energetic cost of distortion of tungstate from the tetrahedral geometry favored in solution to the trigonal bipyramidal geometry stabilized by the AP active site. Nevertheless, this energetic penalty may account for a surprising observation: ablation of the nucleophile (from AP Arg166Ser to Ser102Gly/Arg166Ser), which results in loss of a covalent bond, only causes a fivefold reduction in affinity (Fig. 1c) [6]. Thus, it is possible that the enthalpic contribution from forming the covalent bond with Ser102 is nearly fully offset by distorting tungstate to an energetically unfavorable geometry.
Stabilization of the trigonal bipyramidal geometry of the presumed transition state is observed for both tungstate and vanadate in the AP active [23]. However, tungstate, but not vanadate, passes the litmus test for a transition state analog—that is, a linear correlation with a slope of one between the logarithms of catalytic efficiency and ligand binding affinity (Fig. 3) [31,32]. Two prior studies challenged vanadate as a transition state analog for phosphoryl transfer [31,33], and our work extends those reports in a critical way. Vanadate and tungstate have frequently been inferred to be transition state analogs based on high binding affinity to the WT enzyme (e.g., Refs. [34–36]) or, especially for vanadate, active site stabilization of the ligand in trigonal bipyramidal geometry (reviewed in Ref. [26]). To our knowledge, only two studies have performed a mutational test of vanadate’s transition state analog energetics (and none has similarly examined tungstate); three and five active site mutants of RNase E [32] and protein tyrosine phosphatase [33], respectively, showed vanadate binding behavior to be inconsistent with the prediction of linearity for a transition state analog. Extending this analysis to 20 variants of AP enables us to localize vanadate’s deviation from transition state analog behavior to a specific moiety—the Mg2+ ion—in the AP active site, a mechanistic insight afforded by the scope of the mutants presented herein. With this test, we further established that tungstate is a more suitable transition state analog. Studies of AP•tung-state complexes may help elucidate the catalytic contributions of the Mg2+ ion in AP and may be useful in future mechanistic studies of AP and other phosphoryl transfer enzymes.
Materials and Methods
Protein expression and purification
AP was purified from a fusion construct that contained an N-terminal maltose-binding protein tag and a C-terminal factor Xa cleavage site and StrepII tag. E. coli SM547 (DE3) cells were transformed with this construct and grown at 37 °C in rich media supplemented with glucose (10 g of tryptone, 5 g of yeast extract, 5 g of NaCl, and 2 g of glucose per liter). Once the OD600 reached 0.6, expression of the AP fusion construct was induced by addition of IPTG to 0.3 mM. Cultures were grown for an additional 16–20 h at 30 °C. Cells were harvested by centrifugation at 4400 × g for 20 min and lysed by osmotic shock. The pellet was resuspended in 800 mL 20% sucrose solution [30 mM Tris–HCl (pH 8.0) and 1 mM EDTA] per original 2 L culture and incubated at 4 °C for 10 min on a shaking table. Cells were re-pelleted by centrifugation at 13,000 × g for 10 min and resuspended in column buffer [10 mM Tris–HCl (pH 7.4), 200 mM NaCl, and 10 μM ZnCl2] at 4 °C. The sample was passed over a 10 mL amylose resin gravity column (New England BioLabs, Ipswich, MA). The column was washed with 10 column volumes of column buffer and eluted with the same buffer supplemented with 10 mM maltose. Fractions containing protein were concentrated by centrifugation through a filter (Amicon) with a 10 kDa cut-off and buffer-exchanged twice into 10 mM Na–Mops (pH 7.0), 50 mM NaCl, 100 μM ZnCl2, and 1.0 mM MgCl2. In the case of AP mutants containing the E322Y mutation, MgCl2 was omitted from the buffer. Purity was determined to be greater than 95% by SDS-PAGE gel electrophoresis with staining by Coomassie Blue.
Inhibition measurements
Inhibition constants for phosphate, tungstate, and vanadate were measured in 0.1 M MOPS (pH 8.0), 0.5 M NaCl, 100 μM ZnCl2, and 500 μM MgCl2 at 25 °C, except for E322Y mutants, for which MgCl2 was excluded. The maltose binding protein tag was not excised from AP for these measurements; this tag has previously been shown to not affect AP’s rate constant [4,37]. Inhibitor concentration was varied at least fivefold below and above the observed Ki at a constant concentration of enzyme and a sub-saturating concentration of methyl p-nitrophenol phosphate, a diester substrate. To prevent polymerization of vanadate and tungstate, stock ligand was stored at pH 13, and maximum concentrations of 4.6 and 13 mM, respectively, of the inhibitor were used. Formation of the product p-nitrophenolate was monitored continuously at 400 nm. The inhibition constant was calculated with a nonlinear least squares fit to the data using the following equation for competitive inhibition:
The above equation is most commonly used to describe non-covalent inhibition, but it is also applicable to covalent inhibition when the non-covalent and covalently-bound species equilibrate more quickly than the timescale of the measurement. The measured rates were linear over time at all concentrations of inhibitor, indicating an absence of time dependence to the inhibition and thus fast equilibration of the covalent and non-covalent species relative to the measurement.
Correlation between log(kcat/KM) and log(Ka) was modeled by total least squares regression. The slope for the linear fit was calculated by performing principal component analysis; the ratio of the values of the first eigenvector of the covariance matrix yields the slope, m, and the y-intercept, b, can be recovered from: . Additionally, the optimal linear fit was calculated when the slope was constrained to m = 1. Goodness of fit was assessed by computing the RMSD of the minimal (orthogonal) distance between each data point [log(Ka), log(kcat/KM)] and each linear model. Finally, the coefficient of determination, r2, was computed from the square of the Pearson correlation coefficient; the latter is given by the following formula:
Inhibition constants were additionally measured at pH 9.0 for 16 of the 19 mutants listed in Table 2, and the same trends and correlations as reported in Fig. 3 were observed (data not shown). We were unable to measure inhibition constants below pH 8.0 due to polymerization of vanadate and tungstate at neutral pH and above pH 9.0 due to an enzymatic pKa [6] that raises the inhibition constant above the threshold that we can measure for most mutants.
Crystallization
WT AP was purified as described above, and the maltose-binding protein tag was cleaved with factor Xa. Enzyme and tag were separated by passage over a 5 mL HiTrap Q HP column (GE Healthcare, Amersham, UK). Enzyme was buffer-exchanged into 10 mM Na–MOPS, pH 8.0), 50 mM NaCl, 10 μM ZnCl2, and 100 μM MgCl2, concentrated to 200 μM, and pre-incubated with 500 μM sodium tungstate. Crystallization was performed by the hanging drop method at 18 °C, with equal volumes (2 μL each) of enzyme and precipitant solution (18% PEG3350 and 0.2 M ammonium fluoride) placed over a reservoir of 1 mL precipitant solution. Crystals were soaked in cryoprotectant solution [30% glycerol, 0.1 mM Bis–Tris (pH 5.0), and 0.2 mM ammonium sulfate] and frozen in liquid nitrogen. Crystallographic data were collected at Stanford Linear Accelerator beamline 12–2 at a wavelength of 0.9795 Å.
Structure determination
Data integration was performed with MOSFLM [38]; scaling and merging were carried out in AIMLESS [39] with 5% of reflections set aside to calculate Rfree. Molecular replacement was completed with PHASER [40] using WT AP (PDB 3TG0 [20]) stripped of ligand and metals as a search model. Alternating rounds of manual model building and automated refinement were performed with COOT [41] and REFMAC5 [42], respectively. The tung-state ion was modeled in stages near the end of the refinement process. First, an anomalous scattering map was generated from the scaled dataset and partially refined model using PHENIX [43], which enabled the positioning of the tungsten atom into the center of the anomalous scattering peak. After a round of automated refinement, negative density appeared in the difference map at the position of the tungsten atom, so its occupancy was reduced to 0.5. A tetrahedral tungstate ion was then loaded from the JLigand library [44] and substituted for the tungsten atom. Automated refinement corrected the geometry to trigonal bipyramidal, consistent with the appearance of the difference density map prior to addition of the tungstate oxygen atoms. Omit maps generated in PHENIX [43] provided additional validation of the trigonal bipyramidal geometry. Two positive density peaks remained in the active site after modeling in the tungstate; these were modeled as half-occupied water molecules that coordinate the Zn2+ ions. Stereochemistry was validated by MOLPROBITY [45], and images were generated with PYMOL [46]. Coordinate error was determined by the diffraction-data precision indicator estimate [47].
Supplementary Material
Acknowledgments
This work was funded by a grant from the US National Institutes of Health to D.H. (GM49243). A.P. was funded by a National Science Foundation Graduate Research Fellowship. L.D.A. was supported in part by an NIH training grant (R1GM064798). The SSRL Structural Molecular Biology Program receives support from the Department of Energy, Office of Biological and Environmental Research, the National Institutes of Health, National Center for Research Resources, Biomedical Technology Program, and the National Institute of General Medical Sciences. We thank Daniel Roston and Qiang Cui for instructive discussions, Susanne Ressl for help with crystallo-graphic data collection, Artem Lyubimov and James Fraser for useful discussions about crystallographic refinement, Ishraq AlSadhan for help with enzyme purification, and Julia Salzman for advice about statistics. We are grateful to members of the Herschlag group for discussions and comments on the manuscript.
Abbreviations used:
- AP
alkaline phosphatase
- WT
wild-type
Footnotes
Accession numbers
The accession number for the tungstate•AP crystal structure is PDB ID: 5C66.
Conflict of interest:
The authors declare no conflict of interest.
Appendix A. Supplementary Data
Supplementary data to this article can be found online at http://dx.doi.org/10.1016/j.jmb.2016.05.007.
References
- [1].Coleman JE, Structure and mechanism of alkaline phosphatase, Annu. Rev. Biophys. Biomol. Struct 21 (1992) 441–483, 10.1146/annurev.bb.21.060192.002301. [DOI] [PubMed] [Google Scholar]
- [2].Lassila JK, Zalatan JG, Herschlag D, Biological phosphoryl-transfer reactions: understanding mechanism and catalysis, Annu. Rev. Biochem 80 (2011) 669–702, 10.1146/annurev-biochem-060409-092741. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].O’Brien PJ, Herschlag D, Alkaline phosphatase revisited: hydrolysis of alkyl phosphates, Biochemistry 41 (2002) 3207–3225, 10.1021/bi012166y. [DOI] [PubMed] [Google Scholar]
- [4].Zalatan JG, Fenn TD, Herschlag D, Comparative enzymology in the alkaline phosphatase superfamily to determine the catalytic role of an active-site metal ion, J. Mol. Biol 384 (2008) 1174–1189, 10.1016/j.jmb.2008.09.059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].O’Brien PJ, Lassila JK, Fenn TD, Zalatan JG, Herschlag D, Arginine coordination in enzymatic phosphoryl transfer: evaluation of the effect of Arg166 mutations in Escherichia coli alkaline phosphatase, Biochemistry 47 (2008) 7663–7672, 10.1021/bi800545n. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Andrews LD, Fenn TD, Herschlag D, Ground state destabilization by anionic nucleophiles contributes to the activity of phosphoryl transfer enzymes, PLoS Biol 11 (2013), e1001599, 10.1371/journal.pbio.1001599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Lu Z, Dunaway-Mariano D, Allen KN, The catalytic scaffold of the haloalkanoic acid dehalogenase enzyme superfamily acts as a mold for the trigonal bipyramidal transition state, Proc. Natl. Acad. Sci. U. S. A 105 (2008) 5687–5692, 10.1073/pnas.0710800105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Lu Z, Wang L, Dunaway-Mariano D, Allen KN, Structure–function analysis of 2-keto-3-deoxy-D-glycero-D-galactonono-nate-9-phosphate phosphatase defines specificity elements in type C0 haloalkanoate dehalogenase family members, J. Biol. Chem 284 (2009) 1224–1233, 10.1074/jbc.M807056200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Peisach E, Selengut JD, Dunaway-Mariano D, Allen KN, X-ray crystal structure of the hypothetical phosphotyrosine phosphatase MDP-1 of the haloacid dehalogenase super-family, Biochemistry 43 (2004) 12,770–12,779, 10.1021/bi0490688. [DOI] [PubMed] [Google Scholar]
- [10].Chu HM, Wang AHJ, Enzyme-substrate interactions revealed by the crystal structures of the archaeal Sulfolobus PTP-fold phosphatase and its phosphopeptide complexes, Proteins Struct. Funct. Genet 66 (2007) 996–1003, 10.1002/prot.21262. [DOI] [PubMed] [Google Scholar]
- [11].Brandão TAS, Robinson H, Johnson SJ, Hengge AC, Impaired acid catalysis by mutation of a protein loop hinge residue in a YopH mutant revealed by crystal structures, J. Am. Chem. Soc 131 (2009) 778–786, 10.1021/ja807418b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Reynolds RA, Yem AW, Wolfe CL, Deibel MR, Chidester CG, Watenpaugh KD, Crystal structure of the catalytic subunit of Cdc25B required for G2/M phase transition of the cell cycle, J. Mol. Biol 293 (1999) 559–568, 10.1006/jmbi.1999.3168. [DOI] [PubMed] [Google Scholar]
- [13].Hamda K, Kato M, Shimizu T, Ihara K, Mizuno T, Hakoshima T, Crystal structure of the protein histidine phosphatase SixA in the multistep His–Asp phosphorelay, Genes Cells 10 (2005) 1–11, 10.1111/j.1365-2443.2005.00817.x. [DOI] [PubMed] [Google Scholar]
- [14].Chen Y, Jakoncic J, Wang J, Zheng X, Carpino N, Nassar N, Structural and functional characterization of the C-terminal domain of the ecdysteroid phosphate phosphatase from Bombyx mori reveals a new enzymatic activity, Biochemistry 47 (2008) 12,135–12,145, 10.1021/bi801318w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Felts RL, Ou Z, Reilly TJ, Tanner JJ, Structure of recombinant Haemophilus influenzae e (P4) acid phosphatase reveals a new member of the haloacid dehalogenase superfamily, Biochemistry 46 (2007) 11,110–11,119, 10.1021/bi701016m. [DOI] [PubMed] [Google Scholar]
- [16].Davies DR, Interthal H, Champoux JJ, Hol WGJ, Insights into substrate binding and catalytic mechanism of human tyrosyl-DNA phosphodiesterase (Tdp1) from vanadate and tungstate-inhibited structures, J. Mol. Biol 324 (2002) 917–932, 10.1016/S0022-2836(02)01154-3. [DOI] [PubMed] [Google Scholar]
- [17].Leiros I, McSweeney S, Hough E, The reaction mechanism of phospholipase D from Streptomyces sp. strain PMF. Snapshots along the reaction pathway reveal a pentacoordi-nate reaction intermediate and an unexpected final product, J. Mol. Biol 339 (2004) 805–820, 10.1016/j.jmb.2004.04.003. [DOI] [PubMed] [Google Scholar]
- [18].Sunden F, Peck A, Salzman J, Ressl S, Herschlag D, Extensive site-directed mutagenesis reveals interconnected functional units in the alkaline phosphatase active site, Elife 4 (2015) 1–31, 10.7554/eLife.06181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Stec B, Holtz KM, Kantrowitz ER, A revised mechanism for the alkaline phosphatase reaction involving three metal ions, J. Mol. Biol 299 (2000) 1303–1311, 10.1006/jmbi.2000.3799. [DOI] [PubMed] [Google Scholar]
- [20].Bobyr E, Lassila JK, Wiersma-Koch HI, Fenn TD, Lee JJ, Nikolic-Hughes I, et al. , High-resolution analysis of Zn2+ coordination in the alkaline phosphatase superfamily by EXAFS and x-ray crystallography, J. Mol. Biol 415 (2012) 102–117, 10.1016/j.jmb.2011.10.040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Shannon RD, Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides, Acta Crystallogr. Sect. A: Found. Crystallogr 32 (1976) 751–767, 10.1107/S0567739476001551. [DOI] [Google Scholar]
- [22].Harris SE, Orpen a.G., Bruno IJ, Taylor R, Factors affecting d-block metal-ligand bond lengths: toward an automated library of molecular geometry for metal complexes, J. Chem. Inf. Model 45 (2005) 1727–1748, 10.1021/ci0500785. [DOI] [PubMed] [Google Scholar]
- [23].Holtz KM, Stec B, Kantrowitz ER, A model of the transition state in the alkaline phosphatase reaction, J. Biol. Chem 274 (1999) 8351–8354. [DOI] [PubMed] [Google Scholar]
- [24].Harding MM, Geometry of metal–ligand interactions in proteins, Acta Crystallogr. Sect. D: Biol. Crystallogr 57 (2001) 401–411, 10.1107/S0907444900019168. [DOI] [PubMed] [Google Scholar]
- [25].Murphy JE, Stec B, Ma L, Kantrowitz ER, Trapping and visualization of a covalent enzyme–phosphate intermediate, Nat. Struct. Biol 4 (1997) 618–622, 10.1038/nsb0897-618. [DOI] [PubMed] [Google Scholar]
- [26].Davies DR, Hol WGJ, The power of vanadate in crystallographic investigations of phosphoryl transfer enzymes, FEBS Lett 577 (2004) 315–321, 10.1016/j.febslet.2004.10.022. [DOI] [PubMed] [Google Scholar]
- [27].Allen FH, The Cambridge structural database: a quarter of a million crystal structures and rising, Acta Crystallogr. Sect. B: Struct. Sci 58 (2002) 380–388, 10.1107/S0108768102003890. [DOI] [PubMed] [Google Scholar]
- [28].Wolfenden R, Transition state analogues for enzyme catalysis, Nature 223 (1969) 704–705, 10.1038/223704a0. [DOI] [PubMed] [Google Scholar]
- [29].Mader MM, P.a. Bartlett, Binding energy and catalysis: the implications for transition-state analogs and catalytic antibodies, Chem. Rev 97 (1997) 1281–1302, 10.1021/cr960435y. [DOI] [PubMed] [Google Scholar]
- [30].Wolfenden R, Transition state analog inhibitors and enzyme catalysis, Annu. Rev. Biophys. Bioeng 5 (1976) 271–306, 10.1146/annurev.bb.05.060176.001415. [DOI] [PubMed] [Google Scholar]
- [31].Messmore JM, Raines RT, Pentavalent organo-vanadates as transition state analogues for phosphoryl transfer reactions, J. Am. Chem. Soc 122 (2000) 9911–9916, 10.1021/ja0021058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Bartlett PA, Marlowe CK, Phosphonamidates as transition-state analogue inhibitors of thermolysin, Biochemistry 22 (1983) 4618–4624, 10.1021/bi00289a002. [DOI] [PubMed] [Google Scholar]
- [33].Deng H, Callender R, Huang Z, Zhang Z-Y, Is the PTPase–vanadate complex a true transition state analogue? Biochemistry 41 (2002) 5865–5872, 10.1021/bi016097z. [DOI] [PubMed] [Google Scholar]
- [34].VanEtten RL, Waymack PP, Rehkop DM, Transition metal ion inhibition of enzyme-catalyzed phosphate ester displacement reactions, J. Am. Chem. Soc 96 (1974) 6782–6785, 10.1021/ja00828a053. [DOI] [PubMed] [Google Scholar]
- [35].Georgalis Y, Zouni A, Hahn U, Saenger W, Synthesis and kinetic study of transition state analogs for ribonuclease T1, Biochim. Biophys. Acta 1118 (1991) 1–5. [DOI] [PubMed] [Google Scholar]
- [36].Stankiewicz PJ, Gresser MJ, Inhibition of phosphatase and sulfatase by transition-state analogues, Biochemistry 27 (1988) 206–212, 10.1021/bi00401a031. [DOI] [PubMed] [Google Scholar]
- [37].O’Brien PJ, Herschlag D, Functional interrelationships in the alkaline phosphatase superfamily: phosphodiesterase activity of Escherichia coli alkaline phosphatase, Biochemistry 40 (2001) 5691–5699, 10.1021/bi0028892. [DOI] [PubMed] [Google Scholar]
- [38].Battye TGG, Kontogiannis L, Johnson O, Powell HR, Leslie AGW, iMOSFLM: a new graphical interface for diffraction-image processing with MOSFLM, Acta Crystallogr. Sect. D: Biol. Crystallogr 67 (2011) 271–281, 10.1107/S0907444910048675. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Evans PR, Murshudov GN, How good are my data and what is the resolution? Acta Crystallogr. Sect. D: Biol. Crystallogr 69 (2013) 1204–1214, 10.1107/S0907444913000061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].McCoy AJ, Grosse-Kunstleve RW, Adams PD, Winn MD, Storoni LC, Read RJ, Phaser crystallographic software, J. Appl. Crystallogr 40 (2007) 658–674, 10.1107/S0021889807021206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [41].Emsley P, Lohkamp B, Scott WG, Cowtan K, Features and development of Coot, Acta Crystallogr. Sect. D: Biol. Crystallogr 66 (2010) 486–501, 10.1107/S0907444910007493. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42].Murshudov GN, Skubák P, Lebedev AA, Pannu NS, Steiner RA, Nicholls RA, et al. , REFMAC5 for the refinement of macromolecular crystal structures, Acta Crystallogr. Sect. D: Biol. Crystallogr 67 (2011) 355–367, 10.1107/S0907444911001314. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Adams PD, Afonine PV, Bunkóczi G, Chen VB, Davis IW, Echols N, et al. , PHENIX: a comprehensive Python-based system for macromolecular structure solution, Acta Crystallogr. Sect. D: Biol. Crystallogr 66 (2010) 213–221, 10.1107/S0907444909052925. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44].Lebedev AA, Young P, Isupov MN, Moroz OV, Vagin AA, Murshudov GN, JLigand: a graphical tool for the CCP4 template-restraint library, Acta Crystallogr. Sect. D: Biol. Crystallogr 68 (2012) 431–440, 10.1107/S090744491200251X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45].Chen VB, Arendall WB, Headd JJ, Keedy DA, Immormino RM, Kapral GJ, et al. , MolProbity: all-atom structure validation for macromolecular crystallography, Acta Crystal- logr. Sect. D: Biol. Crystallogr 66 (2010) 12–21, 10.1107/S0907444909042073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [46].DeLano WL, The PyMOL molecular graphics system Schrödinger LLC Wwwpymolorg, 2002. Version 1: http://www.pymol.org(doi:citeulike-article-id:240061). [Google Scholar]
- [47].Murshudov GN, Dodson EJ, Simplified error estimation a la Cruickshank in macromolecular crystallography, Bailey S (Ed.) CCP4 Newletter, Daresbury Laboratory, Cheshire, UK, 1997. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.