Gating interaction maps reveal a noncanonical electromechanical coupling mode in the Shaker K⁺ channel

Abstract

Membrane potential regulates the activity of voltage-dependent ion channels via specialized voltage-sensing modules but the mechanisms involved in coupling voltage-sensor movement to pore opening remain unclear due to lack of resting state structures and robust methods to identify allosteric pathways. Here, using a newly developed interaction energy analysis, we probe the interfaces of the voltage-sensing and pore modules in the drosophila Shaker K⁺ channel. Our measurements reveal unexpectedly strong equilibrium gating interactions between contacts at the S4 and S5 helices in addition to those between S6 and S4–S5 linker. Network analysis of MD trajectories shows that the voltage-sensor and pore motions are linked by two distinct pathways- canonical one through the S4–S5 linker and a hitherto unknown pathway akin to rack and pinion coupling involving S4 and S5 helices. Our findings highlight the central role of the S5 helix in electromechanical transduction in the VGIC superfamily.

INTRODUCTION

Electrical signaling underlies a variety of fundamental biological processes that include nerve impulses, rhythmic contraction of the heart, hormonal secretion to name a few. Members of the voltage-gated ion channel (VGIC) superfamily are primarily responsible for electrical excitability in higher organisms. They share a common structural feature wherein four discrete voltage-sensing modules surround a central pore module¹. Each voltage-sensing module is made up of four transmembrane segments whereas the central pore module has a total of eight transmembrane segments contributed by four subunits. Changes in membrane voltage drive the movement of the charge-carrying transmembrane segments in the voltage-sensing domain, which is coupled, to the pore gates in the central pore module. Over the past decade, it has become increasingly evident that the differences in coupling between the voltage-sensor domain and the pore are a crucial determinant of channel behavior^2,3.

In a definitive study, Lu and colleagues^4,5 were the first to show that the two transmembrane segment KcsA channel exhibits voltage-dependent activity when fused to the voltage-sensing domain of Shaker potassium channel as long as the contacts between the S4–S5 linker and the lower S6 helix was conserved. High-resolution structures of the voltage-gated ion channels suggest a plausible model of electromechanical coupling^1,6–8. Accordingly, the movement of the S4 transmembrane segment pushes or pulls the attached S4–S5 linker which is in juxtaposition with a portion of the S6 helix that forms the pore gate (S6_CT). The notion that the S4–S5 linker is central to electromechanical coupling in the VGIC superfamily is supported by sophisticated structure function studies in potassium and sodium channels which show that mutations in this intracellular gating interface alters channel gating and make voltage-dependent opening less efficient^5,9,10.

Recent studies, however, have raised new questions about the role of the S4–S5 linker and the mechanism of electromechanical coupling^11,12. Using a split channel strategy, Lörinczi, et. al¹⁴ found that the EAG channels are still gated by voltage despite the deletion of the S4–S5 linker. High-resolution cryo-EM structures of wild type EAG channels¹³ show that these channels have a non-domain swapped architecture and that the S4–S5 linker is a short loop rather than distinct helix as in Kv1.2–2.1 chimeras. This raises the possibility that the S4–S5 helix is only involved in coupling in channels with domain swapped architecture such as the Shaker potassium channel whereas in non-domain swapped configuration there exists a non-canonical pathway that bypasses the S4–S5 linker region.

What are the alternate mechanisms for coupling between the voltage-sensor and pore? Even though the voltage-sensor is a discrete and somewhat portable module, in every structure of a voltage-gated ion channel, there are residues in the voltage-sensing domain which form intimate steric contacts with residues in the S5 transmembrane helix^1,14–20. While there are no structures of the same protein in both resting and activated state, comparisons of the putative resting state models and multiple structures in various conformations suggest that this interface changes with channel gating^21,22. Previous studies have also shown that non-charged residues in this transmembrane interface account for dramatic differences in the gating behavior between different potassium channel families^23–25 mainly due to alterations in coupling. We wondered whether in the prototypical domain swapped architecture, alternate pathway for transducing voltage-sensor movement to the pore gates exist. Here, we broadly probe the transmembrane as well as intracellular interfaces between the voltage-sensing and pore modules by measuring how the trans-interaction energies at specific contact sites change during channel activation. To this end, we combined Generalized Interaction energy Analysis (GIA), which is currently the most rigorous way to experimentally measure site-specific interactions, with network analysis of molecular simulations to identify the allosteric signaling pathways. We find that in addition to contacts at the intracellular interface, the residue contacts at the transmembrane interface between the voltage-sensor domain and the pore contribute substantially to channel gating. Network analysis of molecular dynamics trajectories support our experimental findings and show that the S4 movement triggers a conformational change in the pore gate via a canonical as well as a non-canonical pathway involving contacts on the S5 helix. These experimental and computational studies provide a remarkably congruent view of signal propagation between voltage-sensor and pore in a prototypical domain swapped VGIC.

RESULTS

Examination of the interface between the voltage-sensing and pore module in the Kv 1.2/2.1 chimera shows that there are a number of contact points involving residues at this interface suggesting that voltage-sensor movement relative to the pore will likely alter the interactions at this interface^1,7,15,17. Unless the net interaction energy at this interface between resting and activated states is completely balanced, the changes in these trans-interactions contribute to the strength of coupling between the voltage-sensor and pore. There is no available structure of the Kv 1.2/2.1 chimera in the resting state but distance matrices obtained from long time scale MD simulations of Kv 1.2/2.1 channel shows that deactivation causes the S4 helices to move downward as well as undergo a helical screw motion (Supplementary Figure 1). To determine how these interactions change upon channel gating, we focused at the contact sites in the intracellular gating interface (S4–S5 linker with S4 or S6 helices) and the transmembrane gating interface formed by S4 and S5 helices (Figure 1).

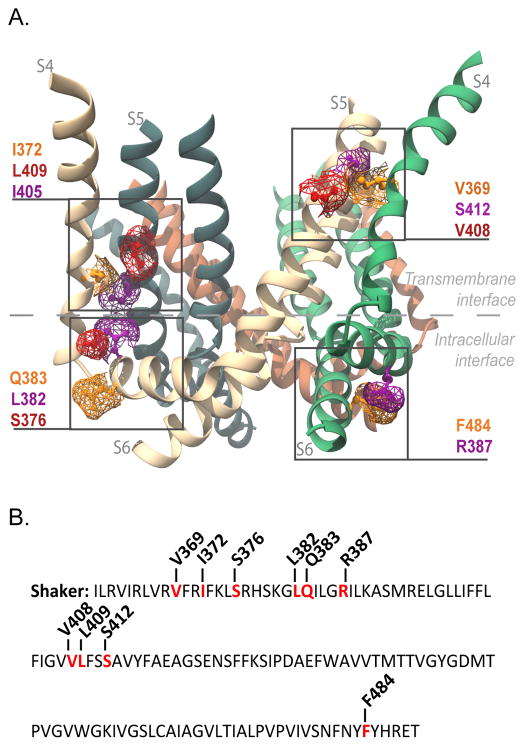
Figure 1. Interfacial regions and residues tested for electromechanical coupling.

(A) Side view of Kv1.2/2.1 chimera (PDB 2R9R). Only S4, S4–S5 linker, S5 and S6 helices are shown for clarity. Highlighted in purple, orange and red are the residues in the transmembrane gating interface of S4 and S5 of neighboring subunits (V369 with V408 and S412; I372 with I405 and L409), and those at the intracellular gating interface (S4–S5 linker (R387) with S6 (F484), and the S4 (S376) with S4–S5 linker (L382 and Q383) of the same subunit). The residue numbering corresponds to positions in the Shaker potassium channel (see Supplementary Figure 6 for alignment). (B) Shaker sequence from residue I360 to T489. Residues that were mutated to alanine are in red and the position noted.

To measure the strength of the interactions at the contact sites, we used the recently introduced GIA method^26,27. This method measures the median voltage-activity of gating charge-voltage (Q-V) curves to calculate the net activation energy of channel gating (see Materials and Methods)^28–30. In contrast to conductance measurements (G-V curves) which provides the free energy difference between the open and undefined closed states of the channel (which can correspond to intermediate gating states of the voltage sensor domain), Q-V curves allow us to calculate the free-energy difference between the two end states, namely, the initial resting state and the final activated state. Free-energy calculations based on G-V curves are highly susceptible to type I errors because mutations may alter the intermediate states without affecting the net free-energy of activation²⁶. Only in a two-state model do the free-energies calculated from G-V curves correspond to the net-free energy of activation. The GIA approach based on the Q-V measurements is robust and allows us to calculate the free-energy of activation without any consideration about the complexity of the underlying model. In order to obtain the net free-energy of activation, this median voltage value from the Q-V curve is multiplied by the total gating charge per channel. In this report, we estimated both the median voltage and the total gating charge per channel at the same time by combining fluorescence intensity measurements with gating current measurements.

Coupling clusters at Intracellular Gating interface

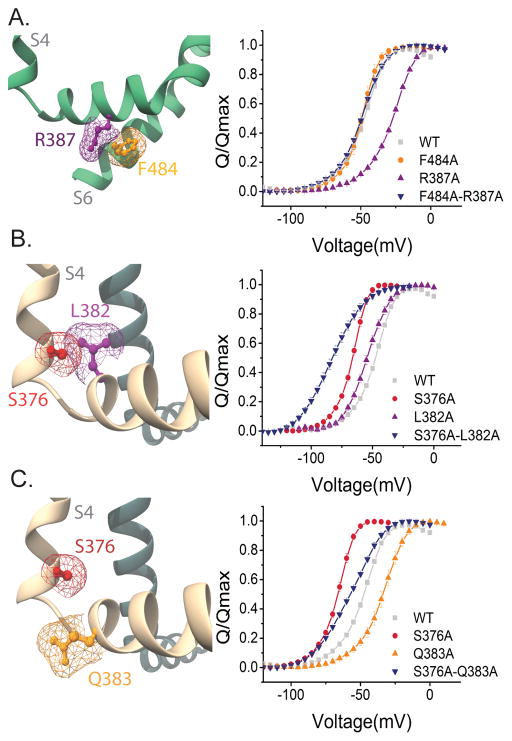
Previous studies have suggested that the mutation of residues in the S4–S5 linker modify channel gating and possibly alter electromechanical coupling strength^31–34. Based on the structure, we first tested the interaction between R387 in the S4–S5 linker and F484 from the lower S6 segment. Gating current measurements reveal that the Q-V curves of F484A and F484A-R387A double mutant is left shifted whereas R387A shifts to the right compared to the WT (Figure 2) (see also Supplementary Table 1). All gating current measurements were obtained in the non-conducting W434F background. Although the rightward shift for R387A is large, a corresponding rightwards shift is not observed in the double mutant implying that at least the median voltage activities are non-additive. The Q_max values for single mutants and the double mutants are identical to the wildtype channels (Supplementary Figure 2), therefore, the calculated ΔΔG of interaction is −5.37 ± 0.5 kcal/mol, indicating a relative stabilization of the activated state. This interaction energy is significantly above our cut-off of 1.8 kcal/mol of functional channels, which corresponds to 0.45 kcal/mol for each subunit. Given that this interaction is between an arginine and phenylalanine, it is quite likely that these two form unusually strong cation-pi interaction³⁵ stabilizing the activated state.

Figure 2. Interaction energy analysis residues in the intracellular gating interface.

(A) (Left panel) Side view of the F484 (orange) and R387 (purple) mapped on Kv 1.2/2.1 chimera structure. Only the S4–S5 and S6 domains of the same subunit are shown for clarity. (Right panel) Normalized Q-V curves of WT (grey squares), R387A (purple triangles), F484A (orange circles) and R387A-F484A (blue inverted triangles). (B) (Left panel) Side view of the S376 (red) and L382 (purple). The S376 residue is at the end of the S4 segment and the L382 is at the beginning of the S5 segment in the neighboring subunit. (Right panel) Normalized Q-V curves of WT (grey squares), L382A (purple triangles), S376 (red circles), S376A-L382A (blue inverted triangles). (C) (Left panel) Side view of the S376 (red) and Q383 (orange), which is at the start of the S4–S5 linker. (Right panel) Normalized Q-V curves WT (grey squares), S376 (red circles), Q383A (orange triangles), and S376A–Q383A (blue inverted triangles). Mesh (A–C) represents the surface based on the Van der Waals radii for selected atoms. Error bars represent SEM in all Q-V plots.

Next, we tested a triad of residues located at the intersection of S4 (S376) and S4–S5 linker (L382, Q383). We observed that single mutants L382A and S376A as well as the corresponding double mutant S376A-L382A, all left shift the Q-V curves relative to the wild type. Q_max measurements (Supplementary Figure 2) show that these mutations apparently alter the total charge per channel but we wondered whether a significant fraction of the total charge moves at potentials beyond +50 mV. Previously, L382V mutation has been shown to move a significant fraction of the total charge at potentials corresponding to channel opening which is also extremely right shifted compared to the WT^36,37. Our measurements of conductance-voltage (G-V) curves show that channel opening is also highly right shifted for both L382A and S376A-L382A mutants (Supplementary Figure 3). To correctly account for all the gating charge per channel, Q-V curves have to be extended to potentials where the G-V curves saturate. However, we were not able to obtain reliable Q-V measurements beyond +50 mV using the cut-open oocyte method due to low expression of these mutants and increased endogenous currents at those potentials. Given these issues, we are unable to determine unambiguously whether these two sites interact although both these two sites have been shown to be crucial for concerted final opening transitions^24,38–40. On the other hand, similar analysis of S376 and Q383 shows that these mutations do not modify the Q_max. Taking the shifts in the Q-V curve into account, the interaction energy between these two positions is 0.57 ± 0.4 kcal/mol (Supplementary Table 2). Thus, even though S376 is important for concerted transitions, it does not seem to involve a change in interaction with the Q383 site going from resting to activated state.

Coupling interaction clusters at transmembrane gating interface

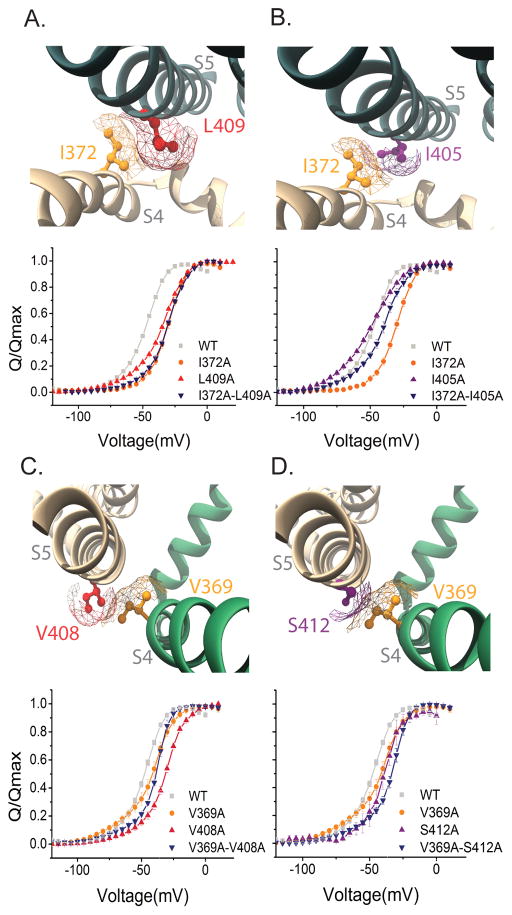
In channels with domain swapped architecture, the S4 helix forms an interface with the S5 helix of the neighboring subunit. Mutations in this region have been shown to affect channel gating^25,41–43 in particular I372 and V369 are part of the well-studied ILT triple mutant²⁴. Our measurements reveal that the interaction energy between I372 and I405 is −2.45 ± 0.4 kcal/mol and that between I372 and L409 is −4.15 ± 0.5 kcal/mol (Figure 3)(Supplementary Table 2). Since the G-V curves of all I372A mutants is far right shifted (Supplementary Figure 3) and the Q_max values (Supplementary Figure 2) calculated at +50 mV are lower than the WT, these should be considered as apparent interactors that stabilize the activated state as discussed earlier.

Figure 3. Interaction energy analysis of residues in the transmembrane gating interface.

(A–D) (Top panels) Top-down view of the S4 and S5 helices from neighboring subunits obtained from the Kv1.2/2.1 chimera structure. (A and B) (Top panels) Top-down view of the S4 and S5 helices from neighboring subunits. Mapped in the structures are I372 (orange), L409 (red) and I405 (purple). (A) (Bottom panel) Normalized Q-V curves of WT (grey squares), I372A (orange circles), L409A (red triangles) and I372A-L409A (blue inverted triangles) (B) (Bottom panel) Normalized Q-V curves of WT (grey squares), I372A (orange circles) I405 (purple triangles) and I372A–I405A (blue inverted triangles). (C and D) Top-down view of the S4 and S5 helices from neighboring subunits. Mapped in the structure V369 (orange) and V408 (red) and S412 (purple). (C) (Bottom panel). Normalized Q-V curves of WT (grey squares), V369 (orange circles), V408A (red triangles) and V369A–V408A (blue inverted triangles). (D) (Bottom panel) Normalized Q-V curves which in addition to WT (grey squares) and V369 (orange circles) also shows S412 (purple triangle) V369A–S412A (blue inverted triangles). The mesh (A–D) represents the surface based on the Van der Waals radii for the residue within the helix, please note that only the mesh for the selected residue is shown.

Next we examined the interaction between V369 (S4) with V408 and S412 both in the S5 segment. Our measurements show that the interaction energy between V369 and V408 is −2.2 ± 0.9 kcal/mol whereas that between V369 and S412 (in S5) is +1.79 ± 0.8 kcal/mol (Supplementary Table 2) (Figure. 3). Thus, both these pairs interact but, interestingly, the V369–V408 interaction is a stabilizing interaction in the activated state whereas the V369–S412 is destabilizing. Despite uncertainties of gating interaction measurements at other sites, these findings unambiguously establish that, specific residues in S4 and S5 transmembrane helices interact to drive electromechanical coupling in the Shaker potassium channel.

Long-range interactions at the gating interfaces

In the last set of experiments, we explore interactions between pairs of residues that are not in direct steric contacts but are likely to be part of the energy transduction pathway between voltage-sensor domain and pore. Although a network of long-range interactors had been previously identified using functional mutant cycle analysis in the Shaker potassium channel^44,45, a follow up analysis using GIA showed that many of these were false positives²⁶. Here, we measure gating interaction energies between V369 with S376 (bottom of S4) and R387, which is in the S4–S5 linker. The interaction energy between V369 and S376 is 5.09 ± 0.75 kcal/mol whereas that between V369 and R387 is 2.64 ± 0.71 kcal/mol. Thus, perturbations at V369 are transmitted to residues in the bottom part of the S4 helix and to those in S4–S5 linker. These findings also show that the GIA method is not just limited to identifying residues which are involved in short range interactions but can be useful to track the long-range interaction pathways (Figure 4, Supplementary Table 2).

Figure 4. Long distance interactions between the S4 and the S4–S5 linker of the same subunit.

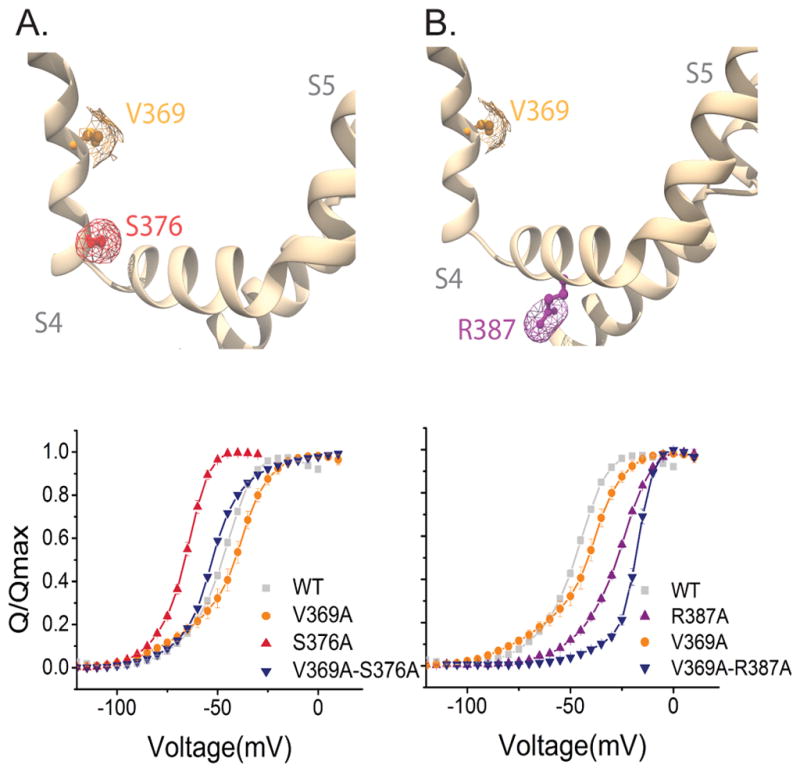
(A and B) (Top panels) Side view of S4 and S4–S5 linker from the same subunit of the Kv1.2/2.1 chimera structure. Mapped in the structure V369 (orange), S376 (red) and R387 (purple). (A) (Lower panels) Normalized Q-V curves of WT (grey squares), V369A (orange circles), S376A (red triangles) and V369A–S376A (blue inverted triangles). (B) Normalized Q-V curves of WT (grey squares) and V369A (orange circles), R387A (purple circles) and V369A–R387A (blue inverted triangles). The mesh (A and B) represents the surface based on the Van der Waals radii for the selected residue.

Two pathways of electromechanical transduction from network analysis of molecular dynamics trajectories

To reveal the structural details of the allosteric pathways linking the voltage sensor domain and the pore, we analyzed multi-microsecond simulations of the resting/closed and the activated/open state Kv1.2/2.1 chimera produced by Jensen et. al using network analysis²¹. In brief, we constructed a network where the nodes represent protein residues and the edges represent interactions between pairs of residues. The weight of the edges is a measure of how efficiently information is transferred from one residue to another. This was determined by measuring the how the fluctuations of residue pairs are covarying over the course of the simulation. The underlying premise is that if the pairs interact tightly, then the covariance will be high. Mathematically, the weights of the edges are information distances between residue pairs (measured as negative logarithm of the covariance measurements of pairs in contact more than 75% of the trajectory time) (see materials and methods). This analysis can be carried out between all possible residue pairs to identify residues that are on pathways with short information distance (or conversely, of high covariance, from here on referred to as shortest pathways). Typically, network analyses are carried out on MD trajectories obtained from a single initial structure. However, here, we carried out independent network analyses on a trajectory of the crystallographic activated state structures and of a resting/closed state model (obtained from long time scale simulations²¹). This allows us to draw comparisons with our experimental data, which measure the changes in gating interactions as the channel goes from resting to activated state. We focused on the pathway linking R365 (R2), the residue on Shaker which moves the most gating charge, and V474 (using the shaker K_V numbering for consistency), which is part of the narrow PVP motif on the S6 helix that constricts during pore closure^33,46–48.

The shortest pathways present in the activated/open state simulation can be classified into two modes of allosteric transmission (Supplementary Fig 4 A–D). One mode, present in two subunits, shows the pathway moving down S4, along the S4–S5 linker and then across to S6 (Supplementary Fig 4 A,B). Whereas, the other mode shows the pathway first moving to the neighboring S5 subunit rather than moving down S4 (Supplementary Fig 4 C,D). To account for pathways originating in the rest of the VSD, we measured the shortest pathways linking residues located on average in a sphere of 9 Å radius from R365 and the V474 gate residue (see methods for details). In order to identify the key residues involved in allosteric coupling, we calculated the number of times a specific residue is present on the shortest pathway between VSD residues in a 9 Å radius sphere around R365 and the V474 gate residue (a quantity known as betweenness) (Fig 5). Residues with high betweenness are hubs in the network because many shortest paths travel through these residues. This implies these residues are important for the transfer of information between the VSD and pore domain. When multiple voltage-sensor domain residues are considered as the origin of the allosteric pathway, the pathways are more degenerate but the structural trend of having two subunits where the pathway is dominated by the intrasubunit mode while the other two subunits are dominated by the intersubunit mode remains (Fig 5). In this way, these modalities are shown to be robust to a range of specific starting residues on the voltage sensor. Unlike the activated state, the resting/closed state shows an intrasubunit pathway in each of the 4 subunits (Supplementary Fig 4 G–L). This difference in connectivity in the resting vs. activated state suggests that the intersubunit pathway is a unique feature of the activated state. This is also consistent with our experimental data showing that the three interaction pairs between residues located on S4 and S5 372/405, 372/409 and 369/408 are stabilized in the activated state.

Figure 5. Residue betweenness for pathways between S4 and S6 in the activated/open state.

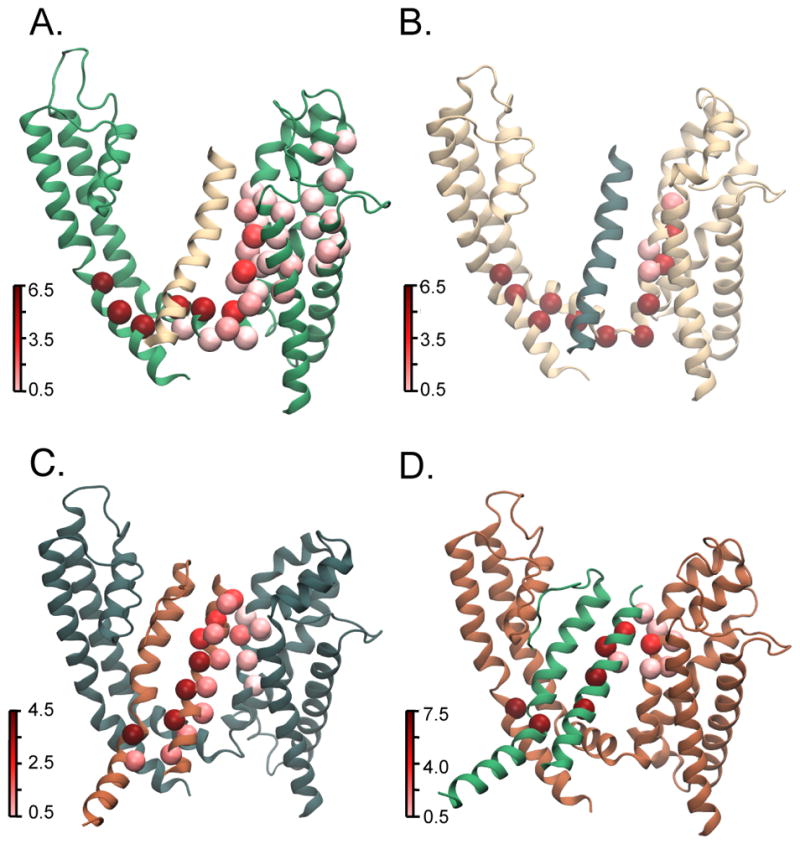
Betweenness is a measure of centrality of a residue in various allosteric pathways that link source and sink residues in that it calculates the number of shortest paths a residue is on. Residues with higher betweenness are hubs in the network and are therefore important for information flow along the network. Betweenness is calculated for residues of each individual subunit since in MD simulations, each subunit will evolve differently over time due to the stochasticity inherent in this process. (A–D) Each panel represents one of the four subunits where the subunit colors, source and sink residues were selected following the convention described in Fig. 1. Residue betweenness for each subunit is mapped on to the activated state structures. It is calculated using source residues where the c-α is, on average, within 9 Å of Arg 365 (R2). Residues with high betweenness are shown in dark red whereas low betweenness residues are shown in light red. In the top two panels showing subunits A and B, residues of high betweenness are within a single subunit and travel down S4 and along the S4–S5 linker finally linking up with the gate residues in the S6 subunit. In the bottom two panels showing subunits C and D, residues of high betweenness are on multiple subunits and travel from S4 to the neighboring subunit S5 then down the S5 helix. In these panels, the S6 helix of the neighboring subunit is also shown to identify the position of the sink residue. The intersubunit pathway remains consistent whether the sink residue is on the same or the adjacent subunit (Supplementary Fig. 4 G,H).

With regards to the long-range interactions identified experimentally, V369–S376 and V369–R387, the network analysis shows that for one subunit in the activated state, both Val 369 and S376 fall on the optimal pathway and have a betweenness of 3 and 4.5, respectively (significantly higher than the average betweenness of all residues on these pathways, 1.63±1.94) (Supplementary Fig 4 M). In the resting/closed state, for one subunit, V369 and R387 fall on the optimal pathway and have betweenness values of 2.0 and 6.5 respectively (with an average betweenness of all residues of 2.77±2.7) (Supplementary Fig 4 N). These long-range interactions may occur because the voltage sensing process requires coupling of two domains over considerable distance and therefore can be perturbed by modulating residues that fall along this pathway. More pertinently, the fact that these long-range interactions are determined experimentally and can also be independently deduced from simulations indicates a remarkable congruity of such approaches.

DISCUSSION

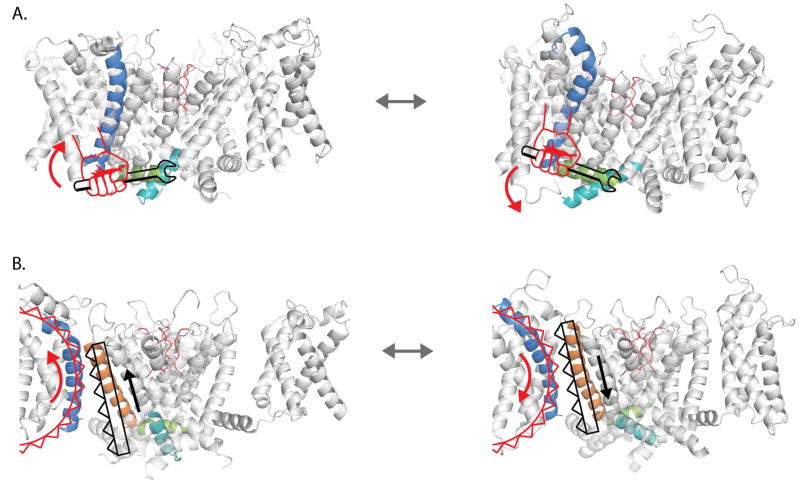
Mutations of residues in the S4–S5 linker and the C-terminal end of the S6 region impairs the activation of channel opening and voltage-sensor movement in a manner consistent with models that predict a loss of coupling^9,31,49. According to the canonical model (Figure 6), upward movement of the S4 segment exerts a torque on the S4–S5 linker, which moves like a lever arm, and allows the helices of S6_CT to rotate outwards resulting in an open channel¹⁹. These mutations in the intracellular gating interface presumably disrupt the non-covalent interactions between the S4–S5 and S6_CT. The upshot of this model is that voltage-sensing is considered to be a relatively independent module with very few meaningful tertiary contacts with the pore domain especially within the membrane⁵⁰. Indeed, it has been shown that the voltage-sensing module from Ci-VSP can drive the voltage-dependent opening of pore only viral potassium channels⁵¹.

Figure 6. Schematic showing the two modes of electromechanical coupling in a prototypical potassium channel.

(A) In the canonical mode, S4 (blue) acts a lever arm moving the S4–S5 linker (green) directly and thereby causing the lower half of the S6 helix (cyan) to readjust. In the resting state, the S4 helix is down which through the S4–S5 linker keeps the lower half of S6 in the closed state (left panel). When the S4 helix is up, the S4–S5 linker rotates upwards and allows the lower S6 helices to splay open (right panel). (B) Gear like movement of S4 helices directly shifts the position of the neighboring S5 helix. In this rack and pinion type of coupling, when S4 is in the resting state (left), it holds the S5 helix in a down position which forces the S6 gates to remain closed. The upward movement of the S4 helix (right panel), drives the S5 helix up and causes the S6 helices to open.

Nevertheless, mutations in residues on the S4 and S5 transmembrane segments are also known to exhibit a phenotype corresponding to a loss of coupling^24,25,43. This raises the possibility that there are alternate pathways of electromechanical coupling. These pathways are presumably more important in non-domain swapped channels where the S4–S5 linker is either non-existent or truncated^12,13,52. Our study reveals that specific interaction pathways involving residues in the S4 and S5 transmembrane segments mediate voltage-dependent activation of the channel pore. Therefore, in addition to the intracellular gating interface, the transmembrane gating interface plays a central role in electromechanical coupling in the Shaker potassium channel. While we do not have a quantitative estimate of the relative contributions of each of the two pathways, it is clear that the disruption of the transmembrane pathway dramatically reduces the coupling between the two modules.

Taking into account our findings from both experiments and network analysis, we can speculate as to the mechanism of how the two different pathways combine to control pore gating. Examination of the MD trajectory corresponding to ultra-long simulation of a single Kv 1.2/2.1 chimera suggests a possible alternate mechanism of voltage-sensor coupling. In response to hyperpolarizing voltage, the S4 undergoes a helical screw movement but the pitch of the screw axis describing this movement is longer than an alpha-helix- second arginine rotates about 90 degrees in the anticlockwise direction and undergoes a translation corresponding to two helical turns (see supplementary movie). Thus, S4 residues which act like cogs of a pinion drive the interacting S5 helix (rack) downward (about a half helical turn). Thus, the gear ratio between S4 and S5 movements is about 4:1. This displacement of S5 and the movement of the S4 together pushes the S4–S5 linker which directly regulates the position of the S6 gates. This rack and pinion type of coupling between voltage-sensors and pore gates could be the primary mode of coupling in EAG or other non-domain swapped channels. The difference being that rather than the S4–S5 linker, the movements of the S5 may directly influence the conformation of the S6 gates in those channels.

The number of trans-interactions identified in this study was limited in part due to the shortcomings of our approach. GIA provides estimates of interactions between specific residues only and only if the interaction strength changes upon channel activation. Thus, by definition, we can only identify interactions that contribute to the net free-energy of open/closed equilibrium and not the other class of coupling interactions that contribute to interactions only in the intermediate states^28,31. For instance, interactions that increase the strength of positive coupling by destabilizing the intermediate states result in a steeper voltage-dependent opening. The other limitation of this method is that experimentally, it is still difficult to estimate accurately the charge per channel. The errors associated with these measurements are relatively large. In some cases, we were not able to measure the full Q-V curve because a significant fraction of the charge moved at very positive potentials (Supplementary Figure 2–4). This introduces uncertainty in the V_M and Q_max values.

Network analysis reduces the dimensionality of complex motions that occur during MD simulations. With a network of residues, it is possible to describe pathways of interactions that are difficult to quantify using other methods. Network theory has been successfully applied to understand other interaction interfaces such as amino acid tRNA synthetase: tRNA interface and long-range interactions between substrate binding and the gate in the LeuT transporter^53,54. While covariance is a proxy for interactions between residues, as opposed to a method such as free energy perturbation, which rigorously calculates this interaction energy, the fact that covariance can be calculated for all residues simultaneously provides for richer exploratory analysis. Therefore, in combination with network theory, covariance measurements provide a unique and more efficient approach to elucidate pathways that link distant moving parts of the channel.

Nevertheless, it is quite remarkable that despite the limitations of experimental and computational approaches, they both delineate the same two pathways in voltage-sensor pore coupling. Unlike the canonical pathway, the one involving the transmembrane gating interface may be common to both domain and non-domain swapped channels. Indeed in the non-domain swapped channels, this appears to be the only pathway involved in voltage-transduction¹¹ but further studies are needed to test the generality of these ideas.

MATERIALS AND METHODS

Mutagenesis and expression in Xenopus Laevis oocytes

All mutants were made in the fast inactivation-removed Shaker Kv channel (Δ6-46)⁵⁵ background using the QuickChange mutagenesis. For gating current measurements, the background is mCherry containing W434F construct. mCherry is inserted after the 5^th residue in the N-terminus. W434F renders the channel non-conducting⁵⁶ and facilitates gating currents measurements. All mutations were confirmed by cDNA sequencing. Mutant cDNAs were linearized using NotI enzyme (Fermentas-Thermo Fisher Scientific) and transcribed into cRNAs using mMESSAGE mMACHINE T7 kit (Life Technologies).

Xenopus oocytes were removed surgically and treated with 1mg/ml collagenase for 1–1.5h to remove the follicular layer. 50nl cRNA at a concentration of 50–500 ng/μl was injected into oocytes. After the injection, oocytes were incubated in ND-96 solution supplemented with, 100 U/ml Penicillin-Streptomycin, 50 μg/ml Tetracycline, 0.1mg/ml Amikacin, 50 μg/ml Ciprofloxacin, 100 μg/ml Gentamicin and 0.5 mg/mL bovine serum albumin at 16 °C before recording. Ionic current measurements were performed 24–48 hrs after injection whereas gating currents were obtained 2–5 days after injection.

Electrophysiology

Gating currents were obtained by applying a 200ms long depolarizing pulse to voltages from −150 mV to +100 mV every 5mV. The holding potential used was −110 or −120 mV. Depolarization pulses were preceded by a 50 ms pre- and post-pulses to −120 mV. The capacitive transients and linear leak currents were subtracted online using the P/−4 method with a substep holding potential of −110 mV. After baseline adjustments, the on-gating current records were integrated over the duration of the depolarization pulse to obtain the gating charge displaced, which was used to compute the fractional gating charge displacement versus V curve (Q/Q_max vs. V).

Ionic currents were measured in a modified cut-open oocyte voltage clamp (COVG) set-up (CA-1B; Dagan Corporation) as described previously⁵⁷. The external solution used was (in mM) 50RbCl, 50 NaCl, 1 MgCl2, 5 HEPES, pH 7.4. The internal solution was (in mM) 95RbCl, 5 NaCl, 2 EGTA, 5 HEPES, pH 7.4. Ionic currents were obtained by applying 50 ms depolarizing pulses from −120mV to 190mV every 3mV. The holding potential was −110mV. Capacitive transients and linear leak currents were subtracted online using the P/−4 method, during which the holding potential was −100 mV. After baseline subtraction, peak tail current amplitude, elicited by repolarization pulses to −110 mV, were used to generate the conductance versus voltage (G/G_max vs. V) curves.

Fluorescence Measurements

Fluorescence and gating current measurements were obtained from the same oocyte on a customized cut-open fluorometry setup as described previously⁵⁷. A xenon lamp (Hamamatsu Photonics, Bridgewater, NJ) controlled by a feedback stabilized power supply was used an excitation light source. The microscope was equipped with a filter cube (excitation filter: 562/40, emission filter: 628/40 and dichroic 593 DiO₂, Semrock Inc, NY) optimized for mCherry fluorescence measurements. Fluorescence measurements were obtained right before the gating current measurements. From a family of gating current traces, the maximum total charge (Q_max) was calculated and plotted with respect to the mCherry fluorescence intensity values.

Data analysis

The fractional gating charge displacement curves for all of the mutants were obtained by averaging measurements performed on at least more than 3 oocytes. The median voltage of activation, V_M, for each normalized Q-V curve was extracted by calculating the area between the Q-V curve and the ordinate axis, using the trapezoid method. For a Q-V curve with n points, the V_M is calculated as:

$$V_M=\sum _{i=1}^{n-1}\frac{(Q_{(i+1)}-Q_{(i)})(V_{(i+1)}+V_{(i)})}{2}$$

Where Q_i and V_i correspond to charge and voltage for the i^th point on the Q-V curve. The net free energy of activation of the channel is calculated as ΔG_c=Q_maxFV_M, where Q_max is the maximum number of charges transferred during voltage-dependent activation of the channel.

In order to determine whether our point mutations alter the charge per channel, we calculated the relative Q_max value for each mutant using a modification of the fluorescence method described previously⁵⁸. The absolute membrane fluorescence of each mCherry tagged construct was measured along with the maximum voltage-dependent charge displacement going from a membrane potential of −120 mV to +50 mV. At these potentials, Q-V curves of most mutants were saturated and the channels are fully open. Fluorescence intensity values were plotted against the Q_max from the same oocyte to obtain Fluo-Q_max scatter plots. We observed that the slopes of these scatter plots varied from batch to batch even for the wild type channels but within the same batch they were tightly correlated. Therefore, for every mutant, we obtained Fluo-Qmax curves for the WT injected with the same batch. The slopes of the WT and mutant channels were calculated by linear regression. By using the equation-(Mutant slope/WT slope) × 13.2 - we obtained Q_max values for the mutant (Supplementary Table 1). 13.2 is total charge per channel for the Shaker potassium channel as estimated previously ^59–61.

To determine the confidence intervals associated with fitting the Q_max-Fluo plots (Supplementary Figure 5), we performed a linear fitting using the Excel Software command LINEST. LINEST computes statistics for a least-squares straight line through a given set of data. From the data array, we compute the confidence intervals for every data point (with 95% confidence and (n−2) degrees of freedom where n is the numbers of data points) by using the following equation:

$$d{y}_i=\pm t_{(0.05,\mathit{dof})}S{E}_y(x)\sqrt{\frac{1}{n}+\frac{{(\overline{x}-x_i)}^2}{{\mathrm{\sum }}_{i=1}^n{(\overline{x}-x_i)}^2}}$$

where t is the calculated t-score corresponding to 95 % confidence with n−2 degrees of freedom; SEy is the standard error for the y estimate.

Given the errors of these Q_max measurements and that none of these mutations target the known gating charges in the Shaker potassium channel, it is fair to assume that the mutations do not substantially alter the total charge per channel (Supplementary Figure 2). In those few instances, where the Q_max values for mutants are substantially lower than 13.2, we note that the G-V curves (Supplementary Figure 3 and Supplementary Table 1) are also far right shifted to the right, therefore indicating that the channels are not fully activated at + 50 mV. Some of these mutants are known to saturate at +200 mV^24,36,37. Since, we are not able to reliably measure gating currents beyond +50 mV with the cut-open oocyte technique, we have assumed that the total charge per channel is the same as the wild type although the median voltage values are quite different.

Interaction free energy between two positions was calculated by measuring the non-additivity in a mutant cycle based on the charge-voltage curves as described previously^26,27. Briefly, gating interaction free-energy between sites S1 and S2 is:

$$\mathrm{\Delta }\mathrm{\Delta }G=Q_{\mathit{max}}F(V_{M(WT)}+V_{M(S12)}-V_{M(S1)}-V_{M(S2)})$$

where the subscripts WT stands for WT, S12 for double mutant and the two single mutants (S1 and S2).

The uncertainty in interaction energy calculation was calculated as Q_max FδV_M, where δV_M is the standard error of the V_M estimation. As described earlier, the Q_max values were considered to be unchanged. The standard error of gating interaction energy, δΔΔG, was calculated as:

$$\mathrm{\Delta }\mathrm{\Delta }G=Q_{\mathit{max}}F\sqrt{{\{\delta {(V_M)}_{WT}\}}^2+{\{\delta {(V_M)}_{S1}\}}^2+{\{\delta {(V_M)}_{S2}\}}^2+{\{\delta {(V_M)}_{S12}\}}^2}$$

where δ (V_M)_WT, δ (V_M)_S1, δ (V_M)_S2 and δ (V_M)_S12 are the uncertainties (standard error of the mean) associated with V_M measurement of the WT channel and the single and the double mutant channels respectively.

The G-V curves for each mutant was obtained by averaging the curves obtained from n>3 oocytes. The curves were fitted individually to a Boltzmann equation:

$$\frac{G}{G_{\mathit{max}}}=\frac{1}{1+exp(\frac{zF(V_{1/2}-V)}{RT})}$$

Where z is the Boltzmann slope and V_1/2 is the voltage that elicits half-maximal response.

Molecular simulations analyses

Molecular dynamics simulations of the K_v1.2/2.1 chimera structure in the activated and resting states from the D.E. Shaw group using Anton were analyzed²¹. The activated state corresponds to simulation 1 (77.85 microseconds in length) in supplementary table S1 and the resting state corresponds to simulation 9 (126 microseconds in length), where analysis began after ~10 e₀ of the gating charges are displaced (the last 72.2 microseconds of simulation 9). Residue-based networks were built and visualized using the Network View plugin within Visual Molecular Dynamics (VMD)^62,63. The network is a residue-based matrix where each residue of the protein is a node (vertex) and edges (connections) between nodes are created for residues that are within a distance of 4.5 Å for at least 75% of the trajectory. Edge weights were calculated using −log (|C_ij|) where C_ij is the normalized covariance of α-carbon positions calculated using Carma⁶⁴. C_ij and r_i are defined as:

$$\begin{gathered} C_{ij}=\frac{{\langle \mathrm{\Delta }\overrightarrow{r_{𝚤}}(t)·\mathrm{\Delta }\overrightarrow{r_{𝚥}}(t)\rangle }_t}{\sqrt{{\langle \mathrm{\Delta }\overrightarrow{r_{𝚤}}{(t)}^2\rangle }_t·{\langle \mathrm{\Delta }\overrightarrow{r_{𝚥}}{(t)}^2\rangle }_t}} \\ \mathrm{\Delta }\overrightarrow{r_{𝚤}}(t)=\overrightarrow{r_{𝚤}}(t)-{\langle \overrightarrow{r_{𝚤}}(t)\rangle }_t \end{gathered}$$

Where 〈…〉_t denotes an ensemble average over time.

Shortest pathways and betweenness calculations were performed using the Dijkstra’s algorithm as implemented in the NetworkX python library⁶⁵. Betweenness calculations using a sphere of residues as source(starting) nodes were calculated using the average α-carbon distance during the simulation. We calculated betweenness for each subunit as the source radii was expanded and found that when R365 residue was used as a source, betweeness values saturate at 9 Å in all the subunits (data not shown). Visualization and image creation of networks was done using VMD⁶³.

Because the K_v1.2/2.1 and shaker K_v channels are not completely homologous, a sequence alignment between the crystal structure of K_v1.2/2.1 and the shaker channels sequence was performed in order to determine residues that are at homologous sites between the two channels (Supplementary Fig. 6).

Data availability

Source data for the figure 2,3 and 4 are available online. Source data for supplementary figures 1, 3 and 5 is also available online. The source values for free-energy calculations and supplementary table 1 is provided. Source data for Figure 5 and supplementary figure 4 can be provided on request.