Investigation of Chiral Recognition by Molecular Micelles with Molecular Dynamics Simulations

Abstract

Molecular dynamics simulations were used to characterize the binding of the chiral drugs chlorthalidone and lorazepam to the molecular micelle poly-(sodium undecyl-(L)-leucine-valine). The project’s goal was to characterize the nature of chiral recognition in capillary electrophoresis separations that use molecular micelles as the chiral selector. The shapes and charge distributions of the chiral molecules investigated, their orientations within the molecular micelle chiral binding pockets, and the formation of stereoselective intermolecular hydrogen bonds with the molecular micelle were all found to play key roles in determining where and how lorazepam and chlorthalidone enantiomers interacted with the molecular micelle.

Introduction

Separation of the enantiomers of both natural and synthetic chiral compounds is a continuing challenge in many areas of chemistry. For example, in the medical and pharmaceutical fields, it is well known that the enantiomers of chiral drugs often have different physiological activity [1,2]. Since 1994, the United States Food and Drug Administration has required the separate testing of the optical isomers of all drugs that exist in enantiomeric form [3]. Consequently, there is a need for efficient chiral chromatographic techniques to separate drug enantiomers [4,5]. These separations are challenging because they are based on small differences in binding free energies between analyte enantiomers and the separation medium [6,7]. This small difference in binding energies is what often makes capillary electrophoresis (CE) an ideal method for enantiomeric separations.

The use of CE for enantiomeric separations has many advantages over the other two commonly used chromatographic techniques: gas chromatography and liquid chromatography. These advantages include lower operating costs, smaller sample sizes, shorter analysis time, versatility, simplicity, and typically much higher separation efficiency [8–13]. Many pseudostationary phases including chiral surfactants, crown ethers, cyclodextrins, and molecular micelles have been employed in chiral CE separations. Advances in the field between 2012 and 2016 have been reviewed by Sciba [14].

This research is part of an ongoing project to use molecular dynamics (MD) simulations to investigate the intermolecular interactions between chiral molecules and a class of chiral molecular micelles (MM) used as pseudostationary phases in CE separations. A MM is a macromolecule in which covalent bonds connect individual surfactant monomers to one another [8,15]. The MM investigated in this study was poly-(sodium undecyl-(L)-leucine-valine) or poly(SULV). In this macromolecule, twenty surfactant monomers are connected by covalent bonds at the end of each monomer’s hydrocarbon tail. The headgroup of each surfactant monomer is a chiral leucine-valinate dipeptide [16]. The structure of poly(SULV) is shown in Figure 1(a). Previous CE work has shown that poly(SULV) is a versatile and effective chiral selector in CE experiments. For example, in a study by Shamsi, et al. poly(SULV) was able to resolve enantiomers in 75% of the 75 racemic mixtures investigated [16].

Figure 1:

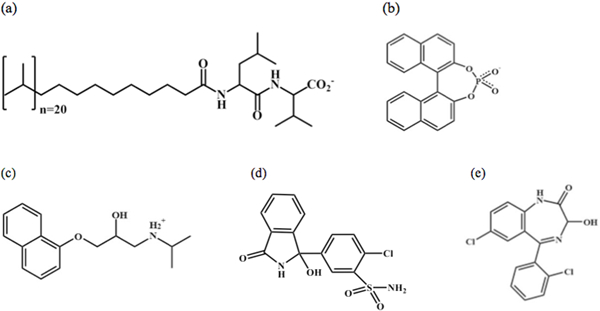
Chemical structures of (a) poly-(sodium undecyl-(L)-leucine-valine) poly(SULV), (b) 1–1’-binaphthyl-2–2’-diyl hydrogenphosphate (BNP), (c) propranolol, (d) chlorthalidone, and (e) lorazepam.

The long-term goal of this project is to use MD simulations to characterize the mechanism of chiral recognition in CE separations using molecular micelles like poly(SULV). Insights from MD simulations will then be combined with experimental results to build predictive models to identify the best MM and experimental conditions for a given chiral CE separation problem.

Previous work with poly(SULV) has shown that the MM contains four independent sites or pockets where chiral ligands can bind [17,18]. These pockets are shown in Figure 2 where each pocket is represented as a surface, with non-polar or hydrophobic pocket regions colored green and polar or hydrophilic regions colored purple. Each pocket also contains alpha spheres that are used to further identify hydrophobic and hydrophilic regions [19–21]. A hydrophilic or red alpha sphere identifies a good hydrogen-bonding environment within the pocket, while a hydrophobic or white alpha sphere identifies a poor hydrogen-bonding environment [19–21].

Figure 2:

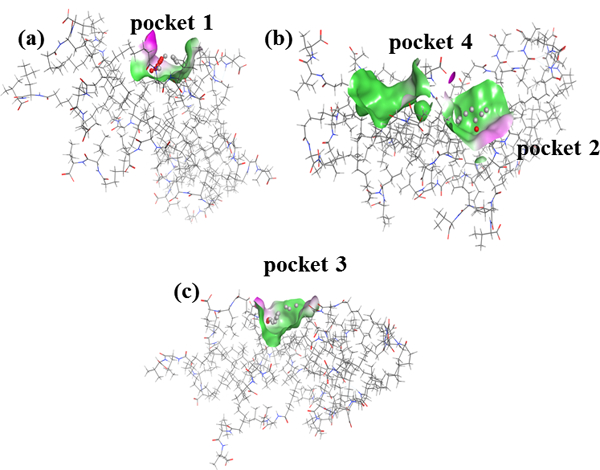
(a) surface map of pocket 1 of poly(SULV), (b) surface map of pocket 4 and pocket 2 in poly(SULV), and (c) surface representation of pocket 3 in poly(SULV)

Figure 2(a) shows that pocket one is relatively narrow and deep and would, therefore, likely accommodate chiral ligands with a similar shape. Pocket one also contains five hydrophilic and six hydrophobic alpha spheres, meaning that within the pocket ligands can interact with the MM through both hydrophobic and hydrogen-bonding interactions. Pocket two in Figure 2(b) is wider and more dish-shaped and contains seven hydrophobic, but only one hydrophilic alpha sphere. Pocket three in Figure 2(c) is similar to pocket two. It is also relatively wide and shallow and contains three and thirteen hydrophilic and hydrophobic alpha spheres, respectively. Finally, pocket four in Figure 2(b) contains only hydrophobic spheres, suggesting it is a primarily non-polar pocket near the MM surface. The size, shape, stereo and electrostatic properties of these four pockets are likely important in governing their interactions with enantiomers in chiral CE separations.

MD simulations have been used to investigate the binding of chiral compounds to poly(SULV) and to probe how the compounds’ shape and charge distribution causes them to preferentially associate with one of the MM binding pockets described above [17,18]. In order to validate and compare MD simulation results to experiment, compounds whose binding to poly(SULV) had been studied experimentally were chosen for these initial investigations. [6,16]. The first chiral compound investigated was 1–1’-binaphthyl-2–2’-diyl hydrogenphosphate (BNP) [17]. As shown in Figure 1(b), this molecule has a rigid, fused-ring structure with very little conformational flexibility. It also has an anionic phosphate group containing several hydrogen bond acceptor atoms and a chiral plane instead of a single chiral atom. MD simulation analyses showed that both enantiomers of BNP bound preferentially to poly(SULV) pocket two, which is shallow and dish shaped and could, therefore, likely best accommodate the BNP ligand. The MD simulations also showed that that (S)-BNP had a lower poly(SULV) binding free energy than (R)-BNP and thus interacted more favorably with the MM than the (R) enantiomer [17]. This result was consistent with CE and NMR experiments [6,13]. (S)-BNP was also shown to penetrate deeper into the poly(SULV) micelle core and it formed more hydrogen bonds than (R)-BNP with atoms in the poly(SULV) dipeptide headgroup.

The binding of the β-blocker drug propranolol to poly(SULV) has also been investigated [18]. Propranolol’s structure is shown in Figure 1(c). Note that unlike BNP, propranolol has a narrow cylindrical shape, with two fused aromatic rings at one end of the molecule connected to a more hydrophilic side chain containing the molecule’s chiral center. The size, shape, and orientation of propranolol’s hydrophobic and hydrophilic moieties caused both its enantiomers to bind to MM pocket one, where the most favorable alignment of the ligand could be achieved. MD simulations with poly(SULV): propranolol intermolecular complexes also showed that propranolol’s fused aromatic rings penetrated into the MM hydrocarbon core and the ligand’s chiral side chain was placed near the MM surface and the chiral dipeptide headgroups. In addition, (S)-propranolol formed more hydrogen bonds than (R)-propranolol with the MM headgroup atoms, giving the former a lower free energy of MM binding. This result was consistent with CE and NMR results, both of which showed that (S)-propranolol bound more favorably to poly(SULV) than (R)-propranolol [18].

This study presents MD simulation analyses of the intermolecular interactions between the chiral drugs chlorthalidone and lorazepam and poly(SULV). Chlorthalidone and lorazepam are, respectively, thiazide diuretic and benzodiazepine drugs. Chlorthalidone is used to treat fluid retention in patients with hypertension and lorazepam is prescribed to treat anxiety, nausea, insomnia, and seizures [22,23]. The enantiomers in racemic mixtures of both drugs have been separated in CE experiments using poly(SULV) as the chiral selector [16]. These separations showed that both drugs experienced strong chiral interactions with the MM, meaning that high chiral resolution of the enantiomers was achieved with a relatively low concentration of poly(SULV) [16].

The structures of lorazepam and chlorthalidone are shown in Figures 1(c) and 1(d), respectively. Chlorthalidone contains a relatively hydrophobic, fused pyrole ring containing the compound’s chiral center. The fused rings are bound to a second aromatic ring containing a chlorine atom and a polar sulfonamide functional group. Therefore, the chlorthalidone structure is somewhat similar to propranolol with its nonpolar fused rings at one end of the molecule, chiral atom near the center, and polar quaternary amine at the other end. Both chlorthalidone and propranolol also have a hydroxyl group connected to the chiral atom. The binding of the chiral drug lorazepam to poly(SULV) was investigated as well. While the chlorthalidone structure is similar to propranolol, lorazepam has a structure similar to BNP. Both molecules have fused rings, are of comparable size, and adopt an overall bent or V-shape. The binding of chlorthalidone and lorazepam enantiomers to poly(SULV) was compared to the behavior previously reported for propranolol and lorazepam in order to further characterize chiral recognition in CE separations with MM. This study will, therefore, investigate whether compounds with similar shape and charge distributions bound preferentially to the same poly(SULV) pocket and experience similar stereoselective interactions with the MM dipeptide headgroups.

Experimental Details

The docking and MD simulation procedures used in this study are described in detail in reference [18]. A brief overview of the methods employed is presented here. An MD simulation was first carried out on a system containing poly(SULV), twenty Na⁺ counter-ions and approximately 9000 H₂O molecules [24]. An average structure was then calculated, along with the root mean squared deviation (RMSD) of each MD simulation structure with respect to the average. A representative poly(SULV) structure with a low RMSD with respect to the average structure was then extracted. This represented the structure from the MD simulation that was most similar to the average and was the structure used in the ligand docking analyses [17,18].

In the docking analysis, the chlorthalidone or lorazepam enantiomers were built and energy minimized in MOE (Molecular Operating Environment, Chemical Computing Group. Inc.) [19]. The poly(SULV) representative structure described above was then imported into MOE and binding pockets were identified using MOE’s Site Finder module. This module located binding sites using alpha sphere and discrete-flow methods developed by Edelsbrunner and Mucke [19–21]. After binding site identification, either the (R) or (S) enantiomer of chlorthalidone or lorazepam was docked separately into each poly(SULV) binding site. During the docking process, the receptor or MM was rigid, while the ligand enantiomer was set as completely flexible [19]. Hundreds of docking poses were examined and MOE used the dG scoring function to score each pose based upon the free energy of the ligand: receptor complex [25]. The highest scoring or lowest free energy pose was then chosen for MD simulation analysis.

MD simulations of all intermolecular complexes were carried out using AMBER12 and the parm99 force field [26,27]. Each MD simulation contained the poly(SULV): enantiomer complex, twenty Na⁺ counterions and approximately 9000 TIP3P water molecules. Before MD simulations were run, each complex was energy minimized. Next a 20 ps MD simulation was used to warm the system to 300 K followed by a one ns MD simulation to equilibrate to a pressure of one atmosphere. A 20.0 ns MD simulation production run was then carried out with a time step of two fs and structures stored every 0.2 ps. In the production run, cubic periodic boundary conditions were employed. All analyses of the MD simulation trajectories were carried out using the ptraj or cpptraj utilities in AMBER12 [26]. Free energy of binding calculations were performed in AMBER12 using the mm-PBSA method [28].

Results and Discussion

Docking analysis

Before comparing the interactions of lorazepam and chlorthalidone with poly(SULV) to those of BNP and propranolol, we first assessed whether the docking analysis placed all four chiral compounds in the same region of the MM. This analysis was done by determining which MM chains were closest to the ligand enantiomers in each of the four MM pockets. Poly(SULV) has twenty covalently bound surfactant chains. For this analysis, the chains were numbered one through twenty.

The nearest-chain analysis was performed after the initial ligand docking, but before the MD simulations were run. Table I compares the closest MM chains for BNP, propranolol, lorazepam, and chlorthalidone. There is some variability in the nearest chains for the individual ligands, however, overall it can be concluded that at the beginning of the MD simulations the chains nearest each molecule in each of the four pockets was largely the same for all four molecules.

Table I.

poly(SULV) molecular micelle chains nearest the docked chiral ligands at the beginning of the BNP, lorazepam, propranolol, and chlorthalidone MD simulations.

Pocket Number	BNP	Lorazepam	Propranolol	Chlorthalidone
One	2, 9, 12	2, 8, 9	2, 9, 15	2, 8, 12
Two	6, 13, 18	6, 13, 18	6, 13, 18	6, 10, 13
Three	8, 10, 11	7, 11, 17	7, 10, 11	7, 10, 11
Four	4, 5, 7	3, 4, 6	3, 4, 6	3, 4, 6

Analysis of MD simulations

After docking analyses, MD simulations with either the (R) or (S) enantiomer of chlorthalidine or lorazepam docked into one of the poly(SULV) binding pockets were carried out. MD simulation analyses included the free energy of ligand enantiomer binding to each MM binding site. These analyses allowed the lowest free energy or preferred binding site for each ligand enantiomer to be identified. Also, the solvent accessible surface areas (SASA) of the chlorthalidone and lorazepam enantiomers were calculated. This quantity reports the surface area of the ligand molecule that is exposed or accessible to solvent. An enantiomer binding deep in the MM hydrocarbon core would be expected to have a low SASA, while the SASA would be higher for an enantiomer binding near the MM surface. Finally, intermolecular hydrogen bond formation between poly(SULV) and the enantiomers are also presented. Hydrogen bond analyses were used to rationalize why certain enantiomers preferred binding to a particular poly(SULV) binding pocket and why the enantiomers of chlorthalidone and lorazepam interacted differently with the MM. Representative structures from the MD simulations were also imported into MOE to investigate further intermolecular hydrogen bond formation and to examine the orientation of the ligand enantiomers within the MM chiral pockets.

Lorazepam Binding to poly(SULV)

The association of (R) and (S)-lorazepam with poly(SULV) will now be presented and compared to previously reported work for BNP. Binding free energies and the fractional occupancies, f_i, for the lorazepam enantiomers in each MM pocket are shown in Table II. The binding free energy corresponds to the difference in free energy between each MM: enantiomer complex and the sum of the free energies of the separate MM receptor and ligand. The fractional occupancy corresponds to the fraction of time that the ligand binds to each pocket, based upon the calculated free energies of binding. Fractional occupancies were calculated with equation (1).

$$f_i=\frac{e^{-G_i/k_{B}T}}{{\displaystyle \sum _{i=1}^N{e}^{-G_i/k_{B}T}}}$$ (1)

G_i is the binding free energy of the (S) or (R) enantiomer in the i^th pocket of the MM, k_B is Boltzmann’s constant, T is Kelvin temperature, and the summation is over all binding sites. Table II also includes the pocket-averaged MM binding free energies for each enantiomer. These average free energies were calculated by multiplying the f_i value of the i^th pocket by that pocket’s binding free energy, G_i, and summing over the four binding sites.

Table II:

Free energies of MM binding and fractional occupancies for lorazepam and chlorthalidone enantiomers in the four MM binding pockets.

	(S)-Lorazepam		(R)-Lorazepam
Pocket	Free Energy (kJ∙mol−1)	Fraction Occupied	Free Energy (kJ∙mol−1)	Fraction Occupied
1	−63.93	0.21	−60.88	0.93
2	−67.03	0.70	−42.55	5.9 × 10−4
3	−31.42	4.3 × 10−7	−52.89	0.037
4	−62.13	0.099	−52.47	0.032
Average Free Energy	−66.24		−60.22
	(S)-Chlorthalidone		(R)-Chlorthalidone
Pocket	Free Energy (kJ∙mol−1)	Fraction Occupied	Free Energy (kJ∙mol−1)	Fraction Occupied
1	−71.54	0.999	−65.75	0.824
2	−38.45	1.57 × 10−6	−53.19	5.18 × 10−3
3	−41.94	6.42 × 10−6	−61.72	0.140
4	n/a	n/a	−54.48	8.72 × 10−3
Average Free Energy	−71.47		−63.57

Table II shows that (S)-lorazepam had the lowest binding free energy in poly(SULV) pockets one (−63.93 kJ∙mol⁻¹) and two (−67.03 kJ∙mol⁻¹) with respective f_i values of 0.21 and 0.70. (R)-lorazepam had the lowest binding free energy in pocket one (−60.88 kJ∙mol⁻¹) where the f_i value was 0.93. Furthermore, the MD simulations predict that (S)-lorazepam interacts more strongly with poly(SULV) than (R)-lorazepam because the (S)-enantiomer has the more negative average binding free energy. In the BNP analyses, (S)-BNP also had a lower MM binding free energy than (R)-BNP [17]. Therefore, the (S)-enantiomers of both lorazepam and BNP bound to poly(SULV) more strongly than the (R)-enantiomers. In addition, lorazepam enantiomers have been successfully separated in CE experiments using poly(SULV) as the chiral selector [16]. The binding free energies in Table II are consistent with this experimental result, in that the pocket averaged free energies of binding are different for the two lorazepam enantiomers.

The lorazepam interactions with poly(SULV), though, are not identical to BNP. For example, (S)-BNP bound to pocket two with f_i near one. (S)-lorazepam also preferred MM pocket two with f_i = 0.70. (R)-BNP preferred MM pocket two as well with f_i = 0.91 [17]. However, (R)-lorazepam binds most favorably to MM pocket one with f_i = 0.93. (S)-lorazepam also had affinity for MM pocket one (f_i = 0.20). Lorazepam may be able to interact favorably with MM pocket one, while BNP does not, because the lorazepam ligand is slightly smaller. The lorazepam enantiomers also likely have some flexibility with respect to the conformation of the seven-membered ring and rotation about the bond connecting the fused rings to the compound’s other aromatic ring. This flexibility may allow lorazepam to adopt a shape or conformation that allows it to bind to the MM in pocket one. In contrast, BNP is larger and more rigid, with very little conformational flexibility, forcing it to always bind to MM pocket two which is relatively wide and shallow.

In order to determine how deeply the lorazepam enantiomers penetrated into the hydrocarbon core in each MM pocket, solvent accessible surface area (SASA) analyses were carried out. A small SASA indicates that the ligand is bound deeper in the MM core, and a large SASA indicates that the ligand is bound nearer the MM surface. Figures 3(a) and 3(b) show plots of the SASA vs. simulation time for (S)-lorazepam and (R)-lorazepam bound to each of the MM pockets. For comparison, Figure 3 also includes analogous SASA plots from an MD simulation containing only lorazepam and water but no MM. Figures 3(a) and 3(b) show that the behavior of the bound lorazepam ligands is split into two distinct groups for both enantiomers. Pockets one and two have smaller SASA and pockets three and four have larger SASA. This result suggests that the relatively high f_i values for (S)-lorazepam in pocket two and (R)-lorazepam in pocket one are in part because these pockets allow the deepest penetration of the enantiomers into the MM hydrocarbon core. Finally, the SASA of (S)-lorazepam in pockets one and two and (R)-lorazepam in pocket one are similar throughout the MD simulation so, although the lorazepam enantiomers prefer to bind in MM pockets where they have a small SASA, the SASA alone does not explain why (S)-lorazepam had a lower average binding free energy than (R)-lorazepam.

Figure 3:

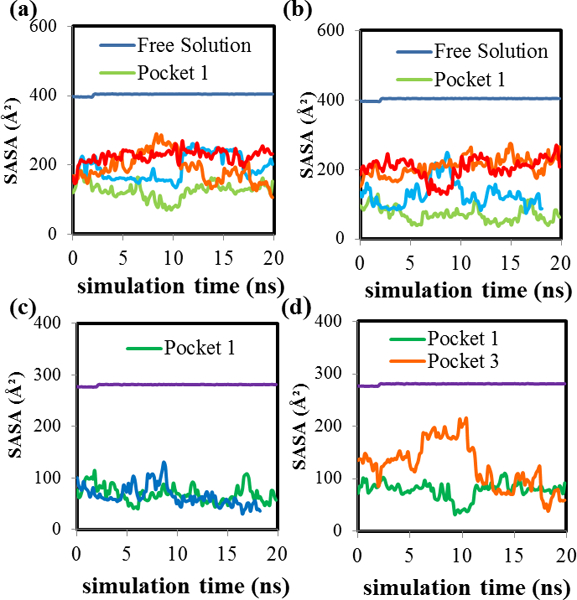
SASA versus simulation time plots for (a) (S)-lorazepam in pockets 1 (green), 2 (blue), 3 (orange) and 4 (red), (b) (R)-lorazepam in pockets 1–4 (color coding is the same as (a)), (c) aromatic rings of (S)-lorazepam in pockets 1 (green) and 2 (blue), and (d) aromatic rings of (R)-lorazepam in pockets 1 (green) and 3 (orange). The horizontal plot in each figure is the free solution SASA versus simulation time.

In order to gain further insight into the orientation of the lorazepam enantiomers within each MM pocket, the SASA of only the atoms in the molecule’s aromatic rings were also calculated. Figures 3(c) and 3(d) show the SASA of the aromatic rings of (S)-lorazepam and (R)-lorazepam in MM pockets one and two, and one and three, respectively. These were the two pockets for each enantiomer with the highest f_i values. When (S)-lorazepam is bound to pockets one and two, its aromatic rings have nearly the same SASA throughout the MD simulation. This result indicates that the (S)-enantiomers in these two pockets must have a similar orientation with the aromatic rings similarly exposed to the solvent. For (R)-lorazepam bound to MM pockets one and three, the behavior is different. (R)-lorazepam has a similar SASA in both pockets for the last five nanoseconds of the MD simulation. However, at the beginning of the MD simulation, the aromatic rings of (R)-lorazepam in pocket three had a larger SASA than the aromatic rings of (R)-lorazepam in pocket one. This result suggests that the aromatic rings of (R)-lorazepam in pocket one are oriented deeper in the pocket and are less accessible to the solvent during the MD simulation when compared to the aromatic rings of (R)-lorazepam in pocket three.

Additionally, hydrogen bond formation between poly(SULV) and the lorazepam enantiomers was investigated. The hydrogen bonds that formed during the MD simulation between the enantiomers of lorazepam and the MM chains are presented in Table III. Included in Table III are the donor and acceptor atoms that form the hydrogen bonds and each hydrogen bond’s percent occupancy. The percent occupancy is the percentage of the MD simulation that a hydrogen bond was present. Table III shows the intermolecular hydrogen bonds present for at least 10% of the MD simulation. If an MD simulation had no H-bonds above 10%, then the H-bonds with the two highest occupancies are listed. Overall, compared to the BNP analysis, lorazepam formed more hydrogen bonds with the MM and the hydrogen bonds that formed had much higher percent occupancies. For example, (S)-lorazepam in pocket two and (R)-lorazepam in pocket one formed hydrogen bonds with the MM that were present for 27.81% and 20.68% of the MD simulation, respectively. These hydrogen bonds were both between the poly(SULV) Leu-CO and the lorazepam NH atoms. In contrast, the hydrogen bond with the highest percent occupancy in the (S)-BNP MD simulation analyses formed between a leucine NH atom in the MM dipeptide headgroup and one of the BNP phosphate oxygens. The percent occupancy of this H-bond was 11.88% and all (R)-BNP H-bond occupancies were less than 1% [17].

Table III:

Hydrogen bonds and percent occupancies from the (S)-lorazepam and (R)-lorazepam MD simulations in MM pockets 1–4.The symbols Lor, Leu, and Val represent, respectively lorazepam and either the leucine (Leu) amino acid or valine (Val) amino acid of of the poly(SULV) headgroup. The number in parentheses indicates the poly(SULV) momomer chain containing the H-bond donor or acceptor atom.

	(S)-Lorazepam			(R)-Lorazepam
Pocket 1	Donor	Acceptor	% occupied	Donor	Acceptor	% occupied
	Lor-CO	Leu-NH (9)	74.21	Leu-CO (8)	Lor-NH	20.68
	Lor-CO	Val-NH (9)	17.32	Lor=N	Leu-NH (2)	16.81
	Val-CO (9)	Lor-OH	13.68
Pocket 2	Donor	Acceptor	% occupied	Donor	Acceptor	% occupied
	Leu-CO (18)	Lor-NH	27.81	Lor-CO	Leu-NH (6)	72.06
	HC-CO (9)	Lor-OH	12.51	Val-CO (6)	Lor-NH	48.48
				Lor-CO	Val-NH (6)	44.99
				Leu-CO (18)	Lor-OH	43.10
				Val-CO (6)	Lor-NH	17.83
				Leu-CO (16)	Lor-OH	12.01
Pocket 3	Donor	Acceptor	% occupied	Donor	Acceptor	% occupied
	Val-CO (17)	Lor-OH	5.82	Val-CO (11)	Lor-NH	15.75
	Lor-OH	Leu-NH (11)	5.30	Leu-CO (17)	Lor-NH	11.35
Pocket 4	Donor	Acceptor	% occupied	Donor	Acceptor	% occupied
	Val-CO (7)	Lor-NH	7.48	Leu-CO (6)	Lor-OH	0.69
	Val-CO (7)	Lor-NH	2.65	Val-CO (7)	Lor-OH	0.58

Returning to the lorazepam H-bond analysis, Table III shows that significant hydrogen bonding occurred between the lorazepam enantiomers and MM in all but the (R)-lorazepam pocket four MD simulation. It is also interesting to note that the largest percent occupancy intermolecular hydrogen bonds did not form in the preferred binding pockets. For example, (S)-lorazepam in pocket one and (R)-lorazepam in pocket two formed hydrogen bonds that were present for 74.21% and 72.06% of the MD simulation, respectively. However, (S)-lorazepam in pocket one and (R)-lorazepam in pocket two both had relatively low f_i values (0.21 and 5.9×10⁻⁴, respectively). In addition, the fact that the pockets with the lowest free energies of binding ((S)-lorazepam pocket two and (R)-lorazepam pocket one) had hydrogen bonds resident for over 20% of the MD simulation suggests that hydrogen bond formation is likely an important contributor to the low free energies of binding for (S)-lorazepam pocket two and (R)-lorazepam pocket one. However, MM hydrogen bond formation alone does not explain why (S) and (R)-lorazepam prefer binding to MM pockets one and two, respectively because hydrogen bonds with higher percent occupancies were detected in pockets with higher free energies of binding.

Finally, structures were extracted from the MD simulations to assess the orientation of the lorazepam enantiomers in the MM pockets with the lowest free energies of binding. As reported previously, structures with low RMSD values with respect to the average structure were chosen for this analysis. Figures 4(a) and 4(b) show MM: (S)-lorazepam structures extracted, respectively, from the pocket one MD simulation at 10.6 ns and the pocket two MD simulation at 10.4 ns. Figures 4(c) and 4(d) correspond to, respectively MM: (R)-lorazepam structures extracted from the pocket one MD simulation at 10.9 ns and pocket two at 10.1 ns. In the structures, the binding pocket is displayed as a surface with green and red corresponding to, respectively hydrophobic and hydrophilic pocket regions. The annotation IN labels atoms or rings inserted into the binding pocket and OUT labels atoms pointing toward the bulk aqueous phase.

Figure 4:

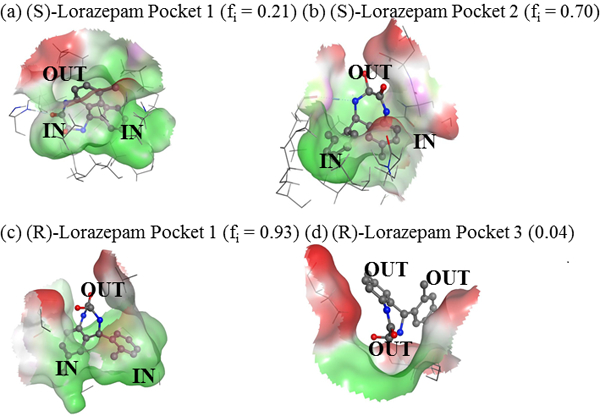
MM: lorazepam structures extracted from the MD simulation. (a) (S)-lorazapem in MM pocket 1 at 10.6 ns, (b) (S)-lorazepam in pocket 2 at 10.4 ns, (c) (R)-lorazepam in pocket 1 at 10.9 ns, and (d) (R)-lorazepam in pocket 3 at 10.3 ns.

Figure 4(c) shows that in pocket one, (R)-lorazepam has both of its aromatic rings oriented into the core of the MM pocket and its seven-membered ring containing the chiral atom oriented towards the aqueous phase. (S)-lorazepam in pocket two is oriented in a similar, favorable manner with its aromatic rings pointing deep in the MM pocket and its seven-membered ring facing out of the pocket towards the MM surface and solvent. In this orientation, (R)-lorazepam in pocket one and (S)-lorazepam in pocket two are also able to form hydrogen bonds with the MM and solvent molecules because the seven-membered ring is facing towards the MM surface and bulk aqueous phase. Adopting this favorable orientation likely contributes to (S) and (R)-lorazepam having low SASA values and binding free energies in these pockets.

Figures 4(a) and 4(d) also show that (S)-lorazepam in pocket one and (R)-lorazepam in pocket three have different orientations than those described above. In Figure 4(a), (S)-lorazepam in pocket one has its seven-membered ring and one of its aromatic rings oriented deep in the MM pocket and the other aromatic ring pointing towards the surface of the MM. This orientation is less favorable than the (S)-lorazepam orientation in Figure 4(b) because in pocket one the lorazepam polar ring containing the chiral atom points towards the hydrophobic MM core. Figure 4(d) shows that (R)-lorazepam in pocket three is oriented with its seven-membered ring in the MM pocket and its aromatic rings pointing toward the MM surface. This orientation is consistent with (R)-lorazepam in pocket three having a relatively large SASA. In this orientation, the polar seven-membered ring points into the MM core creating unfavorable interactions with the MM.

Overall, the structures in Figure 4 suggest that (S)-lorazepam in pocket two and (R)-lorazepam in pocket one have lower binding free energies than the (S)-enantiomer in pocket one and the (R)-enantiomer in pocket three because in the former case the enantiomers adopt favorable orientations within the MM pockets that point their aromatic rings toward the MM core and their polar seven-membered ring toward the MM surface. The enantiomers bound to the latter pockets adopt less favorable orientations with either one or both aromatic rings pointing away from the MM core. The orientations adopted by the lorazepam enantiomers in the MM pockets also highlights another difference between the lorazepam and BNP binding to poly(SULV). In the BNP analyses, the compound’s phosphate functional group remained oriented toward the bulk aqueous phase throughout the MD simulations for both the (R) and (S)-enantiomers. This result is expected since the phosphate group is anionic. In the (R)-BNP MD simulations, the chiral ligand pointed its phosphate group toward the aqueous phase and remained near the surface of the micelle. The (S)-enantiomer in contrast penetrated more deeply into the MM hydrocarbon core, but still kept its phosphate functional group oriented toward the bulk aqueous phase [17]. Therefore, the orientation of the ligand within the chiral pocket is an important factor in governing the interactions of lorazepam with poly(SULV), while in the BNP analyses the ligand remained in the same orientation throughout the MD simulation.

Chlorthalidone Binding to poly(SULV)

The binding free energies for (R) and (S)-chlorthalidone associating with each of the four MM pockets are given in Table II. The fractional population for the (R)-enantiomer in pocket one is the highest (0.824), while pocket three had an f_i value of 0.140. Table II also shows that the fractional population of the (S)-enantiomer in pocket one is 0.999. The f_i values for the (S)-chlorthalidone in the other pockets are very small. There is no energy listed for (S)-chlorthalidone in pocket four because the ligand drifted away from the MM at the beginning of the pocket four MD simulation. As discussed above, both propranolol enantiomers also bound predominately to MM pocket one with f_i values ≈ 1 [18]. Therefore, both chlorthalidone and propranolol enantiomers interacted preferentially with MM pocket one, likely because the molecules have similar shapes and electrostatic properties, with their hydrophobic and charged functional groups on opposite ends of the molecule. It is also interesting to note that for both chlorthalidone and propranolol, the (S) enantiomer had a lower MM binding free energy than the (R) enantiomer. Therefore, within their preferred binding pocket, the stereoselective interactions between the MM and both chlorthalidone and propranolol were likely similar because the (S) enantiomer of both compounds experienced more favorable interactions with the MM.

To assess the depth of penetration of the chlorthalidone enantiomers into the MM and to determine if chlorthalidone like propranolol inserted its hydrophobic fused rings into the hydrocarbon core, the SASA of the chlorthalidone enantiomers in the MM binding pockets were calculated [18]. We will first consider the SASA of all the chlorthalidone atoms and then consider separately the SASA of atoms in the molecule’s fused pyrole and sulfonamide containing rings. Figure 5(a) compares the SASA of (R)-chlorthalidone in MM pockets one and three. Figure 5(b) compares the (R)-chlorthalidone SASA in pocket one with the (S)-chlorthalidone SASA in the same pocket. Pockets one and three were included for the (R)-ligand because the f_i values for those pockets were both relatively high. Only pocket one was included for (S)-chlorthalidone because it had an f_i value near one. Each figure also contains the SASA for chlorthalidone from an MD simulation containing only the ligand and water (SASA = 471±1 Ų).

Figure 5:

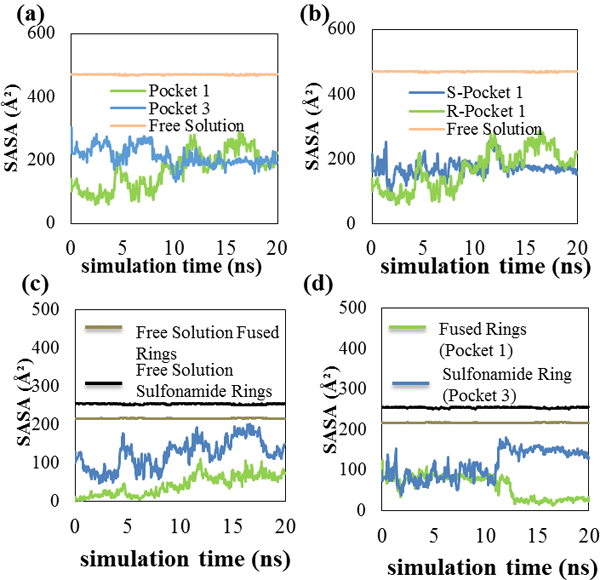
5(a) SASA graph for (R)-chlorthalidone in pockets 1 and 3, 5(b) SASA graph for (S)-chlorthalidone and (R)-chlorthalidone in pocket 1. 5(c) shows a SASA graph comparing the (R)-enantiomer atoms and their orientation pocket, and 5(d) represents the (S)-enantiomer in pocket 1.

Figure 5(a) shows that the SASA of (R)-chlorthalidone in pocket one at the start of the MD simulations was lower than that of pocket three. The two values remained different with the pocket one value being lower for the first half of the MD simulation. After 9 ns, the SASA of the (R)-enantiomer in pocket one increased and from 9–20 ns the SASA of the (R)-enantiomer in both pockets was similar. The MD simulation average SASA for (R)-chlorthalidone in pockets one and three were respectively, 167 ± 59 Ų and 211 ± 30 Ų. Table II showed that (R)-chlorthalidone in pocket one had a higher f_i value (0.824) than in pocket three (f_i = 0.140). The SASA analyses suggest that compared to pocket three, the (R)-enantiomer in pocket one spent more of the MD simulation with its rings inserted into the MM core. Penetration of the (R)-enantiomer into the MM core in pocket one likely shielded its fused pyrole ring from the solvent and allowed the enantiomer to experience favorable hydrophobic interactions with the MM hydrocarbon chains. This behavior likely contributed to the lower binding free energy calculated for the (R)-enantiomer in pocket one.

Figure 5(b) compares the SASA of (R)-chlorthalidone in pocket one to (S)-chlorthalidone in the same pocket. The (R) enantiomer in pocket one had a lower SASA for the first half of the MD simulation. From approximately 9 to 14 ns, the SASA of the (R) and (S)-enantiomers in pocket one were similar. Finally, from 14 to 20 ns, the (S)-enantiomer in pocket one had the lower SASA. The MD simulation average (R)-chlorthalidone and (S)-chlorthalidone SASA in pocket one were 167 ± 59 Ų and 173 ± 25 Ų, respectively. A t-test showed these values were the same at the 95% confidence level. Therefore, the SASA results suggest that in pocket one, (R) and (S)-chlorthalidone penetrate into the MM core to a similar degree. Other intermolecular interactions such as hydrogen bond formation are thus likely responsible for the difference observed in the (R) and (S)-chlorthalidone pocket one binding free energies reported in Table II.

In order to gain additional insight into how the chlorthalidone rings interacted with the MM core, and to further assess similarities with propranolol binding, separate SASA calculations were done for the atoms in the chlorthalidone fused pyrole and sulfonamide-containing rings. Results were then compared to their respective free solution values. In these analyses, a large difference between the free solution SASA and the SASA for a ring bound to the MM indicates that the ring is shielded from water and located within the MM core [18]. A smaller decrease indicates that the ring is found nearer the MM surface. Figure 5(c) plots the separate SASA for the (R)-chlorthalidone fused pyrole and sulfonamide-containing rings when the enantiomer is bound to pocket one. The SASA of these rings in free solution (217 ± 1 Ų, and 254 ± 1 Ų, respectively) are plotted as well. When bound to MM pocket one, the fused pyrole ring SASA is significantly lower than that of the sulfonamide-containing ring. Analysis of the Figure 5(c) data showed that in moving from free solution to MM pocket one, the (R)-chlorthalidone fused pyrole ring SASA decreased on average by 80.4%. In contrast, the SASA of the sulfonamide-containing ring decreased only 51.0%. This result suggests that upon MM binding, the more hydrophobic fused pyrole ring is shielded to a greater degree from solvent than the sulfonamide-containing ring and, therefore, is likely inserted into the MM core.

In Figure 5(d) the (S)-chlorthalidone fused pyrole ring SASA decreased 78.2% upon MM binding, while the sulfonamide-containing ring SASA decreased on average 51.0%. These percentages are almost identical to those observed when (R)-chlorthalidone bound to the same pocket. This behavior is also very similar to the propranolol enantiomers. In the (S)-propranolol analysis, the SASA of the atoms making up the molecule’s fused aromatic rings decreased by 86% moving from free solution to the MM-bound state. In contrast, the SASA of the atoms in propranolol’s chiral side chain decreased by only 65%. The SASA of the fused rings in (R)-propranolol was found to have an 80% decrease, while the side chain had a 59% decrease [18]. Therefore, these SASA analyses suggest that the binding of chlorthalidone and propranolol enantiomers to poly(SULV) is quite similar with both compounds placing their more hydrophobic fused rings in the MM core and their more hydrophilic atoms nearer the micelle surface and bulk aqueous phase.

Structures were extracted from the chlorthalidone MD simulations to further test the binding model suggested by the ring SASA analyses and to visualize chlorthalidone’s orientation with respect to the MM core. Figure 6(a) and 6(c) show, respectively (S)-chlorthalidone and (R)-chlorthalidone pocket one structures extracted from the MD simulation at sixteen ns for the (S) enantiomer and ten ns for the (R) enantiomer. In these structures, the MM is shown as a mesh and the ligand is shown as a ball and spoke model. The annotation IN labels atoms or rings inserted into the MM core and OUT labels atoms pointing toward the bulk aqueous phase. In both structures, the sulfonamide-containing ring (note the yellow sulfur atom) points out of the MM core and towards the bulk aqueous phase, while the enantiomer’s fused pyrole ring is inserted into the MM hydrocarbon core. This orientation was also suggested by the SASA analyses and is very similar to the manner in which the propranolol enantiomers bound to poly(SULV).

Figure 6:

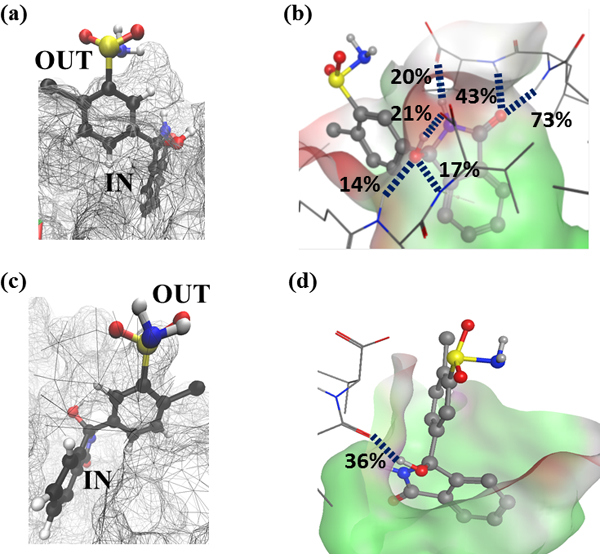
Representative structures of (S)-chlorthalidone and (R)-chlorthalidone in pocket 1. 6(a) and 6(b) show (S)-chlorthalidone at 6 ns, 6(c) and 6(d) shows (S)-chlorthalidone at 16 ns, and 6(e) and 6(f) shows (R)-chlorthalidone at 10 ns.

While the results discussed above give insight into the chlorthalidone: poly(SULV) binding mechanism, they do not fully explain why the binding free energies for the (R) and (S) chlorothiadone enantiomers in pocket one are different. Recall from Table II, the (R)-chlorthalidone and (S)-chlorthalidone binding free energies in pocket one were −65.75 kJ·mol⁻¹ and 71.54 kJ·mol⁻¹, respectively. The fractional occupancies reported in Table II also show that both chlorthalidone enantiomers interacted with the MM by associating predominately with pocket one. Therefore, different intermolecular interactions experienced by the ligand enantiomers in this pocket are likely an important factor governing the chiral resolution of chlorthalidone enantiomers in CE separations with poly(SULV). Previous work showed that t(S)-propranolol interacted with the MM more strongly than the (R)-propranolol because the (S)-enantiomer formed more and longer-lived hydrogen bonds with the polar MM headgroups [18]. Therefore, an analysis of hydrogen bond formation between the chlorthalidone enantiomers and the donor/acceptor atoms of the MM dipeptide headgroups in pocket one was carried out.

Table IV gives the results of hydrogen bond analyses from the MD simulations with (S)-chlorthalidone and (R)-chlorthalidone in MM pocket one. Only hydrogen bonds with percent occupancies greater than 10% are reported. These percentages refer to the percent of the MM simulation time for which each hydrogen bond was resident. The Table IV results show that for (S)-chlorthalidone and (R)-chlorthalidone in pocket one, no high occupancy hydrogen bonds formed between the MM and sulfanamide functional group_. If the sulfanamide functional group points into the bulk aqueous it would be expected that relatively few hydrogen bonds would form with the dipeptide headgroups of the MM surfactant chains. Previous work has also shown that chlorthalidone experiences strong chiral interactions with poly(SULV) [16]. The MD simulation results suggest that this behavior may be due to in part to ligand:MM hydrogen bonding occuring predominately with chlorthalidone atoms on the fused pyrole ring. This ring also contains the ligand’s chiral atom, so formation of H-bonds by the fuse pyrole ring likely brings together the ligand and MM chiral centers and are thus likely be stereoselective.

Table IV:

Hydrogen bonds formed between the (R) and (S) enantiomers and MM dipeptide headgroups in binding pockets one, three, and six. The symbols Cth, Leu, and Val represent, respectively chlorthalidone and either the leucine (Leu) amino acid or valine (Val) amino acid of of the poly(SULV) headgroup. The number in parentheses indicates the poly(SULV) momomer chain containing the H-bond donor or acceptor atom.

Pocket 1	(R)-Chlorthalidone
	Donor	Acceptor	% Occupied
	Cth-OH	Leu-CO (18)	38.25
	Leu-NH (8)	Cth-OH	25.72
Pocket 1	(S)-Chlorthalidone
	Donor	Acceptor	% Occupied
	Leu-NH (9)	Cth-CO	73.28
	Val-NH (9)	Cth-CO	42.75
	Cth-OH	Val-CO2− (2)	20.66
	Cth-NH	Val-CO2− (2)	20.42
	Val-NH (2)	Cth-OH	16.66
	Leu-NH (2)	Cth-OH	13.52
	Cth-OH	Val-CO2− (2)	13.40
	Cth-SO2NH2	Val-CO2− (2)	11.52

(R)-chlorthalidone in pocket one had two relatively high occupancy hydrogen bonds formed between the ligand hydroxyl group and the MM leucine carbonyl oxygen (38.25%) and the ligand hydroxyl group and the MM leucine amide NH (25.72%). In MM pocket one, (S)-chlorthalidone also had several high occupancy hydrogen bonds including one between the ligand carbonyl and leucine amide NH (73.28%), the ligand carbonyl and valine amide NH (42.75%), the ligand amide NH and valine CO₂^- (20.66%), the ligand hydroxyl group and valine CO₂^-, and between the ligand hydroxyl group and valine amide NH (16.66%). Therefore, in the (S)-chlorthalidone pocket one analyses, multiple high occupancy hydrogen bonds were detected suggesting that during the (S)-chlorthalidone MD simulation there were times when multiple ligand enantiomer:MM hydrogen bonds formed simutaneously.

In the AMBER trajectory analysis, the distance cut-off between the heavy atoms making up a hydrogen bond was 3.0 Å. The angle cut-off between hydrogen bond donor and acceptor atoms was ± 30º [26]. These criteria were used to determine the times during the (R) and (S)-chlorthalidone pocket one MD simulations when each hydrogen bond listed in Table IV formed. Overall this analysis showed that two or more intermolecular H-bonds formed for 58% of the (S)-chlorthalidone pocket one MD simulation. In contrast, two or more hydrogen bonds formed for only 8% of the MD simulation in which (R)-chlorthalidone was bound to MM pocket one. Furthermore, the H-bond analysis showed that in the (R)-chlorthalidone pocket one MD simulation there was no sustained period of time when two or more hydrogen bonds were present, with the longest time during which two simultaneous hydrogen bonds formed being only 0.42 ns. In contrast, in the (S)-chlorthalidone pocket one MD simulation, there were sustained periods of time during during which multiple hyrogen bonds formed. For example, at ~4 ns multiple hydrogen bonds formed for 4.62 ns, at 9.3 ns more than one hydrogen bond formed for 2.13 ns, and at 17.6 ns more than one hydrogen bond formed for 2.43 ns.

Finally, Figure 6(b) shows hydrogen bonds formed between the MM headgroups and (S)-chlorthalidone in the pocket one MD simulation. The Figure 6(b) structure was extracted from the MD simulation at 16 ns. This structure shows the formation of multiple simultaneous high occupancy H-bonds between the (S) enantiomer and MM. At this time step, two hydrogen bonds formed with percent occupancies of 73% and 43% between the ligand carbonyl oxygen and, respectively the leucine and valine NH atoms of MM chain nine. A H-bond with a 21% occupancy also formed between the ligand OH group and an oxygen atoms in the valine -CO₂^- group of MM chain two. Intermolecular H-bonds also formed connecting the (S)-chlorthalidone NH and the valine carboxylate of chain two (20%), the ligand -OH group and an oxygen atoms of the chain two valine carboxylate group (17%), and the (S)-chlorthalidone –OH and the leucine NH of MM chain two (14%). In contrast, Figure 6(d) shows H-bonds formed between (R)-chlorthalidone and the MM at a time step of 10 ns. This structure has only one H-bond with a percent occupancy of 38% connecting the ligand –OH group to the leucine carbonyl oxygen of chain 18.

Therefore, the MD simulations suggest that not only do both chlorthalidone and propranolol insert their hydrophobic fused rings into the MM core, but that the mechanism of chiral discrimination is also similar for both ligands [18]. In the propranolol analyses, (S)-propranolol was found to bind more strongly to poly(SULV) than (R)-propranolol because the former formed more hydrogen bonds with the MM [18]. An analogous result was obtained in the chlorthalidone analyses described here with again (S)-chlorthalidone having a lower free energy of binding to the MM than the (R)-enantiomer. Furthermore, the chlorthalidone hydrogen bond analyses showed that, like propranolol, a larger number of intermolecular H-bonds formed between the (S)-enantiomer and MM than between the (R)-enantiomer and poly(SULV). Formation of these H-bonds is likely a major contributor to the lower MM binding free energy calculated for the (S)-chlorthalidone enantiomer.

Conclusions

The association of lorazepam enantiomers with poly(SULV) was found to be similar to that of BNP. Lorazepam enantiomers preferentially associated with MM pockets one and two. In these pockets, the lorazepam aromatic rings where shielded from solvent and the enantiomers formed hydrogen bonds with the MM dipeptide headgroups. Also, in the MM pockets with the lowest binding free energies, the lorazepam enantiomers adopted a favorable orientation that pointed their aromatic rings toward the MM core and their more hydrophilic atoms toward the micelle surface. Chlorthalidone binding to poly(SULV) was in contrast very similar to that of propranolol. Both chlorthalidone and propranolol preferentially bound to the same MM pocket where they placed their more hydrophobic rings into the MM core and their polar functional groups toward the bulk aqueous phase. The (S) enantiomer of both chlorthalidone and propranolol was also found to have a lower MM binding free energy than the (R) enantiomer. For both compounds, this result was attributed to the (S) enantiomer experiencing stronger hydrogen bonding interactions with poly(SULV). Overall, it can be concluded that chiral compounds with similar shape and charge distribution bind preferentially to the same poly(SULV) pocket and in that pocket experience similar stereoselective interactions with the MM dipeptide headgroups. Work is currently underway to use MD simulations to gain additional insights into the nature of chiral recognition by molecular micelles and to use those insights to design new surfactant-based chiral selectors for CE separations.