Functional brain connectivity is predictable from anatomic network’s Laplacian eigen-structure

Abstract

How structural connectivity (SC) gives rise to functional connectivity (FC) is not fully understood. Here we mathematically derive a simple relationship between SC measured from diffusion tensor imaging, and FC from resting state fMRI. We establish that SC and FC are related via (structural) Laplacian spectra, whereby FC and SC share eigenvectors and their eigenvalues are exponentially related. This gives, for the first time, a simple and analytical relationship between the graph spectra of structural and functional networks. Laplacian eigenvectors are shown to be good predictors of functional eigenvectors and networks based on independent component analysis of functional time series. A small number of Laplacian eigenmodes are shown to be sufficient to reconstruct FC matrices, serving as basis functions. This approach is fast, and requires no time-consuming simulations. It was tested on two empirical SC/FC datasets, and was found to significantly outperform generative model simulations of coupled neural masses.

Introduction

The interplay between the brain’s function and structure is of immense interest in neuroscience, and its elucidation can potentiate novel approaches for mapping and treating brain diseases. Structural connectivity (SC) measures anatomical white matter fiber connectivity between gray matter regions and is obtained from diffusion tensor imaging (DTI) (Hagmann et al., 2008; Iturria-Medina et al., 2008; Gong et al., 2009). Functional connectivity (FC) is typically defined as the temporal correlation of neurophysiological time series obtained via fMRI or EEG (Chang and Glover, 2010). Euclidean distance between regions is a good predictor of FC (Pineda-Pardo et al., 2015; Vertes et al., 2012). Strong correlation is known between functional and structural connections, where the former appears to be constrained by the latter (Honey et al., 2009; van den Heuvel et al., 2009; Hermundstad et al., 2013; Rubinov et al., 2009; Ghosh et al., 2008; Wang et al., 2014; Park and Friston, 2013). Important graph properties are shared by both SC and FC networks, such as small world, power-law degree distribution, hierarchy, modularity, and highly connected hubs (Bullmore and Sporns, 2009; He et al., 2007; Filippi et al., 2013).

However, a full exposition of the structure-function relationship requires mathematical, rather than statistical modelling. Some progress in this area has been made (Galán, 2008; Honey et al., 2007; Ghosh et al., 2008; Vertes et al., 2012; Goni et al., 2014; Abdelnour et al., 2014), but the field has eschewed simple models in favor of complex generative models, involving large-scale neural simulations of synthetic activity time series (Honey et al., 2007, 2009; Deco et al., 2011). Anatomic connectivity between nodes is employed indirectly, as coupling constants between node-level dynamics. Function is therefore only deducible indirectly from thousands of trial runs of time-consuming simulations, and the essential minimal rules of organization and dynamics of the brain remain invisible.

Here we demonstrate, for the first time, that in fact, SC and resting state FC are related in a simple and deterministic fashion via just a few eigenvectors of the graph Laplacian. This strong relationship is not apparent at the node-pair level, but rather at the level of eigen-spectra of the brain graph. We had previously reported that the brain network can be decomposed into its constituent “eigenmodes”, which play an important role in both healthy brain function and pathophysiology of disease (Raj et al., 2012; Abdelnour et al., 2014, 2015). We show that presented eigen-relationships arise naturally from a biophsysical abstraction of fine-scaled and complex brain activity into a simple linear model of how mutual dynamic influences or perturbations can spread within the underlying structural brain network, a notion advocated previously (Goni et al., 2014). We present a simple fitting procedure to predict functional eigenvectors and eigenvalues from structural ones. In turn, eigenvectors are combined to construct the full functional connectivity in a completely analytical, i.e. closed-form, manner. The resulting model is verified using empirical healthy SC/FC data, and compared against the previous graph diffusion (Abdelnour et al., 2014) and nonlinear neural mass model (NMM) simulations (Honey et al., 2009; Breakspear et al., 2003; Abdelnour et al., 2014). Further, it is shown that Laplacian eigenvectors can efficiently predict classic functional networks computed from independent components analysis, e.g. default-mode, executive, etc, networks, at least at group level.

Such an analytical approach is quite rare in brain science. Its power derives from the general property that any physical linearized system can be described by a few constituent eigenmodes. Eigenfunctions are key features of classical mechanics; e.g., standing waves in continuous media are eigenfunctions. In quantum mechanics, the “probability cloud” of the electron’s orbit around the nucleus is described via eigenfunctions of the Schrodinger wave equation (Schrodinger, 1940). In structural biology, the so-called “normal modes” that describe the degrees of freedom of large molecules are the eigenfunctions of pairwise atomic bonds (Heller, 1981). The sinusoids of the celebrated Fourier basis are eigenfunctions of bounded-energy linear time-invariant filter (Candan et al., 2000). Similarly, the field of spectral graph theory (Ng et al., 2002) studies how signals on graphs can be efficiently described via constituent graph eigenmodes. Our approach is therefore a “spectral graph theory of brain functional connectivity”. It is closely related to our earlier proposal that diffusion processes, or equivalently, random walks, constrained on the structural network, can predict functional covariances via the so-called graph diffusion kernel $FC=\text{exp}\left(-\beta t\mathcal{L}\right)$, involving the Laplacian of SC, ℒ (Abdelnour et al., 2014, 2015). The kernel is computed via the eigen decomposition of ℒ , hence eigenvectors and eigenvalues of SC and FC must be related (Abdelnour et al., 2015). In this paper we make these eigen-relationships explicit and independent of graph diffusion or any other model. To our knowledge, these results have not appeared before.

Materials & methods

Network notation

In a brain network each node represents a gray matter region located on either the neocortex or in deep brain subcortical areas. We define a network 𝒢 = (V,ℰ ) with a set of N nodes given by $V=\left\{v_i|i\in 1,\dots ,N\right\}$ and a set of edges given by an ordered node pair $E=\left\{\left(i,j\right)|i\in V,j\in V\right\}$ (Chung, 1997). Between any two nodes i and j there might exist a fibre pathway whose connectivity weight 𝑐_ij ∈ [0,∞) can be measured from dMRI tractography, and this defines a connectivity matrix ${\text{C}}_s=\left\{c_{i,j}|\left(i,j\right)\in \mathcal{E}\right\}$. Although some individual neurons are known to be directional, dMRI does not allow measurement of directionality. Major fiber bundles resolvable by dMRI, especially cortico-cortical pathways are generally bidirectional, having roughly equal number of connections in either direction (Albright, 1984). We define the connectivity strength or the weighted degree of a node i in this graph as the sum of all connection weights: ${\delta }_i={\displaystyle \sum _{j|\left(i,j\right)\in \mathcal{E}}{c}_{i,j.}}$

The table below describes the various parameters and variables used in this work (see Table 1).

Table 1.

Summary of the variables and definitions used in this text.

Parameter or variable	Role
𝒢	structural network of N nodes
𝒱	set of nodes of 𝒢
𝒱i	ith node of 𝒢
ℰ	set of edges of 𝒢
Cs	structural connectivity matrix
Ci,j	element (i,j) of Cs
Cf	functional connectivity matrix
${\text{C}}_f^{GD}$	graph diffusion estimate of Cf
${\text{C}}_f^{eig}$	eigen decomposition estimate of Cf
δi	weighted degree of node i
ℒ	Laplacian of Cs
Ul	eigenvectors of ℒ
Λl	eigenvalues of ℒ
${\Lambda }_f^{eig}$	proposed model eigenvalues
${\Lambda }_f^{GD}$	eigenvalues of the GD model
ui	ith eigenvector of ℒ
Δ	diagonal degree matrix of Cs
β	diffusion rate

The graph diffusion model

We had previously described a linear graph model predicting a subject’s functional connectivity matrix from their structural connectivity matrix via graph diffusion (GD) (Abdelnour et al., 2014), briefly described here for completeness. Two cortical regions R_i and R_j are connected by a fibre population with weight c_i;j, then activity in one region affects activity in the other via the first-order diffusion-like dynamics

$$\frac{d{x}_i\left(t\right)}{dt}=\beta \left({\delta }_i^{-\frac{1}{2}}{\displaystyle \sum _j{c}_{i,j}{\delta }_i^{-\frac{1}{2}}\left(t\right)-x_i\left(t\right)}\right)$$

where the last term reflects self-decay within regions as a result of local inhibition, desynchronization and other effects that serve to limit local activity. Over the entire network, the resulting graph diffusion FC estimate, ${\text{C}}_f^{GD}$, is given simply by

$${\text{C}}_f^{GD}\left(t\right)=e^{-\beta \mathcal{L}t}$$ (1)

where $\mathcal{L}=I-{\Delta }^{-1/2}{\text{C}}_s{\Delta }^{-1/2}$. Matrix Δ is diagonal with ${\Delta }_{ii}={\delta }_i$ and C_s is the structural connectivity matrix with elements C_i;j. Matrix ℒ is simply the symmetric normalized Laplacian matrix of C_s. At some diffusion point t_max the correlation R between the estimated functional connectivity matrix ${\text{C}}_f^{GD}$ and the empirical FC matrix reaches a maximum.

By factoring matrix ℒ into its eigenvalues 𝛬_l and eigenvectors U_l matrices we have $\mathcal{L}={\text{U}}_l{\text{Λ}}_l\text{U}.$ From Eq. (1) the GD model can be written as ${\text{C}}_f^{GD}={\text{U}}_l{e}^{-\beta {\Lambda }_{l}t}{\text{U}}_l^{\text{'}}.$

Proposed eigen decomposition model

From the above, the structural connectivity’s Laplacian matrix ℒ and the GD estimated functional connectivity matrix ${\text{C}}_f^{GD}$ must share the same eigenvectors U_l = U_f and the eigenvalues must be directly related by ${\Lambda }_f^{GD}=e^{-\beta {\Lambda }_{l}t}$, where ${\Lambda }_f^{GD}$ is the functional adjacency matrix ${\text{C}}_f^{GD}$ eigenvalues.

In this work we focus on and expand this eigen relationship, and model the functional eigenvalues 𝛬_f and their Laplacian counterparts 𝛬_l by a more general exponential relationship:

$${\Lambda }_f^{eig}=a{e}^{-\alpha {\Lambda }_l}+b\text{I}$$ (2)

where ${\Lambda }_f^{eig}$ is the diagonal matrix containing the estimated functional eigenvalues, and where diffusion depth t is now absorbed into parameter α. The eigen decomposition model eigenvectors are assumed to be identical to the Laplacian eigenvectors, similar to (Abdelnour et al., 2014). Functional connectivity matrix is then estimated from ${\text{C}}_f^{eig}={\text{U}}_l{\Lambda }_f^{eig}{\text{U}}_l^{\text{'}},$ or since the Laplacian eigenvectors are always orthogonal we obtain

$$\begin{gathered} {\text{C}}_f^{eig}=a{\text{U}}_l{e}^{-\alpha {\Lambda }_l}{\text{U}}_l^{\text{'}}+b\text{I} \\ ={\displaystyle \sum _{i=1}^N{\text{u}}_i\text{u}{\text{'}}_i\left(s{e}^{-\alpha {\lambda }_i}+b\right)} \end{gathered}$$ (3)

where N is the order of the graph 𝒢 and ${\lambda }_i$ is the ith eigenvalue of ℒ. It can be easily shown that the above “eigen” model corresponds to a linear first order differential equation:

$$\frac{\text{dx}\left(t\right)}{dt}=-\beta \mathcal{L}\left(\text{x}\left(t\right)-{\text{x}}^{*}\right)$$

where x* is the steady state solution. The solution of this differential equation is given by

$$\text{x}\left(t\right)={\text{x}}^{*}+e^{-\beta \mathcal{L}t}\left(\text{x}\left(0\right)-{\text{x}}^{*}\right)$$

Following (Abdelnour et al., 2014), this signal dynamics, when evaluated repeatedly with initial signal x(0) concentrated at each node, gives a predicted FC matrix

$${\text{C}}_f^{eig}=a{e}^{-\beta \mathcal{L}t}+\text{K}$$

for some constant matrix K. Here we assert $\text{K}\text{=}b\text{I,}\text{a}\text{=}\text{E}\left\{\text{x}{\left(0\right)}^T\text{x}\left(0\right)\right\}$ which $\alpha =\beta t,$ which makes the above equation equivalent to (3).

Although the summation in (3) involves all eigenvectors, in this work, we will exclude eigenvectors u₁ and u₂. Eigenvector u₁ simply captures uniform background connectivity (K above), and is usually regressed out from fMRI data. Eigenvector u₂ reflects left-right connectivity, which is poorly measured by DTI tractography, and this aspect of functional connectivity is well known to be underestimated by SC measurements. When only a single hemisphere is considered, only eigenvector u₁ is excluded, but not u₂. Equation (3) makes it possible to find the contribution of subsets of the eigen components. We show in Results that only a handful of the eigen components are needed to capture the essentials of the FC adjacency matrix, which is usually rather low-rank. Hence, a small subspace spanned by a handful of structural Laplacian eigenvectors is sufficient to construct FC.

NYU MR imaging and preprocessing

26 healthy subjects were recruited. The subjects underwent scanning on a Siemens Allegra 3T scanner at New York University Center for Brain Imaging. All participants had a T1-weighted MRI sequence optimized for gray-white matter contrast. (TR = 2530 ms, TE = 3.25 ms, T1 = 1100 ms, flip angle = 7 deg, field of view (FOV) = 256 mm, matrix = 256 256 192, voxel size = 1 1:33 1:33 mm). Images were corrected for nonlinear warping caused by nonuniform fields created by the gradient coils. Resting state fMRI scans included 197 contiguous echo planar imaging functional volumes for each subject (TR = 2000 ms; TE = 25 ms; flip angle = 90, 39 slices, matrix = 64 64; FOV = 192 mm; acquisition voxel size = 3 3 3 mm). All participants were instructed to lie as still as possible with their eyes open for the duration of the 6 min, 38 s scan.

DTI data were acquired with 65 isotropically distributed diffusionencoding directions at b ¼ 1000 s=mm² and one at b ¼ 0 s=mm², obtained at 47 2:5 mm thick interleaved slices with no gap between slices and 96 × 96 matrix size with a FOV of 117:5 mm.

Structural and diffusion MR volumes were coregistered using SPM tools in MATLAB (Aleman-Gomez et al., 2006; Friston et al., 1994), and then parcellated into 90 cerebral cortical structures as per (Tzourio-Mazoyer et al., 2002). Parcellated regions were used to seed probabilistic tractography in coregistered diffusion MRI volumes. Connectivity between any two regions was given by the sum of tracts going between them (Iturria-Medina et al., 2007). Simple statistical thresholding was performed to remove spurious weak connections, defined as those below the p = 0:001 level of significance. Probabilistic masks, including both white and GM, were obtained. Threshold level p > 0:001 has been previously reported in (Ivkovic et al., 2012). A voxel was included in the mask if both its GM and WM probabilities exceeded 0.5.

All fMRI data were preprocessed using DPARSF version 2.1 (Song et al., 2010). The first seven time points for each subject were discarded. Spatial resolution was set at 2×2×2mm³. Standard steps in fMRI preprocessing were followed, including head motion correction, normalization across the subjects, smoothing, linear trend removal, bandpass filtering (0.01–0.08 Hz), and finally nuisance covariates removal closely following (Song et al., 2010). The latter step includes the removal of the global signal, the cerebrospinal fluid (CSF) and white matter signals so as to reduce the effects of head motion and non-neuronal BOLD fluctuations. The time series of all voxels were averaged to 90 regions for each subject using the anatomical AAL atlas (Song et al., 2010) (cerebellum not included). Due to the weak recovery of the left and right pallidum in addition to their extremely small size, they were excluded from the networks. Thus the structural and functional networks used had 88 nodes each.

NYU functional and structural matrices

The FC matrix elements were obtained by evaluating the Kendall tau correlation between all 88 time series for all subjects. We opt for the Kendall tau because it is nonparametric and thus makes no a priori assumption on the distribution of the functional time-series from which the FC connectivity matrix is obtained. Weak functional connectivity, defined as smaller than 0:05 ${\text{C}}_f^{max}$ in the absolute, is set to zero, with ${\text{C}}_f^{max}$ the largest absolute value of interregional functional connectivity matrix C_f .

Segmentation: For each subject, tissue probability maps (GM, WM, CSF) were obtained with the SPM New Segment module which relied on the DARTEL nonlinear transformation TNative → MNI from native to MNI space (Ashburner, 2007). The subject brain mask was computed by applying a series of morphological operations on the resulting tissue probability maps. A 96-region parcellation of each subject T1 volume was obtained by applying the inverse of the previously calculated native → MNI transform to the AAL 116-region GM atlas and excluding the 20 regions associated to the cerebellum. The warped atlas in subject space was masked by the thresholded subject GM mask. The intersection between the dilated GM mask and the WM mask provided the interface between WM and GM.

Connectivity: The diffusion data was fitted to the diffusion tensor with FSL (Smith et al., 2004) in order to obtain FA maps. The transform TFA → T1 between diffusion and T1 space was computed by registering FA to T1 with a nonlinear deformation initialized from a linear registration (FSL FNIRT and FLIRT toolboxes respectively). The inverse transform TT1 → FA was calculated and applied to the WM/GM interface, so as to provide a seed mask for tractography, as well as to the 90-region parcellation to give the target ROIs required to obtain connectivity matrices. Whole-brain deterministic tractography was performed based on the previous seed mask and on fiber directions extracted from the diffusion profile estimated with Q-Ball ((Tuch, 2004; Hess et al., 2006)) as implemented in Camino (Cook et al., 2006). The count and average length of fibers connecting each pair of regions in the parcellated volume were calculated, and provided two connectivity matrices (associated with fiber count and average length respectively). In this work we use fiber count between two regions to construct the structural network.

ICA computation

Group level independent components analysis (ICA) of all the NYU subjects’ BOLD EPI volumes was performed using toolbox GIFT (Calhoun et al., 2009) and the infomax algorithm, resulting in 20 spatial ICA components. Individual subjects’ expression of the group level components were obtained. Finally, the resulting components are each averaged over each ROI region, leading to a 88×1 vector (after removing the two pallidum nodes) for each ICA component.

Correlation metrics used

Pearson correlation R is used as a measure of how close the models discussed in this work are to the empirical FC connectivity matrix C_f . Importantly, we exclude the diagonal elements of both matrices in the Pearson correlation computation, as their inclusion appears to cause an upward bias of R.

Results

We show that the SC and FC connectivity matrices reveal an exponential relationship predicted by the Laplacian’s eigen components between the eigenvalues λ_f and λ_l, and the tight relationship between the corresponding eigenvectors U_l and U_f . The Laplacian and functional eigenvalues (𝛬_l𝛬_f) and eigenvectors (U_lU_f ) were obtained. For each subject an exponential curve fit of the {λ_f} and {λ_l} eigenvalues of the form ae^−αx + b was computed via unconstrained non-linear minimization (Lagarias et al., 1998). To evaluate the accuracy of the FC connectivity matrix estimate, we compute the Pearson correlation between the estimated and the empirical FC matrices, excluding the matrices’ diagonal elements. All three models (GD, NMM, eigen decomposition) are explored and evaluated on 26 subjects obtained from NYU (Methods Section). The eigen decomposition model is additionally tested on a separate cohort of eight subjects obtained at Weill Cornell Medicine, See Sec SI-1 for MR imaging and networks construction.

Performance of the graph diffusion and neural mass models

Given that the current model is motivated by the GD model of (Abdelnour et al., 2014), we first evaluate how well it performs on the NYU subjects. As in (Abdelnour et al., 2014), the GD model was evaluated over a range of diffusion depths βt, Eq. (1). The resulting FC estimates give an R range of 0.29–0.41, with a mean of 0:35 ± 0:03. Fig. 1(a) depicts the resulting R curves for all subjects. In addition to the mean R obtained from the full brain network, Fig. 1(b) gives the mean R obtained when the GD model is applied to the full network as well as individual hemispheres only. Additional properties of R and βt can be found in Sec SI-2.

Fig. 1.

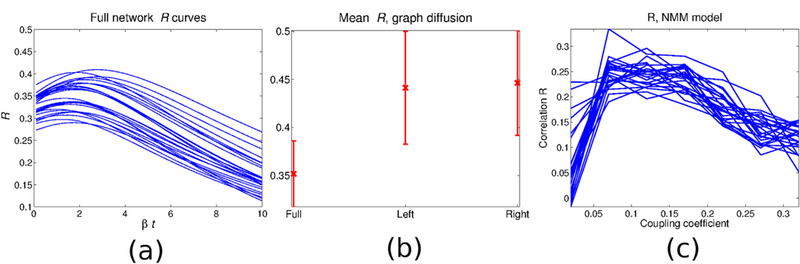
Functional network estimate using the graph diffusion model. and the neuronal mass model: (a) GD model R vs t, full network; (b) Mean GD Pearson correlation R for the full network (left), left hemisphere (middle), and right hemisphere (right); (c) NMM model: Plots of R for all subjects and over a range of the coupling coefficient c. The resulting R has a mean of 0.2622 0.0259. Recall that R here refers to Pearson’s R statistic computed between two FC matrices (model and empirical).

In order to compare proposed and GD models to the more commonly reported generative simulations involving nonlinear neural dynamics, we implemented the NMM model of (Breakspear et al., 2003; Honey et al., 2009), using the same model parameters previously used in (Abdelnour et al., 2014). The free coupling parameter c modulates the inter-regional coupling. In this implementation the model is tested on all subjects with c taking on the values {0:02; 0:07; 0:12; 0:17; 0:22; 0:27; 0:32}. The estimated FC networks give R in the range 0.21–0.33 with a mean 0:2622 ± 0:03. Fig. 1(c) gives R vs coupling coefficient for all subjects and all values of c.

FC and SC Laplacian eigenvectors are related, and their eigenvalues bear an exponential relationship

In both the GD and Laplacian eigen decomposition models, an exponential relationship between the functional eigenvalues, λ_f and the Laplacian ones, λ_l, is expected. Additionally, the model implies that the matrix U^’_lU_f should approximate the identity matrix. We computed the product T = U’_lC_f U_l for each subject, and evaluated the mean value of T over all subjects to reduce the role of inter-subject variability. If the product U^’_lU_f indeed approximates identity, we expect T to be a neardiagonal matrix. FC matrix is predicted from the Laplacian eigenvectors U_l and eigenvalues 𝛬_l, following Eq. (3), where parameters {a, α, b}are estimated from curve fitting of λ_f vs λ_l stacked over all subjects. For all subjects we have b ≥ − 1.

Fig 2(a) gives the empirical λ_f vs λ_l eigenvalues plot for all subjects. The plot closely approximates an exponential curve of the form ae^−αx + b, with {a,α,b}={11.66, 4.08,−0.75}. A semi-log scatter plot of all subjects’ FC eigenvalues λ_f vs the Laplacian eigenvalues λ_l is depicted in Fig. 2(b). The plot reveals an approximately linear relationship between log(λ_f) and λ_l(Fig. 2(c) gives the mean empirical FC eigenvalues λ_f over all subjects as a diagonal matrix. The eigenvectors’ function-structure relationship is observed at group level, where we compute the mean matrix T over all subjects. The resulting matrix is given in Fig. 2(d), where the matrix is nearly diagonal, similar to the empirical mean eigenvalues of Fig. 2(c), suggesting that at least at group level eigenvector matrices U_l and U_f are approximately equal.

Fig. 2.

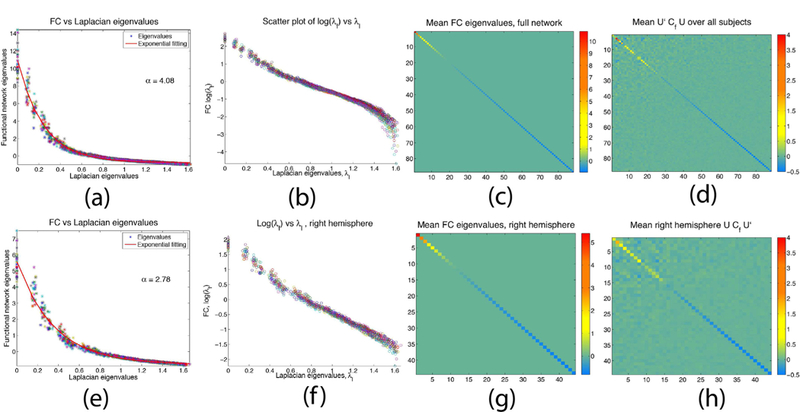
Figs (a-d) Full brain: (a) Curve fitting of λ_f vs λ_l when all subjects’ Laplacian and FC eigenvalues are stacked. The curve is exponential with α = 4:08, (b) Scatter semi-log plot of subjects’ Laplacian and FC eigenvalues, largely a linear plot. (c) Mean empirical 𝛬_f over all subjects, (d) Matrix obtained from mean U^’_lC_fU_l over all subjects. Resulting matrix is nearly diagonal. Figs (e-h) Right hemisphere: (e) Curve fitting when all subjects’ Laplacian and FC eigenvalues are stacked, α = 2:78. (f) Scatter semi-log plot of subjects’ Laplacian vs empirical FC eigenvalues, (g) Mean FC eigenvalues over all subjects. (h) Mean U^’_lC_fU_l over all subjects, leading to a nearly diagonal matrix.

We next examine the case where only the right hemisphere is considered. Consistent with the full network, the functional, λ_f, and Laplacian, λ_l, eigenvalues exhibit largely exponential relationship, see Fig. 2(e) where the stacked FC and Laplacian eigenvalues over all subjects are plotted. The resulting curve fitting coefficients are {a,α,b}={6.40, 2.78, −0.81}. The SC/FC eigenvalues relationship is further revealed in Fig. 2(f) where log(λ_f) vs λ_lscatter plot of all subjects highlights a nearly linear relationship. Fig. 2(g) gives the mean eigenvalues over all subjects as a diagonal matrix. Evaluating the mean value of T over all subjects reveals a near diagonal matrix, Fig. 2(h), similar to the mean eigenvalues matrix depicted in Fig. 2(g). Similar results are obtained in the case of the left hemisphere, where once again the λ_f and λ_l eigenvalues exhibit exponential relationship, and T largely approximates a diagonal matrix. For completeness, matrices U’_lC_f U_l for individual subjects are supplied in Fig SI-1 (Sec SI-3). Although there is clearly a substantial inter-subject variability in these projection matrices, there is also clear evidence of an underlying diagonal-dominant pattern shown in Fig. 2.

FC eigenvalues can be predicted from SC Laplacian eigenvalues

Given that the SC and FC eigenvalues/eigenvectors are related as expected by our model, we predict the FC eigenvalues λ_f given a subject’s Laplacian matrix L , after fitting the coefficients fa;α;bg as described above. The FC eigenvalues are estimated using Eq. (2). Fig. 3(a) gives the scatter plot of ${\lambda }_f^{eig}\text{vs}{\lambda }_f$ The mean correlation between ${\lambda }_f^{eig}\text{and}{\lambda }_f$ for all subjects is R = 0.9907 ± 0.0053. When only the right hemisphere is considered, ${\lambda }_f^{eig}\text{and}{\lambda }_f$ for all subjects have mean correlation R = 0:9890 ± 0.0070, the ${\lambda }_f^{eig}\text{vs}{\lambda }_f$ scatter plot is given in Fig. 3(b). Similar results are obtained in the case of the left hemisphere, where the mean correlation between the empirical and estimated eigenvalues for each subject is R = 0:9892 ± 0:0047. For all three cases the eigenvalues are closely captured. Additionally, for all cases the prediction is less accurate for the larger values of empirical λ_f. Scatter plots of $C_f^{eig}\text{and}{C}_f$ for each subject are given in Fig SI-2 (Sec SI-4).

Fig. 3.

Scatter plots of the estimated functional eigenvalues vs empirical FC eigenvalues, (a) full network, and (b) right hemisphere. For both cases the eigenvalues are closely captured using the eigen decomposition model.

We observe that for the parameters {a,α} at subject level, a and α appear to be correlated across the subjects. Specifically, for the case of the full network a and α correlation gives R ¼ 0:93. Similarly, left hemisphere network gives R ¼ 0:916. Finally, the right hemisphere gives similar results, with R ¼ 0:934. Parameter b appears to depend on α. Furthermore, the Pearson correlation between α and 1/b is 0.86 for the full network, 0.903 for the right hemispheres, and 0.914 for the right hemisphere. The parameters’ properties are further discussed in Sec SI-5 where Fig SI-3 summarizes the values of {a,α,b} over all subjects.

FC can be recovered from the Laplacian

Using the successful prediction of FC eigenvalues and eigenvectors from SC Laplacian, we constructed theoretic FC for each subject. Only a subset of the Laplacian eigenvectors is needed to capture the essentials of the FC connectivity matrix C_f . As discussed in Theory section, the low frequency Laplacian eigenvectors u₁ and u₂ are excluded. We investigated the contribution of subsets of U_l to the FC estimate as the number of eigenvectors progressively increases, and where for the full network u₁ and u₂ are excluded and for the hemisphere networks eigenvector u₁ is excluded. Evaluating Eq. (3) over a subset of eigenvectors, the resulting correlation R was computed; the process was repeated as more eigenvectors contribute to the FC estimate until all of the eigenvectors are exhausted. Fig. 4(a) gives the R values for all subjects starting with u₃ up to and including u₈₈. The resulting correlation R for the full network has a mean of R = 0:39 ±0.07 when only eigenvectors u₃12 were used, and R = 0:41 ± 0.06 when eigenvectors u₃₋₈₈ were used for FC estimation. Proceeding similarly with the right hemisphere, we obtained R = 0:42 ± 0.07 when eigenvectors u₂₋₁₁ were used, and R = 0:45 ± 0.06 when eigenvectors u₂44 were included (Fig. 4(b)). Likewise with the left hemisphere (not shown), the FC estimate gives R = 0:43 ± 0.08 using u₂₋₁₁, and R = 0:46 ± 0.07 when using u₂₋₄₄. It is clear that most of the information in C_f is captured in the first few eigen components. To summarize, the Pearson correlation obtained using the eigen decomposition approach is encapsulated in Fig. 4, where the mean R for the full network as well as the left/right hemispheres is given in Fig. 4(c).

Fig. 4.

(a) Pearson correlation R between model and empirical FC matrices as a function of the number of eigenvectors over all subjects. Recall that R here refers to Pearson’s R statistic computed between two FC matrices - model and empirical - as described in Section 2.7 (b) R for the right hemisphere only. (c) Mean R for the full network and the hemispheres using a subset of the eigenvectors {u_i}. (d) Histogram depicting mean R obtained from random networks preserving the weight, degree, and strength distributions of C_s evaluated over all subjects, and the mean R obtained from the empirical C_s networks

To verify that the model works specifically on the subjects’ SC network and is not simply due to randomness, we applied the above procedure to simulated random networks preserving SC’s weight, degree, and strength distribution using BCT (Rubinov and Sporns, 2010). Fig. 4(d) gives the histogram of R over 1; 000 iterations averaged over all subjects and the mean R obtained from the true SC networks. Clearly, the model is specific to the SC connectivity matrix. The R histograms obtained from the random networks simulation for the individual subjects is given in Fig SI-4, with additional discussion in Sec SI-6.

Fig. 5(a) summarize the eigen decomposition model’s performance vs the GD and NMM models for all subjects. The proposed model consistently results in R equal to or higher than the GD and NMM models. We also show for comparison the direct correlation between empirical SC and FC, since the two are themselves known to be correlated to each other. As observed from Fig 5a, however, their Pearson R is weak, in the range of 0.1–0.2, which is much smaller than what is achieved by the proposed model.

Fig. 5.

Summary of the three models and the resulting R for all subjects, R for each subject and each model. The proposed model consistently results in R equal to or higher than the GD and NMM models. Interestingly, subject 18 has the lowest NMM R but scores the highest eigen decomposition R. (b) Empirical FC for subject 12 in Fig 5(a) above, (c) FC recovery using GD model, (d) Recovery using the NMM model, (e) Recovery using the proposed eigen decomposition model. Recall that R here refers to Pearson’s R statistic computed between two FC matrices (model and empirical), as described in Section 2.7.

Fig. 5(b–e) illustrate the models’ performance for a single subject (subject 12 in Fig. 5(a)). Fig. 5(a) shows the subject’s empirical FC network. Fig. 5(b) gives the FC estimate using the GD model, Fig. 5(d) manifests the estimate obtained via the NMM model. It can be appreciated that the eigen decomposition model (Fig. 5(e)) most closely captures the empirical FC.

Effects of non-stationarity

The model’s linearity and lack of temporal dynamics implies an assumption of stationarity. The underlying fMRI time series are likely non-stationary, which may explain why a high R prediction of the eigenvectors occurs at group level only. To further explore this point, the fMRI time series are windowed into lengths of 60 time points, and the window is repeatedly shifted by 10 time points. For each window shift the FC network is computed from BOLD data, compared against the (stationary) eigenvector model, and the corresponding R is computed. Fig. 6 depicts the model’s performance over all subjects and shifts. Fig. 6(a) gives the resulting R for all subjects and all shifts. Clearly, R changes as the window slides, revealing a degree of non-stationarity. Interestingly, the eigenvector model continues to predict instantaneous FC quite strongly, although not as strongly as against the full time series FC. However, when maximum R for each subject is plotted in Fig. 6(b), the pattern generally follows that of the full time series given in Fig. 5(a).

Fig. 6.

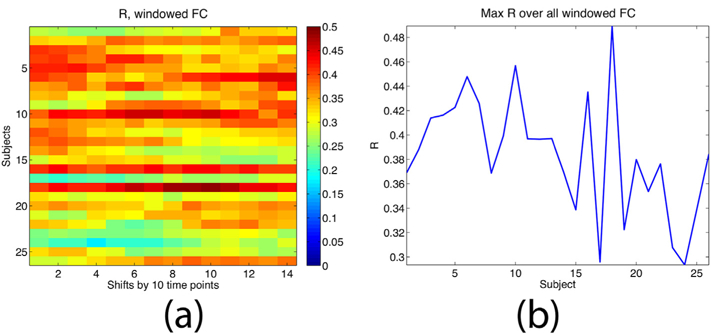
Investigating the effects of non-stationarity. (a) R when the empirical FC is obtained from time series windows of length 60 and shifted by 10 time samples for each bin. There is clear evidence of nonstationarity; however, the proposed model continues to give good match against instantaneous FC. (b) Maximum R for each subject over all shifts. For comparison, the model match against full time series FC is also shown. Despite non-stationarity, the maximum R over all sliding windows is consistent with the model match against FC computed on the full time-series.

Dominant Laplacian components

To illustrate how FC can be constructed using a small number of structural Laplacian eigenvectors, FC estimates using various subsets of eigenvectors is shown in Fig. 7. The matrices u_iu^’_i constitute the building blocks of the FC estimate, with ${\text{C}}_f^{eig}={\displaystyle \sum _{i\in M}{\text{u}}_i{u}_i^{\text{'}}\left(a{e}^{-\alpha {\lambda }_i}+b\right)}$ where M is asubset of indices of eigenvectors used for estimating C_f . Fig. 8 illustrates the leading six Laplacian eigenvectors on glass brain.

Fig. 7.

The first 6 eigenvectors of the graph Laplacian of the average healthy connectome. We hypothesize that these are the most important eigenvectors of the graph, and a linear combination of a few of these eigenvectors can effectively reproduce most eigen-vectors of the FC matrix, as well as the entire FC matrix itself. Blue refers to negative components, while green refers to positive components. Ball size reflects the component’s magnitude.

Fig. 8.

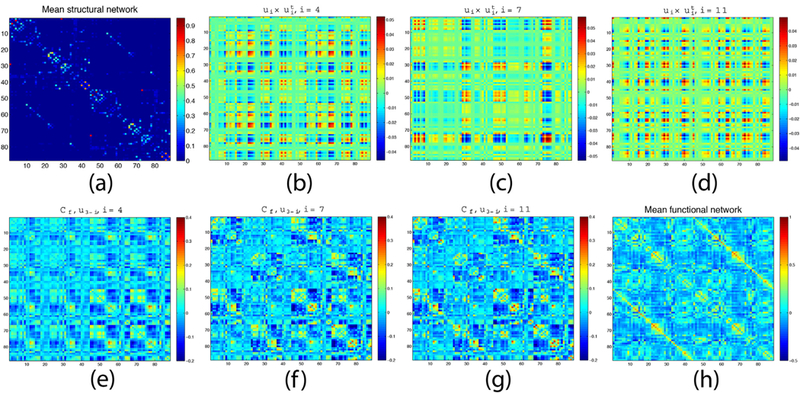
Estimating FC from a subset of the Laplacian eigenvectors. (a) Mean SC matrix, (b-d) FC network “building blocks” u_iu^’_i with i = 4,7,11. FC estimates using eigenvectors u_3–4 (e), u_3–7. (f), and u_3–11 (g). Last panel (h) gives the mean empirical FC.

Fig. 1(a) gives the mean SC matrix of all subjects, and Fig. 1(b–d) show the matrices obtained from eigenvectors u_iu^’_i with i = 4,7,11.. Fig. 1(e) shows the estimated FC ${\text{C}}_f^{eig}$ reconstructed from eigenvectors u₃4 only. The resulting matrix is a poor estimate of FC. Using eigenvectors u₃₋₇ improves the FC estimate (Fig. 1(f)). Finally, eigenvectors u₃₋₁₁ (Fig. 1(g)) give yet closer estimate of the empirical mean functional network depicted in Fig. 1(h).

Proposed model and ICA decomposition

The majority of the brain FC/SC connectivities information is encoded in only a handful of the Laplacian eigenvectors. This is reflected in Fig. 9 where the Pearson correlation between the first six empirical FC eigenvectors (corresponding to the six largest FC eigenvalues) and the Laplacian eigenvectors averaged over all subjects is illustrated.

Fig. 9.

Pearson correlation between each of the six dominant empirical FC eigenvectors and all Laplacian eigenvectors averaged over all subjects. Eigenvector index i refers to the eigenvector indexed by the ith smallest Laplacian eigenvalue. Each panel shows the corresponding FC eigenvector on the glass brain. Blue refers to negative components, while green refers to positive components. Ball size reflects the component’s magnitude. Only a handful of the Laplacian eigenvectors encode most of the FC/SC networks information

To further convey the importance of the Laplacian eigenvectors, we perform independent components analysis (see Sec 2.6). Pearson correlation between each of the first six ICA components and all Laplacian eigenvectors is computed. The results are given in Fig. 10 where once again the network information is encoded only in a handful of the Laplacian eigenvectors. Additionally, each panel of the figure gives the corresponding empirical FC eigenvector on the glass brain. Fig SI-5 gives the full set of correlation plots. Similar steps are followed using the ICA decomposition obtained in Smith et al. (2009) (and using the NYU SC matrices) where once again only a handful of the Laplacian eigenvectors and ICA components are highly correlated (Fig SI-6). Correlation plots for all 20 components are given in Fig SI-7 (see Sec SI-7).

Fig. 10.

Pearson correlation between each of the six dominant empirical FC group level ICA spatial components and all Laplacian eigenvectors averaged over all subjects. Eigenvector index is similar to that of Fig 9. Each panel of the figure gives the corresponding ICA component on the glass brain. Ball size and color uses are identical to Fig 9.

Results from additional cohort

A separate, 8 healthy subjects data set, obtained at Weill Cornell Medicine were used in order to independently confirm the model’s validity (consult Sec SI-1 for MR imaging and preprocessing and networks’ construction). Fig SI-8 shows very similar behavior to the NYU data presented in this work. Fig SI-8(a) gives the scatter plot of the empirical FC eigenvalues vs the eigenvalues of the Laplacian for all subjects. The resulting fitting parameter α = 434 over all stacked subjects is similar to the one obtained with the NYU data. Fig SI-8(b) gives the semi-log plot of FC eigenvalues vs Laplacian eigenvalues for all subjects, approximating a straight line. The functional and Laplacian eigenvectors fit the eigen decomposition model at group level, see Fig SI-8(c) where the elements of matrix U’_lC_f U_l tend to stand out near the diagonal, similar to the empirical C_f eigenvalues in Fig SI-8(d). This strongly suggests that the additional set of data closely fits the proposed eigen decomposition model.

Discussion

Summary of main results

We proposed a novel spectral graph approach that predicts function from the eigen decomposition of the structural network’s Laplacian matrix. The basis of the model is that any well-behaved diffusion process on the structural graph, e.g. (Abdelnour et al., 2014), must lead to an eigen relationship between SC and FC. We exploit this to develop a very simple model-independent analytical predictor of FC from SC Laplacian. When compared with the model developed in (Abdelnour et al., 2014), the eigenvalues estimate has a constant offset b. On a purely mechanical level, perhaps the easiest explanation is that unlike the GD model that can accommodate only non-negative eigenvalues for the estimated FC, here we allow the FC eigenvalues to take on positive as well as negative eigenvalues, which is more realistic. The parameter b reflects this shift. The predictor can be evaluated analytically on the whole brain at once, requiring neither numerical simulations nor explicitly computing pairwise measures of functional connectivity. The presented linear spectral graph model explicitly incorporates the role of macroscopic structural connectivity in governing the stationary covariance structure of functional data in a mechanical fashion without involving any details of local dynamics. While local brain dynamics are not linear or stationary, the emergent stationary behavior of long-range interactions can be independent of detailed local dynamics (Misic et al., 2015), hence amenable to linear modelling. Ensemble-averaged behavior of large connected but individually nonlinear neural populations can be quite linear (Enno Stephan et al., 2008).

We showed that the theoretical SC-FC predictions of both eigenspectra and full connectomes strongly recapitulate empirical data from two independent cohorts of 26 and 8 healthy subjects. We note that although empirical SC and FC are themselves correlated to each other, their Pearson R is weak, in the range of 0.1–0.2, which is much smaller than what is achieved by the proposed model (Fig. 5(a)). Empirical FC eigenvectors were shown identical to SC Laplacian eigenvectors at the group level, and predictable from very few SC Laplacian eigenvectors, spanning low graph frequency components, at the individual level. Further, we showed that Laplacian eigenvectors can efficiently predict, using only 1–3 eigenvectors, many classic functional networks computed from independent components analysis, e.g. default-mode, executive, etc, networks. This suggests that much of the information contained in conventional functional connectomes are already present in SC. The proposed model suggests that the FC network may be largely reproduced by the Fourier transform of the structural network with the domain mapped as an exponential of the Laplacian eigenvalues. This indicates that a large portion of the functional signal can be explained in purely static, mechanistic manner, from the brains structural connectivity organization.

The first structural Laplacian eigenvector u₁ is trivial, with values proportional to node degree. In terms of graph diffusion, it is simply the steady state (infinite time limit) pattern; consequently it has little biophysical interpretability, since actual neural activity is not typically allowed to decay to steady state. In terms of our SC-FC model, this would correspond to the global functional signal correlation, which is typically regressed out. These points were noted previously in (Abdelnour et al., 2014). The second eigenvector u₂ is omitted for a different reason. Previous studies on the eigen-structure of the structural Laplacian showed that u₂ merely captures left-right gradients in diffusion (Wang et al., 2017); this was further confirmed in Fig. 7. In real functional brain activity such a strong lateralization is absent, and both left and right hemispheres show laterally symmetric activity patterns at BOLD frequencies, probably due to shared sensory and thalamic drive. These commissural connections are not easily captured by current DTI and tractography, which significantly underestimates inter-hemispheric callosal connections, as is demonstrated in Fig SI-11, hence the removal of u₂.

There is clearly substantial individual-level variation from the diagonal matrix, and we should not be particularly surprised by this. A purely mechanistic structure-function relationship will not account for timevariant and non-stationary behavior. The proposed model, being linear, can only capture the stationary component of the functional eigenvalues. Therefore one possible explanation of the eigenvectors matching the proposed model only at group level is that the time series leading to the functional connectivity network are non stationary. On the other hand, the ability to predict the eigenvalues at subject level appears to suggest that the functional eigenvalues remain largely stationary. Fig. 6 shows the model match against “instantaneous” functional connectivity, measured using a sliding window. Indeed, we found substantial variability between and even within the same individual. We think this new result has added an interesting new dimension to the issue, and helped clarify the strengths and limitations of the proposed technique.

When compared against two state of the art recent approaches, (analytical) GD and (generative) NMM model, the proposed model yields consistently higher similarity for all subjects, as seen from Fig. 5. The SC/ FC eigenvalues’ exponential relationship gives a close fit to empirical data at both subject and group levels, and holds for full network as well as single hemisphere networks. Notably, the empirical eigenvectors U_l and U_f of individual subjects are not identical as predicted by the eigendecomposition model, even as the mean of U^’_lC_f U_l is nearly diagonal at group level. This is to be expected, as there is considerable inter-subject variability that can not be accounted for in a simple eigen-space model. Despite this, the overall prediction of stationary FC from SC is robustly achieved, with better performance than any competing method we have so far investigated. Ultimately, the maximum R achievable by any predictive model is limited by natural variability, non-stationarity and likely presence of several “meta-stable” states (Deco et al., 2012; Panagiotaropoulos et al., 2013).

In this work we opted to construct the functional networks using Kendall tau correlation rather than the more commonly used Pearson correlation (See Sec SI-8). The results are quite comparable with those obtained using Pearson correlation. Fig SI-9 summarizes the results of applying the eigen decomposition model to FC networks obtained via Pearson correlation. The eigenvalue (Fig SI-9(a)) and group level eigenvectors (Fig SI-9(b)) relationships predicted by the model are preserved. Moreover, the R obtained for the full network (Fig SI-9(c)) and the right hemisphere (Fig SI-9(d)) are comparable with the estimates obtained using Kendall tau. Fig SI-10 shows how the Pearson-generated FC networks of the Weill Cornell data match the proposed model of an exponential relationship between the FC and Laplacian eigenvalues (Figs SI-10(a-b)), and the group level eigenvectors fitting the model (Figs SI10(c-d)).

Related work

Compared with our previous work on graph diffusion, the current proposal is model-independent and also gives better performance. A linear generative model developed by Galan (2008) that predicts neural activity from anatomic connectivity also relies on eigen decomposition, but was proposed for modelling local circuitry only. The model of (Galan, 2008), in turn, is motivated by a large body of work on the eigen structure of memory circuits. Here we favor graph Laplacian of whole brain connectome, compared to Galan’s use of synthetic adjacency matrix of local, intracortical synaptic strengths. The Galan model was adopted by Honey et al. for predicting brain-wide functional connectivity from structural connectivity (Honey et al., 2009), and compared against a nonlinear generative neural mass model (NMM) first reported by (Breakspear et al., 2003). The linear model underperformed the NMM. NMMs have been previously used for predicting function from structure via a system of second order, nonlinear differential equations (Honey et al., 2009; Deco et al., 2011, 2012; Panagiotaropoulos et al., 2013). Neural activities at nodes influence each other via inter-regional couplings weighted by anatomic connectivity. In contrast, our spectral graph model is completely analytical, and can be evaluated for the whole brain FC using only a single matrix exponentiation. In contrast to conventional nonlinear generative simulations, for instance using neural mass models, the proposed model is entirely linear and analytic. Its linearity makes it simple to implement, requiring only the computation of the Laplacian eigen components from C_s. Several analytic measures of functional connectivity based on inter-node communication between pairs of SC nodes were proposed by Goni et al., including~ search information and path transitivity (Goni~ et al., 2014). These measures are superior to previous “shortest path” measures, because they can account for how several possible paths between node pairs are embedded within the rest of the structural network. Although this approach incorporates some of the shortest parts between region pairs, it does not account for all possible paths between them. Further, it requires explicit computation of these FC measures between all region pairs, whereas here we can predict the entire FC matrix via a handful of structural eigenvectors.

Eigen decomposition as a tool for predicting FC from SC, a key component of the proposed model, is not in itself new. In a series of articles, Robinson (2012, 2014) and Robinson et al. (2014) develop a linear relationship between function and structure exploiting spike-based as well as neural field interactions. The model considers excitatory as well as inhibitory activities. Importantly, the authors incorporate delays between the time series in the model using propagator theory. In particular, Robinson et al. (2014) develop a function-structure relationship where matrices C_s and C_f are assumed to share the eigenvectors, similar to (Galan, 2008). Additionally, function and structure eigenvalues are assumed to be related via an inverse square relationship. This is distinctly different from the proposed model where the eigenvectors U_l obtained from the Laplacian (rather than C_s) predict FC eigenvectors, and the functional eigenvalues are obtained via an exponential relationship, as revealed in Fig. 2. We believe this is the key assumption leading to improved R between the empirical FC data and the estimated functional networks. Deco et al. (2013) approximate the nonlinear brain dynamics by assuming stationary covariance of spontaneous fluctuations relating function and structure. The model then is described by a linear first order system. The estimated FC matrix incorporates the eigenvectors of the system’s Jacobian matrix, which in turn is related to the structural connectivity matrix C_s. The resulting R (5 healthy subjects) hovers around 0.45. This is comparable with both the NYU data, Fig. 4(a), and the Weill Cornell, Fig SI-9(c), data when eigenvectors u₃88 are used. However, the proposed model is inherently linear, simple to implement, and does not require a linearization step.

Study limitations and future work

Tractography methods are known to under-estimate inter-hemispheric connections involving long fibers, due to which our predicted FC also shows lower inter-hemispheric FC than observed. Fig SI-11 (Sec SI-9) gives an example of missing inter-hemispheric connectivity. One way of improving the FC estimate may be to apply pre-determined weights to the nodes known to be strongly connected but underestimated by DTI. Next, our prediction gives long-time correlation structure of the stationary portion of functional activity. Hence it cannot account for time varying, non-stationary and possibly chaotic behavior exhibited by real brain signals (Matthew Hutchison et al., 2013). Nonetheless, most current approaches to FC also rely on stationarity. In the fMRI frequency range (< 0:2 Hz) axonal conduction speed is not relevant, but future extensions into higher frequencies will require incorporating temporal delays within the nodes and edges of the network.

Conclusion

In this work we modify the graph diffusion model and explicitly estimate the functional network from the structure Laplacian’s eigen components. The model assumes that the functional network is driven by an external process. It is shown that only a subset of the Laplacian eigen components is sufficient to estimate the functional network. For future work, we plan to incorporate networks’ nodes and edges delays for a more realistic modelling using EEG data.