Summary
The development of optical methods to activate neurons with single-cell resolution has enabled systematic mapping of inhibitory connections. In contrast, optical mapping of excitatory connections between pyramidal neurons (PCs) has been a major challenge due to their high densities in cortical tissue and their weak and stochastic connectivity. Here we present an optogenetic two-photon mapping method in mouse neocortical slices by activating PCs with the red-shifted opsin C1V1 while recording postsynaptic responses in whole-cell configuration. Comparison of delays from triggered action potentials (APs) with those from synaptic inputs allowed us to predict connected PCs in three dimensions. We confirmed these predictions with paired recordings, and used this method to map strong connections among large populations of layer 2/3 PCs. Our method can be used for fast, systematic mapping of synaptic connectivity and weights.
Subject Areas: Optical Imaging, Systems Neuroscience, Techniques in Neuroscience
Graphical Abstract
Highlights
-
•
Two-photon optogenetic mapping of excitatory connectivity and strength in neocortex
-
•
Identification of connected neurons in acute slices through numerical optimization
-
•
Synaptic delays align with location of connected presynaptic cell
-
•
Confirmation of predicted connections by dual patch-clamp recordings
Optical Imaging; Systems Neuroscience; Techniques in Neuroscience
Introduction
Decoding the structural and functional principles of microcircuitry appears necessary to understand neural computations. Most experimental studies of connectivity and strength of connections have employed multiple simultaneous patch-clamp recordings, either in slices or in vivo (e.g., Feldmeyer et al., 2006, Lefort et al., 2009, Hofer et al., 2011, Ko et al., 2011, Jiang et al., 2013, Rieubland et al., 2014, Jiang et al., 2015, Jouhanneau et al., 2015). Although this method provided great insights, it is limited by the amount of neurons that can be recorded from simultaneously. Studying connectivity at the anatomical level, employing, e.g., tracing using a modified rabies virus (Wickersham et al., 2007, Rancz et al., 2011, Sun et al., 2014, Cocas et al., 2016), synapse labeling by mGRASP (Kim et al., 2012, Druckmann et al., 2014), RNA barcoding (Kebschull et al., 2016), or electron microscopic reconstructions (Kasthuri et al., 2015), enables probing of circuitry at a larger scale, yet provides limited information about the function, or strength, of a synaptic connection, and often requires significant analytical processing. Mapping the functionally and strength of synaptic connections is necessary to decipher the functional patterns of a microcircuit, since this cannot be derived from structural connectivity alone. In addition, ideally, functional mapping methods should be usable in living tissue, facilitating experimental approaches such as pharmacological testing, learning or plasticity paradigms, or closed-loop optogenetics or optochemistry.
Using optical tools to map neural connections with single-cell precision is a promising road to perform systematic physiological experiments to probe connectivity between hundreds or thousands of neurons. Indeed, two-photon uncaging of caged glutamate has served as a powerful tool to map the connectivity from hundreds of interneurons to pyramidal neurons (PCs) in the neocortex, revealing a dense, unspecific connectivity (Fino and Yuste, 2011, Packer and Yuste, 2011). Similar studies have employed this method to map excitatory connections between PCs (Nikolenko et al., 2007) or stellate cells of layer 4 (Ashby and Isaac, 2011), but these efforts either remained unproven about their precision, or mapped circuitry at relatively small scales. At the same time, the evidence of specific microcircuitry between excitatory neurons (reviewed in Harris and Mrsic-Flogel, 2013) calls for precise, large-scale connectivity studies between PCs. In addition, establishing and refining the tools needed for such projects would also contribute to the development of methods to precisely map or influence brain activity in neuroscience in general (Alivisatos et al., 2013).
Although glutamate uncaging has been successfully used for functional mapping of connections (Callaway and Katz, 1993, Nikolenko et al., 2007), optogenetic stimulation is desirable since it would enable to map connections among genetically specified cell types. Also, although optogenetic tools have been used to map circuits in two dimensions using conventional, one-photon, laser excitation (Petreanu et al., 2009), circuit mapping with single-cell precision and in three dimensions appears necessary. This is possible employing the non-linear excitation of ultrafast lasers, but such methods are still difficult. This is partly because evoking APs through conventional channelrhodopsin 2 needs highly specialized optics (Rickgauer and Tank, 2009, Andrasfalvy et al., 2010, Papagiakoumou et al., 2010, Baker et al., 2016). To partly supersede these problems, the slower opsin C1V1 was developed as a tool to optogenetically activate neurons with two-photon excitation (Packer et al., 2012, Prakash et al., 2012). Using this opsin to evoke APs with conventional two-photon scanning, we introduce here a mapping method of PC connectivity in slices of mouse visual cortex. By using the latency of AP generation in response to laser stimulation as an indication of potentially connected presynaptic neurons, we overcome the problem that neurons with different opsin expression levels have different excitation properties, and we predict putative connections and confirm them with paired recordings. We demonstrate the capability of our method by mapping higher strength connections in mouse V1. Future refinements of this method could allow mapping weaker connections and using the technique in vivo.
Results
The aim of our study was to develop an optical method to map connectivity between PCs in acute cortical brain slices with single-cell precision. To do so, we first expressed the opsin construct C1V1 in combination with enhanced yellow fluorescent protein (C1V1-p2A-EYFP) in excitatory neurons (under control of the CamKII promoter) in mouse visual cortex via transcranial adeno-associated virus (AAV) injection into neonatal mice. Densely packed expressing neurons could be identified by two-photon-imaging of EYFP at 940 nm. To optically activate neurons, we employed a custom-built two-photon microscope capable of consecutively visiting a pre-programmed set of point stimulations (for stimulation pattern see Transparent Methods, Supplemental Information). For C1V1 stimulation, the Ti:Sapphire laser was set to 1,040 nm.
Calibrating Optical Stimulation Parameters
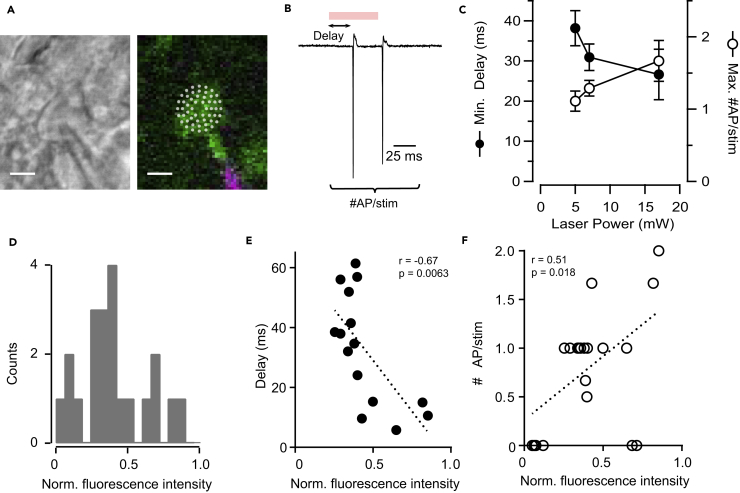
We characterized stimulation conditions by performing extracellular cell-attached patch-clamp recordings of C1V1-p2A-EYFP-expressing layer 2/3 PCs (Figures 1A and 1B). We first explored different power levels (5, 7, and 17 mW) resulting in 61%, 72%, and 82% of neurons firing, respectively. Overall, we found a clear dependency of the number of evoked APs, as well as the latency of the first AP, on laser power on sample (latency: 5 mW: 38 ± 4 ms, n = 12; 7 mW: 31 ± 3 ms, n = 28; 17 mW: 27 ± 6 ms, n = 9; APs per stimulation: 5 mW: 1.1 ± 0.1, n = 12; 7 mW: 1.3 ± 0.1, n = 28; 17 mW: 1.7 ± 0.3, n = 9; Figures 1B and 1C). As expected, AP delay and number of evoked APs (7 mW on sample) were strongly correlated with EYFP fluorescence of the recorded neuron (r = −0.67, p = 0.0063 and r = 0.51, p = 0.018, respectively), indicating that higher expression of the opsin construct favors faster and stronger activation of a given neuron (Figures 1D–1F). This may result in less accurate photostimulation in a heterogeneously expressing population, as high expression level could potentially lead to AP generation, not only when targeting the soma, but also when targeting the dendritic tree. To avoid this, we chose 7 mW at the sample for all further experiments, as this value resulted in AP evoking in most tested neurons, yet was still relatively low to minimize the probability of evoking APs at sites away from the soma.
Figure 1.
Two-Photon Stimulation of C1V1-Expressing Neurons
(A) Left: differential interference contrast image of a layer 2/3 PC recorded in cell-attached configuration. Right: fluorescent image, showing in green expression of C1V1-p2A-EYFP and in magenta Alexa 594 from the pipette solution. White dots represent the pattern of point stimulations performed to excite a neuron. Scale bar, 10 μm.
(B) Example of a response of an EYFP-expressing neuron to a stimulation during cell-attached current recording. Stimulation, red bar, lasts for 54 ms, 1,040 nm, and 7 mW on sample. To characterize the efficiency of stimulation we analyzed the delay of the first AP and the number of APs.
(C) Dependence of mean delay (filled circles) and number of APs (empty circles) on laser power at the sample. In all cases, only neurons that fired after stimulation were considered; n = 12 for 5 mW, n = 28 for 7 mW, and n = 9 for 17 mW. Dots depict mean ± S.E.M.
(D) Distribution of normalized fluorescence intensity of EYFP from cell-attached patched neurons, n = 21 cells.
(E) Plot of AP delay against normalized EYFP fluorescence intensity. Negative correlation is observed, n = 15 cells. Dotted line depicts the linear fitting of the data.
(F) Plot of the number of APs triggered during one stimulation against normalized EYFP fluorescence intensity. Positive correlation is observed, n = 21 cells. Dotted line depicts linear fitting of the data.
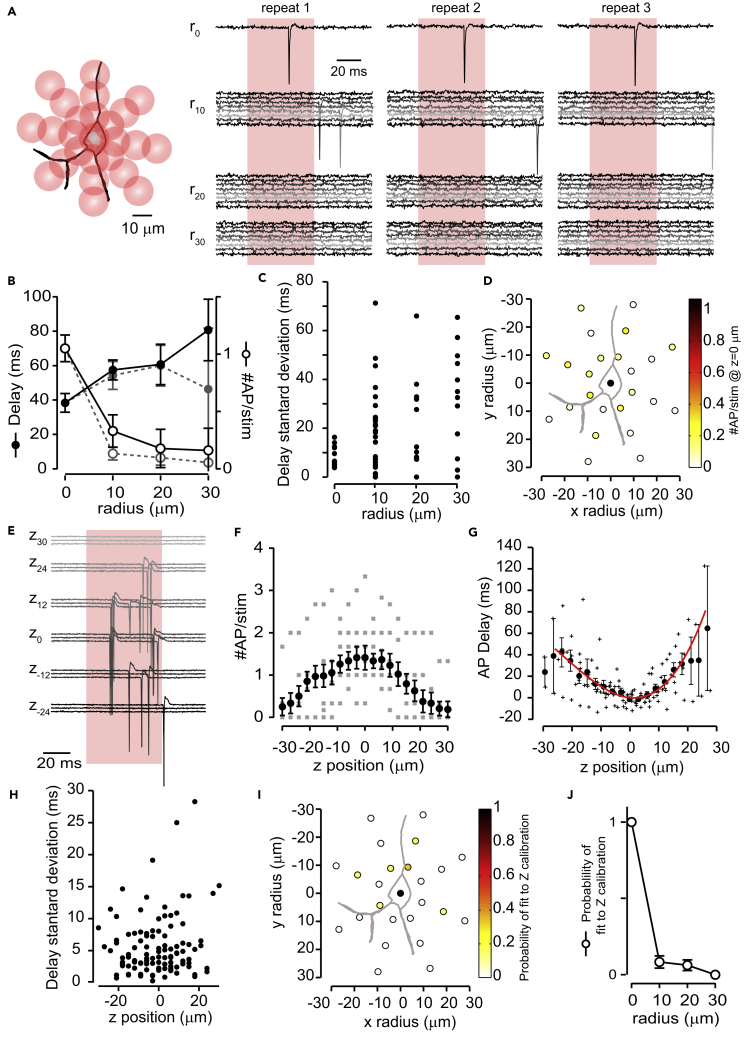
To test the spatial resolution of our system with this power, the excitation pattern was moved laterally from the center of the cell soma in steps of 10 μm. AP probability decreased strongly, and latency increased, with distance (latency: r0: 31 ± 6 ms, n = 15; r10: 49 ± 5 ms, n = 10; r20: 61 ± 6 ms, n = 8; r30: 80 ± 10 ms, n = 7; AP per stimulation: r0: 1.1 ± 0.1, r10: 0.5 ± 0.1, r20: 0.3 ± 0.1, r30: 0.3 ± 0.1; n = 14 in all, Figures 2A and 2B). We also observed that stimulations that evoked APs at longer distances from soma were temporally less reliable, as can be seen by an increase of delay standard deviation in Figure 2C. In fact, nearly all stimulations performed at the center of the cell soma resulted in delays with standard deviations below 18 ms. Because of this, we used 18 ms as a threshold. Excluding AP responses with a delay standard deviation higher than 18 ms across repeats resulted in improved lateral resolution (AP per stimulation: r0: 1.1 ± 0.1, r10: 0.13 ± 0.06, r20: 0.1 ± 0.07, r30: 0.1 ± 0.1; n = 10 in all, Figure 2B, gray traces, and Figure 2D). Thus, we concluded that resolution in the lateral plane, improved by variability restriction across repeats, would be sufficient to reliably map synaptic connections. Testing axial resolution by changing the focus of the excitation pattern revealed a similar behavior for AP latency and number, yet displayed a less steep drop in AP generation probability with distance from the soma than observed for lateral resolution (Figures 2E–2G). The delay standard deviation remained relatively low, even at high axial distances from the soma (Figure 2H). We did not observe a dependency between delay standard deviation and expression level or cell depth (r = 0.24, p = 0.33, n = 18 and r = 0.21, p = 0.41, n = 18, respectively). We felt that lowering the laser power to improve axial resolution would result in a reduction of the number of cells we can activate. We further characterized the change in AP delay in the axial dimension with more detail. This effect was similar across cells, and it could be fitted with a parabolic function, with the minimum centered on the soma position (Figure 2G). These results demonstrate that AP delays indicate the location of the soma of the optically targeted neuron as the point of shortest delay. We also performed stimulations at different axial positions when moving the excitation away from the cell soma in the lateral dimension. The probability of fitting the parabolic function described above (χ2 test with an acceptance threshold of 0.1, see below) was much lower compared to the soma position (probability of fitting: r0: 1 ± 0, n = 6; r10: 0.08 ± 0.04, n = 48; r20:0.06 ± 0.04, n = 48; r30:0 ± 0, n = 48 stimulations, Figures 2I and 2J). This suggested that by fitting the delay of APs to an axial stimulation position, one could distinguish APs evoked by dendritic stimulation or background activity (which do not follow the parabolic function) from those evoked by somatic stimulation. Thus, using the two established criteria based on AP delay, (1) limiting to 18 ms or less standard deviation across repeats and (2) fitting its dependence on axial position to calibration data could in combination be used to identify the soma of a stimulated cell in three dimensions. We used these observations to establish a mapping strategy that reliably identified the exact position of presynaptically connected neurons to the recorded cell.
Figure 2.
Lateral and Axial Resolution of Two-Photon Optogenetic Stimulation
(A) Left: scheme of the stimulations performed during lateral calibration experiments. Each circle represents a stimulation done as in Figure 1A. Each cell was stimulated in the center, and then in radii of 10, 20, or 30 μm from the center with 8 stimulation positions per ring. Right: example of cell-attached current recordings from a cell stimulated during a lateral calibration experiment, repeated three times. Traces are grouped depending on the radius distance. Stimulation duration is highlighted in red. Laser power 7 mW on sample.
(B) Plot of the delay (filled circles) and number of APs (empty circles) per cell against radial distance from the center of the cell from lateral calibration experiments, for delay n = 10 at r0, n = 7 at r10, n = 5 at r20, n = 4 at r30; for number of APs: n = 10 in all cases. In gray, same data when stimulations with delay standard deviation higher than 18 ms were excluded (for delay n = 10 at r0, n = 7 at r10, n = 5 at r20, n = 2 at r30; for number of APs: n = 10 in all cases).
(C) Plot of the delay standard deviation of each stimulation against lateral distance from the center of the cell soma (n = 10 at r0, n = 31 at r10, n = 17 at r20, n = 13 at r30).
(D) Averaged number of APs per stimulation performed at different lateral positions at the soma z position. Stimulations across cells where all aligned, with pia located at the top (n = 10 cells, all stimulated at 25 positions).
(E) Example of cell-attached current recordings from a cell stimulated as in Figure 1A, and changing the focus of the laser in z positions indicated next to the traces, each stimulation was repeated three times. z0 indicates the soma location, positive z values indicate focusing toward more superficial positions, and contrary negative z values indicate focusing deeper into the slice. Laser power is 7 mW on sample, and stimulation duration is shown in red.
(F) Number of APs per cell depending on z position. Individual cells are depicted by gray crosses and the average by black dots, n = 9 stimulated cells.
(G) Delay increase dependence on z position of individual cells (gray crosses) and average (black dots), n = 9. Averaged data were fitted to a parabola with a cubic term to obtain a calibration curve, red line.
(H) Plot of the delay standard deviation of each stimulation against z position, n = 9 cells.
(I) Probability to fit a z calibration curve when axial calibration was performed at different lateral positions (n = 6 cells).
(J) Averaged probability of fitting z calibration curve at different lateral distances (r0: n = 6, r10, r20, r30: n = 48 stimulations from 6 cells). All statistics are presented as mean ± SEM.
Mapping Excitatory Synaptic Microcircuits
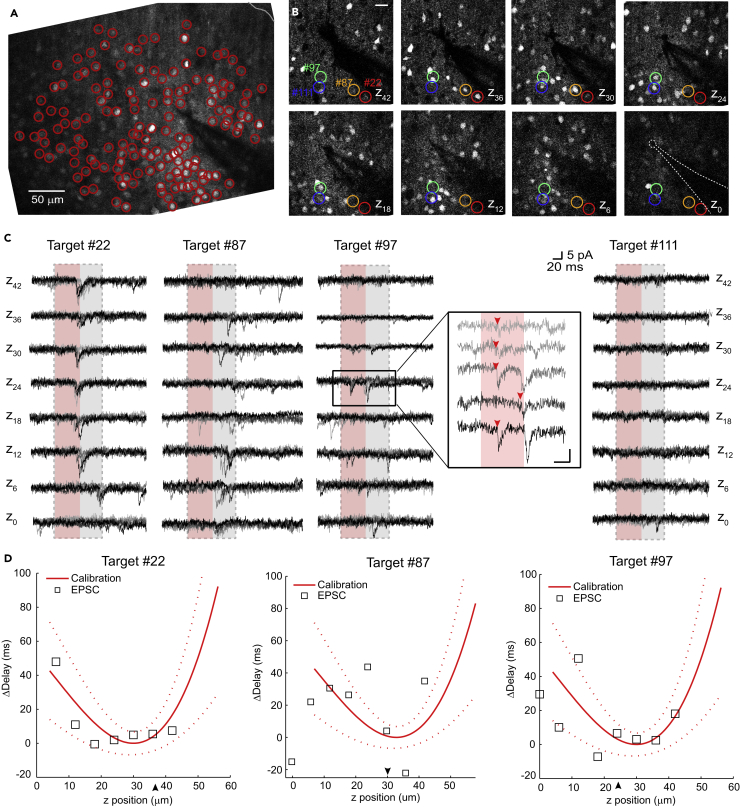
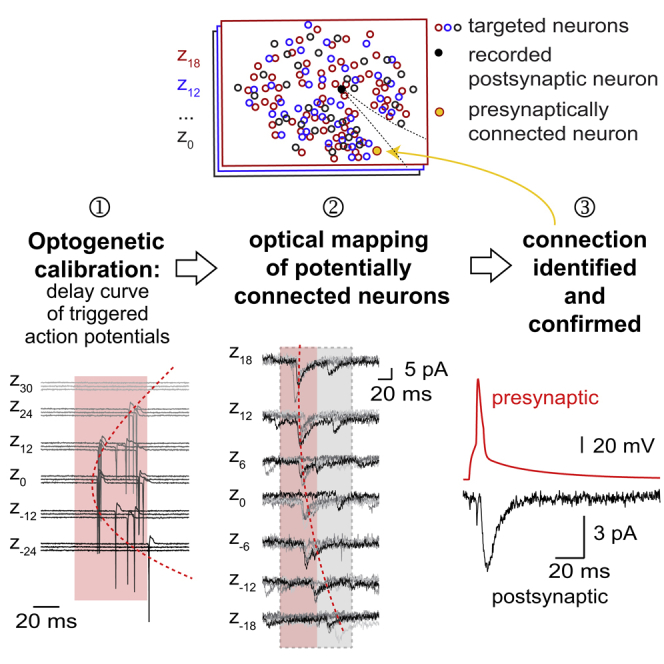
We then explored the application of this photostimulation method to map synaptic microcircuits. To record excitatory synaptic inputs in postsynaptic cells we performed whole-cell patch-clamp recordings of layer 2/3 PCs in slices expressing C1V1-p2A-EYFP, patching non- or low-expressing neurons (to minimize optically stimulating them), localized at 24 to 66 μm depth from the slice surface. Since the internal solution contained Alexa 594, we could visualize the recorded cell via two-photon imaging at 800 nm in the red channel and the expressing neurons surrounding it in the green channel when imaging at 940 nm. We recorded images of 400 × 300 μm in stacks with a step size of 6 μm, spanning 24 to 60 μm. In such a volume, we then manually located 70–200 C1V1-p2A-EYFP-expressing neurons using custom-written MATLAB code. A non-neighbor path in which the neurons would be stimulated was generated (see Transparent Methods, Supplemental Information, for details). In this process, we treated the volume as a 2D image, projecting the z axis down into one plane (Figure 3A). We then performed sequential stimulation of all cell locations at the more superficial end (in z) of the stack and repeated it 5–10 times. Subsequently, we moved 6 μm in z toward the other end of the stack, repeated the stimulations again, and moved again 6 μm in z until we reached the end of the imaged stack. This resulted in each targeted cell being stimulated not only in the focal plane of its soma but also above and below it throughout the stack, performing essentially a resolution test in z on each of the targeted neurons.
Figure 3.
Identifying Putatively Connected Presynaptic Neurons
(A) Image of C1V1-p2A-EYFP-expressing cells in layer 2/3. Sum projection of a z stack of images taken at 940 nm, ranging from 42 μm (on the more superficial side of the slice) down to the focus of the patched cell, in Δz of 6 μm. We selected EYFP-expressing cells for mapping stimulations (red circles, 148 targets). Imaged area is 400 × 300 μm; gray line indicates pia at the top right corner.
(B) Magnification of the mapping area with the localization of some of the stimulation targets, numbered according to the stimulation path, at the different z positions focused during the experiment. The patched neuron is located at z0, and the cell and pipette positions are indicated with a dotted line. Positive z plane values indicate focus on positions superficial to the recorded cell. Scale bar, 20 μm.
(C) Whole-cell voltage-clamp recording of the postsynaptic neuron during stimulation (red area) of 4 representative targeted cells (target numbers 22, 87, 97, and 111). At each z position, the stimulation of all targets was repeated 5 times, repeats are grouped and colored in different tones of gray. Target #22 and #97 are identified as connections as shown in panel D. Gray area depicts time after stimulation considered for the detection of synaptic events (100 ms after the start of stimulation, see Transparent Methods). Inset of target #97 highlights the EPSCs identified as arising from stimulation of a connected neuron (red arrowheads). Calibration bar of the inset is 6 pA and 24 ms. Target #87 shows time-locked synaptic events on the deeper z positions possibly resulting from the stimulation of a neuron with its soma located outside of the imaged volume. In agreement, a slight increase in fluorescence at z0 was observed, probably indicating the very border of a cell located at deeper planes. Target #111 is an example of a neuron stimulation not resulting in EPSCs.
(D) Synaptic delay dependence on z position (empty squares) was compared with the calibration curve from Figure 2G (red line; dotted red lines correspond to a confidence interval of 68%, 1 SD) for target #22, #87, and #97. Synaptic delays are represented as difference from the delay at identified soma position (ΔDelay). The minimum of the calibration curve was assigned within 6 μm of the targeted soma, optimizing the fit to the synaptic delay. We then evaluated the fitting with χ2 test; p values obtained for target #22, #87, and #97 are 0.82, 1.4 × 10−5, and 0.49, respectively, indicating that EPSCs from target #22 and #97 are not random and fit the delay dependence function obtained from AP triggering in calibration. Arrows indicate z positions where the targeted soma was located.
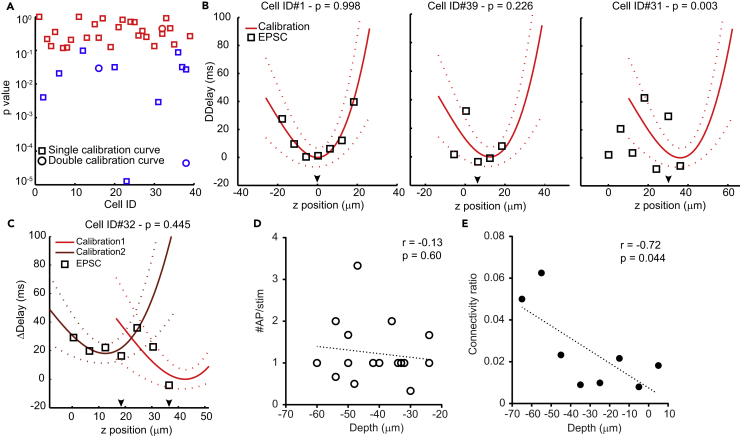
When analyzing recorded synaptic events that occurred during mapping in the patch-clamped neuron, we could clearly observe cases of putative responses from activated presynaptic neurons (see an example in Figures 3B and 3C). To distinguish spontaneous excitatory postsynaptic currents (EPSCs) from ones evoked by our photostimulation, we selected synaptic inputs time-locked to stimulation across repeats according to the calibration data as per the following procedure: (1) we selected those EPSCs with a delay standard deviation lower than 18 ms within the same z position and (2) discarded them if success rate was equal or smaller than 0.2. Latencies of synaptic delays were then compared with the parabolic function of AP latencies obtained in the calibration experiments (Figure 2G) with the lowest point of the fit being within 6 μm of the targeted soma (Figure 3D). We used a χ2 test with an acceptance threshold of 0.1 to compare the delay characteristics of evoked EPSCs with the calibration curve. This threshold excluded targeting sites that did not follow the calibration curve, but still included connections with delay characteristics that, e.g., contained an outlier (Figures 4A and 4B). Using these criteria, we identified targeted neurons as being putatively connected to the recorded neuron (Figures 3C and 3D, target #22 and #97) as well as sites at which targeting in planes lower or higher than the soma location resulted in EPSCs that did not fit the calibration data (Figure 3C, target #87, positions deeper than z18). The latter is probably due to the activation of neurons outside of the volume we imaged. We also calculated a bimodal version of our calibration data fit, which we used to fit EPSC delays in cases in which we observed two neurons on top of each other in the axial dimension. In one case, we identified both neurons as being connected (Figure 4C). AP firing probability in calibration data was not correlated with depth of the recorded cells (r = 0.13, p = 0.60, Figure 4D), ruling out the potential influence of laser power loss with increasing depths. In contrast, connection probability was correlated with the depth of the targeted neurons (r = −0.72, p = 0.044, Figure 4E) probably caused by less cut processes in deeper tissue.
Figure 4.
Comparison of EPSC and AP Delays
(A) Plot of p values obtained when evaluating the fitting of the EPSC delays to our calibration function with a χ2 test. Colored in red are p values higher than 0.1, and colored in blue are p values below 0.1. Squares correspond to tests using simple calibration function (n = 35 targeted cells), whereas circles correspond to cases in which double calibration function was used (n = 3 stimulations).
(B) Examples of fittings resulting in different p values. Left: targeting resulting in EPSC delays highly similar to calibration data (p value = 0.998), middle: targeting resulting in EPSC delays at the border of the acceptation criterion (p value = 0.226), right: targeting resulting in EPSC delays not fitting the calibration data, and excluded as a putative connected cell (p = 0.003). Arrows indicate z positions where the targeted soma was located.
(C) Example of fitting using bimodal calibration function (p value = 0.445) to EPSC delays from cell ID 32; arrows indicate z positions at which each soma was located.
(D) Number of APs triggered optically plotted against depth of the neuron in the slice (slice surface at 0 μm). No correlation was observed, n = 18 cells. Dotted line depicts the linear fitting of the data.
(E) Connectivity ratio plotted against depth of the targeted neurons in the slice (10-μm bins, slice surface at 0 μm). A correlation was observed, n = 8 cells. Dotted line depicts the linear fitting of the data.
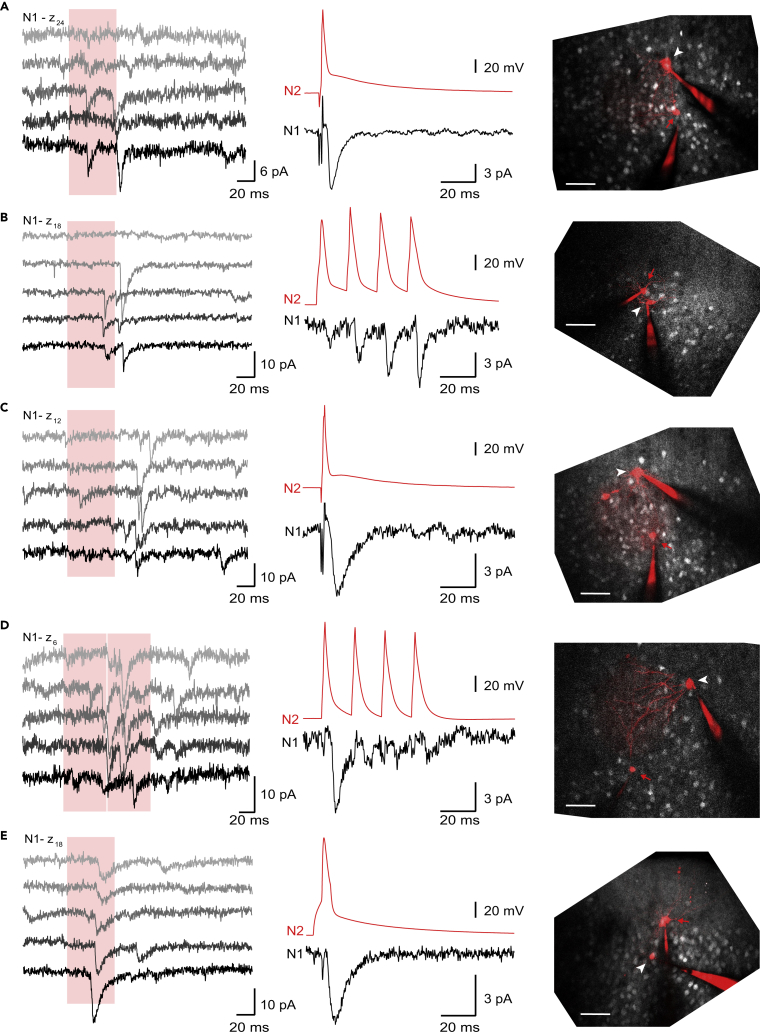
We then verified our mapping predictions online by performing simultaneous recordings of a neuron identified as synaptically connected with a second patch pipette directly after analyzing the synaptic events. In all 5 cases we were able to verify our prediction in layer 2/3 (Figure 5). In addition, we performed one more successful confirmation in a layer 4 mapping experiment (data not shown), for a total of 6/6. In all cases, evoking APs in the second (presynaptic) cell via current injections resulted in synaptic currents in the first (postsynaptic) cell.
Figure 5.
Confirmation of Optically Identified Connections
(A–E) Confirmations of connections from 5 different mapping experiments. Left panels: 5 repeats of whole-cell current recordings of the postsynaptic neuron (N1) during optical stimulation (red area) at the z position of the targeted soma during a mapping experiment. Middle panels: simultaneous voltage recordings of the cell identified online as putatively synaptically connected (N2) and current recording of the postsynaptic cell (N1). APs were triggered by the current injection of either single pulses (1 nA, 2 ms, 1 s interstimulation time, except for E where we injected 500 pA for 10 ms) or trains of 4 APs (1 nA, 2 ms, 15 ms interstimulation time and 5 s between trains). Averaged number of trials: 50, 24, 18, 8, 17 in A, B, C, D, and E respectively. Right panels: overlays of sum z projections from stacked images of each mapping experiment, displaying in white EYFP fluorescence and in red fluorescence of Alexa 594 from internal solution, filling the patched neurons. White arrowheads indicate N1 and red arrows indicate N2. Scale bar, 50 μm; pia is located at the top. Note that A corresponds to target #97 from Figure 3.
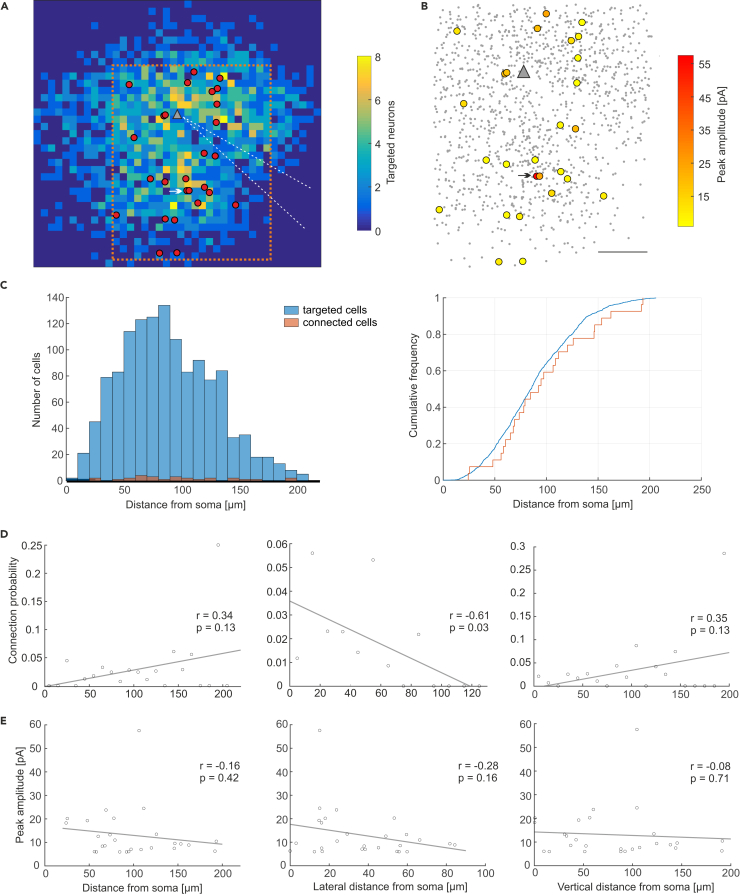
Having proven the validity of our technique, we went on to build presynaptic connectivity maps of neurons in layer 2/3 of primary visual cortex as a proof-of-principle demonstration of the capabilities of our technique. To reduce false-negatives, we excluded targeted neurons with low EYFP fluorescence (7% of targeted neurons, see Transparent Methods, Supplemental Information, for details), as we were probably not able to evoke APs in these, due to low C1V1 expression (Figure 1F). We found EPSCs satisfying the parabola fit criteria in 15 mapping experiments (Figure 4). In those, 27 of 1,729 targeting sites were identified as presynaptically connected neurons. Due to the overall low rate of connectivity (1.6%), partly owing to our strict conservative criteria to ensure that every putative connection was correctly predicted, we pooled all maps into one (Figures 6A and 6B), centering them on the postsynaptic cell. For further analysis, we excluded border regions of the map, because these were mapped at low density. Interestingly, even though the space close to the recorded cell (up to about 50 μm) was mapped at high density, we observed large patches without connections. Connectivity was most robust at about 50–130 μm away from the soma (Figures 6A and 6B). Connection probability (analyzed in bins of 10 μm; Figure 6C) showed no correlation with overall distance from the soma of the recorded neuron (r = 0.34, p = 0.13; Figure 6D), but was correlated with distance when only the lateral (horizontal) distance was taken into account (r = −0.61, p = 0.03). The vertical distance from soma was not correlated with connection probability (r = 0.35, p = 0.13). Peak amplitude of synaptic responses (Figure 6B) was neither correlated with absolute distance from soma (r = −0.16, p = 0.42; Figure 6E) nor with lateral distance (r = −0.28, p = 0.16) or vertical distance (r = −0.08, p = 0.71).
Figure 6.
Mapping Layer 2/3 Connectivity among Pyramidal Cells
(A) Two-dimensional projection of all identified connections pooled from all mapping experiments. The recorded postsynaptic cell is depicted by the gray triangle. Red dots mark the presynaptically connected neurons. The background grid has a spacing of 10 μm. The color code depicts the number of targeted cells pooled from all experiments. Medial is to the left. The pia is located at the top. Orange dotted line indicates the area used for further analysis. The typical patch-clamp pipette location is depicted by white dotted lines. The white arrow marks the position at which two neurons located on top of each other were both identified as connected, based on the bimodal fit. The cell indicators have been set apart slightly to allow for the visualization of two cells.
(B) Similar to A, yet showing the location of all targeted cells as small dots, focusing on the area mapped at high density. Note the gap in cell density to the lower right corner where the patch pipette was usually positioned. The color code of big dots (connected cells) depicts the mean peak amplitude of optically evoked synaptic responses. The arrow marks the position at which two neurons located on top of each other were both identified as connected, based on the bimodal fit. The cell indicators have been set apart slightly to allow for the visualization of two cells. Scale bar, 50 μm.
(C) Histogram (left) and cumulative frequency plot (right) of the Euclidean distance between postsynaptic cell and optically stimulated neuron for all targeted and connected cells.
(D) Absolute, lateral (horizontal), and vertical distances between postsynaptic cell and targeted cells plotted against connection probability of neurons located at the given distance (10-μm bins). A correlation was observed for lateral distance.
(E) Absolute, lateral (horizontal), and vertical distances between postsynaptic cell and targeted cells plotted against the mean peak amplitude of connected cells.
Discussion
In this work, we present a strategy to precisely map connectivity and synaptic strength between PCs in cortical brain slices. For this we use two-photon optical activation of neurons expressing the red-shifted opsin C1V1. Employing a spiral-like point scanning, we demonstrate an inverse correlation between the expression level of C1V1 and latency of APs generated. In addition, AP latency also increased when moving the laser away from the cell soma, both in the lateral and axial planes. We took advantage of a parabolic fit of this latency distribution to accurately map excitatory synaptic connections. By moving the laser to and away from optically targeted cell somata in the axial dimension during the mapping process, and comparing the latency changes of evoked synaptic inputs with those obtained in calibration experiments, we were able to identify connections between PCs. We verified this method by performing targeted patch-clamp recordings of the putative presynaptically connected neuron. In all 6 tested cases, including one performed in layer 4, the predicted connections were verified.
These results demonstrate the ability to precisely map synaptically connected neurons using two-photon optogenetics, even in conditions in which single-cell excitation is technically difficult to obtain. This is often the case in densely packed neuronal populations with heterogeneous opsin expression, because weak expressing neurons will need a certain level of laser intensity to fire, whereas stronger expressing neurons will, at such intensities, also fire APs when their dendrites or axons are targeted. Our strategy, implementing a detailed analysis of the AP delay characteristics, demonstrates that computational approaches can overcome some of these experimental limitations. Other strategies to approach this problem are possible. For example, using temporal-focused excitation or holographic stimulation can limit the problem of dendritic activation (Baker et al., 2016, Shemesh et al., 2017, Forli et al., 2018, Mardinly et al., 2018). However, our method uses relatively simple point stimulations, which, as opposed to complex scanning patterns, can be performed with most conventional laser scanning microscopes. Also, improvements in opsins may enable more selective optogenetic excitation of neurons. In fact, key to two-photon optogenetics was the red-shifted, slowly closing opsin C1V1, designed precisely for two-photon neuronal activation (Packer et al., 2012, Prakash et al., 2012). Indeed, C1V1 has recently been successfully employed in in vivo studies using simultaneous two-photon imaging and activation (Packer et al., 2015, Carrillo-Reid et al., 2016, Yang et al., 2018). In addition, targeting opsin expression to the neuron somata, in combination with some of these optical strategies, might lead to reliable mapping techniques and perhaps enable implementation of our optical mapping technique in vivo. Finally, for mapping synaptic strengths, data collection with a stable access resistance will be especially important.
We used our mapping protocol to perform the first preliminary study of PC connectivity in the visual cortex of juvenile to young adult mice. We highlight that, to preserve the accuracy of the predicted connections, we imposed severely conservative criteria that only enabled us to optically map the strongest and most reliable synaptic connections. This may explain our overall low connection probability, as we are likely discarding the majority of connections that could be weak or unreliable (see Limitations of the Study). Nevertheless, with this caveat, we found in our dataset connection probability negatively correlated with the lateral (horizontal) distance between tested cells, but found no correlations of the strength of synaptic connections with intersomatic distance. These results, generated from a relatively low number of obtained maps, should be seen as an initial demonstration of the capability of our technique.
Conclusions about the connectivity rules between PCs of the neocortex, mostly studied by using multiple patch-clamp recordings, have been diverse. In layer 2/3 of the barrel cortex, connection probability, tested for up to 150 μm, was reported to not depend on intersomatic distance (Lefort et al., 2009, Avermann et al., 2012). In contrast, connection probability, but not connection strength, appears to be negatively correlated with distance in layer 2/3 of the auditory cortex (Oswald and Reyes, 2008, Levy and Reyes, 2012). Holmgren et al. (2003) also reported distance dependence of connectivity (and possibly also synaptic strength) in visual and somatosensory cortex. In an in vivo study, Kwan and Dan (2012) imaged the activity of a group of neurons while inducing bursts in a single neuron close by. Neurons close to the activated cell were more likely to display neuronal activity than those farther away, arguing for a network favoring close-range connections over medium-range ones, whether on the level of absolute connectivity or strength of connections. These differences in experimental results are probably partly explainable by differences of ages, species, and cortical areas used. These considerations might also partly explain the low connection probability we calculated from our mapping data (1.6%). Also, studies in acute slices usually underestimate connectivity rates, due to the processes of superficial neurons being cut (Levy and Reyes, 2012). The studies mentioned above, and including those by Jouhanneau et al. (2015) and Ko et al. (2011), reported connectivity rates ranging from 6% to 19%. We actually achieve similar connectivity rates when mapping at −50 to −70 μm depths in the slice (Figure 4E), a depth that probably corresponds to conditions used in patch-clamp studies. Our present study, however, also included neurons that were located more superficially, as we wanted to explore the capabilities of our method throughout the complete observed volume. Thus, the low observed connectivity rate could to some extent be a result of slicing artifacts. Nevertheless, our calculated connectivity rate is in remarkable agreement with the value of 1.8% in the visual cortex of mice reported in Jiang et al. (2015), although this study used older mice then we did. It needs to be stressed that we did not limit our sampling to the region immediately adjacent to the patched neurons, as is often done in dual patch recordings, but stimulated neurons across the entire field of view. This further limits the comparability of our connection probability calculation to prior studies. However, the distribution of distances between soma tested for connectivity in Jiang et al. (2015) (see Figure S13B, right panel, of the article) is actually very similar to those tested in our study (see Figure 6C).
Although one has to be aware of the limitations of our technique in its current state (see below), our results can be viewed as an important step in the design of optical methods to decipher neuronal connectivity. Such methods are necessary especially for in vivo experiments, in which space for using multiple patch-clamp electrodes can be limited, and thus reaching all neurons in the field of view is very challenging. In addition, even if testing multiple connections sequentially with the same electrode in cell-attached configuration (Barbour and Isope, 2000), moving the electrode around in the brain tissue, or moving it in and out several times, will strongly impair the health of the tested circuits.
Close to the cell soma, we often find patches without connections, despite a high mapping density. At the same time, connection probability does, within our tested volume, not depend on the total intersomatic distance. As pointed out above, the number of experiments needs to be increased to draw final conclusions. However, this observation is in contrast to the connectivity of parvalbumin-positive interneurons on pyramidal cells, which is the highest at short intersomatic distance and declines with higher distance (Packer and Yuste, 2011). This would favor the view that connectivity between excitatory neurons in the cerebral cortex is, in contrast to most inhibitory projections (reviewed in Karnani et al., 2014), non-random and forms specific networks to perform distinct computational tasks. Evidence for this is the observation that excitatory neurons in visual cortex are more likely to form strong connections when their response to sensory stimuli is correlated (Cossell et al., 2015). Also, bidirectional connections are overrepresented in excitatory cortical networks (Jouhanneau et al., 2015) and the output target of cortical neurons is related to the patterns of their intercortical connectivity (Brown and Hestrin, 2009). Wertz et al. (2015) performed in vivo activity imaging of the network presynaptic to a single layer 2/3 PC and found layer-specific modules of motion direction preferences, either aligned or shifted to the postsynaptic neuron. Additional work needs to be done to understand the rules of connectivity in the cerebral cortex, including structural and functional aspects. The mapping technique presented in this work may help to tackle these questions, which are critical to decipher the functional logic of cortical circuitry.
Limitations of the Study
As mentioned in the Discussion, our method, although has the advantage of enabling the testing of hundreds of connections in one experiment, is still not suited to rigorously identify weak synaptic connections or those with high failure rates. Multiple patch-clamp recordings can overcome this limitation by averaging a high number of repeats to the onset of the electrically induced AP. However, as optical activation often has some jitter, with our method one needs a relatively reliable synaptic response, with a clearly detectable postsynaptic signal, to identify a cell as being putatively connected. Due to this limitation, our maps likely favor stronger synaptic connections. We purposefully set high threshold criteria to define putative connections, to avoid false-positives, as confirmed by our dual recordings. This strategy, however, increases the false-negative rate and focuses on identifying strong synaptic connections, which have to be taken into account when considering the observed connectivity rate of 1.6%. With regard to mapping experiments, performing experiments in deeper tissue will reduce underestimation of connectivity rates. In addition, further data collection will be especially important for the analysis of synaptic strength, which can be greatly influenced by access resistance.
Methods
All methods can be found in the accompanying Transparent Methods supplemental file.
Acknowledgments
We thank Drs. Darcy Peterka and Julia Sable for technical support and assistance. We are also grateful to Dr. Yeosook Shin, Dr. Reka Letso, Alexa Semonche, and Mary Bando for mice viral injection and Dr. Carlo Manzo, James Guevara, and Azi Hamzei for technical support. J.J.H. was supported by the Deutsche Forschungsgemeinschaft (research fellowship HI 1728/1-1). M.I.-S. was supported by the Spanish Ministry of economy, Industry and Competition (fellowships FJCI-2014-19556 and IJCI-2016-27577). This work was supported by the NEI (DP1EY024503, R01EY011787), NIMH (R01MH101218, R01MH100561), and the US Army Research Office under contract number W911NF-12-1-0594 (MURI).
Author Contributions
J.J.H. and R.Y. conceived the original idea. M.I.-S., J.J.H., and B.S. designed the experiments. J.J.H. conducted the initial experiments. M.I.-S. conducted the majority of experiments, M.I.-S. and J.J.H. performed analysis and wrote the manuscript. B.S. contributed custom-written code. R.Y. assembled and directed the team, guided the project, edited the manuscript, and provided laboratory space, equipment, and funding.
Declaration of Interests
The authors declare no competing interests.
Published: October 26, 2018
Footnotes
Supplemental Information includes Transparent Methods and can be found with this article online at https://doi.org/10.1016/j.isci.2018.09.008.
Contributor Information
Mercè Izquierdo-Serra, Email: merce.izquierdo@upf.edu.
Jan J. Hirtz, Email: hirtz@bio.uni-kl.de.
Supplemental Information
References
- Alivisatos A.P., Chun M., Church G.M., Deisseroth K., Donoghue J.P., Greenspan R.J., McEuen P.L., Roukes M.L., Sejnowski T.J., Weiss P.S., Yuste R. The brain activity map. Science. 2013;339:1284–1285. doi: 10.1126/science.1236939. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andrasfalvy B.K., Zemelman B.V., Tang J., Vaziri A. Two-photon single-cell optogenetic control of neuronal activity by sculpted light. Proc. Natl. Acad. Sci. USA. 2010;107:11981–11986. doi: 10.1073/pnas.1006620107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ashby M.C., Isaac J.T.R. Maturation of a recurrent excitatory neocortical circuit by experience-dependent unsilencing of newly formed dendritic spines. Neuron. 2011;70:510–521. doi: 10.1016/j.neuron.2011.02.057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Avermann M., Tomm C., Mateo C., Gerstner W., Petersen C.C.H. Microcircuits of excitatory and inhibitory neurons in layer 2/3 of mouse barrel cortex. J. Neurophysiol. 2012;107:3116–3134. doi: 10.1152/jn.00917.2011. [DOI] [PubMed] [Google Scholar]
- Baker C.A., Elyada Y.M., Parra A., Bolton M.M. Cellular resolution circuit mapping with temporal-focused excitation of soma-targeted channelrhodopsin. Elife. 2016;5:e14193. doi: 10.7554/eLife.14193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barbour B., Isope P. Combining loose cell-attached stimulation and recording. J. Neurosci. Methods. 2000;103:199–208. doi: 10.1016/s0165-0270(00)00318-6. [DOI] [PubMed] [Google Scholar]
- Brown S.P., Hestrin S. Intracortical circuits of pyramidal neurons reflect their long-range axonal targets. Nature. 2009;457:1133–1136. doi: 10.1038/nature07658. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Callaway E.M., Katz L.C. Photostimulation using caged glutamate reveals functional circuitry in living brain slices. Proc. Natl. Acad. Sci. USA. 1993;90:7661–7665. doi: 10.1073/pnas.90.16.7661. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carrillo-Reid L., Yang W., Bando Y., Peterka D.S., Yuste R. Imprinting and recalling cortical ensembles. Science. 2016;353:691–694. doi: 10.1126/science.aaf7560. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cocas L.A., Fernandez G., Barch M., Doll J., Zamora Diaz I., Pleasure S.J. Cell type-specific circuit mapping reveals the presynaptic connectivity of developing cortical circuits. J. Neurosci. 2016;36:3378–3390. doi: 10.1523/JNEUROSCI.0375-15.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cossell L., Iacaruso M.F., Muir D.R., Houlton R., Sader E.N., Ko H., Hofer S.B., Mrsic-Flogel T.D. Functional organization of excitatory synaptic strength in primary visual cortex. Nature. 2015;518:399–403. doi: 10.1038/nature14182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Druckmann S., Feng L., Lee B., Yook C., Zhao T., Magee Jeffrey C., Kim J. Structured synaptic connectivity between hippocampal regions. Neuron. 2014;81:629–640. doi: 10.1016/j.neuron.2013.11.026. [DOI] [PubMed] [Google Scholar]
- Feldmeyer D., Lübke J., Sakmann B. Efficacy and connectivity of intracolumnar pairs of layer 2/3 pyramidal cells in the barrel cortex of juvenile rats. J. Physiol. 2006;575:583–602. doi: 10.1113/jphysiol.2006.105106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fino E., Yuste R. Dense inhibitory connectivity in neocortex. Neuron. 2011;69:1188–1203. doi: 10.1016/j.neuron.2011.02.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Forli A., Vecchia D., Binini N., Succol F., Bovetti S., Moretti C., Nespoli F., Mahn M., Baker C.A., Bolton M.M. Two-photon bidirectional control and imaging of neuronal excitability with high spatial resolution in vivo. Cell Rep. 2018;22:3087–3098. doi: 10.1016/j.celrep.2018.02.063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harris K.D., Mrsic-Flogel T.D. Cortical connectivity and sensory coding. Nature. 2013;503:51–58. doi: 10.1038/nature12654. [DOI] [PubMed] [Google Scholar]
- Hofer S.B., Ko H., Pichler B., Vogelstein J., Ros H., Zeng H., Lein E., Lesica N.A., Mrsic-Flogel T.D. Differential connectivity and response dynamics of excitatory and inhibitory neurons in visual cortex. Nat. Neurosci. 2011;14:1045–1052. doi: 10.1038/nn.2876. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holmgren C., Harkany T., Svennenfors B., Zilberter Y. Pyramidal cell communication within local networks in layer 2/3 of rat neocortex. J. Physiol. 2003;551:139–153. doi: 10.1113/jphysiol.2003.044784. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiang X., Wang G., Lee A.J., Stornetta R.L., Zhu J.J. The organization of two new cortical interneuronal circuits. Nat. Neurosci. 2013;16:210–218. doi: 10.1038/nn.3305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiang X., Shen S., Cadwell C.R., Berens P., Sinz F., Ecker A.S., Patel S., Tolias A.S. Principles of connectivity among morphologically defined cell types in adult neocortex. Science. 2015;350:aac9462. doi: 10.1126/science.aac9462. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jouhanneau J.-S., Kremkow J., Dorrn Anja L., Poulet James F.A. In vivo monosynaptic excitatory transmission between layer 2 cortical pyramidal neurons. Cell Rep. 2015;13:2098–2106. doi: 10.1016/j.celrep.2015.11.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karnani M.M., Agetsuma M., Yuste R. A blanket of inhibition: functional inferences from dense inhibitory connectivity. Curr. Opin. Neurobiol. 2014;26:96–102. doi: 10.1016/j.conb.2013.12.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kasthuri N., Hayworth K.J., Berger D.R., Schalek R.L., Conchello J.A., Knowles-Barley S., Lee D., Vázquez-Reina A., Kaynig V., Jones T.R. Saturated reconstruction of a volume of neocortex. Cell. 2015;162:648–661. doi: 10.1016/j.cell.2015.06.054. [DOI] [PubMed] [Google Scholar]
- Kebschull J.M., Garcia da Silva P., Reid Ashlan P., Peikon Ian D., Albeanu Dinu F., Zador Anthony M. High-throughput mapping of single-neuron projections by sequencing of barcoded RNA. Neuron. 2016;91:975–987. doi: 10.1016/j.neuron.2016.07.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim J., Zhao T., Petralia R.S., Yu Y., Peng H., Myers E., Magee J.C. mGRASP enables mapping mammalian synaptic connectivity with light microscopy. Nat. Methods. 2012;9:96–102. doi: 10.1038/nmeth.1784. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ko H., Hofer S.B., Pichler B., Buchanan K.A., Sjostrom P.J., Mrsic-Flogel T.D. Functional specificity of local synaptic connections in neocortical networks. Nature. 2011;473:87–91. doi: 10.1038/nature09880. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kwan A.C., Dan Y. Dissection of cortical microcircuits by single-neuron stimulation in vivo. Curr. Biol. 2012;22:1459–1467. doi: 10.1016/j.cub.2012.06.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lefort S., Tomm C., Floyd Sarria J.C., Petersen C.C. The excitatory neuronal network of the C2 barrel column in mouse primary somatosensory cortex. Neuron. 2009;61:301–316. doi: 10.1016/j.neuron.2008.12.020. [DOI] [PubMed] [Google Scholar]
- Levy R.B., Reyes A.D. Spatial profile of excitatory and inhibitory synaptic connectivity in mouse primary auditory cortex. J. Neurosci. 2012;32:5609–5619. doi: 10.1523/JNEUROSCI.5158-11.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mardinly A.R., Oldenburg I.A., Pégard N.C., Sridharan S., Lyall E.H., Chesnov K., Brohawn S.G., Waller L., Adesnik H. Precise multimodal optical control of neural ensemble activity. Nat. Neurosci. 2018;21:881–893. doi: 10.1038/s41593-018-0139-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nikolenko V., Poskanzer K.E., Yuste R. Two-photon photostimulation and imaging of neural circuits. Nat. Methods. 2007;4:943–950. doi: 10.1038/nmeth1105. [DOI] [PubMed] [Google Scholar]
- Oswald A.-M.M., Reyes A.D. Maturation of intrinsic and synaptic properties of layer 2/3 pyramidal neurons in mouse auditory cortex. J. Neurophysiol. 2008;99:2998–3008. doi: 10.1152/jn.01160.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Packer A.M., Yuste R. Dense, unspecific connectivity of neocortical parvalbumin-positive interneurons: a canonical microcircuit for inhibition? J. Neurosci. 2011;31:13260–13271. doi: 10.1523/JNEUROSCI.3131-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Packer A.M., Russell L.E., Dalgleish H.W.P., Hausser M. Simultaneous all-optical manipulation and recording of neural circuit activity with cellular resolution in vivo. Nat. Methods. 2015;12:140–146. doi: 10.1038/nmeth.3217. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Packer A.M., Peterka D.S., Hirtz J.J., Prakash R., Deisseroth K., Yuste R. Two-photon optogenetics of dendritic spines and neural circuits. Nat. Methods. 2012;9:1202–1205. doi: 10.1038/nmeth.2249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Papagiakoumou E., Anselmi F., Begue A., de Sars V., Gluckstad J., Isacoff E.Y., Emiliani V. Scanless two-photon excitation of channelrhodopsin-2. Nat. Methods. 2010;7:848–854. doi: 10.1038/nmeth.1505. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petreanu L., Mao T., Sternson S.M., Svoboda K. The subcellular organization of neocortical excitatory connections. Nature. 2009;457:1142–1145. doi: 10.1038/nature07709. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prakash R., Yizhar O., Grewe B., Ramakrishnan C., Wang N., Goshen I., Packer A.M., Peterka D.S., Yuste R., Schnitzer M.J., Deisseroth K. Two-photon optogenetic toolbox for fast inhibition, excitation and bistable modulation. Nat. Methods. 2012;9:1171–1179. doi: 10.1038/nmeth.2215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rancz E.A., Franks K.M., Schwarz M.K., Pichler B., Schaefer A.T., Margrie T.W. Transfection via whole-cell recording in vivo: bridging single-cell physiology, genetics and connectomics. Nat. Neurosci. 2011;14:527–532. doi: 10.1038/nn.2765. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rickgauer J.P., Tank D.W. Two-photon excitation of channelrhodopsin-2 at saturation. Proc. Natl. Acad. Sci. USA. 2009;106:15025–15030. doi: 10.1073/pnas.0907084106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rieubland S., Roth A., Häusser M. Structured connectivity in cerebellar inhibitory networks. Neuron. 2014;81:913–929. doi: 10.1016/j.neuron.2013.12.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shemesh O.A., Tanese D., Zampini V., Linghu C., Piatkevich K., Ronzitti E., Papagiakoumou E., Boyden E.S., Emiliani V. Temporally precise single-cell-resolution optogenetics. Nat. Neurosci. 2017;20:1796–1806. doi: 10.1038/s41593-017-0018-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun Y., Nguyen A.Q., Nguyen J.P., Le L., Saur D., Choi J., Callaway Edward M., Xu X. Cell-type-specific circuit connectivity of hippocampal CA1 revealed through cre-dependent rabies tracing. Cell Rep. 2014;7:269–280. doi: 10.1016/j.celrep.2014.02.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wertz A., Trenholm S., Yonehara K., Hillier D., Raics Z., Leinweber M., Szalay G., Ghanem A., Keller G., Rózsa B. Single-cell–initiated monosynaptic tracing reveals layer-specific cortical network modules. Science. 2015;349:70–74. doi: 10.1126/science.aab1687. [DOI] [PubMed] [Google Scholar]
- Wickersham I.R., Lyon D.C., Barnard R.J.O., Mori T., Finke S., Conzelmann K.-K., Young J.A.T., Callaway E.M. Monosynaptic restriction of transsynaptic tracing from single, genetically targeted neurons. Neuron. 2007;53:639–647. doi: 10.1016/j.neuron.2007.01.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang W., Carrillo-Reid L., Bando Y., Peterka D.S., Yuste R. Simultaneous two-photon imaging and two-photon optogenetics of cortical circuits in three dimensions. Elife. 2018;7:e32671. doi: 10.7554/eLife.32671. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.