Abstract
Given its ability to measure multicomponent distance distributions between electron-spin probes, double electron-electron resonance (DEER) spectroscopy has become a leading technique to assess the structural dynamics of biomolecules. However, methodologies to evaluate the statistical error of these distributions are not standard, often hampering a rigorous interpretation of the experimental results. Distance distributions are often determined from the experimental DEER data through a mathematical method known as Tikhonov regularization, but this approach makes rigorous error estimates difficult. Here, we build upon an alternative, model-based approach in which the distance probability distribution is represented as a sum of Gaussian components, and use propagation of errors to calculate an associated confidence band. Our approach considers all sources of uncertainty, including the experimental noise, the uncertainty in the fitted background signal, and the limited time span of the data collection. The resulting confidence band reveals the most and least reliable features of the probability distribution, thereby informing the structural interpretation of DEER experiments. To facilitate this interpretation, we also generalize the molecular simulation method known as ensemble-biased metadynamics (EBMetaD). This method, originally designed to generate maximal-entropy structural ensembles consistent with one or more probability distributions, now also accounts for the uncertainty in those target distributions exactly as dictated by their confidence bands. After careful benchmarks, we demonstrate the proposed techniques using DEER results from spin-labeled T4 lysozyme.
Introduction
Double electron-electron resonance (DEER) spectroscopy is a pulsed electron-spin resonance technique that is widely used to measure long-range distances between paramagnetic species, typically extrinsic probes introduced into biological macromolecules by some form of site-directed spin labeling (1, 2, 3). The main advantage of DEER lies in its ability to go beyond measuring the average distance between labels and resolve complex distance distributions that depend on both the rotameric states of the spin labels and also on differences in backbone structure of the protein or other biomolecule. It is this sensitivity to distinct backbone conformations that allows DEER experiments to give unique insights into the structure and functional dynamics of the protein under study (4).
The translation of an experimental time-domain DEER signal D(t) into a distance distribution P(R) is, however, an ill-posed mathematical problem in that small variations in D(t) can lead to large variations in the P(R) obtained. To address this issue, approaches to the analysis of DEER data impose some degree of smoothness on P(R) either by adding an adjustable smoothness factor to the fit criteria via Tikhonov regularization (TR) (5, 6, 7, 8) or by assuming some smooth functional form, such as a sum of Gaussian components, to model P(R) (9, 10, 11, 12).
The experimental DEER time-domain signal is the product of a factor arising from the dipolar interactions between the small number of spins (typically two) within a labeled molecule, DO(t), and a background signal, DB(t), arising from a large number of intermolecular dipolar interactions. Thus,
| (1) |
Properly accounting for the background signal is therefore necessary to determine the desired intramolecular distance distributions that are reflected in DO(t).
Application of the TR method requires that an estimate of the background factor be made a priori by fitting the latter portion of the time-domain signal D(t). This estimated background factor enables the determination of a background-corrected signal as an estimate of DO(t) that is then analyzed to give a distance distribution. Error estimations are typically made a posteriori by assessing the effects of the background correction and of the experimental noise at an arbitrary statistical-significance level. More recently, a rigorous Bayesian approach has been developed within the TR framework for quantifying the uncertainty in P(R) due to the experimental noise and the uncertainty in the choice of the optimal regularization parameter (13). This Bayesian approach does not, as of yet, allow for an estimate in the uncertainty of P(R) due to the background correction.
An alternative model-based approach, in which P(R) is represented as a sum of smooth basis functions, e.g., Gaussian components, relies on the simultaneous determination of the best-fit parameters modeling both DB(t) and DO(t) by a nonlinear least-squares algorithm. The advantages of a model-based approach for the analysis of DEER data, as opposed to a priori background correction followed by TR, have been detailed previously (9, 10). One of these advantages is the ability to perform a rigorous error analysis on the various fit parameters, including those used to define P(R). For multicomponent distance distributions, however, it can be difficult to appreciate how the parameter uncertainties affect the confidence in the resulting P(R).
In this work, a robust and computationally efficient algorithm is developed to quantify the uncertainty in P(R) in terms of a confidence band about the best-fit solution. This confidence band reflects the influence of both the noise in the measured data and the uncertainty in the estimate of the background correction and can be calculated with no significant increase in computation time.
The algorithm uses the method of propagation of errors, otherwise known as the delta method, to estimate the variance in a function, here P(R), of a set of random variables, here all the best-fit parameters for a given D(t) (14, 15, 16). We demonstrate the validity and robustness of the delta method as applied to the analysis of DEER data using different sets of simulated data. Then, we analyze experimental data from T4 lysozyme (T4L) using the new algorithm. Confidence bands obtained using the delta method quantify the reliability of each of the features of the distance distributions, thus permitting an objective comparison of results from different experiments.
Once estimates of P(R) and its associated error have been obtained, the next step is to use these data for assessing the structural dynamics of the biomolecule. This is a nontrivial task because P(R) reflects both variations in the backbone of the structure and in the configuration of the spin labels. Even for a rigid protein, for example, different rotamers of (1-Oxyl-2,2,5,5-tetramethyl-Δ3-pyrroline-3-methyl) methanethiosulfonate spin labels can result in 10-Å-wide distance distributions featuring multiple peaks (17, 18, 19, 20). Molecular dynamics (MD) simulations are arguably the most rigorous approach to model this variability. Of particular value are advanced simulation approaches that implement a bias on the calculated trajectories so as to reproduce the experimentally determined P(R) while fulfilling the so-called maximal-entropy condition, i.e., when the bias applied is the minimum required (17, 18). To our knowledge, however, none of the biasing techniques of this kind considers explicitly the experimental errors in the target data, which can lead to erroneous interpretations. Here, we generalize one of these advanced simulation techniques, known as ensemble-biased metadynamics (EBMetaD), precisely so as to account for the uncertainty of the input data. Like the original EBMetaD, the method is based on an adaptive biasing algorithm that gradually constructs a molecular ensemble consistent with the target distribution. However, in this version the bias applied is the least required for the simulated P(R) to be consistent with the experimental confidence bands, rather than with the optimal P(R). The EBMetaD method can be applied to probability distributions corresponding to any structural descriptor, either obtained through an experimental measurement or postulated theoretically. This innovative simulation methodology is first benchmarked on a small-molecule system using a hypothetical distribution corresponding to a dihedral angle. Then, EBMetaD is applied to the abovementioned DEER data for T4L to construct the corresponding structural ensembles in explicit water.
Methods
Simulated and experimental DEER signals
Simulated DEER data were generated using the program DEERsim version 2 running in MATLAB R2017a (The MathWorks, Natick, MA) with artificial noise added in the form of normally distributed random numbers with a given SD. DEERsim is based on previously published algorithms for calculating DEER time-domain signals (9) and is freely available at https://lab.vanderbilt.edu/hustedt-lab/software. In some cases, 10,000 replicate data sets were created from the same noiseless time trace and used to evaluate, via Monte Carlo simulations, the proposed methodologies for estimating the confidence in the fit parameters and in P(R). The experimental DEER signals for the three double-labeled mutants of T4L (namely residues 62 and 109, 62 and 134, and 109 and 134) were taken from previously published work (21, 22).
Analysis of DEER data
The simulated and experimental DEER data were analyzed using the program DD version 6C running in MATLAB R2017a as previously described (10) with modifications to allow for 1) the calculation of Bayesian information criterion values, 2) the estimation of parameter uncertainties from the variance-covariance matrix, and 3) the calculation of a confidence band for the best-fit P(R) using the delta method. Details on each of these three new, to our knowledge, procedures are provided below. DD is freely available at https://lab.vanderbilt.edu/hustedt-lab/software.
Assuming an ideal three-dimensional solution, simulated DEER signals, F(t), are modeled according to
| (2) |
where O(t) is the calculated signal for the pair of spins within a molecule,
| (3) |
and E(t) is an exponential to account for the background intermolecular interactions,
| (4) |
Here, Δ is the modulation-depth parameter, λ is a parameter governing the exponential background decay rate, P(R) is any probability distribution for the intramolecular interelectron distance, and G(ωdt) is a kernel function defined previously (5, 13, 23):
| (5) |
where C and S are the Fresnel cosine and sine integrals
| (6) |
and the symbols in the equation for ωd represent the usual physical constants.
Our analysis of DEER data is based on the assumption that P(R) can be described by a sum of n Gaussian components:
| (7) |
and
| (8) |
where , and
| (9) |
and
| (10) |
The Gaussian components are given by
| (11) |
Alternative basis functions with non-Gaussian shapes may also be used (see Supporting Material). The use of the aj > 2 as fit parameters guarantees that for any value of n and any set of 0 ≤ aj > 2 ≤ 1, the resulting P(R) will be normalized. For a given number of components n, the set of 3n − 1 variables r0j, σrj, and aj > 2 define P(R). All of these variables, together with Δ, λ, and a scale factor, constitute the set of parameters βl = 1,2,…,q that need to be determined for a given experimental signal and a given model (i.e., a specific value of n). We define the best-fit values of these parameters as those that minimize the reduced chi-squared value:
| (12) |
where D(t) is the experimental time-domain DEER data, N is the total number of data points, q is the total number of parameters considered in the fit, si is the estimated noise level (SD) of the ith data point, and ti is the time value of the ith data point. Here, the noise level is assumed to be uniform (si = s) at a level estimated from the SD of the imaginary component of the data.
For comparison, the simulated data were also analyzed using DeerAnalysis2016 (http://www.epr.ethz.ch/software/index) using an a priori background correction and TR (6). The zero time, phase correction, and initial start time for background fitting were determined automatically using the “!” button. When necessary, the regularization parameter was manually adjusted to match the corner of the L curve. The “Validation” tool was used to estimate the uncertainty in P(R) due to a range of starting times for background fitting, with results pruned to eliminate those that increased the root mean-square deviation by more than 15% as recommended, although the statistical significance of this increase is unknown.
Bayesian information criterion
Previously, the Akaike information criterion corrected for finite sample size (AICc) has been used to select the optimal model for a given experimental signal (10). Here, the closely related Bayesian information criterion (BIC) is used:
| (13) |
where K = q + 1. BIC can be used to select the optimum number of Gaussians describing P(R) that explain the data without overfitting (24). The optimal value of n is the one that results in the lowest BIC. BIC differs from AICc only in the second term of Eq. 13. For typical values of N and q (i.e., N ≥ 85 and q ≤ 26), BIC will always increase faster than AICc with increasing q. Thus, BIC will favor the same model or a more parsimonious model, i.e., a lower value of n, and in our judgement is preferable. For a given model j, ΔBICj is given by
| (14) |
where BIC0 is the lowest BIC value obtained for a given data set. AICc, BIC, and related criteria have also been recently evaluated by Edwards and Stoll as methods to determine the optimal regularization parameter for TR analysis of DEER data (25).
Parameter uncertainties
The methodology proposed herein aims to not only identify the best-fit values of the set of parameters βl = 1,2,…,q but also their uncertainty. This uncertainty can be rigorously quantified for each parameter by calculating a series of one-dimensional confidence intervals (26, 27) as described in detail elsewhere (10). Alternatively, under appropriate conditions, the parameter uncertainties can be estimated from the standard errors determined from the covariance matrix C = α−1, where α is the curvature matrix whose elements are
| (15) |
where the required partial derivatives are determined numerically via the forward difference method. The standard errors, σl of each of the parameters are determined from the diagonal elements of C,
| (16) |
and the off-diagonal elements give the covariances between parameters. The fit parameters and their uncertainties are reported as
| (17) |
where z = 1, 2, or 3 depending on whether the confidence level desired is 1σ (68.3%), 2σ (95.4%), or 3σ (99.7%). In contrast to the calculation of confidence intervals, estimating the parameter uncertainties from the covariance matrix requires little additional computation. The validity of both approaches will be assessed below using a Monte Carlo approach.
Confidence bands
The confidence band for a P(R) is calculated from the full covariance matrix using the delta method (14, 15, 16). Given that the best-fit parameters are themselves random variables obtained from fitting a given data set, we have
| (18) |
where Λ is a matrix of the partial derivatives of P(R) at a particular distance Ri with respect to all of the fit parameters βl = 1,2,…,q, i.e.,
| (19) |
Here, the partial derivatives of P(R) with respect to aj > 2 are determined analytically; those with respect to r0j and σrj are determined numerically; and those with respect to other parameters such as Δ, λ, and the scale factor are strictly zero. The confidence band for P(R) is then given by
| (20) |
where
| (21) |
and z = 1, 2, or 3 depending on whether a band at the 1σ, 2σ, or 3σ confidence level is desired.
MD simulations
All MD simulations were carried out with NAMD versions 2.9-2.12 (28). The force field used was CHARMM27/CMAP (29, 30), augmented by a force field for the spin labels developed by Sezer et al. (31). The simulations were carried out at 298 K and 1 bar with a 2-fs time step and periodic boundary conditions. Van der Waals and short-range electrostatic interactions were cut off at 12 Å; the particle-mesh Ewald method was used to calculate long-range electrostatic interactions. Two molecular systems are considered, butyramide in a cubic box with 1467 water molecules and T4L in a truncated octahedral box with 12,013 water molecules and Cl− counter ions to neutralize the total charge.
EBMetaD: formalism
We introduce a generalization of the EBMetaD technique (18) to take into account a confidence band around a distance distribution derived from experimental data. In MD simulations based on the EBMetaD method, a function of the atomic coordinates X is defined, namely ξ = ξf[X], and a time-dependent biasing potential V(ξ,t) is added to the standard energy function to ensure that the ensemble of conformations explored during the simulation is consistent with a given target probability distribution, ρ(ξ). The biasing potential is gradually constructed as a sum of Gaussian functions of ξ, added at time intervals τ and centered on the instantaneous value of ξ (18):
| (22) |
where ξ(t′) denotes the value of ξ at time t′, σG is related to the resolution used to describe fluctuations of ξ, w is a scaling parameter of the Gaussians height, and exp{Sρ} is the effective volume spanned by ρ(ξ) (i.e., is the differential entropy of ρ(ξ)). In the original application of the EBMetaD approach to DEER spectroscopy (18), the collective coordinate is the interlabel distance (ξ = R) and the target probability density is the DEER distance distribution (ρ(ξ) = P(R)), thereby assuming that the uncertainty on P(R) is negligible. Following the same notation, from here on, we denote the experimental best-fit distribution as P(ξ), and its uncertainty is represented by δ(ξ).
To account for this uncertainty, the new EBMetaD approach targets not P(ξ) but P(ξ) ± δ(ξ). More specifically, the desired simulated ensemble corresponds to a distribution that satisfies two requirements: first, it is inside the experimental confidence band; and second, it minimizes the amount of bias added to the standard energy function, i.e., it resembles the unbiased probability distribution of a conventional MD simulation as much as possible. In practice, this approach requires that the simulation be biased to sample an adaptive distribution, denoted as ρ(ξ,t). This distribution varies as the simulation evolves so as to ensure both conditions are ultimately fulfilled. An expression for ρ(ξ,t) can be derived either from an extended formulation of the maximal-entropy principle (32) that considers the experimental uncertainty (unpublished data; (33)) or from a Bayesian approach (34):
| (23) |
where kB is the Boltzmann constant, T is the simulation temperature, and CS is a shift constant. Here, denotes the average value of the biasing potential at time t, i.e., which serves as an offset of the instantaneous biasing potential V(ξ,t). The term γ(ξ,t) is a scaling factor of δ(ξ), initially set to 1 and then updated during the simulation, as discussed below. The notation denotes a projection onto the probability simplex (35) and guarantees that ρ(ξ,t) is positive and normalized, i.e., . This normalization condition, in turn, sets the value of CS. That is,
| (24) |
Note that in Eq. 24, the integration is performed only in the region of space where ρ(ξ,t) is different from zero. At any given time t, Eqs. 23 and 24 are solved iteratively and self-consistently until CS converges to a specific value. Note that consistent with the criteria stated above, Eq. 23 implies that a negligible error on P(ξ) leads to ρ(ξ,t) = P(ξ), whereas a large uncertainty on P(ξ) reduces the amount of bias added to the simulation.
In practice, the target distribution ρ(ξ,t) is constantly updated during the simulation, and after a transient period, it typically oscillates around an optimal solution. However, a wide confidence band around P(ξ) can result in wide fluctuations of ρ(ξ,t) during the trajectory, potentially compromising the convergence of the method. To avoid such instabilities, a variation of Eq. 23 is used to update ρ(ξ,t) at a slower pace, namely
| (25) |
where τ is the time range after which ρ(ξ,t) is updated and 0 < η < 1 is an update rate (see below).
The parameter γ(ξ,t) in the previous equations is a weight factor of δ(ξ), leading to an effective noise term . The scale factor γ(ξ,t) is set to attain the largest effective error (i.e., the minimal bias applied to the MD trajectory) that maintains ρ(ξ,t) within the confidence band. This is achieved by imposing the condition | ρ(ξ,t) − P(ξ) |/δ(ξ) = 1, from which the following update rule for γ(ξ,t) can be deduced:
| (26) |
When the uncertainty in P(ξ) is large, update schemes can be also devised for δ(ξ) and P(ξ) to further reduce the time oscillations of ρ(ξ,t). For example, if ρ(ξ,t) is within the confidence band, δ(ξ) can be varied so that it matches approximately the difference between ρ(ξ,t) and P(ξ). Similarly, P(ξ) can be updated to get closer to ρ(ξ,t), provided that the latter distribution remains in the confidence band. Further details and specific guidelines for the choice of the simulation parameters are discussed below.
Like in the original version of EBMetaD, the target distribution ρ(ξ,t) is enforced during the MD simulation by adding the biasing potential in Eq. 22 to the energy function. After an equilibration time te, this potential converges to a well-defined curve, and the resulting stationary distribution ρ(ξ,t > te), calculated over the simulation, approaches the target with the precision dictated by the confidence band. At convergence, the average biasing potential and the calculated probability distribution can be used to deduce the free energy, G, as a function of ξ (18):
| (27) |
As shown previously (18), the current methodology can simultaneously target multiple probability distributions determined using independent experiments (if these distributions can be assumed to be mutually compatible), simply by summing the corresponding biasing potentials.
Finally, a useful metric to compare different structural interpretations of the experimental data is provided by the reversible work W required to construct the biased EBMetaD ensemble. This work is related to the total amount of bias added throughout the simulation:
| (28) |
where <…>EBMetaD stands for a time average over the simulation, again for t > te, and
| (29) |
where ts is the total simulation time. Note that the value of W from Eqs. 28 and 29 can be derived analogously from the Kullback-Leibler divergence of the probability distributions sampled by EBMetaD and by an unbiased, converged MD simulation, i.e., a measure of the distance between the two ensembles. That is,
| (30) |
EBMetaD: implementation
The extension of EBMetaD described herein can be freely used with NAMD 2.12 (28) and LAMPS (36), specifically through the “colvars” module (37). This implementation follows the formalism introduced above. As mentioned, the convergence of this technique is related to the fluctuations of the target probability density ρ(ξ,t) during the trajectory. These fluctuations in turn depend on the value of parameters w, σG, and τ in Eq. 22; on the update rate of ρ(ξ,t); and on the width of the confidence band (P(ξ) ± δ(ξ)). To optimize the performance of EBMetaD, P(ξ) and δ(ξ) may be updated on time according to the following criteria:
| (31) |
and
| (32) |
In these equations, Cδ > 1 and was set to 1.5 for all the simulations. The parameters ηδ and ηP are update rates (0 < ηδ, ηP < 1) that must be selected as a fraction of η in Eqs. 31 and 32. The latter term is also selected as a fraction (0 ≤ Cη ≤ 1) of the biasing potential update rate (18):
| (33) |
The choice of η, ηδ, and ηP in Eqs. 31, 32, and 33 relates to the time required to reach equilibration; the duration of this equilibration stage is on the order of τ divided by the corresponding rate parameter. To accelerate convergence, the rate parameters can be selected larger in the first part of the simulation and then gradually reduced. To assess whether the latter parameters have been set reasonably, it is useful to monitor the time fluctuations of the constant CS and of ρ(ξ,t) (Eqs. 23 and 24). Large oscillations in CS, associated with intermittent values of ρ(ξ,t) that become zero, are an indication of poor convergence, implying that the value of the rate parameters must be reduced.
In the butyramide simulations described below, the variable biased by EBMetaD is the dihedral angle defined by atoms N, C, Cα, and Cβ. Gaussians of height w = 0.025 kcal/mol and width σG = 5 Å were added every 2 ps and were scaled by the target distribution according to Eq. 22. The rate parameters were set as Cη = 1 and ηδ = ηP = η/10. During the initial equilibration stage, lasting 30 ns, the Gaussian height and the rate parameters were gradually reduced to w = 0.01 kcal/mol, ηδ = η/10, and ηP = η/40.
In the simulation of T4L, the variables biased by EBMetaD are the distances between the centers-of-mass of the nitroxide groups in the spin labels. Gaussians of width σG = 5 Å were added every 2 ps. The parameter w was initially set to 0.05 kcal/mol and gradually reduced to 0.01 kcal/mol during equilibration (first 100 ns of simulation). The sampling of the spin interlabel distance was restricted using flat-bottom potentials in the ranges [21.8, 38.6 Å], [37.2, 46.3 Å], and [12.3, 48.8 Å] for spin-labeled pairs 62/109, 62/134, and 109/134, respectively. To avoid the onset of systematic errors at the boundaries of these intervals, the Gaussians added to the biasing potential were reflected beyond the boundaries (38), which translates into a flat biasing potential at the ends of those intervals. Accordingly, the biasing forces were set to zero outside the boundaries. In the EBMetaD simulations including the confidence band, the rate parameters were set according to Cη = 0.25, ηδ = ηP = η/10, and then in the production run, they were scaled down to ηδ = η/10 and ηP = η/40.
Results
Influence of noise level on the confidence band for a P(R)
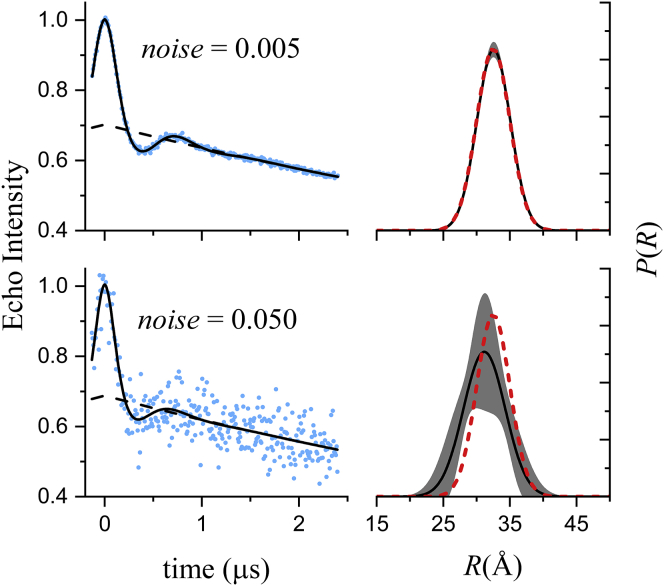
We first evaluate, using simulated DEER signals, how the noise level of the data is reflected in the estimated uncertainties of the fit parameters and the confidence band for the distance distribution. Fig. 1 shows results obtained from fitting a simulated signal at two different noise levels using DD (https://lab.vanderbilt.edu/hustedt-lab/software). Consistent with the fact that they were simulated for a unimodal distance distribution, the n = 1 model gives lower BIC values for both data sets and is thus favored (Table 1). The best-fit P(R) for the low-noise example agrees very well with the true distribution, whereas the best-fit P(R) for the high-noise case is shifted from the true distribution because of the higher variance in the fit parameters.
Figure 1.
Fits to simulated DEER data generated using a single Gaussian to model P(R) (r0 = 32.5 Å and σr = 2.5 Å). Data were simulated for t = −128 to +2400 ns with a time increment of 8 ns. Normally distributed random numbers with SD of either 0.005 or 0.050 were added as noise. (A) The simulated data (blue dots), the fits (solid black lines), and the best-fit background factor (dashed black lines) are shown. (B) The best-fit P(R) (solid black lines), the confidence band (2σ, shaded gray regions), and the true P(R) (dashed red lines) used to generate the simulated signal are shown. Only a portion of the full range (0–100 Å) of R is shown. The values of each of the fit parameters and their uncertainties are given in Table 2. To see this figure in color, go online.
Table 1.
Model Selection for Fits to Simulated DEER Data Generated Using a Single Gaussian
| Noise | n | ΔBIC | |
|---|---|---|---|
| 0.005 | 1 | 0.984 | 0.0 |
| 2 | 0.982 | 13.3 | |
| 0.050 | 1 | 1.054 | 0.0 |
| 2 | 1.0581 | 15.5 |
Model selection was for fits in Fig. 1.
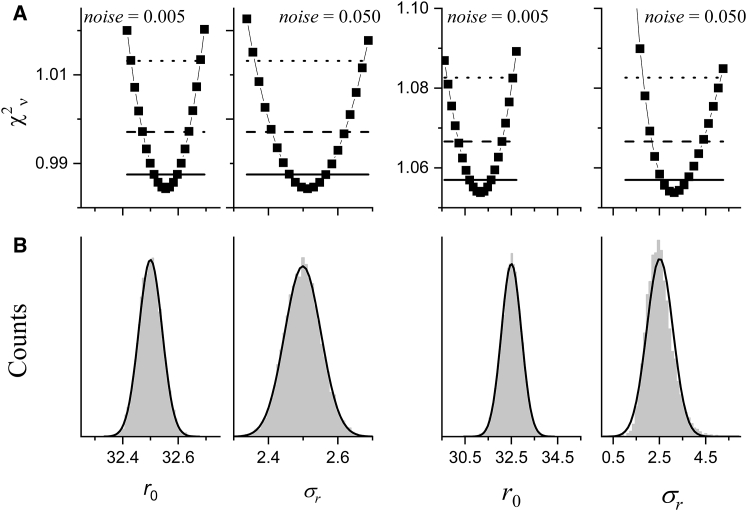
The best-fit parameters from these fits are given in Table 2 along with the parameter uncertainties estimated from the covariance matrix (Eqs. 15, 16, and 17) and the upper and lower parameter bounds estimated from confidence-interval calculations. Example confidence intervals for the parameters r0 and σr are shown in Fig. 2 A. The values reported for the upper and lower parameter limits are measured where each curve intersects the dashed line corresponding to the 2σ confidence level.
Table 2.
Best-Fit Parameters for the Simulated DEER Data Generated Using a Single Gaussian
| Noise = 0.005 | Δ | λ | Scale | r0 | σr | |
|---|---|---|---|---|---|---|
| Best-fit values | 0.2992 | 4.9970 | 1.0024 | 32.555 | 2.513 | 0.984 |
| Uncertaintiesa | ±0.0022 | ±0.0063 | ±0.0024 | ±0.084 | 0.105 | NA |
| CI lower limitb | −0.0022 | −0.0064 | −0.0024 | −0.083 | −0.103 | NA |
| CI upper limitb | +0.0022 | +0.0063 | +0.0024 | +0.083 | +0.107 | NA |
| Average of 10,000 best-fit valuesc | 0.3000 | 5.0000 | 1.0000 | 32.500 | 2.499 | 1.000 |
| 2× std. dev. of 10,000 best-fit valuesd | 0.0022 | 0.0063 | 0.0024 | 0.084 | 0.105 | 0.160 |
| Average of 10,000 uncertaintiese | ±0.0022 | ±0.0063 | ±0.0024 | ±0.084 | 0.106 | NA |
| Noise = 0.050 | Δ | λ | Scale | r0 | σr | |
| Best-fit values | 0.315 | 5.024 | 1.005 | 31.16 | 3.14 | 1.054 |
| Uncertaintiesa | ±0.024 | ±0.061 | ±0.028 | ±0.93 | ±1.27 | NA |
| CI lower limitb | −0.024 | −0.065 | −0.027 | −0.95 | −0.97 | NA |
| CI upper limitb | +0.023 | +0.057 | +0.029 | +0.93 | +1.24 | NA |
| Average of 10,000 best-fit valuesc | 0.301 | 4.998 | 1.001 | 32.50 | 2.52 | 1.000 |
| 2× SD of 10,000 best-fit valuesd | 0.023 | 0.065 | 0.025 | 0.87 | 1.13 | 0.159 |
| Average of 10,000 uncertaintiese | ±0.022 | ±0.064 | ±0.025 | ±0.83 | ±1.04 | NA |
| True valuesf | 0.3 | 5.0 | 1.0 | 32.5 | 2.5 | NA |
Signal parameters are for Fig. 1. NA, not applicable
Upper and lower parameter bounds determined from confidence intervals as shown in Fig. 2. Values given correspond to the 2σ confidence level.
Average best-fit parameters for 10,000 replicate simulated data sets.
Twice the SDs of the best-fit parameters for 10,000 replicate simulated data sets.
Average of the 2σ uncertainties estimated from fits to 10,000 replicate simulated data sets.
The true parameters used to simulate data.
Figure 2.
Comparison of one-dimensional confidence intervals (A) for r0 and σr from the fits in Fig. 1 to histograms (B) from fitting 10,000 replicate data sets. The four panels on the left were obtained for the lower noise level (0.005); the four on the right were obtained for the higher noise level (0.05). (A) Gray dots were obtained by fixing the parameter r0 or σr to a series of values and allowing the other four fit parameters to vary to minimize. The horizontal lines give the 1σ (solid), 2σ (dashed), and 3σ (dotted) confidence levels. Lower and upper bounds on the parameters at a particular confidence level are determined by where the curve intersects the appropriate horizontal line. (B) Histograms of 10,000 parameter values obtained from repetitive fits to data similar to that in Fig. 1 are shown. The solid black lines are normal (Gaussian) distributions calculated for the mean and SD of the distribution of parameter values (see Table 2).
To ascertain the validity of these parameter uncertainties and confidence bands, we analyzed fits for 10,000 replicate signals generated using a Monte Carlo procedure from the same model and with the same level of added random noise. Examining all of these results, three important conclusions can be drawn. First, the distribution of parameter values obtained from 10,000 replicate fits are typically well described by a Gaussian distribution (Fig. 2 B) and the parameter uncertainties estimated from a single fit (at the 2σ confidence level) match (twice) the value of the SD of these parameter distributions (Table 2), as expected. At the highest noise level, the best-fit parameters for a fit to a single data set are shifted from the true values because of the increase in the parameter variance, and both the confidence interval from the single fit and the histogram from 10,000 fits for the σr parameter are slightly distorted by the zero lower bound on the parameter (Fig. 2, far right). Second, as long as the errors are Gaussian, the uncertainties estimated from the covariance matrix match the results of the more rigorous confidence interval calculations. Finally, the parameter uncertainties increase linearly as the noise level increases.
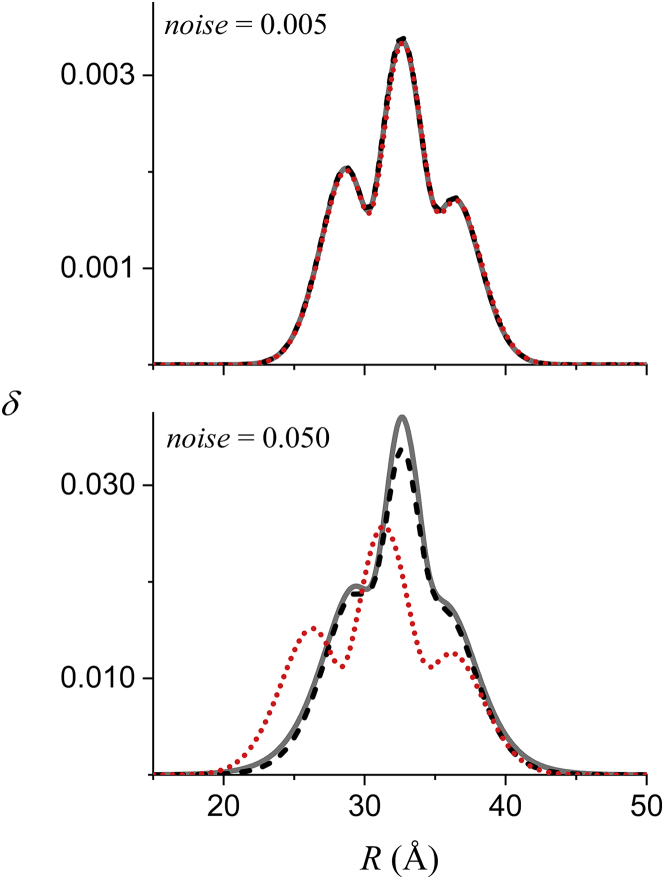
Confidence bands (P(R) ± 2δ(R); Eqs. 18, 19, 20, and 21) for the best-fit distance distributions are shown in Fig. 1 B as gray shaded regions, and the δ(R) themselves are plotted in Fig. 3 (red dotted lines). Fig. 3 also includes the SD of the P(R) obtained from fitting 10,000 replicate data sets (solid gray lines) and the average value of δ(R) from these fits (dashed black lines). The results for the lower noise level (Fig. 3, upper) show that the δ(R) obtained from fitting a single data set overlays the SD in P(R) that would be obtained from fitting a large number of replicate data sets. The results at the higher noise level (Fig. 3, lower) show that the δ(R) from a single fit gives a reasonable order-of-magnitude estimate of this SD that depends linearly on the noise level.
Figure 3.
Comparison of the δ(R) (red dotted line) calculated (Eqs. 18, 19, 20, and 21) for the fits in Fig. 1 to the average δ(R) (black dashed line) and the SD (solid gray line) of all of the P(R) obtained from fitting 10,000 replicate data sets. The results in the upper panel were obtained for the lower noise level (0.005) and the results in the lower panel for the higher noise level (0.05). Only a portion of the full range (0–100 Å) of R is shown. To see this figure in color, go online.
In summary, the results shown in Figs. 1, 2, and 3 demonstrate that the parameter uncertainties and the confidence bands for P(R) both properly account for the noise in the data and give reasonable estimates of the distributions that would be obtained from fitting multiple replicate data sets.
Background correction uncertainty
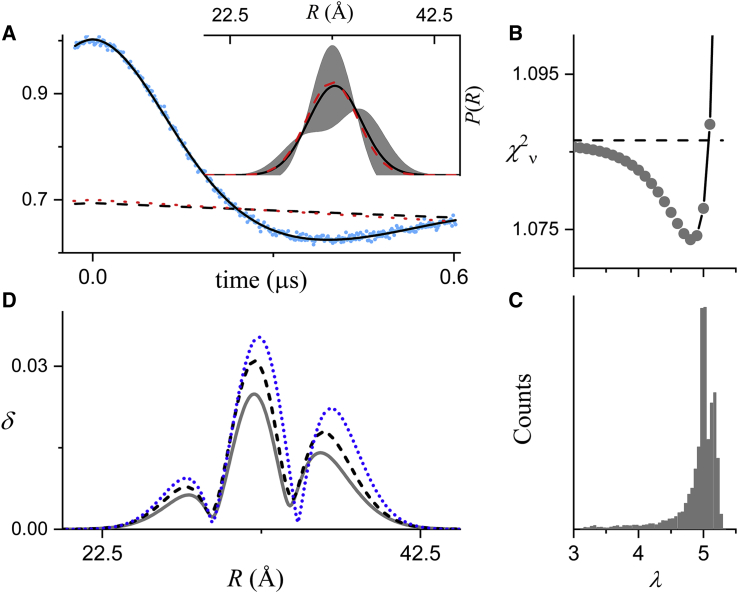
In addition to random noise, other factors can influence the magnitude of parameter uncertainties and confidence band for P(R). In particular, the maximal observed dipolar evolution time determines to what degree the background factor can be resolved at the tail of the full DEER signal. In Fig. 4 A, a “stress test” is performed using DD to fit simulated DEER signal with an extremely short dipolar evolution time generated using the same model parameters and noise level as that in Fig. 1 (upper). The simulated data are well fitted using a single Gaussian to model P(R), whereas a two-component model gives a larger BIC value (see Table S1).
Figure 4.
Fit to simulated DEER data generated using a single Gaussian to model P(R) (r0 = 32.5 Å and σr = 2.5 Å) and a short dipolar evolution time. Data were simulated for t = −32 to +600 ns with a time increment of 2 ns. Other parameters are given in Table S2. Normally distributed random numbers with SD of 0.005 were added as noise. (A) The simulated data (blue dots), the fit (solid black line), the best-fit background factor (dashed black line), and the true background (dotted red line) are shown. The inset shows the best-fit P(R) (solid black lines), the confidence band (2σ, shaded gray regions), and the true P(R) (dashed red lines) for the simulated data. (B) The one-dimensional confidence interval (gray dots) obtained by fixing λ to a series of values and allowing the other four fit parameters to vary to minimize is shown. The green dashed horizontal line gives the 2σ confidence level. (C) Histograms of 10,000 λ values obtained from repetitive fits to replicate data similar to that in (A) are given. (D) The δ(R) (blue dotted line) calculated for the fit A compared to the average δ(R) (black dashed line) and the SD (solid gray line) of all of the P(R) obtained from fitting 10,000 replicate data sets is shown. Only a portion of the full range (0–100 Å) of R is shown. To see this figure in color, go online.
Despite the fact that the background is not resolved for this simulated signal, DD is able to determine a reasonable estimate of the background correction, as can be seen by comparing the best-fit background (Fig. 4 A, dashed black line) with the true background factor (dotted red line) or by comparing the best-fit λ and Δ parameters to the true values (see Table S2). Nonetheless, there is considerable uncertainty in the parameter λ as determined by either the covariance matrix (4.83 ± 0.88) or the one-dimensional confidence interval (Fig. 4 B). This confidence interval for λ and those for most of the other fit parameters (data not shown) strongly deviate from the parabolic shapes seen in Fig. 2. Accordingly, analysis of the 10,000 replicate signals reveals a broad range of λ values (Fig. 4 C), which in turn leads to large variations in the other fit parameters (Fig. S1). Most of these histograms strongly deviate from the Gaussian shapes seen in Fig. 2. The lack of precision in determining the background correction leads to a confidence band for P(R) that is dramatically larger than that obtained for data collected for a longer dipolar evolution time (cf. Fig. 1 upper panel). However, the calculated δ(R) (dotted blue line) gives a reasonable estimate of the SD in P(R) that would be obtained from fitting a large number of replicate data sets (solid gray line). Finally, even under the extreme conditions presented by the simulated data in Fig. 4 A, the best-fit P(R) is very close to the true P(R), demonstrating that the distance distribution and the background factor can be simultaneously estimated using our approach.
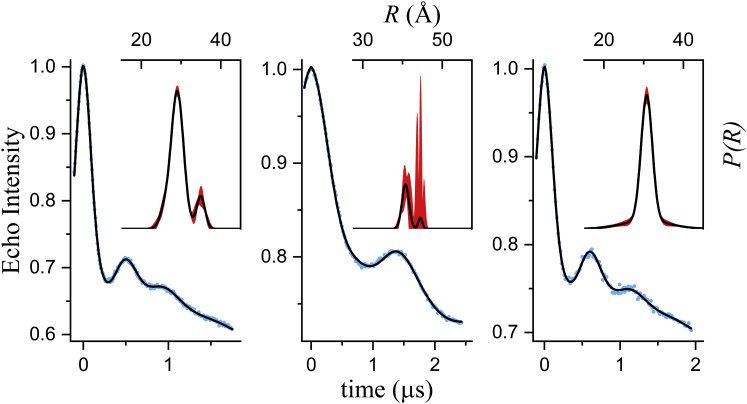
Multimodal Gaussian distribution
Of critical importance is the performance of the proposed analysis method for DEER signals originating from multimodal distance distributions as is typical for systems of biological interest. Fits to simulated DEER signals calculated for two different trimodal distance distributions are shown in Fig. 5 A. As expected for both data sets, the optimal model based on BIC values is a sum of three Gaussians (n = 3, Table S3). The parameter uncertainties estimated from the covariance matrix are in excellent agreement with the results from one-dimensional confidence interval calculations and with the SDs of the parameter values resulting from fitting 10,000 replicate signals (Table S4). Likewise, the δ(R) used to calculate the confidence band for P(R) for each fit closely agrees with the SD of P(R) obtained from fitting 10,000 replicates (Fig. 5 B). For both simulated signals, neither the parameter uncertainties nor the widths of the confidence bands depend on the r0 values of the individual components in a straightforward way. For the data in the upper panel of Fig. 5 A for which the true σr values of the three Gaussians are equal, the parameter uncertainties and width of the confidence band are roughly equal for the three components. For the data in the lower panel of Fig. 5 A, the parameter uncertainties for r0 and σr increase as the value of σr increases for the three components. However, the width of the confidence band decreases as σr increases.
Figure 5.
Fits to two simulated DEER signals generated using three Gaussians to model P(R). Data were simulated for t = −128 to +2400 ns with a time increment of 8 ns. Other parameters are given in Table S4. Normally distributed random numbers with SD of 0.005 were added as noise. (A) The simulated data (blue dots), the fits (solid black lines), and the best-fit background factor (dashed black lines) are shown. The insets show the best fit P(R) (solid black lines), the confidence bands (2σ, shaded gray regions), and the true P(R) (dashed red lines) for the simulated data. (B) A comparison of the δ(R) (solid black lines) calculated for the fits in A to the average δ(R) (dotted blue lines) and the SD (dashed red lines) of all of the P(R) obtained from fitting 10,000 replicate data sets is shown. Only a portion of the full range (0–100 Å) of R is shown. To see this figure in color, go online.
To further clarify how the uncertainty in a component of P(R) varies as its average distance value increases, additional calculations for a unimodal simulated signal were performed as summarized in Table S5. For r0 up to 45 Å, the uncertainties in r0 and σr do not vary significantly, whereas for r0 = 55 Å and beyond, for which a full modulation period is not completed within the dipolar evolution time of 2400 ns, the uncertainties in both r0 and σr increase dramatically.
In summary, the results in Fig. 5 together with Tables S3 and S4 demonstrate that all of the, to our knowledge, new methods presented here perform as expected when DEER data is derived from complex, multimodal distributions.
Comparison to DeerAnalysis
For comparison with the TR method, fits to the simulated signals in Fig. 1 obtained using DeerAnalysis2016 are shown in Figs. S2 and S3. At the lower noise level, the two approaches give similar results and similar estimates of the uncertainty in P(R). At the higher noise level, the DD estimate is considerably larger. This may be due, at least in part, to the fact that, as is commonly done, only the background starting time option was used here in the validation tool of DeerAnalysis2016. For the simulated signals in Fig. 4, it is difficult to find a convincing a priori background correction given the short dipolar evolution time of the data, and therefore this signal cannot be interpreted using DeerAnalysis2016. For the multicomponent simulated signals in Fig. 5, fits obtained with DeerAnalysis2016 are shown in Figs. S4 and S5. For the signal generated from a P(R) calculated as the sum of three Gaussians of equal width, both DD and DeerAnalysis2016 give similar results.
For the data generated from a P(R) using three Gaussians of varying widths, DeerAnalysis2016 adds a fourth component at r0 ≈ 40Å, apparently to account for the component with the broadest width (Fig. S5). This result is due to the fact that TR tends to produce multicomponent distributions with equal component widths. It is important to note that the confidence bands for P(R) obtained from DD (Figs. S4 F and S5 F) do not strictly follow the color-coding scheme for reliability in DeerAnalysis2016 (Figs. S4 D and S5 D).
Evaluation of generalized EBMetaD for a small-molecule system
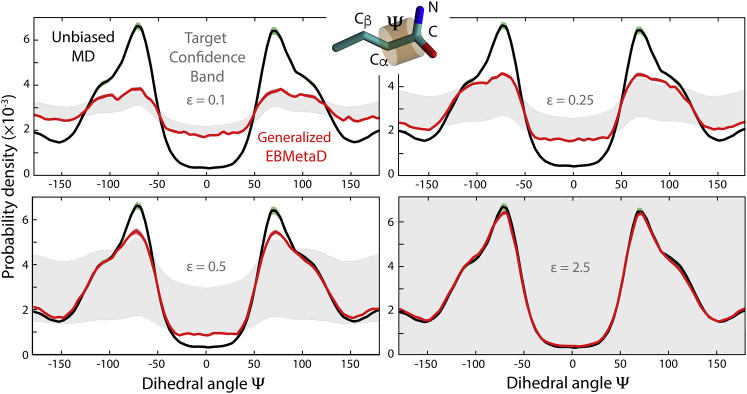
Having established the validity of our signal analysis algorithm, we evaluated the performance and accuracy of the generalized EBMetaD method. We first considered a simple molecular system, namely a butyramide molecule in water. The conformational descriptor considered in this evaluation is the dihedral angle (Ψ) around the Cα-C bond, i.e., ξ = Ψ in Eq. 22 (Fig. 6). We first calculated a 400-ns trajectory using a standard MD simulation so as to obtain a well-converged probability distribution along Ψ. This distribution is symmetric around 0° with peaks at Ψ ≈ ±70° (Fig. 6). We then designed an artificial target distribution for the EBMetaD method that is substantially different from that obtained above, as well as several confidence bands of increasing width around this hypothetical target distribution, such that the widest of these bands encompass the unbiased MD distribution partially or fully (Fig. 6). Using each of these confidence bands as input, we then calculated a 320-ns trajectory with EBMetaD using the same simulation parameters employed for the conventional MD trajectory.
Figure 6.
Evaluation of the generalized EBMetaD method for butyramide in water. The torsional angle Ψ defined by atoms Cβ, Cα, C, and N is considered. The probability distribution obtained from a conventional unbiased MD simulation, ρMD(Ψ) (black), is compared with those obtained using EBMetaD simulations, ρEBMetaD(Ψ) (red), in four independent calculations. Each of these calculations = target a, hypothetical distribution and its uncertainty band (gray), i.e. , where . Note that ρMD(Ψ) is partially encompassed by the target confidence band at and fully encompassed at .
The distributions along Ψ obtained after equilibration illustrate the performance of the proposed method. The EBMetaD distributions draw along the edges of the confidence band so as to fulfill the target data while remaining as close as possible to the unbiased distribution (Fig. 6). Accordingly, when the confidence band is wide enough to encompass the unbiased probability density, the EBMetaD approach does not bias the sampling and produces the same distribution as a standard MD simulation. By contrast, when the confidence band is narrow, the EBMetaD distribution deviates from the unbiased distribution as needed.
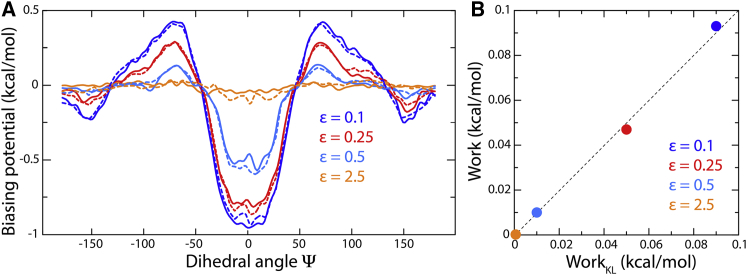
Analysis of the converged biasing potential developed by the EBMetaD algorithm for each of the input confidence bands using Eq. 29 explains these results (Fig. 7 A). It is apparent that the magnitude of the bias added to the simulation is not uniform along Ψ but depends on the difference between the target and unbiased distribution. The overall bias also decreases as the uncertainty of the target distribution is greater; when the input confidence band encompasses the unbiased distribution from standard MD, the EBMetaD potential is nearly flat, i.e., no conformational bias is applied (Fig. 7 A). This result, consistent with the minimal-information condition, can be further quantified by calculating the reversible work performed to enforce the EBMetaD biasing potential using Eq. 28 (Fig. 7 B). Consistent with the data in Fig. 7 A, the value of the work diminishes as the confidence band widens, becoming negligible when the unbiased MD distribution is within the uncertainty.
Figure 7.
Evaluation of the generalized EBMetaD method for butyramide in water. (A) EBMetaD biasing potential is shown as function of Ψ for each of the calculations shown in Fig. 6, i.e., with increasing confidence-band widths (denoted by the scaling factor ). The biasing potential was calculated with Eq. 29, using te = 30 ns and t = 320 ns (solid curves), and compared with a calculation using Eq. 27 (dashed lines), in which G(Ψ) = −kBT ln ρMD(Ψ), where ρMD(Ψ) is the unbiased probability distribution obtained from an unbiased MD trajectory (Fig. 6). (B) Shown are the values of the reversible work required to enforce the EBMetaD biasing potential for each of the four simulations mentioned above. The work values are derived from the Kullback-Leibler divergence of ρMD(Ψ) and ρEBMetaD(Ψ) (Fig. 6) using Eq. 30 and compared with calculations based on the biasing potentials in (A) using Eq. 28. The error bars in the work values, based on from a five-block analysis, range from 10−3 to 10−4 kcal/mol.
Like with any enhanced-sampling simulation method, it is important for EBMetaD to preserve the inherent thermodynamics of the molecular system. To evaluate whether this is the case, the biasing potentials derived with Eq. 29 were compared with calculations based on Eq. 27, i.e., from the free-energy function = G(Ψ) = −kBT ln ρMD(Ψ), which for this simple system can be calculated exactly from an unbiased trajectory (Fig. 7 A). Similarly, the work values calculated using Eq. 28 were contrasted with those deduced from the Kullback-Leibler divergence (Eq. 30) of the unbiased and biased distributions (Fig. 7 B). Both evaluations demonstrate the proposed methodology is robust qualitatively and quantitatively.
In summary, this application demonstrates that EBMetaD constructs a conformational ensemble compatible with the confidence band of a target probability distribution and with the underlying free-energy landscape of the system, and that it does so by applying the minimal bias required. This application also shows that the EBMetaD work is an accurate descriptor of the degree to which an unbiased conformational ensemble might be compatible with a given set of target data. We posit that these features make the EBMetaD method an ideal tool to formulate well-founded molecular interpretations for a range of experimental information e.g. DEER data.
Model-based fitting and EBMetaD simulations for T4L DEER data
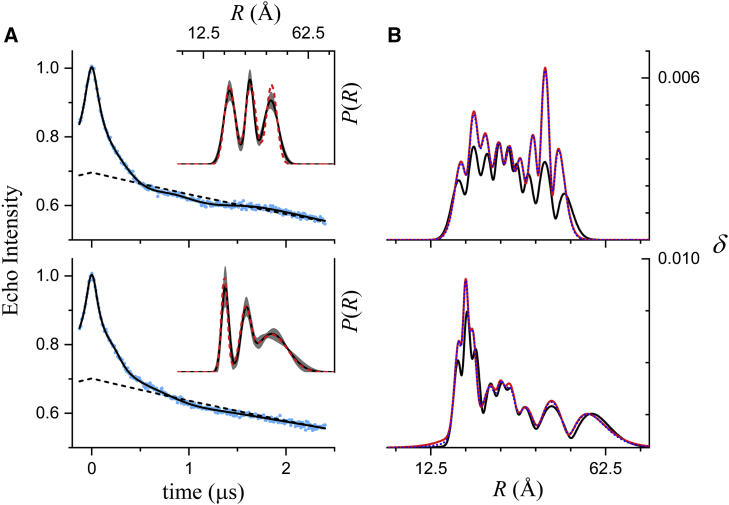
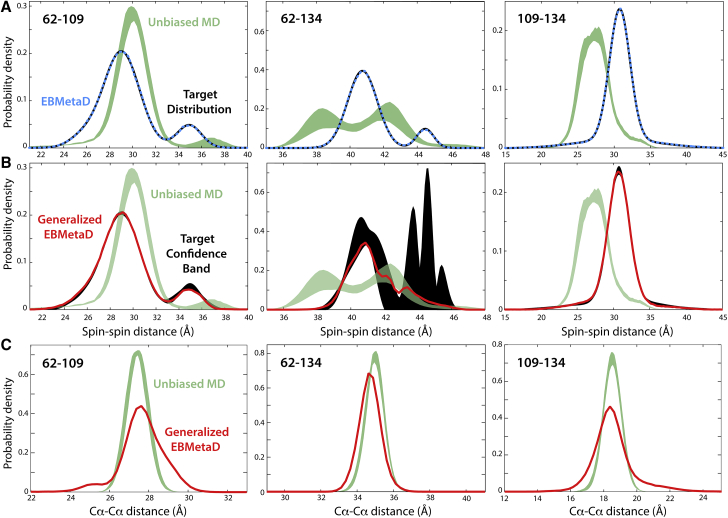
After demonstrating the validity of the extended EBMetaD method on a simple system, we applied this approach to spin-labeled T4L in explicit water. Following our previous work (18), we considered three double-labeled T4L mutants with labels introduced at positions 62, 109, and 134. Experimental DEER data along with the corresponding fits obtained using DD are shown in Fig. 8. Based on BIC values, a three-Gaussian model was found to be optimal for T4L 62/109, whereas a two-Gaussian model was better suited for both T4L 62/134 and T4L 109/134 (Table 3). The best-fit parameters are given in Table S6. Note that the confidence bands for pairs T4L 62/109 and T4L 109/134 are relatively narrow over the entire distance range, whereas that for T4L 62/134 is very broad for the component at the longest distance. These data sets, therefore, constitute a nontrivial test case of EBMetaD methodology.
Figure 8.
DEER signals and associated probability distributions for three spin-labeled pairs in T4L. The DEER data are shown as blue dots, and the fits as solid black lines. The insets show the best fit P(R) (solid black lines), along with the newly obtained confidence bands (2σ, shaded red regions). Best-fit parameters are given in Table S6. To see this figure in color, go online.
Table 3.
Model Selection for T4L Data Sets
| T4L Mutant | n | ΔBIC | |
|---|---|---|---|
| 62/109 | 1 | 3.741 | 377.0 |
| 62/109 | 2 | 0.713 | 4.1 |
| 62/109 | 3 | 0.662 | 0.0 |
| 62/109 | 4 | 0.654 | 10.5 |
| 62/134 | 1 | 1.395 | 9.4 |
| 62/134 | 2 | 1.220 | 0.0 |
| 62/134 | 3 | 1.243 | 15.1 |
| 109/134 | 1 | 1.400 | 25.8 |
| 109/134 | 2 | 1.049 | 0.0 |
| 109/134 | 3 | 0.977 | 2.1 |
To model the DEER data for T4L using EBMetaD, we considered the distance between the centers-of-mass of the nitroxide groups as the reaction coordinate (ξ = R). For simplicity, we enforced the three experimental distance distributions simultaneously, even though the DEER signals were measured for one pair of spin labels at a time. We are implicitly assuming, therefore, that the relative dynamics of any two spin labels is not influenced by the presence of a third spin label. This assumption seems plausible in this case, but it is not a prerequisite for the EBMetaD method, which can be applied to single spin-labeled pairs, as mentioned. To evaluate the new methodology, three calculations were carried out: a 600-ns conventional MD simulation, a 400-ns EBMetaD simulation in which the experimental error is not considered, and a 670-ns EBMetaD simulation that does consider the confidence bands. The resulting distance distributions after equilibration are reported in Fig. 9 (see caption for details). Overall, the unbiased probability distributions obtained with standard MD are outside the confidence bands, particularly for T4L 109/134 (Fig. 9 A). By contrast, and consistent with our previous work (18), the distributions calculated with EBMetaD while neglecting the error match the target with great accuracy (Fig. 9 A). However, when the confidence bands are targeted, the EBMetaD results no longer match the optimal-fit distributions and instead draw nearer the unbiased data while being fully consistent with the experimental confidence bands (Fig. 9 B). A compelling example is the T4L 62/134 pair, for which the second peak near 45 Å in the experimental probability distribution is not fully realized in the results of the EBMetaD sampling (red lines, Fig. 9 B) precisely because the confidence bands (black bands, Fig. 9 B) indicate a very large uncertainty in this region.
Figure 9.
Evaluation of generalized EBMetaD for spin-labeled T4L. (A) Best-fit probability distributions obtained for each of the three experimental data sets (black) are compared with those calculated with standard MD simulations (green bands) or with EBMetaD when the experimental distribution is the target and the confidence bands are not considered (cyan). (B) Confidence bands from Fig. 8 (black bands) but shown at 1σ are compared with probability distributions calculated with EBMetaD now targeting these confidence bands (red) and the unbiased MD data. The standard MD data in (A) and (B) are shown as a band whose width is the standard error over five consecutive blocks of 100 ns each. The standard errors of EBMetaD distributions are barely visible and therefore not shown for clarity. (C) Probability distributions of the distance between the Cα atoms for each of the spin-labeled pairs, either from standard MD (green bands) or from the EBMetaD simulations (red lines) targeting the confidence bands shown in (B), are shown.
Consistent with the maximal-entropy principle underlying our methodology, the overall magnitude of the EBMetaD biasing potential is smaller when the simulation targets the confidence bands. Specifically, the work value calculated using Eq. 28 changes from 0.96 to 0.77 kcal/mol when the confidence bands are targeted rather than the optimal-fit distributions. The small magnitude of these values reflects the limited structural dynamics of T4L, which implies that the unbiased MD distributions are not entirely unlike those measured. Indeed, at the structural level, the ensemble produced by EBMetaD differs from the unbiased simulation primarily in the distribution of rotameric states of the spin-labels (Figs. 9 C and 10 A). Nevertheless, the work values derived from the biasing potential are in good agreement with those predicted from the Kullback-Leibler divergence (Eq. 30) of the unbiased and target distributions (Fig. 9, A and B), namely 0.99 and 0.83 kcal/mol, respectively. It seems clear, therefore, that this methodology will be sufficiently sensitive to conformational changes of a larger scale.
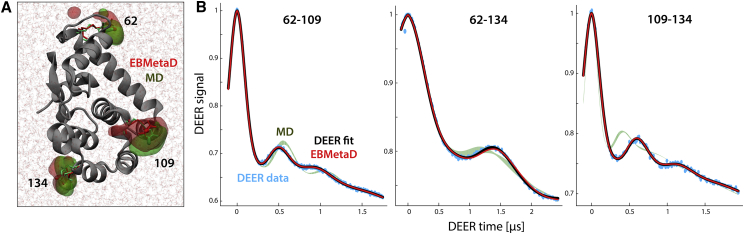
Figure 10.
Evaluation of generalized EBMetaD for spin-labeled T4L. (A) A closeup of T4L in the MD simulation system is given, highlighting the spin labels at positions 62, 109, and 134. Red and green surfaces encompass the regions occupied by the nitroxide groups during the EBMetaD and MD simulations, respectively. The root mean-square deviation of the protein backbone (gray cartoons) relative to the initial x-ray structure (46) is within 2 Å in both cases. (B) For each of the three spin-labeled pairs, the experimental DEER signals (cyan) and the corresponding fits (black) are compared with theoretical signals calculated (Eqs. 2, 3, 4, 5, and 6) from the simulated EBMetaD distributions (red) in Fig. 9B, i.e., in consideration of the confidence bands. The calculated signals from the unbiased MD data are also shown for comparison (green bands). The Δ and λ parameters for each of these calculated time-traces are provided in Table S7.
The molecular ensembles produced by the generalized EBMetaD method not only facilitate a structural interpretation of the DEER data; they also provide a self-consistency check for the model-based analysis of the DEER signal described above and the resulting confidence bands. That is, from each of the simulated EBMetaD ensembles, it is possible to derive the DEER time trace for each of the spin-labeled pairs (9, 10, 13), which can then be compared with the actual experimental measurements. As shown in Fig. 10 B, in the T4L case the EBMetaD ensembles produced for each spin-labeled pair by targeting the confidence bands are in excellent agreement with the DEER measurements, demonstrating the cross-consistency of the model-based analysis and the EBMetaD method. This result is particularly worth-noting for T4L 62/134, for which, as mentioned, the uncertainty band is very broad for the component at the longest distance.
In summary, atomistic simulations of T4L demonstrate that the combined use of the model-based analysis and EBMetaD is a rigorous, self-consistent methodology to efficiently generate conformational ensembles that optimally represent DEER spectroscopic data.
Discussion
Although the importance of defining experimental uncertainty and estimating errors in derived quantities is well established in science, practitioners of DEER spectroscopy have been slow to adopt methods for estimating the uncertainty in the distance distributions obtained from DEER data (13). Within the context of the model-free TR approach to the analysis of DEER data, Jeschke and co-workers (6) have developed a validation tool for estimating the uncertainty in P(R) due to variation in the background correction and the noise in the data. Edwards and Stoll have developed a Bayesian approach for estimating the uncertainty in P(R) due to the noise in the data and the regularization process (13). Alternatively, DEER data can be analyzed by modeling P(R) as a sum of Gaussian components (9, 10). The advantages of this model-based approach include the ability to analyze the data without the need for a priori background correction; the ability to perform global analysis of multiple data sets (e.g., to model functionally relevant ligand-induced conformational changes (39, 40, 41, 42)); and the ability to perform rigorous statistical analysis of the fit results. The major disadvantages are the need to specify particular basis functions that may deviate from the shape of the true distance distribution, and the need to ensure that space has been fully explored to find the true global minimum.
In this work, we have extended our model-based approach to allow for a direct estimation of a confidence band for P(R) using propagation of errors, i.e., the delta method. By construction, this confidence band includes contributions due to both the noise in the data and the uncertainty in the background factor. The robustness of the methodology has been demonstrated through an extensive Monte Carlo analysis of simulated data. In particular, these results establish how the noise level and the maximal observed dipolar evolution time, tmax, influence the uncertainty in the fit parameters and P(R). From the results in Fig. 5 and Tables S4 and S5, it is evident that precise estimates of the contribution of a given component to P(R) can be obtained as long as one full modulation period can be observed within tmax, i.e., . This equation is similar to one proposed by Jeschke for the minimal tmax required to determine an r0 (mean) value (3). Even under less than optimal conditions, with extremely short tmax, reasonable estimates of P(R) can be obtained (see Fig. 4; Table S2). It should be noted that different analysis methods can influence the reliability of the determined P(R) as much as the information content in the data itself.
In conjunction with our approach for determining confidence bands on distance distributions obtained from fitting DEER data, we have also proposed an atomistic simulation method that imposes a minimal-information bias on an MD trajectory so that the conformational ensemble explored reproduces one or more experimental probability distributions as precisely as dictated by their confidence bands. This technique is an extension of the EBMetaD method (18), reformulated here to include the confidence bands in the target distributions. Although there exist other enhanced-sampling approaches that use probability distributions as input data (17, 18), to our knowledge this is the first report of a methodology that also considers the uncertainties in those distributions.
The proposed methodology was evaluated for T4L in explicit water, simultaneously targeting the distance distributions obtained from three spin-labeled double mutants. It was clearly shown how the EBMetaD ensembles deviate from those obtained from conventional MD simulations precisely so that the calculated probability distributions draw inside the experimental confidence bands. For values of R for which the experimental uncertainty of P(R) is small, the simulation approaches the best-fit distributions as accurately as required by their confidence bands. In poorly defined regions, EBMetaD behaves comparably to an unbiased MD simulation. Needless to say, MD trajectories are inexact on account of the many approximations and simplifications inherent to this technique. Thus, although the EBMetaD method guarantees that the simulated ensemble will reproduce the input experimental data, it does not guarantee that this ensemble is free of error otherwise, or that it represents the only possible solution. It follows that the bias required for an MD simulation to reproduce a given experimental target is not universal but will vary depending on the intrinsic accuracy of the underlying force field (e.g., CHARMM versus AMBER, all-atom versus coarse-grained, etc.) and dedicated simulation time. For any one particular choice, however, EBMetaD will apply the minimal bias required to meet the experimental probability distribution (or uncertainty band), consistent with the maximal-entropy principle. Finally, it is also worth noting that the EBMetaD method is not limited to the interpretation of DEER data. Indeed, this approach may be used for any observable for which a probability distribution can be derived experimentally (or postulated theoretically), as long as it is computable during run-time from the set of atomic coordinates in the molecular system.
The EBMetaD simulation methodology is based on the fundamental concept of maximal entropy. This is to say that the simulation uses the minimal information required to reproduce the target data, and therefore the bias introduced to modify the simulated ensemble is also minimal. This notion becomes clear when the magnitude of the bias applied is transformed into a quasi-equilibrium work value: specifically, the smaller the uncertainty, the greater the amount of work required to reproduce a given experimental distribution. It is worth pointing out that not all structural refinement methods satisfy this intuitive minimal-information principle. Standard procedures to construct structural ensembles from NMR data, for example, impose distance restraints on pairs of atoms that imply specific distributions around the target value (43). In doing so, these computational approaches utilize more information than the experiment actually provides, which is only the ensemble-average value of those distances and not their distribution. We therefore anticipate that variations of this maximal-entropy paradigm, together with high-end molecular simulation methods, will become increasingly used to derive a rigorous interpretation of a variety of spectroscopic data.
From a mechanistic standpoint, a notable feature of EBMetaD is that it permits quantifying the minimal work required to generate a conformational ensemble that is most consistent with a given experimental probability distribution. It is not uncommon that different structures are known for a biomolecule, often presumed to represent distinct and interconverting functional states. Using DEER spectroscopy under different experimental conditions, different components of P(R) can be assigned to these different functional states. EBMetaD simulations provide a means to relate structural and spectroscopic data: the experimental structure that, when simulated, requires the least amount of work to reproduce a given set of DEER data can be assumed to be the best representative of the conditions used to collect that spectroscopic signal. It should be noted, though, that the distance between two or more spin labels might not be an appropriate reaction coordinate to drive the reversible exploration of large-scale or intricate conformational changes. In such cases, the EBMetaD approach ought to be combined with other strategies devised to enhance the sampling of those conformational changes. Multiple-walker algorithms such as bias-exchange metadynamics (44, 45) would be a natural choice to integrate EBMetaD with other biasing schemes, but other options are also possible.
Although there are compelling reasons to interpret the P(R) obtained in terms of components corresponding to distinct functionally relevant structures, there are a number of factors that can give rise to artifactual components in the P(R) that do not, in fact, correspond to distinct structural states. These factors include imperfect background correction and orientation-selection effects. The TR approach biases the P(R) obtained to have an equal degree of smoothness across all R. Thus, in situations in which the true P(R) may contain a mix of narrow and broad components, TR will split a single broad component into a sum of multiple narrow components (see Fig. S5 D). As a result, an approach that first fits the time-domain data using TR and then fits the P(R) obtained to a sum of Gaussians can overestimate the number of components.
Instead, our approach directly fits the time-domain data using a sum of components of varying width and uses BIC values to select the optimal number of components based on the principal of parsimony. To lend credence to the structural and functional relevance of these components, a global analysis of multiple DEER signals may reveal how the amplitudes of these components change with conditions that can be manipulated experimentally. Otherwise, care must be taken when assigning structural and biological relevance to terms in the mathematical equation used to model P(R). When using a model-based approach, particularly for high signal/noise data, additional terms may be required for an optimal fit to account for deviations from Gaussian shapes. For example, each of the T4L data sets can be fit using one fewer component (see Fig. S6; Table S8) using alternate basis functions (see Supporting Material). Although these non-Gaussian functions yield very similar fits with comparable values, they are favored by BIC by virtue of their lower number of fit parameters. The differences in the distributions obtained using different basis functions or TR that are shown in Fig. S6 highlight the inherent uncertainty in the shape of P(R) regardless of the method used. Ultimately, molecular simulations based on the EBMetaD method can clarify the interpretation of multicomponent distance distributions inferred from DEER experiments in terms of distinct molecular conformations while taking into account rigorously determined uncertainties in the experimental results.
Conclusion
In this study we propose two complementary computational strategies that, taken together, provide a compelling methodology to derive an objective structural interpretation of DEER measurements for a dynamic biomolecular system. Ultimately, both methodologies underscore the importance of a rigorous error estimate for a correct interpretation of the experimental data.
Author Contributions
The research on the analysis of DEER data was designed by H.S.M., R.A.S., and E.J.H. (Figs. 1, 2, 3, 4, 5, and 10) and then developed and implemented by E.J.H. with the assistance of R.A.S.; the research on EBMetaD (Figs. 6, 7, 8, 9, and 10) was designed by F.M. and J.D.F.-G. and developed and implemented by F.M.; E.J.H., F.M., and J.D.F.-G. wrote the manuscript with the assistance of H.S.M. and R.A.S.
Acknowledgments
E.J.H. and R.A.S. thank the Biostatistics Clinics service of the Vanderbilt University Department of Biostatistics for helpful discussion about the delta method.
F.M. and J.D.F.-G. are funded by the Division of Intramural Research of the National Heart, Lung and Blood Institute, National Institutes of Health. H.S.M. received funding from National Institutes of Health GM 077657.
Editor: Elsa Yan.
Footnotes
Eric J. Hustedt and Fabrizio Marinelli contributed equally to this work.
Supporting Materials and Methods, six figures, and eight tables are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(18)30932-9.
Contributor Information
José D. Faraldo-Gómez, Email: jose.faraldo@nih.gov.
Hassane S. Mchaourab, Email: hassane.mchaourab@vanderbilt.edu.
Supporting Material
References
- 1.Borbat P.P., Freed J.H. Pulse dipolar electron spin resonance: distance measurements. In: Timmel C.R., Harmer J.R., editors. Structural Information from Spin-Labels and Intrinsic Paramagnetic Centres in the Biosciences. Springer; 2014. pp. 1–82. [Google Scholar]
- 2.Jeschke G. DEER distance measurements on proteins. Annu. Rev. Phys. Chem. 2012;63:419–446. doi: 10.1146/annurev-physchem-032511-143716. [DOI] [PubMed] [Google Scholar]
- 3.Jeschke G. Interpretation of dipolar EPR data in terms of protein structure. In: Timmel C.R., Harmer J.R., editors. Structural Information from Spin-Labels and Intrinsic Paramagnetic Centres in the Biosciences. Springer; 2014. pp. 83–120. [Google Scholar]
- 4.McHaourab H.S., Steed P.R., Kazmier K. Toward the fourth dimension of membrane protein structure: insight into dynamics from spin-labeling EPR spectroscopy. Structure. 2011;19:1549–1561. doi: 10.1016/j.str.2011.10.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Bowman M.K., Maryasov A.G., DeRose V.J. Visualization of distance distribution from pulsed double electron-electron resonance data. Appl. Magn. Reson. 2004;26:23–39. [Google Scholar]
- 6.Jeschke G., Chechik V., Jung H. DeerAnalysis2006 - a comprehensive software package for analyzing pulsed ELDOR data. Appl. Magn. Reson. 2006;30:473–498. [Google Scholar]
- 7.Chiang Y.W., Borbat P.P., Freed J.H. The determination of pair distance distributions by pulsed ESR using Tikhonov regularization. J. Magn. Reson. 2005;172:279–295. doi: 10.1016/j.jmr.2004.10.012. [DOI] [PubMed] [Google Scholar]
- 8.Jeschke G., Panek G., Paulsen H. Data analysis procedures for pulse ELDOR measurements of broad distance distributions. Appl. Magn. Reson. 2004;26:223–244. [Google Scholar]
- 9.Brandon S., Beth A.H., Hustedt E.J. The global analysis of DEER data. J. Magn. Reson. 2012;218:93–104. doi: 10.1016/j.jmr.2012.03.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Stein R.A., Beth A.H., Hustedt E.J. A straightforward approach to the analysis of double electron-electron resonance data. Methods Enzymol. 2015;563:531–567. doi: 10.1016/bs.mie.2015.07.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Fajer P., Brown L., Song L. Practical pulsed dipolar ESR (DEER) In: Hemminga M.A., Berliner L.J., editors. ESR Spectroscopy in Membrane Biophysics. Springer; 2007. pp. 95–128. [Google Scholar]
- 12.Pannier M., Schädler V., Spiess H.W. Determination of ion cluster sizes and cluster-to-cluster distances in ionomers by four-pulse double electron electron resonance spectroscopy. Macromolecules. 2000;33:7812–7818. [Google Scholar]
- 13.Edwards T.H., Stoll S. A Bayesian approach to quantifying uncertainty from experimental noise in DEER spectroscopy. J. Magn. Reson. 2016;270:87–97. doi: 10.1016/j.jmr.2016.06.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Tellinghuisen J. Statistical error propagation. J. Phys. Chem. A. 2001;105:3917–3921. [Google Scholar]
- 15.Ver Hoef J.M. Who invented the delta method? Am. Stat. 2012;66:124–127. [Google Scholar]
- 16.Casella G., Berger R.L. Duxbury Press; Pacific Grove, CA: 2002. Statistical Inference. [Google Scholar]
- 17.Roux B., Islam S.M. Restrained-ensemble molecular dynamics simulations based on distance histograms from double electron-electron resonance spectroscopy. J. Phys. Chem. B. 2013;117:4733–4739. doi: 10.1021/jp3110369. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Marinelli F., Faraldo-Gómez J.D. Ensemble-biased metadynamics: a molecular simulation method to sample experimental distributions. Biophys. J. 2015;108:2779–2782. doi: 10.1016/j.bpj.2015.05.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Polyhach Y., Bordignon E., Jeschke G. Rotamer libraries of spin labelled cysteines for protein studies. Phys. Chem. Chem. Phys. 2011;13:2356–2366. doi: 10.1039/c0cp01865a. [DOI] [PubMed] [Google Scholar]
- 20.Fajer P., Fajer M., Yang W. Simulation of spin label structure and its implication in molecular characterization. Methods Enzymol. 2015;563:623–642. doi: 10.1016/bs.mie.2015.07.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Kazmier K., Alexander N.S., McHaourab H.S. Algorithm for selection of optimized EPR distance restraints for de novo protein structure determination. J. Struct. Biol. 2011;173:549–557. doi: 10.1016/j.jsb.2010.11.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Islam S.M., Stein R.A., Roux B. Structural refinement from restrained-ensemble simulations based on EPR/DEER data: application to T4 lysozyme. J. Phys. Chem. B. 2013;117:4740–4754. doi: 10.1021/jp311723a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Milov A.D., Maryasov A.G., Tsvetkov Y.D. Pulsed electron double resonance (PELDOR) and its applications in free-radicals research. Appl. Magn. Reson. 1998;15:107–143. [Google Scholar]
- 24.Burnham K.P., Anderson D.R. Springer-Verlag; New York: 2002. Model Selection and Multimodel Inference: A Practical Information-Theoretic Approach. [Google Scholar]
- 25.Edwards T.H., Stoll S. Optimal Tikhonov regularization for DEER spectroscopy. J. Magn. Reson. 2018;288:58–68. doi: 10.1016/j.jmr.2018.01.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Bevington P.R., Robinson D.K. McGraw-Hill; New York: 1992. Data Reduction and Error Analysis for the Physical Sciences. [Google Scholar]
- 27.Press W.H., Teukolsky S.A., Flannery B.P. Cambridge University Press; New York: 1993. Numerical Recipes in FORTRAN; The Art of Scientific Computing. [Google Scholar]
- 28.Phillips J.C., Braun R., Schulten K. Scalable molecular dynamics with NAMD. J. Comput. Chem. 2005;26:1781–1802. doi: 10.1002/jcc.20289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.MacKerell A.D., Bashford D., Karplus M. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J. Phys. Chem. B. 1998;102:3586–3616. doi: 10.1021/jp973084f. [DOI] [PubMed] [Google Scholar]
- 30.Mackerell A.D., Jr., Feig M., Brooks C.L., III Extending the treatment of backbone energetics in protein force fields: limitations of gas-phase quantum mechanics in reproducing protein conformational distributions in molecular dynamics simulations. J. Comput. Chem. 2004;25:1400–1415. doi: 10.1002/jcc.20065. [DOI] [PubMed] [Google Scholar]
- 31.Sezer D., Freed J.H., Roux B. Parametrization, molecular dynamics simulation, and calculation of electron spin resonance spectra of a nitroxide spin label on a polyalanine alpha-helix. J. Phys. Chem. B. 2008;112:5755–5767. doi: 10.1021/jp711375x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Roux B., Weare J. On the statistical equivalence of restrained-ensemble simulations with the maximum entropy method. J. Chem. Phys. 2013;138:084107. doi: 10.1063/1.4792208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Cesari A., Gil-Ley A., Bussi G. Combining simulations and solution experiments as a paradigm for RNA force field refinement. J. Chem. Theory Comput. 2016;12:6192–6200. doi: 10.1021/acs.jctc.6b00944. [DOI] [PubMed] [Google Scholar]
- 34.Hummer G., Köfinger J. Bayesian ensemble refinement by replica simulations and reweighting. J. Chem. Phys. 2015;143:243150. doi: 10.1063/1.4937786. [DOI] [PubMed] [Google Scholar]
- 35.Wang W., Carreira-Perpiñán M.A. Projection onto the probability simplex: an efficient algorithm with a simple proof, and an application. 2013. https://arxiv.org/abs/1309.1541 arXiv, arXiv:1309.1541.
- 36.Plimpton S. Fast parallel algorithms for short-range molecular-dynamics. J. Comput. Phys. 1995;117:1–19. [Google Scholar]
- 37.Fiorin G., Klein M.L., Hénin J. Using collective variables to drive molecular dynamics simulations. Mol. Phys. 2013;111:3345–3362. [Google Scholar]
- 38.Crespo Y., Marinelli F., Laio A. Metadynamics convergence law in a multidimensional system. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2010;81:055701. doi: 10.1103/PhysRevE.81.055701. [DOI] [PubMed] [Google Scholar]
- 39.Collauto A., DeBerg H.A., Goldfarb D. Rates and equilibrium constants of the ligand-induced conformational transition of an HCN ion channel protein domain determined by DEER spectroscopy. Phys. Chem. Chem. Phys. 2017;19:15324–15334. doi: 10.1039/c7cp01925d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Kazmier K., Sharma S., McHaourab H.S. Conformational dynamics of ligand-dependent alternating access in LeuT. Nat. Struct. Mol. Biol. 2014;21:472–479. doi: 10.1038/nsmb.2816. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Martens C., Stein R.A., Mchaourab H.S. Lipids modulate the conformational dynamics of a secondary multidrug transporter. Nat. Struct. Mol. Biol. 2016;23:744–751. doi: 10.1038/nsmb.3262. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Mishra S., Verhalen B., Mchaourab H.S. Conformational dynamics of the nucleotide binding domains and the power stroke of a heterodimeric ABC transporter. eLife. 2014;3:e02740. doi: 10.7554/eLife.02740. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Schwieters C.D., Kuszewski J.J., Clore G.M. Using Xplor-NIH for NMR molecular structure determination. Prog. Nucl. Mag. Res. Sp. 2006;48:47–62. doi: 10.1016/s1090-7807(02)00014-9. [DOI] [PubMed] [Google Scholar]
- 44.Marinelli F., Kuhlmann S.I., Faraldo-Gómez J.D. Evidence for an allosteric mechanism of substrate release from membrane-transporter accessory binding proteins. Proc. Natl. Acad. Sci. USA. 2011;108:E1285–E1292. doi: 10.1073/pnas.1112534108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Liao J., Marinelli F., Jiang Y. Mechanism of extracellular ion exchange and binding-site occlusion in a sodium/calcium exchanger. Nat. Struct. Mol. Biol. 2016;23:590–599. doi: 10.1038/nsmb.3230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Weaver L.H., Matthews B.W. Structure of bacteriophage T4 lysozyme refined at 1.7 A resolution. J. Mol. Biol. 1987;193:189–199. doi: 10.1016/0022-2836(87)90636-x. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.