Skip to main content
PMC home page
Royal Society Open Science logoLink to Royal Society Open Science
. 2018 Sep 19;5(9):181168. doi: 10.1098/rsos.181168

Spatial scale changes the relationship between beta diversity, species richness and latitude

Rachakonda Sreekar 1,✉, Masatoshi Katabuchi 2, Akihiro Nakamura 3, Richard T Corlett 4, J W Ferry Slik 5, Christine Fletcher 6, Fangliang He 7, George D Weiblen 8, Guochun Shen 9, Han Xu 10, I-Fang Sun 11, Ke Cao 12, Keping Ma 12, Li-Wan Chang 13, Min Cao 3, Mingxi Jiang 14, I A U Nimal Gunatilleke 15, Perry Ong 16, Sandra Yap 17, C V Savitri Gunatilleke 15, Vojtech Novotny 18,19, Warren Y Brockelman 20, Wusheng Xiang 21, Xiangcheng Mi 12, Xiankun Li 21, Xihua Wang 22, Xiujuan Qiao 14, Yide Li 10, Sylvester Tan 23, Richard Condit 24, Rhett D Harrison 25, Lian Pin Koh 1
PMCID: PMC6170539  PMID: 30839691

Abstract

The relationship between β-diversity and latitude still remains to be a core question in ecology because of the lack of consensus between studies. One hypothesis for the lack of consensus between studies is that spatial scale changes the relationship between latitude and β-diversity. Here, we test this hypothesis using tree data from 15 large-scale forest plots (greater than or equal to 15 ha, diameter at breast height ≥ 1 cm) across a latitudinal gradient (3–30o) in the Asia-Pacific region. We found that the observed β-diversity decreased with increasing latitude when sampling local tree communities at small spatial scale (grain size ≤0.1 ha), but the observed β-diversity did not change with latitude when sampling at large spatial scales (greater than or equal to 0.25 ha). Differences in latitudinal β-diversity gradients across spatial scales were caused by pooled species richness (γ-diversity), which influenced observed β-diversity values at small spatial scales, but not at large spatial scales. Therefore, spatial scale changes the relationship between β-diversity, γ-diversity and latitude, and improving sample representativeness avoids the γ-dependence of β-diversity.

Keywords: β-deviation, ForestGEO, null model, pairwise dissimilarity, tree diversity

1. Introduction

Decreasing species richness from the equator to the poles is one of the best-recognized patterns in ecology [1,2]. This latitudinal pattern in species richness is consistent across different spatial scales, habitats and taxonomic groups [3]. However, latitudinal differences in species co-occurrence still remain a core question in ecology because of the lack of consensus on the patterns of site-to-site variability in species composition (β-diversity) across latitudinal gradients [4–7]. Difficulties in disentangling the variation caused by pooled species richness (γ-diversity) and site-to-site variation in species composition (β-diversity), as well as in the estimation of β-diversity itself, pose challenges to understanding the latitudinal β-diversity patterns.

Null-model approaches have been proposed to account for variation caused by γ-diversity, by calculating the rate of deviation of observed β-diversity from a null-model generated stochastic expectation (hereafter β-deviation), and have been widely used in studies on β-diversity [4,6,8–10]. Although recent studies have criticized the use of null models (see discussion) [7,11,12], they still provide heuristic values that may help understand how non-random (biological) processes structure local communities. A β-deviation of zero indicates that the observed β-diversity is similar to random sampling, while positive β-deviation values reflect species aggregation [6,8]. As the degree of species aggregation is known to increase with grain size [13], we should expect spatial scale effects on β-deviation as well [10,11].

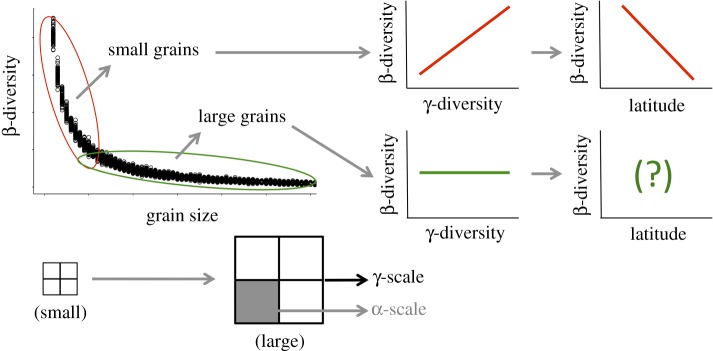
The majority of previous studies that examined latitudinal tree β-diversity patterns used small grain sizes to measure α-diversity (less than or equal to 0.1 ha) [5–7,14]. However, studies have demonstrated that β-diversity metrics may risk false conclusions when data are collected using such small grains [15,16], primarily because biodiversity patterns measured at small grains are weaker and more variable [17,18]. Observations show that β-diversity decreases exponentially with increasing spatial scale [19] and can be divided into two segments (figure 1): the first segment where the grain sizes are small and its influence on β-diversity is high, and the second segment where grain sizes are comparatively large and its influence on β-diversity is low (figure 1). Steeper slopes in the first segment can be caused by sampling at small grains that result in artificially lower local (α) diversity and higher γ:α ratios (β-diversity; statistical Type I errors). A lower influence of α-diversity results in the correlation between β- and γ-diversity [20]. This potentially prevents accurate estimation of β-diversity, especially when γ-diversity varies with environmental gradients such as elevation and latitude [6,21]. Previous studies have shown that the influence of γ-diversity on β-diversity decreases with increasing grain size [6,22] and changes β-diversity patterns across broad-scale ecological gradients [22]. The largest grain size in the previous studies was 0.1 ha [22].

Figure 1.

Figure 1.

Open in a new tab

Illustration of the relationship between observed β-diversity and spatial scale (grain size) showing a bi-phasic curve: (1) large variation at small spatial scales, and (2) small variation at large spatial scales. Decreasing γ-diversity with increasing latitude is well known [3], and if β-diversity is correlated with γ-diversity at small spatial scales, we should also expect β-diversity to decline with increasing latitude. However, reliance of β-diversity on γ-diversity is mathematically invalid as long as α-diversity is large and allowed to vary freely with γ-diversity [15]. Therefore, at large spatial scales, we should expect β-diversity not to be reliant on γ-diversity, and the latitudinal β-diversity patterns in such scenarios remain unknown.

In this study, we compare the relationship between β-diversity, γ-diversity and latitude at multiple spatial scales. First, we use tree census data from two 50 ha plots to determine: (i) the sensitivity of β-diversity to grain size and (ii) if the null-model generated β-deviation is also sensitive to grain size. Second, we use tree census data from 15 plots (greater than or equal to 15 ha) along a latitudinal gradient in the Asia-Pacific region to assess: (iii) if the relationship between β-diversity and latitude changes with increasing grain size and (iv) if the relationship between the null model generated β-deviation and latitude remains similar at all grain sizes.

2. Methods

2.1. Sensitivity of β-diversity

We compared the effects of grain size on classical multiplicative β-diversity and null-model generated β-deviation using woody-plant data from a 52 ha (1040 m × 500 m) forest plot in Lambir Hills National Park, Sarawak, Malaysia (40°186′ N, 114°017′ E; elevation: 104–244 m) and a 50 ha forest plot on Barro Colorado Island (BCI), Panama (9°154′ N, 79°846′ W; elevation: 120–160 m). All stems with a diameter at breast height (DBH) of 1 cm or greater were identified to species and precisely mapped across the entire area. The Lambir and BCI plots contain more than 350 000 and 200 000 mapped trees (greater than or equal to 1 cm DBH) belonging to ca 1200 and ca 300 species, respectively [23–27]. All stems that are greater than or equal to 1 cm were identified to species and precisely mapped across the entire area. Nothing is omitted and nearly all individuals are assigned to distinct taxa. The Lambir and BCI plots have been censused approximately every five years since 1991 and 1981, respectively. Our analysis of Lambir and BCI plots is based on the 2007–08 census and 2010 census, respectively. The 52 ha (1040 m × 500 m) Lambir plot was trimmed to 50 ha (1000 m × 500 m) to evenly fit multiple non-overlapping grains ranging from 10 m × 10 m to 150 m × 150 m.

A grain is a sample at the local scale (α) and an extent (γ) is a set of multiple grains. In this study, each extent had a set of nine grains of varying sizes (10 m × 10 m to 150 m × 150 m), all contained within one of the two 50 ha plots (Lambir and BCI). We chose the first sampling grain randomly and the remaining eight were chosen alongside this in a 3 × 3 matrix design. We then repeated the sampling 25 times for each grain size. We measured α-diversity as the mean species richness of each grain and γ-diversity as the species richness of an extent.

We calculated three classical measures of β-diversity (multiplicative β-diversity, proportional β-diversity and z-value of the species–area relationship) and three multivariate distance measures of β-diversity (mean pairwise Sørensen distance, multiple-site Sørensen distance, Hellinger's distance). We calculated:

  • (i) Classical multiplicative β-diversity as γ/α.

  • (ii) Classical proportional β-diversity as 1 − (α/γ).

  • (iii) z-value [28] of the species–area relationship as log(γ) − log(α)/log(grain number).

  • (iv) Mean pairwise Sørensen distance using ‘beta.pair’ function in betapart package in R (http://www.r-project.org/).

  • (v) Multiple-site Sørensen distance using ‘beta.multi’ function in betapart package in R.

  • (vi) Hellinger's distance using ‘beta.div’ function in adespatial package in R.

In this paper, we only present the results of classical multiplicative β-diversity because all metrics were highly correlated with each other (Pearson r > 0.95).

To determine if β-diversity deviated from the null expectations of random sampling (standardized β-deviation, which we refer to as β-deviation), we compared β-diversity of observed and randomized datasets [4,6]. Specifically, we generated randomized datasets by randomizing trees (greater than or equal to 1 cm DBH) across all nine grains, while retaining the relative species abundance across the extent and the total number of individuals in each grain. This accounts for variation in γ-diversity [4,6]. We generated 1000 randomized datasets for each sampling design. We calculated β-deviation = (βobs − βrand)/s.d.rand, where βobs is the observed β-diversity, and βrand and s.d.rand are the mean and s.d., respectively, of the expected β-diversity. Under the null hypothesis of equal values for the observed and expected β-diversity, the distribution of β-deviation is approximately standard normal [29], which we assumed when calculating p-values (i.e. 95% of β-deviation values are expected to fall in the range of −1.96 to 1.96) [6].

2.2. Latitudinal β-diversity patterns

We used tree data from 15 long-term, large-scale forest dynamics plots along a latitudinal gradient from Papua New Guinea to northern China. The Center for Tropical Forest Science/Smithsonian Institution Global Earth Observatories (CTFS/SIGEO; http://www.sigeo.si.edu/) and the Chinese Forest Biodiversity Network (CForBio; http://cfbiodiv.org/) coordinated data collections in all plots: Badagongshan, Fushan, Gutianshan, Hainan, Heishiding, Lambir, Lienhuachih, Mo Singto, Nonggang, Palanan, Pasoh, Sinharaja, Tiantongshan, Wanang, Xishuangbanna (electronic supplementary material, figure S1) [30,31]. Each of the 15 plots covers 15–52 ha of forest in which all stems with DBH of 1 cm or greater were identified and precisely mapped across the entire area.

For analyses of latitudinal β-diversity patterns, we use 20 grains of varying sizes: 10 m × 10 m (0.01 ha), 20 m × 20 m (0.04 ha), 30 m × 30 m (0.09 ha), 50 m × 50 m (0.25 ha), 70 m × 70 m (0.49 ha) and 100 m × 100 m (1 ha). We used a nested design, where we chose the first grain randomly and the remaining 19 next to each other in a 4 × 5 matrix design. We did not fit 100 m × 100 m grains into Palanan and Nonggang plots due to their small size (less than 20 ha). Extent size represents the combination of 20 grains, and therefore the extent size (γ-scale) varies with grain size (α-scale). We measured α-diversity as the mean species richness of each grain and γ-diversity as the species richness of an extent (electronic supplementary material, figure S2 and figure S3). We used the two most widely used measures of β-diversity, classical multiplicative β-diversity (β = γ/α) [32] and mean pairwise Sørensen dissimilarity distance, as measures of β-diversity [33]. These two metrics were highly correlated with proportional beta, z-value, multiple-site Sørensen and Hellinger's distance (Pearson r > 0.89; electronic supplementary material, figure S4).

The multiple-site Sørensen distance can be partitioned into nestedness and turnover components [34]. Nestedness represents the result of the variation in species richness, and turnover represents the result of the variation caused by species replacement [34,35]. Thus, turnover could be used as a true measure of species replacement. In this study, turnover caused ca 94% (range: 85–98%) of the variation and was highly correlated with multiple-site Sørensen distance at all spatial scales (Pearson r > 0.93). Therefore, we did not partition multiple-site Sørensen distance.

We used a randomized null-model approach to measure the deviation of observed β-diversity from the null expectations of random sampling (β-deviation; see above for details). We also calculated the rate of deviation of observed mean pairwise Sørensen from a null-model generated stochastic expectation (hereafter pairwise Sørensen deviation). We extracted mean monthly temperature and mean annual precipitation data for each plot from the WORLDCLIM database v. 1.4 [36].

3. Data analysis

Tree β-diversity often shows a nonlinear bi-phasic curve with spatial scale, with a faster change in β-diversity values at small spatial scales and slower change at comparatively larger spatial scales (figure 1) [19]. We therefore fitted a regression model with segmented relationships between β-diversity and spatial scale to estimate a threshold between small and large spatial scale (figure 1). Segmented regression is a method where two regression lines are fitted onto an independent variable (grain size in our analysis), which are joined together at a break point [37]. It can be used to detect changes in model fits and can be important in decision-making.

We used general linear models with normal error structure to determine the change in β-diversity and β-deviation of different grain sizes with γ-diversity and latitude. We did not include a temperature in the models as it was highly correlated with latitude (Pearson r = 0.9, p < 0.001), but precipitation was included as a covariate. We used a backward elimination technique to simplify the models. We loge transformed γ-diversity prior to analysis and used absolute values of latitude. We removed the Lambir site from the models determining the change in β-deviation with varying γ-diversity and latitude because of high heteroscedasticity. Lambir had β-deviation (spatial aggregation) values up to two times higher than any other site, which may be caused by the presence of distinct soil types and strong habitat associations within this particular plot [38,39]. All analyses were conducted in the statistical program R (R Core Team, v. 3.3.1). The data are available in electronic supplementary material, appendix S1 and on request from ForestGEO (http://forestgeo.si.edu) and CForBio (http://cfbiodiv.org).

4. Results

4.1. Sensitivity of β-diversity

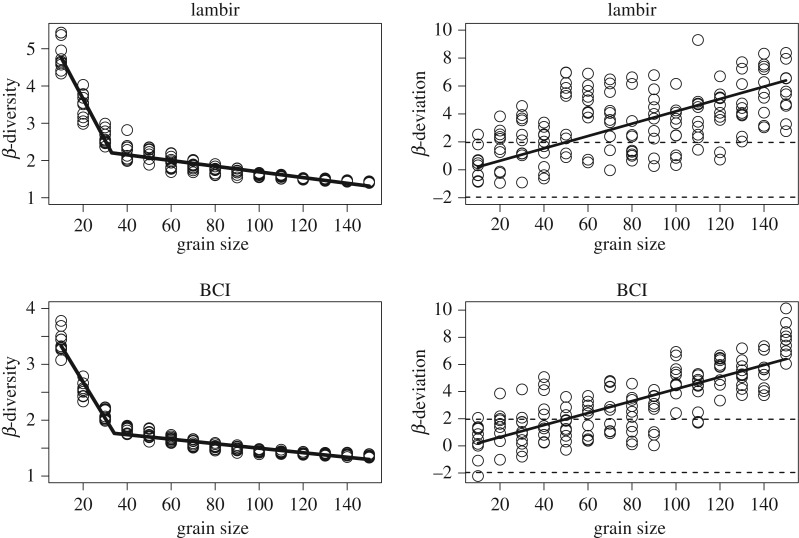
Grain size significantly influenced classical multiplicative β-diversity at both tropical forest sites with a sharp decrease in values at very small grains (Lambir: R2 = 0.94, p < 0.001; BCI: R2 = 0.97, p < 0.001; figure 2). The slope of the first segment (10 m × 10 m to 35 m × 35 m; Lambir: −0.110 ± 0.005 [s.e.]; BCI: −0.066 ± 0.003) was ca 16 times higher than that of the second (Lambir: −0.007 ± 0.0006; BCI: −0.004 ± 0.0003) at both sites (figure 2). Grain size had a very strong relationship with both the number of individuals sampled and γ-diversity (R2 > 0.95). For both Lambir and BCI sites, β-deviation did not differ from stochastic expectation at small grain sizes (β-deviation| < 1.96), but increased with grain size (Lambir: R2 = 0.28, p < 0.001; BCI: R2 = 0.63, p < 0.001; figure 2).

Figure 2.

Figure 2.

Open in a new tab

Variation in classical multiplicative β-diversity and β-deviation with increasing grain size in Lambir, Malaysia and BCI, Panama. β-deviation of zero indicates that the observed pattern does not differ from random sampling. The dashed lines in β-deviation plots represent the criterion (±1.96 s.d.) for assessing the statistical significance. The x-axis represents grain size at α-scale (e.g. 50 = 50 m × 50 m).

4.2. Latitudinal β-diversity patterns

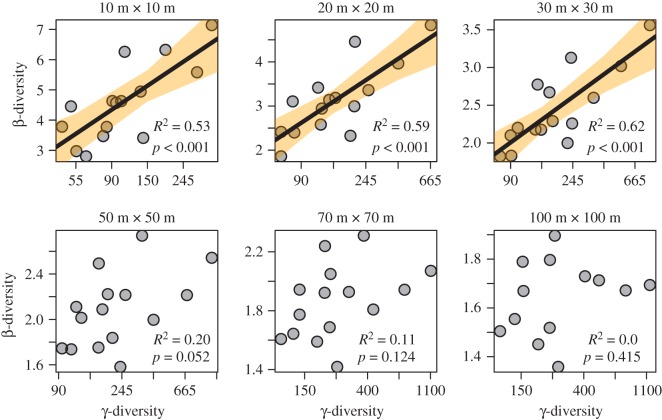
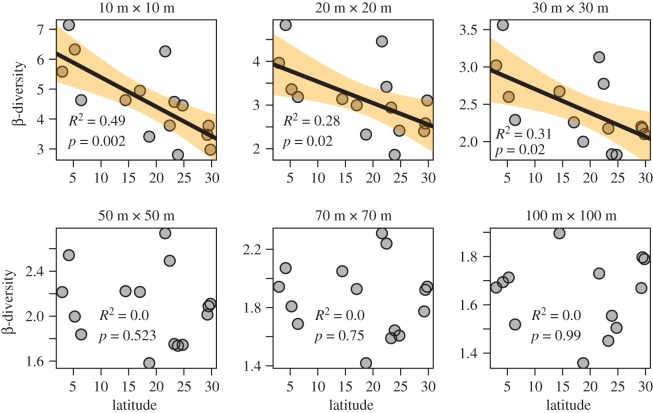
Changes in precipitation did not affect either of the β-diversity metrics (classical multiplicative and mean pairwise Sørensen) at any grain size (electronic supplementary material, table S1), and precipitation was therefore eliminated from all models. Both the β-diversity metrics increased significantly with γ-diversity at small grains (10 m × 10 m to 30 m × 30 m), but showed no relationship with γ-diversity at larger grains (50 m × 50 m to 100 m × 100 m; figure 3; electronic supplementary material, figure S5). Latitudinal β-diversity patterns were similar. Both the measured β-diversity indices decreased significantly with increasing latitude while sampling at small grains (10 m × 10 m to 30 m × 30 m), but showed no relationship with latitude at relatively larger grains (50 m × 50 m to 100 m × 100 m; figure 4; electronic supplementary material, figure S5). The γ-diversity was highly correlated with α-diversity at all grain sizes (R2 > 0.84, p < 0.01), and the number of individuals in each grain did not change with latitude (R2 = 0.001; p = 0.85).

Figure 3.

Figure 3.

Open in a new tab

Classical multiplicative β-diversity increased with γ-diversity when sampling at small grains (10 m × 10 m to 30 m × 30 m) within each ForestGEO plot, but showed no relationship with γ-diversity at larger grains (50 m × 50 m to 100 m × 100 m).

Figure 4.

Figure 4.

Open in a new tab

Classical multiplicative β-diversity decreased with increasing latitude when sampling at small grains (10 m × 10 m to 30 m × 30 m) within each ForestGEO plot, but showed no relationship with latitude at larger grains (50 m × 50 m to 100 m × 100 m).

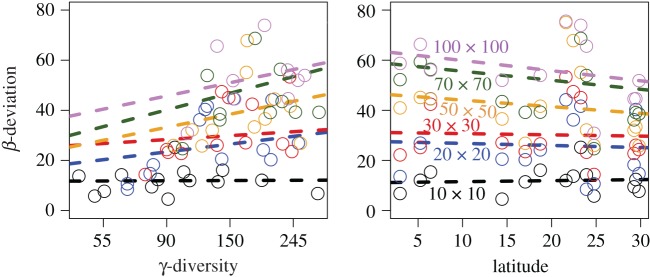
Changes in precipitation did not affect either β-deviation or Sørensen deviation at any grain size, and so precipitation was eliminated from all models (electronic supplementary material, table S2). Standardized β-deviation did not vary with either γ-diversity or latitude at all grain sizes (figure 5; electronic supplementary material, table S3). The pairwise Sørensen deviation was similar to β-deviation. The values of pairwise Sørensen deviation also did not vary with either γ-diversity or latitude at all grain sizes (electronic supplementary material, figure S6).

Figure 5.

Figure 5.

Open in a new tab

Standardized β-deviation did not vary significantly with γ-diversity and latitude at any grain size. However, β-deviation values increased significantly with grain size, indicating stronger intraspecific aggregation at larger spatial scales. Dashed lines indicate non-significant relationships.

5. Discussion

Our results demonstrate that spatial scale (grain size) changes the relationship between β-diversity and latitude. We found that β-diversity was highly dependent on γ-diversity at small grains, but not at large grains (figure 3; electronic supplementary material, figure S4). Our study therefore confirms that the use of large grains still remains to be the best-known method for measuring γ-independent β-diversity [15,40,41], unless questions specific to β-diversity at smaller spatial scales are being addressed. Their correlation is problematic because variation in γ-diversity alone can account for gradients in β-diversity [6]. At relatively large grains (greater than or equal to 0.25 ha), where β-diversity is not influenced by γ-diversity, β-diversity remained similar across the latitudinal gradient (figure 4; electronic supplementary material, figure S4).

It should be noted that the grain size is relative and will vary with sampling method and taxon. Our study sampled all trees ≥ 1 cm DBH, but when sampling trees ≥ 10 cm DBH even a grain size of 100 m × 100 m can be considered small [42]. Sampling using small grains could explain the correlation between β- and γ-diversity. For example, let us assume a homogeneous community with 100 species and a β-diversity (β = γ/α) of one, i.e. α-diversity is equal to γ-diversity. But, if only 40 individuals are sampled at α-scale, the probability of β-diversity being one is zero, simply caused by constraining α-diversity that makes β-diversity dependent on γ-diversity [15]. Therefore, β-diversity at small grains is higher at the equator because of sampling inadequacy, which makes it dependent on γ-diversity [6,15,20].

Methods to account for γ-dependence of β-diversity have received strong scientific attention and stirred discussions [6,7,10–12]. Previous studies used null-model generated β-deviation to account for γ-dependent effects [4,6,10]. But recent studies have challenged the use of β-deviation for comparing between habitat types [11,12], as studies that used β-deviation have resulted in contrasting conclusions within and across studies [4,6,7]. Recently, Ulrich et al. [12] have shown that the use of null models can result in high artificial rejection rates of focal patterns (Type II statistical errors). Our case study, along with several previous studies, suggests that the use of large grains is the best available method to avoid γ-dependence of β-diversity [15,40,41].

Our data were limited to forests in the tropics and subtropics and we did not have data from permanent plots in the temperate region (greater than 30° latitude). Recently, Castro-Insua et al. [43] investigated if there were any latitudinal thresholds in β-diversity, and showed that different β-diversity patterns exist on either side of a threshold at ca 30° latitude. Although we found no relationship between β-diversity and latitude, this relationship might change in the temperate region. Our plots also have a broader longitudinal spread that is not ideal in a study of latitudinal effects, and 7 of 15 plots are on islands. Future studies should examine latitudinal β-diversity patterns using large spatial scales in a different region that includes temperate plots. Studies using more sites, across American and African latitudinal gradients, and using multiple growth forms and larger distances between grains, will be useful to determine spatial scale effects on β-diversity patterns and differences in the mechanisms that drive community assembly.

6. Conclusion

Our results suggest that sampling at large sampling grains can remove the influences of γ-diversity on β-diversity. Specifically, we show that observed β-diversity does not change with increasing latitude (3–30° latitude; figure 3). Therefore, our results support the idea that β-diversity in the tropics is similar to β-diversity in the subtropics. These results have important implications for community ecology and demonstrate that the general β-diversity patterns and the processes structuring communities are still open for discussion.

Supplementary Material

Supplementary material
rsos181168supp1.docx (1.6MB, docx)

Supplementary Material

Supplementary material
rsos181168supp2.csv (8KB, csv)

Acknowledgements

Adelaide Scholarship International and Australian Research Council supported R.S. and L.P.K., respectively. We thank Robert Colwell, Stuart Davies, Akira Itoh, David Burslem, Paulo A. V. Borges and three anonymous reviewers for helpful suggestions. We thank the many people who contributed to the long-term ecological plots in Asia-Pacific. The Lambir 52-ha Long-Term Ecological Research Project is a collaborative project of the Forest Department of Sarawak, Malaysia, the Center for Tropical Forest Science of the Smithsonian Tropical Research Institute, the Arnold Arboretum of Harvard University, USA and Kyoto Universities, Japan. The Barro Colorado Island (BCI) forest dynamics research project was founded by S.P. Hubbell and R.B. Foster and is now managed by R. Condit, S. Lao, and R. Perez under the Center for Tropical Forest Science and the Smithsonian Tropical Research in Panama. We acknowledge the Sarawak Forest Department for supporting and maintaining the project in Lambir Hills National Park. We thank Shameema Esufali for helping with the Sinharaja plot data. The PIs of Sinharaja plot (I.A.U.N.G and C.V.S.G) gratefully acknowledge the Forest Department and the Post-Graduate Institute of Science at the University of Peradeniya, Sri Lanka for supporting this project, and the local field and laboratory staff who tirelessly contributed in the repeated censuses of this plot. The 50-ha Wanang Forest Dynamics Plot is a collaborative project of the New Guinea Binatang Research Center, the Center for Tropical Forest Science of the Smithsonian Tropical Research Institute, the Forest Research Institute of Papua New Guinea, the Czech Academy of Sciences and the University of Minnesota. We acknowledge the government of Papua New Guinea and the customary landowners of Wanang for supporting and maintaining the plot. The Mo-Singto plot was supported by the Thai National Park, Wildlife and Plant Conservation Department, Thai Ministry of Natural Resources and Environment, National Center for Genetic Engineering and Biotechnology (Thailand) and National Science and Technology Development Agency (Thailand). The Lienhuachih plot was supported by the Taiwan Forestry Research Institute, Taiwan Forestry Bureau, Taiwan Academy of Ecology, Tunghai University (Taiwan), and the Center for Tropical Forest Science of the Smithsonian Tropical Research Institute. The Fushan plot was supported by the Taiwan Forestry Bureau, Taiwan Forestry Research Institute, Tunghai University (Taiwan), Institute of Ecology and Evolutionary Biology, National Taiwan University, and the Center for Tropical Forest Science of the Smithsonian Tropical Research Institute (USA).

Ethics

Field efforts in Fushan and Lienhuachih were supported by the Taiwan Forest Bureau and Taiwan Forest Research Institute. Field efforts in Mo Singto were supported by the Thai National Park, Wildlife and Plant Conservation Department. Field efforts in Sri Lanka were supported by the Sri Lanka Forest Department. Field efforts in Wanang were supported by the government of Papua New Guinea and the customary landowners of Wanang. Field efforts in Lambir were supported by the Forest Department of Sarawak, Malaysia.

Data accessibility

Data are available from the electronic supplementary material, appendix S1, and available via CTFS-ForestGEO website at http://www.forestgeo.si.edu and CForBio website at http://cfbiodiv.org.

Authors' contributions

R.S., M.K., A.N., R.T.C., J.W.F.S., R.H.D. and L.P.K. designed the study; C.F., F.H., G.D.W., G.S., H.X., I.-F.S., K.C., K.M., L.-W.C., M.C., M.J., I.A.U.N.G., P.O., R.C., S.Y., S.T., C.V.S.G., V.N., W.Y.B., W.X., X.M., X.L., X.W., X.Q. and Y.L. acquired tree data; R.S. and M.K. analysed the data; R.S. drafted the article. All authors gave final approval for publication.

Competing interests

The authors have no competing interests.

Funding

Financial support for the Tiantongshan plot came from the National Natural Science Foundation of China (31470487 to G.S., 31210103920 to X.W.). Financial support for the Nonggang plot came from the National Natural Science Foundation of China (31660130 and 31760131). Financial support for Sinharaja plot came from the University of Peradeniya, Center for Tropical Forest Science of the Smithsonian Tropical Research Institute, Arnold Arboretum of Harvard University, USA, with supplementary funding from the John D. and Catherine T. MacArthur Foundation, the National Institute for Environmental Science, Japan, and the Helmholtz Centre for Environmental Research-UFZ, Germany. Financial support for the Lambir plot came from the Forest Department of Sarawak, Malaysia, the Center for Tropical Forest Science of the Smithsonian Tropical Research Institute, the Arnold Arboretum of Harvard University, USA (under NSF awards DEB-9107247 and DEB-9629601), and Osaka City, Ehime and Kyoto Universities, Japan. Financial support for the Barro Colorado Island (BCI) plot came from numerous organizations, principally the US National Science Foundation. Financial support for the Heishiding plot came from Sun Yat-sen University in Guangzhou, China. Financial support for the Wanang plot came from the Czech Academy of Sciences (grant no. GACR 16-18022S) and the University of Minnesota supported by NSF DEB-1027297 and NIH ICBG 5UO1TW006671.

References

  • 1.Wallace AR. 1878. Tropical nature and other essays. London, UK: Macmillan and Company. [Google Scholar]
  • 2.Rosenzweig ML. 1995. Species diversity in space and time. Cambridge, UK: Cambridge University Press. [Google Scholar]
  • 3.Hillebrand H. 2004. On the generality of the latitudinal diversity gradient. Am. Nat. 163, 192–211. ( 10.1086/381004) [DOI] [PubMed] [Google Scholar]
  • 4.Ashton LA, et al. 2016. Vertical stratification of moths across elevation and latitude. J. Biogeogr. 43, 59–69. ( 10.1111/jbi.12616) [DOI] [Google Scholar]
  • 5.Koleff P, Lennon JJ, Gaston KJ. 2003. Are there latitudinal gradients in species turnover? Glob. Ecol. Biogeogr. 12, 483–498. ( 10.1046/j.1466-822X.2003.00056.x) [DOI] [Google Scholar]
  • 6.Kraft NJB, et al. 2011. Disentangling the drivers of β diversity along latitudinal and elevational gradients. Science 333, 1755–1758. ( 10.1126/science.1208584) [DOI] [PubMed] [Google Scholar]
  • 7.Qian H, Chen S, Mao L, Ouyang Z. 2013. Drivers of β-diversity along latitudinal gradients revisited. Glob. Ecol. Biogeogr. 22, 659–670. ( 10.1111/geb.12020) [DOI] [Google Scholar]
  • 8.Myers JA, et al. 2013. Beta-diversity in temperate and tropical forests reflects dissimilar mechanisms of community assembly. Ecol. Lett. 16, 151–157. ( 10.1111/ele.12021) [DOI] [PubMed] [Google Scholar]
  • 9.Catano CP, Dickson TL, Myers JA. 2017. Dispersal and neutral sampling mediate contingent effects of disturbance on plant beta-diversity: a meta-analysis. Ecol. Lett. 20, 347–356. ( 10.1111/ele.12733) [DOI] [PubMed] [Google Scholar]
  • 10.Mori AS, Fujii S, Kitagawa R, Koide D. 2015. Null model approaches to evaluating the relative role of different assembly processes in shaping ecological communities. Oecologia 178, 261–273. ( 10.1007/s00442-014-3170-9) [DOI] [PubMed] [Google Scholar]
  • 11.Bennett JR, Gilbert B. 2016. Contrasting beta diversity among regions: how do classical and multivariate approaches compare? Glob. Ecol. Biogeogr. 25, 368–377. ( 10.1111/geb.12413) [DOI] [Google Scholar]
  • 12.Ulrich W, Baselga A, Kusumoto B, Shiono T, Tuomisto H, Kubota Y. 2017. The tangled link between β- and γ-diversity: a Narcissus effect weakens statistical influences in null model analyses of diversity patterns. Glob. Ecol. Biogeogr. 26, 1–5. ( 10.1111/geb.12527) [DOI] [Google Scholar]
  • 13.Clark AT, et al. 2017. Functional traits of tropical trees and lianas explain spatial structure across multiple scales. J. Ecol. 106, 795–806. ( 10.1111/1365-2745.12804) [DOI] [Google Scholar]
  • 14.Xu W, Chen G, Liu C, Ma K. 2015. Latitudinal differences in species abundance distributions, rather than spatial aggregation, explain beta-diversity along latitudinal gradients. Glob. Ecol. Biogeogr. 24, 1170–1180. ( 10.1111/geb.12331) [DOI] [Google Scholar]
  • 15.Beck J, Holloway JD, Schwanghart W. 2013. Undersampling and the measurement of beta diversity. Methods Ecol. Evol. 4, 370–382. ( 10.1111/2041-210x.12023) [DOI] [Google Scholar]
  • 16.Pitman NCA, Terborgh J, Silman MR, Nunez P. 1999. Tree species distributions in an upper Amazonian forest. Ecology 80, 2651–2661. ( 10.1890/0012-9658(1999)080%5B2651:TSDIAU%5D2.0.CO;2) [DOI] [Google Scholar]
  • 17.Field R, et al. 2009. Spatial species richness gradients across scales: a meta-analysis. J. Biogeogr. 36, 132–147. ( 10.1111/j.1365-2699.2008.01963.x) [DOI] [Google Scholar]
  • 18.Mittelbach GG, et al. 2001. What is the observed relationship between species richness and productivity? Ecology 82, 2381–2396. ( 10.1890/0012-9658(2001)082%5B2381:WITORB%5D2.0.CO;2) [DOI] [Google Scholar]
  • 19.Rosindell J, Hubbell SP, Etienne RS. 2011. The unified neutral theory of biodiversity and biogeography at age ten. Trends Ecol. Evol. 26, 340–348. ( 10.1016/j.tree.2011.03.024) [DOI] [PubMed] [Google Scholar]
  • 20.Tuomisto H, Ruokolainen K. 2012. Comment on ‘Disentangling the drivers of β diversity along latitudinal and elevational gradients'. Science 335, 1573 ( 10.1126/science.1216393) [DOI] [PubMed] [Google Scholar]
  • 21.Sreekar R, et al. 2017. Horizontal and vertical species turnover in tropical birds with differing land use. Biol. Lett. 13, 20170186 ( 10.1098/rsbl.2017.0186) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 22.Tello JS, et al. 2015. Elevational gradients in β-diversity reflect variation in the strength of local community assembly mechanisms across spatial scales. PLoS ONE 10, e0121458 ( 10.1371/journal.pone.0121458) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 23.Condit R. 1998. Tropical forest census plots. Berlin, Germany: Springer-Verlag and R. G. Landes Company. [Google Scholar]
  • 24.Condit R, Lao S, Perez R, Dolins SB, Foster RB, Hubbell SP.2012. Barro Colorado forest census data, 2012 version . See . . [DOI]
  • 25.Lee H, Davies SJ, LaFrankie JV, Tan S, Itoh A. 2002. Floristic and structural diversity of 52 hectares of mixed dipterocarp forest in Lambir Hills National Park, Sarawak, Malaysia. J. Trop. For. Sci. 14, 379–400. [Google Scholar]
  • 26.Lee HS, et al. 2005. The 52-hectare forest research plot at Lambir Hills, Sarawak, Malaysia: tree distribution maps, diameter tables and species documentation. Kuching, Malaysia: Forest Department Sarawak, The Arnold Arboretum-CTFS Asia Program, Smithsonian Tropical Research Institute. [Google Scholar]
  • 27.Hubbell SP, et al. 1999. Light gap disturbances, recruitment limitation, and tree diversity in a neotropical forest. Science 283, 554–557. ( 10.1126/science.283.5401.554) [DOI] [PubMed] [Google Scholar]
  • 28.Koleff P, Gaston KJ, Lennon JJ. 2003. Measuring beta diversity for presence-absence data . J. Anim. Ecol. 72, 367–382. ( 10.1046/j.1365-2656.2003.00710.x) [DOI] [Google Scholar]
  • 29.Gotelli NJ, Rohde K. 2002. Co-occurrence of ectoparasites of marine fishes: a null model analysis. Ecol. Lett. 5, 86–94. ( 10.1046/j.1461-0248.2002.00288.x) [DOI] [Google Scholar]
  • 30.Vincent JB, Henning B, Saulei S, Sosanika G, Weiblen GD. 2015. Forest carbon in lowland Papua New Guinea: local variation and the importance of small trees. Austral Ecol. 40, 151–159. ( 10.1111/aec.12187) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 31.Co L, et al. 2006. Forest trees of Palanan, Philippines: a study in population ecology. Quezon City, Philippines: University of the Philippines Center for Integrative and Development Studies. [Google Scholar]
  • 32.Whittaker RH. 1960. Vegetation of Siskiyou Mountains, Oregon and California. Ecol. Monogr. 30, 279–338. ( 10.2307/1943563) [DOI] [Google Scholar]
  • 33.Santini L, et al. 2017. Assessing the suitability of diversity metrics to detect biodiversity change. Biol. Conserv. 213, 341–350. ( 10.1016/j.biocon.2016.08.024) [DOI] [Google Scholar]
  • 34.Baselga A. 2010. Partitioning the turnover and nestedness components of beta diversity. Glob. Ecol. Biogeogr. 19, 134–143. ( 10.1111/j.1466-8238.2009.00490.x) [DOI] [Google Scholar]
  • 35.Carvalho JC, Cardoso P, Gomes P. 2012. Determining the relative roles of species replacement and species richness differences in generating beta-diversity patterns. Glob. Ecol. Biogeogr. 21, 760–771. ( 10.1111/j.1466-8238.2011.00694.x) [DOI] [Google Scholar]
  • 36.Hijmans RJ, Cameron SE, Parra JL, Jones PG, Jarvis A. 2005. Very high resolution interpolated climate surfaces for global land areas. Int. J. Climatol. 25, 1965–1978. ( 10.1002/joc.1276) [DOI] [Google Scholar]
  • 37.Muggeo V. 2010. Package ‘segmented’. Biometrika 58, 525–534. [Google Scholar]
  • 38.Davies SJ, Tan S, Lafrankie JV, Potts MD. 2005. Soil-related floristic variation in the hyperdiverse dipterocarp forest in Lambir Hills, Sarawak. In Pollination ecology and rain forest diversity, Sarawak studies (eds Roubik D, Sakai S, Hamid A), pp. 22–34. New York, NY: Springer. [Google Scholar]
  • 39.Katabuchi M, Kurokawa H, Davies SJ, Tan S, Nakashizuka T. 2012. Soil resource availability shapes community trait structure in a species-rich dipterocarp forest. J. Ecol. 100, 643–651. ( 10.1111/j.1365-2745.2011.01937.x) [DOI] [Google Scholar]
  • 40.Chao A, Jost L. 2012. Coverage based rarefaction and extrapolation: standardizing samples by completeness rather than size. Ecology 93, 2533–2547. ( 10.1890/11-1952.1) [DOI] [PubMed] [Google Scholar]
  • 41.Tuomisto H. 2010. A diversity of beta diversities: straightening up a concept gone awry. Part 2. Quantifying beta diversity and related phenomena. Ecography 33, 23–45. ( 10.1111/j.1600-0587.2009.06148.x) [DOI] [Google Scholar]
  • 42.Condit R, Hubbell SP, LaFrankie JV, Sukumar R, Manokaran N, Foster RB, Ashton PS. 1996. Species-area and species-individual relationships of tropical trees: a comparison of three 50 ha plots. J. Ecol. 84, 549–562. ( 10.2307/2261477) [DOI] [Google Scholar]
  • 43.Castro-Insua A, Gomez-Rodriguez C, Baselga A. 2016. Break the pattern: breakpoints in beta diversity of vertebrates are general across clades and suggest common historical causes. Glob. Ecol. Biogeogr. 25, 1279–1283. ( 10.1111/geb.12507) [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary material
rsos181168supp1.docx (1.6MB, docx)
Supplementary material
rsos181168supp2.csv (8KB, csv)

Data Availability Statement

Data are available from the electronic supplementary material, appendix S1, and available via CTFS-ForestGEO website at http://www.forestgeo.si.edu and CForBio website at http://cfbiodiv.org.

Articles from Royal Society Open Science are provided here courtesy of The Royal Society

RESOURCES