Numerical encoding in early visual cortex

Abstract

The ability to estimate the number in a visual array arose early in evolution, develops early in human development, and is correlated with mathematical ability. Previous work with visually presented arrays indicates that the intraparietal sulcus (IPS) represents number. However, it is not clear if the number signal originates in IPS or is propagated from earlier visual areas. Previous work from our group has demonstrated a rapidly instantiated representation of number in low-level regions of visual cortex using the high temporal resolution of event-related electro-encephalography (EEG). Here, we use a rapid event-related functional magnetic resonance imaging (fMRI) paradigm and find convergent evidence for a number signal in low-level visual cortex (areas V1, V2, and V3). Employing a stringent set of stimulus controls, we demonstrate that this signal cannot be explained by the total extent of the array, the density of the items in the array, the aggregate visual area of the items, the size of individual items, the proportion of the array covered by items, nor the overall scale of the array and items. Our findings thus provide strong support for the hypothesis that number is rapidly and directly encoded early in the visual processing stream.

1. Introduction

The number sense describes our ability to estimate the number of objects or events without counting them (Dehaene, 1997). Symbolic mathematics is unique to educated adult humans, but we share the number sense with infants (Izard et al., 2009; Xu and Spelke, 2000), adults from cultures that lack a verbal counting system (Pica et al., 2004), and diverse vertebrate taxa including monkeys (Brannon and Terrace, 1998), rodents (Meck and Church, 1983), and birds (Honig and Stewart, 1989). Although the number sense is distinct from symbolic calculation, the acuity of numerical estimation is correlated with math achievement (e.g. Chen and Li, 2014; Halberda et al., 2008, 2012), and the number sense is theorized to provide a cognitive scaffold for more complex mathematical concepts (Feigenson et al., 2004; Spelke, 2003).

Research into the neural basis of the number sense has implicated a parieto-frontal network in approximate enumeration (Nieder, 2016). The number of items is thought to be encoded in the intraparietal area (IPS) and utilized for decision-making processes in the dorsolateral prefrontal cortex (DLPFC) (Nieder and Dehaene, 2009). Single-cell recordings in monkeys have revealed neurons tuned to particular numerosities (Nieder and Miller, 2004) and other neurons that vary monotonically with number (Roitman et al., 2007). Functional imaging studies have shown that the horizontal segment of the IPS in humans includes topographic representations that are tuned to the number of items in a visual array (Harvey et al., 2013; Piazza et al., 2004). Furthermore, multi-voxel pattern analysis (MVPA) approaches have been able to decode stimulus number from the blood oxygen level dependent (BOLD) signal in IPS (Eger et al., 2009).

Recently, however, new evidence for number encoding in early visual cortex (EVC) arose in several human scalp electroencephalography (EEG) studies. In particular, Park et al. (2016) demonstrated event-related potentials specifically sensitive to number very early in visual processing (75 ms) over medial occipital regions. This signal varied monotonically with number: larger numbers were associated with greater scalp voltage. A subsequent experiment counter-balanced the visual hemifield (upper versus lower) within which the stimuli were displayed and demonstrated a polarity reversal in the number-related scalp potential; the polarity reversal provides strong evidence that the early number signal originated in V2 or V3 with a potential contribution of V1 (Fornaciai et al., 2017).

There are several open questions regarding the EVC signal and how it relates to IPS signals reported previously. Although EEG has very high temporal resolution, it is intrinsically limited in spatial resolution, and the exact source of the number signal within EVC is still unclear. It is also unclear whether the EVC signal is tuned to individual numbers as previously reported in IPS (Harvey et al., 2013; Nieder and Miller, 2004; Piazza et al., 2004) or varies monotonically with number as the EEG findings suggest. Finally, the IPS signal is robust enough to allow stimulus numerosity to be decoded from recorded BOLD signal using MVPA (Eger et al., 2009), but it is unclear if the same could be done using the EVC signal.

Here we used a fast-event-related functional MRI design to test for a numerical signal in EVC with greater spatial resolution. Using a whole-brain approach allowed us to compare the EVC number signal to any potential number signals in IPS. Our stimuli sampled a three-dimensional stimulus space that allowed number to be disentangled from multiple key non-numerical visual stimulus dimensions, including the visual area of the array, the density of the items in the array, the combined visual area of the items, the size of individual items, the proportion of the array covered by items, and the overall scale of the array and items. Participants viewed these stimuli while performing an orthogonal detection task unrelated to magnitude.

We utilized a continuous carry-over (CCO) sequence of stimulus presentation (Aguirre, 2007; Aguirre et al., 2011), which has been used to probe the representational structure of object shape and color in the ventral visual stream (Drucker and Aguirre, 2009; Drucker et al., 2009) and of locations in hippocampus and scene selective cortex (Morgan et al., 2011). CCO sequences have the unique advantage of allowing the simultaneous estimation of the effect of viewing the stimulus on BOLD signal and the modulation in BOLD signal caused by any neural adaptation to the previous stimulus. This approach allowed us to conduct three analyses previously utilized in different paradigms to discover number signals in the brain and apply all three to the hypothesized EVC and IPS number signals. First we examined the monotonic effect of changes in number on signal intensity to test and extend the EEG finding of a number signal in EVC (Fornaciai et al., 2017; Park et al., 2015). Second, we examined the modulatory effect the previous stimulus had on the signal. We note that this allowed us to look for adaptation effects as a result of habituation to the immediately previous stimulus rather than by a long stream of stimuli as in previous work (Jacob and Nieder, 2009; Piazza et al., 2004, 2007). Finally, we attempted to decode numerosity from signal intensity using MVPA. This approach could provide evidence for encoding of numerosities in a given region even if no univariate effects were found in that area (e.g. Bulthé et al., 2015; Eger et al., 2009; Lyons and Beilock, 2011).

The results demonstrate a robust number signal in EVC, which cannot be explained by any of the other non-numerical visual features we tested. In contrast, no number signal was found in the IPS or in any other areas of the brain, contrary to many prior reports. We conclude that our data provide strong evidence for a number signal in EVC and discuss the possible reasons we did not find numerical coding in IPS despite the rich literature that implicates IPS in numerical coding.

2. Methods

2.1. Participants

Participants were 16 right-handed participants aged 19.0 – 35.4 (mean 24.4), with no history of neurological disorders, and normal or corrected-to-normal vision. All participants gave written informed consent, and all procedures were approved by the University of Pennsylvania Institutional Review Board. Participants received monetary compensation. Two participants were excluded for excessive head motion (greater than 1 mm between successive volumes or greater than 3 mm over a run), and two participants were excluded for poor performance on the target-detection task to be described below (lapse rate greater than 10%); all analysis were performed on the remaining 12 participants.

2.2. Stimuli

Stimuli were arrays of dots constructed to evenly sample the three-dimensional stimulus space described in DeWind et al. (2015). This stimulus space is designed to deal with the intrinsic problem of multi-collinearity among the visual features of dot-array stimuli. Number is one cardinal dimension in the stimulus space; the other two are size and spacing. Size is the feature that varies when the size of dots is varied while number is held constant, and so it is necessarily proportional to total item area and to individual item area. Space is the feature that varies when a fixed number of dots are spread out over a greater or lesser extent, and it is necessarily proportional to density (or its reciprocal sparsity) and to field area. Stimuli were constructed to evenly sample this space at three levels of number, three levels of size, and three levels of spacing on a logarithmic scale resulting in 27 unique locations in the stimulus space (Figure 1).

Figure 1. Examples of dot array stimuli from each of the 27 unique stimulus space locations.

Dot arrays were evenly sampled from the three-dimensional stimulus space. Three levels of number, size, and spacing yielded 27 unique stimulus conditions.

By fitting regression models with regressors for number, size, and spacing, we could determine if any of the features that are linear combinations of those three variables caused changes in BOLD signal intensity. The features are listed in Table 1, are logarithmically scaled, and are described as follows: number is the number of dots; size is the feature that varies when a fixed number of dots change size, and spacing is the feature that changes when a fixed number of dots are spread out over a greater or lesser portion of the display; total area is the combined visual area of all dots; item area is the visual area of a single dot; field area (also convex-hull) is the visual area within which the dots are drawn; sparsity (also inverse of density) is the field area divided by number; coverage is the proportion of the field area covered by dots; and scaling is the feature that changes when an entire array (dots and field area) is scaled up or down without changing the number of dots.

Table 1. Visual features that can be described as linear combinations in the log stimulus space.

These feature abbreviations are used throughout the text. Formulae show relationship between each feature and the number, size, and spacing variables used in the regression model.

Visual Feature	Abbr.	Equation in terms of log of number, size and spacing
Number	Num	log (Num)
Size	Sz	log (Sz)
Total Area	TA	$\log (TA)=\frac{1}{2}\log (Num)+\frac{1}{2}\log (Sz)$
Item Area	IA	$\log (IA)=-\frac{1}{2}\log (Num)+\frac{1}{2}\log (Sz)$
Spacing	Sp	log(Sp)
Field Area	FA	$\log (FA)=\frac{1}{2}\log (Num)+\frac{1}{2}\log (Sp)$
Sparsity	Spar	$\log (Spar)=-\frac{1}{2}\log (Num)+\frac{1}{2}\log (Sz)$
Scale	Sc	$\log (Sc)=\frac{1}{2}\log (Sz)+\frac{1}{2}\log (Sp)$
Coverage	Cov	$\log (Cov)=-\frac{1}{2}\log (Sp)+\frac{1}{2}\log (Sz)$

Log scaling of the features is mathematically parsimonious and theoretically motivated. Log scaling means that all features in Table 1 are related to number, size, and spacing by linear equations. As a result, fitting a regression with number, size, and spacing terms, allows the effects of all the features in Table 1 to be inferred from just three coefficients. At a theoretical level, numerosity judgments follow the Weber-Fechner law: the discriminability of two stimuli is related to their ratio. Equal ratios correspond to equal distances on a log scale. Thus, evenly sampling numbers from a log scale stimulus space results in values that are equally discriminable; 17 and 24 differ by a similar ratio to 24 and 34. This same relationship is true for all the features in Table 1.

Importantly for the analysis approach outlined below, number, size, space, total item area, individual item area, sparsity, and field area all varied by a 2:1 ratio over the entire stimulus set and each was partially independent of the rest. This helped ensure that there was equal sensitivity to detect an effect of any of these features on BOLD signal intensity, and that our analysis was not biased towards the discovery of a numerical effect over and above an effect of any other feature. Equal ratios also maximized our ability to discriminate between the effects of different features, in that the “angle analysis” outlined below works best when standard errors of coefficient estimates are approximately equal.

However, we did not collect psychometric data on size and spacing, and there is no guarantee that equal ratios were also consistent on a perceptual scale. Indeed, previous work has suggested that number and density are perceived via different mechanisms with different acuity and different rates of maturation (Anobile et al., 2016a). Similarly, object size has been reported to be perceived with much greater acuity than number (Anobile et al., 2018) and is unaffected by education (Piazza et al., 2013). As a result, a 1:2 ratio in number may have differed in salience compared to other features. In this sense our analysis was designed to balance the detectability of a feature’s effect on BOLD signal on an absolute, but not necessarily perceptual scale.

We carefully controlled many non-numerical features, but one set of features we did not explicitly control was spectral power. Castaldi et al. (2016) demonstrated that adding items to an array of dots increased power across the spatial frequency spectrum. In that study, they were able to explicitly control spectral power by decreasing contrast with increasing numerosity. The stimuli we used here differ from those used by Castaldi et al. (2016) in that we varied the size of the items as well as their number. As a result, a subset of our stimuli had the same total surface area but differed in number, and another subset had the same item surface area but differed in number. To assess the effect of spectral power we compared the mean spectral power over all frequencies of for each of the three numerical values for the subset of stimuli with constant item size and constant surface area (see Table S1). Like Castaldi et al. (2016), we found that when item area was constant mean spectral power increased with more items, but when total area was constant we found that spectral power decreased slightly with increasing number. As a result, effects of number on BOLD signal were unlikely to have been driven by differences in average spectral amplitude.

2.3. Continuous carry over presentation counterbalance

During scanning, participants were instructed to fixate a central cross and were presented with a stimulus stream at a rate of 1 hz, with a 500 ms stimulus-on period followed by a 500 ms stimulus-off period (50% duty cycle). Stimuli were presented centrally according to the continuous carry-over protocol using a de Bruijn cycle (Aguirre, 2007; Aguirre et al., 2011). The de Bruijn cycle is a stimulus-order counter-balancing that ensures that every stimulus is preceded and succeeded by every other stimulus an equal number of times. This allows for two types of effects to be independently modeled: “direct effects” are simply the effect of a stimulus or stimulus category on BOLD signal intensity; “adaptation effects” are the modulatory effects of the previous stimulus on the BOLD signal intensity of the current stimulus (Aguirre, 2007).

As noted above, there were 27 stimulus conditions (3 number × 3 size × 3 spacing), as well as a null-trial condition when no stimulus was presented, resulting in 28 unique trial types. Each of these was presented 28 times in one de Bruijn cycle giving 28² or 784 stimulus presentations. These presentations were spread over three runs, and three complete cycles were presented over nine runs, resulting in 2352 presentations per participant. While viewing the stimuli, participants performed an orthogonal target-detection task that required pressing the response button whenever the fixation cross turned red (15% of trials).

2.4. Localizer task and region of interest (ROI) definition

We used a localizer task adapted from Cantlon and Li (2013) to obtain subject-specific estimates of the number-related areas in parietal cortex. The localizer was a blocked matching task with four conditions. In each run participants saw 12 blocks of three trials each. In all conditions participants viewed two stimuli simultaneously and were instructed to push the response button to indicate a match or to do nothing if there was no match. On each trial the stimulus pair was presented for two seconds with a two-second inter-trial interval and eight seconds between blocks. In the face condition participants saw a pair of photographs of faces and indicated whether they were the same person or different people; in the shape condition participants saw a pair of shape silhouettes and indicated whether the shapes were the same or different; in the word condition participants indicated whether two words were the same or different while ignoring font and capitalization; in the number condition participants indicated whether a single numeral was the same or different in magnitude to an array of dots.

We fit a general linear model (GLM; Friston et al., 1994) with terms for each of the four conditions in the localizer task, as well as nuisance regressors for motion to the whole-brain data for each subject. We ran a contrast testing the hypothesis that activation in the number condition was greater than the mean activation in the other three conditions. We defined the ROI for each participant as the 100 voxels in parietal cortex with the greatest t-statistic of this contrast.

2.5. Retinotopic ROIs

Prior studies have derived maps of the retinotopic areas of IPS and visual cortex at the single-subject level. These single-subject maps were normalized and combined across many subjects, generating probabilistic maps corresponding to the likelihood of each voxel in human cortex being part of a retinotopic map (Silver and Kastner, 2009; Wang et al., 2014). We used this probabilistic atlas to address two questions. First, we sought to confirm the anatomical locus of the early visual EEG signal observed previously (Park et al., 2015) using bilateral ROIs for V1, V2, and V3. Second, retinotopically organized IPS regions are not necessarily the same as the mathematical and calculation regions obtained by our parietal localizer task. Accordingly, we used the parietal retinotopic regions as another separate ROI. ROIs were constructed from the probabilistic atlas, such that each voxel belonged to a maximum of the one ROI that was most likely to contain it. The seven parietal ROIs, IPS0 – IPS5 and the superior parietal area (SPL1), were combined into a single ROI representing all the parietal regions likely to be part of a retinotopic map. This gave us four ROIs from the probabilistic maps: V1, V2, V3, and an IPS-SPL ROI. Results from these ROI analyses are presented in the supplementary results.

2.6. Scanning parameters

MRI data was collected in a 3T Siemens Prisma scanner using a 64-channel head coil in the Stellar Chance Labs at the University of Pennsylvania. High-resolution T1-weighted structural images were collected in 160 axial slices and 1 mm isotropic voxels (TR = 2200 ms, TE = 4.67 ms, TI = 900 ms). Functional blood-oxygenation-level-dependent (BOLD), 6x-multiband accelerated, echoplanar data were acquired in 2 mm isotropic voxels (TR = 750 ms, TE = 30 ms) in 79 axial slices with 79 × 95 in plane resolution. Nine runs of 402 TRs of functional data were collected while participants viewed the dot-array stimuli. Afterward, an additional two runs of 320 TRs of functional data were collected while participants performed the matching localizer task.

2.7. General linear models

We fit two GLMs to the nine runs of functional data collected while participants viewed the dot arrays. In both models, nuisance regressors were included for 6-axis motion and for button presses for the detection task. Both the GLMs were fit using SPM 12 (Wellcome Trust, London, UK). Family-wise-error correction was accomplished using random field theory (Worsley et al., 1992).

2.7.1. GLM coding of direct and adaptation effects

The first GLM included 9 parametric regressors of interest: three modeling the “direct” effects of number, size, and spacing; three modeling the “tuned adaptation” effects of the same features (see below); and three modeling the “monotonic adaptation” effects of the same features. The “direct” effect regressors were simply parametric regressors coding the three levels of number, size, and spacing (Aguirre, 2007).

The regressors for “tuned adaptation” were designed to detect tuning curve responses in the neuronal code for number (e.g. Harvey et al., 2013; Nieder and Miller, 2004; Piazza et al., 2007). The theoretical basis for such a model is that, for each numerosity presented, a subset of the neural population tuned to that number will be activated. If the same number of items is presented again on the next trial the response will be attenuated (for a general discussion of fMRI adaptation effects and hypothesized mechanisms see Grill-Spector et al., 2006; Krekelberg et al., 2006). If the number of items presented is very different from (distant from) the previous, the response will be at full strength, because the neurons tuned to that number of items will not have been previously activated. An intermediate effect may be observed at intermediate distance from the previous number of items, because such values activate a partly overlapping set of neurons. Thus, the tuned adaption regressor for numerosity is expected to increase inversely with the numerical distance (maximum adaptation effect when numerical distance is zero); in addition to numerosity we included two more adaptation regressors to detect any tuned representations of size (Harvey et al., 2015) or spacing.

The “monotonic adaptation” regressors rely on the same theoretical idea as tuned adaptation, but account for the possibility that neurons may be responding to numerosity with monotonic increasing or decreasing activation (Roitman et al., 2007). If adaptation is proportional to the degree of activation to the preceding stimulus, and activation is governed by a monotonic function, adaptation would be proportional to the absolute magnitude of the preceding stimulus, rather than the distance between the preceding and current stimuli as in the tuned adaptation model. Thus, the three monotonic adaptation regressors parametrically encoded the number, size, and spacing of the previous stimulus, but with a reversed sign, to match the prediction that a larger value of the previous stimulus would decrease signal for the current stimulus.

We performed three separate F-tests on the output of the GLM to test for any direct effects, any tuned adaptation effects, and any monotonic adaptation effects. These tests were equivalent to comparing a model with direct effects to a null model without direct effects, a model with tuned adaptation effects to one without, and a model with monotonic adaptation effects to one without. Whenever significant F statistics were obtained from any of these test, we performed follow-up t-tests to determine which regressors were significant (number, size, or spacing).

At the crux of the difficulty dissociating the effect of number from those of non-numerical features is the mathematical fact that number cannot be orthogonalized from all non-numerical features simultaneously. As a result, simply observing a significant number coefficient from the GLM is necessary but not sufficient for determining if there was a real effect of number that was not merely the effect of some other visual feature that is correlated with number. We took two approaches to determining which feature was driving significant direct and monotonic adaptation effects after determining that such effects existed with the F test: an “angle analysis” to determine which features best correlated with changes in activation, and a contrast to test to determine if number had some relation with signal after accounting for the best correlated feature.

First, we performed an “angle analysis” to determine which visual feature best correlated with changes in activation (Park et al., 2015). This analysis takes direct effect coefficients for number, size, and spacing (β_{Direct − Num}, β_{Direct − Sz} and β_{Direct − Sp}) and treats them as a “parameter vector” (${\overrightarrow{\beta }}_{Direct}$) in three-dimensional parameter space. Different possible directions of ${\overrightarrow{\beta }}_{Direct}$ correspond to different visual features that could be driving changes in BOLD signal. We calculated the angle (θ_Feature) between ${\overrightarrow{\beta }}_{Direct}$ and each feature’s direction. To test whether the θs calculated for different features were significantly different from each other, a bootstrapping approach was used. Specifically, we resampled our participants with replacement 1,000 times and derived two-tailed p-values from the proportion of bootstraps when θ_x> θ_y, where x and y are different visual features.

The angle analysis could demonstrate that a particular feature had the strongest influence on activation; however, we also wanted to know if there was residual variance that could be explained by number. So, in addition to the angle analysis, we performed post-hoc contrasts to subtract the variance attributable to one feature and test if there was still variance explained by number. In particular, we wanted to know if number had explanatory value after accounting for field area. If field area were the only feature affecting signal, we would expect β_Num to equal β_sp (Table 1). So, to test the hypothesis that number has an effect over and above field area, we tested whether β_Num was significantly greater than β_sp.

2.7.2. Categorical GLM

We also fit a second “categorical” GLM with a unique regressor for each of the 27 stimulus conditions. We used these parameter estimates to plot the heatmap in Figure 2 below and as the input for the support vector machine (SVM) classification described below.

Figure 2. Significant direct effects of number and spacing in early visual cortex.

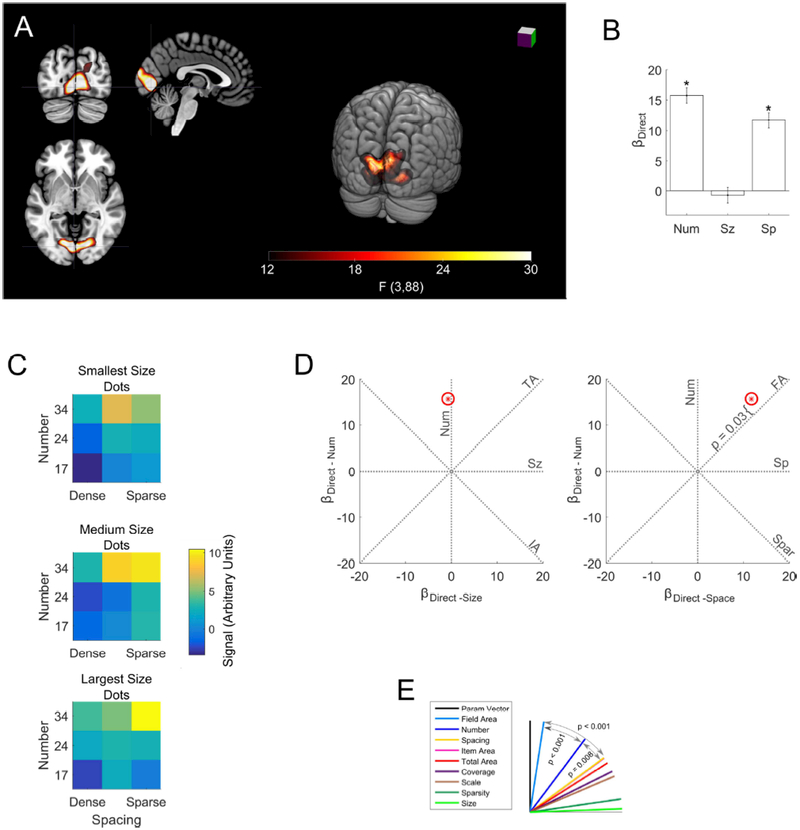
(a) The single significant cluster revealed by the whole-brain analysis is shown in red (threshold F > 12.15, p < 0.05 FWE). Slices at x = −4, y = −80 z = −2 in MNI space. (b) Bars indicate coefficients for the number, size and spacing regressors within the significant whole brain cluster. Error bars indicate standard errors across subjects. There were significant effects of number (t(88) = 12.2, p < 0.0001) and spacing (t(88) = 9.1, p < 0.0001), but not size (t(88) = −0.6, p = 0.57. (c) Mean signal response to each of the 27 dot arrays in the cluster. Number is on the y-axis, spacing is on the x-axis, size increases across the three heat maps from top to bottom. More numerous arrays of greater extent generated the greatest response, but the size of the dots had no significant effect. (d) ${\overrightarrow{\beta }}_{Direct}$ displayed as a red star in two plots: as β_{Direct − Num} plotted against β_{Direct − Sz} and as β_{Direct − Num} plotted against β_{Direct − Sp} Red ellipse indicates the standard error of the estimates (these may appear circular if the standard errors for two coefficients are similar). Dashed lines indicate where ${\overrightarrow{\beta }}_{MonoAdapt}$ would fall if activity was exactly proportional to the feature abbreviation labeling it. P-value demonstrates the significant deviation of ${\overrightarrow{\beta }}_{Direct}$ from the field area line towards the number line. (e) The angle (θ) between each feature line and ${\overrightarrow{\beta }}_{Direct}$ θs serves as an index of how well each feature describes changes in signal across stimuli. ${\overrightarrow{\beta }}_{Direct}$ was significantly closer to field area and number than to any other feature, indicating that these features were the main drivers of changes in signal intensity.

2.8. Multi-voxel decoding of number

We applied an SVM classification algorithm to attempt to decode stimulus identity from voxel-level signal in each ROI. Classification was performed on parameter estimates from the “categorical” GLM described above. We performed pair-wise classification between each of the 27 stimulus conditions using leave-one-run-out crossvalidation. Mean classification accuracy was calculated for each pair within subject. Depending on the analysis, the accuracy for different pairs was averaged together. For the overall number decoding, all the pairs with a 1:1.4 numerical ratio were averaged together and all the pairs with a 1:2 numerical ratio were averaged together to produce two mean SVM accuracies. Averaging of pairs always occurred within subject. To determine if SVM accuracy differed from chance, we performed t-tests of the subject-level SVM accuracies to test if the mean was significantly different from chance performance (50%).

For the analysis of number decoding while controlling for non-numerical features, we used the same subject-level pair-wise classification accuracies described above. We averaged accuracy of pairs with both a 1:2 numerical ratio and a 1:1 ratio of the nonnumerical feature that was being controlled. For example, when controlling for field area, we averaged accuracy of pairs that had both a 1:2 numerical ratio and a 1:1 (constant) field area. We then performed t-tests to determine if mean accuracy across subjects was significantly above chance performance.

3. Results

3.1. Direct effect of stimulus

A whole-brain analysis for significant direct effects of number, size, or spacing revealed a single significant cluster in early visual cortex (Figure 2A; p < 0.05 FWE). Follow-up univariate ROI analysis in this cluster found a significant effect of number and spacing, but not size (Figure 2B, Table 2).

Table 2. Significant effects of number and spacing in early visual cortex, but not the parietal localizer region.

F tests were performed to determine if there was a direct effect in each ROI. The first row are the results from the cluster found in the whole brain analysis shown in Figure 2. The second row are the results from the individually defined localizer ROIs shown in Figure 3. We did not perform follow-up T tests in the localizer ROIs because the F test was not significant at p < 0.1, and so there was no evidence of a direct effect of stimulus on signal. Degrees of freedom for the F tests were (3,88) and for the T tests were (1,88).

	F test for any direct effect		Number		Size		Space
	F stat	p value	T stat	p value	T stat	p value	T stat	p value
Whole Brain Sig. Cluster	77.4	< .0001	12.2	< .0001	−0.6	0.57	9.1	< .0001
Parietal Localizer	1.6	0.19	-	-	-	-	-	-

We examined the number, size and spacing coefficients in more detail as a three-dimensional parameter vector (${\overrightarrow{\beta }}_{Direct}$ Figure 2D). We assessed how well changes in different visual features of the dot arrays corresponded to signal changes by examining how closely ${\overrightarrow{\beta }}_{Direct}$ aligned with different dimensions in the parameter space. Figure 2D and 2E shows that ${\overrightarrow{\beta }}_{Direct}$ falls between the number (θ_Num = 36.7°, 95% CIs = 30.1° − 42.0°) and the field area (θ_FA = 8.6°, 95% CIs = 4.7° − 16.6°) dimensions in the parameter space. A bootstrap analysis (see Methods) showed that field area was significantly better aligned with ${\overrightarrow{\beta }}_{Direct}$ than any other feature, including number (maximum p < 0.001). However, number was the second-best feature and was significantly better than all features other than field area (maximum p = 0.008). Although field area had a stronger effect on signal than number, field area alone could not fully explain signal change. We found that ${\overrightarrow{\beta }}_{Direct}$ significantly deviated from the field area dimension towards the number dimension, indicating that after accounting for the effect of field area there was still a significant effect of number (t(88) = 2.2, p = 0.03; Figure 2D).

Since the whole-brain analysis failed to detect direct effects of numerosity in parietal cortex, we next focused the ROI defined by our localizer task, which was designed to delineate neural regions sensitive to numerical comparison (Cantlon and Li, 2013). The localizer task generated subject-specific ROIs (Figure 3A) that generally fell within the horizontal segment of the intraparietal sulcus (hIPS) and superior parietal lobule (SPL), consistent with many previous studies on the neural bases of numerical and mathematical cognition (e.g., Ansari, 2007; Arsalidou and Taylor, 2011; Dehaene et al., 2003). Here, however, we found no significant direct effect of stimulus in these ROIs (F(3,88) = 1.6, p = 0.19).

Figure 3. No significant direct effect of number, size or spacing was found in the individual parietal localizer ROIs.

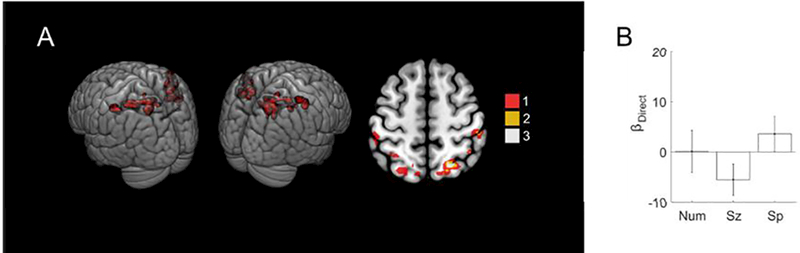
(a) Additive penetrance map of the 12 individual localizer ROIs. Voxels falling in the ROI of a single subject are in red, of two subjects in gold, and of three subjects in white. There were no voxels with significant effects in more than three subjects. Axial slice z = 56 mm MNI. (b) Coefficient values for the direct effect regressors. Error bars indicate standard errors across subjects.

3.2. Adaptation effects

In addition to modeling the effect of stimulus on BOLD signal, we modeled how the signal was modulated by the previously viewed stimulus through the use of two different sets of adaptation regressors, tuned and monotonic. The tuned adaptation regressors tested the hypothesis that neurons were tuned to a specific numerosity, size, or spacing, that the response would be suppressed if that value were repeated, and that the response would be less suppressed with increasing distance from that value. Positive tuned adaptation coefficients would indicate suppression for repeated number, size, or spacing. The monotonic adaptation regressors tested the hypothesis that neurons varied in response monotonically with numerosity, size, or spacing and that responses would be suppressed proportional to the absolute magnitude of the numerosity, size, or spacing of the previous stimulus, irrespective of the current stimulus. Positive monotonic adaptation coefficients would indicate greater suppression following larger magnitudes and imply that neurons increased activation for greater number, size or spacing.

We found no significant effect of tuned adaptation in the whole-brain analysis (threshold FWE p < 0.05). Nor did we find significant tuned adaptation in the individual parietal localizer ROIs (F(3,88) = 0.32, p = 0.81), nor in any of the retinotopic ROIs V1, V2, V3, or IPS-SPL (maximum F(3,88) = 0.5, p = 0. 68).

We did, however, find a significant monotonic adaptation cluster in early visual cortex (Figure 4). This cluster overlapped closely with the direct-effects cluster (Figure 2). Similar to the direct-effects analyses, we found significant effects of number and spacing but not size (Table 3).

Figure 4. Field area drives significant monotonic adaptation effects in EVC.

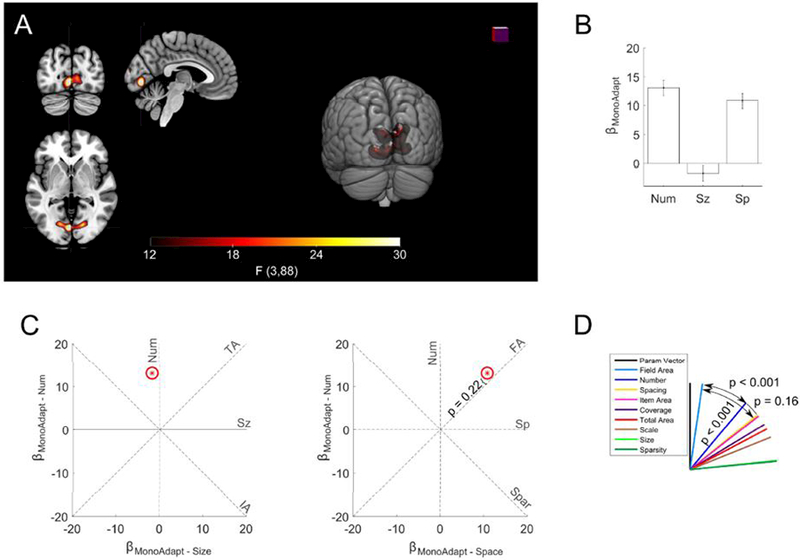
(a) A significant monotonic adaptation cluster was found in early visual cortex (threshold FWE p < 0.05). Slices at x = −4, y = −80, z = −2 in MNI space. (b) Bars indicate coefficients for the monotonic adaptation of number, size, and spacing within the significant whole brain cluster. Error bars indicate standard errors across subjects. Signal was depressed if the previous stimulus had a larger total extent. The size of the items in the previous stimulus had no significant effect on subsequent activation. (c) ${\overrightarrow{\beta }}_{MonoAdapt}$ displayed as red star in two plots as β_{MonoAdapt – Num} plotted against β_{MonoAdapt – Sz} and as β_{MonoAdapt – Num} plotted against β_{MonoAdapt – Sp} The red ellipses indicate the standard error of the estimates. Dashed lines indicate where ${\overrightarrow{\beta }}_{MonoAdapt}$ would fall if monotonic adaptation was exactly proportional to the feature abbreviation labeling it. P-value fails to demonstrate any significant deviation of ${\overrightarrow{\beta }}_{Direct}$ from the field area feature line. (d) θs (angle between feature line and ${\overrightarrow{\beta }}_{MonoAdapt}$) for each feature. ${\overrightarrow{\beta }}_{MonoAdapt}$ was significantly closer to field area than to any other feature.

Table 3. Significant monotonic adaptation effects of number and spacing in early visual areas, but not parietal regions.

F tests were performed to determine if there was a monotonic adaptation effect in each ROI. The first row is the monotonic adaptation cluster found in the whole-brain analysis shown in Figure 4. The second row gives the results from the individually defined localizer ROIs shown in Figure 3. Although, there was a significant number coefficient in the whole-brain cluster, follow-up analysis (Figure 4) found that it was driven by field area. Degrees of freedom for the F test were (3,88) and for the T test was (88).

	F test for any monotonic adaptation effect		Number		Size		Space
	F stat	p value	T stat	p value	T stat	p value	T stat	p value
Whole Brain Sig. Cluster	54.5	< .0001	9.8	< .0001	−1.3	0.19	8.1	< .0001
Localizer	3.0	0.03	0.0	0.98	−1.7	0.08	2.5	0.02

We modified the angle analysis by defining ${\overrightarrow{\beta }}_{MonoAdapt}$ comprised of the number, size, and spacing monotonic-adaptation coefficients. This allowed us to determine the features causing monotonic adaptation. The analysis revealed that monotonic adaptation was primarily driven by field area (θ_FA = 8.2°; 95% CIs = 3.1° − 16.9°) and was significantly closer to ${\overrightarrow{\beta }}_{MonoAdapt}$ than the second closest feature of number (θ_Num& = 39.8°; 95% CIs = 32.9° − 46.8°; p < 0.001). We also found that after accounting for field area, number had no significant effect (t(88) = 1.2, p = 0.22).

We did find a weak, but significant monotonic adaptation effect in the parietal localizer ROI (f(88,3) = 3.0; p = 0.03). Follow-up t-tests revealed a significant monotonic adaptation effect of spacing and a marginal negative effect of size, but no effect of number (Table 3; Figure 5). The angle analysis failed to find any significant differences between features (minimum p = 0.09), making the effect difficult to interpret.

Figure 5. No significant monotonic adaptation effect of number in the parietal localizer regions.

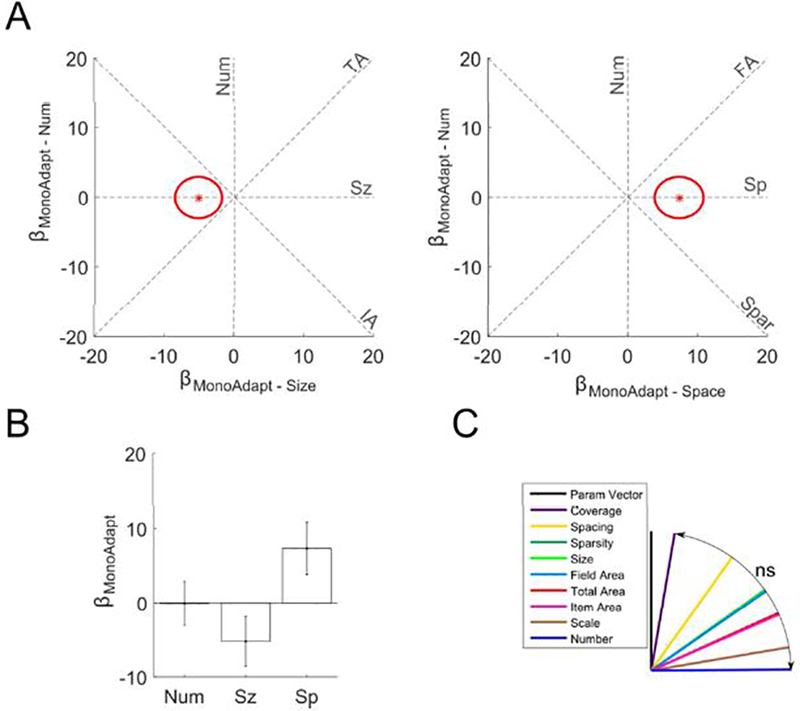
(a) ${\overrightarrow{\beta }}_{MonoAdapt}$ in the localizer ROI displayed as red star in two plots as β_{MonoAdapt – Num} plotted against β_{MonoAdapt – Sz and as} β_{MonoAdapt – Sp.}Red ellipses indicate the standard error of the estimates. Dashed lines indicate where ${\overrightarrow{\beta }}_{MonoAdapt}$ would fall if monotonic adaptation was exactly proportional to the feature abbreviation labeling it. (b) Bars indicate coefficients for the monotonic adaptation number, size, and spacing regressors within the subject-specific localizer ROI. Error bars indicate standard errors across subjects. The number of the items in the preceding stimulus had no significant effect on current activation. (c) θs (angle between feature line and ${\overrightarrow{\beta }}_{MonoAdapt}$) for each feature. There were no significant differences between features.

3.3. Decoding number from multi-voxel patterns

To confirm number encoding in EVC we used a SVM classifier to decode number from multi-voxel signal intensity in the ROIs already considered. We found that number could be decoded in the cluster obtained from our direct effects whole-brain analysis, but not from the parietal localizer ROIs (Figure 6). Because the SVM compared two stimuli, we could calculate accuracy at two numerical ratios, 1:1.4 (17 to 24 and 24 to 34) and 1:2 (17 to 34). As expected, we found that performance was higher comparing a 1:2 numerical ratio than a 1:1.4 ratio.

Figure 6. Number can be decoded from multi-voxel signal intensity in EVC but not the parietal localizer ROI.

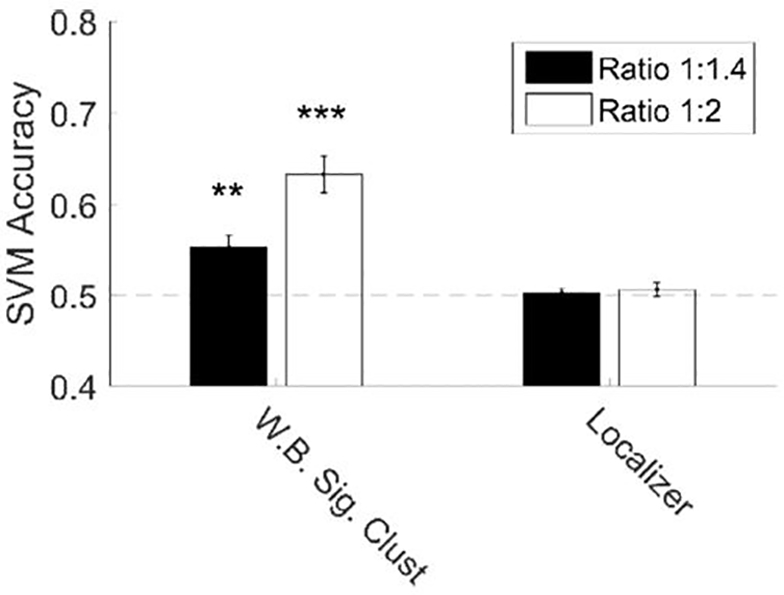
We found significant decoding of number at 1:2 and 1:1.4 ratios in the whole brain (WB) significant cluster (Figure 2), but not in the subject specific parietal localizer. Error bars denote standard error across subjects. * p < 0.05; ** p < 0.01; *** p < 0.001.

Critically, our even sampling of the 3D stimulus space resulted in subsets of the pairwise comparisons where number varied, but another feature was fixed. By examining these subsets, we could determine if SVM decoding was dependent on a non-numerical feature or could be attributed to number itself (Figure 7). In the cluster from direct-effect whole-brain analysis, we found that number was decoded significantly above chance in all control conditions. This means that the number signal in these regions could not be explained by variation in field area, sparsity (or density), total area covered by the dots, area of individual dots, the overall scale of the array, or the proportion of the array covered by dots. In the subject specific parietal localizer ROIs, the SVM failed to classify above chance in all the control conditions.

Figure 7. Number drove classification performance in EVC while controlling for eight non-numerical features.

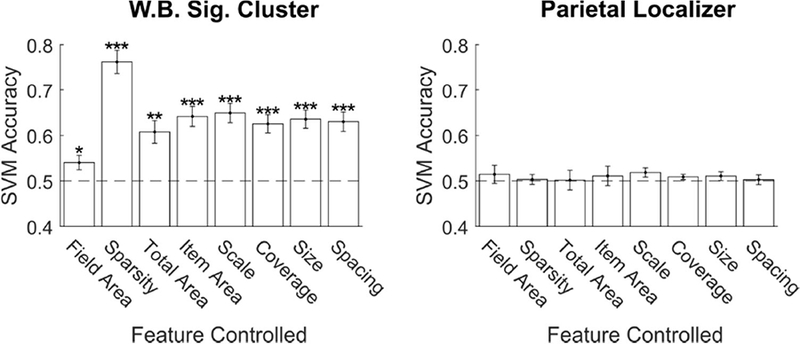
Mean SVM classification accuracy on pair-wise comparisons where number changed by a 2:1 ratio, but the non-numerical stimulus feature on the x-axis was held constant. The process was repeated for the whole brain significant cluster (Figure 2) and the subject specific parietal localizer ROIs. Error bars indicate standard error across subjects. * p < 0.05; ** p < 0.01; *** p < 0.001.

3.4. Retinotopic ROIs

We extended our analyses to four ROIs derived from an atlas of the probable locations of retinotopic maps based on anatomical position (see section 2.4; Silver and Kastner, 2009; Wang et al., 2014). The results of the GLMs, the angle analyses, and the SVM analyses are included in the supplementary materials. In general, these analyses confirmed that number and field area are encoded in EVC, but no reliable stimulus information could be obtained in parietal cortex.

4. Discussion

Recent EEG studies have demonstrated an early number signal in occipital cortex (Park et al., 2015), and that these signals primarily originated in V2 and V3, with a potential contribution of V1 (Fornaciai et al., 2017). Here we used a rapid event-related fMRI design to demonstrate that the BOLD signal intensity in V1, V2, and V3 increases with number of items in a visual array. More importantly, we found that, although there was a strong effect of the field area of the array as expected in retinotopic visual areas, number also modulated the signal, and the field area effect could not account for the number effect. Our SVM analysis confirmed that number could be decoded from EVC signal intensity when field area, or any other feature tested, was held constant while number varied. Our findings thus lend strong support to the proposal that number is encoded at very low levels in visual processing independent of other visual features. In this sense our findings support the claim that number is a “primary” perceptual feature (Anobile et al., 2016b).

We also found adaptation-like effects in EVC; however, they differed from those reported previously in IPS (Piazza et al., 2004, 2007). These previous studies reported what we term “tuned adaptation,” the repetition of a numerosity resulting in a partially suppressed response to the second presentation. This type of adaptation is evidence for tuned numerosity detectors, neurons that fire maximally in response to a particular numerosity and attenuate their response to increasingly distant numerosities. Here, however, we found no evidence of tuned adaptation in any ROI, nor in the whole-brain analysis. Instead, we found what we term “monotonic adaptation:” the greater the numerosity of the previous stimulus, the more attenuated the response to the current stimulus, regardless of the numerosity of the current stimulus. This type of adaptation is consistent with units that have monotonically increasing activation for greater number or field area. It is then not surprising that we saw a close overlap between the areas showing monotonic adaptation and the areas with a direct increase in signal with increasing number and field area.

The adaptation effects, however, were not as unambiguously numerical as the direct effects. In most of the EVC ROIs we considered, field area was sufficient to explain the monotonic adaptation effects: signal was suppressed following arrays with a large visual angle regardless of the number of items. However, in V1 we found an additional significant adaptation effect of number beyond the effect of field area.

The discrepancy between the direct effects and the SVM classification that both were driven by number on the one hand and the monotonic adaptation effects that may have been driven by field area alone on the other hand, is difficult to interpret. One possibility is that the number effect on monotonic adaptation was present throughout EVC, but we failed to detect it in some ROIs because of experimental noise. Another possibility is that single neurons in EVC do not encode number and single-neuron encoding of number is necessary to drive adaptation effects (Grill-Spector et al., 2006; Krekelberg et al., 2006). This makes sense given the small receptive fields in EVC areas, which might not be large enough to contain multiple dots. Lack of single-neuron encoding of number in EVC is consistent with the possibility that the EVC signal represents the object-normalization layer theorized in computational models of number perception (Dehaene and Changeux, 1993; Verguts and Fias, 2004). In this layer, units represent the presence or absence of an item in a local receptive field, but do not increase activation with more items in the array. Thus, individual neurons might not show a monotonic relationship with array numerosity, but their summed response across the ROI would, just as we observed in our univariate analysis of direct effects.

The hypothesis that EVC numerical encoding is based on spatially anchored receptive fields rather than trans-spatial numerosity detectors is also supported by previous empirical findings. More specifically, it has been found that number can be decoded from EVC, which required classifier training and testing on patterns of fMRI activity elicited by stimuli presented in the same spatial location, whereas cross-decoding across spatial location failed. This suggests that the number code is specific to a spatial location (Eger et al., 2013). The hypothesis is also supported by the observation of summation numerosity signals in occipital regions, but not adaptation numerosity signals (Roggeman et al., 2011).

In contrast to many previous studies, we were unable to find any number signal in the parietal cortex. There are a variety of possible explanations for this discrepancy, including large differences in stimulus design, stimulus presentation, task, and scanning parameters. Below we consider some of these differences.

Several studies that have used multi-voxel pattern analysis to decode number in IPS rely on data obtained while participants performed an explicit numerical comparison task (Bulthé et al., 2014, 2015; Eger et al., 2009; Lyons et al., 2015). Another study found that number could only be decoded from IPS during active comparison (Cavdaroglu et al., 2015). In the present study, participants passively viewed the dot arrays while performing an irrelevant detection task on the fixation cross. Thus, one possibility that deserves future study is that explicit attention and active numerical processing contributes to the representation of number in the IPS. In the absence of such a task, these signals may be weaker or absent, thus explaining our inability to detect them.

Several studies, however, have also demonstrated IPS number signals in the absence of an explicit number comparison task using an adaptation paradigm. Adaptation studies do not require a number discrimination, but several have found tuned-adaptation effects in IPS (Cantlon et al., 2006; Jacob and Nieder, 2009; Piazza et al., 2004, 2007). One clear difference between these studies and our protocol is that the prior studies used extended habituation phases before each probe stimulus. During habituation, 3–11 stimuli with the same numerosity were presented consecutively such that the response to subsequent presentations would be maximally depressed (Piazza et al., 2004). When a probe stimulus that differed in numerosity was presented, the greatest possible rebound from this depressed state might then have been elicited and thus have been observable. In contrast, in our CCO procedure, a continuous stream of changing stimuli was presented. The CCO allows thousands of stimulus presentations in a single session, all of which could be analyzed for direct and adaptation effects. However, there may have been a drawback in that adaptation effects could only be defined only with respect to the immediately previous stimulus presentation, not the previous 3–11. We had hoped that the signal-to-noise improvement of so many observations would outweigh the drawback of a smaller habituation effect, but it is distinctly possible that there were tuned-adaptation effects in IPS, but that they were too small to observe with the CCO approach. In support of this possibility, it has been reported that at least four adaptation trials may be needed to generate behavioral adaptation to numerosity (Aagten-Murphy and Burr, 2016). If the same is true for neural adaptation in IPS, our paradigm may have been inadequate to generate adaptation.

It is also worth considering an attentional explanation for our failure to detect tuned-adaptation in IPS. Adaptation paradigms are designed to cause neural habituation and detect rebound from this habituated state after the presentation of a deviant stimulus. However, these conditions similarly cause habitation of attentional processes, as in infant habituation studies. When a deviant is presented in the stimulus stream it may cause a refocusing of attention on the stimuli or a surprise reaction. It could be this attentional signal, rather than rebound from neural adaptation, that drives the numerosity effects reported previously (Cantlon et al., 2006; Jacob and Nieder, 2009; Piazza et al., 2004). Under this scenario, because our paradigm varied number pseudo-randomly and by the same 1:2 proportion as other non-numerical visual features, we never generated this attention-induced enhancement of processing. Thus, it is possible that the IPS number signals found using adaptation paradigms reflect an attentional process rather than a purely perceptual number representation. In support of this possibility is the finding that the presentation of a surprising saccade target increases BOLD signal in the IPS (O’Reilly et al., 2013). Against this possibility is the finding that shape deviants did not cause recovery from adaptation, although the salience of this manipulation is unclear (Piazza et al., 2004). Future research will be necessary to test these hypotheses.

Harvey et al. (2013) found topographic representation of number in the superior parietal area in the absence of a task. Although our SVM was theoretically capable of detecting such a signal, we failed to find any significant decoding of number in the localizer ROI or in the IPS-SPL retinotopic region. Our paradigm differs in several key ways that could account for the difference in findings. Perhaps most importantly, we only varied the number of items between 17 and 34, a 1:2 ratio. Harvey et al. varied numerosity between 1 and 20, a ratio ten times greater than the one we used. The larger ratio could have generated more distinct activation profiles and made it easier to identify numerically dependent changes in signal. The difference in range may also have been significant. The Harvey et al. experiment used values in and just above the subitizing range, whereas in the present experiment we exclusively used numbers outside the subitizing range. Values in the subitizing range may be represented differently from larger values (Cutini et al., 2014). Another possibility is that the Harvey et al. study may have caused participants to allocate more attention to numerosity. Number but not non-numerical visual features was modulated systematically in a slow and obvious cycle (1 to 20 to 1 repeating many times). This slow systematic change over such a large range of values may have caused subjects to attend to the number of items or to entrain to the repeating stimulus pattern.

Castaldi et al. (2016) demonstrated number decoding in the IPS using only numerosities outside the subitizing range, without an explicit numerical task, and without the habituation-dishabituation design used in other adaptation paradigms. It is thus difficult to reconcile their finding with ours. One contributing factor may be that in their study number varied over a 1:4 ratio, giving them more power to detect an effect of number on BOLD signal. They also did not systematically vary non-numerical features, which possibly could have caused participants to focus attention on number. Future work is necessary to explore the attentional hypothesis of IPS number representation, which currently remains speculative.

Finally, we note that our stimuli were carefully controlled for multiple non-numerical visual features. However, we do not think that such stimulus control can explain our failure to find numerical effects in IPS. Some of the features we controlled for, such as size, have been controlled in previous studies (e.g. Eger et al., 2009). Further, follow-up analyses have demonstrated that numerical tuning curves in parietal cortex cannot be explained by non-numerical stimulus features (Harvey and Dumoulin, 2017). Most importantly, our paradigm not only controlled non-numerical features, but also varied them independently of number. As a result, if previous findings were driven by non-numerical features, then we should have been able to detect those effects and differentiated them from putative number effects, as we did with field area and number effects in EVC.

4.1. Conclusion

Here we report an effect of stimulus numerosity on the BOLD signal in EVC that cannot be explained by the non-numerical visual features we tested. This effect is quite strong and, at least in the paradigm we used here, is more robust than any number signal in IPS, which we failed to detect. This EVC signal thus deserves further investigation, as it may represent the instantiation of the object-normalization stage of processing posited in computational models of the number sense. Mapping the stages of visual processing that lead to a robust number signal should ultimately afford a greater understanding of the link between the number sense and symbolic mathematical ability.