Body and tail-assisted pitch control facilitates bipedal locomotion in Australian agamid lizards

Abstract

Certain lizards are known to run bipedally. Modelling studies suggest bipedalism in lizards may be a consequence of a caudal shift in the body centre of mass, combined with quick bursts of acceleration, causing a torque moment at the hip lifting the front of the body. However, some lizards appear to run bipedally sooner and for longer than expected from these models, suggesting positive selection for bipedal locomotion. While differences in morphology may contribute to bipedal locomotion, changes in kinematic variables may also contribute to extended bipedal sequences, such as changes to the body orientation, tail lifting and changes to the ground reaction force profile. We examined these mechanisms among eight Australian agamid lizards. Our analysis revealed that angular acceleration of the trunk about the hip, and of the tail about the hip were both important predictors of extended bipedal running, along with increased temporal asymmetry of the ground reaction force profile. These results highlight important dynamic movements during locomotion, which may not only stabilize bipedal strides, but also to de-stabilize quadrupedal strides in agamid lizards, in order to temporarily switch to, and extend a bipedal sequence.

1. Introduction

Lizards are an important study system for understanding locomotory transitions, as some lizard species can begin strides on four limbs but transition onto their hindlimbs during a sprinting bout [1–3]. Why they do this is unclear, but suggestions that bipedalism increases speed or endurance have been unsupported [4]. Instead, forward dynamic modelling, proposed the pitching rotation that lifts the head and trunk is a mechanical consequence of a rearward shift in the body centre of mass (BCOM), combined with the lizard's forward acceleration [5]. This model suggested that above a threshold acceleration, the nose up pitching moment about the hip would become so great, that the front limbs would lose contact with the ground passively. Thus bipedalism need not have been selected for per se, but could have evolved as a consequence of a high acceleration and a posterior shift in the BCOM. This model was supported by Clemente & Withers [4] who showed that acceleration during strides better separates bipedal against quadrupedal strides, than variation in speed. Further, Clemente [6] showed a rearward shift in the BCOM is associated with bipedalism among 124 species of lizards.

This passive model suggests that acceleration is important for bipedal running [5], yet some lizards appear able to run bipedally at low accelerations, deviating from mathematical models of rigid bodied lizards [4,7,8]. These deviations from the model were predicted to be an exaptation; an exploitation of accidental bipedalism [5,9]. Such exploitations were supported by Clemente [6] who showed a continuous increase between predicted acceleration thresholds and actual acceleration thresholds over evolutionary time; lizards were beginning to run bipedally at lower than expected accelerations.

Other modelling studies suggested that several kinematic parameters may act to reduce the acceleration threshold, and therefore, allow bipedalism to be achievable at these low accelerations. For example, changing the angle of the body or tail relative to the ground would aid in bipedalism through changes in the BCOM [10]. Rearward trunk rotation will cause the BCOM to shift posteriorly reducing the nose-down pitching effect of gravity, and extending a bipedal sequence [11]. Similarly, increases in the height of the hip throughout the stance phase, will increase the proportion of the stride where the BCOM lies above the hindlimb ground reaction force (GRF) vector, which would further contribute to a nose-up pitching moment about the hip [11]. Active tail lifting during the acceleration phase would act to destabilize the trunk, causing it to rotate posteriorly (upwards and backwards), through the high angular moment of the tail, making bipedalism possible at lower accelerations [1,5,12]. This mechanism has previously been demonstrated, where it was used to stabilize the pitch of the body during jumping in lizards [13,14]. Spatial and temporal footfall patterns may also be an important factor extending bipedal stretches. Placing the foot further forward during the stride, or modifying the GRF profile such that a greater proportion of the vertical impulse is applied shortly after initial foot contact, would increase the duration in which the ground-reaction force vector is anterior to the BCOM, further increasing the nose-up pitching moment [11].

To understand which mechanisms are most important for the exploitation of bipedalism in Australian agamids we examined kinematics and GRF profiles among Australian agamids and compared these to acceleration thresholds. Since bipedal running is a dynamic movement, we included not only estimates of the average position of body segments relative to one another throughout the stride, but also attempted to include estimates of the inertial forces which can act in a free body by including estimates which relate the angular speed and acceleration about body joints.

The mechanisms associated with bipedalism were explored in two ways. Firstly, we hypothesized that there were distinct kinematic or kinetic variables that distinguish quadrupedal, bipedal and transitional strides. Second, we hypothesized that the kinetic variables distinct for bipedal strides that best correlated with differences between the predicted passive threshold [5] and the actual (empirically measured) thresholds [6] will contribute most to extending bipedal sequences among lizards. These variables may be the inspiration for robotic vehicles which will benefit from both bipedal and quadrupedal modes of locomotion.

2. Methods

(a). Study species

Lizards were collected using hand foraging techniques from various non-protected sites in Queensland and Western Australia permitted by the Queensland Department of Environment and Heritage Protection (WISP11435612) and the Department of Conservation and Land Management (SF0003846). In total, we measured 342 strides from 31 individuals from eight agamid species (table 1). All animal care, handling, and experimental procedures in this study were carried out in accordance with The University of Queensland's Animal Ethics act (SBS/195/12/ARC), and that of the University of Western Australia ethics (AEC/00/100/151).

Table 1.

Australian agamid species investigated in this study. N denotes number of individuals used in the experiment for each species; n denotes number of trials for each species.

species	N	mass (g)	n	% bipedal stridesa	accelerationb
Ctenophorus cristatus	4	28.7 ± 2	30	52.6 ± 17	−
Ctenophorus isolepis	3	18.7 ± 0.8	24	3.37 ± 2	+c
Ctenophorus nuchalis	7	22.8 ± 5.4	33	8.3 ± 4.1	+
Ctenophorus ornatus	3	28.1 ± 0.7	26	30 ± 6	−
Ctenophorus reticulatus	1	36.6	15	16.67 ± 10.8	+
Ctenophorus scutulatus	2	22.3 ± 2.7	26	40.4 ± 19	−
Lophognathus gilberti	4	58.7 ± 6	82	83	−c
Intellagama lesueurii	7	46.5 ± 13	106	40 ± 7.9c	+c

^aMean ± s.e. % bipedal strides from Clemente & Withers [4].

^bPositive (+) indicates bipedalism only when during acceleratory strides, and negative (−) indicates bipedal strides with accelerations below zero [6].

^cIndicates results from this study.

(b). Morphometrics

The horizontal BCOM (BCOM_hori) was measured using the reaction board method [6], which was shown to be highly reliable in comparison to other methods [15]. Each specimen was placed along the beam, in a neutral posture, suspended between two scales (±0.01 g; SF-718; SouFei Electronic Co. Ltd; Jiangsu, China). The length of the BCOM_hori from the snout tip was calculated using equation (2.1):

2.1

where, L = length of the beam, m₁ was the mass recorded at the snout tip, and m₂ on the distal scale. BCOM forward of the hip was calculated using equation (2.2):

2.2

where, SVL = snout–vent length and VH = vent–hip (VH) length.

(c). Experimental set-up

A horizontal racetrack (3.6 m × 0.6 m × 0.6 m) was composed of hardwood, with sandpaper adhered to the floor to provide traction, with one side composed a clear Perspex sheet. A HiSpec1 (Fastec Imaging Inc., San Diego, USA; 120, 240 or 250 fps) positioned laterally to the racetrack filmed side views. A second camera, a Fastec IL3-100 (Fastec Imaging Inc., San Diego, USA; 250 fps) or a Casio FX200 (Casio, Japan; 120 or 240 fps) was positioned dorsally above the racetrack to provide top views. Both cameras were synchronized using either internal triggers, or a light pulse from a battery powered LED mounted on the racetrack. Prior to recording, nine landmarks (top of head, shoulder joint, elbow joint, hip joint, knee joint, ankle joint, metatarsal joint, tip of the fourth toe (excluding claw) and tail (1/4 of tail length from the base) were painted on each lizard, using Liquid Paper™ to facilitate digitizing video images (electronic supplementary material, figure S1A,B). We wished to film the acceleration phase of the lizards' run, but excluded the first three steps, as kinematics during these show considerable variation [16], but attempted to use strides shortly following this.

Each stride began at footfall (FF) of a hindlimb, and ended with the subsequent footfall of the same limb, thus each stride consists of two hindlimb steps, and the touchdown of the third. Since lizards typically used a quadrupedal trotting gait [17], the lateral camera was used to classify steps as being bipedal or quadrupedal, by the presence or absence of a touch of the contralateral forelimb. The stride was then classified as being quadrupedal or bipedal gait if all three steps were classified similarly, or a transitional stride if steps changed from quadrupedal to bipedal, or bipedal to quadrupedal.

(d). Kinematics

3D coordinates of each body marker during stance phase were calculated using Direct Linear Transformation (DLTdv5.m) software [18] in Matlab (v. R2012b, Mathworks, Inc., Natick, MA, USA). The calibration object used was a custom-built array of 21 markers, of which the exact position of each marker was known relative to an axis origin point. The x-axis described anterior–posterior direction, the y-axis described medio-lateral direction, and the z-axis described dorsoventral direction perpendicular to the x–y plane (electronic supplementary material, figure S1A,B). Marker positions over time were smoothed using the mean square error algorithm, implemented via spaps.m, as this approach was least error prone [19].

Markers were used to define segments of the body, and from these, segment angles were calculated (electronic supplementary material, figure S1C and table S1). The trunk segment was defined between the hip and the shoulder marker, and the trunk angle (BS) was calculated by the tangent of the trunk segment relative to the global horizontal plane, such that positive values indicated an elevated trunk, while negative values indicated a declined trunk. The tail segment was defined from the hip to the tail marker, and tail angle (TA) was similarly defined relative to the horizontal global coordinate system, such that positive values indicated elevation from horizontal. The following 3D angles were calculated using law of cosines: head–body angle (HB) was the angle between the head segment (between the head and shoulder marker) and the body segment–body tail angle (BT) angle between body segment and the tail segment, upper forelimb angle (UFL) was the angle between the forelimb segment (between the shoulder and elbow) with the body segment. For each angle we calculated the mean angle, as well as the mean angular velocity (° s⁻¹), and acceleration (° s⁻²) throughout the stance phase. We also determined the horizontal distance of the toe and metatarsal marker relative to the hip (toehip, metahip) at FF, at end of stance (ES), and the mean value throughout the stance phase. Similarly we calculated the vertical position of the hip (HH) relative to the y coordinates of the toe at FF, ES and the mean value throughout the stance phase.

(e). Ground reaction forces

The GRF was collected for both the fore- and hindlimbs though only the latter could be measured during bipedal strides. GRF was measured with either an ATI force plate (Nano 17, ATI Technologies, Ontario Canada), or a custom built force plate based on Clemente et al. [20]. Force data were collected at 10 000 Hz and synchronized to the high-speed cameras by an external trigger. The resulting force–time profiles for each trial were converted to newtons (N), and smoothed using the smoothing spline function spaps.m in a custom built Matlab GUI. GRF curves were analysed with respect to two measures of temporal asymmetry which indicated the distribution of vertical impulse throughout the stance [20]; (electronic supplementary material, table S1). Force 1 was the percentage of the stance phase at which half of the total vertical impulse had been produced; values below 50% indicate early skew, values above 50% indicate late skew. Force 2 was the percentage of the total vertical impulse that was produced before temporal mid-stance; values above 50% indicate early skew, values below 50% indicate late skew (electronic supplementary material, table S1).

(f). Acceleration threshold experiments on running lizards

Acceleration was calculated for each stride as the mean acceleration throughout the entire stride, measured using the hip marker. Five different methods were used to estimate the empirical acceleration transitional threshold; the acceleration at which lizards change from quadrupedal to bipedal running (ACC_trans electronic supplementary material, table S1). The first estimate (Estimate 1) used the average acceleration of all transitionary strides as the estimate of empirical transitional threshold. The second estimate (Estimate 2) used only transitionary strides in which the gait changed from quadrupedal to bipedal (i.e. the start of a bipedal bout). The third estimate (Estimate 3) used only transitionary strides where the gait changed from bipedal to quadrupedal (i.e. at the end of a bipedal bout). The fourth estimate (Estimate 4) used the highest recorded quadrupedal acceleration, with the assumption that higher acceleration leads to bipedal strides. The last estimate (Estimate 5) used the inflection point of a binomial logistic regression between quadrupedal and bipedal acceleration to estimate the 50% probability for ACC_trans from quadrupedal to bipedal strides [6].

We compared the empirically measured acceleration thresholds above to the passive acceleratory threshold (ACC_pred) based upon the 2D model presented by Aerts et al. [5]. From this model the vertical force supported by the forelimbs reaches zero at an acceleration given by equation (2.3).

2.3

Ax was then used to represent the predicted acceleration threshold for each species (ACC_pred). BCOM_hori was used for each individual and vertical acceleration over the stride was assumed to be negligible (Az = 0). If BCOM_hori was not available for an individual than the species mean was used. The hip height at midstance was assumed to approximate BCOM_vert. The origin of the GRF vector (xfh) was assumed to be halfway between the toe tip and the metatarsal, and the mean position of these forward of the hip throughout the stance was used. We then calculated the difference between estimated thresholds with predicted thresholds (ACC_trans − ACC_pred = Diff.T), resulting in five different Diff.T estimates.

(g). Statistical analysis

All analyses were performed in RStudio v. 1.0.136 [21]. Data are either presented as means ± standard error (s.e.), or individual data points depending on the nature of the data, and α was set at 0.05 for all statistical tests. Data that were not normally distributed were log-transformed prior to appropriate analysis. Details of statistical analyses and assumptions for each dataset were presented in the electronic supplementary material. In summary, a linear discriminant analysis (LDA) and Wilks lambda (λ) was used to calculate a set of weightings for each kinematic variable (electronic supplementary material, table S1) between gaits, and determine which variables were strongly loaded between gaits. A linear mixed effects model was used to examine the significance of each load between gaits with Tukey contrasts performed for multiple comparisons of means between gaits. Kinematic variables were the response variables, gait as fixed effect, and individual identity and species as random effects to account for repeated measurement among gaits for each species. For each analysis, the mean of trials for each stride type (quad, bi, trans) of each individual animal of each species was used. The relative importance of kinematic parameters with the difference between the estimated and actual threshold (Diff.T) was determined using partial least-squares regression, after each variable was scaled between 0 and 1, to remove magnitude bias.

3. Results

(a). Kinematic differences between gaits

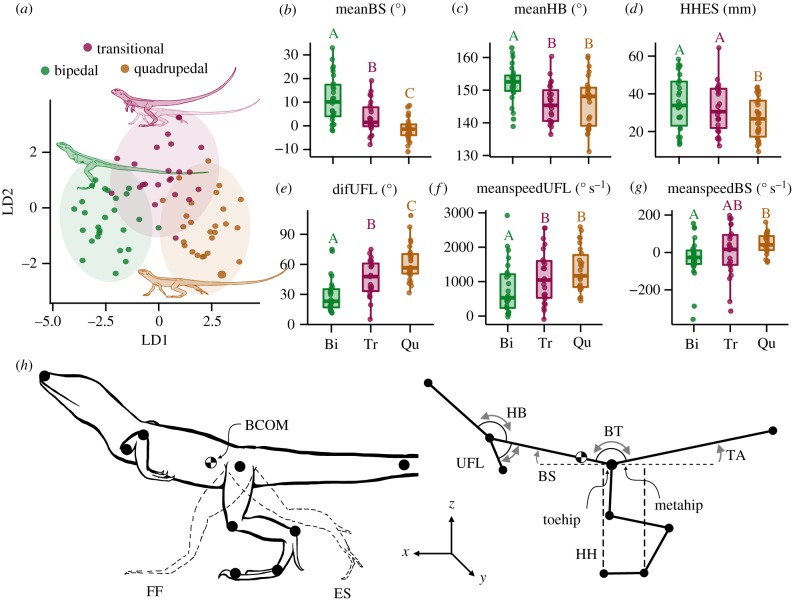
Linear discriminant analysis (LDA) revealed a distinct separation of kinematic variables between quadrupedal, transitional and bipedal gaits, and Wilks λ revealed 10 variables that were significantly different between gaits (F_2,85= 2.75, p < 0.0001; Wilks λ = 0.117). The first discriminant function (LD1) explained 83.4% of total variance and appeared to separate bipedal and quadrupedal strides (figure 1a; electronic supplementary material, table S2). Bipedal strides loaded negatively revealing greater trunk rotation (meanBS) and head-to-body angle (meanHB), and a higher hip height at end stance (HHES; figure 1b–d). Conversely quadrupedal strides loaded higher for the mean angular speed of the trunk (meanspeedBS) and at the shoulder (meanspeedUFL), and a greater difference in forearm displacement (difUFL; figure 1e–g). Therefore, lizards during bipedal strides exhibited a more upright body posture, were higher during endstance, better aligned the head with the body, and reduced upper forelimb movement compared to quadrupedal strides. The second discriminant function (LD2) accounted for 16.6% of the total variation and separated transitional strides from bipedal and quadrupedal strides (figure 1a). Transitional strides loaded positively for the difference in trunk angle (difBS), the difference in the head-to-body angle (difHB), and the angular rotation speed of the tail (meanspeedTA; electronic supplementary material, table S2).

Figure 1.

Linear discriminate (LD) loads between gaits, with boxplots of top three loads for positive (mean body–shoulder: meanBS, mean head–body: meanHB, hip height at end stance: HHES), and negative (difference in upper forelimb angle: difUFL, mean angular speed of the forelimb: meanspeedUFL, mean angular speed of the body–shoulder: meanspeedBS) loadings for LD1. (a–g) Data are presented as individual data points for bipedal (green dots, n = 26), transitional (purple dots, n = 23), and quadrupedal (orange dots, n = 26) strides for each animal. Boxplots show 25th and 75th percentile, and the centreline is the 50th percentile, lines represent the max/min values (within the 1.5 × IQR) and dots represent outliers (< Q1 − 1.5 × IQR || > Q3 + 1.5 × IQR). Letters represents significance between gaits. (h) Schematic diagram of kinematic changes during bipedal strides with grey arrow representing direction of changes in angle during bipedal stride. Full names of abbreviations and descriptions of direction of angle change provided in electronic supplementary material, table S1. Summary statistics in electronic supplementary material, tables S2 and S3. (Online version in colour.)

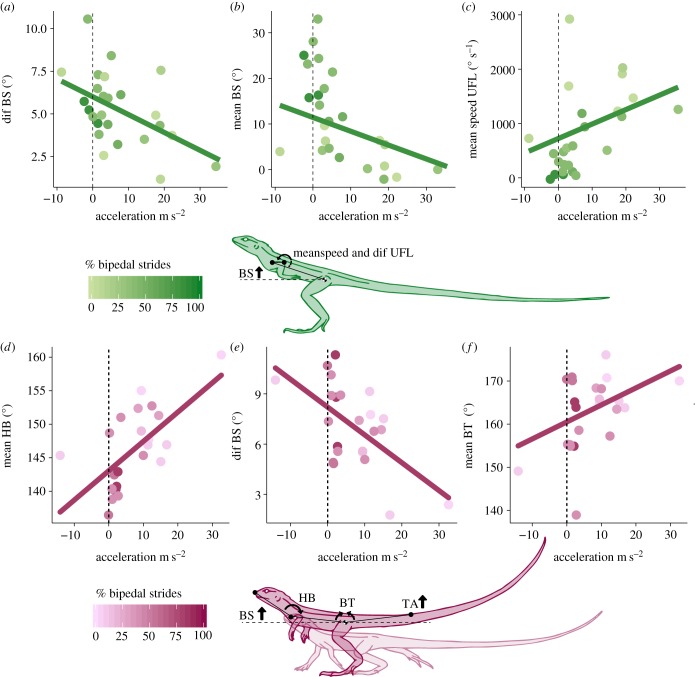
Of the 10 kinematic variables that were significantly different between gaits (electronic supplementary material, table S3), four kinematic variables showed significant correlation with stride acceleration during bipedal gaits (electronic supplementary material, table S4). Mean and difference in trunk angle (meanBS, and difBS) increased as acceleration decreased, while mean angular speed of the forearm displacement (meanspeedUFL and difUFL) decreased as acceleration decreased (figure 2a–c), suggesting an uplift of the body and stabilization of the forelimb and head as the animal reduces acceleration. The remaining six kinematic variables (meanHB, meanspeedBS, HHES, difHB, meanspeedTA, meanBT) showed no significant correlation with stride acceleration (electronic supplementary material, table S4).

Figure 2.

Summary of change in body kinematics during acceleration (m s^–2) of bipedal (a–c) and transitional (d–f) strides. Data presented as individual data points for bipedal (•, n = 25), and transitional (•, n = 23) strides for each animal. Gradient colours represent the percentage of bipedal strides from Clemente & Withers [4] and this study for the individuals of each species. Regression lines presents model prediction, and vertical dash lines represents no acceleration. Summary statistics in electronic supplementary material, tables S4 and S5. (Online version in colour.)

During transitional strides there were five kinematic variables that were significantly correlated with stride acceleration (electronic supplementary material, table S5). MeanBS, difBS, and mean speed TA angle significantly increased as acceleration decreased. MeanHB angle, and meanBT angle decreased as acceleration decreased, suggesting that animals with transitional strides at lower acceleration have greater uplift of body, and tail posture above hip height, and uplift of head relative to body compared to higher acceleration strides (figure 2d–f). The remaining four kinematic variables (HHES, meanspeedUFL, difUFL, difHB) showed no significant correlation with stride acceleration (electronic supplementary material, table S5), suggesting no change.

(b). Asymmetry in ground reaction force between gaits

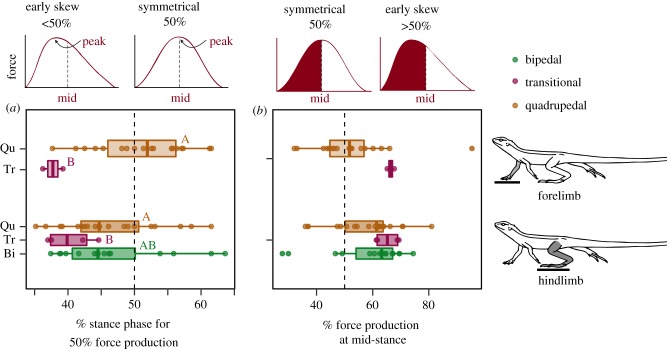
We tested variation in GRF among gaits and between the limbs. There was a significant difference in percentage of stance phase when 50% of force is produced (Force 1) among gaits, but not among limbs. A post hoc test revealed that during the transitional strides, there was a disproportional larger force produced early during the stride, when compared to both bipedal and quadrupedal strides (figure 3a), however, there was no significant difference in asymmetry between bipedal and quadrupedal strides (electronic supplementary material, table S6). There was also no significant difference in percentage of force produced at midstance (force 2) between gaits nor between the limbs (electronic supplementary material, table S6). However, like the results above transitional strides produced over 60% of the force by midstance, while quadrupedal and bipedal strides had a much wider distribution of asymmetry profiles (figure 3b).

Figure 3.

Asymmetry of force measurements for each gait between forefoot and hindfoot. For (a) the percentage of the stance phase at which half of the total vertical impulse had been produced (force 1), and (b) percentage of force produced at midstance (force 2). Boxplots as for figure 1. Data presented as individual data points each stride for each animal (quadrupedal: orange dots, forelimb n = 18, hindlimb n = 20, transitional: purple dots, forelimb n = 2, hindlimb n = 4, bipedal: green dots, n = 15). Top bell curve graphs represents shift in force symmetry for force 1 (left), and force 2 (right). Within the panels, the top sets present forelimb GRF profiles, while the bottom sets represent hindlimb GRF profiles. Letters represent significance between gaits. Vertical dashed line indicates predicted response for a symmetrical vertical GRF pattern. Summary statistics in electronic supplementary material, table S6. (Online version in colour.)

(c). Acceleration threshold analysis

The passive threshold calculated from the Aerts et al. [5] model were not significantly different among the different gaits reported (F_2,65 = 2.77, p = 0.070), when using individual mean estimates in a linear mixed effects model with species included as a random factor. When comparing the passive threshold with the empirically derived acceleration estimates, the results appear mixed depending on which estimate is used. The inflexion point of a binomial logistic regression (Estimate 5) shows the strongest effect (electronic supplementary material, table S7), though this appears in most part to be driven by the high quadrupedal acceleration measured from a single individual. This results in a model showing a low slope estimate of 0.118 (slope = 1.0 suggests perfect agreement). The second best performing estimate used the mean of transitional strides moving from quadrupedal to bipedal (Estimate 2). This showed a higher slope agreement of 0.58 (electronic supplementary material, table S7). No other estimates showed a significant relationship between these estimates.

(d). Kinematics associated with threshold differences

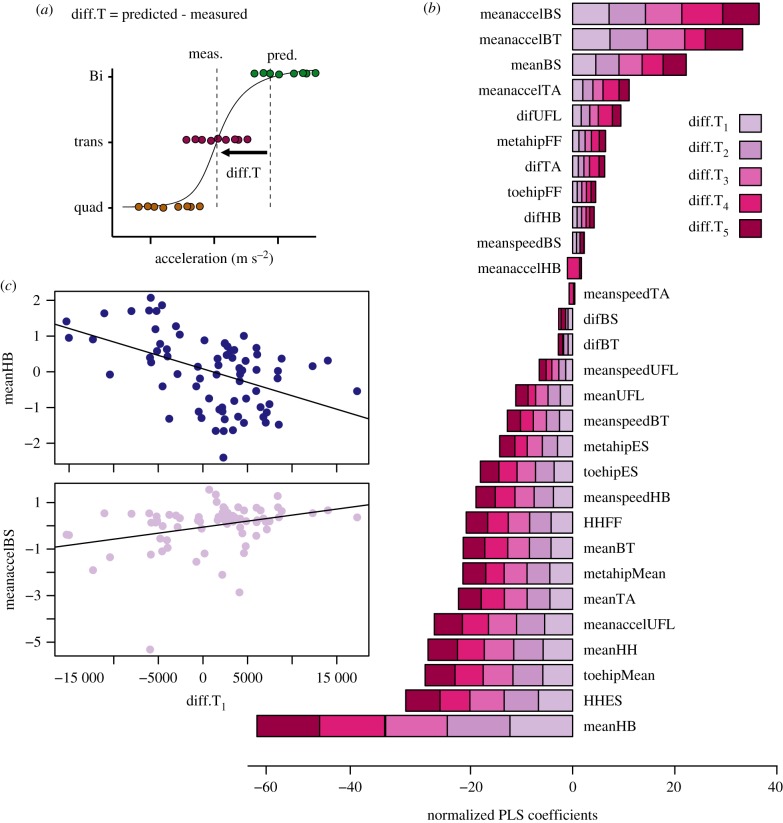
The relative importance of kinematic variables for each of the five threshold differences (diff.T) were shown in figure 4b. The results indicate several kinematic variables were associated with these threshold differences. The mean angle between the head and body appeared to have the highest weighting among all the variables studied. In each case there was a negative relationship between diff.T and meanHB suggesting that greater positive variation from the model (i.e. going bipedal earlier than predicted) was associated with small head–body angles, likely indicating the head is tilted more posteriorly (figure 4c). The mean acceleration of the body–shoulder angle and the body–tail angle (and to a lesser extent Tail angle) were positively associated with diff.T, indicating that rapid changes in position of the body and tail segments relative to the horizontal were better associated with greater positive variation from the model (i.e. earlier bipedal bouts) (figure 4c).

Figure 4.

The relative importance of 30 different kinematic variables in predicting the differences between estimated and empirically derived acceleration thresholds. Data presented are for 75 observations from eight species, including 26 bipedal strides, 26 quadrupedal strides, and 23 transitional strides. Each kinematic variable is compared to the difference between predicted and estimated acceleration thresholds (a). Shows example data of the difference between the model prediction and estimates for empirical thresholds (electronic supplementary material, table S1), and results are shown stacked for each kinematic variable (b). The significant relationship between this difference and two example kinematic variables is shown in (c), for the mean head to body angle (meanHB), and the mean acceleration of the body–shoulder segment about the hip (meanaccelBS). (Online version in colour.)

Several other variables showed a strong negative correlation with diff.T indicating a reduction in these variables was associated with transition to the bipedal gait at lower than predicted accelerations (figure 4b). These include three hip height estimates; hip height at the end of stance phase, mean hip height, and the toe to hip height. Mean acceleration of the forelimbs was also negatively related to diff.T, suggesting movement of the forelimbs is reduced in species which run bipedally sooner than model predictions.

4. Discussion

Among extant vertebrates, bipedalism appears to have evolved multiple times, and fossil evidence suggests it may have been used early on in the evolution of squamates [22]. Bipedalism in lizards, was suggested to have occurred through an accidental consequence of changes to the BCOM, however, it was clear that some lizards appear able to run bipedally in the absence of acceleration [4,5] and further biomechanical modelling suggested several kinematic mechanisms through which this could be achieved [11]. These lizards were thought to be exploiting bipedal locomotion, by modifying biomechanics to extend the length of bipedal sequences. We explored kinematic and kinetic evidence for this hypothesis in the current study.

Previous studies which compared kinematics of bipedal and quadrupedal strides among lizards, have showed several key differences between these gaits [10] supporting the findings of the current study. Trunk angle was highlighted as an important predictor for bipedal locomotion, which also support previous modelling efforts [5,11]. Positive rotation of the trunk shifts the BCOM posteriorly and therefore reduces the nose-down pitching moment caused by gravity, extending bipedal sequences [11]. This current study had also shown other differences were evident too; the head appears to be tilted forward during bipedal locomotion, probably to compensate for the rearward tilting of the trunk and to re-align the head with the direction of travel, likely aiding the visual field. Movement of the forearms was also reduced among bipedal strides. This seems reasonable given the forearms are actively used to propel the body forward during quadrupedal locomotion, but it also highlights that the forelimbs are actively tucked backwards during bipedal locomotion (figure 1e). Tucking back of the forelimbs may not only help reduce interference with the hindlimbs, one of the early perceived benefits of bipedal locomotion [1], but may also help contribute to the overall shift of the body COM rearward, extending bipedal sequences.

These measurable kinematic differences between bipedal and quadrupedal strides, support previous studies suggesting bipedal strides may be distinct from quadrupedal strides in at least a few species of lizards [10], though these differences are perhaps not as pronounced as gait changes seen in other groups (e.g. mammals; [23–25]). For several kinematic variables, bipedal strides appear to be at one end of a continuum of variation from quadrupedal to transitional to bipedal strides (figure 1b–g), highlighting the overall similarity of leg mechanics between these gaits. Yet the LD analysis revealed distinct differentiation in kinematics during transitional strides, specifically relating to the uplifting of the tail and head to allow bipedal locomotion. These trends follow Van Wassenbergh & Aerts [11] prediction for the requirements to transition towards bipedal strides. Active tail lifting during the acceleratory phase was highlighted by Aerts et al. [5], to affect trunk angle positively, via increased local and remote angular momentum to the tail, which may become important for increasing the kinetic energy available to rotate the body.

Transitional strides also differed from bipedal and quadrupedal strides in the shape of the GRF profiles. While all gaits showed a characteristic early skew, transitional strides had a significantly earlier skew than both bipedal and quadrupedal ones, suggesting that more force is applied early on in the stance phase of the stride. The significance of this for bipedalism was demonstrated mathematically by Van Wassenberg & Aerts [11]. Asymmetrical GRFs will increase the nose-up pitching moment during running by increasing the proportion of the stride when the GRF vector is anterior to the BCOM. Asymmetrical GRFs have been previously shown during bipedal and quadrupedal running in agamids [20], quadrupedal running in Tegus [26], and bipedal water-running in basilisks [27], which suggested that some level of asymmetry is common among all lizard species. However, the exaggerated asymmetry reported here for transitional strides may indicate that this kinetic characteristic may be exploited by some species of lizards in order to transition to the bipedal strides.

However, comparing variations in kinematics between bipedal and quadrupedal strides cannot describe the mechanism behind the transition, and is complicated by a strong link to acceleration [4]. We were interested in the extent to which lizards were actively attempting bipedal locomotion, thus we compared the acceleration threshold expected from a purely passive lizard model Aerts et al. [5] to the empirically derived threshold estimates. Overall the agreement between passive thresholds and empirical thresholds estimates was weak. Yet, of the five empirical estimates tested, Estimate 2, the transition acceleration from quadrupedal to bipedal, best related to the passive model, suggesting the start of bipedal locomotion may closely follow the model proposed by Aerts et al. [5]. Alternative models show greater variation, and a likely explanation for this is that they contain strides where lizards are using kinematic or kinetic mechanisms to extend bipedal runs. Deviations from the passive model appear to be greatest where strides return from bipedally running to quadrupedally running (Estimate 3), which may indicate different mechanics in action between the quadrupedal to bipedal transition compared with the opposite scenario. Yet all estimates show a slope below 1, suggesting species are generally running bipedally at lower accelerations than we might predict.

To understand which kinematic mechanisms lizards use to run bipedal sooner, we compared kinematics to the difference between the passive model and each empirically derived estimate. We reasoned that differences from the passive model may be the result of active movements of the body, and the greater these movements are at creating the nose-up pitching moment then the more likely they will correlate with these differences. Our analysis revealed that the more dynamic movement of segments, for example, angular acceleration of the trunk about the hip (meanaccelBS), and of the tail about the hip (meanaccelBT) were critical in bipedal locomotion. These are significant as the high angular acceleration of the tail implies a large amount of torque is being applied to the hip, which has the ability to impart large angular moments to the body [14], meaning less explosive accelerations may be required to produce nose-up rotational moments.

These dynamic changes to the position of segments throughout a stride may give insight into the control strategies underlying performance and may be based at different levels of organization. Changes in the muscular skeletal systems, (e.g. small changes in the size, origins and insertions of muscles, or limb segment lengths) may change over evolutionary time among species and determine differences in dynamics (e.g. [28]). This may explain the result of Clemente [6] who showed an evolutionary trend over time towards greater differences between passive and empirical estimated thresholds among 10 species of agamids. Alternatively changes to the muscle activation patterns may be under behavioural control and kinematics may be altered within a species between quadrupedal and bipedal strides to exploit bipedalism. There is further evidence for this latter strategy among lizards. Experiments which have varied the height of obstacles in a trackway down which lizards are run, have recorded behavioural differences in the frequency of bipedal strides [29].

This study highlights the importance of including not only positional estimates of limbs during steady-state locomotory trials, but of the inclusion of variables which are able to indicate the magnitude and rate of change between segments throughout the stride. Numerous studies have highlighted the importance of swinging appendages to aid stabilization in human walking [30,31], arboreal jumping and climbing in primates [32–34] as well as rodents [35] and cats [19]. Further, in lizards, tails have been shown to allow righting and turning in mid-air to aid stabilization while jumping [14] or gliding [36]. Here we show the lizard tail may also be used to de-stabilize quadrupedal locomotion, in order to temporarily switch to, and extend a bipedal sequence while running. The functional purpose of these bipedal stretches remains to be conclusively demonstrated, but increased obstacle negotiation seem likely [7]. These findings may have important implications for the design of bioinspired robotic devices. Similar de-stabilization efforts can be incorporated into robot devices, which may not only aid jumping performance as has previously be shown [13,14] but to benefit robots attempting to transverse complicated or uneven environments.

Ethics

All animal care, handling, and experimental procedure in this study were carried out in out in accordance with The University of Queensland's Animal Ethic act (SBS/195/12/ARC), and that of the University of Western Australia ethics (AEC/00/100/151).

Data accessibility

Codes, data and electronic supplementary material are available via (https://drive.google.com/open?id=1Z-ZjNYN6_F8FyGrJsyJjZenb5vZajitc).

Authors' contributions

C.J.C. conceived the project, collected the data, analysed the data and wrote the manuscript. N.C.W. collected the data, analysed the data and co-wrote the manuscript.

Competing interests

We declare we have no competing interests.

Funding

This study was financially supported by an ARC DECRA Fellowship to C.J.C. (DE120101503), and an ARC Discovery award to C.J.C. (DE180100220).