Computational modelling suggests complex interactions between interstitial flow and tumour angiogenesis

Abstract

Angiogenesis, the growth of capillaries from pre-existing ones, plays a key role in cancer progression. Tumours release tumour angiogenic factors (TAFs) into the extracellular matrix (ECM) that trigger angiogenesis once they reach the vasculature. The neovasculature provides nutrients and oxygen to the tumour. In the ECM, the interstitial fluid moves driven by pressure differences and may affect the distribution of tumour TAFs, and, in turn, tumour vascularization. In this work, we propose a hybrid mathematical model to investigate the influence of fluid flow in tumour angiogenesis. Our model shows the impact of interstitial flow in a time-evolving capillary network using a continuous approach. The flow model is coupled to a model of angiogenesis that includes tip endothelial cells, filopodia, capillaries and TAFs. The TAF transport equation considers not only diffusive mechanisms but also the convective transport produced by interstitial flow. Our simulations predict a significant alteration of the new vascular networks, which tend to grow more prominently against the flow. The model suggests that interstitial flow may produce increased tumour malignancies and hindered treatments.

1. Introduction

At the early stages of tumour development, cancerous cells rely on the pre-existing vasculature for their nourishment [1]. However, their accelerated cellular multiplication eventually renders this supply insufficient and creates regional hypoxia (oxygen- and nutrient-deprived regions) [1]. Under these conditions, some mutated tumour cells are able to release signalling factors, commonly known as tumour angiogenic factors (TAFs). When these factors bind to the endothelial cells that form the pre-existing vasculature they initiate angiogenesis, i.e. the growth of new capillaries [2–4]. TAFs promote a phenotype change in endothelial cells: some cells known as tip endothelial cells (TECs) become migratory, while others known as stalk endothelial cells become proliferative. The mechanism that selects the phenotypical change is called lateral inhibition [5]. TECs direct their migration towards the tumour following gradients of TAF aided by cytoplasmatic projections or filopodia [6,7]. Stalk cells trail behind them forming a new capillary by proliferation. The process continues until the stimuli end or the new capillary fuses with another one (anastomosis). As a result, the tumour becomes vascularized, hypoxic regions become normoxic and the lesion continues its growth.

Tumour angiogenesis research has been driven by the discovery of the biochemical signalling pathways that regulate the process. The role of biophysical cues, however, is receiving increasing attention. Significant progress has been made in understanding how pressure and shear stresses produced by intravascular flow control angiogenesis by remodelling vessel networks [8–15]. The role of interstitial flow in tumour angiogenesis has received little attention. However, since tumour angiogenesis is tightly regulated by soluble substances that are transported through the extracellular matrix (ECM), the influence of convective transport produced by interstitial flow may be significant, especially in the tumour micro-environment, where strong interstitial flows have been reported [16,17] (figure 1). Although recent noteworthy advances in microfabrication and microfluidic technology that allow the creation of in vitro multicellular microvascular tissues with simultaneous control of interstitial flow and the TAF spatial concentration gradient have demonstrated the importance of interstitial flow [18], the mechanistic understanding of the process has remained elusive. Achieving further progress requires controlling and/or measuring simultaneously TAF concentrations and interstitial flow in an experiment that recreates conditions similar to those encountered in vivo. This is challenging because there is a tight two-way coupling: flow has a strong impact on angiogenesis, at least modifying the spatial distribution of TAF; and the TAF distribution controls the geometry and topology of the neovasculature, which, in turn, determines flow. Computational modelling may be beneficial to study this problem because, under certain assumptions, it provides high-resolution information of the fluid flow and TAF distributions. Previous mathematical models have shown their potential as predictive tools in angiogenesis (see [19–23]) but, to the best of our knowledge, none of them has coupled angiogenesis with a multidimensional description of the intra-, trans- and extravascular flow in a capillary network that evolves in time. Although our interest is the effect of extravascular (i.e. interstitial) flow on angiogenesis, the fluid flow in the interstitium is to a great extent determined by the intravascular and transvascular flow in the growing vascular network. Therefore, we propose a model that couples intra-, trans- and extravascular flow with tumour angiogenesis, accounting for the convective transport of TAFs. We show that the model naturally predicts the experimental observation that new vasculature grows more prominently against the flow. We also use the model to make predictions on the impact of interstitial flow on the angiogenic switch¹ of small tumours and the effect of elevated intratumoral pressure that produces flow radially outward of a cancerous lesion.

Figure 1.

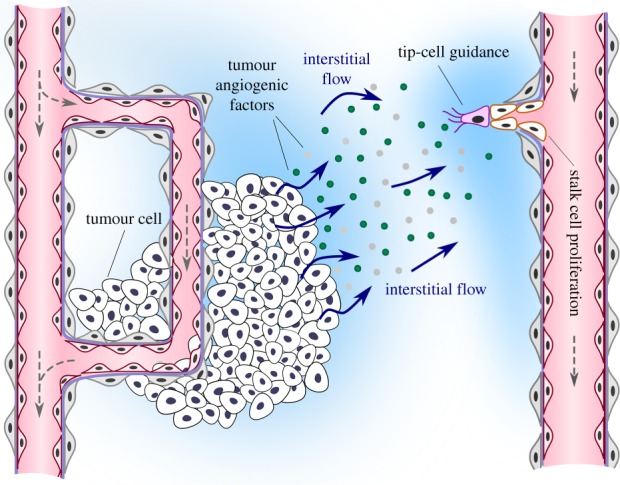
Angiogenesis starts with the activation of tip endothelial cells by tumour angiogenic factors, which are released in hypoxic regions and transported to nearby capillaries. Tumour angiogenic factor transport is usually assumed to be purely diffusive, but convective transport by interstitial flow may significantly influence tumour angiogenesis.

2. Model of convection-mediated angiogenesis

Our theoretical framework is based on an angiogenesis model that is coupled to a fluid flow theory. The angiogenesis model, based on the work developed in [24–28], is a hybrid theory with two continuous partial differential equations and a set of discrete agents. The continuous equations describe the location of the capillaries and the concentration of TAFs. There are several relevant TAFs, but the vascular endothelial growth factor (VEGF) is considered one of the most potent ones [29]. For simplicity, our model for TAFs considers VEGF only. The discrete agents represent TECs which lead the growth of new capillaries in angiogenesis. The fluid flow model is based on Darcy's Law and its unknowns are fluid velocity, u, and pressure, p. The angiogenesis and the fluid flow models are fully coupled: the fluid transports TAF, which modifies the capillary field (both through endothelial cell proliferation and through the creation of TECs), and the distribution of capillaries controls the fluid flow—much of the fluid transport occurs through the capillaries, but the model accounts for extravasation and interstitial flow. In the rest of the section, we describe the models separately.

2.1. The angiogenesis model

2.1.1. The continuous variables (c and f)

The location of capillaries (defined by c) and the VEGF concentration f comprise the continuous part of the model. These equations will be later coupled to the flow model which determines the velocity and pressure inside and outside the capillaries. Therefore, to avoid meshing the vessels, we resort to the phase-field method [30–32], which permits an implicit description of the capillaries through a continuous field c defined on the entire tissue. The phase-field c is governed by the equation

2.1

where M > 0 is the mobility and is the Heaviside function. The function μ(c) = −c + c³ represents the derivative of a double-well potential that drives the solution to c = 1 or to c = −1, which can be interpreted as stable uniform solutions in the absence of TAF. The regions of the tissue where c ∼ 1 represent the capillaries, while c ∼−1 represents the ECM. The transition between the capillaries and the extravascular space is smooth and occurs across a length scale proportional to λ; see a one-dimensional solution to equation (2.1) in figure 2. The function represents the endothelial cell proliferation and is defined as

2.2

Here, B is the proliferative rate constant and f_p is the TAF condition for highest proliferation.

Figure 2.

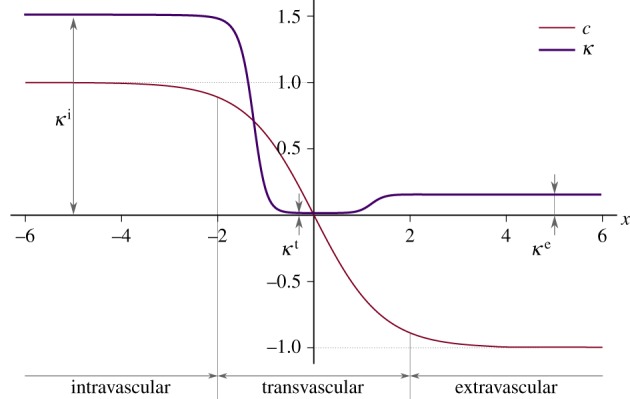
Hydraulic conductivity function. We plot 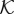as a function of 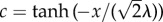, that is, the one-dimensional solution to the phase-field equation on an infinite domain. The phase-field creates smooth interfaces that permit the differentiation of intravascular, transvascular and extravascular regions. Accordingly, the hydraulic conductivity displays three plateaus, one per region, connected by smooth transitions. In this plot, we take κ^e = 0.15, 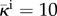, 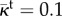and λ = 1. Although these values are not realistic, we use them in the plot to enable a simple visualization of the hydraulic conductivity as a function of c.

The TAF is produced in hypoxic regions, diffuses throughout the ECM, and is consumed by endothelial cells [33]. In the proposed model, additionally, the TAF is convected by the fluid [34]. The proposed governing equation is

2.3

where D is the diffusion constant of VEGF, u is the fluid velocity, f_hyc is the maximum TAF produced in a hypoxic region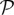, and and 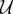are the TAF production and uptake by capillaries, respectively. These functions are defined by

2.4

and

2.5

where P is the production rate, d is the distance to the closest hypoxic cell, R is an average cell radius, U_u is the endothelial cell uptake rate and U_d is the TAF natural decay rate and uptake rate by other cells. The value of t* is zero, except when there is a capillary in the neighbourhood of a hypoxic cell. When a capillary is at a distance short enough so as to effectively provide oxygen to a hypoxic cell, t* starts counting time and the VEGF production rate decreases as per (2.5). We assume that the VEGF production rate starts decreasing (t* > 0) when a capillary is at a distance δ_nox or lower to the hypoxic cell, where δ_nox is the oxygen diffusion length scale.

2.1.2. The discrete agents (tip endothelial cells) and their coupling to the continuous description

TECs are modelled as circular discrete agents with radius R. Discrete agents can be created at any point in the domain if the following conditions are met: (1) c > c_act, (2) f > f_act and (3) the distance to the closest TEC is greater than δ₄. The first condition indicates that TECs can only be located in regions of the tissue occupied by endothelial cells; the second one expresses that TEC activation requires that VEGF has reached the existing capillaries with sufficient concentration; the third one accounts for the lateral inhibition mechanism that prevents the formation of several sprouts in the same region. An active TEC initially moves with a constant velocity v_tec = χ(∇f/|∇ f|), where χ is the chemotactic speed. Once a TEC is outside its parent capillary, it develops filopodia, which we model as a set of check points distributed in an annular sector, centred in the direction of the TAF gradient, with angle 2π/3, and with internal and external radius 2R and 4R, respectively (see fig. 2 in [28]). A positive check in one of these points (c > −0.9) implies that filopodia have detected a nearby endothelial cell and the TEC alters its velocity direction towards it. Finally, TECs get deactivated if they fail to meet any of the above-mentioned conditions for activation or if they encounter another TEC or capillary in their migration path (anastomosis).

There is a two-way coupling between the discrete agents and the continuous variables. On the one hand, the activation, movement and deactivation of the agents depend on point-wise evaluations of the continuous variables. On the other hand, the value of the phase-field c is overwritten at the region occupied by each TEC (a circle with radius R). In particular, c takes the value one within this region such that TECs form automatically part of the intravascular region defined in this theory (see electronic supplementary material, text T1, for more details of the discrete agents).

2.2. The fluid flow model

Our goal is to understand how fluid flow controls angiogenesis through VEGF convection in the extravascular space. Therefore, we are mainly interested in the interstitial flow. However, interstitial flow emanates from capillaries and we need some notion of intravascular flow. Developing an accurate computational model that accounts for coupled intravascular and extravascular flow on a time-evolving capillary network is an open research problem that is out of the scope of this paper [35–40]. Therefore, we resort to a porous media flow model in which capillaries are modelled as highly permeable regions and the vascular wall as a low hydraulic conductivity layer. The extravascular space is assigned a hydraulic conductivity value taken from experiments. Thus, considering that blood plasma and the interstitial fluid have the same properties, and under the assumptions of incompressible, stationary and creeping flow, the governing equations may be written as

2.6

and

2.7

where 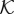is the hydraulic conductivity function. We define 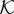by using three constant values associated with the intravascular, the transvascular and the extravascular regions. The value of 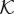transitions smoothly as we move from one of the regions to another. As one of the main variables of the angiogenesis model is the location of capillaries c, we could straightforwardly delineate the extra- and intravascular regions. More interestingly, recalling that the dynamics of c is governed by a phase-field equation that generates thin but smooth transitions between these regions, we make use of this property to define the following hydraulic conductivity function:

2.8

where κ^e is the extravascular hydraulic conductivity, 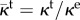is the normalized transvascular hydraulic conductivity and κ^t is the transvascular hydraulic conductivity. Figure 2 shows the spatial variation of 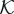across a cut-line perpendicular to a capillary wall. The red line shows a generic solution of the phase-field equation, which transitions from c ∼ 1 (intravascular region) to c ∼−1 (extravascular space). In equation (2.8), ϑ is a function of the phase field that accounts for the different permeabilities of the intravascular and extravascular regions through the expression

2.9

where 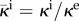is the normalized intravascular hydraulic conductivity and κⁱ is the intravascular hydraulic conductivity. The last factor of equation (2.8), 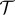, can be understood as a weighting function that modifies ϑ in the transvascular region and is defined as

2.10

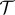depends on the gradient of the phase-field in such a way that only affects 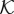in the transvascular region, that is, where the gradient is large. The term 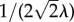and the factor 10λ are needed to ensure that if the thickness of the capillary wall changes, the hydraulic conductivity function will adapt accordingly. Although, in principle, it should be possible to define 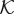using the value of c only, we found that using also ∥∇ c∥ permits a more accurate location of the transvascular region. This formulation is also less sensitive to numerical errors in the computation of c.

2.3. Parameters

Table 1 summarizes the values of the parameters of the model. There, we categorize the parameters according to the different sub-models. Those for which there was no available data are estimated, as explained below. The rest are taken from experimental measurements or have been used in previous models of tumour angiogenesis.

Table 1.

Values of the parameters grouped by sub-models.

	description	value	reference
M	mobility	1.002 × 10−11 cm2 s−1	[28]
λ	interface width	1.25 μm	[41]
B	proliferative rate	4.987 × 10−6 ml (ng s)−1	[24]
fp	VEGF condition for highest proliferation	54 ng ml−1	[24]
D	diffusion	1.002 × 10−7 cm2 s−1	[42]
fhyc	maximum VEGF production	180 ng ml−1	[43,44]
P	production	6.410 × 10−2 l s−1	numerical
Uu	endothelial cell uptake	4.006 × 10−1 l s−1	estimated
Ud	natural decay	6.410 × 10−5 l s−1	[45]
χ	chemotactic speed	0.194 μm s−1	[46,47]
δnox	nutrient and oxygen diffusion length	25 μm	[48,49]
cact	condition for TEC activation	0.9	[24]
fact	condition for TEC activation	0.72 ng ml−1	[28]
δ4	condition for TEC activation	80 μm	[48,49]
R	TEC radius	5 μm	[50]
κe	extravascular hydraulic conductivity	5.008 × 10−8 cm2 (s mmHg)−1	[15,51]
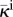	normalized intravascular hydraulic conductivity	10.0	[52,53]
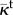	normalized transvascular hydraulic conductivity	0.1	[54]

The fluid flow problem is completely defined by three parameters, namely, κ^e, κⁱ and κ^t. As shown in the table, the extravascular hydraulic conductivity is 5.008 × 10⁻⁸ cm² s⁻¹ mmHg⁻¹, which is within the range of data from the literature [15,51]. In the intravascular region, the fluid flows more easily than through the interstitium, thus, κⁱ ≫ κ^e. For the capillary networks considered in this paper, taking κⁱ/κ^e = 10³ would produce intravascular velocities of the order of approximately 0.1 mm s⁻¹, which are consistent with the estimates in the literature for non-tumoral capillaries [52]. However, the heterogeneous leakiness of tumour vessels along with other morphological abnormalities of the network produce a velocity that is one to three orders of magnitude lower [52,53]. Therefore, we took κⁱ/κ^e = 10. Tumour-induced capillaries are characterized by being leaky, but their permeability is difficult to estimate. In addition, vascular permeability depends on the local VEGF concentration. In this paper, we take the constant value κ^t = 5.008 × 10⁻⁹ cm² s⁻¹ mmHg⁻¹, which is approximately 5 times larger than the value reported in [54] for oxygen permeability through a physiological vascular wall.

The remaining parameters belong to the continuous and discrete angiogenesis model, many of which have been already used in other mathematical models. In particular, following [42], we set the diffusion coefficient of VEGF to D = 1.002 × 10⁻⁷ cm² s⁻¹. The mobility of the phase-field sets the time scale for the capillary remodelling dynamics, which is much slower than the diffusion of VEGF. Following [28], we set the same ratio D/M, so that M = 1.002 × 10⁻¹¹ cm² s⁻¹. The length scale λ is proportional to the width of the intravascular region, that is, the capillary wall. We set its value to 1.25 μm so that we obtain an intravascular region of the order of 1 μm [41]. The values of the proliferative constant and the TAF condition for maximum proliferation were defined following the parametric study in [24]. The endothelial cell uptake is U_u = D/R² = 4.006 × 10⁻¹ s⁻¹ so that the TAF cannot penetrate inside a capillary farther than the radius of a TEC R. We take R = 5 μm, which is within the range of measured values [50]. Taking an average value for the half-life of VEGF equal to 3 h [45], the value of the natural decay rate results U_d = 6.410 × 10⁻⁵ s⁻¹. P is a purely computational constant that acts as a penalty parameter. We found through numerical simulations that the value of P has almost no influence on the solution. Therefore, we set it to a value high enough to drive the value of f to f_hyc in the hypoxic regions without affecting the convergence of the numerical method. In particular, we used the value P = 6.410 × 10⁻² s⁻¹. In the absence of an equation for the nutrient diffusion as in [48,49] and considering the high nutrient uptake of cancer cells and the faulty structure of tumour-induced capillaries we have set δ_nox to 25 μm. Furthermore, we have set δ₄ to 16R, so that TECs impede the activation of other TECs in their neighbourhood.

The value f_hyc = 180 ng ml⁻¹, which defines the maximum concentration of VEGF, was taken from mouse cornea micropocket angiogenesis assays [43,44]. By setting the chemotactic speed χ to 0.194 μm s⁻¹, we obtain TEC velocity values within the range observed in [46,47]. Under physiological conditions, every cell is at a maximum of 100–200 μm from a blood vessel. We have set the TAF condition for TEC activation f_act = 0.72 ng ml⁻¹ so that hypoxic cells located farther than 200 μm away from a capillary can activate TECs.

2.4. Numerical method

Our mathematical model is composed of a continuous and a discrete part. The continuous compartment is described by partial differential equations. The discrete part involves algorithms for the activation, movement and deactivation of TECs and filopodia probing, as well as the coupling with the continuous variables. We developed an efficient numerical method that robustly handles these complexities. The spatial discretization of the continuous equations is performed using isogeometric analysis [55]—a generalization of the finite-element method that permits a straightforward discretization of equations with spatial derivatives of order higher than two, such as equation (2.1). Our variational formulation is based on the Galerkin method. We confirmed that for the elemental Peclet numbers (see electronic supplementary material, text T1) considered in this paper our formulation did not present convective instabilities. This was done by performing a mesh refinement study and comparing our Galerkin solutions with those obtained using the streamline upwind Petrov–Galerkin method—a standard stabilized finite-element method [56]. The coupling between the continuous and the discrete compartments was performed using the concept of templates, which allows one to blend the discrete agents into the continuous formulation using a generalization of an exact solution to the phase-field equation; see [25]. Time integration was performed using the generalized-α method, which is a second-order scheme that features unconditional linear stability. The details of the algorithm may be found in electronic supplementary material, text T1.

2.5. Basic features of the model

Here, we study angiogenesis with and without VEGF convection. These simulations illustrate the features and capabilities of the model, showing the type of information that can be extracted from our computational approach. As shown in figure 3 and electronic supplementary material, video V1, we perform simulations on a square piece of tissue of size 375 × 375 μm. We place two 6.25 μm thick capillaries along the left and right sides of the square and a hypoxic region at its centre, mimicking a 68.75 μm radius, hypoxic tumour. Note that the initial conditions of capillaries and hypoxic region in this simulation (as well as in the remaining simulations in this work) are symmetric, so that we can isolate the effect of interstitial flow with respect to geometric asymmetry. We arbitrarily define the left-hand side capillary to be the arterial side of the vascular bed and the right-hand side capillary to be the venous side. Following [15,57,58], we assume that the pressure difference between the arterial and the venous side in a capillary bed is approximately 10 mmHg. Therefore, we impose the boundary condition p = 10 mmHg and p = 0 mmHg on the left-hand side and right-hand side capillaries, respectively. The remaining boundary conditions are free-flux conditions. We choose this configuration because it allows us to quantify the importance of interstitial flow in a common setting: a small growing tumour placed far enough from the capillaries to be hypoxic and trigger angiogenesis.

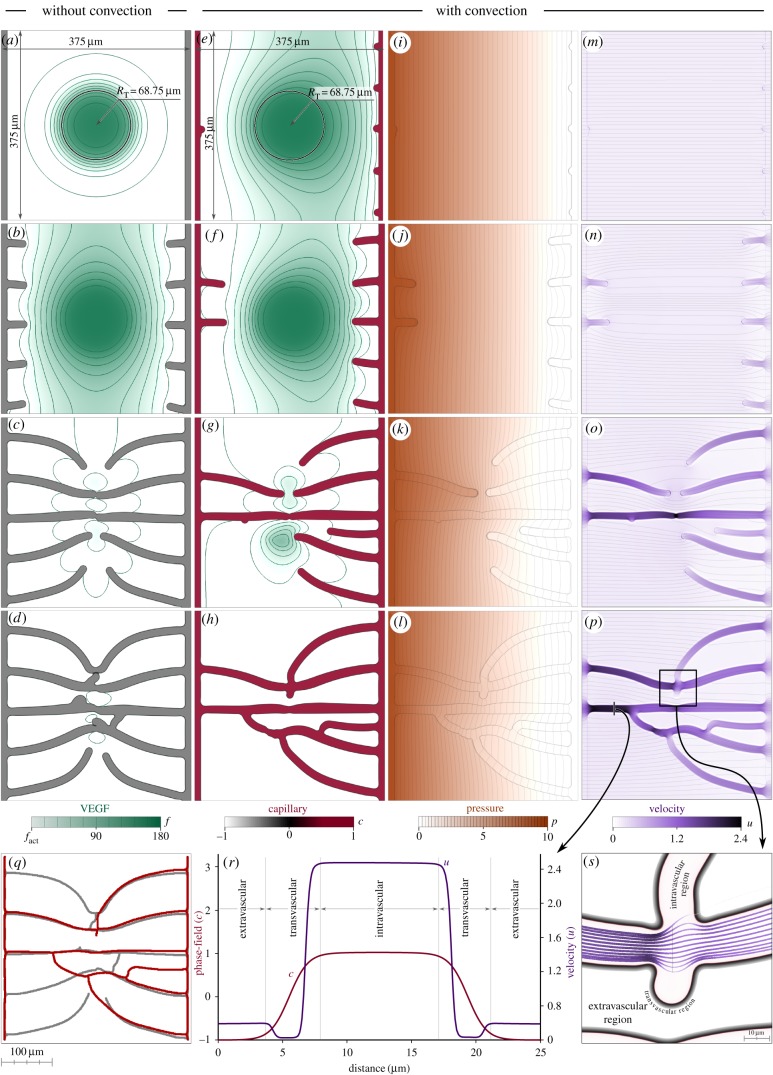
Figure 3.

Non-convective versus convective vascular patterns. Vascular patterns without VEGF convection (a–d) and with VEGF convection (e–p) create different vascular networks (q). The numerical method captures the fluid velocity and the phase-field, as shown by the velocity magnitude, u, and the phase-field profile, c, along a cut-line (r) and streamlines (s). We used a mesh composed of 512 × 512 elements in these simulations.

Figure 3 shows two numerical simulations: one in which VEGF convection is neglected (figure 3a–d) and one with the full model (figure 3e–p). For the simulation that accounts for interstitial flow, the figure shows snapshots of the evolution of the four unknowns of the model. Initially, there is a constant pressure drop from the higher pressure on the left-hand side capillary to the lower one in the right-hand side capillary (figure 3i). Fluid particles travel from left to right following straight trajectories as shown by the streamlines (black lines) in figure 3m. The fluid carries VEGF to the right-hand side (figure 3e) altering the symmetric distribution obtained when only diffusive mechanisms are in action (figure 3a). Early after the simulation starts, the non-symmetric VEGF distribution promotes dissimilar TEC activation: while the purely diffusive VEGF distribution activates five TECs from each capillary, convection promotes the early activation of only two TECs from the left-hand side parent capillary (figure 3f). This incipient vascular network has already altered the pressure and velocity fields (figure 3j,n) highlighting how strongly the variables of the model are coupled. Later in the simulation (figure 3c,g), the newly created capillaries have pervaded the tumour and the VEGF production has stopped. This is accompanied by the anastomosis of capillaries at the centre of the tissue. In this case, the connection of the capillaries is enabled by the filopodia of the leading TECs which detect each other and change their migration paths to coalesce. When interstitial flow is considered, there is only one anastomosis at a similar time (figure 3g) because convection delays the activation of TECs from the left-hand side capillary.

The fourth row of figure 3 shows the final results of these simulations. At this point, the vascular networks are fully developed and they completely pervade the tumour and its surroundings. Their shape is, however, remarkably different. We show in figure 3q the superimposed skeletons of these networks which are obtained using twofold-iteration parallel thinning algorithm based on [59] plus a sequential thinning algorithm. The neo-vessels that approximately match in both simulations are those created by the first activated TECs, when the VEGF distributions were most similar. After that moment, convection altered the distributions leading to different patterns. As shown in figure 3p, the highest velocities are attained in the two leading vessels that join the arterial and venous sides of the capillary bed. The majority of the fluid that flows through the new vascular network goes through these vessels, whose reduced calibres increase the velocity.

In figure 3r, we show the velocity magnitude and phase-field profiles along a cut-line marked with black colour in figure 3p. The cut is perpendicular to one of the main capillaries that connect the parent vessels and includes part of the extravascular region. The smoothness of the profiles shows that the numerical methods are able to capture not only the phase-field interface but also the large gradients of the velocity field. The velocity curve plateaus in the intra- and extravascular regions, being almost 10-fold higher inside the capillaries. These two plateaus are connected through smooth transitions to a third one that is smaller and corresponds to the transvascular region. The low hydraulic conductivity in the transvascular region hinders the extravasation of the fluid. We show this in figure 3s, where we draw fluid streamlines that cross the black line at the centre of the figure. The streamline colour and thickness are plotted according to the velocity of the fluid: the darker and thicker the streamline, the higher the velocity. Note that all streamlines but one remain within the intravascular region. The only one that transverses the vascular wall is thin, indicating a small velocity. Figure 3s also shows that the model captures how the streamlines separate from each other at the centre of the plot as they go through a capillary intersection and the velocity is reduced. This highlights the accuracy of the simulations.

Electronic supplementary material, figure S1 shows four additional simulations in which we modified the arterio/venous conditions of capillaries by modifying the boundary conditions for the pressure field in the initial capillaries. There, different configurations of the parent capillaries alter the vascular patterns, although in every one the tumour and its surroundings get pervaded by capillaries. The main difference is that the location of connections of the networks to the vascular patterns tends to be at the venous side of the capillary bed.

3. Results

3.1. The neovasculature grows more prominently against the flow

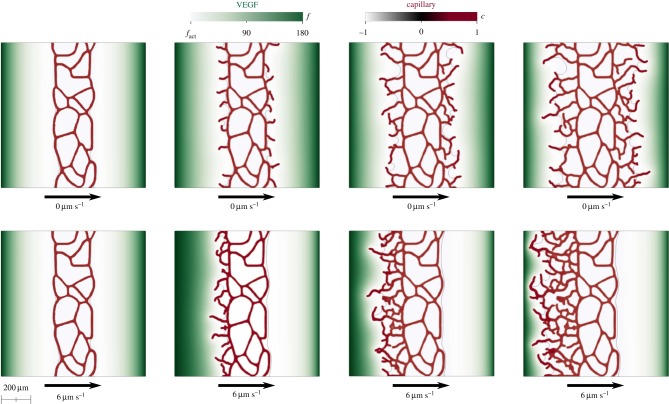
Although our model predicts intra-, trans- and extravascular flow in a tissue with a time-evolving vascular network, we will initially use it to study a flow-controlled experiment in which the fluid velocity is constant and known. The goal is to provide a fluid-dynamics explanation of the experiments reported in [18]. In these experiments, a microfluidic device allows one to create in vitro microvascular tissues with simultaneous control of the VEGF spatial concentration gradient and the interstitial flow. Initially (left-hand side of figure 4), there is a pre-existing vascular network in the central part of the device. When the experiment starts, a constant concentration of VEGF is established on the lateral boundaries and a uniform flow in horizontal direction is applied. When a controlled interstitial flow is applied, the experiments show a strikingly non-symmetric distribution of the neovasculature, while similar experiments without flow produce symmetric growth; see [18] for more details. The detailed mechanisms that control the symmetry breaking are not well understood. A potential explanation for this observation is that TECs detect the flow and bias their migration direction; in fact, a similar behaviour was recently observed for cancer cells [60]. Although this has not been observed for endothelial cells, it is a plausible mechanism because, by migrating against the flow, TECs travel in the direction of a positive pressure gradient. When the migrating TEC anastomoses with another capillary, the newly created vessel will be effectively carrying flow because it joins two points with different pressures. Another relevant hypothesis is that interstitial flow alters the TEC activation process by accelerating the transition from a quiescent to a migratory phenotype [61]. Our model, however, indicates that no direct sensing is necessary to reproduce preferential migration against the flow. The simplest hypothesis that flow only modifies angiogenesis by altering the VEGF distribution allowed us to qualitatively reproduce the experimental observation. Figure 4 shows the computational results for vanishing interstitial flow (top) and for a constant flow rate with velocity 6 μm s⁻¹. The results clearly show that the new vessels grow symmetrically with no flow (top) and preferentially upstream with flow (bottom). The model suggests that this happens due to a non-symmetric distribution of VEGF. If the VEGF transport was purely diffusive, the concentration distribution would be symmetric, but the combination of convective and diffusive transport, with the consumption of VEGF by the initial capillary network produces a non-symmetric VEGF distribution that leads to preferential vascular growth against the flow.

Figure 4.

Flow-mediated angiogenesis with a controlled, uniform fluid velocity. In the top-row simulation, there is no flow. In the bottom-row simulation, the fluid velocity is 6 μm s⁻¹. For both computations, time grows from left to right. The results show that our model predicts more prominent growth of the neovasculature against the flow, as observed in a recent experiment [18]. The VEGF was kept constant on the lateral boundaries with concentration f = f_hyc. Boundary conditions in the vertical direction were assumed to be periodic. The computation was performed on a tissue of size 1000 × 1000 μm. As this computation is performed on a larger piece of tissue, we added random perturbations to the TEC velocity field orientation [27] to produce a more realistic vascular pattern. We have verified (data not shown) that this does not have an impact on the symmetry breaking mechanism. Similar computations without random perturbations also produce more prominent capillary growth against the flow.

3.2. Interstitial flow may facilitate the angiogenic switch of small tumours

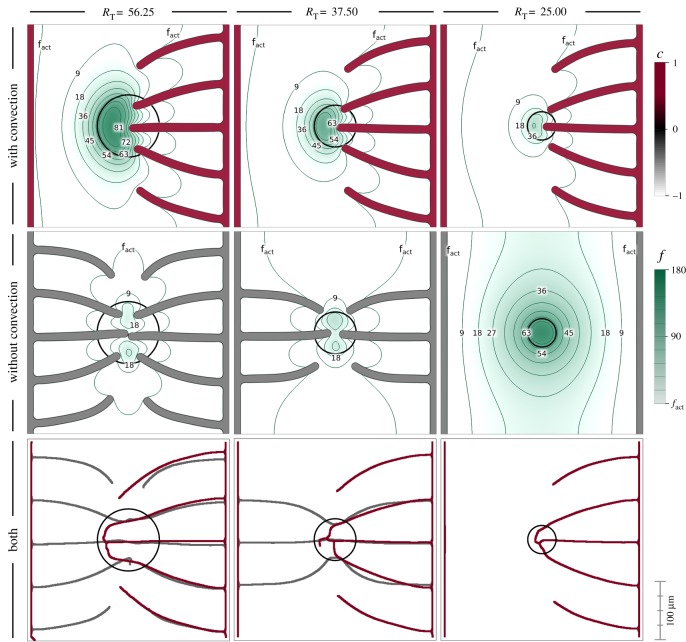
Here, we study the effect of interstitial flow on the avascular to vascular switch of a small tumour. We perform a parametric study in which we alter the size of the tumour that is producing VEGF. We analyse whether interstitial flow enhances the tumour's ability to trigger angiogenesis. Our results are shown in figure 5, where we present simulations for tumours of radius R_T = 56.75, 37.50 and 25.00 μm, from left to right. The top and middle rows of this figure correspond to intermediate time steps of simulations with and without VEGF convection, respectively. The bottom row corresponds to the final vascular patterns for all cases. For these simulations, we have used the same setup, mesh, boundary and initial conditions as the simulations in the previous example (figure 3a).

Figure 5.

Convection-increased angiogenesis. VEGF reaches the initial capillaries at different times when the tumour radius is varied (56.25, 37.50 and 25.00 μm). In the absence of convection, the smaller tumour is not able to trigger angiogenesis. The green colour scale represents VEGF concentration.

We observe a significant impact of interstitial flow on the results. For all the simulations with VEGF convection, the vascular network develops only from the right-hand side capillary, while in the absence of convection, when angiogenesis occurs, new vessels grow from both parent capillaries. The main conclusion from these simulations is that interstitial flow may play a role in enhancing the malignancy of small tumours. As shown in the simulations at the right-most column of the figure, small tumours, may not be able to trigger angiogenesis in the absence of convection. On the contrary, the model with convection predicts that the same tumour gets fully vascularized and becomes malignant.

3.3. Intratumoral pressure may increase the tumour's ability to induce angiogenesis through stronger interstitial flow

So far we have assumed the fluid pressure inside the tumour to be equal to that in the host tissue. This is, however, not necessarily true. Cancer cells replicate rapidly and group forming densely packed tumours. The growth generates mechanical stress, which is transmitted to the fluid leading to a pressure rise. Furthermore, this high fluid pressure is not alleviated due to the absence of functional lymphatic and blood vessels. We use our computational method to study whether an intratumoral pressure higher than that of its micro-environment affects angiogenesis through VEGF convection.

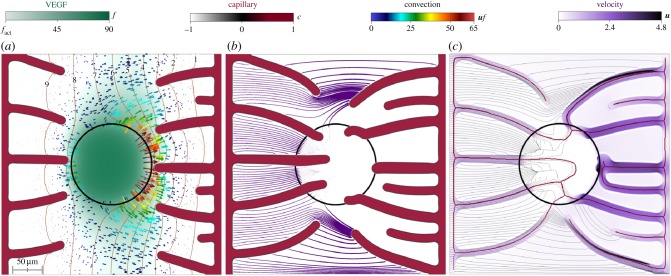
The proposed mathematical model does not explicitly consider cancer cell density; instead, we assume that the tumour is located in a fixed hypoxic circular region at the centre of the tissue (figure 6). This region is assigned an intratumoral pressure p = p_t. From a computational point of view, we impose this constraint using the penalty method [62]. Figure 6 and electronic supplementary material, video V2, show the result of a simulation in which p_t = 7.4 mmHg and f_hyc = 90 ng ml⁻¹. The computation starts with two initial capillaries at the left and right edges of a 375 × 375 μm square tissue and one approximately 60 μm radius hypoxic region at its centre. The left capillary is considered to be on the arterial side of the microcirculatory system and have a constant pressure p = 10 mmHg that we impose by way of a boundary condition. The initial capillary on the right-hand side represents the venous side and its associated pressure boundary condition is p = 0 mmHg.

Figure 6.

Influence of intratumoral pressure. Intratumoral pressure alters the distribution of VEGF which, in turn, drives capillaries around the tumour. The fluid velocity inside the tumour is low, even within the capillaries that transverse the tumour.

Figure 6a displays the results before the TECs reach the tumour. There, we plot contour lines of pressure (orange) and VEGF (green), a black circle rendering the contour of the tumour, glyphs representing the convective term uf, and the distribution of VEGF and capillaries. The pressure contour lines are mostly parallel to the initial capillaries as in other simulations, showing the pressure drop between them. The imposed intratumoral pressure, however, disrupts the parallelism in the central region and reveals the location of the tumour. In particular, the contour line p = 7 bends towards the right surrounding the tumour and exposing its location. The tumour produces all the VEGF in the domain that reaches the capillaries through diffusion and convection. Convection is, however, virtually non-existent inside the tumour as shown by the absence of glyphs in the intratumoral region. After being produced, the VEGF escapes the tumour by diffusion only. Once in the ECM, interstitial flow starts to play a role in the VEGF distribution. This is specially noticeable on the right-hand side of the tumour, as shown by the colour arrows representing the convection term. There, the transition between the intratumoral pressure and the extravascular pressure in a small region generates high-pressure gradients. In turn, convection is increased and drives VEGF away from the tumour creating a region with low values of VEGF. As a result and contrary to previous simulations, electronic supplementary material, video V2, shows how capillaries originated from the venous side turn at the tumour boundary, rather than going through it. This trend continues as the simulation evolves. Figure 6b shows how one of these venous capillaries has stopped its growth and anastomosed, while the other two have run along the tumour boundary. Only when the VEGF has been consumed in the vicinity of the tumour do they penetrate the lesion. Figure 6b also displays streamlines of the extravascular fluid velocity. Each streamline starts at the left-hand side capillary and its thickness varies according to the norm of the fluid velocity. Interestingly, few streamlines transverse the tumour and those that do are very thin, indicating small velocities. The highest fluid velocity in the extravascular region occurs between capillaries that are very close to each other but have not anastomosed yet. The vascular network continues evolving until all the VEGF in the domain has been consumed. We present a snapshot of this last step in figure 6c, where we show the final vascular network represented by its skeleton (red lines), streamlines of the velocity field (black lines) and the continuous velocity field (shades of purple). As in previous simulations with a similar setup, the final vascular network is non-symmetric, being denser towards the venous side due to the effect of convection. The difference here is that the intratumoral pressure has prevented capillaries from entering the tumour. The velocity field highlights, first, that the fluid flows more rapidly within the capillaries and, second, that the velocity inside the tumour is very low. In fact, the capillaries that transverse the tumour present velocities close to zero. The intratumoral pressure has rendered these capillaries non-functional. Finally, as in figure 6b, the streamlines barely penetrate the tumour.

Importantly, the simulation predicts that even though the tumour is vascularized, nutrients, oxygen, or systemically administered drugs cannot easily reach the tumour's interior, resulting in an increased tumour malignancy [63]. The fluid flow both within the capillaries and in the extravascular region does not favour their penetration into the tumour.

4. Discussion

The role of interstitial flow in tumour angiogenesis is not well understood. In principle, interstitial flow could affect angiogenesis in multiple ways, such as for example, modifying the VEGF concentration distribution via convective transport, altering the TEC activation process, or biasing the migration direction of tip cells. Here, we used a computational model to show that accounting for the VEGF convective transport mechanisms with a physiological flow rate produces significant changes in the angiogenesis process, with a striking bias of vascular growth upstream the flow. Our results provide a fluid-dynamics explanation for the experiments reported in [18], which show non-symmetric neovasculature with more prominent growth against the flow. Although the simplest hypothesis that flow only modifies angiogenesis by altering the VEGF distribution allowed us to qualitatively reproduce a non-trivial experimental observation, it is unlikely that cells are unable to interpret signals directly. In fact, as an indication of the ability of cells to sense flow directly, it was observed that TECs travelling against the flow have more filopodia that those moving with the flow [64]. However, our model suggests that active sensing may not be the dominant mechanism.

The model also predicts that TAF convection may play a role in enhancing the malignancy of small tumours. Including the high intratumoral fluid pressure in the model shows an increased ability of the tumour to trigger angiogenesis. In addition, the delayed capillary penetration and the low fluid velocity within the tumour suggest a potential increase in tumour malignancy, as oxygen, nutrients or even drugs may not reach tumour cells.

The model can be extended and improved in multiple ways. The major limitation of our model at this point is that the intravascular flow compartment does not capture the complex haemodynamic interactions occurring across a microcirculatory network. This includes the shear-thinning behaviour of blood and the heterogeneous flow resistance produced by a non-uniform distribution of erythrocytes. However, an accurate computation of the intravascular flow on a time-evolving vascular network is an open scientific problem that is out of the scope of this paper. Therefore, since our main interest is interstitial flow rather than intravascular flow, we employed a simplified intravascular flow model that produces realistic extravascular flows. The model may also be enhanced by the inclusion of convection–diffusion equations for nutrients, oxygen, or systemically delivered drugs. Also, the initial geometry of capillaries and tumours has been simplified. The predictive capabilities of the model could be augmented using geometries from in vivo three-dimensional imaging. Its extension to three dimensions does not require any modification of the model neither of the numerical methods. Another possible refinement of the model is to consider the fact that several TAFs are known to increase the patency of capillaries [4]. This mechanism may be built into the model by transforming the parameter κ^t into a function that depends on the concentration of that particular TAF. Finally, a proposed line of further research is to change the definition of the hydraulic conductivity to capture the intratumoral pressure.

Data accessibility

This article has no additional data.

Authors' contributions

G.V., M.B. and H.G. conceived and designed the research. M.B. and G.V. ran the simulations. G.V., M.B., H.G. and I.C. analysed the data and participated in the preparation and editing of the manuscript.

Competing interests

We declare we have no competing interests.

Funding

H.G., M.B. and G.V. were partially supported by the European Research Council (contract no. 307201). I.C. was partially supported by Consellería de Cultura, Educación e Ordenación Universitaria of the Xunta de Galicia (grant no. GRC2014/039).