Nonlinear Elasticity of the ECM Fibers Facilitates Efficient Intercellular Communication

Abstract

Biological cells embedded in fibrous matrices have been observed to form intercellular bands of dense and aligned fibers through which they mechanically interact over long distances. Such matrix-mediated cellular interactions have been shown to regulate various biological processes. This study aimed to explore the effects of elastic nonlinearity of the fibers contained in the extracellular matrix (ECM) on the transmission of mechanical loads between contracting cells. Based on our biological experiments, we developed a finite-element model of two contracting cells embedded within a fibrous network. The individual fibers were modeled as showing linear elasticity, compression microbuckling, tension stiffening, or both of the latter two. Fiber compression buckling resulted in smaller loads in the ECM, which were primarily directed toward the neighboring cell. These loads decreased with increasing cell-to-cell distance; when cells were >9 cell diameters apart, no such intercellular interaction was observed. Tension stiffening further contributed to directing the loads toward the neighboring cell, though to a smaller extent. The contraction of two neighboring cells resulted in mutual attraction forces, which were considerably increased by tension stiffening and decayed with increasing cell-to-cell distances. Nonlinear elasticity contributed also to the onset of force polarity on the cell boundaries, manifested by larger contractile forces pointing toward the neighboring cell. The density and alignment of the fibers within the intercellular band were greater when fibers buckled under compression, with tension stiffening further contributing to this structural remodeling. Although previous studies have established the role of the ECM nonlinear mechanical behavior in increasing the range of force transmission, our model demonstrates the contribution of nonlinear elasticity of biological gels to directional and efficient mechanical signal transfer between distant cells, and rehighlights the importance of using fibrous gels in experimental settings for facilitating intercellular communication.

Introduction

The cellular actomyosin machinery actively generates forces that are transmitted to the cell surroundings to induce loads (displacements, strains, and stresses) within the extracellular matrix (ECM); these can persist hundreds of microns away (1) and are known to influence cell morphology, migration, and differentiation (2). Long-range loads have thus been proposed as a means for cells to mechanically communicate with each other and have been shown to play a key role in various biological, physiological, and pathological processes as diverse as capillary sprouting (3), cancer invasion (4), heartbeat synchronization (5) and morphogenesis (6).

The fibrous ECM demonstrates nonlinear-elastic behavior that is manifested by compressive softening and tension strain stiffening (7, 8). These are attributed to the mechanical behavior of the individual fibers contained in the matrix, showing strain stiffening in tension (7, 9, 10, 11, 12) and microbuckling under compression (12, 13, 14). The fibrous structure of the ECM also contributes to its macroscale elastic nonlinearity owing to fiber reorganization under applied loading, resulting in fiber alignment and densification (15, 16, 17). Previous experimental studies have demonstrated that the nonlinear elasticity of the ECM facilitates long-range transmission of loads, enabling cells to sense and respond to mechanical signals sent by other cells located at far distances. For example, Notbohm et al. (18) found that the contraction of fibroblasts within a fibrin matrix with nonlinear-elastic behavior induced displacements that traveled considerably further than predicted by linear elasticity. Vanni et al. (19) similarly demonstrated that the contraction of a single fibroblast within a collagen gel induced strains that propagated up to 800 μm through the substrate. Winer et al. (20) found that local strain stiffening of fibrin gels facilitates the transmission of forces between fibroblasts or mesenchymal stem cells up to ∼500 μm (∼30 cell diameters) apart. In linear-elastic gels, such as polyacrylamide (PAA) gels, the displacements induced by the contraction of a sphere were found to decay faster than in collagen gels (21). This concurs with experiments with cells cultured on PAA gels, which demonstrated that cells sense and respond to loads induced by other cells at a distance limited to ∼25 μm, a relatively shorter distance than those reported for biological gels (22). These experimental findings have been elucidated by numerous analytical procedures, finite-element (FE) simulations, and other computational models developed to study the effects of ECM elastic nonlinearity on the transmission of cell-contraction-induced loads through the network in which the cell(s) are embedded. Safran and colleagues (23, 24) presented an analytical model demonstrating the long-range decay of displacements induced by the contraction of a circular cell embedded in a medium showing nonlinear-elastic behavior. These predications were later supported by computer simulations of fibrous networks demonstrating that fiber buckling results in displacements and stresses traveling considerably farther than in a linear-elastic medium (25, 26, 27). In addition, the fibrous structure of the ECM, and particularly the load-induced geometric rearrangement of the network, have been found to contribute to the nonlinear-elastic behavior (especially stiffening) of the ECM and to act as a mechanism considerably increasing the range of force transmission and sensing (1, 15, 16, 17, 28, 29, 30, 31). These studies identified nonlinear mechanical behavior of the ECM as a mechanism supporting long-range force transmission through the matrix. However, less is known about the effect of the mechanical behavior of the ECM fibers on force transmission between cells.

Previous experimental studies (3, 4, 28, 32, 33, 34) have revealed that contraction of multiple cells embedded in fibrous biological gels induces structural remodeling of the ECM fibers, manifested by the formation of aligned and densely packed fiber “bands” connecting the cells. This observation demonstrates not only the long-range nature of the force transmission through the ECM—which is both facilitated by and contributes to such structural remodeling—but also reflects the tendency of cell-contraction-induced loads to be delivered in a highly directional manner toward neighboring cells. Harris et al. (32) were the first to show that the forces exerted by tissue explants placed millimeters apart in a collagen gel stretched and aligned the fibers between the explants, resulting in the formation of intercellular “bands.” More recent studies have demonstrated that cells respond to such intercellular bands. Korff and Augustin (3) found that forces applied by two endothelial cell spheroids embedded in a collagen gel and placed up to 700 μm apart resulted in directional sprouting of capillaries along aligned fibrils between the spheroids. Shi et al. (4) further showed that the directional remodeling of collagen fibers accelerated the transition of gel-cultured mammary acini cells to an invasive phenotype. Such biological observations highlight the importance of the structural remodeling of the intercellular matrix in supporting long-range intercellular mechanical interactions, which, in turn, regulate various biological processes. Still, the physical mechanisms facilitating the formation of such ECM “bands” and the manner in which they mediate force transmission between cells are poorly understood. Particularly, despite the fact that several computational models were able to capture the tendency of loads to concentrate within the intercellular medium and align the fibers in this region (17, 28, 29, 30, 34), a quantitative exploration of the influence of ECM elastic nonlinearity on regulating matrix-mediated mechanical interaction between cells is warranted.

In this work, we explore the contribution of the nonlinear-elastic properties of the ECM fibers to the structural remodeling and to the transfer of mechanical loads between neighboring cells. Experimentally, we show that fibroblast cells structurally align and densify the fibers between them shortly after being seeded in fibrin gels, when they are still mostly rounded. Based on our experimental setting, we develop two-dimensional (2D) FE simulations of two contracting cells (separated by 1.5–19 cell diameters) embedded within fibrous nonlinear-elastic networks. The simulation outcomes indicate that cell-contraction-induced loads are highly directed toward neighboring cells owing to the nonlinear-elastic behavior of the matrix and its constituting fibers; this observation is coupled with increased structural remodeling of the intercellular region of the ECM. We link these observations with efficient transfer of mechanical loads between cells. We also show that intercellular interactions manifest by attraction forces occurring between neighboring cells and also lead to the onset of force polarity on the cell boundaries. The model presented herein contributes to the understanding of biological processes involving ECM-mediated interactions, which can influence cell differentiation, migration and morphogenesis. It can also expand the knowledge basis required for designing biomaterials that support efficient intercellular mechanical interactions.

Materials and Methods

Biological experiments

Approximately 5000 NIH3T3-GFP-actin cells were seeded in 20 μL fibrin gel (5 mg/mL fibrinogen) labeled with Alexa Fluor 546-NHS ester (succinimidyl ester) (ThermoFisher, Waltham, MA), as described in previous studies (e.g., (18)). The gel was scanned at several time points post seeding using a confocal laser scanning microscope (laser scanning microscope 880 lens ×40, water immersion; Carl Zeiss, Oberkochen, Baden-Württemberg, Germany) to capture distant cells forming “bands” between them (18). The cell pairs selected for analysis were within an average intercellular distance of 51.3 ± 17.5 μm (n = 5 cell pairs). Image analysis used ImageJ (National Institutes of Health, Bethesda, MD; https://imagej.nih.gov/ij/) and the OrientationJ plugin (École polytechnique fédérale de Lausanne, Switzerland, 2017; http://bigwww.epfl.ch/demo/orientation/#soft) to examine the orientation and intensity (indicative of the fibrin density and normalized to the mean intensity of the entire image) of several regions between two interacting cells or far away from the cells.

Computational modeling

A 2D FE model was developed to explore the effects of the mechanical behavior of the ECM on the mechanical loads occurring within the medium between contracting cells. The cell-to-cell distance and the mechanical properties of the fibers contained in the network were adjusted to create model variants (31 cell-to-cell distances, six types of fiber mechanical properties, and three levels of cell contraction). The model was largely based on computational models described in previous studies (mainly Notbohm et al. (25) and Liang et al. (35)) with some major modifications, which are described below.

Network geometry and architecture

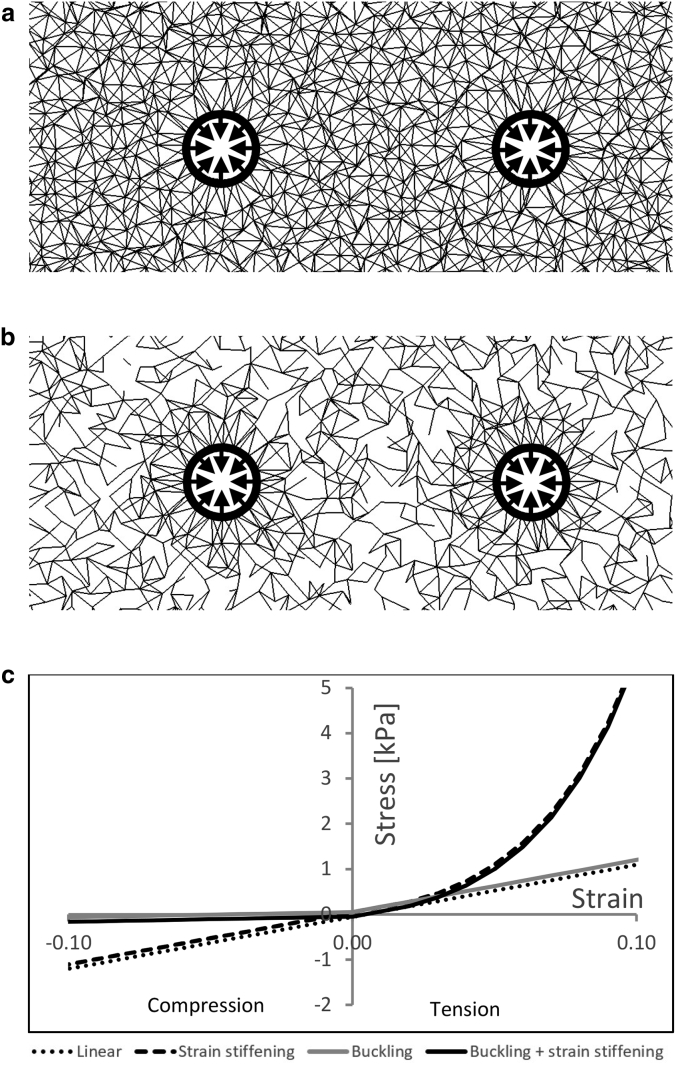
A 2D array of multiple identical square box X units was initially created. Each unit contained four corners acting as nodes and two horizontal, two vertical, and two diagonal sides acting as elements. Each of the four horizontal/vertical sides was shared with another box X unit; similarly, each of the four corners was shared between four identical units meeting at this corner. This resulted in each corner/node being the edge of eight sides/elements (i.e., connectivity, C = 8.0; Fig. 1 a). The network was also modified to reduce the mean network connectivity from 8.0 to 6.5, 5.0, and 3.5 (25) by randomly removing a fraction of the network elements so that the average number of elements meeting at each node reached the desired connectivity value (Fig. 1 b).

Figure 1.

Details of the 2D finite-element (FE) model. (a) A small portion of the FE model of two cells contracting within the fibrous network of connectivity, C = 8.0, is shown. The contracting cells were modeled as void regions (thick circles) to which a boundary condition of radial contractile displacement (thick arrows) was applied. (b) The same as above, for C = 3.5, is shown. (c) Stress-strain curves representing the mechanical properties of the fiber elements comprising the FE model are shown. Four material models were used to simulate the mechanical behavior of the ECM fibers, as listed in Mechanical Properties. Lines are slightly shifted for visualization purposes.

The locations of all nodal positions were modified by relocating each node to a randomly selected location contained within a circular region of a radius equal to the length of the horizontal/vertical sides of the aforementioned square box X. This created a random array of elements of different lengths and orientations in which each linear element connecting a pair of nodes represented a fiber segment between two cross-linking points. Elements were removed from the network to create two circular void regions (16, 17, 25, 26, 27, 35) representing cells embedded within the ECM. The centers of both circles were coincident with a horizontal line passing through the center of the network (Fig. 1, a and b). Equivalent model variants with a single cell each (the center of which was coincident with the center of the network) were also generated. Cell diameter and mean fiber-segment length were set at 15.2 and 3.5 μm, respectively, according to our biological experiments with fibroblast cells embedded in fibrin gel (Fig. 2; Biological Experiments). For selected model variants, the mean fiber length was increased to 7 μm so that the cell diameter/mean fiber length ratio was set at 15.2 μm/7.0 μm = 2.2 (Fig. S12). Cell-to-cell distances ranged between 1.5 and 19 cell diameters (i.e., ∼23–289 μm, based on our laboratory experiments; full list of cell-to-cell distances: 1.5, 1.8, 2.1, 2.9, 3.4, 4.0, 4.6, 5.3, 5.9, 6.5, 7.1, 7.8, 8.4, 9.0, 9.6, 10.3, 10.9, 11.5, 12.1, 12.8, 13.4, 14.0, 14.6, 15.2, 15.9, 16.5, 17.1, 17.8, 18.4, 19.0). The diameter of the network was 100 times larger than that of the cell (i.e., 1520 μm) so that the distance between each cell and the boundaries of the network was at least twice as large as the cell-to-cell distance.

Figure 2.

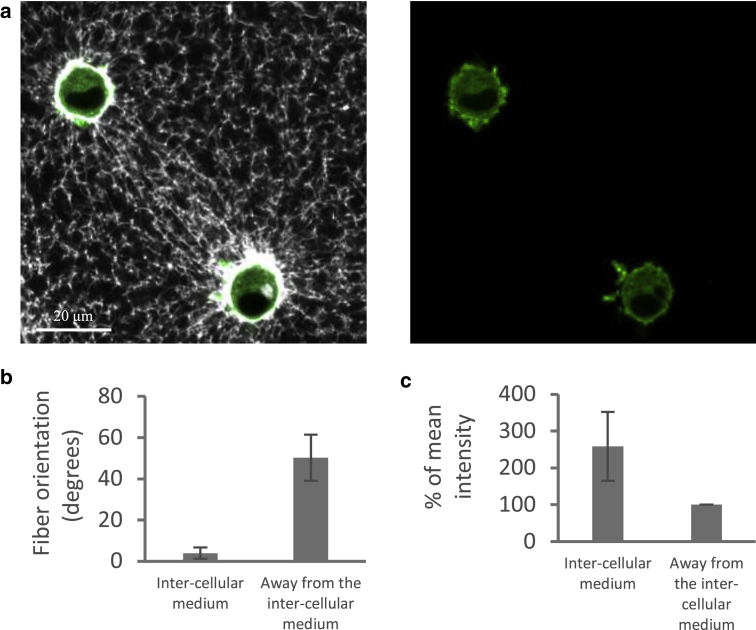
Experiments of intercellular mechanical interaction. (a) Two GFP-actin cells (gray) embedded in fluorescently labeled fibrin gel (white) are shown. The images show the overlay of cells and fibrin matrix (left) and the cells only (right). (b) The mean orientation of the fibers in the intercellular region of the ECM and far away from the cells is shown; 0° is defined as the line connecting the centers of the two cells. (c) The fluorescence intensity of the matrix as measured both within the intercellular region of the matrix and far away from the cells is shown. For a full-color version of this figure, the reader is referred to the online version of the article.

Mechanical properties

Four material models were used to simulate the mechanical behavior of the ECM fibers (Fig. 1 c; Eq. 1; (25, 35)):

• 1)“linear”: linear-elastic material with both tensile and compressive elastic moduli (Young’s moduli, E) of 11.5 kPa (buckling ratio, which is the ratio between tensile and compressive E, is ρ = 1).
• 2)“buckling”: elastic material with tensile E of 11.5 kPa and compressive E 2- (buckling^1/2, ρ = 0.5), 5- (buckling^1/5, ρ = 0.2), or 10- (buckling^1/10, ρ = 0.1) times smaller, which simulates fiber buckling. Throughout the text, unless stated otherwise, “buckling” is referring to buckling^1/10, i.e., ρ = 0.1.
• 3)“strain stiffening”: hyperelastic material with compressive E of 11.5 kPa and tensile E of 11.5 kPa within the engineering-strain range of 0–0.02 (ρ = 1); for tensile strains larger than 0.02, stress increases exponentially to simulate strain-stiffening behavior.
• 4)“buckling + stiffening”: hyperelastic material with tensile E of 11.5 kPa within the logarithmic strain range of 0–0.02, which increases exponentially for strains larger than 0.02; compressive E is 10 times smaller than 11.5 kPa (ρ = 0.1).

$$E=\{\begin{array}{c}\rho \times E_{ref},\lambda <0\\ E_{ref},0\le \lambda <{\lambda }_s\\ E_{ref}\times e^{\frac{\lambda -{\lambda }_s}{{\lambda }_0}},\lambda \ge {\lambda }_s\end{array}$$ (1)

Equation 1 gives the values of the elastic modulus (Young’s modulus, E) assigned to the elements of the FE model. E_ref = 11.5 kPa is the reference elastic modulus, λ = Δl/l is the engineering strain occurring within an element of length l, λ_s = 0.02 is the strain above which strain stiffening occurs, λ₀ = 0.05 is the strain-stiffening coefficient, and ρ is the buckling ratio (12, 35).

Boundary conditions

Cell contraction was modeled by applying a boundary condition of radial contractile displacement (equals to 10%, 25%, and 50% of the cell radius) to all nodes constituting the cell boundaries (Fig. 1, a and b) (in line with (25, 28, 29, 30, 31, 35)). These levels of cell contraction have been shown to fall within the physiological range of muscle-cell contraction (both skeletal (36) and smooth muscle cells (37)). The circular boundary of the entire network was fixed for translations and rotations in all directions (16, 29, 30, 35). In all simulations, the possibility of the boundary fixation affecting the model outcome measures was eliminated by ensuring that the strains, stresses, and strain energy densities (SEDs) occurring along the network boundaries were negligible compared with those occurring in the cell vicinity (16).

Numerical method

Linear truss elements (i.e., supporting uniaxial tension and compression and unrestrained rotation about the nodes but with infinite resistance to bending) were used to model the fiber segments. For selected model variants, beam elements instead of truss elements were used. The selection of element type (beam/truss) showed marginal influence on the model outcomes (Fig. S11; in line with (16, 17, 35)). The cross-sectional area of all elements was assumed to be constant at 0.031416 μm² (Supporting Information). The model included ∼590,000 elements and ∼148,000 nodes. The ABAQUS Standard/Implicit FE solver (Version 2017; Dassault Systèmes Simulia, Providence, RI, 2017) in its nonlinear analysis mode was used to process all model variants, with running time of ∼5 min per simulation (on an i7, 3.60-GHz central processing unit and 32-gigabyte random-access-memory station).

Outcome measures

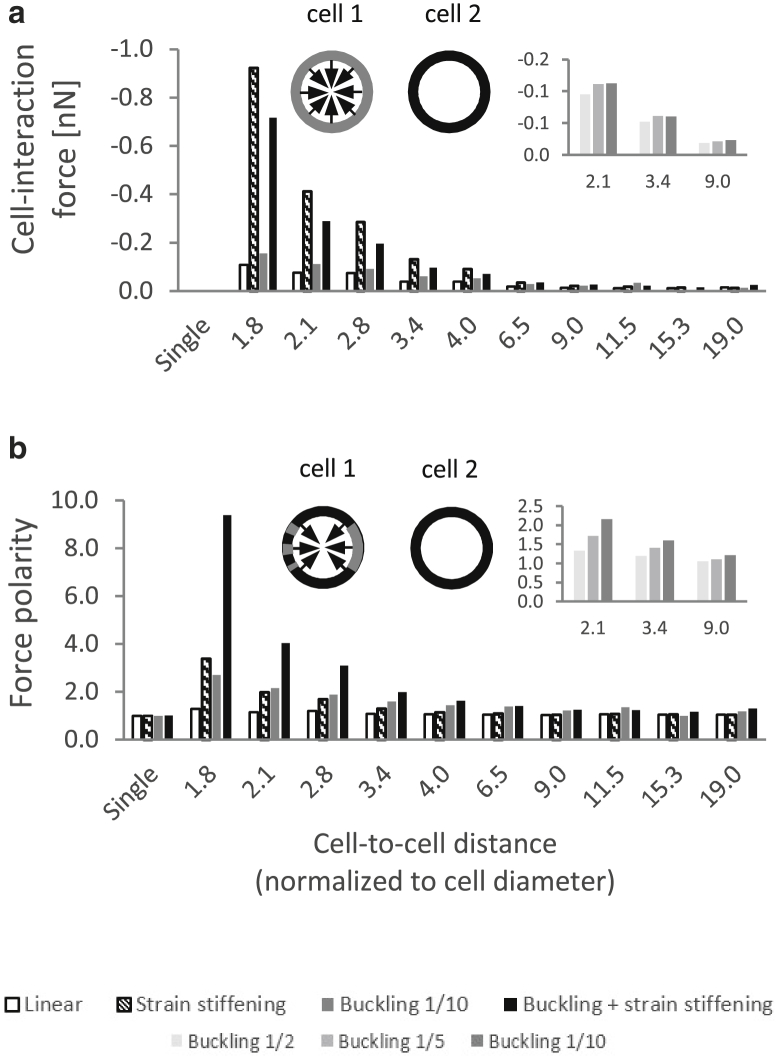
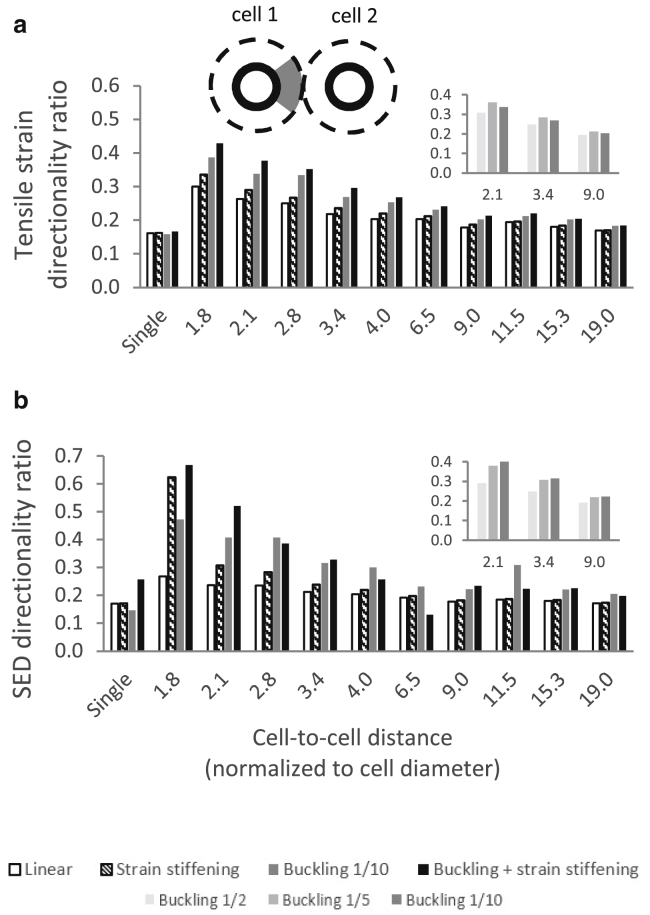
Values of displacement, strain, stress (logarithmic/true tensile and compressive strains and stresses), SED, and reaction force were calculated at the nodes and/or centroids of all elements. A script coded in MATLAB (version R2016b; The MathWorks, Natick, MA) was used to determine the following outcome measures for all model variants: 1) total cell-contraction force: the sum of all reaction forces occurring in the nodes constituting the cell perimeter along the radial axis toward the cell center (arrows at the top panel of Fig. 7 a); 2) net cell-interaction force: the sum of projections of the radial contraction forces on the line connecting the centers of the two cells. This outcome measure is indicative of the level of intercellular attraction (negative) or repulsion (positive); 3) contraction-force front-to-rear polarity ratio: the fraction of the cell-contraction force occurring within a 60° arc of the cell boundary pointing toward the neighboring cell (gray arc at the top panel of Fig. 7 b) to that occurring in the arc pointing toward the exactly opposite direction (dashed gray arc). This outcome measure is used to evaluate the relative amount of cell-contraction force directed to sending signals toward the neighboring cell; it can also be used as an indication of the direction (toward/away from the neighboring cell) in which the cell is likely to spread or migrate (force polarity is known to affect cell motility and morphology (38)); 4) the mean loads (strains, stresses, and SED) occurring within a disk surrounding an individual cell, of a radius equal to half of the cell-to-cell distance (gray disk at the top panel of Fig. S7 a); 5) directionality ratio: the fraction of the sum of loads occurring in all elements falling within a 60° sector pointing toward the neighboring cell (gray sector at the top panel of Fig. 5 a) versus the sum of loads occurring within the entire aforementioned disk. This outcome measure is used to evaluate the relative amount of the load (strain, stress, or energy) caused by cell contraction directed toward the neighboring cell. A directionality ratio of 0.17—corresponding with the area of the aforementioned 60° sector divided by that of the aforementioned disk (360°) surrounding the individual cell—indicates no preferred orientation of loads toward the neighboring cell; 6) the relative change (in %) in the number (i.e., density) of elements contained in the 60° sector pointing toward the neighboring cell (gray sector at the top panel of Fig. 8 a) as a result of cell contraction. This was derived by counting the number of element centroids contained in the aforementioned sector before and after cell contraction; and 7) change in the mean angle of the orientations of the fibers contained in the aforementioned 60° sector as a result of cell contraction. The size of the aforementioned sector was set at 60°, as it visibly captures most of the highly deformed area within the intercellular matrix. For selected model variants we also calculated the aforementioned outcome measures for sector sizes of 50° and 70° and found that the trends and conclusions reported below are largely insensitive to the sector size. For the two-cell model variants, all aforementioned outcomes were derived for both cells; the mean of the outcomes of the two cells was then calculated and was regarded as the model outcome (as presented below). Finally, the tensile strains, compressive strains, and SEDs occurring in the ECM fibers falling within the intercellular band and within the opposite areas of the matrix were plotted as a function of the location along the horizontal line connecting the cell centers (as detailed in Fig. S8).

Figure 7.

(a) Net cell-interaction force occurring on the cell boundary (as projected on the line connecting the cell centers; outcome measure 2 in Outcome Measures), for 25% contraction. The interaction force is defined as positive for repulsion and negative for attraction. (b) The polarity ratio of the contraction force occurring on the cell boundary (outcome measure 3 in Outcome Measures) is shown. Polarity ratio of 1.0 indicates no preferential orientation of loads toward the neighboring cell.

Figure 5.

Directionality of load toward the neighboring cell for tensile strains (a) and SEDs (b). The fraction of load occurring within a 60° sector pointing toward the neighboring cell (gray sector at the top panel) to the total loads falling within the entire disk (outcome measure 5 in Outcome Measures) for 25% contraction, is shown. The model variants shown include several cell-to-cell distances (in terms of cell diameter, D) and four of the material models (Fig. 1c). A directionality ratio of 0.17 indicates no preferential orientation of loads toward the neighboring cell. The values calculated for the single-cell model variants are shown for comparison. On the top right, equivalent bar charts with fewer cell-to-cell distances for different buckling ratios (ρ = 0.5, ρ = 0.2, and ρ = 0.1; Eq. 1) are shown.

Figure 8.

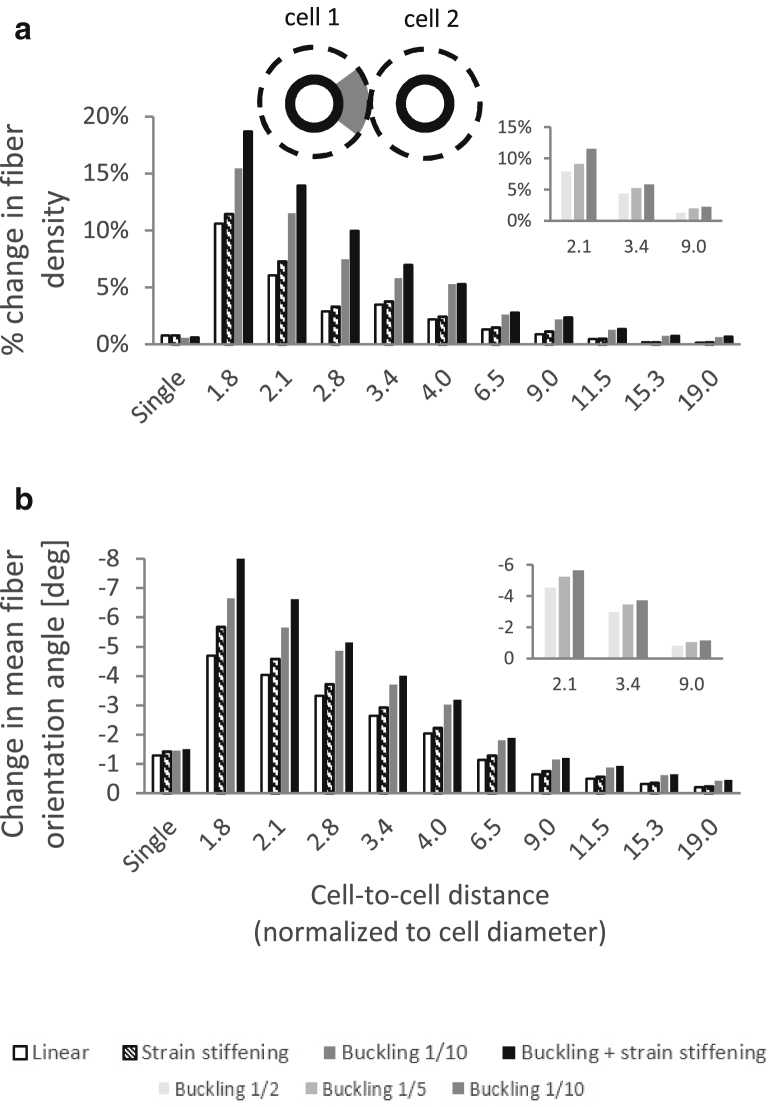
(a) Relative change in the density of fiber segments contained in the intercellular medium and (b) mean change in the orientation of the fibers contained in the intercellular medium (gray sector at the top panel) as a result of 25% cell contraction. 0° is defined as the horizontal line pointing toward the center of the neighboring cell; accordingly, negative change indicates realignment of the fibers to point toward the center of the neighboring cell (i.e., to be aligned more horizontally).

Results

Biological experiments of intercellular mechanical interactions

Fibroblast cells were embedded in fluorescently labeled fibrin gels at a low cellular density such that cells were well separated from each other. Within 2 h of seeding, although most of the cells were still mostly rounded (without major protrusions), some cells were observed to deform the fibrous matrix in a highly directional manner toward neighboring cells, creating highly remodeled matrix “bands” between pairs of neighboring cells (Fig. 2 a). Image analysis of the fibrous structure of the ECM confirmed that the area between such cell pairs was of elevated fiber density and alignment compared with those located farther away from the cells (Fig. 2, b and c). This directed remodeling of the matrix is in line with the observations of Ma et al. (28) and Vader et al. (39). These biological experiments were used as the motivation and basis to develop a computational model of two spherical cells contracting within a fibrous matrix while accounting for the relative size of the cells, length of matrix fibers, and intercellular distances. Our model was designed to study the role of ECM nonlinear-elastic behavior on the distribution and propagation of loads (forces, displacements, strains, stresses, and SEDs) through the matrix and particularly in the region between neighboring cells.

FE analysis of the transmission of loads induced by cell contraction through a fibrous matrix

In our 2D FE simulations of a single cell contracting within a fibrous matrix, the distribution of loads within the matrix was not homogeneous. Particularly, the majority of loads were carried through a small number of fiber segments constituting “force chains” (mostly apparent in the buckling model variants; Figs. 3 and S4). Despite this nonhomogeneity, the load distribution around a single cell was nearly isotropic about the cell center and did not demonstrate any preferred orientation. Tensile loads were highest in the fibers aligned approximately perpendicularly to the cell edges (thereby forming “tethers” or “force chains” propagating away from the contracting cell; Figs. 3, a and b and S4, a–d). The compressive strains, which were generally approximately twice as large as the tensile strains, were highest within the fibers aligned approximately tangentially to the cell perimeter (thus forming “rings” around the cell; Figs. 3, c and d and S4, e–h).

Figure 3.

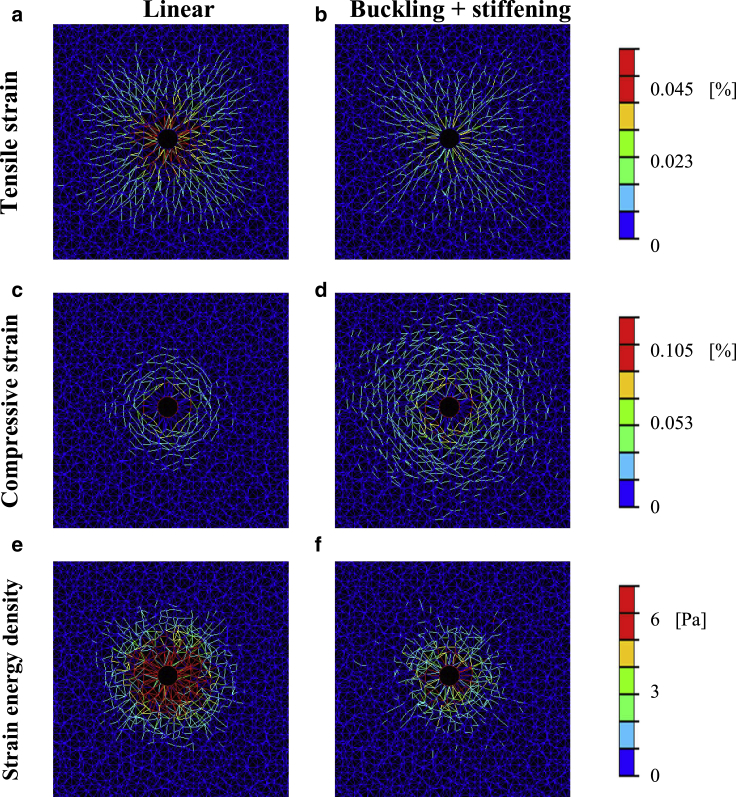
Deformations as a result of the contraction of a single cell. Tensile (logarithmic) strains (top row), compressive (logarithmic) strains (middle row), and strain energy densities (SEDs, bottom row) occurring in the fiber segments around a single, isolated contracting cell for 25% contraction are shown. Plots were produced for linear (left column; a, c, and e), and nonlinear (buckling + strain stiffening; right column; b, d, and f) mechanical models. Equivalent plots produced for all four material models are shown in the Supporting Information available online (Fig. S4). For a full-color version of this figure, the reader is referred to the online version of the article.

The tendency of contraction-induced loads to concentrate in such tethers and rings was greatly augmented by fiber compression buckling, with fiber tension stiffening marginally contributing to this effect (Fig. S4). Fiber compression buckling also resulted in larger compressive strains and smaller tensile loads and SEDs, with tension stiffening again only marginally affecting the magnitudes of loads (Fig. S4). Overall, the contraction of an isolated single cell (without cell neighbors) induces matrix deformations that are symmetrically distributed about the cell center yet propagate through distinct fibrillar arrangements, with magnitudes that are predominantly dictated by fiber microbuckling.

The effect of fiber compression buckling on load transfer between cells

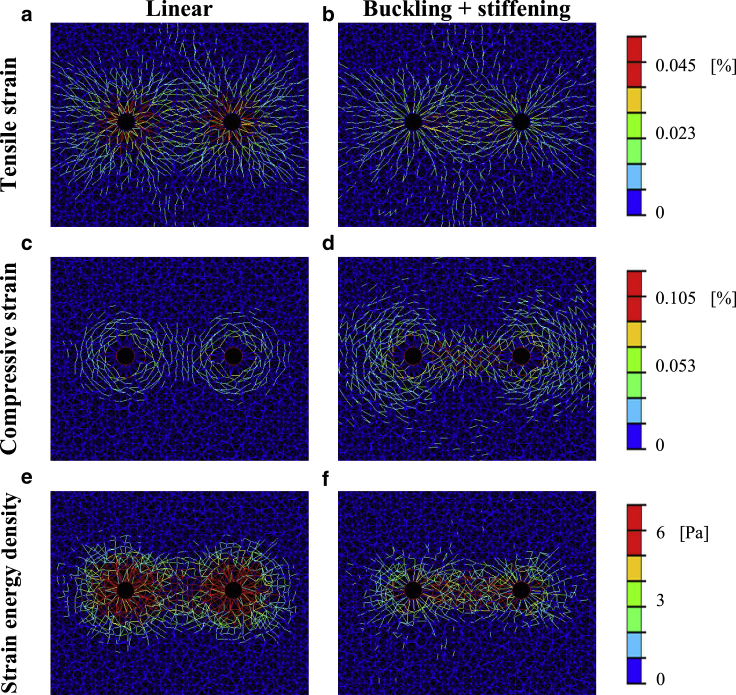
We next analyzed the distribution of loads occurring between two neighboring contracting cells. The contour plots in Figs. 4 and S5 show that fiber microbuckling resulted in tensile strains and SEDs that were generally smaller yet more concentrated within the intercellular matrix, whereas fiber linear elasticity produced a more even distribution of loads around each cell. The mean tensile strain and SED occurring in a disk surrounding each of the cells (outcome measure 4 in Outcome Measures) revealed considerably lower values for the compression-buckling model variants as compared to those in which fibers resisted compression (Fig. S7, a and b). This indicates that it is “easier” for cells to contract within a bucklable matrix, which is ascribable to its lower resistance. To quantify the tendency of loads to concentrate in the intercellular medium, we calculated the fraction of deformations and SEDs falling within the matrix area pointing toward the neighboring cell (outcome measure 5 in Outcome Measures, referred to as “directionality ratio”). We found that fiber buckling resulted in SEDs and tensile strains being more directed toward the neighboring cell (i.e., concentrating in the intercellular region), as reflected by higher directionality ratios (Fig. 5). The most distinct effect was found for SEDs and tensile strains at the shortest cell-to-cell distances tested: at 2.1 cell diameters, for example, fiber buckling resulted in 0.40 of the total SEDs being directed toward the neighboring cell, compared with 0.24 for linear-elastic fibers and 0.17 for a single, isolated contracting cell (Fig. 5 a). “Stronger” buckling ratios (i.e., smaller ρ in Eq. 1) normally resulted in a more considerable fraction of loads falling within the intercellular medium (small panels at the top right of Fig. 5), which further emphasizes the critical role of fiber buckling in directing the ECM loads toward the neighboring cell. The effect of microbuckling was noticeable up to a distance of ∼9 cell diameters, above which the directionality ratios approached the value calculated for a single, isolated cell (0.17, which indicates no preferred orientation of loads), implying that mechanical intercellular signaling no longer occurred (Fig. 5). In general, similar trends were observed for 10% and 50% cell contraction (data not shown), showing elevated directionality of loads for the model variants simulating the fibers as demonstrating nonlinear-elastic behavior. Additionally, when plotting the loads (tensile strains, compressive strains, and SEDs; Fig. S8) occurring in the intercellular band along the line connecting the cells, it was evident that loads were more elevated within the intercellular band with respect to the opposite direction, with networks of bucklable fibers showing a slower decay of loads. These results indicate that fiber microbuckling results in lower-magnitude loads that are more efficiently directed to the neighboring cell.

Figure 4.

Deformations as a result of the contraction of two cells. Tensile strains (top row), compressive strains (middle row), and SEDs (bottom row) occurring around two neighboring contracting cells (here, the cell-to-cell distance is 3.4 cell diameters) and particularly within the intercellular medium for 25% contraction, are shown. Plots were produced for linear (left column; a, c, and e) and nonlinear (buckling + strain stiffening; right column; b, d, and f) models. Equivalent plots produced for all four material models are shown in the Supporting Information available online (Fig. S5). For a full-color version of this figure, the reader is referred to the online version of the article.

The effect of fiber tension strain stiffening on load transfer between cells

Fiber strain stiffening in tension further contributed to concentration of loads in the intercellular medium, as reflected by higher directionality ratios of SEDs, tensile, and compressive strains (Fig. 5). The effect of stiffening was most evident at the smaller cell-to-cell distances and larger cell contractions (50% as opposed to 25% and 10%), which is attributable to the tensile strains exceeding the critical stiffening threshold of 0.02 tensile strain (Eq. 1). For a cell contraction of 25% and a cell-to-cell distance of 1.8 cell diameters, for example, fiber stiffening resulted in a SED directionality ratio of 0.62, compared with 0.27 for the equivalent linear-elastic model variant and 0.17 for a single, isolated cell (Fig. 5 b). When fibers were modeled as both buckling and stiffening, the directionality ratios were substantially elevated, reaching 0.66 at a cell contraction of 25% and cell-to-cell distance of 1.8 cell diameters (SED directionality ratio, Fig. 5 b). For 50% contraction and a cell-to-cell distance of 1.8 cell diameters, fiber nonlinear elasticity contributed to a directionality ratio of up to 0.92 (data not shown). For a cell contraction of 10%, the differences between equivalent strain-stiffening and non-strain-stiffening model variants were marginal, which is ascribable to the tensile strains rarely exceeding 0.025 (strain stiffening was set to occur above 0.02; Mechanical Properties). The influence of fiber tension stiffening was noticeable up to ∼3–4 cell diameters, a relatively smaller distance than that found for the effect of compression buckling (9 cell diameters, The Effect of Fiber Compression Buckling on Load Transfer Between Cells). Overall, at larger cell contractions and smaller cell-to-cell distances, fiber strain stiffening—alone or in combination with compression microbuckling—further contributes to concentration of loads within the intercellular region of the ECM, as demonstrated by the amplification of the directionality ratio of the load distributions.

The effect of fiber nonlinear elasticity on cell-contraction forces

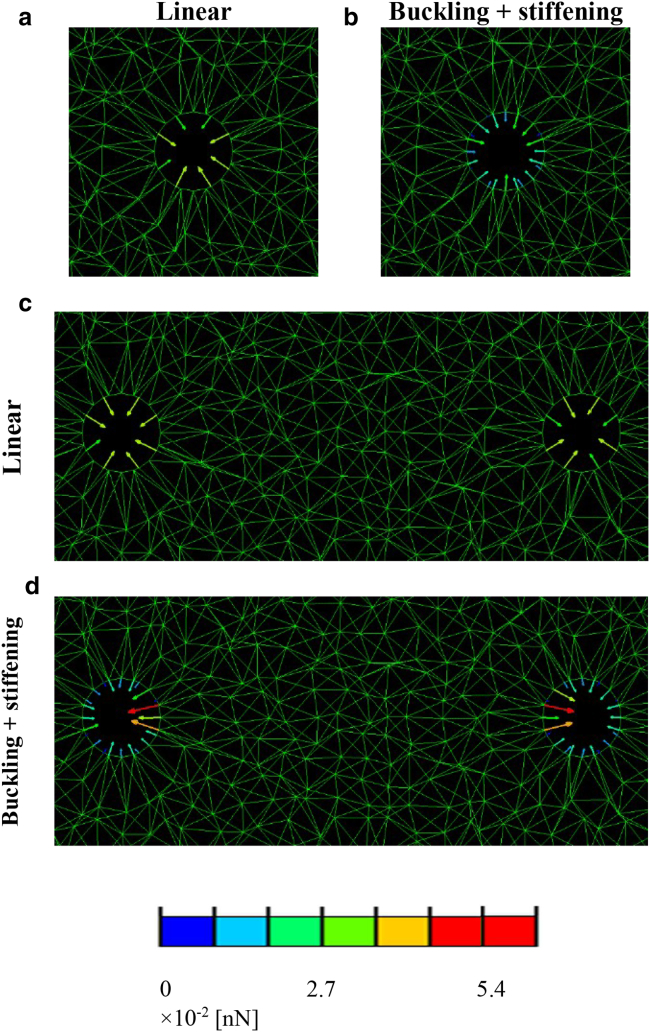
Analysis of the force balance acting on the cell boundaries (Figs. 6 and S9) and its dependency on the cell-to-cell distance can serve as an indication of how the ECM mediates the propagation of forces between contractile cells. A key question is whether the contraction of two neighboring cells results in mutual attraction or repulsion. We thus calculated the projection of the net force applied by the cell to the surrounding ECM on the line connecting the centers of the two cells (outcome measure 2 in Outcome Measures, referred to as “cell-interaction force”) and plotted it against the cell-to-cell distance (Fig. 7 a). We found that the net force applied by the cell to the ECM is consistently in the direction opposite the neighboring cell. It can thus be inferred that the matrix is always pulling the cells together, resulting in attraction forces. The cell-interaction force was only slightly influenced by fiber compression buckling but considerably affected by tension stiffening (with or without microbuckling; Fig. 7 a). For example, at a cell contraction of 25% and a cell-to-cell distance of 2.1 cell diameters, fiber stiffening resulted in an interaction force exceeding 0.4 nN, compared with 0.07 nN (i.e., 5.7-fold) for the equivalent linear-elastic model variant (Fig. 7 a). This effect of strain stiffening was most evident for the larger levels of cell contraction; for 50% contraction, there was an almost 30-fold difference in the interaction force between the strain-stiffening and linear-elastic cases (data not shown). The cell-interaction force decreased with increasing cell-to-cell distance and for all levels of cell contraction reached a plateau at distances larger than 6–7 cell diameters (Fig. 7 a).

Figure 6.

Reaction forces occurring on the cell boundaries for a single ((a) and (b)) and two contracting cells ((c) and (d)). The distance between cells is 3.4 cell diameters, and cell contraction is 25%. Plots were produced for linear ((a) and (c)) and nonlinear (buckling + strain stiffening, (b) and (d)) mechanical models. Equivalent plots produced for all four material models are shown in the Supporting Information available online (Fig. S9). For a full-color version of this figure, the reader is referred to the online version of the article.

Also of interest is the force polarity that develops on the cell boundary. This can potentially trigger cell morphological changes and migratory preference along the direction of force polarization (38). Therefore, we further computed the front-to-rear force polarity ratio (with “front” referring to the direction pointing toward the neighboring cell; outcome measure 3 in Outcome Measures) as an indicator of the direction toward which the cell(s) is likely to spread or migrate (Fig. 7 b). We found that force polarity was greatly elevated when cells were close together, particularly when the matrix fibers exhibited both buckling and stiffening (Fig. 7 b). At a cell contraction of 25% and cell-to-cell distance of 2.1 cell diameters, for example, the force applied in the direction pointing toward the neighboring cell was 1.2- (linear-elastic fibers), 2.2- (compression buckling), 2.0- (tension stiffening), and 4.0- (buckling and stiffening) fold larger than the force applied in the opposite direction (Fig. 7 b). The force polarity considerably increased with the level of cell contraction; at 50% contraction and a cell-to-cell distance of 2.1 cell diameters, it reached as much as 6.2 (tension stiffening) and 22.7 (buckling and stiffening); for a smaller cell-to-cell distance of 1.8 cell diameters, polarity exceeded 100 (data not shown). This is attributable to the large tensile deformations occurring in the fibers contained in the intercellular region of the matrix as a result of cell contraction (The Effect of Fiber Tension Strain Stiffening on Load Transfer Between Cells). These findings indicate that nonlinear elasticity leads to stronger attraction forces acting between cells and contributes to the onset of force polarity on the cell boundaries. Cells are thus more likely to respond to distant cells (e.g., by adapting their shape or migrate toward their neighbors) when embedded within a matrix consisting of nonlinear-elastic fibers compared with linear-elastic ones.

The effect of nonlinear elasticity on structural remodeling of the intercellular matrix

Structural remodeling of the ECM, including fiber densification and alignment, can influence the biological activity of cells, including morphology and migration (38), and is therefore of particular interest. Accordingly, we examined how the above-described preferred directionality of loads and their tendency to concentrate in the intercellular matrix influence fiber density and alignment. We found that the intercellular region of the matrix contained more fibers as a result of contraction. The level of increase in fiber density was considerably greater when the fibers buckled under compression, with strain stiffening under tension further contributing to this effect (Fig. 8 a). The level of increase was larger for higher levels of cell contraction (data not shown).

As a result of cell contraction, the fibers contained in the intercellular medium were also more aligned along the line connecting the centers of the contracting cells (Fig. 8 b), which is the direction of maximal tensile loading imposed by such contractions. The alignment was more considerable when the fibers buckled under compression and stiffened under tension, with buckling again showing a more considerable effect. Higher levels of cell contraction resulted in a more considerable alignment (data not shown). Similarly to the model outcomes discussed above, these trends—along with the changes in fiber density and orientation themselves—were more noticeable when the two neighboring cells were closer together; a plateau was reached beyond a cell-to-cell distance of 11–15 cell diameters (Fig. 8). Overall, nonlinear elasticity of the fibers forming the ECM contributes to an increase in the density and alignment of the fibers contained in the intercellular region of the matrix, facilitating the formation of the “bands” visible in our experiments (Fig. 2) as well as in other biological contexts (3, 4, 38).

Network connectivity

Biological gels typically demonstrate fiber-network connectivity levels smaller than 8.0 as reported in previous experimental studies (e.g., C = ∼3.5 for collagen gel as reported in (40)). We therefore tested the effect of reducing the network connectivity on the concentration of loads between the neighboring cells. We found that the network connectivity affected most outcome measures of interest (directionality ratios and structural remodeling of the intercellular matrix) to a limited extent. Particularly, the trend showing increased directionality of loads and structural remodeling of the intercellular matrix due to fiber nonlinear elasticity was evident for all levels of network connectivity (Figs. 9 and S10). Above the cell-to-cell distance of nine cell diameters and for all levels of network connectivity, the directionality ratios approached the values for a single, isolated cell, implying that mechanical intercellular signaling no longer occurred.

Figure 9.

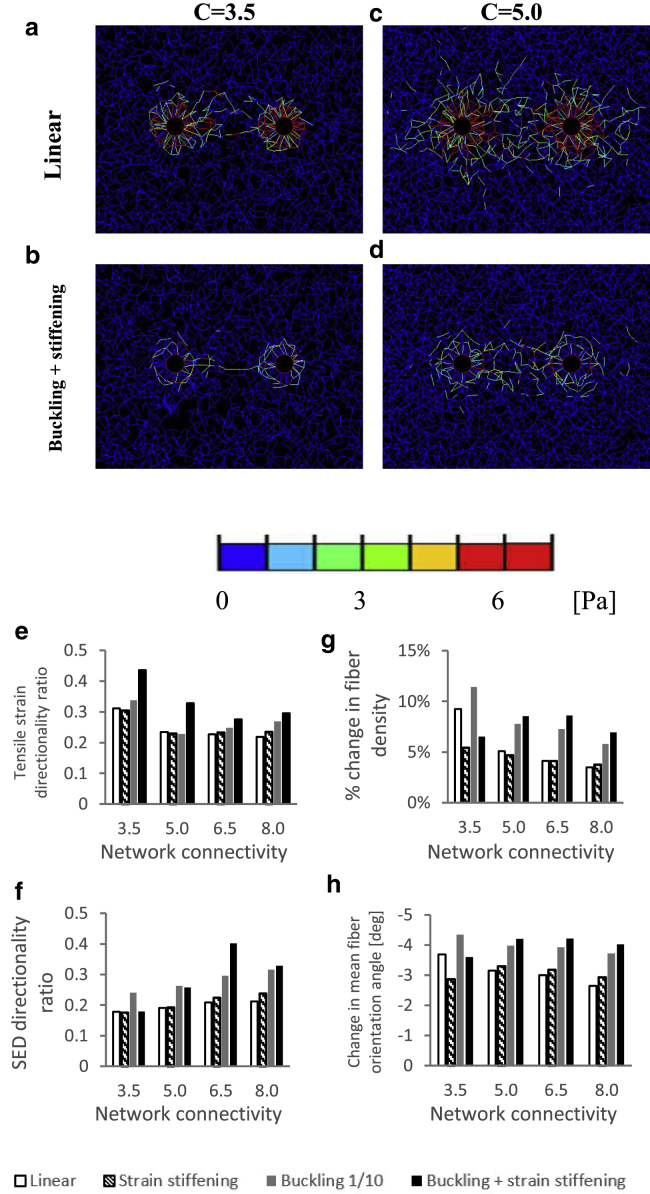
The effects of network connectivity on the model outcomes. (a–d) SEDs occurring around two neighboring contracting cells (here, the cell-to-cell distance is 3.4 cell diameters) for 25% contraction and two levels of network connectivity (C = 3.5, 5.0) are shown. Plots show linear ((a) and (c)) and nonlinear (buckling + strain stiffening; (b) and (d)) model variants. Equivalent plots produced for all four material models are shown in the Supporting Information available online (Fig. S10). (e–h) Bar charts demonstrating the effects of the level of network connectivity on the directionality ratios of tensile strains (e) and SEDs (f) and fiber density (g) and orientation (h) within the intercellular region of the matrix for all four material models at a cell-to-cell distance of 3.4 cell diameters, are shown. For a full-color version of this figure, the reader is referred to the online version of the article.

Discussion

ECM-mediated interaction between cells has been shown to be essential in various biological processes, such as capillary sprouting (3), cancer invasion (4), heartbeat synchronization (5), and morphogenesis (6). This diversity of biological contexts implies that long-range intercellular mechanical interaction has a universal role in cell and tissue function. To explore the role of ECM mechanical properties on the transmission of loads between cells, we developed a 2D computational model of two contracting cells embedded within a fibrous matrix. The model was validated in various aspects, including by juxtaposing its bulk mechanical response to applied load (Fig. S1) and the decay of cell-induced displacements (Fig. S3), to previous theoretical and experimental findings. The model suggests that the nonlinear-elastic behavior of the ECM fibers—manifested by compression microbuckling and tension stiffening—results in loads that are more concentrated within the intercellular matrix and more directed toward the neighboring cell. Efficiency can be regarded as the capacity of a process to occur with a minimal amount of wasted effort; in more quantitative terms, it is the ratio of useful output versus total input. In the context of the current model, efficiency can be related to as the fraction of cell-induced loads applied in the direction pointing toward the neighboring cell (and thus potentially resulting in mechanical signaling, i.e., “useful output”) to the total load induced by the cell contraction (“total input”). Accordingly, the directionality ratio outcomes presented herein (The Effect of Fiber Compression Buckling on Load Transfer Between Cells and The Effect of Fiber Tension Strain Stiffening on Load Transfer Between Cells) indicate that the nonlinear-elastic behavior of the ECM fibers contributes to the efficiency of the transfer of mechanical signals between neighboring cells. When embedded within a bucklable matrix, cells not only induce a more directed mechanical signal toward their neighbor but also exert less energy to contract (which is attributable to the smaller resistance of the matrix to deformations; The Effect of Fiber Compression Buckling on Load Transfer Between Cells). This further highlights the contribution of fiber buckling to efficient mechanical communication between cells via the ECM. Although previous models have revealed the role of elastic nonlinearity to increasing the range of cell-induced loads through the ECM and between neighboring cells (24, 25, 27, 28, 29), to our knowledge our model is the first to demonstrate and quantify the direct effects of ECM nonlinear elasticity on the directionality of mechanical loads and on the efficiency of load transfer between cells.

The elevated concentration of loads and the rearrangement of fibers within the intercellular medium (experimental: Biological Experiments of Intercellular Mechanical Interactions; computational: The Effect of Nonlinear Elasticity on Structural Remodeling of the Intercellular Matrix) were observed in all model variants (albeit to different degrees depending on the modeled fiber elastic behavior, level of cell contraction, and cell-to-cell distance). These trends were found to be largely insensitive to the network connectivity (Network Connectivity), cell diameter/fiber length ratio (Fig. S12), and selection of element type (truss/beam, Fig. S11). The elevated loads in the intercellular matrix are ascribable to the simultaneous contraction of the two cells, which practically pulls the intercellular band from both sides, whereas other regions of the network are not subjected to such elevated loading. The increased tension in this region of the ECM obliges the fibers to stretch and align and also results in perpendicular compression—which is augmented by fiber compression buckling—leading to fiber densification in the intercellular medium (the level of increase in fiber density within the intercellular region was found to be larger when fibers were bucklable; The Effect of Nonlinear Elasticity on Structural Remodeling of the Intercellular Matrix). This may effectively induce “compressive stiffening” of the intercellular ECM band (41, 42), particularly when the fibers are modeled as bucklable (42). The increased effective stiffness of this region of the matrix can lead to the observed preferential orientation of loads toward the neighboring cell, which is more evident in fiber-buckling networks. The further increase in the directionality of loads (mainly SEDs) owing to tension stiffening (The Effect of Fiber Tension Strain Stiffening on Load Transfer Between Cells) is attributable to the greater resistance of the strain-stiffened fibers to tensile deformation (i.e, stiffening).

Previous studies (16, 25, 28, 29) have captured the tendency of cell-contraction-induced loads to concentrate in the intercellular regions of the matrix. For example, Notbohm et al. (25) and Abhilash et al. (29) showed that cell-contraction-induced tensile strains occur almost entirely in the band between the two cells, which was ascribed to fiber microbuckling. Ma et al. (28) further suggested that 24 h after cell seeding in a collagen gel, the preferential orientation of cell-induced stresses toward neighboring cells was facilitated by increased fiber alignment. Our study further provides a systematic quantitative evaluation of the transmission of mechanical signals between neighboring cells and its dependency on ECM nonlinear elasticity, level of cell contraction and distance between the cells. Moreover, our model shows that the preferential orientation of cell-induced loads toward neighboring cells can occur without a priori fiber alignment; in the simulations, both the load anisotropy and network fiber anisotropy occurred simultaneously with cell contraction.

Our simulations demonstrate an increase in fiber density and alignment within the intercellular band, which was most evident when the ECM fibers exhibited nonlinear elasticity (The Effect of Nonlinear Elasticity on Structural Remodeling of the Intercellular Matrix). This finding can explain the elevated fluorescence intensity and alignment in the matrix extending between fibroblast cells embedded in a fibrin gel (Fig. 2). It also highlights the important role played by the nonlinear-elastic behavior of the ECM fibers in the formation of intercellular bands formed in other biological situations, as demonstrated in vitro (1, 3, 25, 28, 33, 34) and in silico (17, 29, 30, 31, 34).

Our FE model allowed us to directly infer the cell-contraction forces and cell-interaction forces acting between neighboring contracting cells and to examine their dependency on the cell-to-cell distance. Contraction forces were estimated to range between 0.2 and 10 nN, in line with previous experimental findings (43, 44, 45). In our simulations, we also found that neighboring contracting cells attract each other up to a cell-to-cell distance of 6–7 cell diameters, with the attraction forces increasing with shorter cell-cell distances (The Effect of Fiber Nonlinear Elasticity on Cell-Contraction Forces). This result has some discrepancy with previous analytical models that identified both attractive and repulsive forces occurring between cells in linear-elastic media (which estimated cellular interactions based on energy considerations) (46, 47). A previous experimental study similarly found that endothelial cells cultured on linear-elastic synthetic gels apply both repulsive and attractive forces to each other (22).

Our simulations predict intercellular mechanical signal transmission to occur at a cell-to-cell distance of up to ∼9 cell diameters. Specifically, we observed structural changes (alignment and densification) within the intercellular region of the matrix when the cells were up to nine cell diameters apart (The Effect of Nonlinear Elasticity on Structural Remodeling of the Intercellular Matrix); directionality ratios of tensile strains and SEDs predicted preferential load orientation to arise at a cell-to-cell distances of up to nine cell diameters (The Effect of Fiber Compression Buckling on Load Transfer Between Cells); and force interactions occurred when the cells were up to 6.5 cell diameters apart (The Effect of Fiber Nonlinear Elasticity on Cell-Contraction Forces). The influence of fiber tension stiffening on intercellular loads was notable at a cell-to-cell distances of up to four cell diameters (The Effect of Fiber Tension Strain Stiffening on Load Transfer Between Cells), whereas the effect of compression buckling spanned a considerably longer distance of up to nine cell diameters. This is supported by the recent analytical predications of Xu et al. (24), which implied that tension stiffening dominates the propagation of matrix displacements in the near vicinity of the contracting cell, whereas compression buckling dictates the distribution of displacements in the more distant regions of the ECM. The range of intercellular mechanical force transmission predicted by our simulations (∼9 cell diameters or 137 μm when assuming that the fibers are bucklable) is larger than that of Humphries et al. (16) (five cell diameters), but similar to that of Wang et al. (30) (both derived computationally). It is also larger and smaller than predicted in the experimental studies of Ma et al. (28) (120 μm) and Winer et al. (20) (500 μm), respectively.

Like in many previous models (16, 17, 24, 25, 26, 27, 35), cells were modeled here as contracting circles. This simplified representation captures the morphology of cells shortly after seeding in biological gels (Biological Experiments of Intercellular Mechanical Interactions; Fig. 2; (28, 33)). It is also in line with the purpose of our model, which was designed to investigate the mechanical signaling occurring between contracting cells embedded in biological gels shortly after seeding, before cell spreading or morphogenesis, and while isolated from any modifications potentially occurring in the ECM at later stages. Similarly, we assumed uniformly distributed (i.e., isotropic) contractile displacements of the cell. It is currently unclear whether cells attempt to control displacements or forces in their vicinity (which may also vary depending on the physiological conditions, e.g., early or late cell-matrix interaction). We chose to model cells as applying uniform contractile displacements as one possible biological scenario occurring, for example, during early cell-matrix interaction, as demonstrated by Ghassemi et al. (48), who found that cells employ a rigidity-sensing system to adjust the force needed to produce a given displacement of the surrounding matrix. Further research exploring intercellular interactions under uniformly distributed cell-contraction forces is warranted. Overall, our computational model mimics the biological scenario of the early stages of cell-ECM and cell-cell interactions and predicts the ability of cells to initiate mechanical cues and communicate through mechanical pathways shortly after their seeding. These early mechanical cues can guide cell growth and expansion toward nearby cells, as previously described for fibroblasts spreading toward each other already 5–7 h post seeding (25).

Our model has notable limitations that should be considered when interpreting the results. First, similarly to most previous models (16, 17, 28, 30), the model simulated an inherently three-dimensional (3D) system, in 2D. Such simplification, however, possesses a considerable computational advantage, which allowed us to run a large number of model variants to explore the effects of several factors on the outcome measures of interest while still capturing all aspects of network mechanics, including the nonlinear mechanical-loading response at the micro- and macroscale levels, and fiber rearrangement (29). In this regard, previous studies, e.g., Notbohm et al. (25) and Rosakis et al. (49), demonstrated that the trends observed in 2D reflected the trends in 3D. Both 2D and 3D systems demonstrated the slow decay of displacements as a result of buckling (albeit with different decay slopes, which were smaller than the linear-elastic decay). Additionally, the mechanical properties assigned to the individual fibers were not directly derived from the literature but from the simulated macroscale properties of the network, which were juxtaposed against previous experimental findings of the bulk response of collagen gels to uniaxial loading (Supporting Information). This is because most of our understanding of the mechanical behavior of fibrous gels comes from bulk measurements, whereas data on the elastic behavior of the individual fibers contained in the gels are sparse and inconsistent (17). Furthermore, most of our model variants employed truss elements, which encompasses the assumption that these are subjected to uniaxial tension and compression (without bending) and are able to rotate freely one with respect to the other (Numerical Method). Some of the previous models (17, 26, 27, 28, 29, 30, 35), however, did account for bending potentially occurring in the fibers and/or between two fibers meeting at a cross-link. A sensitivity study we conducted showed that using beam rather than truss elements affected the model outcomes only slightly while resulting in similar trends (Fig. S11), which concurs with previous findings (16, 17, 25, 29, 35, 50). Considering these and other potential limitations of the model, it is recommended that the data presented here be interpreted mostly as trends of effects rather than as absolute values (51). Particularly, the objective of the study was not to reproduce specific numerical results reached through laboratory experiments but to compare trends of effects of the mechanical behavior of the ECM fibers on the mechanical signaling between neighboring cells; we do not expect the limitations discussed above to affect such comparative findings.

Conclusion

The FE model presented herein predicts that the nonlinear-elastic behavior of the individual fibers constituting the ECM contributes to highly directional and efficient intercellular mechanical signal transmission. Such a mechanism regulating long-range, cell-cell communication elucidates previous experimental observations of biological processes involving intercellular mechanical signaling. In addition, it further highlights the importance of utilizing fibrous biological gels for facilitating long-range intercellular communication in comparison with linear-elastic synthetic gels (such as polyethylene glycol and PAA gels), which are commonly used for cell culturing (52).

Major challenges for future work include a more realistic description of the physiological scenario, including 3D modeling and dynamic modeling accounting for the time-dependent cell morphology and loading, as well as the viscoelastic and plastic nature of ECM.

Author Contributions

A.L. conceived and supervised the project as the principal investigator. R.S.S. and H.T. designed and implemented the computational model. R.S.S. carried out the computations and conducted the data analysis. M.S. validated the material properties assigned to the computational model by running the analysis described in the Supporting Information. S.N. and O.S. conducted the biological experiments and the analysis of their outcome data. R.S.S. and A.L. analyzed and interpreted the data. O.T. assisted in the model design and data analysis. R.S.S. and A.L. wrote the manuscript.

Editor: Cynthia Reinhart-King.

Supporting Citations

Reference (53) appears in the Supporting Information.