Stability of hand force production. II. Ascending and descending synergies

Abstract

We combined the theory of neural control of movement with referent coordinates and the uncontrolled manifold hypothesis to investigate multifinger coordination. We tested hypotheses related to stabilization of performance by covarying control variables, translated into apparent stiffness and referent coordinate, at different levels of an assumed hierarchy of control. Subjects produced an accurate combination of total force and total moment of force with the four fingers under visual feedback on both variables and after feedback was partly or completely removed. The “inverse piano” device was used to estimate control variables. We observed strong synergies in the space of hypothetical control variables that stabilized total force and moment of force, as well as weaker synergies stabilizing individual finger forces; whereas the former were attenuated by alteration of visual feedback, the latter were much less affected. In addition, we investigated the organization of “ascending synergies” stabilizing task-level control variables by covaried adjustments of finger-level control variables. We observed intertrial covariation of individual fingers’ referent coordinates that stabilized hand-level referent coordinate, but we observed no such covariation for apparent stiffness. The observations suggest the existence of both descending and ascending synergies in a hierarchical control system. They confirm a trade-off between synergies at different levels of control and corroborate the hypothesis on specialization of different fingers for the control of force and moment. The results provide strong evidence for the importance of central back-coupling loops in ensuring stability of action.

NEW & NOTEWORTHY We expand analysis of action in the space of hypothetical control variables to hierarchically organized multieffector systems. We also introduce the novel concept of ascending synergies, which reflect covariation of control variables to individual effectors (fingers) that stabilize task-specific control variables at a hierarchically higher, task-specific level (hand).

INTRODUCTION

Two views have dominated the literature on the problem of motor redundancy, which arises due to the excess of variables at the level of effectors as compared to the number of constraints in typical tasks. According to the classical formulation (Bernstein 1967), motor redundancy is a major problem for the controller, which may be solved, for example, using methods of optimization (reviewed in Prilutsky and Zatsiorsky 2002). The alternative view (Gelfand and Latash 1998; Latash 2012) is that the problem of redundancy is merely apparent and that abundant sets of variables at the effector level allow the neural controller to ensure stability of different performance variables in a task-specific way (Latash 2012; Schöner 1995). This view has been developed within the physical approach to motor control (Latash 2016, 2017) that combines the ideas of the neural control of movement with spatial referent coordinates (RCs; Feldman 2015) and the uncontrolled manifold (UCM) hypothesis (Scholz and Schöner 1999).

According to the notion of action control with specification of time-varying RCs, the control of an effector can be described with time profiles of two basic commands, the reciprocal command (R-command) and the coactivation command (C-command). The C-command reflects overlapping spatial zones of activation of action-relevant agonist and antagonist musculature (Feldman 1980, 2015). Depending on external conditions, changes in the R- and C-commands lead to different measurable changes in performance. In particular, in isometric conditions during force production along a coordinate X, assuming that there is a non-zero degree of agonist-antagonist cocontraction (cf. Ghez and Gordon 1987; Gottlieb et al. 1989), the R-command is a neural entity related to changes in spatial referent coordinate (X_R), whereas the C-command is the neural counterpart of the effector’s apparent stiffness (k_X). In a linear approximation, the effector is expected to produce force according to Hooke’s law: F_X = –k_X × (X_A − X_R), where X_A is the current coordinate of the effector. In experiments with smooth changes in X_A, X_R and k_X values can be computed and used to infer the R- and C-commands, assuming that the subject does not change these commands during the change in X_A (Ambike et al. 2016a).

In the present study, we explored four-finger pressing tasks that required the production of a magnitude of total force (F_TOT). According to the theory of control with RCs, a set {R_H; C_H} is specified at the hierarchically highest (task) level to match the desired hand total force magnitude (Fig. 1). Note that we use {R; C} to address neural commands and {X_R; k} for the related pair of variables computed in experiments. Neural mappings from the task level, given the extrinsic and intrinsic conditions, result in the emergence of each individual finger’s {R_f; C_f} values, which lead to individual finger forces (F_f) that sum up to produce total force, F_TOT. For simplicity, the scheme in Fig. 1 skips other levels, such as, for example, propagation of X_R to individual muscles; at the muscle level, X_R is equivalent to threshold of the stretch reflex (λ) as in the classical equilibrium-point hypothesis (Feldman 1966, 1986). Although the scheme in Fig. 1 is essentially feedforward, it implies the existence of feedback loops, which are inherent in the theory of control with referent coordinates, in particular, those that adjust {R_f; C_f} at the finger level to ensure stable performance with respect to the salient task variable, i.e., F_TOT (Latash et al. 2005; Martin et al. 2009).

Fig. 1.

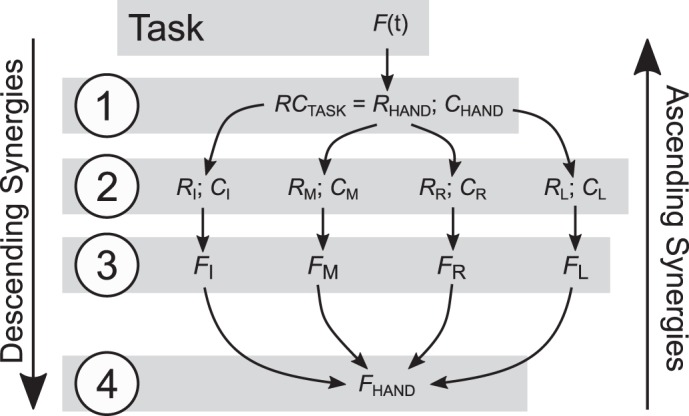
A hypothetical scheme of the neural control of the four-finger total force (F_TOT) production task with referent coordinates for the effectors. At level 1, two variables R_HAND and C_HAND, are specified, based on the desired F_TOT. At level 2, these variables result in the {R_f; C_f} pairs for the individual fingers, f = I (index), M (middle), R (ring), and L (little). At level 3, individual finger forces F_f are produced by the corresponding {R_f; C_f} pairs. At level 4, the finger forces sum up to produce hand force, F_HAND. At each level, pairs of variables computed from experimental data {X_R; k} are used as proxies for the control pairs R and C. Two types of abundant mappings may be associated with synergies, descending (from a higher level to a lower level) and ascending (from a lower level to a higher level).

A number of earlier studies have explored the mapping from the four finger forces to a single variable, F_TOT (reviewed in Latash 2008). Several recent studies have estimated {X_R; k} pairs measured in individual trials and explored their mapping on F_TOT (2-to-1 mapping; Ambike et al. 2016a, 2016b, 2018; Reschechtko and Latash 2017). In both of these examples, numerous solutions at the hierarchically higher level were theoretically available to match the desired mechanical outcome. In the following, we address hypothetical neural mechanisms ensuring stability of the salient performance variable by covaried adjustments within abundant sets of elemental variables, such as finger forces and {X_R; k} pairs, as “descending synergies.”

In the present study, for the first time, we address the role of an intermediate step, the specification of {R_f; C_f} at the finger level, in ensuring stability of performance. One aspect of this exploration is another example of a descending synergy, from the eight-dimensional {R_f; C_f} set (pairs of variables for each finger) to F_TOT and total moment of force (M_TOT) prescribed by the task. This mapping implies two steps: a mapping from {R_f; C_f} to each finger’s force (2-to-1 mapping) and a mapping from the digit forces to F_TOT and M_TOT (4-to-2 mapping). On the basis of earlier reports of a trade-off between synergies in hierarchical systems (Gorniak et al. 2007, 2009), we hypothesized that there would be strong synergies stabilizing F_TOT and M_TOT in the eight-dimensional {R_f; C_f} space (hypothesis 1A), but not necessarily those stabilizing individual finger forces in the two-dimensional {R_f; C_f} space, where f stands for the individual fingers, index, middle, ring, and little (hypothesis 1B). In the present paper, we use the term “descending synergy” to signify all few-to-many mappings in which hierarchically higher sets of elemental variables (kinematic, kinetic, or control) covary to stabilize hierarchically lower outputs. This nomenclature is a generalization of previous work on multielement synergies (reviewed in Latash et al. 2007).

We also explored the role of certain fingers in stabilization of total force and total moment by randomizing the {X_Rf; k_f} pairs (cf. Müller and Sternad 2003) for one finger at a time and quantifying the effects of such randomization on F_TOT and M_TOT variability. Earlier studies in which subjects held and manipulated objects have provided evidence pointing at different functional roles of the “lateral fingers” (index and little) and “medial fingers” (middle and ring): the former were responsible for accurate moment production, whereas the latter ensured accurate production of the grip force (Zatsiorsky et al. 2002, 2003). On the basis of those studies, we hypothesized that F_TOT stabilization would be highly sensitive to randomization of the {X_Rf; k_f} pairs for the middle and ring fingers, whereas M_TOT stabilization would be more sensitive to randomization of the {X_Rf; k_f} pairs for the index and little fingers (hypothesis 2).

In our studies, synergies were estimated at two states, under continuous visual feedback on F_TOT and M_TOT and following a drift in performance caused by turning the feedback off (cf. Ambike et al. 2015; Vaillancourt and Russell 2002). On the basis of earlier studies (Parsa et al. 2016; Reschechtko and Latash 2017), we expected all the mentioned synergies to be strong under visual feedback and to weaken or disappear completely without feedback on one or both salient variables (hypothesis 3).

Finally, we explored a qualitatively different kind of synergies, from the eight-dimensional {X_Rf; k_ƒ} space to the two-dimensional {X_RH; k_H} space at a higher hierarchical level (see Fig. 1). Such “ascending synergies” are natural parts of the idea of hierarchical control with RCs; to our knowledge, they have never been explored quantitatively. We tentatively hypothesized that there would be synergies stabilizing {X_RH; k_H} by covarying across trials adjustments of {X_Rf; k_ƒ} and that those synergies would also be weakened under the removal of visual feedback (hypotheses 4A and 4B).

Our study uses two methods of synergy analysis. One of them is a more traditional method (reviewed in Latash et al. 2002) based on quantifying intertrial variance in two spaces, one of which is compatible with accurate performance of a salient variable (within its UCM, V_UCM) and the other of which leads to changes in that variable (orthogonal to the UCM, V_ORT). This method is used when a linear mapping between elemental variables and the performance variable can be assumed. The other method (cf. Müller and Sternad 2003) uses a permutation technique to create surrogate data sets; the permutation is expected to remove covariation among elemental variables. After permutation, indices of performance variability are compared between the actual and surrogate sets. This method is used when mapping between elemental variables and the performance variable is known but expected to be strongly nonlinear.

METHODS

This is the second paper presenting results of a study with four-finger accurate F_TOT and M_TOT production. Details of the apparatus and procedures are available in the first paper (Reschechtko and Latash 2017). Below we briefly present the main steps of the experimental procedures.

Subjects

Ten adult subjects (5 women; ages 20–35 yr) participated in this study; due to exclusion criteria imposed during analysis (see Analysis), however, data from only nine subjects are analyzed in this article. Subjects were right handed, as assessed via self-reported use for activities of daily living, and reported no injuries or neurological disorders that would interfere with their ability to perform the study procedures. Subjects provided written informed consent according to procedures approved by The Pennsylvania State University Office for Research Protections.

Apparatus

This study used the “inverse piano” apparatus (Martin et al. 2011). This apparatus records finger forces while the fingers can be raised or lowered along the vertical axis. Four unidirectional force transducers (208C01; PCB Piezotronics, Depew, NY) measured force by individual fingers; each transducer was mounted on a linear actuator (PS01-23 × 80; Linmot, Spreitenbach, Switzerland) that allowed the sensor to be raised and lowered. Each force transducer was excited and amplified using an individual signal conditioner (PCB 484B11); analog data from these conditioners were sampled at a rate of 1 kHz at 16-bit resolution using a PCI-6052 analog-to-digital board (National Instruments, Austin, TX). Each linear actuator could be controlled independently using a four-channel servo drive (Linmot E400-AT), which was controlled via serial output from the personal computer used for data collection and feedback presentation.

Each subject sat with her or his right forearm approximately parallel to the ground with the shoulder abducted to ~45° with respect to horizontal and the elbow flexed to ~90°. Subjects placed each finger of the right hand on a corresponding force transducer (17-mm diameter); the transducers were mounted such that the centers of adjacent transducers were 3 cm from each other. Transducer position was adjusted in the anterior-posterior direction such that each finger was slightly curved while the finger pad rested in the middle of the transducer face.

A 19-in. monitor, positioned ~0.8 m from each subject’s face, provided visual feedback on total force produced by the four fingers (F_TOT) and the computed moment of force (M_TOT; see Procedures for computation). A purpose-built application designed in the LabVIEW programming environment (National Instruments) was used to log data for offline analysis, provide real-time visual feedback, and control the inverse piano. An illustration of the experimental setup is available in our earlier article (Reschechtko and Latash 2017).

Procedure

Data collection for this study consisted of three main components. First, subjects produced a four-finger maximal voluntary contraction (MVC). The MVC value recorded in this part of the procedure was used to set force values for subsequent experimental procedures. During this procedure, subjects received visual feedback on F_TOT and were instructed to smoothly increase force to produce maximum force any time during a 6-s time window. Subjects were given one practice trial, followed by a 30-s imposed rest, and were then asked to produce the test MVC trial.

After the MVC trial, subject produced single-finger force ramps. Subjects were required to keep all of their fingers on the force sensors but to press with only one (instructed) finger to follow a 12-s force profile. This profile started with 3 s at 5% of the instructed finger’s contribution to the four-finger MVC (addressed further as this finger’s MVC), followed by a 6-s smooth ramp to 50% of its MVC and then 3 s at 50% MVC. Subjects performed one ramp trial for each finger. Data from the ramp trials were used to quantify finger enslaving (Zatsiorsky et al. 2000), but these data are not presented in the current article.

During the main experimental trials, subjects were instructed to produce a combination of F_TOT and M_TOT according to visual feedback. Subjects controlled a cursor that could move vertically and horizontally on the screen; vertical movement corresponded to changes in F_TOT, whereas horizontal movement tracked changes in M_TOT. M_TOT was calculated about a horizontal axis in the anterior-posterior direction between the middle and ring fingers according to the nominal moment arms of the fingers: 4.5, 1.5, −1.5, and −4.5 cm for the index, middle, ring, and little fingers, respectively. The effects of tangential forces and changes in points of force application were neglected; as such, M_TOT reflected a computed variable rather than the actual total moment of force.

A visual target was shown at the center of the screen; the initial cursor position was computed such that maintaining the cursor position in the target corresponded to specific values of F_TOT and M_TOT. The F_TOT target was set at 20% of the four-finger MVC, whereas the M_TOT value was equal to 7% of the index finger’s contribution to the four-finger MVC multiplied by the moment arm of the index finger (4.5 cm) with respect to an axis of rotation passing through the center of the hand in the proximal-distal direction, yielding a value of 31.5% MVC_I·cm (where MVC_I is the index finger’s contribution to the four-finger MVC). These values were selected on the basis of previous studies (Park et al. 2010; Parsa et al. 2016) such that they would not induce fatigue over multiple trials but had a good chance of inducing drifts in both F_TOT and M_TOT.

Each trial lasted for 21 s. When the trial began, subjects moved the cursor to the target position and maintained its position within the target. After 5 s, the inverse piano raised all four fingers simultaneously by 1.0 cm at a rate of 2.0 cm/s and then returned the fingers to their initial position at the same speed. Subjects were instructed not to react to this perturbation. Furthermore, they made any necessary corrections to bring the cursor into the target. Two seconds later (8 s after trial onset), visual feedback was manipulated in one of three possible ways: in the no-feedback condition, the cursor disappeared completely (while the target stayed on the screen); in the force-feedback condition, the cursor’s movement was frozen along the horizontal axis such that subjects received information only about F_TOT production; and in the moment-feedback condition, the cursor’s movement was frozen along the vertical axis such that subjects received information only about M_TOT production. An earlier study by Ambike et al. (2016a) randomized the timing of the application of the perturbation so that subjects could not predict its timing on the basis of the preceding removal of visual feedback. The present study, however, did not use such a randomization protocol because our subjects received full visual feedback when the perturbation was applied, so they could not use feedback removal as a cue for the perturbation onset. Furthermore, we trained the subjects to ignore the effects of perturbations on finger forces, in particular, the effects clearly seen on the feedback monitor. Subjects were also explicitly asked not to try to predict the timing of the perturbations.

Across conditions, subjects were instructed to continue to press as they had previously been pressing and to maintain cursor position in the target according to any visual feedback available. Eleven seconds after feedback had been changed, all four fingers were again raised by 1.0 cm at 2.0 cm/s and returned to their initial position, at which point the trial ended. Subjects performed three to four practice trials until they reported that they were comfortable with the instructions; they performed 24 trials under each feedback condition, for a total of 72 trials. The feedback manipulations were presented in a fully randomized order. Subjects were allowed to take any rest intervals they desired after each trial.

Data Analysis

Data were processed offline using Python 3 (Python Software Foundation) and packages from the SciPy library (Jones et al. 2001). Before analysis, data were low-pass filtered using a forward-and-reverse 4th-order Butterworth filter with a cutoff frequency of 10 Hz. Data were visually inspected for subjects’ failure to adhere to instructions; across subjects and conditions, the largest number of removed trials was three.

Computation of referent coordinates and apparent stiffness.

Hypothetical control variables R_f and C_f (for each finger f) were reflected in pairs {X_R; k} computed twice for each experimental trial according to methods used by Ambike et al. (2016a). These {X_R; k} pairs, referred to subsequently as initial (ini) and final (fin) values, were computed over 0.5 s between 5 and 5.5 s after trial onset (under visual feedback) and again between 19 and 19.5 s with respect to trial onset. We first verified that the force change occurring while fingers were raised was a linear function of the time-varying finger position. We did this by requiring that the best-fit linear regression of the data explained at least 50% of the observed finger force variance (i.e., R > 0.71). Compared with previous studies (Ambike et al. 2016a, 2016b; Reschechtko and Latash 2017), this threshold is relatively low; this was due to the fact that some fingers produced relatively low force, effectively decreasing the signal-to-noise ratio, as well as the requirement that both episodes of finger raising and lowering within a trial be acceptably linear. Across subjects, this criterion yielded an average of 17.8 usable trials per condition per subject (range: 11–24), and we were forced to remove one subject from analysis due to a low number of usable trials in one condition. Finally, because we used some measures susceptible to outliers, we removed any trials in which any finger’s values of X_R or k were more than 3 SD from the mean values. This reduced the number of trials analyzed by an average of 1.2 trials (range: 0–3) per subject per condition. Note that the number of trials analyzed in the present study is equal to or greater than the number used in previous studies using these methods (Ambike et al. 2016a; Reschechtko and Latash 2017).

On ensuring a relatively linear response of F_f to change in finger position, we computed the average value of F_f during the 50 ms before the fingers were raised, as well as the average value of F_f during the final 10 ms of upward sensor motion. We then subtracted the final value from the initial value to obtain ΔF_f and divided ΔF_f by the change in finger position (1.0 cm), yielding k (apparent stiffness) in units of %MVC/cm. X_Rf (in cm) was subsequently computed as X_Rf = −F_f/k. Our choice of coordinate frame (after Ambike et al. 2016a), in which the initial position of the fingers is defined as 0, yields values of X_R < 0.

We computed average values of X_R and k both before (X_Rini; k_ini) and after (X_Rfin; k_fin) feedback manipulation, as well as the ranges of X_R and k for each subject in each condition. We also computed the changes in X_R and k observed within each accepted trial: ΔX_R = X_Rfin − X_Rini and Δk = k_fin − k_ini.

Permutation analysis in the {X_R; k} space.

F_TOT is related to finger forces (F_i) according to the following equation:

$${\text{F}}_{\text{TOT}}={\displaystyle \sum {\text{F}}_f,f=[\text{I,\hspace{0.17em}index;\hspace{0.17em}M,\hspace{0.17em}middle;\hspace{0.17em}R,\hspace{0.17em}ring;\hspace{0.17em}L,\hspace{0.17em}little}]}.$$ (1)

Furthermore, by setting X_A = 0, F_f can be approximated as

$${\text{F}}_f=-k_f\times X_{\text{R}f}.$$ (2)

Combining these two equations, we obtain

$${\text{F}}_{\text{TOT}}={\displaystyle \sum k_f\times X_{\text{R}f}}.$$ (3)

Because the solution space for this equation is nonlinear, we used the permutation analysis (cf. Müller and Sternad 2003) to generate surrogate data. This analysis estimates the variability of F_TOT expected if X_R and k vary randomly across trials while being sampled from distributions with the same means and standard deviations as the original values. We generated {X_Rf; k_f} pairs by combining values of X_R and k observed in different trials and subsequently computing F_SUR and M_SUR. We then computed the standard deviations of F_SUR and M_SUR (SD_SUR,F and SD_SUR,M, respectively) over 10,000 permutations. Finally, we compared SD_SUR,F and SD_SUR,M with those for the actual data (SD_ACT,F and SD_ACT,M) to obtain a ratio: R_SD = SD_SUR/SD_ACT, which was used as a synergy index. Theoretically, R_SD > 1 means that the original data set included covariation of {X_Rf; k_f}, which made SD_ACT lower than expected in a data set without covariation. However, see discussion for further evaluation of an appropriate null hypothesis; given the nature of computation of X_R values from k values, R_SD > 2 is a more likely criterion, although uncontroversial specification of this criterion is impossible at this time. In the present study, we applied the permutation analysis to various subsets of fingers and individual fingers, as well as to X_Rf or k_f separately.

UCM-based analysis in the finger force space.

Analysis of intertrial variance in the finger force space was performed within the framework of the UCM hypothesis (Scholz and Schöner 1999). To match our methods for permutation analysis, we analyzed F_TOT and M_TOT data using the UCM method during the 0.5 s immediately preceding the onset of perturbations used for computation of X_R and k (initial: 4.5–5 s; final: 18.5–19 s with respect to trial onset). Using this method, we partitioned intertrial variance produced by sets of fingers in two subspaces: the UCM and the subspace orthogonal to it (ORT). As such, variance within the UCM (V_UCM) does not affect the performance (e.g., F_TOT and/or M_TOT) production, whereas variance orthogonal to it (V_ORT) does affect this performance. The UCM was estimated as the null space of the Jacobian matrix for F_TOT (J = [1, 1, 1, 1]) or M_TOT (J = [4.5, 1.5, −1.5, −4.5]). For subsets of fingers, the Jacobian included only those entries corresponding to the digits in question. For more detail regarding the computation of V_UCM and V_ORT, see Scholz et al. (2002) and Latash et al. (2001). We quantified the relative amounts of V_ORT and V_UCM by computing the index of synergy, ΔV = (V_UCM/V_ORT)/V_TOT, where V_UCM, V_ORT, and V_TOT are normalized by their respective dimensionalities depending on the subset of fingers analyzed. Before further statistical analysis, ΔV was z-transformed to produce an index, ΔV_Z.

UCM-based analysis in the finger-level {X_Rƒ; k_ƒ} space.

We also used the UCM framework to investigate whether control variables at the levels of the individual fingers, {X_Rf; k_f}, covaried to stabilize the hand-level control variables {X_RH; k_H}. This question can be split into two components: 1) whether the individual fingers’ k_i covaried to stabilize hand-level k_H, and 2) whether the individual fingers’ X_Rƒ covaried to stabilize hand-level X_RH. Because in a system of parallel springs, the apparent stiffness magnitudes sum up to produce the apparent stiffness of the system, J_k = [1, 1, 1, 1] for the mapping from k_i to k_H. In contrast, there is no a priori mapping from finger-level X_Rƒ to hand X_RH. As such, we used multiple linear regression to define entries in the J_XR matrix:

$$X_{\text{RH}}=a_{\text{I}}\times X_{\text{RI}}+a_{\text{M}}\times X_{\text{RM}}+a_{\text{R}}\times X_{\text{RR}}+a_{\text{L}}\times X_{\text{RL}},$$ (4)

using values of X_RH and X_Rƒ obtained individually for each subject separately for each feedback condition (no feedback, force feedback, and moment feedback) and analysis epoch (initial and final), where subscript I is index finger, M is middle finger, R is ring finger, and L is little finger. The regression equations we obtained accounted for 62% to 99% of variance in X_RH (mean: 90%) across subjects, conditions, and epochs of analysis. The regression coefficients a_f were then combined into the Jacobian, J_XR = [a_I, a_M, a_R, a_L]. Note that our use of such computational methods to reveal approximate mappings among variables at different levels of analysis does not imply the central nervous system (CNS) uses any computations for the purposes of control.

Statistics

To test the effect of visual feedback on the organization of synergies in eight-dimensional space of finger-level {X_Rf; k_f}, we used one-way repeated-measures ANOVAs with the factor Feedback (3 levels: no feedback, force feedback, moment feedback) on the outcome variable ΔR_SD, the change in R_SD under altered feedback with respect to its magnitude under full visual feedback. This ANOVA was run on ΔR_SD computed for M_TOT- and F_TOT-stabilizing synergies in {X_Rf; k_f} space separately.

To test whether different fingers were used to stabilize F_TOT and M_TOT, we compared IL and MR fingers’ R_SD with respect to F_TOT and M_TOT separately, using data pooled across feedback conditions during the full feedback phase (when all trials were identical), using a one-way repeated-measures ANOVA with factor the Fingers Permuted (2 levels: IL, MR).

To test hypothesis 4, regarding so-called ascending synergies, we used the two-way repeated-measures ANOVA with factors Feedback × Phase (2 levels: full feedback, altered feedback) for ΔV_Z with respect to X_RH-stabilizing X_Rf and k_H-stabilizing k_f separately. In addition to the aforementioned tests related to our specific hypotheses, we used a three-way ANOVA with factors Feedback and Phase (as previously described) as well as Finger (4 levels: I, M, R, L) on different outcome variables (force, X_R, and k) to explore differences between individual fingers in their reactions to modified feedback.

To test for the presence of synergies in the {X_Rf; k_f} space, we compared R_SD values with the critical value of 2 using one-sided, single-sample t-tests. To test for the presence of ascending synergies, we compared ΔV_Z values with the critical value of 0.55 using one-sided, single-sample t-tests.

All statistics were run in SAS 9.4 (SAS Institute, Cary, NC). ANOVAs accommodated the repeated-measures nature of the experimental design using mixed models (PROC MIXED), in which subject is treated as a random factor (rather than a classical split-plot repeated-measures design). For this analysis, we assumed a variance components variance-covariance structure. In the case of significant interactions or significant main effects with more than two levels, we used post hoc tests with Bonferroni correction to evaluate which levels were different from one another. F-test degrees of freedom were computed using the Kenward-Roger method (Kenward and Roger 1997), as implemented by SAS 9.4. Unless otherwise stated, numerical data are presented as means ± SE.

RESULTS

General Performance

All 10 subjects were able to satisfactorily complete the full experimental procedure and were included in analysis in our previous paper (Reschechtko and Latash 2017). However, data from only 9 of these 10 analyzed subjects are included in the present paper, because not enough values of {X_Rf; k_f} were recoverable for one of the subjects. With the inclusion of all trials by all subjects, median R² for the linear regression under visual feedback was 0.94 for the whole hand, 0.94 for the index finger, 0.86 for the middle finger, 0.91 for the ring finger, and 0.98 for the little finger. Across all accepted subjects (n = 9; all trials and conditions), the hand-level F_TOT response was within the linearity constraint of R ≥ 0.71 in all conditions during both the first and second perturbations for ~97% of the trials; the changes in force exhibited by the index, middle, and ring fingers were acceptable in ~92–94% of the trials, whereas the little finger showed no appreciable difference from the hand.

Performance Drifts

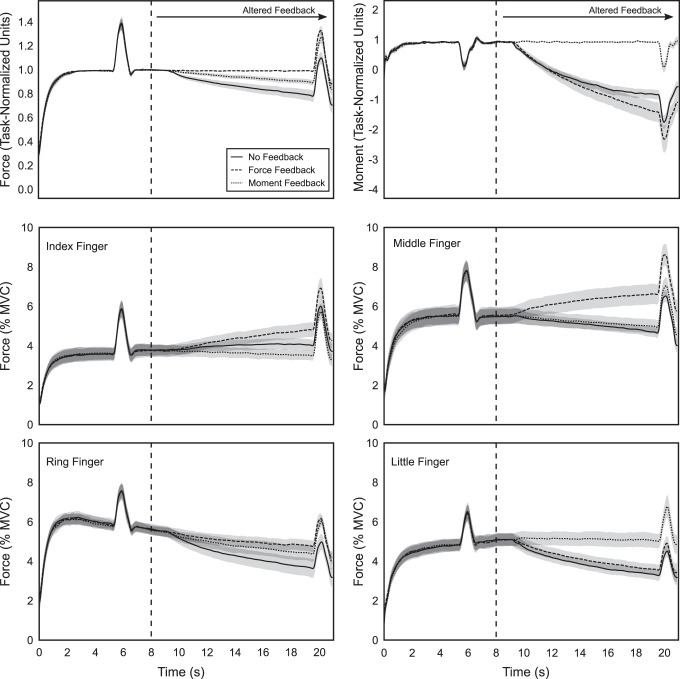
Although no subjects reported fatigue during the experiment, subjects’ performance did drift for the performance variables, F_TOT and/or M_TOT, when they did not receive visual feedback on that variable. When F_TOT feedback was removed (no-feedback and moment-feedback conditions), the subjects showed a drop in F_TOT; when M_TOT was removed (no-feedback and force-feedback conditions), they drifted from the original supination value of M_TOT to a pronation value. Across-subjects average time series plots of this behavior for F_TOT and M_TOT, as well as force produced by each finger, are provided in Fig. 2. Analysis of the force changes in individual fingers indicated that the changes in F_TOT and M_TOT occurred because the ring finger decreased force production in all conditions and the little finger decreased force production in the no-feedback and force-feedback conditions, whereas the index and middle fingers’ force decreased to a smaller extent or even increased. This behavior was especially pronounced in the force-feedback condition: the index and middle fingers increased force, whereas the ring and little fingers decreased force to maintain F_TOT.

Fig. 2.

Top two panels are time series plots of across-subjects average force production and moment of force production. Bottom four panels are time series plots of across-subjects average force production by each finger in feedback condition separately (no feedback, solid line; force feedback, dashed line; moment feedback, dotted line), with shading indicating SE. Vertical dashed line indicates the time of feedback alteration. MVC, maximum voluntary contraction.

Figure 3 illustrates the difference in force (ΔF) from the initial to final phase for each finger in each condition. The two-way ANOVA Feedback × Finger on the magnitude of force drift ΔF showed significant main effects of Feedback (F_2,88 = 10.76; P < 0.001) and Finger (F_3,88 = 21.97; P < 0.0001), as well as a significant interaction (F_6,88 = 5.58; P < 0.001). Post hoc tests on Feedback indicated that ΔF values for the force-feedback condition (−0.09 ± 0.21% MVC) and moment-feedback condition (−0.52 ± 0.17% MVC) were not significantly different from each other across fingers, but both were significantly larger than that observed in the no-feedback condition (−1.05 ± 0.22% MVC). Post hoc tests on Finger indicated that ΔF of the index finger was positive (0.37 ± 0.12% MVC), significantly larger than ΔF of the little finger (–0.85 ± 0.22% MVC) and the ring finger (–1.47 ± 0.24% MVC) across feedback conditions. Additionally, ΔF of the middle finger (–0.26 ± 0.22% MVC) was significantly larger than that of the ring finger. The interaction indicated that ΔF of the middle finger and little finger changed depending on the feedback condition: for the middle finger, ΔF in the force-feedback condition was significantly larger than in the no-feedback or moment-feedback condition; for the little finger, ΔF was significantly smaller in the moment-feedback condition than in the no-feedback condition. ΔF was equivalent across conditions for the index and ring fingers.

Fig. 3.

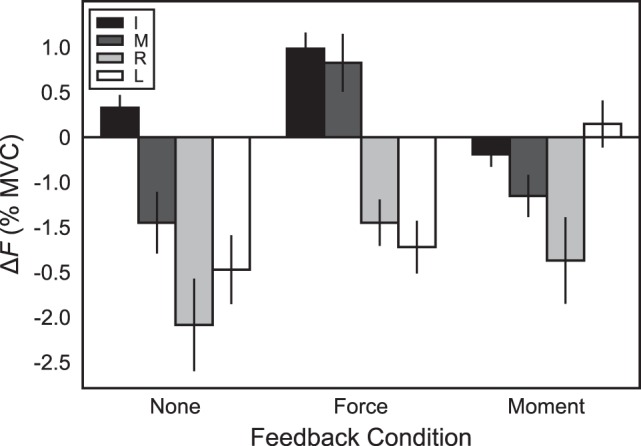
Average across-subjects changes in force production (ΔF) observed during each feedback condition in individual fingers (I, index; M, middle; R, ring; L, little) from the initial time point (under full visual feedback) to the end of the trial (after the feedback was differentially altered depending on the experimental condition). Error bars indicate SE. MVC, maximum voluntary contraction.

{X_R; k} Synergies Stabilizing F_TOT and M_TOT

Our previous analysis of F_TOT- and M_TOT-stabilizing synergies organized at the {X_RH; k_H} level (Reschechtko and Latash 2017) indicated that when visual feedback on F_TOT and M_TOT was provided, {X_RH; k_H} covaried across trials such that both F_TOT and M_TOT were stabilized. A typical data set for the hand-level {X_RH; k_H} data is illustrated in Fig. 4, top Note the very high R² value for the hyperbolic regression under full visual feedback and a drift of the data toward lower k values without visual feedback (no-feedback condition) accompanied by a drop in R².

Fig. 4.

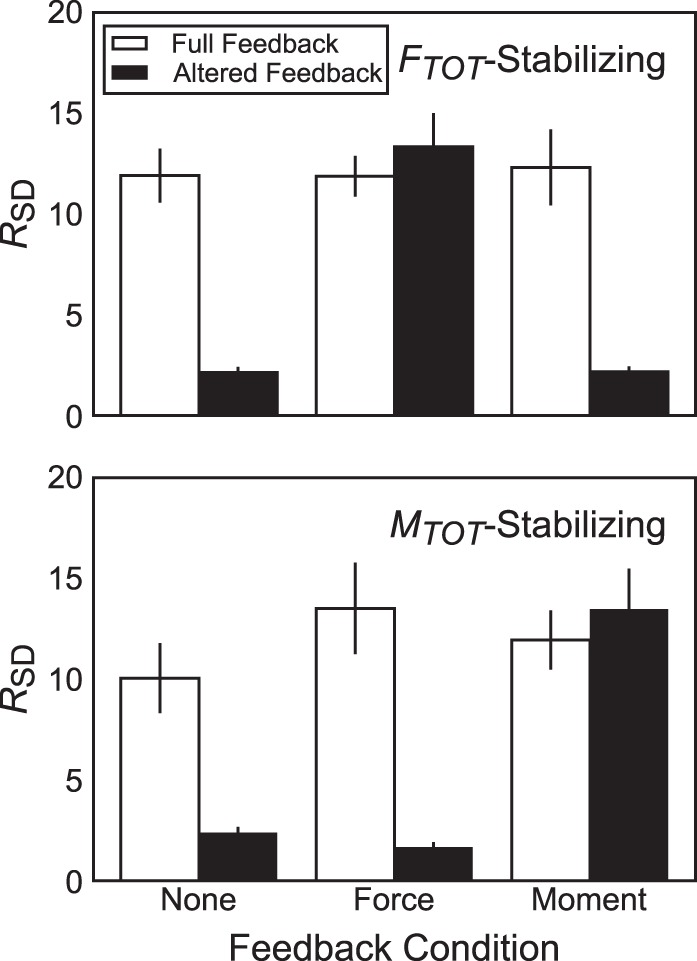
Average across-subjects magnitudes of R_SD, the ratio of the mean standard deviation of permuted data to that of nonpermuted data with respect to total force (F_TOT; top) or moment of force (M_TOT; bottom) under full feedback (open bars) or altered feedback (solid bars). Error bars indicate SE.

Similarly, we found synergies stabilizing F_TOT and M_TOT in the eight-dimensional space of individual finger {X_Rf; k_f} values (we cannot illustrate the data distribution in the 8-dimensional space in a figure). These synergies are reflected in the large magnitudes of R_SD, the ratio of SD of F_TOT or M_TOT derived from the permuted data set, SD_SUR, vs. the SD of the values observed during the experiment, SD_ACT. Because trials in each feedback condition were identical before visual feedback was manipulated, data for the analysis of synergies in the eight-dimensional {X_Rƒ; k_ƒ} space were pooled across feedback conditions to evaluate the presence of F_TOT- and M_TOT-stabilizing synergies predicted by hypothesis 1A. Under full visual feedback, R_SD with regard to F_TOT was 12.03 ± 0.78, whereas R_SD with regard to M_TOT was 11.83 ± 1.03 (i.e., SD_SUR was ~12 times larger than SD_ACT for each task-related variable).

To assess the effect of visual feedback on the organization of F_TOT- and M_TOT-stabilizing synergies in the eight-dimensional {X_Rf; k_f} space, we used the one-way ANOVA with factor Feedback on the change in R_SD (ΔR_SD) over the trial duration for M_TOT and F_TOT separately. For ΔR_SD computed for F_TOT, the effect of Feedback was significant (F_2,16 = 34.50; P < 0.0001), indicating that different feedback alterations affected R_SD differently. Note that this result is expected because in the force-feedback condition, subjects continued to receive feedback regarding F_TOT. Post hoc comparisons indicated that R_SD for F_TOT dropped in the no-feedback (ΔR_SD = –9.77 ± 1.10) and moment-feedback conditions (ΔR_SD = –10.14 ± 1.73), whereas it increased modestly in the force-feedback condition (ΔR_SD = 1.46 ± 1.47).

Similarly, the one-way ANOVA on ΔR_SD for M_TOT showed a significant Feedback main effect (F_2,16 = 24.09; P < 0.0001). Post hoc tests indicated that ΔR_SD for M_TOT in the no-feedback (ΔR_SD = –7.67 ± 1.49) and force-feedback conditions (ΔR_SD = –11.84 ± 2.03) corresponded to a large drop in R_SD, whereas its drop in the moment-feedback condition was much smaller (ΔR_SD = –1.54 ± 1.83). Again, values for ΔR_SD for M_TOT in the no-feedback and force-feedback conditions were not different from one another. Figure 4 illustrates magnitudes of R_SD for F_TOT (top) and M_TOT (bottom) before and after feedback was altered.

{X_R; k} Synergies Stabilizing Force of Individual Fingers

Hypothesis 1B predicted that synergies in the two-dimensional space of {X_Rf; k_f} would stabilize individual finger forces F_f. That is, X_R and k for individual fingers would covary across trials to stabilize an individual finger’s force production. In contrast to the aforementioned synergies stabilizing F_TOT and M_TOT, however, note that no explicit feedback on F_f for any finger was provided: subjects received feedback only on F_TOT and M_TOT.

Figure 5, bottom, illustrates {X_R; k} values for the individual fingers of one subject under the no-feedback condition. Note that under full visual feedback, R² values for individual fingers were lower than for the hand, although still corresponding to statistically significant effects. Across fingers, {X_R; k} values displayed better hyperbolic fits (larger R²) under full visual feedback than after feedback manipulation. There was also a shift in the average values of X_R and k across trials from the values observed under feedback to those observed at the end of the trial. Typically, this shift involved a consistent drop in k and variable adjustments in X_R. Figure 6 shows across-subjects average changes in X_Rf and k_f for individual fingers elicited by the alteration of visual feedback. In the force-feedback condition, the drop in k_f was accompanied by a consistent drop in X_Rf to keep F_TOT on the target. In the other two conditions, X_R adjustments were highly variable across subjects.

Fig. 5.

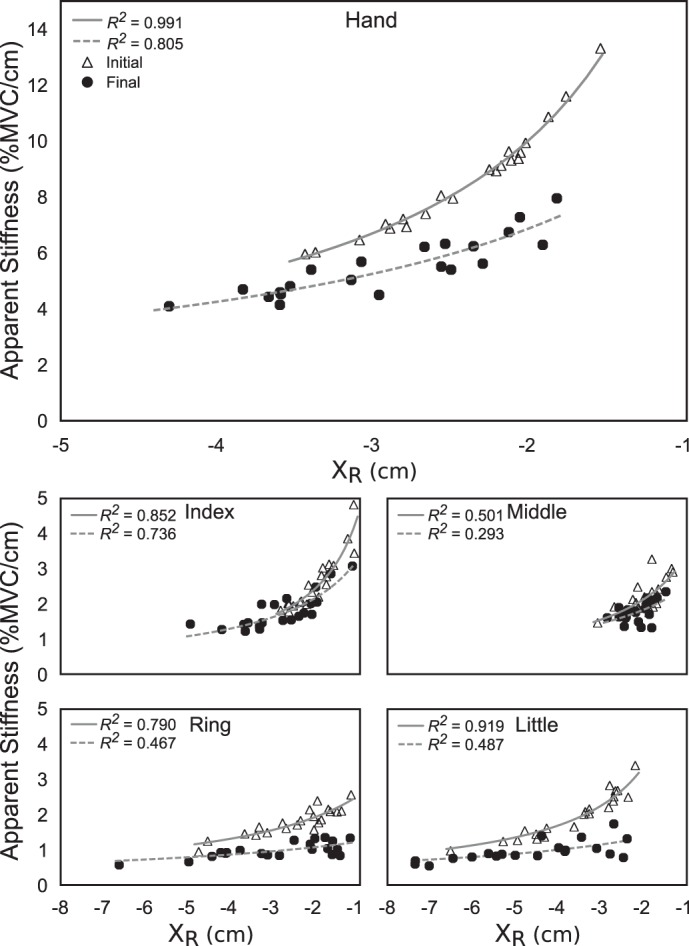
Values of {X_R; k}, the related pair of variables for the spatial referent coordinate and apparent stiffness, for a representative subject at the hand level (top) and individual finger level (bottom) in the no-feedback condition. Triangles represent {X_R; k} pairs recorded under full visual feedback; circles represent pairs recorded after feedback alteration. Best hyperbolic fits are represented with solid (visual feedback) or dashed (altered feedback) lines.

Fig. 6.

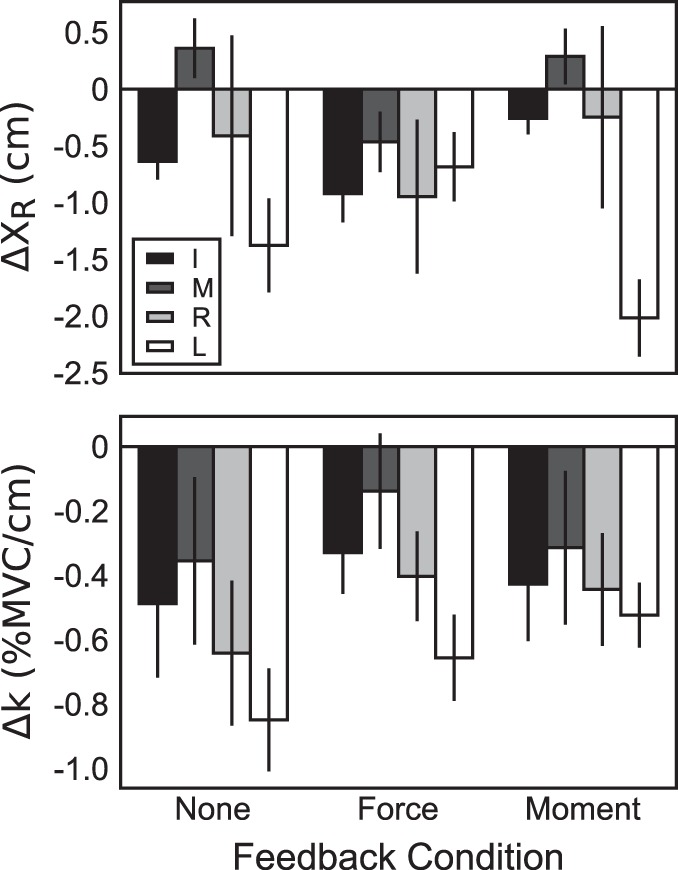
Across-subjects averages of change in finger-level referent coordinate (ΔX_Rf; top) and apparent stiffness (Δk_f; bottom), where f = I (index), M (middle), R (ring), and L (little). Error bars represent SE.

Because trials in each feedback condition were identical before visual feedback was altered, we tested whether synergies in the {X_Rf; k_f} space stabilized individual finger forces by analyzing data pooled across all feedback conditions. We found that X_Rf and k_f for the index and middle fingers stabilized the production of F_f, as indicated by values of R_SD > 2, as assessed by individual, single-sided t-tests for each finger. R_SD was 3.82 ± 0.41 for the index finger (t₂₆ = 4.48; P < 0.0001), 3.04 ± 0.26 for the middle finger (t₂₆ = 4.05; P = 0.0004), 2.27 ± 0.15 for the ring finger (t₂₆ = 1.75; P = 0.09), and 2.09 ± 0.19 for the little finger (t₂₆ = 0.44; P = 0.66). These values, however, were much smaller than those at the hand level: R_SD with respect to F_TOT was 12.03 ± 0.78. A one-way ANOVA with factor Finger on R_SD showed a significant effect of Finger (F_3,96 = 9.30; P < 0.0001). Pairwise contrasts with Bonferroni correction indicated that R_SD of the index finger was significantly larger than that of the ring and little fingers; no other pairs of R_SD values were significantly different from one another.

Figure 7 shows R_SD both before and after visual feedback was altered. We investigated whether removing visual feedback on F_TOT or M_TOT affected R_SD for F_f organized by covariation of {X_Rf; k_f} for individual fingers. For this analysis, we used the three-way ANOVA Finger × Feedback × Phase on R_SD. This ANOVA showed main effects for Finger (F_3,184 = 17.83; P < 0.0001) and Phase (F_1,184 = 20.65; P < 0.0001) without other significant main effects or interactions. The main effect of Feedback shows that, across all fingers and feedback conditions, when feedback was altered (by removing information on F_TOT, M_TOT, or both), R_SD decreased significantly from 2.80 ± 0.14 to 2.09 ± 0.10. Post hoc mean comparisons on the levels of Finger indicated that, across feedback conditions and alterations, R_SD for the index finger (3.16 ± 0.24) and middle finger (2.85 ± 0.19) was greater than for the little and ring fingers (1.84 ± 0.11 and 1.93 ± 0.10, respectively). However, the index and middle fingers were not significantly different from one another, and the ring and little fingers were not significantly different from each other either.

Fig. 7.

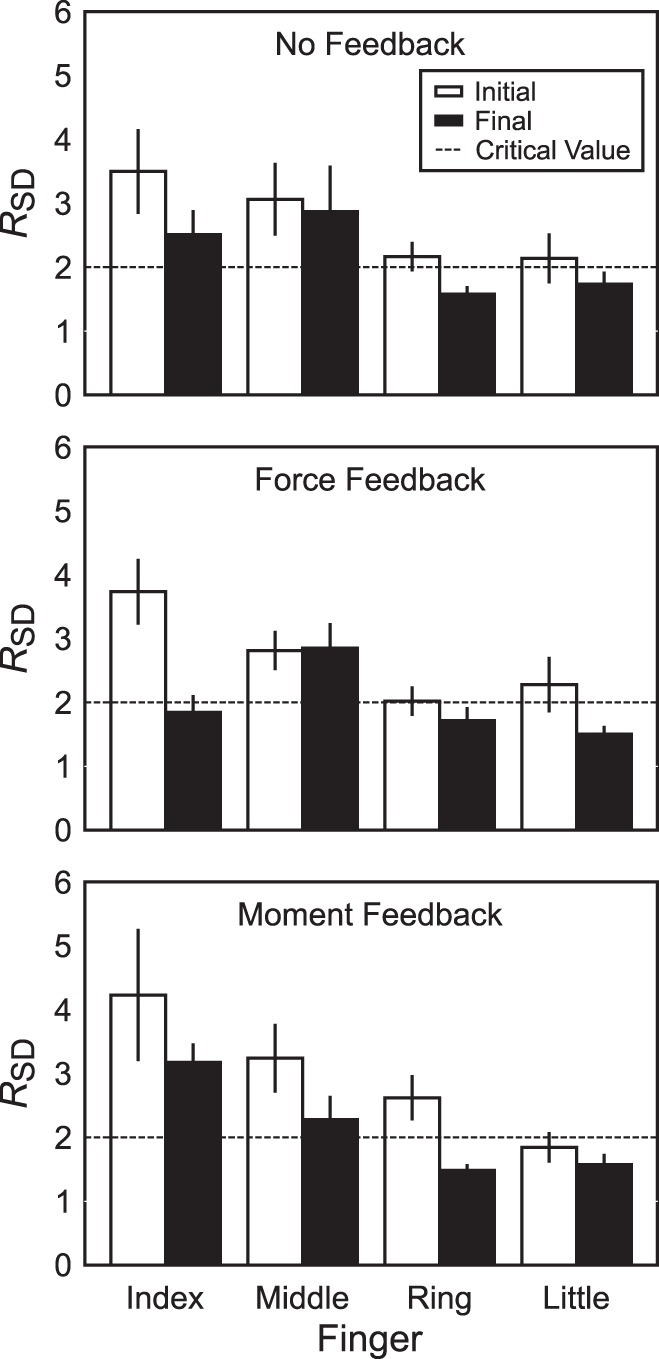
Across-subjects values of R_SD, the ratio of the mean standard deviation of permuted data to that of nonpermuted data, for analysis of individual finger force-stabilizing {X_Rf; k_f}, the pair of variables for the referent coordinate and apparent stiffness, during no-feedback (top), force-feedback (middle), and moment-feedback conditions (bottom). Error bars are SE.

Role of Lateral and Medial Fingers in Stabilization of F_TOT and M_TOT

As indicated by the aforementioned exploratory analysis of R_SD for individual fingers, not all fingers displayed equivalent covariation of X_Rf and k_f. A related question is whether different fingers affected F_TOT and/or M_TOT differently, the subject of hypothesis 2, predicting that F_TOT is primarily stabilized by the medial fingers (middle and ring), whereas M_TOT is primarily stabilized by the lateral fingers (index and little). To test this hypothesis, we again pooled data across feedback conditions and compared R_SD for F_TOT and M_TOT obtained by permuting the {X_R; k} data for the medial and lateral fingers separately under full visual feedback. We then used two separate one-way repeated-measures ANOVA (factor Fingers Permuted) to evaluate whether the lateral and medial fingers stabilized F_TOT and/or M_TOT differentially.

The ANOVA on M_TOT showed that the lateral fingers (R_SD = 11.1 ± 1.0) stabilized M_TOT significantly more strongly than the medial fingers (R_SD = 4.69 ± 0.37; F_1,44 = 49.08; P < 0.0001). In contrast, the ANOVA on F_TOT showed equivocal results that did not reach the significance criterion (F_1,44 = 3.68; P = 0.062), although R_SD was, on average, higher for medial fingers (9.79 ± 0.55) than for lateral fingers (8.51 ± 0.55).

Ascending Synergies

The final goal of this analysis was to investigate so-called ascending synergies. This analysis was split into two parts: analysis of covariation of k_ƒ with respect to k_H, and analysis of covariation of X_Rƒ with respect to X_RH. The latter analysis involved a step of identifying the Jacobian matrix using linear regression. R² values obtained for each multiple linear regression ranged from 0.996 to 0.752 across all 54 computed mappings (9 subjects × 3 feedback conditions × 2 phases); seven values were <0.9, but we observed no obvious relation between R² values and experimental conditions.

After determining X_Rf-to-X_RH mappings, we used the UCM-based methods to evaluate the presence of k_H-stabilizing and X_RH-stabilizing synergies separately. To assess whether feedback manipulations affected these ascending synergies, we used a two-way repeated-measures ANOVA, Feedback × Phase, on ΔV_Z computed for k_H- and X_RH-stabilizing synergies separately (Figs. 8 and 9). These analyses showed a significant main effect of Phase (X_R stabilizing: F_1,40 = 9.17; P = 0.004; k stabilizing: F_1,40 = 4.26; P = 0.046) without other significant effects or interactions. This effect indicates that indices of X_RH-stabilizing synergies increased significantly from ΔV_Z = 0.82 ± 0.09 to ΔV_Z = 1.12 ± 0.09 (Fig. 8, top), and k_H-stabilizing synergies also increased significantly from ΔV_Z = 0.14 ± 0.05 to ΔV_Z = 0.26 ± 0.06 (Fig. 9, top). Given the critical value of ΔV_Z ≈ 0.55, single-sided t-tests indicated that k_H-stabilizing synergies were absent, whereas X_RH-stabilizing synergies were present both with (t₂₆ = 3.02; P = 0.003) and without (t₂₆ = 6.37; P < 0.0001) relevant visual feedback.

Fig. 8.

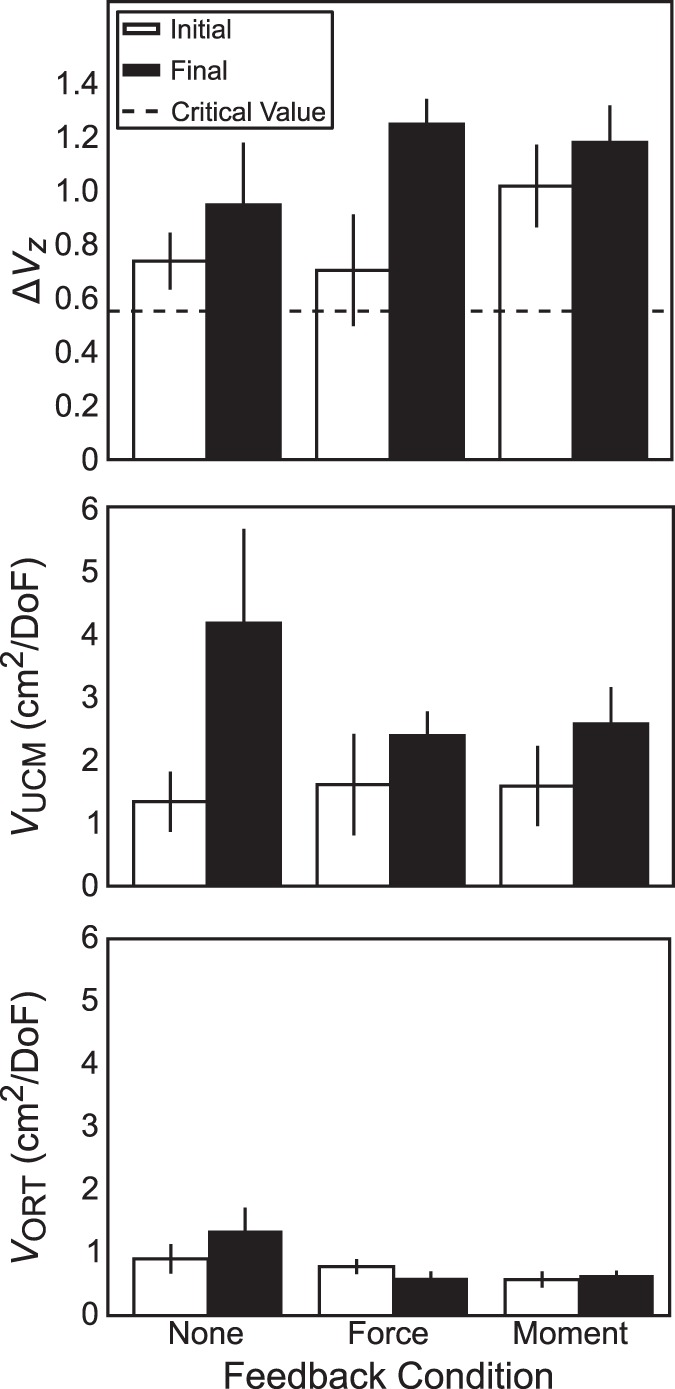
Across-subjects average index of synergy (ΔV_Z; top), variance within the uncontrolled manifold (V_UCM; middle), and variance orthogonal to the uncontrolled manifold (V_ORT; bottom) for hand-level referent coordinate (X_RH)-stabilizing ascending synergy due to covariation of the finger-level reference coordinate (X_Rf). Open bars are data recorded under full visual feedback; solid bars are data recorded after altered visual feedback. Dashed horizontal line indicates the ΔV_Z critical value. Error bars are SE.

Fig. 9.

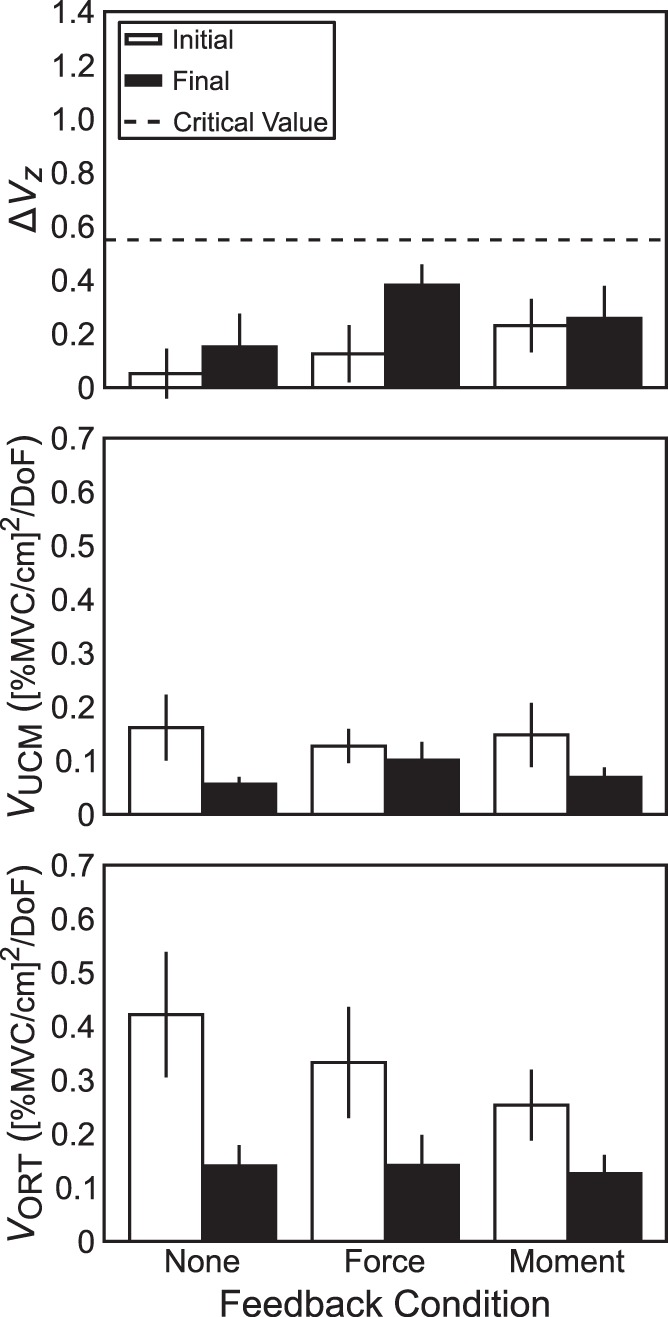
Across-subjects average index of synergy (ΔV_Z; top), variance within the uncontrolled manifold (V_UCM; middle), and variance orthogonal to the uncontrolled manifold (V_ORT; bottom) for hand-level apparent stiffness (k_H)-stabilizing ascending synergy due to covariation of finger-level apparent stiffness (k_f). Open bars are data recorded under full visual feedback; solid bars are data recorded after altered visual feedback. Dashed horizontal line indicates ΔV_Z critical value. Error bars are SE.

Changes in ΔV_Z can come about because V_ORT changes without V_UCM changing, V_UCM changes while V_ORT does not change, or both change simultaneously. We explored which of these might have occurred by using the two-way ANOVA on V_ORT or V_UCM separately, for indices of variance with respect to both k_H and X_RH. Values of V_ORT and V_UCM were log-transformed for normality before analysis. For X_R-related analysis, V_ORT was not significantly affected by removal of feedback (F_1,40 = 2.66; P = 0.11; Fig. 8, bottom, whereas V_UCM significantly increased from 1.51 ± 0.34 to 3.04 ± 0.52 cm² (F_1,40 = 21.12; P < 0.0001; Fig. 8, middle). For k_H-related analysis, V_ORT significantly decreased from 0.34 ± 0.05 (%MVC/cm)² under visual feedback to 0.14 ± 0.02 (%MVC/cm)² under altered feedback (F_1,40 = 36.03; P < 0.0001; Fig. 9, bottom), whereas V_UCM significantly decreased from 0.15 ± 0.03 to 0.08 ± 0.01 (%MVC/cm)² (F_1,40 = 31.54; P < 0.0001; Fig. 9, middle). As such, we conclude that the observed increase in ΔV_Z for X_RH resulted from an increase in V_UCM, whereas the decrease in ΔV_Z for k_H resulted from simultaneous but disproportional drops in both V_ORT and V_UCM.

DISCUSSION

Our experiment was designed to address a set of hypotheses related to a relatively new theoretical development (Latash 2010, 2017) that combines the main ideas of the uncontrolled manifold (UCM) hypothesis (Scholz and Schöner 1999) and the theory of control with spatial referent coordinates (RCs; Feldman 2015). We tested the hypotheses by quantifying stability of hand action within spaces of control variables, R and C, related to the computed pair of variables {X_R; k} of either the hand or individual fingers (cf. Ambike et al. 2016a; Reschechtko and Latash 2017). Our first hypothesis was related to synergies stabilizing the hand force and the individual finger forces in the space of finger-specific {X_Rƒ; k_ƒ} pairs. Our earlier study (Reschechtko and Latash 2017) documented strong synergies stabilizing total hand force (F_TOT) and moment (M_TOT) in the four-dimensional space of finger forces as well as synergies stabilizing F_TOT in the two-dimensional space of hand-level {X_RH; k_H}. The current study documented strong synergies stabilizing hand F_TOT and M_TOT in the eight-dimensional {X_Rƒ; k_ƒ} space in support of hypothesis 1A. Additionally, there were relatively weak synergies in the space of finger-specific {X_Rf; k_f} pairs stabilizing individual fingers’ forces, as predicted by hypothesis 1B.

We also explored finger-level specialization in the {X_Rf; k_f} space to stabilize F_TOT and M_TOT. We found that the lateral fingers (index and little) contributed much more strongly to the stabilization of M_TOT than the medial fingers (middle and ring). The data related to stabilization of F_TOT were less conclusive: the medial fingers showed higher contribution to stabilization of F_TOT, but their difference from the contribution of the lateral fingers was just below the significance level. Overall, we view these findings as supporting hypothesis 2 and being in agreement with earlier conclusions on the digit specialization with respect to force and moment production (Zatsiorsky et al. 2002, 2003).

Turning off visual feedback on one or both task-specific variables, F_TOT and M_TOT, led to a rather dramatic drop in the index of stabilization of the variable deprived of the feedback. These findings support hypothesis 3 and earlier reports on changes in the synergic control of variables without visual feedback (Parsa et al. 2016, 2017).

We view as potentially most exciting the results of our analysis of ascending synergies (see Fig. 1), i.e., analysis of stabilization of the hand-level control variables, {X_RH; k_H}, reflected in intertrial covariation of {X_Rƒ; k_ƒ} for the four fingers. Under full visual feedback, we observed strong synergies in the four-dimensional space of X_Rƒ stabilizing X_RH (in support of hypothesis 4A), whereas no synergies in the four-dimensional k_ƒ space stabilized k_H (against hypothesis 4A). When visual feedback was removed, the index of both X_RH-stabilizing and k_H-stabilizing synergies increased; the latter index, however, remained below the critical level, which indicates that k_H is not stabilized (these data speak against hypothesis 4B).

Furthermore, we interpret the results within the general control scheme described in the introduction (Fig. 1). We address a number of issues related to synergic control in hierarchical systems, stability of performance, the role of visual feedback, and possible further directions of exploring the advantages of synergic control at different levels of analysis.

Methodological Aspects of the Reconstruction of X_R and k

One potential concern regarding the methods used in this study is that X_R and k are reconstructed using a single computational procedure applied to a single data set: k is computed as the ratio of force change to coordinate change: ΔF/ΔX, whereas X_R is computed as the ratio of the initial force level to k: –F/k. Because, for the hand force, F should be close to the task force level, there is an intuition that X_R and k must automatically (and trivially) covary according to the equation F = –X_R · k, leading to a hyperbolic UCM.

An important consideration regarding the covariation of X_R and k, particularly in the present study, is the extent to which F is prescribed. Subjects are never able to perfectly produce the task level of hand force, F_TASK (or moment); as such, F varies across trials, and the values of X_R and k from different trials belong to different hyperbolic UCMs. This variability is relatively small (but never 0) in the presence of visual feedback on the force magnitude, and it becomes substantially larger without visual feedback. Earlier studies used hyperbolic regression to fit {X_R; k} data with a best-fit UCM (Ambike et al. 2016a, 2016b). The aforementioned intertrial variability in F is expected to lead to deviations of the data points from this UCM; however, variability of X_R and k along (rather than orthogonal to) the best-fit UCM is not constrained by the task. In particular, it could be lower than variability orthogonal to the UCM or even zero. In such a case, the points would deviate from the hyperbolic best-fit UCM primarily in the orthogonal direction with little or no deviations along the UCM. The randomization method would lead in such a situation to R_SD < 1, which never happened in our experiment. Therefore, our results show that the data varied along the UCM more than orthogonally to the UCM, which is a consequence of subjects’ behavior, not a trivial outcome of the computation.

In the present study, we also present analysis with respect to variables that received no visual feedback at all, such as the individual finger forces. For these variables, intertrial variability of force values was substantial, leading to relatively large deviations from the best-fit UCM. Despite the higher variability of F_f than F_TOT, however, we still observed values of R_SD indicating X_R and k for individual fingers covaried in a way that left individual finger forces relatively unchanged. Note also that we observed different behaviors of X_R and k across feedback conditions (consistent changes in k that were not matched by consistent changes in X_R; see Fig. 6), which may not be expected if our results were trivial outcomes of the computational procedure.

There is another important issue regarding the present methodology, related to the fact that some of the variables used in the analysis were measured relatively independently (such as force F and its change due to sensor motion, resulting in apparent stiffness k), whereas the second variable at the assumed control level (X_R) was computed from the first two. This procedure, by itself, could lead to covariation among pairs of variables, in particular between X_R and k, as a result of algebra of random variables. This problem is inherent to many studies that analyze covariation in spaces of elemental variables that are not measured independently but computed on the basis of other, directly measured, variables. For example, analysis of covariation in joint configuration spaces typically uses individual joint rotations as elemental variables (e.g., Scholz and Schöner 1999; Scholz et al. 2000). These rotations, however, are not measured but computed from the measured values of marker coordinates. Similar problems emerge with analysis within spaces of activation of muscle groups (M-modes; Krishnamoorthy et al. 2003).

Estimating potential effects of such computations on expected magnitudes of covariation is nontrivial because of a number of factors. First, the precise expectations arising from such operations are dependent on the actual distributions of the measured variables, which are difficult to evaluate in our studies given the relatively small number of trials collected. The situation is also complicated by the fact that the two variables, force and apparent stiffness, which can be viewed as measured more or less independently, are expressed in incommensurate units and are not normally distributed (in particular, they are both nonnegative). The latter issue may be seen as relatively minor because the actual values are far from zero, and so the distributions of F and k may be viewed as approaching normality. To deal with the former issue, we analyzed expected covariation patterns after expressing the two variables in normalized units such that the mean of each equals unity.

Figure 10 illustrates this issue in more detail via simulations in sets of 1,000 samples of F and k that were drawn from independent normal distributions and used to compute X_R values for three different distributions of k, assuming a normal distribution of F with the mean μ_F ≈ 1.0 and standard deviations σ_F ≈ 0.1 (chosen to approximate experimental data under visual feedback). The mean for k was always assumed μ_k ≈ 1.0, whereas its standard deviation varied among the illustrated simulations. In Fig. 10A, σ_F = σ_k; intuitively, this corresponds to the null hypothesis, assuming that variation of elemental variables was comparable to that of the performance variables. Note that the R_SD value computed from these data is ≈1.8, rather than 1.0, as it has been assumed in previous studies. In Fig. 10B, σ_F > σ_k; in this case, R_SD indeed approaches 1.0. Finally, in Fig. 10C, σ_F < σ_k, which we interpret as a synergy in the {X_R; k} space stabilizing the performance variable F. In this case, R_SD is ~22 (>>1.0) as expected.

Fig. 10.

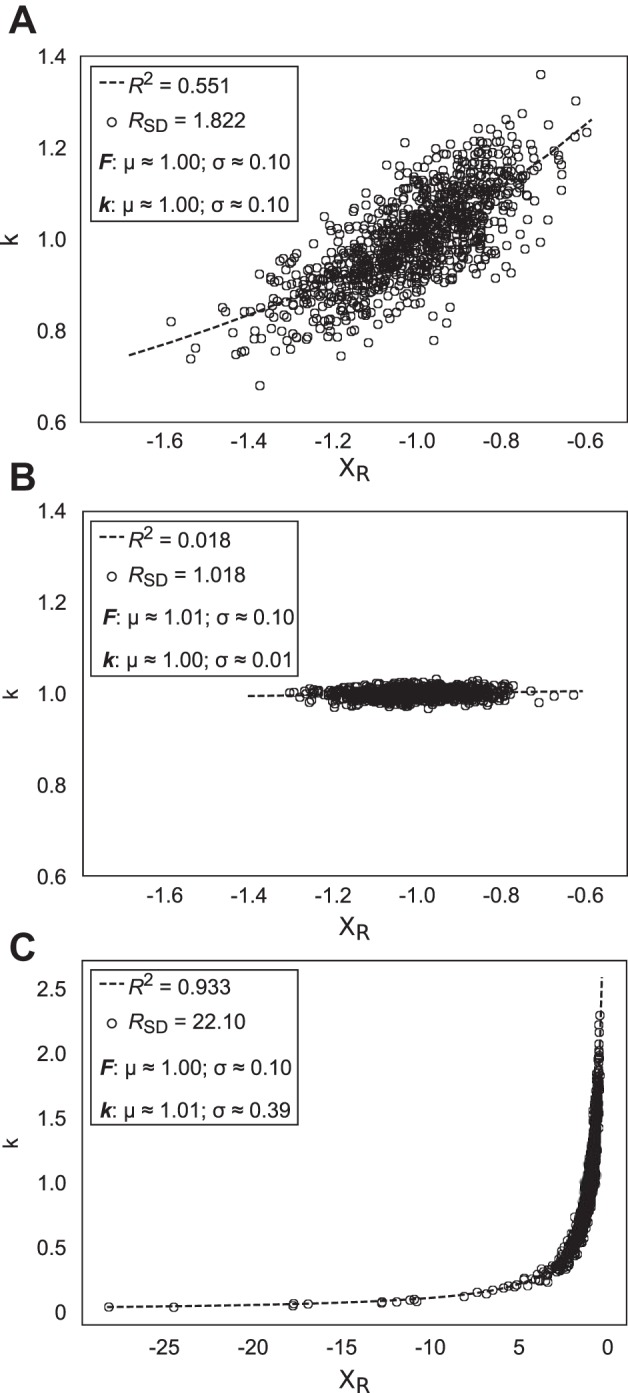
Results of 3 simulations that exemplify the effects of variability of apparent stiffness, k, on the computed metrics R_SD and R². R² refers to the best-fit hyperbola denoted by the dotted lines in A–C; R_SD is the ratio of mean standard deviation of permuted data to nonpermuted data (see methods). In each simulation, 1,000 force (F) and k values (denoted by open circles) were randomly selected from independent normal distributions. In A–C, the mean of the normal distributions from which F samples were selected = 1.0, and standard deviation = 0.1. The mean of the normal distribution for k = 1.0; in A, the standard deviation of the k distribution = 0.1; in B, the standard deviation of this distribution = 0.01; and in C, the standard deviation = 0.4. The values of mean (μ) and standard deviation (σ) in the panels refer to the sample means and standard deviations of the actual data used in the simulations.

The applicability of this particular simulation with its large number of samples and known distributions to the experimental data is still admittedly tenuous. One of the main results of these simulations is revision of the idea that our null hypothesis corresponds to R_SD = 1.0, and subsequent reinterpretation of certain previous results. In particular, in an earlier study, we observed R_SD values ~2.0 after force drifts in the absence of visual feedback (Reschechtko and Latash 2017). We interpreted those results as reflecting a weak synergy stabilizing F, whereas in fact, the synergy could be absent. In future work, we intend to develop a metric directly comparing the relatively independently recorded measures F and k, rather than invoking the computed measure X_R and associated methodological problems.

It must be admitted that, given the aforementioned issues (including incommensurate units and unknown data distributions), there is no way to prove that a given criterion value of R_SD is the applicable threshold in a given experiment. Such problems are, however, by no means unique to the present methodology or application: all studies comparing the variances of computed elemental variables (including joint angles in radians recovered from best-fit kinematic marker paths and muscle modes in mV recovered from processed and dimension-reduced electromyographic recordings) with variances of performance variables expressed in different units (e.g., end-point coordinate in m and center of pressure coordinate in m, respectively) suffer from the same shortcomings, and we attempt to be as transparent as possible about these shortcomings.

Is Redundancy a Problem?

Our approach to the problem of motor redundancy (Bernstein 1967) is based on the principle of abundance (Gelfand and Latash 1998; Latash 2012). According to this principle, the excess of elemental variables (those produced by elements at a selected level of analysis) is not a computational problem for the CNS (e.g., solved using optimization approaches; Prilutsky and Zatsiorsky 2002; Seif-Naraghi and Winters 1990), but a high-dimensional space where lower dimensional subspaces can be stabilized corresponding to the production of stable magnitudes of salient performance variables. This can be done, for example, by using feedback loops from peripheral receptors or central back-coupling loops, as suggested in earlier studies (Latash et al. 2005; Martin et al. 2009). Stabilization of such subspaces allows the controller to ensure natural stability of action based on laws of nature (Latash 2016), as well as offering the ability to perform secondary tasks without interference with the primary one (e.g., Zhang et al. 2008) and to adjust stability of a performance variable in a task-specific way (e.g., in preparation to a quick change in that variable; Olafsdottir et al. 2005).

Until recently, studies of action stability within the UCM hypothesis framework have been limited to analysis of higher dimensional space of performance variables produced by elements, e.g., finger forces, joint rotations, and muscle activations (reviewed in Latash 2008). Merging this framework with the idea of control with spatial referent coordinates (reviewed in Feldman 2015) offers an exciting opportunity to explore the synergic control of performance at the level of hypothetical control variables (Ambike et al. 2016a). This method has so far been applied to studies of single-effector actions, either an individual finger (Ambike et al. 2016a, 2016b) or the hand as a whole (Reschechtko and Latash 2017), controlled with two basic commands, R and C, that translate into changes in the effector X_R and k. Our present study is the first to apply this method to a multieffector task where each of the effectors is controlled with the corresponding {R; C} pair. Our results show that, within the eight-dimensional {X_Rf; k_f} space, two one-dimensional subspaces, corresponding to the desired magnitudes of the performance variables F_TOT and M_TOT, were strongly stabilized. Although subjects could have involved more proximal muscles during the task performance, the isometric conditions and intermediate posture of the fingers used in the present study did not allow passive transmission of forces not mediated by activation of finger muscles. That is why we only analyze the behaviors presented in this article at the finger and hand level.

We do not propose that a given {X_R; k} pair is precomputed at some level of the CNS, but rather that it emerges as a result of selecting values of the R- and C-commands to match the task requirements. The R- and C-commands may be viewed as tools available to humans to perform various tasks; specific patterns of these tools are used, based on experience and available sensory feedback. A given {X_Rf; k_f} pair at the finger level may lead to different combinations of joint-level r- and c-commands in different trials, realized via various combinations of stretch reflex thresholds (λ) of involved muscles. As such, individual joint and muscle actions are not unique even if they originate from the same combination of the R- and C-commands, another facet of the notion of “repetition without repetition” introduced by Bernstein (1967). Joint- and muscle-level control variables emerge and show patterns of covariation, which ensure that the individual effector actions are combined to be compatible with the performance dictated by the {R; C} pair. Neurophysiological mechanisms involved in these transformations are unknown, and in this article we try to develop concepts, such as central back-coupling and ascending synergies, which, at this time, seem promising to address issues of the neural control of performance stability.

We view the relatively large variability of the elemental variables within subspaces corresponding to stable magnitudes of salient performance variables as a consequence of selective stability in different directions of the original multidimensional space. The unavoidable variability of the intrinsic states of the body, and of its interaction with the environment, serves as a source of perturbations for the elemental variables that respond naturally by larger deviations in directions of low stability. The indices of stability such as, for example, indices of the structure of intertrial variance (Scholz et al. 2002), motor equivalence (Mattos et al. 2011), and the R_SD index used in the current study do not reflect computations by the controller (e.g., as in optimal feedback control schemes; Diedrichsen et al. 2010; Todorov and Jordan 2002) but natural processes within the system characterized by different stability in different directions.

Stability of Processes in a Hierarchical System

Stability of variables within a hierarchical system is a nontrivial issue. Stabilization of total force produced by the four fingers implies the existence of a three-dimensional subspace within the original four-dimensional finger force space where processes are less stable and show relatively large variance. The large variance in that subspace means that variance in the behavior of individual effectors is also large. Can the outputs of individual effectors be stabilized at a different level of the hierarchy, e.g., within their {X_Rf; k_f} spaces, given their large variance? An earlier series of studies (Gorniak et al. 2007, 2009) showed that in pressing and prehensile tasks, some mechanical variables were stabilized only at the task-specific level of analysis, whereas other variables were stabilized at both task-specific level and a lower level combining a subset of digits (so-called “virtual finger”; Arbib et al. 1985). These findings led to the conclusion that stabilization at more than one level of a hierarchy may indicate the controller’s prioritization of different performance variables.

In our study, we observed relatively high indices of synergies quantified at the {X_Rf; k_f} level with respect to task-specific performance variables F_TOT and M_TOT (R_SD > 10). These indices for the forces produced by individual fingers (F_f) were much lower (1.5 < R_SD < 4.0). However, all these indices were significantly higher than unity, which may correspond to synergies stabilizing resultant force and moment as well as individual fingers' forces—however, it is unclear whether this criterion is appropriate (see discussion for indication that 2 may be more appropriate). These results are notable as another sign of a trade-off between synergies at different levels of a control hierarchy. They also indicate that the controller cared not only about performing the explicit task accurately but also about stabilizing values of individual finger forces, possibly to keep them within a range perceived as natural or in some sense optimal.

Earlier studies of prehension tasks have suggested that fingers play different roles with respect to resultant mechanical variables applied to the grasped object. In particular, the middle and ring finger forces were highly sensitive to manipulations of the external load (while the external torque was kept constant), whereas the index and little finger forces showed high sensitivity to manipulations of the external torque rather than external load (Gao et al. 2006; Zatsiorsky et al. 2002). We explored this hypothesis at the level of pairs of control variables to individual fingers. This was done by removing possible stabilizing effects of finger subsets with the help of permutation of their {X_Rf; k_f} pairs. Permutation of {X_Rf; k_f} to the lateral fingers (index and little) led to strong effects on accuracy of M_TOT performance, much stronger than permutation of the {X_Rf; k_f} to the medial fingers (middle and ring). The effect on F_TOT was opposite: stronger effect was observed as a result of permutation of the {X_Rf; k_f} to the medial fingers, but the difference between the finger pairs was under the level of statistical significance. Overall, our observations corroborate the original hypothesis by Zatsiorsky and colleagues on specialization of finger pairs in prehensile tasks.

Natural Processes Leading to Performance Drifts

Unintentional drifts in human performance have been reported in multiple contexts, including slow force drifts during force-production tasks (typically to lower magnitudes; Slifkin et al. 2000; Vaillancourt and Russell 2002), faster force drifts in trials with external perturbations (Wilhelm et al. 2013; Zhou et al. 2014), and drifts in other performance variables that may occur over a long series of trials (Heijnen et al. 2012, 2014). In our study, we explored drifts in force and moment after removal of salient visual feedback. These phenomena have commonly been explained in terms of shortcomings in working memory (Vaillancourt and Russell 2002), supported by clinical studies (Prodoehl et al. 2007) and brain imaging studies (Coombes et al. 2011; Poon et al. 2012). There is also evidence, however, that such drifts do not come about because subjects “forget” the required level of force production. For example, when a subject is asked to interrupt a force production trial, relax, and then return to the required force, no force drop is observed (Jo et al. 2016; Solnik et al. 2017). Additionally, when force production by one hand drifts, subjects tend to match the original force level if asked to match the force production with their contralateral hand (Reschechtko et al. 2018).

Within the context of neural control of movement with RCs, explanations of force drift have been proposed suggesting that this phenomenon results from a natural drift of X_R toward the actual effector coordinate. This natural process reflects the tendency of all physical systems to move toward minimum of potential energy but remains compatible with the aforementioned explanations because it takes place at a different level of explanation and has received support in a number of recent studies. In particular, earlier studies have documented drifts in both X_R and k during the unintentional force drift (Ambike et al. 2016b; Reschechtko and Latash 2017). Similarly, we observed such drifts in the {X_R; k} pairs at the level of the hand and individual fingers (see Fig. 5). However, it is notable in the present experiment (and in Reschechtko and Latash 2017) that we saw a consistent drift in k across conditions with and without visual feedback. When visual feedback on F_TOT was present, X_R adjustments allowed keeping the F_TOT at the required level; without visual feedback on F_TOT, this variable showed a drift. The consistent decreases in k may reflect both the high energetic requirements of the C-command (increased agonist-antagonist muscle coactivation), as well as the ecological rarity of tasks that require sustained coactivation: modulation of the C-command is more often observed transiently during fast movements, and it subsides during steady states (as exemplified in the classic triphasic electromyographic patterns observed during single-joint movements; reviewed in Gottlieb et al. 1989).

Role of Different Feedback Modalities in Modulation of Stability

In an isometric force production task, the feedback modalities that can stabilize variables including F_TOT and M_TOT are relatively limited. It is unsurprising, therefore, that visual feedback is particularly important for allowing the CNS to stabilize force or moment of force in isometric conditions. A less trivial finding in our previous study was that {X_RH; k_H} synergies at the hand level were strongly attenuated by the removal of visual feedback but that they did not completely disappear: R_SD was never observed to drop below the critical value of 1. This indicated that even during the force drift without visual feedback, intertrial variability in X_RH and k_H was still structured to stabilize F_TOT, which could result from aforementioned central back-coupling processes (Latash et al. 2005) or other feedback modalities, including somatosensation in the fingertips and proprioceptors in the involved muscles. The fact that the subjects were unaware of the force and moment drifts despite their large magnitudes, however, casts doubt on the latter hypothesis.

In our present study, we again observed the strong attenuation of synergies in the {X_Rƒ; k_ƒ} space stabilizing F_TOT and M_TOT during unintentional drifts in these variables. These results confirm previous findings (Ambike et al. 2016b; Parsa et al. 2016; Reschechtko and Latash 2017), but our present findings also extend to processes involving multiple effectors. In particular, we found relatively weak synergies in the {X_Rf; k_f} space stabilizing individual finger forces, which again were attenuated but not extinguished by feedback alteration. This finding is somewhat surprising given that feedback on individual finger forces was never provided, so any organization of {X_Rf; k_f} synergies took place without visual feedback, and it is not clear why feedback alteration should further affect these synergies. Nevertheless, existence of such synergies at the individual finger level suggests that processes governing the {X_RH; k_H}-to-{X_Rf; k_f} transformation are somewhat stable, possibly to stabilize certain solutions in the {X_Rf; k_f} space, which may serve various functions, including the stabilization of digit posture or maintenance of some baseline level of cocontraction.

The observed drifts in performance were associated with consistent drifts of k toward lower magnitudes, whereas X_R adjustments depended on available feedback. This observation suggests lower stability of processes associated with specifying k compared with those associated with specifying X_R, a finding that may be partially resultant from the study of isometric action rather than free motion, and one that we address further below.

Ascending Synergies

A primary goal of this paper is to introduce the notion of ascending synergies and make an (admittedly naive) effort to quantify them. We use the term “ascending” to highlight the idea that a high-dimensional space at certain intermediate levels of a hierarchy may be organized to stabilize its input rather than its output, an assumed aspect of control with RCs. This statement may appear to violate the causal relations within the system illustrated in Fig. 1, but this is only a seeming violation. The X_RH and k_H inputs into the lower level may be seen as structuring the eight-dimensional space of finger level {X_Rƒ; k_ƒ} pairs in a way compatible with stabilization of both X_RH and k_H, naturally leading to the stabilization of total hand force F_TOT, which is a direct function of X_RH and k_H.

We split the problem of {X_RH; k_H} stabilization into two problems because the problem of k_H stabilization in the four-dimensional {k_ƒ} subspace is linear and independent of variations in X_Rƒ. We emphasize, however, that our choice in splitting the problem is done for computational purposes and is in no way an endorsement of the idea that the CNS actually splits the problem or performs such computations. Although we do not know how such synergies are organized, some kind of central back-coupling could be used for this purpose (Latash et al. 2005).

To our surprise, we did not find k_H-stabilizing synergies even when full visual feedback was available. Moreover, the synergy index ΔV_Z was consistently much lower than the critical value, suggesting that individual finger k_ƒ values covaried positively across trials. This could be due to the organization of extrinsic finger flexors, which are multitendon muscles serving all four fingers. As a result, natural intertrial variations in muscle activation could lead to parallel changes in the apparent stiffness of the individual fingers, resulting in the very low ΔV_Z values.

Analysis of the X_RH-stabilizing synergies led to a very different outcome. Despite the fact that our linear model was merely based on multiple regression, strong synergies were observed in the {X_Rƒ} space stabilizing X_RH. This result supports a hypothesis suggested earlier by Feldman (2015) that the R-command (which is linked to X_R in our study) plays a primary role in the control of actions, whereas the C-command (which is linked to k) is subordinate to the R-command.

Without visual feedback, the index of the synergy stabilizing X_RH increased, in contrast to other synergies described in the study. This was primarily due to a less stereotypical set of solutions in the {X_Rƒ} space, as reflected by the significant increase in the V_UCM component of variance, without a major change in the other component, V_ORT. Although a similar trend was seen in the index of synergy stabilizing k_H, this resulted from disproportionate decreases in both V_UCM and V_ORT, indicating that k_f changes became more stereotypical. Furthermore, the increase in ΔV_Z was insufficient to constitute a synergy stabilizing k_H. These results show the particular sensitivity of mechanisms related to X_R production to feedback manipulations, whereas mechanisms related to k production remain relatively immune. Because the present study investigates only performance variables, and not configuration of the hand, limbs, and/or body (as may be expected in studies with free motion), the values of and changes in X_R and k may also differ from those that would be observed during tasks requiring such movement.

Concluding Comments

In the present study, we have made an attempt to quantify ascending synergies, which result from the mapping of a low-dimensional task control variables on a high-dimensional space of redundant control variables to individual effectors. We also admit to shortcomings in our current methodology. For example, the range of feedback alterations and tasks performed was quite limited, albeit due to the amount of time subjects could focus on the task without fatigue. The lack of physiological measurement (e.g., surface electromyography) also limits our ability to interpret our results in terms of muscle activations; this is undoubtedly an important level of analysis, and one that we hope to use in future studies. Furthermore, the method we used to link finger- and hand-level X_R values is admittedly crude, and we are open to the possibility that it may prove to be a suboptimal practice as the exploration of ascending synergies commences. Finally, the index used in this and previous studies to compare variability of the performance and control variables, R_SD, suffers from computational problems related to algebra of random variables. Although similar computational assumptions are commonplace in the literature, we plan to avoid such methodological problems in future work by comparing variables that are measured independently when such measurements are possible, and we believe that the methodologies employed in this study display no unique shortcomings.

GRANTS

This work was supported by National Institute of Neurological Disorder and Stroke Grant R21-NS95873 (to M. L. Latash).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

S.R. and M.L.L. conceived and designed research; S.R. performed experiments; S.R. and M.L.L. analyzed data; S.R. and M.L.L. interpreted results of experiments; S.R. and M.L.L. prepared figures; S.R. and M.L.L. drafted manuscript; S.R. and M.L.L. edited and revised manuscript; S.R. and M.L.L. approved final version of manuscript.