Modulating enzyme activity by altering protein dynamics with solvent

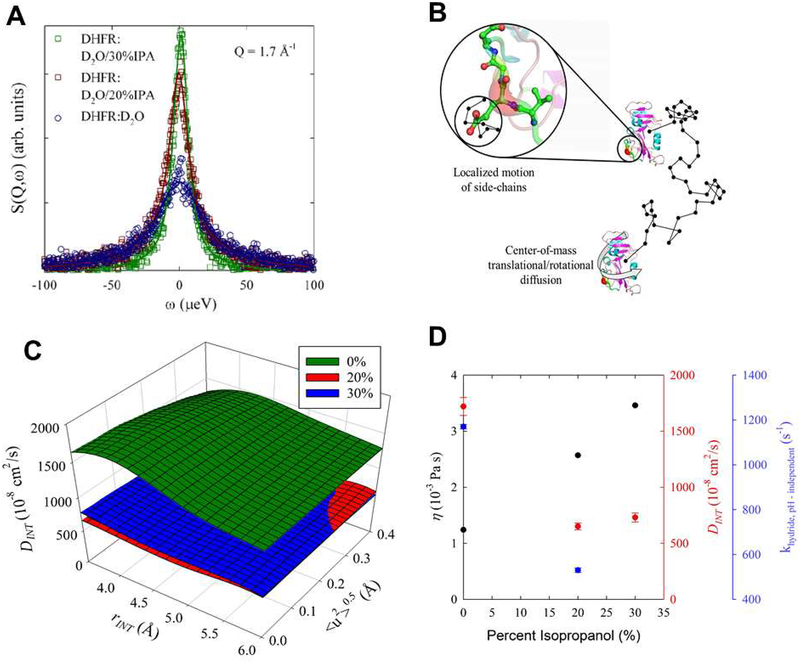
Abstract

Optimal enzyme activity depends on a number of factors, including structure and dynamics. The role of enzyme structure is well recognized, however, the linkage between protein dynamics and enzyme activity has given rise to a contentious debate. We have developed an approach that uses an aqueous mixture of organic solvent to control the functionally relevant enzyme dynamics (without changing the structure), which in turn modulates the enzyme activity. Using this approach, we predicted that the hydride transfer reaction catalyzed by the enzyme dihydrofolate reductase (DHFR) from Escherichia coli in aqueous mixtures of isopropanol (IPA) with water will decrease by ~3 fold at 20% (v/v) IPA concentration. Stop flow kinetic measurements find that the pH-independent k_hydride rate decreases by 2.2 fold. X-ray crystallographic enzyme structures shows no noticeable differences, while computational studies indicate that the transition-state and electrostatic effects were identical for water and mixed solvent conditions; and quasi-elastic neutron scattering studies show that the dynamical enzyme motions are suppressed. Our approach provides a unique avenue to modulating enzyme activity through changes in enzyme dynamics. Further it provides vital insights that show the altered motions of DHFR cause significant changes in the enzyme’s ability to access its functionally relevant conformational sub-states, explaining the decreased k_hydride rate. This approach has important implications for obtaining fundamental insights into the role of rate-limiting dynamics in catalysis and as well as for enzyme engineering.

TOC Graphic

INTRODUCTION

Control of enzyme function has fundamental implications for cells as regulation of enzymes is a vital part of normal biochemical processes. In industrial and laboratory applications, the abilityto regulate enzyme catalytic efficiency is also widely desired. Teasing apart the roles of various factors in enzyme mechanism has proven to be a challenging task.^1–16 The contributions of individual active-site residues and secondary structural elements in enzyme mechanisms have been well established by decades of investigations.^{17, 18} More recently, the role of internal protein motions (or dynamics) in aiding enzyme catalysis has been the topic of an intense and ongoing debate.^{1, 8, 19, 20} The difficulty in investigating the contribution of motions arises due to challenges associated with isolating the right sub-set of protein motions and to selectively control and examine their effect on enzyme function. What makes the task even more challenging is the fact that structure and dynamics are closely inter-connected; even small changes in enzyme structure often lead to changes in dynamics,²¹ making it difficult to tease apart their specific contributions.

Current understanding suggests that enzyme structure, in addition to serving as a scaffold for correctly positioning the critical residues around the active-site, also enables sampling of functionally relevant conformational sub-states.^{5, 6, 22–25} The rate of sampling these sub-states, enabled by conformational fluctuations, has been found to coincide with the rate of enzyme turnover.^{3, 7, 26} Enzyme structures catalyzing the same or similar reactions, even with low sequence similarity, frequently share the same overall shape (fold) and exhibit similar motions.6 A sub-set of these motions allows the enzyme to sample regions of the conformational landscape corresponding to populations where the active-site (and other) residues are in proper orientations to facilitate the chemistry to be catalyzed.⁵ Evidence indicates that these function promoting motions, in addition to structural features, may be a conserved feature of the enzyme folds, rather than coincidental.⁶

Understanding how enzyme structure and dynamics are then further influenced through interaction with local solvent environment, or the cellular milieu, is a more complex question. Enzymes inside the cell work in an environment which significantly differs from the typical laboratory conditions of dilute aqueous solutions. The cytosol is a crowded environment with each molecule surrounded and interacting with a wide variety of cellular components. This introduces further variables in the investigations and an increasing number of recent in-vivo and related studies are motivated to address this issue.^{27, 28} However, understanding of the relationship between solvent conditions and the enzyme structure-dynamics and function remains fairly limited.

Motivated to understand distal control of enzyme function, we developed a strategy of changing solvent conditions to investigate the possibility of changing enzyme motions to control enzyme activity. The solvent surrounding the enzyme impacts internal protein motions, such that solvent motions may enslave the protein dynamics.^29–32 Therefore, we hypothesized that changes in solvent conditions could be used as a mechanism for changing protein motions. Enzyme catalysis in aqueous mixtures of organic solvents has been investigated for some time.^33–36 Enzymes can show decreases in activity under these conditions, but have also been known to maintain or even show increased catalytic activity in a variety of cosolvents.^{33, 34} The impact on protein structure in cosolvents has been well investigated,³⁵ while the investigations of dynamics in cosolvents have only recently attracted attention. We used computer simulations to model changes in solvent conditions and characterize its impact on functionally important conformational substates. The enzyme system used for the studies is dihydrofolate reductase (DHFR) from E. coli, which has been widely investigated for the role of enzyme dynamics in catalysis. DHFR plays an important role in folate metabolism by catalyzing the conversion of dihydrofolate (DHF) to tetrahydrofolate (THF) by using nicotinamide adenine dinucleotide phosphate (NADPH) as the cofactor for hydride transfer.³⁷ In particular, we examined DHFR structure and function in isopropanol (20–25% v/v) as a cosolvent. Detailed characterization indicated changes in solvent conditions altered the enzyme motions impacting access to the functionally important sub-states. Under these conditions computer simulations predicted that the enzyme activity should be decreased by 2–3 fold compared to the enzyme working under aqueous conditions, due to changes in conformational sub-states in the transition state area of the rate limiting hydride transfer. Stop flow reaction kinetics in the presence of 20% isopropanol indicated a 2.2 fold decrease in hydride transfer rate, consistent with the prediction. X-ray structures under aqueous and cosolvent conditions were nearly identical, while quasi-elastic neutron scattering experiments confirmed that the protein dynamics is significantly decreased in the presence of isopropanol. Overall, these studies have allowed the isolation and characterization of rate-limiting protein dynamics successfully explaining the decrease in enzyme rate, and therefore providing new insights into the debate regarding the role of protein dynamics in enzyme function.

METHODS

Computer Simulations:

The E. coli DHFR was modeled as described previously.⁶ The cofactor NADPH present in the PDB file (PDB code: 1RX2) was included in the model, and the substrate (as protonated dihydrofolate) was modeled based on the folate molecule present in the PDB file. The protonation states for the various ionizable residues of the enzyme were based on neutral pH. Counterions were added to the protein and the enzyme-complex was solvated using the SPC/E water model. AMBER parm 98 force-field was used for simulations.

Isopropanol model:

For simulations with isopropanol, AMBER force-field parameters for isopropanol were taken from the study of Martin³⁸ on the vapor-liquid coexistence curves and liquid densities for several organic solvents. The ionization states and other conditions were similar to the water only system preparation.

Model preparation and equilibration protocol:

Water and isopropanol molecules at the appropriate volume ratio u were randomly placed in a 64 Å-side simulation box until the volume (V) was filled. Mild steric clashes were allowed in the placement process. The number of water and isopropanol molecules is determined assuming no volume of mixing:

$${\text{N}}_{\text{ISO}}=\upsilon \cdot {\rho }_{\text{ISO}}/{\text{M}}_{\text{ISO}}$$

$${\text{N}}_{\text{WAT}}=\left(1-\upsilon \right)\cdot \text{V}\cdot {\rho }_{\text{WAT}}/{\text{M}}_{\text{WAT}},$$ (1)

using appropriate densities (ρ) and molecular weights (M) for water and isopropanol (Table 1). DHFR plus ligand and cofactor were placed at the center of the periodic box prior to solvent placement. The protocol that was followed for system relaxation to equilibrium includes a series of energy minimizations and equilibration steps, and has been described previously.³⁹

Table 1:

Density and molecular weights for water and isopropanol

	ρ (g/cm3)	M (g/mol)
water	1.00	18.01
isopropanol	0.786	60.10

Hydride transfer modeling with empirical valence bond:

For modeling the hydride transfer step, we used protonated substrate (DHF⁺) and the empirical valence bond (EVB) method as implemented in AMBER (v14), which was developed by Warshel and coworkers.^{40, 41} The modeled enzyme reaction is the hydride transfer from NADPH (cofactor) to protonated DHF to produce NADP⁺ and THF. The present study involves the modeling of the hydride transfer from the C4N carbon on the cofactor (C_D) to the C6 carbon on the protonated substrate DHF (C_A). The bonds between the donor-hydride atoms and the acceptor-hydride atoms were modeled using a Morse potential. The Morse potential parameter α, which is dependent on the force constant of the C‒H bond (340 kcal/mol), was set to 1.817 A^‒1. D_e is the dissociation constant and is 103.0 kcal/mol, while R_e is the equilibrium C‒H bond length of 1.09 Å. The EVB method, in combination with classical molecular mechanics, was used for sampling of the conformations along the hydride transfer reaction. A total aggregate sampling of 114 ns was performed along the reaction pathway (6 ns for each of the 19 EVB simulations for mapping parameter λ = 0.05, 0.10, 0.15, …., 0.90, 0.95). Note that for each λ, we started from 5 different starting structuresand 5 complete independent trajectories (each 1.2 ns) were generated to ensure reproducibility. Starting from the X-ray structure following equilibration, a simulation of 10 ns was performed for the reactant complex. Five independent structures after the equilibration step (2, 4, 6, 8 and 10 ns) were used as starting points for the EVB simulations after minimization. A total of 11,400 conformations (600 conformations from each λ simulation) were collected representing the enzyme-substrate conformations sampled along the reaction pathway. These conformations were used structural analysis, enzyme motion analysis and computations of the reaction-coupled modes. Note, more conformations were stored for λ = 0.45, 0.50, and 0.55 to calculate the transition state structure and electrostatic potential calculations (see below). Three completely independent sets of EVB simulations were performed for 0%, 20% and 25% IPA concentrations (see Figure S1 is supporting information).

Quasi-anharmonic analysis (QAA):

This new computational methodology was used for identification of conformational sub-states associated with the hydride transfer catalyzed by DHFR. The collected conformational snapshots along the EVB simulations, 11,400 for each the three systems (0%, 20% and 25% IPA) were separately analyzed and characterized using QAA. Only the protein coordinates (excluding the cofactor and substrate) were used for the QAA, with the matrix only constructed using backbone C_α. The QAA provides a set of independent vectors or independent components that correspond to conformational fluctuations in the protein. This has been validated for a number of enzyme systems.⁵ The projections of conformations on the independent vectors s allow characterization of the sub-states. In this study, the conformations were characterized using the value of the collective reaction coordinate. The reaction coordinate value associated with each snapshot was obtained from the EVB method. More details about identification of conformational sub-states associated with enzyme catalyzed reactions are available in ref. ⁵ and ⁴², and further details of the EVB method and collective reaction coordinate for hydride transfer catalyzed by DHFR are available in ref. ⁶ and ⁴³.

Average transition state structure calculation:

In the EVB methodology, the transition state is defined as the highest point on the free energy profile (approximately at collective reaction coordinate value of −5.0 kcal/mol as seen in Figure S1). For the 3 simulations of hydride transfer (0%, 20% and 25% IPA), the free energy profiles were obtained and the corresponding value of the collective reaction coordinate was obtained to identify 1,000 structures that were within ± 1.0 kcal/mol. These were averaged to obtain the averaged structure corresponding to the transition state. For more details see ref. ⁴⁴

Electrostatic potential calculations:

For the 1,000 structures extracted above, within the ± 1.0 kcal/mol of the highest point on the free energy profile, the electrostatic surfaces were computed using the Adaptive Poisson-Boltzmann Solver (APBS) software.⁴⁵ The surfaces for the 1,000 structures were averaged to correspond to the representative electrostatic surface for the transition state.

DHFR expression and purification.

E. coli DHFR used in the stopped flow and isothermal titration calorimetry experiments was purified according to Grubbs et al.⁴⁶ Briefly, a gene for DHFR with a mutant (up) promoter⁴⁷ and a C-terminal histag was synthesized by Genscript and cloned into the pJET1.2 vector. The protein was expressed in D H 5α E. coli cells. Protein was purified by nickel-NTA (Invitrogen) and methotrexate-affinity columns. To remove folate used in the affinity column elution, the protein was passed over a DEAE column. The protein was dialyzed against deionized water and lyophilized. The presence of the histag was previously found not to alter ligand binding.⁴⁶

For DHFR used for X-ray and neutron scattering studies, a different method for protein expression was used. Recombinant DHFR was purified from E. coli JM109 bearing the plasmid encoding for the DHFR genes, pTZwt1–3. The plasmid and bacterial strain were provided by Richard Wagner (University of Minnesota). Ampicillin selection (50 mg/L) was used in all cultures. A single transformed colony was picked from an LB agar plate and transferred to 50 ml LB medium start culture containing 5 μg/ml trimethoprim (TMP). The starter cultures were grown for overnight at 37°C. The starter culture (10 ml) was inoculated into each of four 1 liter LB-AMP medium without trimethoprim. The cells were harvested by centrifugation (6000 ×g for 20 mins) when OD₆₀₀ values over 1.3 was observed. The cells were lysed by sonication, followed by ammonium sulfate precipitation prior to the chromatographic purification. As previously reported,^{48, 49} two chromatography steps were used. A methotrexate affinity column (Sigma) was utilized followed by a DEAE column (G.E. Healthcare) for an anion exchange step to remove folate. A SDS gel and DHFR activity assays were used to detect the purity of the protein fractions. Eventually the fractions containing pure DHFR were combined using a centrifugal filtration unit.

Rapid Kinetics:

Stopped flow experiments were performed at 27°C on an SX20 model Applied PhotoPhysics system with a dead time of 1 millisecond (ms). The samples were excited at 290 nm and a 455 nm filter was used to monitor energy transfer from DHFR to the NADPH cofactor. DHFR (30 μM) and NADPH (200 μM) were preincubated for five minutes prior to starting the kinetic scans. The DHFR-NADPH complex and DHF (250 μM) in MTEN buffer (50 mM MES, 25 mM Tris, 25 mM ethanolamine, 100 mM NaCl, 5 mM β-mercaptoethanol) were mixed and the resulting data were fit using Pro-Data SX software. Two events were observed: an exponential process that corresponds to the hydride transfer (k_hydride) rate and a slower steady state rate. 5–10 traces of the fast phase (2 ms to 25 ms time interval) were averaged and fit to a single exponential plus a linear rate:

$$F\left(t\right)=A{e}^{\left(-k_{hydride}*t\right)}+k_a*t+B$$ (2)

where F(t) is the fluorescence intensity as a function of time, A is the amplitude of the quench, k_app and k_a are the exponential and linear rates, respectively, and B is the final fluorescence. The linear rate corrects for the small contribution of the steady state rate on the fast time scale. Rates for k_hydride were collected over a pH range of 6.0 to 9.0.⁵⁰ Experiments were repeated in MTEN buffer with 20% (v/v) isopropanol. For the latter, the syringe concentration of DHF was increased to 600 μM due to the increase in K_d for DHF in the presence of isopropanol. Plots of k_hydride versus pH were fit for both MTEN buffer and MTEN buffer with 20% isopropanol and the pH-independent hydride transfer rates and reaction pK_as were determined:

$$k_{hydride}=\frac{k_{hydride,pH-independent}}{1+\frac{{10}^{-pka}}{{10}^{-pH}}}$$ (3)

where k_hydride is the hydride transfer rate at a particular pH and k_{hydride, pH -independent} is the pH-independent k_hydride.

Isotherm al Titration Calorimetry:

The effects of isopropanol on the K_d of NADPH or DHF binding to E. coli DHFR were monitored using a MicroCal VP-ITC. Titrations of NADPH (190 μM) were performed with 13 μM DHFR. DHF (500–650 μM) was titrated into the binary complex of DHFR (8–12 μM) and NADP⁺ (200 μM). Titrations were performed in duplicate at 25°C in 100 mM Tris, 50 mM MES, 50 mM acetic acid, 1 mM EDTA, 5 mM β-mercaptoethanol, pH 7.0 (MTA) buffer. Data from two separate titrations were globally fit to determine a single set of thermodynamic parameters using the single-site binding model in the SEDPHAT program.⁵¹

Preparation of DHFR Ternary Complex:

The purified DHFR was exchanged three times into 10 or 20 mM imidazole hydrochloride, pH 7.0, and concentrated using the centrifugal filtration unit to 1 mg/ml, as determined by absorbance at 280 nm. For making folate•DHFR binary mixture, 1mM folic acid powder was added into the protein solution, which was stirred gently to totally dissolve. The binary complex was incubated at 4°C overnight. The mixture was concentrated to 30mg/ml in concentrators, and re-diluted in 71mM Tris-Cl, pH 7.0 with a trace of folic acid added. The process of re-dilution and re-concentration was repeated for two more times to remove excess folic acid and the previous buffer. A 5 fold molar excess of solid NADP⁺ powder (Sigma) was added to the 30 mg/ml solution of folate•DHFR and incubated overnight, in order to make the folate•NADP⁺•DHFR ternary complex.

Preparation of BASIS beam samples for quasi-elastic neutron scattering (QENS) studies:

The folate•NADP⁺•DHFR ternary complex was used in the QENS experiments. To make the ternary complex in deuterated buffer was similar to the process of making the complex in hydrogenated buffer. Before adding substrate and cofactor, the purified DHFR was exchanged into D₂O buffer by adding D₂O buffer to hydrogenated protein solution with a 1:10 ratio. The protein again was concentrated to 1 ml. This process was repeated for a total of three times to exchange hydrogenated buffer with deuterated buffer. DHFR in D₂O was diluted to 2 mg/ml to make binary complex. To make ternary complex, the concentration of binary complex in D₂O was 40 mg/ml. Finally, the folate•NADP⁺•DHFR ternary complex was sequentially concentrated to 80 mg/ml.

To make a standard sample without isopropanol, 700 μl of the ternary complex was mixed with 300 μl of D₂O. The final Tris-Cl D₂O buffer concentration is 50 mM and the protein concentration is 56 mg/ml. The sample with 20% isopropanol was made by mixing 700 μl of ternary complex with 200 μl of D8-isopropanol and 100 μl of D₂O. The sample with 30% isopropanol was prepared by mixing 700 μl of the sample and 300 μl of D8-isopropanol. All three samples (0%, 20% and 30% isopropanol) and the three corresponding solvent samples used for background measurements were individually sealed into Teflon pouches and then inserted into standard aluminum sample cans.

Crystallization:

Crystals of DHFR were grown by hanging drop vapor diffusion in drops containing 2 μl of the protein solution mixed with 2 μl of 0.2 M CaCl₂, 20–35 % (w/v) PEG 6000, 0.1M NaHEPES pH 7.5 equilibrated against 900 μl of the same solution. Crystals typically grew to a maximum dimension of 150 pm in two weeks. For isopropanol soaks, crystals were transferred to 25 % (w/v) PEG 6000, 0.1M NaHEPES pH 7.5 that was supplemented with isopropanol. Crystals were allowed to soak for an hour and then immediately mounted in a nylon loop, and flash frozen in liquid nitrogen. All data were collected at 100 K at the SERCAT beamline at the Advanced Photon Source, Argonne National Laboratory using a Mar345 CCD detector. The diffraction data were scaled and indexed using HKL2000. PDB coordinates and structure factors have been deposited in the RCSB Protein Data Bank under the accession codes 5EAJ (0% IPA) and 5UJX (20% IPA).

RESULTS

Past investigations of DHFR using nuclear magnetic resonance (NMR) spin relaxation dispersion experiments suggested that the enzyme cycles through different conformational states as the reaction proceeds through the catalytic cycle.²⁶ The conformational states investigated included DHFR in binary or ternary complexes; these studies suggested that at each of these states, the enzyme also samples a minor set of conformations that correspond to the nearby states in the catalytic cycle. One of these states corresponds to the ground state for the hydride transfer reaction, with the enzyme bound to substrate (DHF) and cofactor (NADPH). In this state, the enzyme samples higher energy conformations at the rate of 1200 s⁻¹. Interestingly, this coincides with the rate of hydride transfer of 950 ^s−1 mentioned in that study as well as our measurement of 1170 ^s−1 (see below). It has been hypothesized that the minor population samples the functionally relevant conformational sub-states for hydride transfer.

The solvent surrounding the enzyme impacts internal protein motions, with some evidence even indicating that the connection may be very strong, such that solvent motions may enslave the protein dynamics.^29–31 Therefore, we hypothesized that changes in solvent conditions could be used as a mechanism for changing protein motions. DHFR activity was initially screened in aqueous binary mixtures with different types of cosolvents: methanol, ethanol, isopropyl alcohol (IPA), acetone, acetonitrile, dimethyl sulfoxide, and dimethylformamide (Figure S2 in supporting information). The cosolvents in this screen contain different functional groups, so as to provide different hydrophilic (and hydrophobic) interactions on the enzyme surface to represent the interaction of enzyme with other biomolecules in the cellular environment.^{28, 52} Enzyme activity was screened as a function of increasing concentration of binary mixtures of these cosolvents with water (buffer), and their impact on structure was investigated with circular dichroism (data not shown) and X-ray crystallography. The case of DHFR activity (measured by a change in absorbance with contributions from the cofactor NADPH and the substrate DHF) in IPA-water binary mixtures of up to 20% of IPA (v/v) provided the most interesting case for detailed analysis.

Controlling protein dynamics using isoproponal as a cosolvent

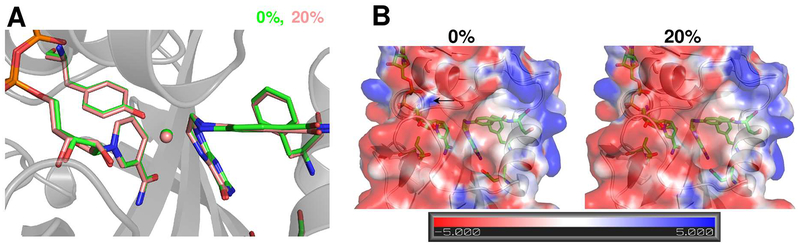
For E. coli DHFR, the hydride transfer step is rate-limiting at pH >8.4 and this enzyme has been investigated widely for a connection between dynamics and enzyme mechanism. We used computational simulations to identify the conformational sub-states associated with the hydride transfer reaction catalyzed by DHFR. Using empirical valence bond (EVB), ⁵³ conformations were sampled along the hydride transfer pathway. Simulations were performed in water and in binary mixtures with IPA at 20% and 25%. The results indicated that the transition state (TS) for hydride transfer in water (0%) and 20% isopropanol is nearly identical (see Figure 1). Previously, it was suggested that changes in solvents can impact enzyme catalysis through changes in electrostatics.⁵⁴ However our comparison of the averaged electrostatic potential for the active-site between the 0% and 20% IPA shows very little difference (Figure 1). This result rules out the direct impact of the dielectric constant in altering the reaction rate for the case of IPA, as previously suggested.

Figure 1: Impact of isopropanol-water mixture on the transition state for hydride transfer.

(A) The averaged transition state structure calculated based on EVB computer simulations indicates no difference in the active-site residues (Phe31 and Tyr100 are shown) as well as cofactor (NADPH) and substrate (protonated DHF). 1,000 structures within ± 1kcal/mol (collective reaction coordinate) of the activation energy barrier were used to calculate the average structure. The transferring hydride is shown as a sphere. (B) The averaged electrostatic potential (+5kT/e in blue and −5kT/e per electron in red) for the transition state structures is practically the same (obtained by averaging the APBS calculated electrostatic potential of 1,000 TS structures). The only minor difference between the 0% and 20% IPA cases occurs around residues 98–99 (marked by small black arrow).

The dielectric constant in condensed phase accounts for screening of the interactions by the medium present between electrostatic charges. The dielectric constant of the bulk solvent changes as the IPA concentration is increased, so it could be argued that the changes in bulk dielectric constant would also change the active-site interactions. However, the computational calculations suggest the averaged electrostatic potential as well as the TS structure is identical for the case of 0% and 20% IPA. Specifically, residues Phe31 and Tyr100 show identical orientation in the active-site, as do the substrate and cofactor (Figure 1). It is widely proposed that hydride the transfer rate is highly sensitive to the donor-acceptor distance in DHFR. This is a clear indication of the unique properties of enzymes to create a unique micro-environment in the active-site to shield the reactive species from the properties of the bulk medium. The peripheral residues between the active-site and the bulk solvent thus shield the long-range electrostatic interactions such that the micro-environment at the active-site is optimal for attaining the TS. This is indicated by various observations that the pK_as of active-site residues in enzymes can be significantly different from those on the solvent exposed surfaces. It is possible that some effect of solvent interactions on the surface could change the behavior of dynamical trajectories (such as barrier re-crossings) and therefore impact of bulk dielectric constant could indirectly influence active-site interactions through minor fluctuations. However, the computational results indicate, the averaged TS structures and electrostatic interactions are nearly identical, even under different bulk solvent conditions. This could be of biological significance, since the cellular environment contains different molecules randomly diffusing with a wide range charges and enzymes need to function under constantly varying conditions and changing external electrostatic forces.

Note that our simulations indicated that in the case of DHFR, no IPA molecules enter the active-site (also see the discussion about X-ray structures below), therefore, the impact of IPA on the electrostatic environment is possible only through alteration o f enzyme structure. Collectively these results ruled out changes in the enzyme structure and electrostatics environment as impacting the mechanism of hydride transfer.

Functionally critical conformational sub-states

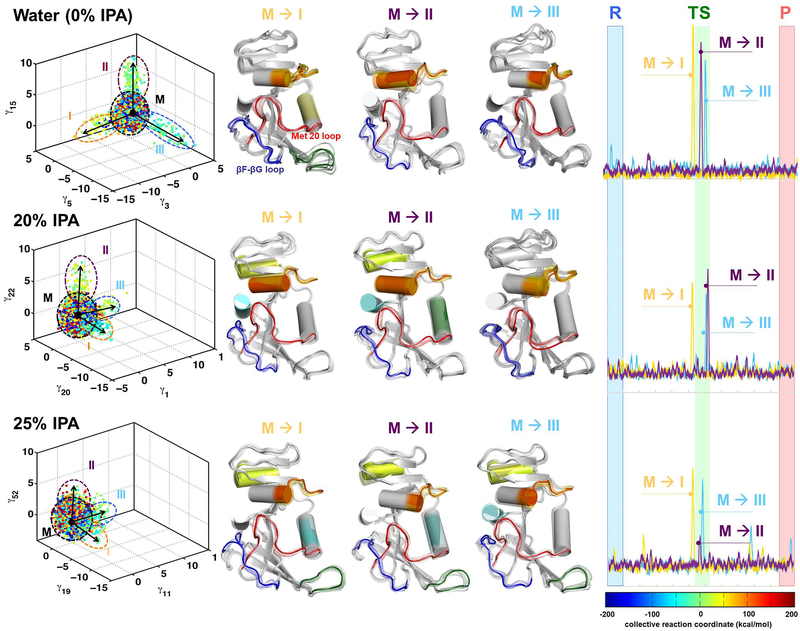
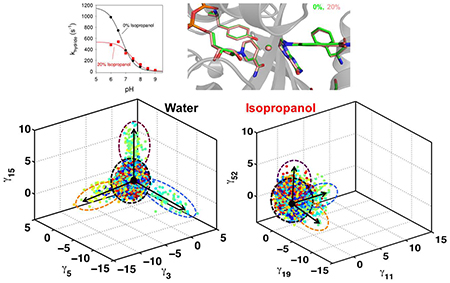
The sets of enzyme complex conformations collected were characterized using quasi-anharmonic analysis (QAA).⁵ QAA has previously been used to identify and characterize functionally relevant conformational states in cyclophilin A and other enzymes.^{5, 42} We focused on identification of the conformational sub-states along the reaction pathway associated with hydride transfer and characterized the sub-states associated with the transition-state (TS) area. As depicted in Figure 2, the conformational sub-states that sample the TS area are enabled by the motions of the dynamical loop regions including the Met20 and βF-βG loops. This result is in agreement with the previous NMR studies.²⁶ For the 0% IPA case, these conformational substates are well defined and show three sub-states that enable the sampling of the TS area due to conformational transitions. The results indicate that DHFR spends a majority of time sampling conformational states that have mixed properties (labeled M in Figure 2, left panels). However, certain protein motions (depicted as movie frames in the central panel of Figure 2) enable conformational transitions that allow sampling of rarely populated states such as those that correspond to the transition states. These conformational transitions (marked by black arrows in the left panels of Figure 2) correspond to the motions that are detected by NMR and other experimental techniques. Note that the motions that are visible in these results are consistent with the previous studies. It is well known that the Met20 and βF-βG loops show reaction coupled motions.²⁶ As depicted on right hand side in Figure 2, these conformational transitions are activated in the vicinity of the TS for 0% but not in the case of 25% IPA. In case of the 20% they are activated near the TS however their magnitude is reduced. These activation profiles were calculated by projecting the conformations sampled during the hydride transfer reaction on the QAA modes.

Figure 2: IPA alters the functionally relevant conformational sub-states for catalysis.

Computer simulations with the EVB method were used to model the rate-limiting hydride transfer reaction in water (0% IPA), 20% IPA and 25% IPA. (The color coding is based on the reaction coordinate. See the free energy profiles in supporting information for details.) The 3-D plot (left panel) shows three different independent component vectors from QAA and the ellipses identify the conformational sub-states for each of the simulations. Each dot represents a single enzyme conformation along the reaction pathway of hydride transfer (color coded according to the value of the reaction coordinate). For each of the simulations, we identified conformational sub-states close to TS area (cyan-green-yellow dots). The mixed sub-state (M) represents a mixture of all other sub-states. The conformational fluctuations that enable the sampling of these sub-states are indicated by arrows (M ⟶I, M ⟶II, and M⟶III). In the middle panel, the structural changes in DHFR associated with fluctuations are shown in a movie like fashion, with regions displaying the largest fluctuations shown in color (Note these colors have no connection to reaction coordinate colors but are used to indicate same regions of protein that show motion). In these conformational fluctuations, the enzyme regions including Met20 and βF-βG loops show the largest displacements. The right-most panel indicates the activation of enzyme (visit into the TS conformational sub-states) by these protein motions. These activation profile corresponds to the 3 QAA modes shown on left hand side and are calculated by projecting the sampled conformational snapshots on each mode. Note that the conformational sub-states are clearly defined for 0% IPA; however, the enzyme landscape is altered significantly by addition of IPA in solution. At 20% and 25% these sub-states are not clearly defined, which indicate difficulty in sampling the motions (see the activation profiles in right panel) and reaching the functionally relevant sub-states in the TS area.

Note that in the 3D plots in the left most panel of Figure 2, the axes correspond to QAA modes; these modes are ranked by degree of kurtosis (thus corresponding to the degree of anharmonicity of the protein motions).⁵ The selection of the modes is based on the modes which identify the functionally relevant conformational sub-states near the TS. For the 0%. 20% and 25% IPA, the QAA modes corresponding to the x, y and z axes show different labels, as they are ranked differently by kurtosis. Even though they are ranked differently, these modes correspond to the same motions as indicated by the corresponding motions as depicted in middle panel of the Figure 2. Further, it should be noted that all enzyme conformations have the optimal/suitable orientation of the active-site (and other) residues, that is not all enzyme conformations are catalytically competent. The color-coding of conformations (dots in 3D panel) corresponds to the reaction coordinate. The conformations in the proximity of and at TS area are considered to be catalytically competent (green colored dots). For the sub-states, where the conformations have different colors, the state has catalytically competent and incompetent conformations (mixed properties), as compared to TS sub-states which are homogeneous sub-states with mostly catalytically competent conformations.

Significantly, in the presence of IPA (20% and 25%), there are marked changes in the nature of the conformational sub-states. At 20% IPA, the sub-states are less well defined and are not clearly present in these sub-states, indicating less sampling of the functionally relevant substates. An interesting observation is that these conformational transitions show movement in new regions of the protein in the presence of IPA. At 25% IPA concentration, the simulations indicate that these conformational sub-states are significantly altered and not clearly defined. The altered motions due to the presence of IPA change the energetic landscape of the enzyme and consequentially sampling of the functionally relevant sub-states (as seen in the case of 0% IPA) separated from the mixed conformations and a comparatively smaller number of conformations is not achieved. In the context of previous NMR studies,²⁶ the presence of IPA in solution changes the enzyme’s ability to sample functionally important conformational sub-states.

Quantitative comparisons provide more detail about the impact of altered dynamics on the hydride transfer reaction (see Table 2). For the 0% IPA case, 302 conformations (of the 11,400 used for the computational analysis) are able to sample the TS sub-states enabled by the 3 conformational transitions (identified by the QAA vectors), while for the 20% IPA simulations only 95 conformations were able to sample the TS sub-states for the top 3 conformational transitions (M⟶I, M ⟶II, and M⟶III in Figure 2). This is more than a three-fold decrease. A further increase in IPA concentration to 25% leads to a further decrease in the TS sub-state sampling. Additionally, to understand the nature of these visits of conformations to TS substates, we compared the computer simulation trajectories. The visits to the conformational states are possible in two ways. First, systematic activations of the conformational transitions are enabled by protein motions as identified by our analysis (right panels of Figure 2). The second path is through stochastic motions, where random changes allow the system to sample a value of the reaction coordinate that is typical of the TS area but these types of changes are quickly reversed as the environment is unfavorable. Simulations with 20% and 25% IPA show that about 4 fold more visits to the TS region are stochastic. Note that for our analysis, we define a stochastic visit to the TS area as part of the trajectory that exactly has one conformation in the TS vicinity. Furthermore, even the systematically activated visits to the TS region by protein motions are shorter for the systems with 20% and 25% IPA (6.7 fs in water as compared to 5.5 fs in presence of 20%/25% IPA). These combined results indicate that the global conformational fluctuations enable the protein to sample functionally relevant conformational sub-states. In the presence of IPA, even though the overall protein structure is not altered and dynamics are suppressed, the major effect comes from the inability of the protein to sample conformations that are functionally relevant.

Table 2:

Analysis of conformations in the TS sub-state

IPA concentration	0%	20%	25%
Conformations in TS sub-statesa	302/11,400	95/11,400	89/11,400
Stochastic TS visitsb,c	8,049/40,000	32,036/40,000	28,935/40,000
Averaged timed (fs) in TS area for systematically activated (non-stochastic) visitsc	6.7	5.5	5.5

^a= Of the 11,400 conformations used for QAA, the number of conformations identified in the TS conformational sub-state as defined by the 3 QAA vectors. These 11,400 conformations were obtained by sampling 19 separate EVB windows along the reaction pathway.

^b= For the EVB simulation in the vicinity of TS (EVB parameter λ = 0.5), trajectories were analyzed for a visit in the TS region. 40,000 sampled conformations were used for this analysis.

^c= For this calculation, the TS area is defined as ± 5 kcal/mol. of the TS (top-most point on the EVB free energy profile).

^d= Averaged number of molecular dynamics steps for all the TS visits (as defined by c). A step of 1 femto-second was used for the EVB simulations.

Overall the computational simulations show that with increasing concentrations of IPA, there are significant changes to the conformational sub-states associated with the hydride transfer reaction. For the reaction in water, conformational fluctuations enable systematic visits to TS sub-states that show motions in the Met20 and βF-βG regions of the protein. In contrast, the presence of IPA significantly alters the conformational fluctuations, allowing a much smaller number of conformations to sample the TS sub-states. Based on the quantitative characterization of conformational sub-states associated with TS sub-states (Table 2), it is expected that 95/302 or ~3 fold less conformations access the TS sub-states. Therefore, we predicted that the reaction rate should be decreased by about 3 fold. Note that given the nature of computational calculations and limitations associated with the force-fields, this number should be considered as a qualitative prediction rather than a quantitative prediction.

Stopped-flow kinetics measurement

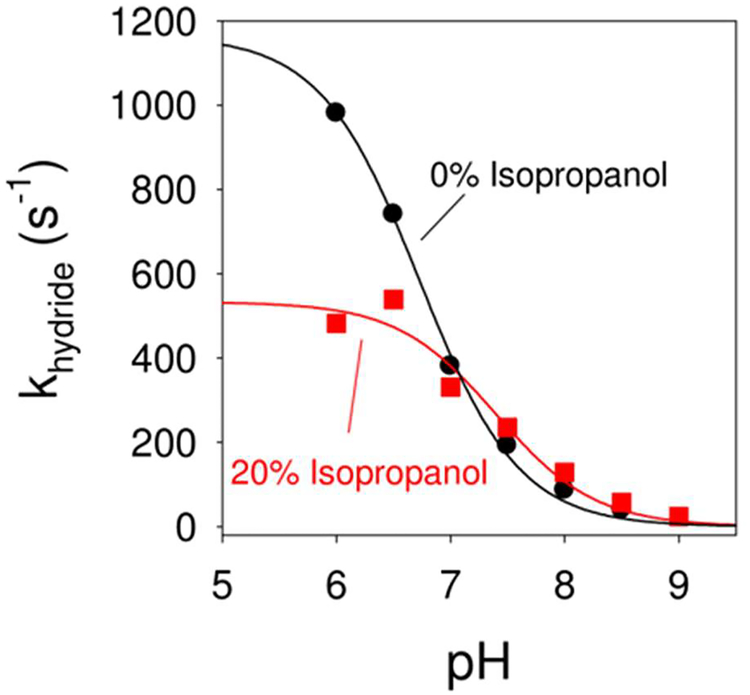
The effect of IPA on the hydride transfer rate (k_hydride) for DHFR was monitored using stopped-flow kinetics. Using steady state kinetics, hydride transfer catalyzed by DHFR is rate determining above pH > 8.4 while product release is rate determining at lower pH values.⁵⁰ Thus we elected to monitor the hydride transfer rate directly using stopped flow. As addition of cosolvents can alter pK_a values,⁵⁵ the pH independent hydride transfer rates were compared. The k_hydride rate was monitored for DHFR in MTEN buffer over the pH range of 6.0 to 9.0 (see Figure 3), as well as in buffer with 20% IPA. All experiments were performed at 27°C. The hydride transfer rate increased with decreasing pH, and became pH independent below pH 6. The data were fit to a pH titration equation yielding a pH-independent k_hydride of 1170 ± 10 s⁻¹. The pH-independent khydride is higher than previously reported (950 ^s−1) for DHFR,^{50, 56} though those studies were performed at 25°C. A pK_a of 6.7 ± 0.1 was obtained in the absence of IPA. The corresponding pH independent hydride transfer rate with 20% IPA was 530 ± 10 ^s−1, corresponding to a 2.2 fold decrease. This is consistent with the prediction of ~3 fold decrease from the computational studies. The pK_a in 20% IPA was shifted upwards to 7.4 ± 0.1. It should be noted that organic solvents could also affect catalysis indirectly, through changes in the binding of cofactor (NADPH) and substrate (DHF), through changing the binding affinity of these molecules to the enzyme. This scenario was considered using isothermal titration calorimetry studies as described in the supporting information. It is also possible that the enzyme dynamics impacts the cofactor/substrate binding and/or cofactor/product release. Characterization and obtaining quantitative estimates is currently difficult. Future investigations that combine the analysis described in Figure 2 with computer simulations of the ligand binding and release process will provide more information about these aspects. (Method development and validation of such an approach for other enzyme system is currently underway in our group).

Figure 3: Effect of isopropanol-water mixture on DHFR catalyzed hydride transfer.

Stop flow kinetics indicates that the pH independent rate for hydride transfer is 1170 ± 10 ^s−1 (black curve) for 0% isopropanol (buffer only), while it is 530 ± 10 ^s−1 with 20% isopropanol.

Impact of cosolvent on enzyme structure

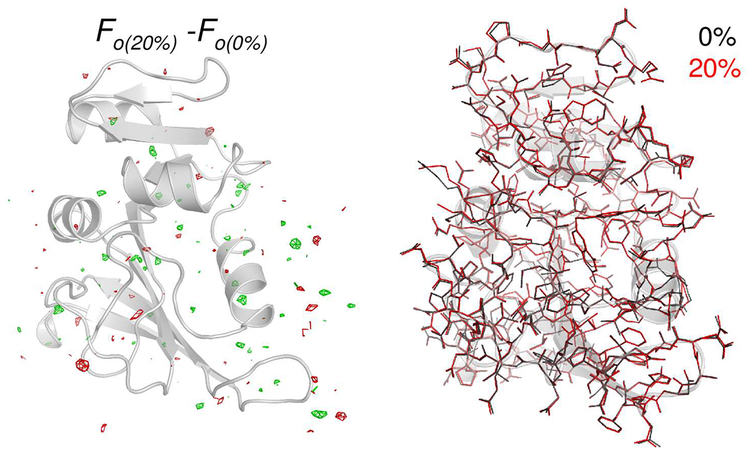
X-ray crystallography was used to examine the effects of the IPA cosolvent on enzyme structure. Enzyme structures determined in buffer, 5%, 10% and 20% IPA showed no significant changes at the 1.7 Å resolution of the analyses, with overall RMS differences of < 0.09 Å (see Figure 4). In addition to the overall structure of the enzyme, the previously implicated dynamical regions of the enzyme including the Met20 and βF-βG loops, and the active-site residues (Tyr100 and Phe31) show no discernable differences in local structure or orientation.⁵⁷ Crystal structures were obtained for the binary complex (folate with enzyme) and other conditions were also similar to protocols followed previously.⁵⁷ See supporting information for additional details.

Figure 4: Effect of isopropanol-water mixture on DHFR structure.

The X-ray structure indicates little difference in the electron density (left) and fitted structure (right) for the two cases. The gray cartoon shows the 0% IPA structure for orientation purposes only.

Impact of cosolvent on DHFR dynamics

Quasi-elastic neutron scattering (QENS) was used to identify changes in protein dynamics with increasing IPA concentrations. Hydrogen atoms have a much higher neutron scattering cross section than deuterium.⁵⁸ Therefore, measuring hydrogenated proteins in D₂O solvent allows characterization of the motion of the hydrogen atoms in the protein, and thus, of the protein itself. QENS studies were performed at 0% (buffer), 20% IPA and 30% IPA. Note that prior to sample preparation, the labile hydrogens on the protein were exchanged with D₂O (see supporting information). After solvent background subtraction, the scattering signal (see Figure 5) is almost entirely from the remaining hydrogen atoms on the protein, with minor contributions from other protein atoms. As seen in Figure 5A, the quasi-elastic signal narrows with increasing IPA concentration, indicating slower protein motions. The scattering signal consists of contributions from three different motions: the translation diffusion (D_COM) and rotational motions (D_ROT) of the protein through the solution, and the local dynamics of the protein hydrogens (D_INT, modeled as a diffusion in a sphere) as illustrated in Figure 5B. Over this concentration range, the solvent viscosity increases significantly with increasing IPA concentration, which is expected to impact the translational diffusion and rotational motion of the entire protein and perhaps to a lesser degree, the local dynamics of the protein hydrogens. QENS was used to probe the diffusional dynamics of DHFR at 16 momentum transfers, 0.4 Å⁻¹< Q< 1.9 Å⁻¹ corresponding to length scales relevant to both center-of-mass and internal motions (local dynamics). A model was constructed (see supporting information for full details) that described the three types of protein hydrogen motion described above with an additional term for harmonic, vibrational oscillation. Translations and rotations were related through the Stokes-Einstein (S-E) and Stokes-Einstein-Debye relationship using measured values for solvent viscosity.^{59, 60} Internal motions were described by a model we developed previously to characterize protein samples.⁶¹ The QENS results indicate that with solutions of increasing concentrations of IPA, the local, internal motions (D_INT) of the enzyme are significantly decreased (Figure 5C) by as much as 60% between water and the 20% IPA cosolvent concentration.

Figure 5: Effect of IPA on DHFR dynamics.

(A) Background subtracted quasi-elastic neutron scattering (QENS) data from DHFR hydrogen atoms in solution at the indicated IPA concentration. The points show experimental data and line indicates fit to the model as described in supporting information. (B) The contribution to the QENS signal comes from hydrogen local motions and the translational and center-of-mass rotational movement of the entire enzyme in solution. A random path is illustrated by the black line where the center-of-mass translational and rotational motion of DHFR will be affected by the viscosity of the solution. The local dynamics of hydrogens (D_INT) attached to the side chain were modeled as diffusion in a sphere. (C) The internal motion diffusion coefficient, D_INT, at the indicated IPA solvent concentrations. The plot shows the sensitivity of D_INT at fixed values of the radius defining the extent of internal motion and the vibrational, oscillation Debye-Waller factor. As IPA concentration is initially increased to 2 0 %, D_INT decreases by approximately 60%. There is little difference between the 2 0 % and 30% samples. (D) Dependence of viscosity (η), D_INT, and pH independent rate for hydride transfer (k_{hydride,pH ‒ independent}) with isopropanol concentration. The first two quantities are for deuterated solutions while the last is from protonated solutions. Note, the uncertainties associated with the viscosity measurements are less than the size of the symbols. D_INT is from Table S3.

Collectively, stopped-flow kinetics and X-ray crystallography indicate that the enzyme shows a decrease in the rate of hydride transfer with increasing IPA concentration, while there is no impact on the structure. The neutron scattering studies indicated that the protein dynamics are impacted by addition of IPA as cosolvent. In addition, it is also important to consider the impact of long-range electrostatic effects on the catalyzed reaction.⁶²

Contribution of electrostatic effects

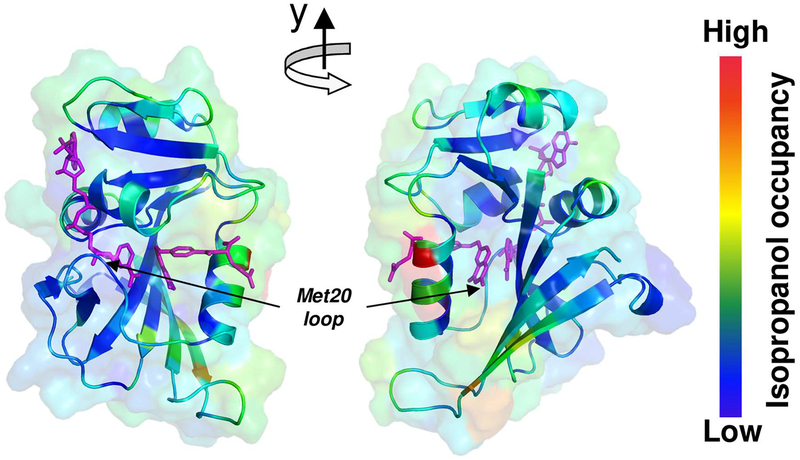
Previous investigations monitored changes in DHFR activity in cosolvents, where the lack of correlation of enzyme activity with the bulk viscosity of the cosolvents, was presented as evidence for a lack of connection between global dynamics and enzyme activity.^{54, 63} In particular, it was given as evidence that global motions (on slow time-scales) do not affect the hydride transfer reaction. The neutron scattering results discussed above indicated that there are changes in both global and internal dynamics in the presence of IPA, which raises questions about the correlation of bulk viscosity with dynamics. Furthermore, the correlation of bulk viscosity and enzyme activity may not be totally appropriate. Viscosity depends on the interaction between different layers of a fluid and therefore the bulk viscosity would correspond to measurements between cosolvent and solvent layers, especially in the case of miscible solvents. The organization of water and IPA around the DHFR is not uniform. Computer simulations show that several regions of the enzyme exhibit preferential IPA interaction compared to other regions (see supporting information). Therefore, not all the dynamics of the enzyme would be altered similarly. In particular, the dynamically important surface loop regions, Met20 and βF-βG, show preferential interaction with water⁶⁴ even in the presence of IPA (see Figure 6).

Figure 6: Differential interaction of IPA with DHFR surface residues of DHFR.

100ns molecular dynamics trajectories were used to calculate relative occupancies of IPA molecules close to the surface of DHFR (see supporting information for more details). Regions of low interaction are shown in blue and higher occupancy in red. The cofactor and substrate are shown in magenta. The dynamical regions Met20 and βF-βG loops show little preference for IPA (and therefore more preference for water). Note, these results are based on difference between simulations with 15% and 30% IPA, other results were qualitatively similar.

A possible concern is the effect of IPA on protonation of the DHF N5 atom that is proposed to occur before the hydride transfer step.⁶⁵ Results from previous isotope effect studies and analysis of mutants are consistent with protonation of the N5 atom of DHF preceding hydride transfer.⁶⁶ Additional studies propose the observed pK_a associated with hydride transfer describes the pK_a of DHF in the ternary complex where the enzyme provides an environment that increases the N5 pK_a from 2.59 free in solution⁶⁷ to ~6.5 when bound to the enzyme-NADPH complex.^{66, 68, 69} Our studies remain consistent with the proposal of a more hydrophobic solvent (20% IPA) increases the observed pK_a to 7.4 (Figure 3). Note, our QAA results describe ~3 fold decreased ability of the bound, protonated DHF-NADPH complex to reach the transition state, under mixed solvent conditions. The measured pH independent hydride transfer rate also describes a 2.2 fold decreased turnover of bound, protonated DHF into THF. The altered pK_a could arise due to changes in the dynamic balance between the tightly closed and partially closed/open states associated with the M20 loop, as the M20 loop conformation has been proposed to greatly influence the N5 DHF pK_a value (see Figure 6 in ref. ⁶⁹). An additional possibility is that small fluctuations in the M20 loop have been proposed to allow access of water to bound DHF to enable protonation. Changes in solvent could impact this accessibility and affect the resulting pK_a.^{70, 71} Also, histidine pK_a values in DHFR have been observed to vary up to 0.7 pH units depending on the bound ligand identity.⁷² These various studies indicate the whole protein as well as the solvent likely contribute to the observed pK_a value.

DISCUSSION

Enzyme mechanisms are influenced by a number of factors, with the role of structure well established, and the role of protein motions currently being widely debated. Our investigations extend the previous hypothesis that certain large scale conformational fluctuations (or protein motions at long time-scales) influence catalysis, and changes in these motions due to changes in the surrounding solvent alter the rate of hydride transfer activity catalyzed by DHFR.

Our new computational approach, quasi-anharmonic analysis, enables the identification and quantitative characterization of the function promoting dynamics. The underlying technique based on accurate description of protein motions (particularly the anharmonicity of large scale motions) enables identification of conformational sub-states associated with the transition states, and therefore, the rate-limiting fluctuations that enables access to these sub-states.5 For hydride transfer catalyzed by DHFR, QAA predicted that the changes in solvent conditions alter the energetic landscape of enzyme and its ability to sample conformational sub-states that are relevant for enzyme catalysis. Specifically, ~3 fold decrease in hydride transfer rate was predicted going from aqueous conditions to mixed solvent conditions with IPA. Note, that this computational approach is general and can be extended to other systems (enzymes and nonenzymatic proteins) for identification of function promoting conformational sub-states and associated conformational transitions.^{5, 42} As compared to the approach presented here based on the characterization of the TS conformational sub-states, previously dynamical effects of enzymes have been quantified using a pre-exponential term in the transition state theory. This term, known as transmission co-efficient is estimated based on fractions of successful reaction trajectories that cross the dividing surface at the activation barrier. The ratio of transmission coefficient for 0% and 20% IPA systems is calculated to be approximately 1.20 (see SI text for details). Therefore, the predicated rate based on such calculations will only be 1.20 fold lower (approximately 20% slower) for the case of 20% IPA. This difference in the estimates based on using only the transmission coefficient and experimentally observed rates is due to the limitation of the TST theory in estimating the effects of enzyme dynamics. The use of conformational substates analysis provides a more accurate estimation of the impact of functionally relevant dynamics in catalysis.

Stopped flow kinetics measurement of DHFR in a 20% IPA-water binary mixture, shows a 2.2 fold decrease in the rate of hydride transfer (pH independent rate), compared to the enzyme activity in fully aqueous conditions. X-ray crystallography indicates that there is no significant difference between the enzyme structure in water and 20% IPA mixture, while quasi-elastic neutron scattering indicates that the local dynamics of the enzyme are suppressed with increasing concentration of IPA. Note, a number of other solvents mixtures were also investigated, however, IPA provide the most interesting case where the changes in dynamics and enzyme activity were observed, without any significant changes in the structure.

The debate about role of dynamics in protein function, including enzyme catalysis, has been vigorous. Based on a number of past investigations, it seems clear that not all types of motions will have a direct influence on enzyme function. Our computational methodology aided by experiments, enables identification, quantitative characterization and validation of rate-limiting protein dynamics. The results from our present investigations indicate that rather than changes in any set of enzyme motions, it is changes in a specific sub-set of functionally promoting motions that impacts enzyme catalysis. These results also indicate that the energetic landscape of an enzyme is likely to be influenced by interaction with cellular components other than water, which could also affect catalysis. The extent of a dynamical contribution to the overall rate-acceleration will depend on the enzyme system. Therefore, it must be emphasized that the specific set of motions that are related to enzyme activity must be isolated, before their role can be investigated.

The emerging paradigm indicates that the fold (topology), in addition to serving as a structural scaffold, also preserves the dynamical features that allow sampling of the conformational substates that promote reaching the transition state. Studies from the groups of Friedman, Agmon and Frauenfelder have provided significant insights into the link between hierarchy of protein motions, conformational states and protein function.^{23–25, 73–75} In particular for hemeproteins, kinetic hole burning effect has indicated that both the disordered conformational coordinate and the resulting distribution of kinetic barriers are important for protein function.²³ Recent evidence also suggests that the turnover of the enzyme may be limited due to the enzyme’s ability to sample these conformational sub-states. Once the catalytically competent conformational substates are sampled, the actual chemistry (or other rate limiting events) will be relatively fast. A clear understanding and delineation of functionally important protein dynamics has implications for identifying the role of remote regions in protein function, as well as allosteric and cooperative effects.

Abbreviations:

DHF

dihydrofolate

DHFR

dihydrofolate reductase

EVB

empirical valence bond

IPA

isopropanol

NADP+/NADPH

oxidized/reduced form of nicotinamide adenine dinucleotide phosphate

QAA

quasi-anharmonic analysis

QENS

quasi-elastic neutron scattering