Observation of long-range dipole-dipole interactions in hyperbolic metamaterials

Metamaterials mediate long-range dipole-dipole interactions between quantum emitters.

Abstract

Dipole-dipole interactions (V_dd) between closely spaced atoms and molecules are related to real photon and virtual photon exchange between them and decrease in the near field connected with the characteristic Coulombic dipole field law. The control and modification of this marked scaling with distance have become a long-standing theme in quantum engineering since dipole-dipole interactions govern Van der Waals forces, collective Lamb shifts, atom blockade effects, and Förster resonance energy transfer. We show that metamaterials can fundamentally modify these interactions despite large physical separation between interacting quantum emitters. We demonstrate a two orders of magnitude increase in the near-field resonant dipole-dipole interactions at intermediate field distances (10 times the near field) and observe the distance scaling law consistent with a super-Coulombic interaction theory curtailed only by absorption and finite size effects of the metamaterial constituents. We develop a first-principles numerical approach of many-body dipole-dipole interactions in metamaterials to confirm our theoretical predictions and experimental observations. In marked distinction to existing approaches of engineering radiative interactions, our work paves the way for controlling long-range dipole-dipole interactions using hyperbolic metamaterials and natural hyperbolic two-dimensional materials.

INTRODUCTION

Engineering of dipole-dipole interactions has led to demonstrations of long-range qubit interactions in circuit quantum electrodynamics (QED) (1), superradiance of atoms and quantum wells mediated by photonic crystals (2, 3), collective lamb shifts of atoms in cavity QED (4), enhanced energy transfer between molecules in cavities (5), and quantum phases in optical lattices (6). A unifying theme in these approaches is the enhancement of radiative interactions and departure from the far-field (V_dd ~ 1/r) scaling of interaction with distance. A significant challenge is the control of the nonradiative Coulombic near-field interactions that scale considerably faster with distance (V_dd ~ 1/r³) and are conventionally limited to the extreme near field (7).

The canonical understanding of dipole-dipole interactions in cavity/waveguide QED stems from modification of the vacuum density of states and spectral tuning of atoms toward regions where the group velocity goes to zero and the corresponding density of states diverges. The two conventional approaches to achieve this criterion, as shown in Fig. 1 (A and B), use either metallic waveguides operating near the cutoff frequency or cavities operating near a photonic band edge (8–10). The resonant nature of the density of states modification leaves little room for tolerance in terms of the range of emitters that can be used, as well as the environmental conditions necessary for direct experimental observation. All experiments so far have relied on a resonant interaction intrinsically requiring emitters with linewidths much smaller than the resonance linewidth of the cavity or waveguide mode; this condition inherently requires either cold atom systems where the linewidths of the atoms are on the order of gigahertz or less, or circuit QED systems where the metallic waveguide is cooled to ultralow temperatures.

Fig. 1. Comparison of dipole-dipole interactions (V_dd) in metallic waveguides, photonic crystal band-edge structures, and hyperbolic metamaterials.

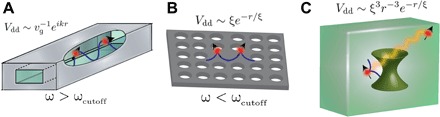
Here, r is the distance between interacting emitters, v_g is the group velocity of the waveguide mode with wave vector k, ω_cutoff is the cutoff frequency of the metallic waveguide mode or photonic crystal, and ξ is an interaction range. (A) When the transition frequencies of interacting atoms lie above the cutoff, they will have a sinusoidal-type interaction. (B) On the other hand, at the band edge of a photonic crystal, there occur interactions with a divergent strength and range. (C) Hyperbolic media exhibit fundamentally different Coulombic long-range interactions, which diverge for specific angular directions in the low-loss effective medium limit.

Here, we provide the first experimental demonstration of long-range dipole-dipole interactions in metamaterials consistent with the super-Coulombic theory recently proposed for hyperbolic media (11). We use many-body dipole-dipole interactions between quantum emitters mediated by a nanostructured hyperbolic metamaterial to show the marked increase of interactions compared to conventional media. We develop a first-principles numerical approach of many-body dipole-dipole interactions to compare the ideal super-Coulombic behavior in homogeneous hyperbolic media as opposed to a practical multilayer realization, which includes absorption, finite unit cell size, and few coupled metal-dielectric layers. Our work also provides a direct comparison between first-principles theory and an experiment of this modified long-range dipole-dipole interaction mediated by metamaterials.

Resonant dipole-dipole interactions (RDDI) in metamaterials with hyperbolic dispersion are fundamentally different from photonic crystal waveguides (2) or circuit QED waveguides (1). The unique RDDI properties of the hyperbolic medium (12), which is a homogeneous material with dielectric tensor ϵ = diag[ϵ_x, ϵ_x, ϵ_z] with ϵ_xϵ_z < 0, arises from the topology of the k surface of extraordinary waves (see the Supplementary Materials). It takes on a hyperboloidal relation ($({\mathit{k}}_{\mathit{x}}^2+{\mathit{k}}_{\mathit{y}}^2)/{\mathrm{ϵ}}_{\mathit{z}}-{\mathit{k}}_{\mathit{z}}^2/|{\mathrm{ϵ}}_{\mathit{x}}|={\mathrm{\omega }}^2/{\mathit{c}}^2={\mathit{k}}_0^2$) between wave vector (k = [k_x, k_y, k_z]) and frequency (ω) instead of the usual spherical form for conventional media. This k surface allows for giant interactions mediated by real and virtual hyperbolic polaritons (11) along the asymptotes of the hyperboloid when the radius vector joining the two emitters makes an angle ${\mathrm{\theta }}_{\mathrm{R}}\approx \text{arctan}\sqrt{-{\mathrm{ϵ}}_{\mathit{x}}/{\mathrm{ϵ}}_{\mathit{z}}}$ with respect to the optic axis (z axis). To illustrate the unique properties of the super-Coulombic interaction, we consider a hyperbolic medium where the permittivity along the optic axis is modeled as a free-electron Drude metal with plasma frequency ω_p, ${\mathrm{ϵ}}_{\mathit{z}}=1-{\mathrm{\omega }}_{\mathrm{p}}^2/{\mathrm{\omega }}^2$, while ϵ_x is equal to one (11), resulting in the RDDI for hyperbolic media (ω < ω_P)

$${\mathit{V}}_{\text{dd}}~\frac{{\mathrm{\omega }}^3{\mathit{e}}^{-\mathit{r}/\mathrm{\xi }}}{{\mathrm{\omega }}_{\mathrm{p}}^3\sqrt[3]{{\text{sin}}^2\mathrm{\theta }-{\mathrm{\omega }}^2/{\mathrm{\omega }}_{\mathrm{p}}^2}}\left(\frac{1}{{\mathit{r}}^3}\right)$$ (1)

where the interaction range is given by ${\mathrm{\xi }}^{-1}=\frac{{\mathrm{\omega }}_{\mathrm{p}}}{\mathit{c}}\sqrt{{\text{sin}}^2\mathrm{\theta }-{\mathrm{\omega }}^2/{\mathrm{\omega }}_{\mathrm{p}}^2}$ in this ideal limit. We emphasize that the super-Coulombic behavior occurs in both type 1 (ϵ_x > 0,ϵ_z < 0) and type 2 (ϵ_x < 0,ϵ_z > 0) hyperbolic media. In our experiments, we have used a type 2 hyperbolic metamaterial. This equation shows a marked similarity to the RDDI in band-edge cavities or cutoff waveguides outlining the origin of the singular super-Coulombic interaction strength and diverging spatial range. In stark contrast to the single-frequency divergence that occurs near a band edge, the anisotropy of the medium provides an additional degree of freedom (directional angle θ), allowing the interaction strength to diverge for a broad range of wavelengths. This result provides an interesting interpretation of the hyperbolic medium as a directionally dependent band-gap medium where certain directions (θ < θ_R, θ ∈ [0, π/2]) allow propagating modes with traditional Coulombic dipole-dipole interactions limited only to the near field, while other directions (θ > θ_R, θ ∈ [0, π/2]) only allow for exponentially decaying evanescent-type interactions. Exactly at the resonance angle θ_R (or cutoff angle) of propagating modes, there exists a diverging interaction strength similar to photonic crystals and waveguides. We further note that the RDDI in hyperbolic media contains a dominant Coulombic r⁻³ power law dependence consistent with three-dimensional (3D) band-gap media (13) as opposed to purely exponential decay or sinusoidal dependence (see Fig. 1). Thus, quantum emitters interacting along these special angular directions will have a Coulombic power law scaling irrespective of their physical separation (11, 14) curtailed only by material absorption. We also note that the 2D quasi-static (Coulombic) equation in the hyperbolic medium remarkably resembles a wave equation implying the extension of Coulombic near fields to infinity (11, 14). Figure 2A shows the point-to-point scaling of RDDI along the resonance angle for a hyperbolic medium with realistic loss compared to metal (Ag) and dielectric (SiO₂). These long-range Coulombic (nonradiative) interactions are fundamentally different from long-range radiative interactions (15) and interactions in plasmonic waveguides (16–18).

Fig. 2. Förster resonance energy transfer (FRET) as a probe for dipole-dipole interactions.

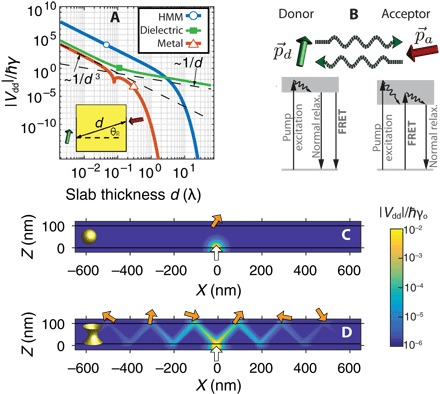
(A) The calculated vacuum fluctuation-induced dipole-dipole interaction potential for two molecules separated by a realistic (dissipative) slab of HMM, SiO₂, and Ag. γ_o is the free-space decay rate. The hyperbolic metamaterial (HMM) provides strong dipole-dipole interactions along the asymptotes of the resonance cone, which show a Coulombic near-field scaling (1/r³) even for distances comparable with the free-space wavelength—orders of magnitude stronger than conventional materials. The HMM dielectric constants are ϵ_x ≈ −4.2 + 0.2i, ϵ_z ≈ 5.4 + 0.01i. (B) FRET is used as a probe for long-range super-Coulombic RDDI. The donor atom’s radiative dipole transition is resonant with the acceptor absorption dipole transition. (C and D) The enhanced RDDI mediated by directional hyperbolic polaritons for a dipole located below a 100-nm slab of SiO₂ and HMM. The HMM allows a single dipole (white arrow, bottom) to interact with many physically separated acceptors (orange arrows, bright regions, top), giving rise to unique super-Coulombic enhancements for thin films of acceptors and donors.

RESULTS

The real part of the RDDI (Re(V_dd)) generally predicts a cooperative frequency shift, while the imaginary part (I m (V_dd)) predicts a cooperative decay rate between resonant atoms. Isolating these effects is quite difficult at room temperature due to inhomogeneous broadening and vibrational dephasing mechanisms that destroy coherence between atoms. Nevertheless, it is still possible to isolate dipole-dipole interactions at room temperature through the well-known FRET process (19). This type of dipole-dipole interaction is an energy transfer process that occurs when two distinct molecules with overlapping emission and absorption spectra are in the extreme near field (<10 nm apart). The FRET rate is dependent on the squared magnitude of the RDDI, Γ_ET = 2πℏ⁻¹|V_dd|²δ(ℏω_d − ℏω_a), thus providing a direct probe of the super-Coulombic dipole-dipole interaction (Fig. 2). This energy transfer provides an additional decay channel for the excited state of the donor, and here, we use this increased relaxation rate of the donor excited state as a distinct signature of FRET across a 100-nm metamaterial (Fig. 2, C and D). The broadband and nonresonant nature of hyperbolic dispersion (20, 21) allows us to observe the emergence of super-Coulombic interactions through FRET at room temperature and at optical frequencies. In the experiment, we choose the following as interacting FRET molecules: the organic dyes Alq3 (donor; peak emission, λ ≈ 523 nm) and R6G (acceptor; peak absorption, λ ≈ 525 nm) whose FRET radius we estimate to be R_o ≈ 5.1 ± 0.1 nm using their photoluminescence (PL) and absorption spectra (see section S2).

Extremely thin films (<2 nm) of Alq3 donor molecules are spin-cast onto glass substrates. On top of these dyes, we then fabricate a metal-dielectric thin-film implementation of a hyperbolic medium: electron beam evaporation of a multilayer stack of alternating silver/silicon dioxide layers (20 ± 2–nm–thick layers ≪ λ_Alq3 = 525 nm). The acceptor R6G dye molecules are also spun-cast on the metamaterial but physically separated from the donor molecules by the multilayer metal-dielectric metamaterial. Deviations from the effective medium theory (EMT) are expected, but ellipsometric transmission and reflection measurements confirm that hyperbolic dispersion is achieved within the entire bandwidth of the overlap between the donor emission and acceptor absorption spectra. The effective dielectric constants can be approximated by ϵ_x ≈ −4.2 + 0.2i, ϵ_z ≈ 5.4 + 0.01i at λ = 525 nm (22). This confirms the effective hyperbolic dispersion behavior essential to create super-Coulombic interaction pathways.

Figure 3A shows the comprehensive set of samples required to demonstrate super-Coulombic interactions in the metamaterial, not present in any conventional material. We isolate the role of the metamaterial on enhancing RDDI as opposed to its role in increasing two competing physical phenomena—the local photonic density of states (LDOS) and nonradiative quenching of donor molecules on top of the metal (23–25). This is achieved using a careful comparison between the donors with acceptors (hybrid; Fig. 3A, front row) and the donor-alone and acceptor-alone cases (Fig. 3A, middle and back rows). Along with the metamaterial, we fabricate Ag and SiO₂ control samples of equal thickness to the metamaterial (100 nm).

Fig. 3. Evidence of long-range dipole-dipole interactions across metamaterials.

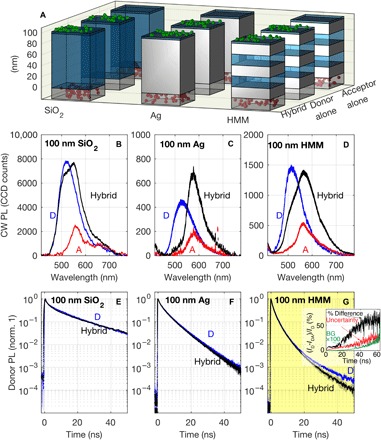
(A) The sample types used to isolate RDDI in various material systems (donors, Alq3, shown green). (B to D) The transmitted continuous-wave excitation PL spectra (CW PL) is shown for the donor and acceptor separated by dielectric, metal, and metamaterial. The spectra are in units of spectrometer charge-coupled-device (CCD) counts. We note that energy transfer is visible in all three material systems; that is, the donor-excited state is causing the acceptor to be excited and subsequently relax and emit a photon. This is concluded by noting an increased intensity of acceptor emission and a quenched donor emission when the emitters are placed in the hybrid geometry (black curve) relative to the donor-only (blue curve) and acceptor-only (red curve) control systems (see the Supplementary Materials for quantitative differential spectra). (E to G) The time-resolved donor fluorescence for donor-only (blue) and hybrid (black) samples are shown for the three material systems. For the donors/acceptors separated by 100 nm of SiO₂ or Ag (E and F), the hybrid decay traces reveal no additional lifetime reduction compared to the donor-only case, indicating no long-range RDDI. When the donor and acceptors are separated by a 100-nm Ag/SiO₂ multilayer metamaterial (G), we observe a marked excited-state lifetime reduction when the acceptor molecules are present, providing evidence of long-range super-Coulombic RDDI. The percentage change in the signal is plotted in the inset. It is seen that the signal is many SDs away from the uncertainty level and the background throughout the time trace. We emphasize that the net time integrated difference in counts is far greater, providing conclusive evidence of the emergence of super-Coulombic interactions.

To demonstrate evidence of energy transfer from donors to acceptors, we measure the steady-state fluorescence intensity, I, of the hybrid samples (denoted hybrid) in contrast to the control samples (donor alone and acceptor alone, denoted D and A, respectively). Figure 3 (B to D) shows the transmitted PL spectra of the control samples and the hybrid samples for the three types of material systems. The samples are optically pumped with steady-state fluence of ≈25 μW per 1 mm² from a 405-nm continuous wave laser. We note evidence of energy transfer from donors to acceptors in all three material systems. We conclude this by observing that when acceptors are present on the opposite side of the donors (hybrid, black curve), there is an increase in the acceptor emission intensity compared to acceptors alone (red curve). This is accompanied by a decrease in donor emission intensity (relative to donors alone, blue curve). The differential spectra (I_hybrid − I_D − I_A) obtained from Fig. 3D at constant pump intensity provides striking evidence of this energy transfer and is discussed in detail in the Supplementary Materials.

To gain insight into the nature of this energy transfer process, we use time-resolved emission kinetics of the Alq3 donor and isolate the additional increase to the donor relaxation rate with the presence of R6G acceptors across the metamaterial. Figure 3E compares the decay trace for the 100-nm SiO₂ film with and without acceptors. We denote these traces by D (blue data points) and Hybrid (black data points). We note that the introduction of acceptors to the far side of the SiO₂ film produces no change in the emission kinetics, despite the fact that the steady-state fluorescence indicates that there is energy transfer from donors to acceptors. This shows that the energy transfer mechanism is radiative, mediated by a photon emitted by the excited donor which propagates through the 100-nm SiO₂ film and is subsequently absorbed by the acceptor. The 100-nm Ag material system only causes the well-known decrease in lifetime of the donor lifetime due to the metallic environment and increased LDOS (26, 27). Similar to the SiO₂ thin film, this system also lacks strong long-range interactions since no additional decrease in lifetime is observed when the acceptors are introduced on the opposite side of the metal (28).

Figure 3G shows the fundamentally different emission kinetics of the donor in the HMM system. The donor-only sample shows a decreased excited-state lifetime relative to the pure Ag sample (Fig. 3F, blue). This is due to the enhanced optical density of photonic states in the near field of HMMs (20, 23). When acceptors are introduced on the opposite side of the HMM in the hybrid sample (black data points), we observe a marked additional reduction in the excited-state lifetime of the donor. This lifetime reduction offers proof of long-range metamaterial-enhanced dipole-dipole coupling of donors and acceptors with a physical separation distance of 100 nm. In the inset of Fig. 3G, we show the percent difference in the decay traces that arise after the introduction of the acceptor. Taking into account the dark count, laser intensity fluctuations, and sample fabrication variations, we plot the uncertainty level and also show the background PL of the metamaterial samples. It is seen that the signal due to the emergence of long-range RDDI behavior is consistently between two and three SDs away from the random noise in our experiment. Furthermore, it should be noted that the total time integrated difference in counts is significantly larger, providing evidence of long-range interactions. A full analysis of the systematic and random noise in our experiment is provided in the Supplementary Materials.

To elucidate the distance scaling law of dipole-dipole interactions mediated by metamaterials, we fabricate additional structures displaying varying strengths of RDDI owing to the different separation distances (20 and 60 nm) between donors and acceptors. We robustly quantify the effective FRET strength between the donors and acceptors using the harmonic mean of the measured decay rates of the donor emission kinetics with and without the presence of acceptors (see the Supplementary Materials) (19). If the observed decay traces I(t) are normalized to unity at time zero, then the integral of the trace over time yields the average excited-state lifetime, that is, ${\overline{\mathrm{\gamma }}}^{-1}=\overline{\mathrm{\tau }}=\int \mathit{d}\mathit{t}\mathit{I}(\mathit{t})$. Since we are in the weak coupling limit, the difference between the average decay rate of the donors with and without acceptors present yields the effective FRET rate of donors to acceptors: ${\overline{\mathrm{\Gamma }}}_{\text{ET}}={\overline{\mathrm{\gamma }}}_{\text{DA}}-{\overline{\mathrm{\gamma }}}_{\mathrm{D}}$. We have shown enhancements in the RDDI at two different distances between the acceptor and donor as compared to conventional media (metal or dielectric). The 20-nm silver layer is only used as a reference point to calibrate the difference in behavior between a conventional metal and metamaterial as the distance per number of layers grows.

DISCUSSION

The observed effective FRET rates and their scaling for the three separation distances between donor and acceptor molecules are shown in Fig. 4. To connect these data with theory, we have developed a rigorous theoretical framework of many-body dipole-dipole interactions, which allows for quantitative comparison of the metamaterial response in the ideal EMT limit and the practical absorptive-dispersive, finite-sized multilayer structure. The calculation uses many-dipole spatially integrated Green’s function for finite multilayer structures and homogeneous hyperbolic media. Using only physical quantities extracted independently from experiment (permittivity, layer thicknesses, FRET radius, donor decay rate, and acceptor concentration) and no fitting parameters, the many-body super-Coulombic interaction theory shows excellent agreement with experimentally observed FRET rates across the metamaterial (Fig. 4A). To understand whether these observations are consistent with the theory of super-Coulombic behavior for the specific metal-dielectric structure, one can use homogenization to compare results between the practical structure and the ideal effective medium limit. The enhancement of FRET due to the HMM is close to two orders of magnitude compared to the dielectric and one order of magnitude compared to the metal. We note that our simulations take into account the discrete nature of the metamaterial and that the sawtooth behavior of the RDDI enhancement is related to the influence of the metamaterial termination layer (metal or dielectric).

Fig. 4. Spatial scaling of long-range interactions.

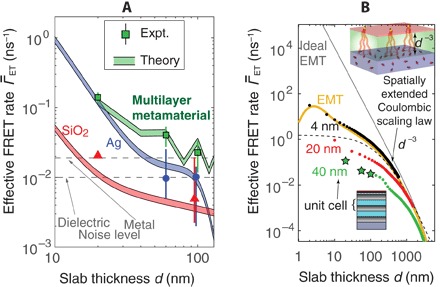
(A) Experimental confirmation of enhanced energy transfer rates due to the long-range dipole-dipole interactions in a hyperbolic metamaterial (green) compared to a silver film (blue) and a SiO₂ film (red). The noise levels are denoted by dashed curves, and the numerically calculated many-body dipole-dipole interaction curves are denoted by the colored bands (no free-fitting parameters). The theoretical predictions include 10% error bands accounting for uncertainty in the independently extracted physical parameters. (B) We now compare the ideal super-Coulombic behavior to the experimental observations. The curves show the numerically simulated spatial dependence of sheet-to-slab (2D sheet of donors and thin slab of acceptors) many-body dipole-dipole interactions demonstrating an enhanced FRET rate of the effective medium model (yellow) with d⁻³ power law dependence. Multilayer lattice structures with unit cell sizes of 40, 20, and 4 nm, respectively, are also shown exhibiting an extended spatial range with enhanced Coulombic interactions beyond the scale of a wavelength. The green stars correspond to the experimentally measured data. It is seen that the ideal EMT (yellow) has excellent agreement with the numerical simulations for 4-nm unit cell sizes. The same numerical simulations show excellent agreement with experimental data points for 40-nm unit cell sizes only limited by nanofabrication of ultrathin layers. The solid gray line shows the ideal limit obtained from Eq. 1 of adsorbed quantum emitters on a hyperbolic medium, whereas the dashed black line presents the analytical scaling law, taking into account the finite distance between the emitter from the metamaterial.

We now compare the ideal super-Coulombic interaction predicted by Eq. 1 and the regime of enhanced FRET rate observed in the experiment. We emphasize that the characteristic Coulombic scaling Γ_ET ~ r⁻⁶ only occurs for point-to-point interactions along the resonance angles. In contrast, for sheet-to-slab (2D sheet of donors and thin-film slab of acceptors) interactions, a many-body behavior starts manifesting since each donor molecule can interact with multiple acceptor molecules at the base of a conical region formed at the resonance angles. Using the FRET radius, concentration of dye molecules, PL and absorption spectra, collection optics, and beam size, we estimate a single donor to interact with approximately 16,000 acceptors. The characteristic scaling of Coulombic energy transfer in this many-dipole interacting limit is given by ${\mathrm{\Gamma }}_{\text{ET}}={\mathrm{\gamma }}_{\mathit{D}}{\mathit{c}}_{\mathrm{A}}{\int }_{\mathit{d}}^{\infty }\mathit{d}{\mathit{z}}_{\mathit{a}}\iint \mathrm{\rho }\mathit{\text{d}}\mathrm{\rho }\mathrm{\theta }{({\mathit{R}}_{\mathit{o}}/\mathit{r})}^6={\mathrm{\gamma }}_{\mathit{o}}{\mathit{c}}_{\mathrm{A}}\mathrm{\pi }{\mathit{R}}_{\mathit{o}}^6/6{\mathit{d}}^3~{\mathit{d}}^{-3}$, where d is the distance between the sheets and c_A is the concentration of acceptors (see the Supplementary Materials).

Motivated by the excellent agreement between theory and experiment (Fig. 4B, green stars and green dots), we compare the scaling law of interactions for the experimental realization of the metamaterial to the ideal EMT limit of super-Coulombic RDDI for adsorbed quantum emitters on a hyperbolic medium (light gray line). The yellow curve shows the EMT calculation of dipole-dipole interactions in hyperbolic media, whereas the black dots depict the practical multilayer metal-dielectric structure. As the unit cell size is decreased to 4 nm, a very strong agreement is noticed between EMT (yellow curve) and the multilayer system (black dots). We emphasize that the marked spatial extension of the Coulombic scaling law (Γ_ET ~ d⁻³) to beyond the wavelength scale (d > 500 nm) despite losses, dispersion, absorption, and finite unit cell size of the metamaterial can be observed directly in future experiments. Furthermore, the dashed black curve in Fig. 4B presents our analytical model of super-Coulombic FRET taking into account the finite distance between the emitter and metamaterial (z_a). This modified Coulombic scaling law shown in the figure as a dashed black curve takes into account the proximity effect and is given

$${\mathrm{\Gamma }}_{\text{ET}}~{(\mathit{d}\text{Re}[\sqrt{{\mathrm{ϵ}}_{\mathit{x}}/{\mathrm{ϵ}}_{\mathit{z}}}]+{\mathit{z}}_{\mathit{a}})}^{-3}$$ (2)

A strong agreement in the scaling law between EMT and multilayer simulations occurs when the unit cell size is significantly smaller than the molecule-interface separation distance (see the Supplementary Materials and Fig. 4B, dashed black curve). The spatial range of the long-range super-Coulombic interaction is ultimately curtailed by material absorption (ϵ″), and the resulting interaction range becomes ${\mathrm{\xi }}^{-1}=\frac{\mathrm{\omega }}{\mathit{c}}\sqrt{\frac{{\mathrm{ϵ}}_{\mathit{z}}^{″}|{\mathrm{ϵ}}_{\mathit{x}}^{\prime }|+{\mathrm{ϵ}}_{\mathit{z}}^{″}|{\mathrm{ϵ}}_{\mathit{x}}^{\prime }|}{|{\mathrm{ϵ}}_{\mathit{x}}^{\prime }|+|{\mathrm{ϵ}}_{\mathit{z}}^{\prime }|}}$.

We now explain how the agreement between theory and experimental results is consistent with the theory of super-Coulombic behavior. Equation 1 is derived for two interacting quantum emitters embedded inside homogeneous hyperbolic media in the ideal EMT limit using the Green’s tensor approach. The same Green’s function formalism has been adopted for many-body dipole-dipole interactions in the practical metal-dielectric thin multilayer realization of hyperbolic media, taking into account finite distance of emitters from the surface, finite unit cell size, absorption, dispersion, and few-layer behavior. It is seen that for 4-nm unit cell sizes, there is excellent agreement between the ideal theory and the many-body numerical simulations. The experiments function away from this ideal homogeneous limit since our current unit cell sizes are 40 nm limited by nanofabrication roughness effects. However, our experiment shows enhancement and agreement with the first-principles numerical simulations. The comparison with measured lifetime data includes no fitting parameters and only uses data obtained through experiments (detailed flowchart available in the Supplementary Materials). The long-range interaction is related to the emergence of directional resonance cones, which occur even for few layers but is not present for a single layer of thin-film silver (see the Supplementary Materials). We have shown enhancements in the RDDI at two different distances between the acceptor and donor as compared to conventional media (metal or dielectric). The 20-nm thin-film silver layer is only used as a control sample to calibrate the difference in behavior between a conventional metal and metamaterial as the number of layers increases. We emphasize that previous work in the field has shown the emergence of metamaterial behavior in the few-layer limit such as topological transitions and hyperlens (21, 23).

This metamaterial-mediated nonradiative Förster interaction should be contrasted with the previously reported superradiant lifetime change in quantum dots, which only showed a radiative interaction and V_dd ~ 1/R scaling at the comparable distance of 150 nm (29). Furthermore, two mesoscopic atomic clouds have shown Förster interaction at 40 μm (30). However, the transition wavelength is 1 cm, placing the experiment in the extreme near-field regime (d ≈ λ/250). For comparison, if similar mesoscopic atomic systems were interacting through a hyperbolic metamaterial functioning at ω = 30 GHz ≡ 1 cm, then the interaction distance would be a centimeter.

In conclusion, we have demonstrated the emergence of long-range dipole-dipole interactions mediated by metamaterials curtailed only by material absorption and finite unit cell size effects. A rigorous analysis of the noise and systematic uncertainties in the experiment shows that our observed super-Coulombic effect is three times stronger than our experimental uncertainties. These interactions fundamentally extend the nonradiative near fields as opposed to engineering radiative interactions, and the ideal limit can be achieved through lower unit cell sizes or moving to homogeneous hyperbolic media such as hexagonal boron nitride. We envision that super-Coulombic interactions can affect deterministic entanglement creation between remote emitters (31) and quantum coherence (32, 33) in metamaterial-mediated photosynthetic energy transfer, lead to many-dipole interactive states in metamaterials (9), increase the range of biomolecular FRET rulers and FRET imaging systems (34), and accelerate progress toward the long-standing goal of strongly coupled quantum systems at room temperature (V_dd > k_BT_room).

MATERIALS AND METHODS

Time-resolved fluorescence emission was measured via time-correlated single-photon counting (TCSPC). The samples were pumped with a 25- to 40-fs laser pulse centered at 400 nm, detuned from the acceptor absorption edge of the donor emission band; the subsequent fluorescence emission was transmitted through a band-pass filter centered at the blue edge of the donor emission band and is measured by a silicon-based single-photon avalanche diode. The emission kinetics were inferred via TCSPC. We took into account imperfections of the nanofabrication by averaging the measured decay traces from 10 different physical areas of a given sample. From this procedure, we calculated a mean decay trace and its corresponding variation (SD of the 10 decay traces). The Supplementary Materials details our analysis of the random and systematic noise in our experiments (11, 14, 19, 22, 23, 35–46). Thin-film metamaterial sample fabrication was performed using electron beam evaporation of metal (silver) and dielectric (silica). The acceptor and donor molecules were spun-cast in PMMA [poly(methyl methacrylate)] solution to obtain ultrathin dye-doped uniform layers.

A detailed theory of dipole-dipole interactions in practical metamaterials taking into account experimental non-idealities was developed specifically for comparison with experimental observations. The ideal theory of super-Coulombic dipole-dipole interactions applies to the case of two quantum emitters embedded inside homogeneous effective medium hyperbolic media. Here, we consider a collection of emitters, not embedded, in the near field of a practical metal-dielectric superlattice, taking into account absorption, dispersion, and finite unit cell size. The random orientations of the emitters are taken into account by 3D averaging of dipole moments. There are no fitting parameters in the theory, and critical physical variables for the calculation such as quantum efficiency of the dye molecules and concentration were obtained from experimental measurements. The optical constants (dielectric permittivity of constituent layers) and thickness of the fabricated thin film layers were obtained by ellipsometry.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/4/10/eaar5278/DC1

Section S1. Theory of resonant dipole-dipole interactions in hyperbolic media

Section S2. Experimental verification of super-Coloumbic dipole-dipole interactions

Fig. S1. Flowchart of comparison between experiment and theory.

Fig. S2. Long-distance sheet-to-sheet super-Coulombic dipole-dipole interactions in a hyperbolic medium.

Fig. S3. Interplay of length scales causing deviations from EMT.

Fig. S4. Experimental apparatus for obtaining time-resolved fluorescence.

Fig. S5. Collecting fluorescence system and acceptor/donor plots.

Fig. S6. Fabrication process flow for multilayer metamaterials displaying super-Coulombic interactions.

Fig. S7. Background fluorescence.

Fig. S8. Donor lifetime measurements.

Fig. S9. Raw donor lifetime traces and extracted measurements.

Reference (47)