Reproducible automated breast density measure with no ionizing radiation using fat-water decomposition MRI

Abstract

BACKGROUND

Increased breast density is a significant independent risk factor for breast cancer, and recent studies show that this risk is modifiable. Hence, breast density measures sensitive to small changes are desired.

PURPOSE

Utilizing fat-water decomposition MRI, we propose an automated, reproducible breast density measurement, which is non-ionizing and directly comparable to mammographic density (MD).

STUDY TYPE

Retrospective study.

POPULATION

The study included two sample sets of breast cancer patients enrolled in a clinical trial, for concordance analysis with MD (40 patients) and reproducibility analysis (10 patients).

FIELD STRENGTH/SEQUENCE

The majority of MRI scans (59 scans) were performed on a 1.5T GE Signa scanner using radial IDEAL-GRASE sequence, while the remaining (7 scans) were performed on a 3T Siemens Skyra using 3D Cartesian 6-echo GRE sequence with a similar fat-water separation technique.

ASSESSMENT

After automated breast segmentation, breast density was calculated using FraGW, a new measure developed to reliably reflect the amount of fibroglandular tissue and total water content in the entire breast. Based on its concordance with MD, FraGW was calibrated to MR-based breast density (MRD) to be comparable to MD. A previous breast density measurement, Fra80—the ratio of breast voxels with <80% fat fraction—was also calculated for comparison with FraGW.

STATISTICAL TESTS

Pearson correlation was performed between MD (reference standard) and FraGW (and Fra80). Test-retest reproducibility of MRD was evaluated using the difference between test-retest measures (Δ_1–2) and intra-class correlation coefficient (ICC).

RESULTS

Both FraGW and Fra80 were strongly correlated with MD (Pearson ρ: 0.96 v.s. 0.90, both p<0.0001). MRD converted from FraGW showed higher test-retest reproducibility (Δ_1–2 variation: 1.1%±1.2%; ICC: 0.99) compared to MD itself (literature intrareader ICC ≤0.96) and Fra80.

DATA CONCLUSION

The proposed MRD is directly comparable with MD and highly reproducible, which enables the early detection of small breast density changes and treatment response.

Introduction

Breast cancer is the most commonly diagnosed cancer and second most common cause of cancer death among women in the U.S (1). Higher mammographic density (MD) has been consistently associated with elevated breast cancer risk (2–5). Consistent with this risk relationship, breast cancer patients with high MD have been reported to have a two-fold greater risk of developing a new primary contralateral breast cancer compared to low MD (6). In a recent study of 18,437 breast cancer cases and 184,309 controls, having extremely dense breasts was identified as the most prevalent risk factor for breast cancer (3), with the population attributable risk proportion of ~39% for premenopausal women and ~26% for postmenopausal women. These authors concluded that a sizable fraction of breast cancer could be prevented by decreasing MD. Based on this positive association between MD and breast cancer, MD has been suggested as an intermediate risk biomarker for breast cancer that is potentially modifiable (7–11) such as by tamoxifen and other pharmaceuticals.

As such, accurate breast density estimation has emerged as a priority for assessing breast cancer risk. Breast tissue is composed of adipose and fibroglandular tissue where MD is a radiologic measure of the proportion of these two types of tissues. Dense breasts have more fibroglandular tissue and less fatty tissue (12). Currently, MD is obtained by exposing a compressed breast to low dose x-rays, which leads to several limitations. Slight differences in x-ray exposure calibration and the degree of compression can induce high variation in MD (13) with low and wide intrareader reliability [intra-class correlation coefficient (ICC): 0.88~0.96] (14–16). Further, even using 3D tomosynthesis (17), the images are still acquired from a compressed breast at limited angles which causes overlapping of the breast tissue and impacts the accuracy of MD (18). These factors, and the underlying concerns regarding the undesirable exposure to ionizing radiation, limit mammography for accurate and sensitive measurement of small changes in breast density over short periods of time, as would be desirable in intervention studies aimed at reducing breast density.

Magnetic resonance imaging (MRI) provides a safer alternative for breast density estimation of the entire breast volume, as it is free of ionizing radiation. Most current studies used standard T1-weighted MRI for breast density evaluation (13,19–22). However, none are considered to actually represent true breast tissue composition (23). In contrast, fat-water decomposition MRI is particularly useful because of its ability to separate the MRI signals from protons in water and in fat using a Dixon-like approach (24–26). Recently, a technique called “iterative decomposition of water and fat with echo asymmetric and least-squares estimation” (IDEAL) (27,28) incorporated the asymmetric acquisition of multi-echo data with an iterative least-squares decomposition algorithm for fat-water separation with optimized noise performance. IDEAL has been applied to the gradient- and spin-echo (GRASE) technique to reduce scan time (29). The radial IDEAL-GRASE technique (30) combines IDEAL-GRASE with radial data acquisition to reduce motion effects. With this MRI acquisition technique, fat-only images and water-only images can be quickly reconstructed from multi-echo data by applying a signal model to the phase evolution at different echo times.

Breast segmentation is the first and an important step for accurate and reproducible BD estimation. The conventional cumbersome and bias-prone manually drawn regions-of-interest (ROIs) need to be improved using an automated segmentation method (9,31–34). In addition, the consistency between manual and automated segmentation needs to be validated not only by comparing the breast ROIs but also for the purpose of assessing breast density.

Based on fat-water decomposition MRI, previous publications have studied breast density measurements using thresholding methods. Tagliafico et al. (23) used a semi-automated technique where the radiologists adjusted the intensity threshold for determining the dense region, and the breast density measurement was calculated as the percentage of the dense region in the whole breast volume. Thomson et al. (9,35) established a breast density measurement termed Fra80, which was representative of the ratio of breast voxels with < 80% apparent fat fraction (the ratio of the fat signal to the sum of the fat and water signals). This method used a hard threshold of 80% in the fat fraction map to identify the dense breast region. Wengert et al. (34,36) recently developed an automated approach by assigning each voxel to either fatty tissue or fibroglandular tissue based on its intensity in the fat-only image and water-only image, and the breast density was measured by the percentage of the fibroglandular tissue volume within the entire breast. This technique, effectively, is also a thresholding method with a self-adjusted threshold. All these previous thresholding methods, however, have several limitations: Using a threshold to determine whether the breast voxel is dense (fibroglandular) tissue causes the breast density quantification to be susceptible to partial volume effect. Consequently, this type of technique may have difficulty detecting changes of small structures in the breast tissue composition. In addition, the chemical-shift based Dixon fat-water decomposition MRI technique has intrinsic limitations due to the imperfection of the signal model, which causes fat-water signal intensity bias and fat-water signal shine-through. Meanwhile, due to the differences in proton density between fat and water and the fact that fat signal is stronger than water in gradient echo MRI images, the amount of fat would be misestimated if no correction is performed. All three methods mentioned above did not calibrate this fat-water signal intensity bias, leading to potentially inaccurate breast density estimations. Furthermore and more importantly, MD is still the most widely used breast density measurement in clinical practice. Previous MRI-derived methods were not directly comparable to the existing MD (23,35) and, in fact, a significant difference was shown (34), which limited their applications in clinical breast cancer studies.

The purpose of this study is to develop a new automated breast density measurement based on fat-water decomposition MRI, which overcomes the limitations of the previous methods as described above. One of the previous thresholding measurements, Fra80, was calculated for comparison.

Materials and Methods

Study Population

This study used de-identified data from a completed clinical trial (clinical trials number: NCT01391689, from February 2011 to July 2016) which was approved by the Institutional Review Board. The study sample included two sample sets (see Table 1) of pre- and post-menopausal women who were enrolled in the randomized, placebo-controlled trial, receiving tamoxifen as either adjuvant therapy after primary treatment of early-stage breast cancer (stage 0–III) or primary chemoprevention due to the high risk of breast cancer. Sample 1 included 40 patients receiving digital mammography within 6 months from the data of MRI scan and with MD change ≤10% between baseline and follow-up mammograms (1–2 years apart). The purpose of Sample 1 was to evaluate the concordance of MRI-derived breast density with MD. Sample 2 included 26 test-retest scans from 10 patients (7 patients with test-retest at 3 time-points, 2 with test-retest at 2 time-points, 1 with test-retest at 1 time-point; for the same patient, scans at different time-points are approximately 6 months apart), which was used to assess the test-retest reproducibility of the breast density measures based on fat-water decomposition MRI. For each repeated scan, the patient completely left the scanner and was immediately repositioned in the scanner, re-registered and re-localized by the same technician. Breasts containing implants or treated with radiation therapy in both samples were excluded from the study. Only the unaffected breasts (without cancer) were analyzed.

Table 1.

Summary characteristics of the samples used in the different analysis.

Study samples	Sample 1	Sample 2
Purpose	To evaluate the concordance by comparing with MDa	To assess the test-retest reproducibility
Inclusion criteria	Patients underwent digital mammography within 6 months from the date of MRI scan	Patients received test-retest scans (For each test-retest scan, the patient left the scanner and was immediately repositioned in the scanner, re-registered and re-localized)
Exclusion criteria for the analysis	The change of MD was larger than 10% between baseline and follow-up mammograms (1–2 years apart).b	n/a
Number of patients (age)	n=40 (age mean ± SD: 56.1 ± 8.4 years)	n=10 (age mean ± SD: 56.4 ± 10.4 years); 7 with test-retest at 3 time-points, 2 with test-retest at 2 time-points, 1 with test-retest at 1 time-point; for the same patient, scans are 6 months apart
Number of scans	40 (35 from GE scanner, 5 from Siemens scanner)	26 × 2 (24 from GE scanner, 2 from Siemens scanner)
Number of unaffected breasts	42 (both breasts of 2 patients from GE scanner were unaffected)	26 × 2 (all patients had one unaffected breast)

^aMD: mammographic density

^bThis is to exclude patients with large breast density fluctuations

MR Imaging Protocol

As demonstrated in Table 1, the majority of MRI scans in both Sample 1 and 2 were performed on a 1.5T GE Signa NV-CV/i scanner with an 8 channel breast coil (GE HD Breast) using the radial IDEAL-GRASE sequence in the axial orientation with acquisition parameters: 19 slices, acquisition matrix 256×256, pixel size = 1.33×1.33 mm², slice thickness/gapping = 7mm/1mm, 8 spin echoes with 4 gradient echoes per spin echo, 1 average, repetition time (TR) = 6s, acquisition time = 198s, bandwidth = ±125kHz. A saturation band was placed on the heart to reduce motion-induced image artifacts. The remaining MRI scans were performed on a 3T Siemens Skyra with a 16 channel breast coil (Sentinel) using a 3D Cartesian 6-echo gradient echo pulse sequence. The following acquisition parameters were used: 48 slices, acquisition matrix 256×152 (80% phase sampling), pixel size = 1.63×1.63 mm², slice thickness/gapping = 4mm/0mm, flip angle = 6°, TR = 9.67ms, 6 echoes with echo time (TE) = 1.18, 2.38, 4.76, 5.94, 7.10, 8.26ms, 1 average, acquisition time = 24s, bandwidth = 1220Hz/pixel, a saturation band was placed on the heart.

MR Imaging Processing

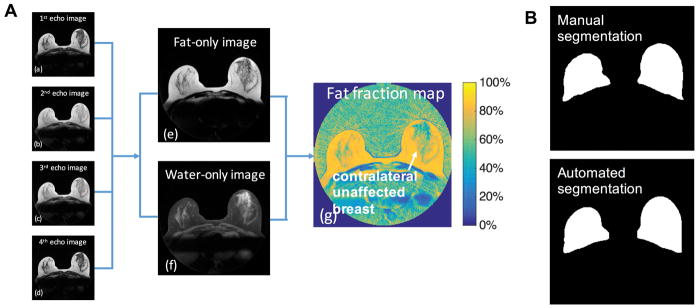
For images acquired on the GE scanner, IDEAL fat-water separation was performed using a Multi-mask Multi-seed Free Growing algorithm (37). For images acquired on the Siemens scanner, a similar fat-water separation technique with T2* correction was performed with multipeak (38). The fat-water separation was processed using in-house software written in Matlab to ensure long-term compatibility, which generates the fat-only images, water-only images and fat fraction maps (reflecting the relative percentage amount of fat signal in each voxel) of the entire breast volume. Images of a breast slice collected on the GE scanner are shown in Figure 1A.

Figure 1.

Derivation of the fat fraction map from data acquired using the radial IDEAL-GRASE technique and the breast segmentation results. A, (a)–(d) Images obtained from data acquired with each of the 4 gradients echoes of the radial IDEAL-GRASE sequence and the calculated (e) fat-only image, (f) water-only image and (g) fat fraction map (calculated voxel-wise as the ratio of the fat signal to the sum of the fat and water signals). B, the corresponding manual, and automated breast segmentation results. The average Dice index was 0.9121 with a standard deviation of 0.0306 based on the data from Sample 1.

Breast Segmentation

A fully automated breast segmentation (39) was applied to all scans. This automated technique is similar to the method of Rosado-Toro J, et al (31), where k-means++ and dynamic programming were used to identify the breast boundary by taking advantage of the different tissue contrasts in the fat-only and water-only images [Figure 1A(e) and (f)]. A 3D regularization was performed with a 3D order-statistic filtering (40) to smooth the breast mask and eliminate the nipple region, which is an improvement over the previous method (31). See Appendix 1 for details of the automated breast segmentation method. Manual ROIs were drawn (20–35 minutes per volume) according to the manual tracing protocol in the study by Rosado-Toro J, et al (31). The automated breast segmentation was quantitatively examined against manual ROI drawings by Dice index using the data from Sample 1 (41), which measures the similarity for two image segmentation results, and was further validated by a task-based comparison on the reproducibility of the breast density measures using the data from Sample 2.

Fat-water Decomposition MRI-based Breast Density Measures

Fra80

Fra80 (9,35) was a previously proposed MRI-based breast density measure calculated as the ratio of breast voxels with < 80% apparent fat fraction for the data collected on the GE scanner as in the previous study. We chose Fra80 to be the representative method of the previous thresholding-based breast density measurements to compare with our proposed method. Fra80 uses 80% as the threshold on apparent fat fraction maps to quantify the proportional amount of “dense” tissues in the breast. Due to scanner hardware and acquisition sequence differences, the data collected on the Siemens scanner were fit to a different threshold that was matched to the GE Fra80 using data from five volunteers whose images were acquired on both the GE and Siemens scanners on the same day.

FraGW

Because MD depends on both the amount of fibroglandular tissue and its distribution, we propose a new MRI-based breast density measure that accounts for both: FraGW = (FraGland + FraWater).

FraGland is the volumetric fraction of fibroglandular tissues present in the breast, which is a measure representing the distribution of fibroglandular tissues. See Appendix 2 for details.

FraWater is a measure quantifying the amount of water signal in the breast (vs. fat signal), which is a measure of the amount of fibroglandular tissues. Due to the limitation of IDEAL-GRASE, the inaccurate separation occurred with the residual fat signal appearing in water images. Here, the apparent fat fraction maps were calibrated to reflect their true volume fraction using a linear signal model.

For each pixel in the breast region,

$$\{\begin{array}{c}{\mathrm{S}}_{\text{fat}}={\text{aV}}_{\text{fat}}+{\text{bV}}_{\text{water}}\\ {\mathrm{S}}_{\text{water}}={\text{cV}}_{\text{fat}}+{\text{dV}}_{\text{water}}\end{array},$$ [1]

where S_fat is the fat signal intensity, S_water is the water signal intensity, V_fat is the fat volume, and V_water is the water volume. Four correction factors a, b, c, and d were solved based on the image intensities in “pure” fat (subcutaneous fat) and “pure” water regions (muscle). See Appendix 2 for details of the linear correction.

Mammographic Density (MD) measures

MD was used as the reference standard as it is currently the accepted measure of breast density. Craniocaudal views of mammograms were obtained during the study for breast density analysis using a previously published method (42,43). No personal identifiers were contained in the digital mammograms. MD was measured using a computer-assisted thresholding software called Cumulus (42). All mammograms for each patient were assessed during the same session. Based on this interactive software, the reader selected a first threshold value (grayscale on the screen) to distinguish the breast region from the dark background and a second threshold value to identify the edges of the mammographic dense areas within the breast outline. The total breast area and the dense area were measured by the number of pixels in the two areas, and MD for each breast was the percent density calculated as the ratio of dense to total breast area. Quality control was performed using 27 images assessed in duplicate readings of the same radiologist; the intrareader reliability (measured by Spearman correlation coefficients) for total breast area, dense breast area, and MD were 0.99, 0.96, and 0.92, respectively.

Statistical Analysis

Concordance with MD (reference standard)

To test the concordance of Fra80 and FraGW, Pearson correlation analysis was performed to compare Fra80 or FraGW and MD using Sample 1. Further, based on their correlation relationships, both Fra80 and FraGW measures were converted to an “MR-based breast density” (MRD) using a conversion function y = ax^b. To evaluate the concordance of MRD derived from FraGW and Fra80, the root mean square errors (RMSEs) of leave-one-out cross-validation were calculated respectively.

Reproducibility

Based on the 26 repeated scans in Sample 2, the Δ_1–2 values, calculated as the difference between the test and retest measures, were generated to represent the within-subject discrepancy. Test-retest reproducibility was evaluated statistically using the mean of |Δ_1–2| and standard deviation of Δ_1–2 and ICC analyses in Matlab. ICC (44) was performed on the logarithm of the Fra80 and FraGW. The same test-retest analyses were performed using the converted MRD, to determine if these converted MRD can be directly compared with MD for use in clinical practice.

Results

Imaging Processing

Figure 1B shows that the manual and automated segmentation have excellent agreement visually. Based on the data from Sample 1, the average Dice index between the manual and automated ROIs was 0.91 with a standard deviation of 0.03. Our automated breast segmentation was further validated on the reproducibility of Fra80 and FraGW to objectively compare the manual and automated segmentation (task-based comparison) using Sample 2 as discussed in the next section (Table 2).

Table 2.

Concordance and Reproducibility of the Fra80 and FraGW.

Breast segmentation fat-water decomposition MRI-based breast density		Manual segmentation		Automated segmentation
		Fra80	FraGW	Fra80	FraGW
Pearson correlation coefficient with MDc (* P-values < 0.0001)a		R= 0.88*	R=0.94*	R= 0.90*	R=0.96*
Test-retest reproducibilityb	mean |Δ1–2|	0.0231	0.0149	0.0174	0.0130
	standard deviation Δ1–2	0.0282	0.0186	0.0214	0.0146
	dynamic range	0.0809~ 0.6483	0.0695~ 0.6896	0.0902~ 0.6601	0.0735~ 0.6696
	Mean |Δ1–2|/ dynamic range	4.07%	2.40%	3.05%	2.18%
	ICCd [95% confidence interval]	0.9653 [0.9251, 0.9842]	0.9846 [0.9662, 0.9930]	0.9870 [0.9715, 0.9941]	0.9901 [0.9783, 0.9955]

^acorrelation analysis was performed using Sample 1

^btest-retest analysis was performed using Sample 2.

^cMD: mammographic density

^dICC: intra-class correlation coefficient

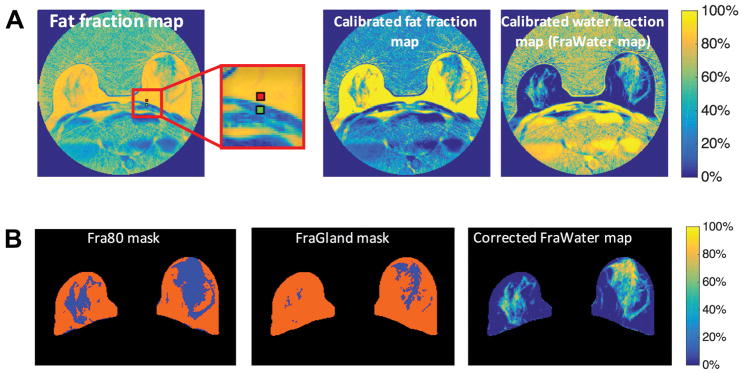
To obtain FraWater for the proposed FraGW measure, the calibration procedure was performed as mentioned in materials and Methods. For the same breast slice shown in Figure 1, the apparent fat fraction map and the corresponding calibrated fat fraction map and the calibrated FraWater map are shown in Figure 2A. The fat fraction in the subcutaneous fat region increased from 86% to 100% after correction, and fat fraction in the muscle region decreased from 17% to 2%. Figure 2B shows the Fra80 mask, FraGland mask, and corrected FraWater map. The Fra80 mask shows the proportion of the voxels with <80% fat fraction within the breast. The FraGland mask captures the amount of the voxels with predominant fibroglandular tissues, while the corrected FraWater mask provides the true volume fraction of the water signals in the entire breast after correcting the signal bias.

Figure 2.

Fat-water decomposition MRI-based breast density estimation. A, correction for the signal intensity bias to calculate FraWater, the original fat fraction map (left), and the corresponding calibrated fat fraction map (middle) and calibrated FraWater map (right). The red and green regions in the original fat fraction map (left) represent the subcutaneous fat and muscle regions used for calibration, respectively. B, breast density measures. Fra80 mask (left), FraGland mask (middle), and FraWater map after correction for fat-water signal contamination (right). Blue regions in Fra80 mask (left) and FraGland mask (middle) indicate the dense areas with <80% fat fraction and the fibroglandular tissue, respectively.

Concordance of FraGW with MD and Reproducibility

A total of 42 unaffected breasts without prior surgery were identified from 40 patients (both breasts of 2 patients were unaffected) in Sample 1. Table 2 shows the concordance and reproducibility analyses of Fra80 and FraGW based on manual and automated segmentation algorithms. As shown, based on the data from Sample1, both Fra80 and FraGW were strongly correlated with MD, with FraGW having a stronger correlation using automated breast segmentation (Pearson correlation coefficient = 0.96, p-value < 0.0001). Based on 26 repeated scans in Sample 2 (multiple test-retest scans from the same patients were treated as independent scans), both Fra80 and FraGW exhibit superior test-retest reproducibility (both ICCs > 0.985 using automated breast segmentation) compared to MD values from the literature (reported intrareader ICC <=0.96) (14–16). FraGW was superior to Fra80 in all measures tested. In addition, our automated breast segmentation protocol was associated with more concordant and reproducible breast density estimations compared to the labor-intense manual segmentation method.

MR-based breast density (MRD)

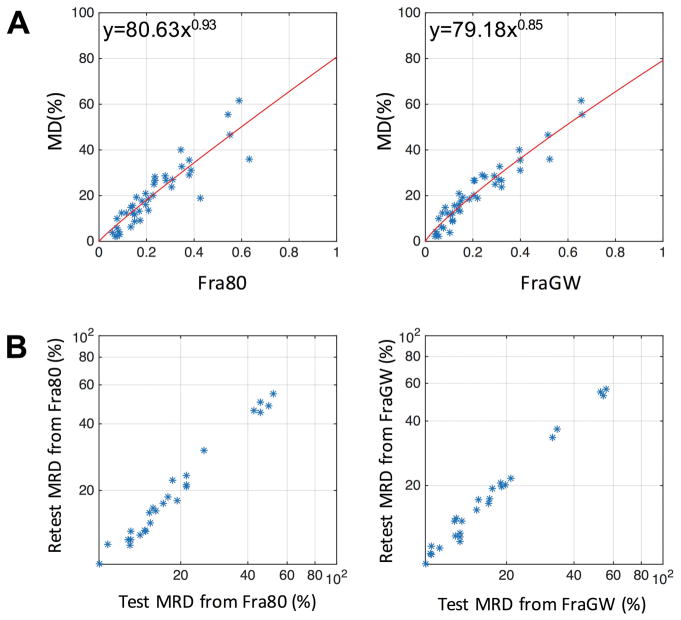
Figure 3A illustrates the correlation between MD and Fra80, MD and FraGW, respectively, of Sample 1 using automated breast segmentation method, with the data points fitted to exponential function y = ax^b as the calibration curve. RMSEs of the conversion based on leave-one-out cross-validation of Fra80 and FraGW were 6.64% and 4.17%, respectively. Using the calibration curves in Figure 3A, both Fra80 and FraGW were calibrated to MRD, to be directly comparable to MD. Using Sample 2, Figure 3B and Table 3 demonstrate the test-retest reproducibility of the converted MRD from Fra80 and FraGW. The MRD converted from our proposed FraGW method produced more reproducible breast density measurements with minimal test-retest variation (1.2%) and high ICC (0.99).

Figure 3. Concordance and test-retest reproducibility assessment.

A, correlation plot between MD and Fra80 (left) and FraGW (right) based on the automated segmentation. The statistics are shown in Table 2. The red line represents the fitted calibration curve. B, test-retest reproducibility plot of MRD measures converted from Fra80 (left) and FraGW (right). The statistics are shown in Table 3.

Table 3. Reproducibility analyses of the MRD measures converted from Fra80 and FraGW.

based on automated breast segmentation.

MRD converted from		Fra80	FraGW
Test-retest reproducibility	mean |Δ1–2|	1.43%	1.10%
	standard deviation Δ1–2	1.73%	1.20%
	ICCa [95% confidence interval] (logarithm)	0.9870 [0.9715,0.9941]	0.9901 [0.9783,0.9955]

^aICC: intra-class correlation coefficient

Discussion

In this work, we offer a new MRI-based breast density measure that has a superior concordance with MD and test-retest reproducibility compared to the previously published thresholding measure, Fra80. Further, we develop a fully automated breast segmentation protocol that yields more concordant and reproducible breast density measurements than manual segmentation. We also correct the fat-water signal intensity bias due to the intrinsic limitation of the fat-water decomposition MRI technique, and convert our method to an MRI-based breast density measurement, MRD, which is directly compared to MD obtained by mammography. In total, this non-contrast MRI method requires less than 5 minutes of scan time, avoids ionizing radiation, and provides more robust measurements of breast density compared to mammographically determined values, enabling the detection of individual breast density changes for clinical trials and treatment response assessment.

Breast density has been proposed as a risk biomarker and an intermediate surrogate biomarker for assessing strategies aimed at reducing breast cancer risk including determining the efficacy of hormone-modulating drugs for breast cancer prevention (7–11). In the IBIS-II Breast Cancer Chemoprevention Trial, a ≥10% decrease in MD after 12–18 months of tamoxifen use was predictive of clinical benefit, especially in younger, premenopausal women with baseline higher MD (45). In contrast, several attempts to demonstrate an effect of aromatase inhibitors on MD have failed. This may reflect the low sensitivity of MD to the smaller breast density changes in postmenopausal women who receive aromatase inhibitors or may indicate that the anti-cancer benefit of aromatase inhibitors is independent of an effect on breast density. Thus, the ability to detect small changes in breast density in response to therapeutic interventions and at earlier time points is highly desirable and may require more sensitive methods. The ability to do so with repeated measures and without ionizing radiation provides an opportunity to identify non- or poor-responders early for dose modification or agent change, as well as to encourage drug adherence for responders.

The proposed MRD measurement derived from FraGW overcomes some of the limitations of MD and outperforms a representative previously published MRI-derived measurement of breast density based on thresholding methods, Fra80. FraGW is more strongly correlated with MD, with superior reproducibility compared to Fra80. In addition, based on the calibration curves of FraGW with MD (Figure 3A), MRD determined with FraGW enables a direct comparison to MD, achieves a 31% smaller test-retest standard deviation compared to that of Fra80 (1.20% v.s. 1.73%, Table 3) and an extremely high ICC of 0.99. Note that this calculation was based on 26 test-retest scans from 10 patients and might introduce biases to the result, however, the comparison is still valid since both measures were derived using the same data sets. Also note that in the quality control mentioned in the Materials and Methods, the intrareader correlation coefficient of MD was only 0.92. It is noteworthy to point out that MD test-retest difference is often > 4% (14–16). The improved concordance and reproducibility of breast density measurements presented in this work may allow clinicians to track changes in breast density as small as 1.2%. Further research is warranted to investigate if this enhanced quantitative concordance can be employed in clinical trials to guide treatment response assessments more quickly and drive chemoprevention strategies.

This study also exhibits other, methodological strengths compared with the previously published studies that developed fat-water decomposition MRI based breast density measurements (9,23,34–36). First, previous studies lacked the validation of their semi- or fully-automated breast segmentation against ground truth manual segmentation. In our method, we quantitatively validate our fully automated breast segmentation with manual segmentation using Dice index; moreover, we demonstrate that automated segmentation leads to more reproducible breast density measures. Second, as mentioned in the Introduction, previous thresholding methods, including Fra80, simply measured the amount of dense or fibroglandular breast tissue by assigning each voxel to a single class. This could be a potential limitation as the partial volume effect would influence the accuracy of their breast density estimation. In comparison, we quantify breast density based on the fraction of fibroglandular tissue and actual water content in each voxel after correcting the fat-water signal bias, enabling a more reliable estimation. Third, the previous breast density measurements were not directly comparable with MD, and Wengert et al. (34,36) along with other previous studies based on T1-weighted MRI (19–21) showed that their MRI-derived breast density measurements were systematically lower than MD. However, MD is still the most widely accepted method for breast density evaluation in clinical practice and clinical research, and a large number of studies reported their findings using MD, including clinical trials. In this study, we calibrate our FraGW to an MRD measure, which is directly comparable to MD. This “backward compatibility” is another important strength of our measurement as it is much easier for clinicians to use and for patients to understand, especially when comparing with their previous MD and interpreting cancer risk associated breast density.

A limitation of this work is that the range of MRD in Sample 2 individuals with test-retest scans was not as broad as the distribution of individuals in Sample 1 used for correlation analysis (Figure 3A). Also, MR imaging processing is currently dependent on our in-house software, which limits the potential impact of MRD for research and clinical application; this is further limited by the fact that our work was conducted on two MRI scanners and on a cancer patient population. Further studies are needed to validate this new MRD measure on a larger sample including more women with no diagnosis of breast cancer for primary prevention, and across breast density distributions, scanners, centers, vendors, and field strengths. In addition, a true gold standard for breast density is lacking in this study, and the use of MD for this purpose could be controversial. Previous studies (36,46) developed anthropomorphic breast phantoms that can be used as the ground truth for breast density assessment. However, the similarity of these phantoms to real human breasts with more complex tissue composition needs to be further investigated. As MD is currently the most widely used method for breast density quantification in clinical practice, it is reasonable and potentially more relevant to use MD as a reference standard in this study. The data shown in this work prove that MRD derived from FraGW is superior to MD in terms of reproducibility, as discussed before.

In conclusion, the proposed automated MRI-based breast density measure derived from FraGW, which quantifies the entire fibroglandular and water content of the breast, is more reliable than the previously published MRI-derived method, Fra80, and is superior to MD. The next step is to apply this method in longitudinal studies to assess the detection of small changes in breast density. This will be useful for evaluating the efficacy of hormonal therapy or other chemoprevention strategies that mediate the anti-cancer actions through effects on breast density.

Abbreviations Key

GRASE

gradient- and spin-echo

ICC

intra-class correlation coefficient

IDEAL

iterative decomposition of water and fat with echo asymmetric and least-squares estimation

MD

mammographic density

MRD

MR-based breast density

MRI

magnetic resonance imaging

RMSE

root mean square error

ROI

region-of-interests

TE

echo time

TR

repetition time

Appendix 1: Fully Automated Breast Segmentation

Breast segmentation is the first and very critical step for accurate and reproducible BD estimation. The automated segmentation was developed based on the different features in the fat-only and water-only images, which is similar to the method of Rosado-Toro et al.(31) but with an improved 3D regularization. It includes the following steps:

• Step 1: In the fat-only images, as the example shown in Figure 1A(e), the signal intensities of pectoral muscle are much lower than those of the breast tissue, which provides a clear boundary. This lower pectoral muscle boundary thus can be captured in the image gradient (y direction) of the fat-only images using a linear programming algorithm with a smoothing window to minimize the penalty (31).

• Step 2: In the water-only images, as shown in Figure 1A(f), the k-means++ approach (47) is applied to classify the image pixels into three clusters. This method is a variation of the original k-means classification and the centroids for each cluster are not selected at random but based on its distance to the existing centroids to reduce the probability of finding incorrect centroids. After the k-means++ classification in the water-only images, the cluster with the lowest mean signal intensity is the non-object region and can be excluded. In this way, the upper boundary of the breast is identified.

• Step 3: After combing the lower and upper boundaries, the chest tissue between two breasts can be automatically removed by a 3D region growing method by setting the distance between the left and right breasts.

• Step 4: The inclusion of nipple region is a limitation of the segmentation method of Rosado-Toro et al.(31). In the last step, we perform a 3D regularization using a 3D order-statistic filtering (40) to automatically smooth the breast mask and successfully eliminate the nipple region.

Appendix 2: Fat-water Decomposition MRI-based Breast Density Measure: FraGW

FraGW

We propose a new MRI-based breast density measure that accounts for the amount of fibroglandular tissue and its distribution, FraGW = (FraGland + FraWater).

FraGland measures the volumetric fraction of fibroglandular tissues in the entire breast, representing the distribution of fibroglandular tissues. A 3D automated segmentation based on localized robust statistics of the image intensity is utilized for extracting the glandular region on the fat-only image. In particular, a few seeds (the initial points selected to start the algorithm) are placed inside the glandular region automatically based on the fat signal intensity. At each seed point, a 3× 3× 3 neighborhood is scanned through and the three local robust statistics are computed. Specifically, the local median intensity, the median absolute deviation, and the interquartile range are computed to represent the local characteristics of the intensity distribution as well as the robust variance around the seed region. Then, a non-parametric density estimation is performed to compute the distribution of the three features. In particular, the kernel density estimation is performed with a Gaussian kernel whose standard deviation is 1/10 of that of each feature. The estimated probability density function will further be used to evaluate the similarity of a new location with the seeded region. Then, for any non-determined point in the entire volume, the shortest path is constructed from the seeded region. The distance along the path is determined by both the spatial and image discrepancy along the path. As such, the distance between two points in the image not only represent their spatial distance but also the accumulated intensity difference along the path connecting them. Specifically, at any non-determined point, its local robust statistics feature vector is computed. The 3D feature vector is fed into the pdf computed above and the probability is computed. This probability value evaluates the similarity of the features between the current point with those seed points. However, this value does not take the spatial distance of the current point with the seed points. In order to consider both the appearance similarity and the spatial vicinity, an optimal path connecting this point (and any other non-determined point) to any seed point, is computed. Such optimal path is computed from the local distance between each point and its neighbors, detailed as follows. The distance between any point and its neighbor is defined as the absolute difference between their probability value computed above, then the dynamic programming is used to trace back to the seed points and find the optimal path. If the final optimal path connects it to the few gland seeds, it is determined to be within the gland region. On the other hand, if the optimal path connects it to the background non-breast region, it is categorized into background(48).

FraWater represents volumetric water fraction after correcting the fat-water signal contamination in the fat fraction maps due to the intrinsic limitations of this fat-water decomposition technique. The relationship (assumed linear) between the signal fraction and volume fraction can be established as below:

For each pixel in the breast region,

$$\{\begin{array}{c}{\mathrm{S}}_{\text{fat}}={\text{aV}}_{\text{fat}}+{\text{bV}}_{\text{water}}\\ {\mathrm{S}}_{\text{water}}={\text{cV}}_{\text{fat}}+{\text{dV}}_{\text{water}}\end{array},$$ [Eq.1]

where S_fat is the fat signal intensity, S_water is the water signal intensity, V_fat is the fat volume, and V_water is the water volume. Four correction factors a,b,c,d refer to the volume contribution to the signal intensity. The fat signal faction, $S_{\mathit{fat}}\%=\frac{S_{\mathit{fat}}}{S_{\mathit{fat}}+S_{\mathit{water}}}$ can be obtained directly from the fat fraction map [Figure 1A(g)]. Our goal is to find the water volume fraction in each pixel, $V_{\mathit{water}}\%=\frac{V_{\mathit{water}}}{V_{\mathit{fat}}+V_{\mathit{water}}}$, which requires the determination of a,b,c and d.

On the fat fraction map (Figure 2A), we take a small region in pectoral muscle tissue as pure water region, and take another small region in the nearby subcutaneous fat tissue as a pure fat region. By taking the average of the signal intensity in each region, we acquire two fat signal fraction values fra_pw and fra_pf. In order to make the values more accurate, this procedure was repeated on four patients’ images to get the average fra_pw and fra_pf. Then, the fat fraction map can be normalized using fra_pw and fra_pf: values smaller than fra_pw are set as fra_pw whereas values greater than fra_pf are set as fra_pf. In order to set up enough equations to solve the four coefficients:

First,

• in pure water region: V_fat = 0, V_water = 1, plug into Equation [1]⇒ S_fat = b, S_water = d ⇒

  $$S_{\mathit{fat}}\%=\frac{S_{\mathit{fat}}}{S_{\mathit{fat}}+S_{\mathit{water}}}=\frac{b}{b+d}={\mathit{fra}}_{pw}$$ [Eq.2]
• in pure fat region: : V_fat = 1, V_water = 0, plug into Equation [1]⇒ S_fat = a, S_water = c ⇒

  $$S_{\mathit{fat}}\%=\frac{S_{\mathit{fat}}}{S_{\mathit{fat}}+S_{\mathit{water}}}=\frac{a}{a+c}={\mathit{fra}}_{pf}$$ [Eq.3]

Next, the fat image [Figure 1A(e)] and the water image [Figure 1A(f)] are added, and the same method is conducted on this “fat+water image” to find a pure water region and a pure fat region. Then, the ratio of the signal intensity in pure fat region and the signal intensity in pure water region, r, can be determined,

$$\frac{S_{\mathit{fat}}+S_{\mathit{water}},\mathit{pure}\mathit{fat}\mathit{region}}{S_{\mathit{fat}}+S_{\mathit{water}},\mathit{pure}\mathit{water}\mathit{region}}=\frac{a+c}{b+d}=r$$ [Eq.4]

This procedure was also repeated on four patients’ images to determine a more accurate r.

Since what we care about here is the “fraction”, one of the coefficients can be set as 1.

$$\text{Here}\text{we}\text{take}d=1.$$ [Eq.5]

Combing the [Eq.2] ~ [Eq.5], the four correction factors a,b,c,d were solved. Therefore, FraWater, the averaged water volume fraction in the entire breast volume, could be easily achieved by solving the matrix equations (Eq.1) for each pixel based on the normalized fat fraction maps.