Assessment of Head Tremor with Accelerometers Versus Gyroscopic Transducers

Abstract

Background

Accelerometers and gyroscopes are used commonly in the assessment of hand tremor, but their validity in the assessment of head tremor has not been studied. We hypothesized that gyroscopy would be superior to accelerometry because head tremor is rotational motion, and gyroscopes record rotational motion, free of gravitational artifact. We also hypothesized a strong logarithmic relationship between 0 to 4‐point tremor ratings and the transducer measures of tremor amplitude, similar to those previously reported for hand tremor.

Methods

Head tremor was recorded for 1 minute in each of the five head positions used in the Essential Tremor Rating Assessment Scale, using a triaxial accelerometer and triaxial gyroscope mounted at the vertex of the head. Mean and maximum 3‐second burst displacement tremor and rotation tremor were computed by spectral analysis. The minimum detectable change for the transducers was estimated using the residual mean squared error from repeated‐measures analysis of variance.

Results

Tremor displacement and rotation (T) were logarithmically related to tremor ratings (tremor rating score; TRS): log(T) = α TRS + β, where α ≈ 0.47 for displacement and ≈0.64 for rotation, and β ≈ −1.8 and −1.4. Tremor ratings correlated more strongly with gyroscopy (r = 0.83–0.87) than with accelerometry (r = 0.71–0.75). Minimum detectable change (percent reduction) was approximately 66% of the baseline geometric mean.

Conclusions

Gyroscopic transducers are superior to accelerometry for assessment of head tremor. Both measures of head tremor are logarithmically related to tremor ratings. The minimum detectable change of the transducer measures is comparable to those previously reported for hand tremor.

Accelerometers and gyroscopes are used commonly in the assessment of hand tremor,1, 2, 3, 4, 5 but there are only a few published studies in which accelerometry was used to assess head tremor6, 7, 8, 9 and no reports in which gyroscopes were used. In general, body motion has six degrees of freedom: three‐dimensional (3D) translation and 3D rotation. Most accelerometers measure translational motion, and gyroscopes measure rotation. Head tremor is almost entirely rotational motion, so gyroscopes should be ideal for measuring this tremor. Accelerometers detect rotation to the extent that they are mounted some distance from the axis of rotation,10 and accelerometers are subject to gravitational artifact, whereas gyroscopes are nearly free of this artifact.10 Neither transducer has been compared to clinical ratings of head tremor.

The overall aim of this work was to examine the convergent validity of accelerometry and gyroscopy versus clinical ratings and estimate the sensitivity to change of these transducers in the measurement of head tremor. We hypothesized that gyroscopic recordings, compared to accelerometry, would correlate better with head tremor ratings. We also hypothesized that both transducer measures would be logarithmically related to tremor ratings, as previously reported for hand tremor,11 and this relationship would be evidence of convergent validity for both transducers in the measurement of head tremor. The repeated measures in this study were used to estimate the minimum detectable change (MDC) for accelerometry and gyroscopy. MDC is the smallest change in tremor that is not the result of measurement error or random variability in tremor amplitude.

Materials and Methods

Using data from a preliminary study,12 a power analysis revealed that 19 patients were needed to demonstrate correlations of 0.6 or greater, assuming a significance level of 0.05 and power of 0.8. Therefore, 17 patients with tremulous cervical dystonia and 9 with essential tremor (ET) were studied after giving their informed written consent, approved by the institutional review boards of the two participating universities. Nine ET patients were recruited and studied at an ET support group meeting, and the other patients were recruited from our outpatient clinics. We included patients with tremulous cervical dystonia because the purpose of this study was to examine the ability of accelerometry and gyroscopy to quantify head tremor, not to quantify or diagnose a particular form of head tremor. Tremor was the dominant problem in all of the dystonia patients. Patients’ medications were not altered. We did not include healthy controls because our preliminary study revealed that our transducers lacked sufficient sensitivity to record normal head tremor.

Head tremor was recorded with a Kinesia motion sensor (Great Lakes Neurotechnologies, Cleveland, OH) that contained a triaxial accelerometer and a triaxial gyroscope (see Appendix S1 for technical specifications). This device was fastened to a plastic head harness taken from the interior of a safety hat (hard hat). This adjustable harness was worn snugly with the transducer positioned at the vertex of the head (see Appendix S1). The transducer axes were oriented vertically (axially), laterally, and anteroposteriorly.

Tremor was recorded while subjects sat in a chair with the head in each of five positions used in The Essential Tremor Rating Assessment Scale (TETRAS): head forward; head rotated fully to the left and then to the right; and head forward while patient gazes to the left and then to the right.13 Each head position was held for 1 minute while tremor was recorded with the transducers. The nose and chin were used as landmarks to rate the largest tremor excursions during the examination. During the recording, a movement disorders specialist (R.J.E.) rated head tremor 0 to 4, using the Fahn‐Tolosa‐Marín (FTM)14 rating scale and TETRAS. We originally planned to compare the FTM and TETRAS ratings, but their 0 to 4 anchors are so similar (see Appendix S1) that the ratings with the two scales were identical in 24 of 26 patients. We therefore used the TETRAS ratings, which are based on the following estimates of tremor amplitude: 0, no visible tremor; 1, <0.5 cm; 2, 0.5 to <2.5 cm; 3, 2.5 to 5 cm; and 4, >5 cm. The entire recording session lasted approximately 15 minutes.

Displacement head tremor was computed from the accelerometer recording, and rotational head tremor was derived from the gyroscope. We computed mean peak‐to‐peak tremor over the entire duration of each 1‐minute recording (“mean tremor amplitude”) and the mean peak‐to‐peak tremor amplitude over the 3‐second interval with greatest tremor during each recording (“maximum burst amplitude”). Tremor was computed in each axis of recording using MATLAB software (The MathWorks, Inc., Natick, MA) and two methods of spectral analysis: the fast Fourier transform (FFT) and the Morlet wavelet transform.15 The Morlet wavelet transform was used to compute the maximum 3‐second burst amplitude because it was our impression that this method has a better time‐frequency resolution than the short‐time Fourier transform.16 Theoretically, the results should be nearly identical.15, 16

Peak‐to‐peak tremor displacement and rotation amplitudes were derived from the tremor spectral peaks in the x, y, and z accelerometer and gyroscope spectra. Tremor displacement (cm) was estimated by dividing tremor acceleration by the squared tremor frequency (radians/s), and tremor angular rotation (degrees) was computed by dividing tremor angular velocity by the tremor frequency. Tremor amplitude was computed as the resultant of the x, y, and z displacements and rotations.

Linear regression analysis was performed with MedCalc software (http://www.medcalc.org) to compute the relationship between tremor ratings (tremor rating score; TRS) and the transducer measures (mean displacement and rotation, and maximum burst displacement and rotation). Regression was performed with and without log₁₀ transformation of the transducer measures to determine which relationship produced the best linear fit (greatest r² and homoscedasticity), as described previously for hand tremor.11 The tremor rating was based on the maximum tremor observed in any of the five head positions, according to TETRAS guidelines.13 Each head position was not rated separately. These ratings were compared to the greatest transducer measures in the five head positions. Statistical comparison of correlation coefficients for TRS versus displacement (accelerometry) and TRS versus rotation (gyroscopy) was performed with a web‐based calculator,17 using the method of Steiger.18

MDC was estimated as follows. Displacement and rotation data were positively skewed and were log (base 10) transformed to achieve gaussian distributed data. The standard error of the measurement (SEM) is the square root of the within‐subjects residual mean squared error in the two‐way repeated‐measures analysis of variance (ANOVA), using the five head positions as the repeated measure factor and tremor rating as the grouping factor.19 This ANOVA was performed on the mean and maximum burst tremor displacement and rotation tremor amplitudes. For each measure of tremor amplitude, MDC = SEM·1.96·√2.19 The percentage of the baseline geometric mean was computed using the formula MDC% = (1 − 10^−MDC) 100, where MDC is on log₁₀ scale and MDC% is the percentage decrease in the geometric mean.20 When MDC represents an increase from baseline, the percentage increase in the geometric mean is computed using the formula MDC% = (1 − 10^MDC) 100.

Results

The mean (standard deviation; SD) age of the 17 dystonia patients (61 ± 9 years) was less than that of the 9 ET patients (74 ± 5; F _(1,24) = 15.12; P = 0.001), and the ratio of men to women was significantly greater in ET (7:2) than in dystonia (2:15; χ² ₍₁₎ = 10.894; P = 0.001). The 26 patients had the following distribution of tremor ratings: 7 with TRS 1, 15 with TRS 2, 4 with TRS 3, and no patients with TRS 4 or 0. The geometric mean and 95% confidence intervals (CIs) for each rating are summarized in Table 1. The results of FFT and Morlet wavelet spectral analyses did not differ significantly. Example FFT amplitude spectra are shown in Figure 1.

Table 1.

Geometric means and 95% CIs for each tremor rating

Measure of Tremor Amplitude	Spectral Method	Geometric Mean (95% CI) for each TRSc
		TRS = 1	TRS = 2	TRS = 3	All TRS
Mean displacement (cm)a	Morlet wavelet	0.0401 (0.0176–0.0916)	0.101 (0.0711–0.142)	0.367 (0.148–0.911)	0.0959 (0.0646–0.142)
Mean displacement (cm)a	FFT	0.0347 (0.0154–0.0782)	0.0888 (0.0651–0.121)	0.339 (0.124–0.930)	0.0848 (0.0573–0.125)
Mean rotation (deg)a	Morlet wavelet	0.143 (0.0857–0.240)	0.665 (0.501–0.882)	2.539 (0.531–12.133)	0.541 (0.345–0.847)
Mean rotation (deg)a	FFT	0.130 (0.0877–0.192)	0.618 (0.474–0.804)	2.358 (0.517–10.756)	0.499 (0.320–0.776)
Maximum burst displacement (cm)b	Morlet wavelet	0.0698 (0.0355–0.137)	0.197 (0.132–0.294)	0.555 (0.275–1.117)	0.175 (0.119–0.256)
Maximum burst rotation (deg)b	Morlet wavelet	0.222 (0.124–0.398)	1.128 (0.800–1.591)	4.202 (0.920–19.188)	0.891 (0.555–1.433)

Number of patients = 7, 15, and 4 for tremor ratings 1, 2, and 3.

^aMean peak‐to‐peak amplitude for the 1‐minute recording of head position with greatest tremor.

^bMean peak‐to‐peak amplitude for the 3‐second interval with greatest tremor for the head position with greatest tremor.

^cTremor rating score.

Figure 1.

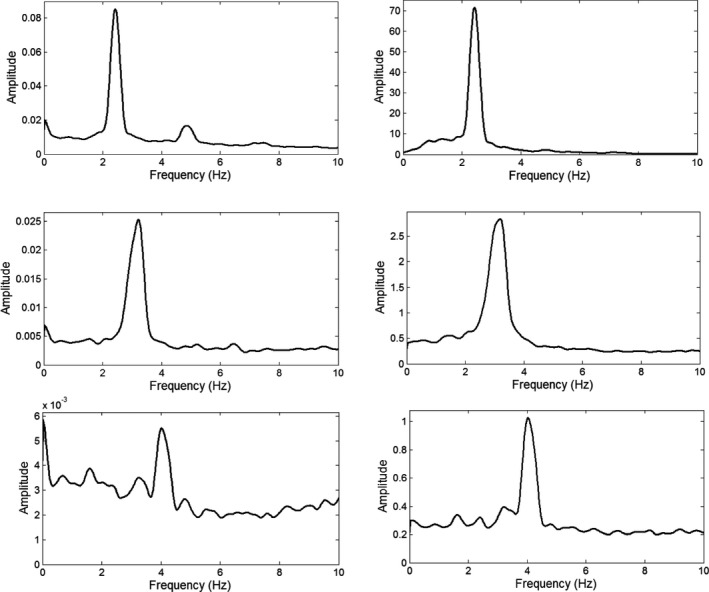
Representative amplitude (one‐half peak‐to‐peak) spectra for a patient with TRS 3 (top row), TRS 2 (middle row), and TRS 1 (bottom row). The spectra were computed with an FFT. Amplitude (square root of power) is plotted versus frequency. Amplitude units are in units of gravity (g = 980 cm/s²) for accelerometry and deg/s for gyroscopy. For accelerometry (left column) and gyroscopy (right column), the tremor spectral peak becomes an increasingly dominant part of the amplitude spectrum with increasing tremor severity. The small harmonic peak at twice the tremor frequency in the upper left acceleration spectrum could be attributed, at least in part, to gravitational artifact.10

Repeated‐measures ANOVA of log‐transformed mean and maximum burst tremor amplitudes in the five head positions was performed with diagnosis (dystonia vs. ET) as a grouping variable. There was no statistically significant effect of head position or group by head position interaction. In other words, no particular head position had a consistent effect on tremor amplitude. The distribution of head positions with greatest tremor for the 26 patients was as follows: head forward 6, head right 3, head left 3, head forward eyes right 7, and head forward eyes left 7. Diagnosis had a significant effect on mean tremor amplitude (F _(1,24) = 6.59; P = 0.017) and maximum burst tremor amplitude (F _(1,24) = 7.37; P = 0.012). The geometric mean tremor amplitude (displacement, rotation) in the dystonic patients (0.125 cm, 0.803 degrees) was more than twice that in the ET patients (0.058 cm, 0.256 degrees). This was also true for the geometric means of maximum burst tremor amplitudes (dystonia: 0.235 cm; 1.343 degrees; ET: 0.100 cm; 0.411 degrees).

Head tremor frequency ranged from 2.3 to 6.4 Hz. The mean ± SD tremor frequencies for mean displacement tremor were 4.35 ± 0.93 (FFT method) and 4.59 ± 0.96 Hz (wavelet method) and for rotation tremor were 4.25 ± 0.93 (FFT method) and 4.56 ± 0.97 Hz (wavelet method). Two‐way repeated‐measures ANOVA revealed no effect of diagnosis (dystonia vs. ET) or any of the five head positions on tremor frequency.

The transducer measures of tremor amplitude (T) were logarithmically related to tremor ratings (TRS): log(T) = α TRS + β (Table 2; Fig. 2). The correlation coefficients between log(T) and TRS were consistently greater (P < 0.05) for gyroscopy than for accelerometry (Table 2). Log₁₀ mean displacement was strongly correlated with log₁₀ mean rotation (r = 0.853 using wavelet transform and r = 0.847 using FFT), and log₁₀ maximum burst displacement was strongly correlated with log₁₀ burst rotation (r = 0.848).

Table 2.

Summary of regression analyses

log(T) = α TRS + β				Spectral Method	Transducer
T	α	β	r
Mean displacement (95% CI)	0.467 (0.278–0.657)	−1.899 (−2.277 to −1.521)	0.720	Morlet wavelet	Accelerometer
Mean displacement (95% CI)	0.481 (0.300–0.662)	−1.978 (−2.339 to −1.617)	0.745	FFT	Accelerometer
Mean rotation (95% CI)	0.631 (0.468–0.794)	−1.456 (−1.770 to −1.142)	0.852	Morlet wavelet	Gyroscope
Mean rotation (95% CI)	0.637 (0.488–0.786)	−1.503 (−1.800 to −1.207)	0.874	FFT	Gyroscope
Maximum burst displacement (95% CI)	0.450 (0.263–0.637)	−1.601 (−1.977 to −1.233)	0.712	Morlet wavelet	Accelerometer
Maximum burst rotation (95% CI)	0.650 (0.467–0.833)	−1.274 (−1.639 to −0.910)	0.831	Morlet wavelet	Gyroscope

r, correlation coefficient, which were all significant at P < 0.0001; T, transducer measure of tremor amplitude; TRS, tremor rating.

Figure 2.

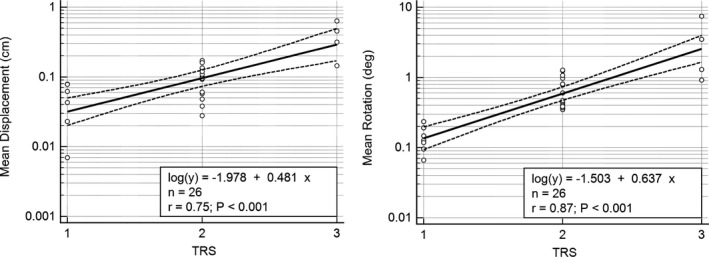
Linear regression and 95% confidence limits for log₁₀ displacement (accelerometry) and rotation (gyroscopy) versus TRS. Tremor displacement and rotation amplitudes were computed with a FFT. Without log₁₀ transformation, the relationships between the two transducer measures and TRS were clearly nonlinear and heteroscedastic, with increasing variance in transducer measures with higher TRS.

Using the five head positions as repeated measures, MDCs were computed for the mean displacement and rotation tremor amplitudes and for maximum burst displacement and rotation tremor amplitudes. The results for the wavelet and FFT spectral analyses did not differ significantly, so the results from wavelet spectral analysis are reported here. The MDCs for mean displacement tremor and mean rotation tremor were 66% and 65% reduction in baseline geometric mean. The MDCs for maximum burst displacement and rotation tremor were 66% and 67% reduction in the baseline geometric means. We also computed the MDCs for patients with each tremor rating (Table 3).

Table 3.

Minimum detectable change for patients with each tremor rating

Measure of Tremor Amplitude	MDC%a
	TRS = 1	TRS = 2	TRS = 3	All TRS
Mean displacement	51.6 (106)	68.0 (213)	71.6 (252)	65.6 (191)
Mean rotation	53.2 (114)	68.6 (219)	67.8 (210)	65.2 (188)
Maximum burst displacement	59.3 (145)	69.3 (226)	64.7 (183)	66.4 (198)
Maximum burst rotation	59.7 (148)	68.6 (218)	72.4 (262)	67.1 (204)

^aPercentage minimum detectable change: % decrease (increase) of geometric mean for patients with each tremor rating.

Discussion

The logarithmic relationship between transducer measures of tremor amplitude and tremor ratings is predicted by the Weber‐Fechner law of psychophysics (see Appendix S1),11 and our results for head tremor are very similar to those previously reported for upper limb tremor.11 The equation log(T) = α TRS + β can be used to estimate the actual tremor amplitudes associated with clinical ratings,3 and this relationship has been used to generate clinical ratings from accelerometry and gyroscopy.21 We previously used this method to compare changes in accelerometric measures with changes in tremor ratings in published treatment trials of ET hand tremor.3 The percentage change in a transducer measure of tremor T can be computed from the change in TRS using the following equation, where subscripts 1 and 2 denote the initial and final assessments.

$$\left(\frac{{\mathrm{T}}_2-{\mathrm{T}}_1}{{\mathrm{T}}_1}\right)100=\left[{10}^{\mathit{\alpha }({\text{TRS}}_2-{\text{TRS}}_1)}-1\right]100$$

Using this equation, a 1‐point reduction in head tremor rating is equivalent to a 66% reduction in tremor displacement (α = 0.47) and a 77% reduction in rotation (α = 0.64). Similarly, a 1‐point increase in head tremor rating is equivalent to a 195% increase in tremor displacement (α = 0.47) and a 337% increase in rotation (α = 0.64). These values are comparable to the computed MDCs for accelerometry and gyroscopy in Table 3. The MDCs in this study are also comparable to those previously reported for hand tremor, using accelerometry and digitizing tablets.22, 23 Transducers are much more precise and sensitive than clinical ratings, but the random test‐retest variability in tremor amplitude appears to mitigate these advantages of transducers, resulting in MDCs that are comparable to those of 0 to 4 clinical ratings.

The gyroscopic measures of tremor rotation correlated better with clinical ratings than did accelerometric measures of tremor displacement. This result is not surprising, because head tremor is primarily rotational motion and because accelerometric recordings of rotational motion contain significant gravitational artifact at all frequencies of motion.10 This gravitational artifact cannot be removed by filtering.10 However, despite these limitations of accelerometry, accelerometry performed surprisingly well in the assessment of head tremor. FTM and TETRAS ratings are based on estimates of the displacement of the nose or chin caused by head rotation, and this may explain why accelerometry correlated so well with clinical ratings, despite the rotational nature of tremulous head motion. Accelerometry and gyroscopy performed equally well in a study of Parkinson hand tremor.1

However, accelerometry has other limitations. Gyroscopes record head rotation regardless of where they are mounted on the head. Accelerometers detect rotational motion only to the extent that they are mounted some distance L from the axis of rotation.10 Therefore, the results of accelerometry will vary with location, whereas the results of gyroscopy are independent of location. Translational acceleration, detected with an accelerometer, is equal to L times the angular acceleration. Thus, linear acceleration and displacement of an accelerometer depends on its distance from the axis of rotation, which varies in time and is generally not known. The displacement amplitudes in Table 1 are small because the accelerometer was mounted close to the axis of rotation. Mounting the accelerometer on the forehead or chin would increase the accelerometric measures, but the accelerometric values will vary with head size, axis of rotation, and transducer location. This limitation of accelerometry and gravitational artifact are strong reasons for using gyroscopes in assessing tremor in most body segments.

Clinicians are instructed to base FTM and TETRAS ratings on the largest tremor amplitude observed during the examination. Therefore, we expected maximum burst tremor amplitude to correlate more strongly than mean tremor amplitude with TRS. However, this expectation was not confirmed (Table 2). This is possibly explained by the fact that burst amplitudes and mean amplitudes were strongly correlated in our patient population (r = 0.9 for displacement and rotation). Burst amplitude might correlate more strongly with TRS in a different patient population with very intermittent or paroxysmal tremor or in a patient population with very severe (TRS = 4) head tremor. Furthermore, we arbitrarily defined burst tremor amplitude as the average tremor amplitude during the 3‐second interval with greatest tremor. It is possible that a shorter interval (e.g., 1 or 2 seconds) would yield different results.

Theoretically, the FFT and Morlet wavelet transform should produce statistically identical estimates of tremor amplitude and frequency.15 This was indeed the case in our study. We used the Morlet wavelet transform for computing maximum 3‐second burst amplitudes. Other methods may be as good as those used in this study.16

In TETRAS, each head position is held for 10 seconds, but in our study, each head position was held for 60 seconds in order to provide ample time for transducer recordings. The optimum durations of recording and clinical observation have not been studied, and the duration of clinical observation and head positions are not specified in the FTM.14 We found no consistent variation in head tremor with the five head positions. Therefore, if a transducer is used in conjunction with TETRAS, it seems likely that head tremor could be recorded continuously as the patient executes the five head positions for 10 seconds each, and the 50‐second recording could be analyzed in toto.

This study has four noteworthy limitations. The first limitation is that the patient population did not include patients with TRS of 4 and had only 4 patients with TRS 3. TRS of 4 requires head tremor to be greater than 5 cm, which is very uncommon for dystonic and essential head tremor. Nevertheless, one cannot assume that our results can be extrapolated to very severe head tremor. In addition, MDC may vary with severity of tremor, and we did not have enough patients with each tremor rating to exclude this possibility. A second limitation is that our patient population did not include patients with TRS of 0, and we did not include healthy controls. Our preliminary study12 revealed that our transducers lacked sufficient sensitivity to record normal head tremor. Studies of controls will require transducers with greater resolution and accuracy than those used in our study (see Appendix S1).

A third limitation is that our repeated measures were only a few minutes apart. For studies of test‐retest reliability and responsivity, the repeated measures should be separated by longer intervals (e.g., days or weeks) that are comparable to the intervals used in most studies. There is significant diurnal variability in ET24 and probably in dystonic tremor, so estimates of MDC might have been larger if the repeated measures were days or weeks apart. The fourth limitation is that our repeated measures involved five different tasks or head positions, not the same task, and this could have increased the test‐retest variability, producing inflated estimates of MDC. However, we also computed the MDC using only the two positions in which the head was straight while the patient gazed left or right, and the MDC% decrease (increase) estimates were 69 (220), 59 (145), 76 (323), and 63 (167), for mean displacement, mean rotation, maximum burst displacement, and maximum burst rotation. These values are comparable to those in Table 3. Therefore, we believe that it is unlikely that significantly different results will be obtained when MDC is computed by repeating precisely the same task.

In conclusion, we have demonstrated good convergent validity among accelerometry, gyroscopy, and TETRAS head tremor ratings. Gyroscopes are recommended over accelerometers for measuring head tremor because the rotational movement recorded with gyroscopes correlates best with tremor ratings, the gyroscopic recordings do not contain significant gravitational artifact, and the results of gyroscopy do not vary with location on the head. Both transducers correlated strongly with tremor ratings, but the displacement estimates from accelerometry were artificially small because of transducer location near the axis of rotation. The optimum duration of recording requires further study. Accelerometers and gyroscopes measure tremor much more precisely than rating scales, but the considerable random variability in head tremor amplitude mitigates this advantage of transducers in the assessment of tremor severity. However, the linear precision of these transducers would be an advantage in a study of tremor variability.25 The MDC for transducers is comparable to a 1‐point change in TETRAS and is also comparable to the MDC reported for transducers and 0 to 4 ratings of hand tremor.

Author Roles

(1) Research Project: A. Conception, B. Organization, C. Execution; (2) Statistical Analysis: A. Design, B. Execution, C. Review and Critique; (3) Manuscript: A. Writing of the First Draft, B. Review and Critique.

R.E.: 1A, 1B, 1C, 2A, 2B, 2C, 3A, 3B

H.H.: 1A, 1B, 1C, 2C, 3B

J.R.: 1A, 1B, 2C, 3B

G.D.: 1A, 1B, 2C, 3B

Disclosures

Ethical Compliance Statement: We confirm that we have read the Journal's position on issues involved in ethical publication and affirm that this work is consistent with those guidelines.

Funding Sources and Conflicts of Interest: This study work was supported by the German Research Council (SFB 855) and by the Spastic Paralysis Research Foundation of Kiwanis International, Illinois‐Eastern Iowa District. The authors report no conflicts of interest.

Financial Disclosures for previous 12 months: Rodger Elble received research funding from the Spastic Paralysis Research Foundation of Kiwanis International, Illinois‐Eastern Iowa District. He is employed by Southern Illinois University HealthCare. He received consultant fees from Sage Therapeutics. Helge Hellriegel received a travel grant for the DGN congress from Ipsen Pharma GmbH. Jan Raethjen received travel support and consultant fees from Novartis. Günther Deuschl has received lecture fees from Medtronic and Desitin and has been serving as a consultant for Medtronic, Sapiens, and Boston Scientific. He received royalties from Thieme publishers. He is a government employee and receives through his institution funding for his research from the German Research Council, the German Ministry of Education and Health, and Medtronic.

Supporting information

Appendix S1. Transducer specifications.