RF coils: A practical guide for nonphysicists

Abstract

Radiofrequency (RF) coils are an essential MRI hardware component. They directly impact the spatial and temporal resolution, sensitivity, and uniformity in MRI. Advances in RF hardware have resulted in a variety of designs optimized for specific clinical applications. RF coils are the “antennas” of the MRI system and have two functions: first, to excite the magnetization by broadcasting the RF power (Tx‐Coil) and second to receive the signal from the excited spins (Rx‐Coil). Transmit RF Coils emit magnetic field pulses ( ${\mathrm{B}}_1^{+}$) to rotate the net magnetization away from its alignment with the main magnetic field (B₀), resulting in a transverse precessing magnetization. Due to the precession around the static main magnetic field, the magnetic flux in the receive RF Coil ( ${\mathrm{B}}_1^{-}$) changes, which generates a current I. This signal is “picked‐up” by an antenna and preamplified, usually mixed down to a lower frequency, digitized, and processed by a computer to finally reconstruct an image or a spectrum. Transmit and receive functionality can be combined in one RF Coil (Tx/Rx Coils). This review looks at the fundamental principles of an MRI RF coil from the perspective of clinicians and MR technicians and summarizes the current advances and developments in technology.

Level of Evidence: 1

Technical Efficacy: Stage 6 J. Magn. Reson. Imaging 2018;48:590–604.

Starting with the initial studies by Lauterbur1 and Mansfield and Grannell,2 magnetic resonance imaging (MRI) has seen a tremendous growth as a diagnostic and research imaging modality. MRI offers excellent soft‐tissue contrast at high spatial and temporal resolutions, with the ability to have a 3D tomographic representation of the subject of interest. MRI is unique in its ability to move beyond anatomical imaging, as it allows visualizing metabolic functions and chemical processes via spectroscopic imaging, and offers advanced methods to measure physiologic properties such as tissue oxygenation, flow, diffusion, and perfusion.

While advances in the MRI hardware such as increased field strength and improved gradient performance have been substantial, advances in the radiofrequency (RF) technology have also proved to be valuable to improve the resolution and shorten the duration of MRI examinations. MRI RF coils are essential components for every MRI examination, as they are responsible for the excitation and the reception of the MR signal.

This review on MRI RF Coils and their basic principles is written from the perspective of clinicians and MR technicians, and is divided into three sections. Basic Concepts and Terminology of MRI RF Coils are explained and a broad overview of the application fields is given. Then an in‐depth explanation of current state‐of‐the‐art transmit and receive RF coils is given, and novel technologies, approaches, and current advances in the field of MRI RF Coils are discussed in the last part. Every part includes topic‐specific, selected references and further literature recommendations.

Part A: Basic Concepts and Overview

Transmit and Receive RF Coils and Basic Terminology

Every MRI system (Fig. 1) is a mix of several subsystems that each provide necessary functionality to generate images of an object.

Figure 1.

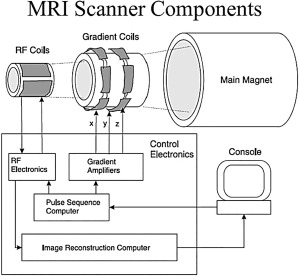
The basic components of any MRI system: The main magnet produces the B₀ field, necessary to align the spins and achieve equilibrium. Gradient coils enable image encoding in the x, y, and z direction (ie, the frequency, phase, and slice‐encoding directions). The RF coil is the part of the MRI system that excites the aligned spins and receives an RF signal back from the sample. All the components are controlled and interfaced with the user via a console.

In general, RF coils act like a broadcasting station: they transmit and receive signals. As a patient is positioned in an MRI scanner, the tissue obtains a small magnetization that aligns with the magnetic field, M₀. A RF transmit coil (Tx) generates an RF pulse that produces a small magnetic field perpendicular to the main magnetic field, which rotates net magnetization away from its alignment with the main magnetic field. The stronger the RF pulse (energy), the farther the magnetization will tilt or flip, which is called the flip angle, θ. The RF receive coil (Rx) detects the precessing magnetization resulting in an induced electric current via electromagnetic induction. The induced current is the MR signal, and represents the mixture of the magnetizations from the tissue within the field of view (FOV) of the Rx‐Coil.

The Tx‐Coils generate the electromagnetic ${\mathrm{B}}_1^{+}$‐field, which is perpendicular to the main (static) magnetic field B₀, and oscillates at the resonance frequency, also known as the Larmor Frequency ω _r. The Larmor frequency ω _r depends on the type of nucleus and the strength of the main magnetic field (ie, 128 MHz for ¹H at 3T). This precession frequency corresponds to the frequency range of radio waves (MHz).

Modes of Operation: Tx, Rx, Tx/Rx

RF coils can be differentiated by their mode of operation: Transmit‐Only (Tx) and Receive‐Only (Rx) (Fig. 2A,B). Usually, these modes are realized in separate coils, but in a third possibility, both functions are combined in a transmit/receive (Tx/Rx) coil (Fig. 2C). The combination of a transmit and receive RF coil in a single device can be useful for applications with X‐nuclei MR spectroscopy or at ultrahigh‐field MRI due to lack of body transmitter,3 but the separation of the two functionalities has the advantage of individually optimizing the coil design for each function.

Figure 2.

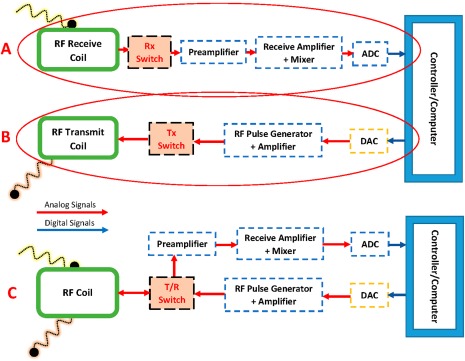
(B) To excite the spins, the transmit coil receives a signal from the controller/computer via a digital‐to‐analog converter (DAC). (A) The receive coil takes up the response from the excitation, amplifies, and digitizes (ADC) it. (C) The schematic of a transmit‐receive RF coil: the T/R‐switch controls the transmission and reception of RF signals.

Both the Tx‐ and the Rx‐Coil are resonant circuits that consist of electrical components that store electric (Capacitor C) and magnetic energy (Inductor L) to obtain a magnetic field when electric current flows. These coil circuits need to be correctly tuned and matched. Tuning a coil means adjusting the capacitance (and sometimes the inductance) so that the frequency of the electrical resonance of the coil circuit matches the frequency of the nuclear MR of the spins in the tissue. At the electrical resonance, a small external perturbation—due to the precessing magnetization—produces a large response from the coil, much like rubbing the lip of a wine glass can produce a loud tone. Matching the impedance of the coil ensures the maximum power transfer from the power amplifier to the coil, minimizing the reflected power from the coil, and ensuring that the greatest possible fraction of the power is delivered to the spins. The better an RF coil is tuned and matched the better/stronger the signal, like in any radio or television broadcast. In order to create an image, the analog signals received by the Rx‐Coil have to be amplified, which is done by the preamplifier. The preamplifier is an electronic circuit that increases the amplitude of the received signal to a level that can be digitized.

When the transmit coil is active (ie, transmitting power), the receive coil has to be off‐resonance, in order to prevent the transmit field to be affected by an RF field of the receiver coil caused by RF coupling. Coupling in electronics is the often undesirable transfer of energy from one medium to another. As the transmit power is orders of magnitude greater than the received signal, the preamplifier of the Rx coil needs to be protected from damage due to the high power of the RF transmission.4 The prevention of coupling from the transmit coil to the Rx coil caused by the transmitted power of the Tx Coil is usually achieved using a detuning circuit. The active detuning circuit or “trap” is a resonant circuit with a PIN (positive intrinsic negative) diode, an inductor L, and a capacitor C. When a forward DC bias is applied to the PIN diode, the resonant parallel LC circuit inserts a high impedance in series with the coil loop, blocking current flow at the Larmor frequency during the transmit phase. Depending on the size of the resonant coil and the operating frequency, one or more blocking networks are used per coil element. In Tx/Rx‐Coils, such as using the built‐in body coil for reception, a so‐called T(/R)‐switch5 is used to separate the RF line of the coil between the transmit and receive line of the MRI system.6

The MR signal induced in the receive coil is on the order of millivolts, and therefore, the most important properties of an RF receive coil are a maximal signal‐to‐noise ratio (SNR), and a high coverage of the RF receive response over the imaged volume, which will be discussed next.

SNR and Design Parameters

Many factors determine the SNR available in a nuclear magnetic resonance (NMR)/MRI experiment. In the early days of MRI, two somewhat parallel paths towards more efficient MRI experiments evolved: one was to improve the gradient technology and pulse sequence design to increase spatial resolution and decrease imaging time, and the other one was the development of RF coil technology.

Regardless of the field strength, the key requirement of any receiver coil is achieving the maximum SNR in order to obtain the best possible image quality. The SNR fundamentally represents the statistical confidence one can have in the robustness of the appearance of features in the image (or spectrum, in the case of MR spectroscopy). If the signal is far stronger than the random variations in the intensity due to noise, then one can have confidence that apparent features in the image (a bright spot in a particular location) reflect the physical characteristics of the sample. When detected by the receiver, the noise may start as Gaussian white noise, but will generally take on a Rician shape and be further altered by the reconstruction process, particularly with Array Coils.7, 8

Every physical experiment includes either random or systematic noise, which can seriously affect the accuracy of the measurement. The degree to which noise affects an experiment is generally characterized by the SNR (Fig. 3). Noise in MRI can be considered a random signal, which is superimposed on top of the real signal. Due to its random character, the mean value is zero, which gives no indication of the noise level, and so the quantitative measure of the noise level is conventionally the standard deviation of the noise. It follows, therefore, that SNR can be increased by repeating the same scan several times, which is called “signal averaging”: every factor of √2 improvement in SNR costs a factor of two in scan time. Or in other words, a factor of √2 improvement in SNR by RF coils can be used to decrease scan time by a factor of 2. The trade‐off for this signal averaging is the additional scan time required for data acquisition.9

Figure 3.

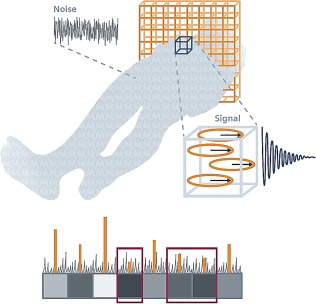
Noise in the image appears as a grainy random pattern similar to snow on a TV screen. It represents statistical fluctuations in signal intensity that do not contribute to image information, and have two basic sources: Brownian motion of molecules in the human body and electronic noise of the receiver, which both add up. If the signal from a slice is too weak, it may be “washed over” by noise (Courtesy of Ref. 93).

The signal of every MRI experiment is originated from dipoles that rotate in the transverse plane.10 While a single receiver coil can pick up one dimension from this rotating field (LP, linear polarized mode), two properly aligned RF coils can pick up both dimensions of the rotating field. This so‐called circular polarized (CP) mode of the coil pair can be realized using a Quadrature Hybrid that sums the two signals from both coils with a 90° phase difference11 (Fig. 4). Compared to a single RF coil, the CP receiver coil pair gains a √2 in SNR.12 This is the signal polarization concept (electromagnetic wave propagation) in MRI, which is similar to that in optics, as polarized lenses of sunglasses only allow specified constrained light rays to pass through the glass, and block all other polarized rays.

Figure 4.

The rotating magnetization induces a voltage at the terminals of the loop, which can cause a current in a single loop or coil. Linearly polarized RF coils detect the rotating magnetization (MR signal) along a single direction. Quadrature (circularly polarized) coil arrangements detect the MR signal in orthogonal directions.

In Tx coils, the CP‐mode has the advantage of requiring half the power of a linearly polarized system to provide the same ${\mathrm{B}}_1^{+}$‐field.

The Evolution of MRI RF Coils

In 1978, Hoult first explained and discussed the NMR receiver.13 These single‐segment coils for various regions of the body had to be moved several times to image larger areas like the spine, and therefore switchable or ladder arrays were developed in 1990. Early MRI machines accepted only one single quadrature receiver channel at a time, and the introduction of switchable multi‐element coils was a huge step.14

Soon after the first publications, researchers recognized that a small region of interest (ROI) could also be imaged by a small RF coil, closely fitted to the ROI. This approach solved the problem of the decreased SNR in high‐resolution MRI, as the close fit of small coils allowed a more localized high SNR. The major breakthrough towards modern RF coil design was explored by Ackerman et al in 1980: by placing a small coil on the surface of the sample, close to the ROI, a significant SNR gain was achieved.15 This small local RF coils act as a spatial filter, eliminating the noise from outside of the ROI, and are called “surface”‐coils. These coils, first introduced in 1951 by G. Surygan and later by J.R. Singer in 1959 for NMR flow measurements, play a major role in the acceleration of dynamic imaging, spectroscopy, and generally all experiments using NMR/MRI.16

The resulting trend towards small surface coils, initiated by miniaturization of RF coil loop size, necessitated consideration of noise dominance. Noise dominance determines where the loss, and therefore the lower SNR, comes from: the sample or the coil. In the early days, cooling RF coils was a way to maintain the RF coil in sample noise dominance, but due to higher field strength and thereby higher operating frequencies, the sample noise generally maintains dominance in recent MRI systems without the need for cooling, providing coil dimensions are not too small.17

Next, switched loop elements arranged in arrays, which received the MR signal individually by detuning the other elements in the array, were developed to adjust the sensitivity pattern of such an array, in order to optimize the single receiver for use in arrays.18, 19, 20 A major step in the development of arrays was the adaptation of mobile phased‐array radar technology, in the reception of NMR signals. In 1990, Roemer and colleagues proposed phased‐array technology, which uses small coil elements that are grouped together or fed into separate receive‐channels.21, 22 Combining large groups of small antennas enhances the overall signal or transmission properties.23 Shortly after Roemer et al, Hayes's group explored the application of the phased‐array in volume imaging.24 To obtain the maximal SNR at each point, the individual signals from each loop of the phased‐array have to be weighted differently at each point. As long as the SNR maintains high enough, root sum of squares signal combination is generally adequate. However, when SNR per element is low (ie, in diffusion tensor imaging,22 the weights need to be obtained with a separate high SNR scan: At a point where only one loop detects significant signal, the other loop still contributes noise, and should therefore not be included in the reconstruction. At points where both loops detect, the signals have to be put in phase to constructively sum the signals. The necessary amplitude and phase correction information is referred to as weighting coefficients (Fig. 5).

Figure 5.

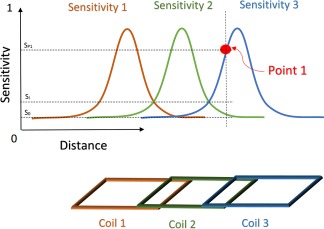
The optimal combination of signals from an array coil requires knowledge of the spatial variation of each element's sensitivity. A pixel at point 1 of a 3‐element (channel) array, has contributions from Coil 3 and 2, but very little from Coil 1. Coil 1 will contribute primarily noise leading to a suboptimal combination of the pixel at point 1. If the contribution is weighted by the sensitivity at this location, the contribution of Coil 1 will be weighted close to zero, reducing the combined noise and hence increasing the SNR.

Soon after that, researchers explored the possibility to incorporate the spatial heterogeneity of the receiver elements from the array in spatially reconstructing the MR image. The spatial variance of RF fields between receivers was used to accelerate image acquisition and is called parallel imaging. Phased‐array technologies are considered the current state of the art.

At higher field strength, ie, >3T, the wavelength for ¹H signals is smaller than the dimensions of the human body. This means that the traditional near‐field approximation for the design of RF coils no longer holds and that antenna concepts are being explored as new ways to transmit or detect the RF waves. In the last 10 years, several works have introduced different RF antennas for MRI, like patch antennas, dipoles, multipole antennas, and many more, enabling efficient and homogeneous B₁ field despite the shorter wave length.25, 26

Types of RF Coils and Their Application

The following chapter gives an overview of various types of RF coils and their fields of application, without a claim of completeness, as the field is still rapidly developing. RF Coils can also be distinguished, for example, by their homogeneity of the B₁ field or, if viewed from a usage perspective, into Surface Coils, Array Coils, or Volume Coils.

Volume Coils

Volume coils (eg, the body coil) completely encompass the anatomy of interest and are mostly operated as transmit coils but also capable to be operated as transmit/receive coils. Volume coils are typically cylindrical and rely upon a sinusoidal distribution of currents arranged circumferentially around the tube and running the length of the coil to create a transverse magnetic field. Such coils as the birdcage 27 and the transverse electromagnetic (TEM) resonator 28 were designed to generate a very homogeneous RF excitation field B₁ across the entire covered volume.

Surface Coils (and Arrays)

An RF surface coil consists of a partial loop of wire having dimensions that match the area of interest and its inductance in resonance with the capacitance at the Larmor frequency. The inhomogeneous field profile of surface coils restricts their use primarily to the Rx‐only mode, except in the case where adiabatic pulses or trains of pulses are used to reshape the flip angle profile.29, 30 However, they are, as their name suggests, good for detecting signals at much higher SNR close to the surface of the patient.

Another but similar approach to a more localized SNR is the concept of dipole antennas. Already well described by communications or astronomy, dipole antennas are still relatively unknown in the broad MR community. Various types of dipoles used in MRI already exist: monopole antenna,31 the folded dipole antenna,32 circular dipole antenna,33 fractionated dipole,25, 34 and combinations of loop coils and dipole antennas.26 Compared to standard loop surface coils, electric dipoles are more likely used in ultrahigh‐field systems, where wavelengths are much shorter than the dimensions of the tissue.35, 36

A combination of several surface coils or dipole antennas is called an Array. Array Coils represent a methodology to gain a high SNR over a large ROI. As array coils have coil elements that operate at the same time, care must be taken to minimize crosstalk between elements, else efficiency in SNR and acceleration performance is compromised. Figure 6 highlights several coil array configurations.37

Figure 6.

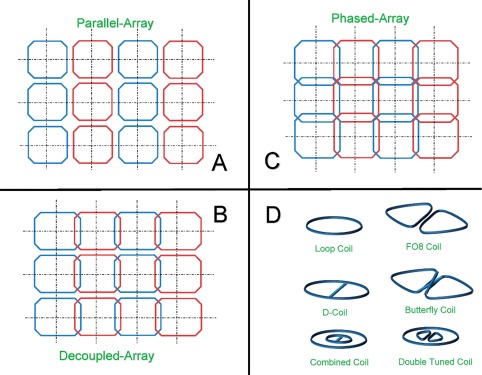
Different types of array coil combinations: (A) parallel array, (B) decoupled array, (C) phased array, (D) representation of various loop‐shaped surface coil designs.

RF array coils are used to reduce imaging time by their ability to spatially localize signals.38, 39 In some cases, small coils are used to maximize SNR in restricted regions.

Figure 7 shows the relationship between array channel count and sensitivity for a 1D profile across the head. Dense arrays of small coils provide an SNR gain over uniform volume coils (“CP”). The SNR gain is greatest near the periphery, and as the channel count grows, the incremental SNR gains are increasingly confined to the peripheral areas closest to the coil elements. While array coils provide no SNR gain at the center of the FOV versus a size‐matched volume coil, in practice, array coils are often built on conformal housings (such as helmets for brain imaging). Because these conformal arrays have a better filling‐factor (see Part B) than typical volume coils, the arrays provide an SNR gain even at the center of the FOV. In clinical settings, there is often a practical trade‐off between maximizing SNR with close‐fitting arrays on the one hand, and optimizing patient comfort and clinical workflow on the other hand. For example, clinicians often opt far larger, looser‐fitting helmet arrays rather than the tightest‐fitting coils available, even though this trade‐off incurs an SNR loss.

Figure 7.

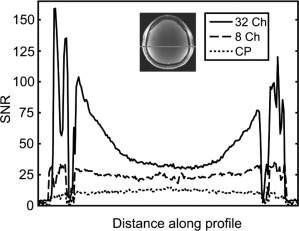
SNR along a 1D profile as a function of channel count for a few representative arrays (courtesy of Ref. 94).

A list of coils including their application and properties as well as suggested references, are shown in Table 1.

Table 1.

MRI RF Coils grouped by their Clinical Field of Application. Designs from Low Field to High and Ultra‐High Field Strengths (>7 Tesla).

Clinical Application	Type (examples)	# of Channels	Suggested References
Head/Neck and Brain	Birdcage, Surface Coil Arrays, Dipole Antennas, Local Shim‐Array Coils	4–128	25, 26, 46, 94, 95, 100
Spine	Surface Coil Arrays	15–75	18, 36
Extremities	Resonator, Volume Coils, Flexible or Adaptive Coil Arrays	2–32	28, 82, 83, 84, 101
Breast, Chest, Abdomen	Surface Coil Arrays	6–32	27, 28, 70, 98
Rectum or prostate area, inner surfaces	Surface Coils, Meanderline Coil, Litz Coil, Spiral Coil, Catheter Coil, Micro Coil	1–6	91, 92, 97, 99
Whole body	Body Coil, Surface Coil Arrays, Dipole Antenna, Flexible or Adaptive Coil Arrays	12–128	28, 48, 76, 87

Part B: Advanced Concepts and Details

In the following Part B, the transmit and receive RF coil concepts are explained and analyzed in detail.

Transmit Coils (Tx)

The transmit RF Coil is used to excite the spins in the sample. This is achieved by the broadcast of a well‐defined RF pulse to the sample of interest. The primary focus of transmit RF coils is to generate a homogeneous ${\mathrm{B}}_1^{+}$‐field. The secondary focus to minimize the time needed to tip the net magnetization from its previous state (eg, equilibrium state). The amount of rotation of the net magnetization due to the ${\mathrm{B}}_1^{+}$‐field is called the flip angle, θ. The flip angle is dependent on the gyromagnetic ratio $\gamma \left(42.6\frac{Mhz}{Tesla}for1H\right)$, the transmit field B ₁, and τ_RF, the amount of time needed to generate the desired rotation.

$$\theta =\gamma B_1{\tau }_{RF}$$

The magnitude of B₁ is determined by the delivered power P _Amp of the RF amplifier and characteristics of the RF coil. The power delivered to the coil depends on the impedance match to the transmission line from the amplifier, and the current excited in the coil that created the B₁ field, depends on the impedance. When the frequency of the electrical resonance of the coil is the same as the center frequency of the incident RF pulse, the maximum current will flow in the coil and produce the largest B₁ field. When the coil is matched to the impedance of the transmission line (50 Ω), the greatest fraction (1/2) of the incident power will be delivered to the coil and available to produce this field. B₁ scales linearly with current, and the power and current relation in a matched condition is as follows:

$$P_{Amp}=I^{2}R$$

which is the product of the transferred current I squared through the RF coil and the resistive losses seen by the coil at the Larmor frequency ω. These resistive losses R _eff comprise the resistance of the coil conductor and its components R _Coil, the electronic losses R _Electronics, and tissue losses R _Sample.40

$$R_{eff}=R_{Sample}+R_{Coil}+R_{Electronics}$$

Ideal homogeneous resonators create a homogeneous magnetic field, either by a uniform distribution on a sphere or by a cosine dependent distribution of currents, flowing parallel to a cylinder axis. The closest approximations to ideal homogeneous resonators are the axial resonators (eg, Helmholtz Coil,41 Four Coil Configuration,42 Solenoid Coil43). Transverse resonators are another approach for Tx‐Coils and have a cylindrical shape. They produce a magnetic B₁‐field perpendicular to their main axis and are used with any size of axial magnets, either horizontal or vertical. Transverse resonators are also known as volume coils. An early example for a transverse homogeneous resonator is the saddle coil.44 Further examples for RF coils with a homogeneous B₁‐field are the Alderman‐Grant Coil,45 and the Cosine or Bolinger coil, which is designed to improve the homogeneity without the complexity of a birdcage design.46

A resent approach called parallel (Multi‐) Transmit RF coil, or pTx, increases the homogeneity of the transmit field due to more accurate excitation. In a pTx RF coil the transmit coil is divided into individually powered and controlled elements, like in a receive array coil, to produce separate B₁ transmit fields. The increased homogeneity of the transmit field increases the received MR signal, and results in better imaging quality or improved scan time.47

Specific Absorption Rate (SAR)

Another important but often underestimated aspect of RF transmit coils is the fact that RF energy can be deposited in the body as heat. At field strengths up to 1.5T, the wavelength of the RF is so long that energy deposition in the body is relatively simple to predict. The move towards higher field strengths and therefore wavelengths shorter than the body puts the safety problem of increased local RF power deposition in the body into focus.

The SAR describes the potential heating of the patient's tissue due to the interaction of the transmit coil's electric fields with electrically conductive tissue in the body. The SAR distribution depends on the geometry and electrical properties of the conductive tissue of the subject, the coil geometry, and the applied RF pulses. A distinction is made between local and global SAR. Averaging the deposited power by the Tx coil over the whole sample exposed by the RF coil leads to global SAR. The global SAR reflects the total power deposited in the tissue, and is well estimated through power monitors on modern MR systems by measuring the total incident power. Local SAR is due to the inhomogeneity of both the electric field and the distribution of conductive tissues, which leads to localized deposition of energy. Unlike global SAR, the local SAR is not directly accessible by measurement.

In order to reduce SAR, the duty‐cycle and the power of the transmitted RF pulses can be reduced, at the cost of longer scan times and altered contrast. The doubling of the field strength of the main magnet from 1.5T to 3T could lead to a quadrupling of SAR. This problem becomes even more important at field strengths beyond 3T,48 and needs proper SAR management to enable 7T systems in the clinic.49 There are government guidelines that regulate the acceptable limits of SAR of radiation deposited in the body. In most countries, standard MRI systems are limited to a global maximum SAR of 4W per kg.

Receive Coils (Rx)

A Simple RF Coil Loop

From an engineering point of view, an MRI RF Coil is a piece of conductive wire with an inductance (L) and capacitance (C), eg, an LC circuit, which is “tuned” to a certain frequency (resonance frequency ω). In this circuitry, the coil wires form the inductor, and capacitance is added in parallel, in order to tune the coil to the appropriate frequency. A simple version of a typical RF receive circuit is shown in Fig. 8.

Figure 8.

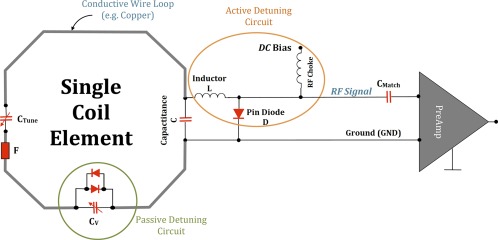
A typical circuit schematic for a receive‐only coil element. In this case, the loop comprises a conductive wire with two tuning capacitors (C_Tune and C) to fine‐tune the coil frequency, a detuning trap (L and pin diode D) to actively deactivate/detune (turn off) the loop while RF excitation by the transmit coil, and a matching capacitor (C_Match) to transform the element impedance to 50 Ω of the preamplifier, which finally amplifies the MR signal. The pin diode D is powered by a certain DC bias. The passive detuning circuit, consisting of an adjustable capacitor CV and crossed diodes and serves, like the RF fuse F, as a second stage of safety to the Rx loop during transmission by the Tx coil, and as well for the patient. This example coil thus has three redundant safety features to prevent interactions between the Tx coil and the receive loop that could cause heating or other safety concerns.

The tuning of an RF Coil can be imagined as the adjustment to a radio station: The more accurate the tuning, the better the sound. The angular resonance frequency ω _r, respectively the resonance frequency ${\omega }_r=2\pi f_r$, of the LC circuit, is given by:

$${\omega }_r=\frac{1}{\sqrt{L{C}_{Tune}}}\hspace{0.17em}or\hspace{0.17em}{f}_r\approx \frac{1}{2\pi \sqrt{L{C}_{Tune}}}$$

The RF signals are usually transferred via coaxial cables, with a characteristic impedance of 50 Ω. In order to avoid signal losses during transmission of the MR signal, the tuned RF circuitry should also have an input and output impedance of 50 Ω.50

SNR in Detail

The basic goal of RF receiver coils is to achieve the highest possible SNR. The MR signal, which is resolved into voxels, can be approximated with a rotating net magnetization vector at the resonance frequency. A time‐varying electromagnetic field generated by the rotating magnetization will induce an electromotive force (EMF) in the RF coil, producing a current flow, which causes a voltage at the open terminals of the loop and constitutes the NMR signal.10, 51

The SNR has already been discussed in several publications52, 53 and, besides other factors illustrated in Fig. 9, very much depends on the coil's loop size and the electrical properties. The loop‐coil has a very high local sensitivity depending on the penetration depth. The penetration depth is defined as the depth at which the coils sensitivity drops to 37% of that at the center of the coil. As a rule of thumb, the penetration depth of a circular, sample noise‐dominated loop‐coil is approximately equal to its diameter.54 Kumar et al showed that, when coil sizes are large, the interaction with the sample is strong. In other words, in large coils tissue noise dominates over coil noise. Figure 10 shows the optimal coil radii r _R, that yields the maximum SNR at a given target depth along the axes as well as a graphical plot of the full‐wave analysis by Kumar et al.55

Figure 10.

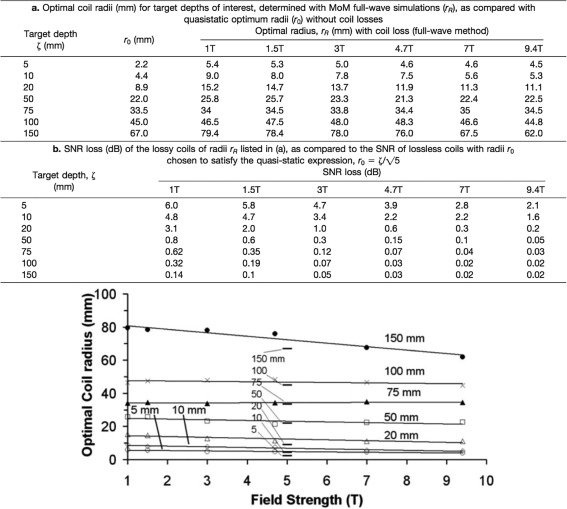
Table a,b display the optimal coil radii (mm) of a surface coil loop for target depths of interest, determined with full‐wave simulations and SNR loss of the lossy coils of radii r _R measured and calculated (courtesy of Ref. 90). The graph below table b shows the optimal coil radius r _R (mm), including coil losses, as a function of field strength (T) for various target depths, as determined by full‐wave numerical method of moments (MoM). The quasistatic optimum coil radii r ₀, without coil losses, are indicated by horizontal bars in the center of the plot (courtesy of Ref. 55).

Figure 9.

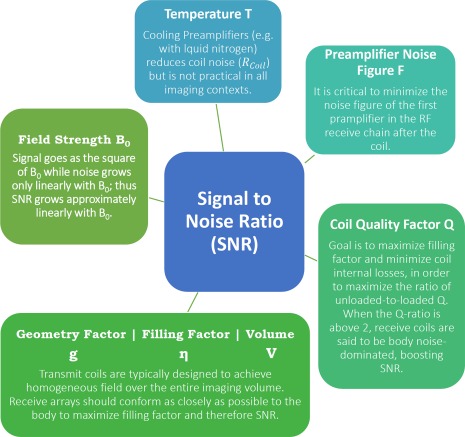
The SNR is influenced by several factors: The effective temperature factor T or T_eff at room temperature which includes the losses of all components; the performance of the preamplifier to amplify the EMF, which is described through the noise figure; the coil quality factor Q, which is the ratio of stored energy to dissipated energy; the filling factor η, which is the ratio of magnetic field energy stored inside the sample volume versus the total magnetic energy stored by the loop; the geometry or g‐factor, which is simply the ratio in noise between accelerated and unaccelerated imaging important in parallel imaging; and the volume of interest and the field strength B₀.

Quality Factor

The quality factor (Q) is a measure to compare coil loops in their efficiency to detect the MR signal. The Q‐factor is a dimensionless indicator for the loss mechanisms in the coil.50 It is the ratio of the stored and dissipated energy:

$$Q=\frac{Maximum\hspace{0.17em}Energy\hspace{0.17em}Stored}{Average\hspace{0.17em}Energy\hspace{0.17em}Dissipated\hspace{0.17em}per\hspace{0.17em}Cycle}=\frac{\omega L}{R}$$

where L is the inductance of the coil and R _Coil the coil resistance. When summing up all loss resistances of a loop without considering the sample, the corresponding Q is called unloaded (Q _Unloaded), while when incorporating the sample losses it is called Q _Loaded.

Typical Q values for loaded coils range from 10–100 and for unloaded coils from 50–600. The Q‐factor of a coil can be estimated by using an RF probe with a network analyzer on the bench. The relation between the loaded Q and the unloaded Q is an indicator of the coil sensitivity:

$$Q_{ratio}=\frac{Q_{unloaded}}{Q_{loaded}}=\frac{R_{Coil}+R_{Sample}}{R_{Coil}}$$

A good design should have R _Sample ≫ R _Coil. Note that an increase of R _Sample will also increase the noise and the power needed to excite the spins. With a Q _ratio < 2, the coil‐noise dominates the sample‐noise, which results in reduced SNR. Therefore, a minimization of the loss mechanism of the loop, eg, reduction of R _Coil, leads to an SNR improvement. If Q _ratio ≫ 2, the sample noise is dominant, a reduction of the loop's resistance would still lead to an SNR improvement but quite small. It is always incumbent on the RF coil designer to minimize the losses in the coil. Although some methods like cooling the copper or using superconductors can lower R _Coil, it is usually easier to improve the Q by increasing R _Sample in a way that also improves the sensitivity of the signal detection (by more tightly coupling to the tissue) and leaves R _Coil unaffected. This is done via the filling factor.

Filling Factor

The filling factor, η, should be as close as possible to 1 to gain maximum SNR. The unitless filling factor is the ratio of the magnetic field energy stored inside the sample volume versus the total magnetic energy stored by the loop. The filling factor (near‐field approximation) is

$${\eta }_f=\frac{B_1^2}{QP}$$

where B ₁ is the value of the RF magnetic field in a particular point in space and P is the input power. To maximize the filling factor, and thereby the SNR, the coil resistance R _Coil, also called equivalent series resistance (ESR), is relatively minimized (increasing the Q‐ratio) by improving the electronics and the antenna, and maximizing the sample resistance R _Sample by moving the coil closer to the sample. In other words, by choosing a coil that fits closer to the ROI, you potentially gain better images.

The filling factor is derived from quasisteady‐state approximation and thus it does not apply to field strengths above 3T for body imaging and 4.7T and higher for head imaging.

Preamplifiers and (Analog/Digital) Signals

A major role to maintain high SNR with individual loop elements is for the preamplifier. The preamplifier is important to amplify the weak MR signal detected by the RF coil. Characteristics of a preamplifier, such as the noise figure,55 affect the SNR. Modern low‐noise (LN) preamplifiers amplify the induced voltage in the coil by ∼27 dB.56 The second role of the low‐input‐impedance preamplifier is to limit interelement coupling in large receiver arrays. The preamplifier decoupling (active decoupling) does not directly reduce the mutual inductance; instead, it causes a high impedance in the coil that reduces the current in the coil, which suppresses the effect of mutual inductance. To mitigate SNR losses that might occur as a result of preamplifier noise coupling, the strategy of overmatching57 or broadband matching58 can be applied. A recent strategy proposed by Zhang et al59 includes the use of coupled transmission lines to realize a tuned RF Coil with an intrinsic high impedance. The corresponding current of the standing wave in the inner conductor is shifted by half the coil length with respect to the mirror current in the shield, thereby maintaining a reasonably uniform current density over the entire loop. The consequence of such a design is that coils can be put in close proximity without substantial coupling, and even facilitates reshaping the coil to a certain extent without causing SNR reduction.

Parallel Imaging

Another milestone in MRI was the introduction of parallel imaging (PI), enabled by phased‐array coils. The key concept behind PI is that acquisition time is proportional to the number of phase‐encoding steps in a Cartesian acquisition. Increasing the distance between phase‐encoding lines in k‐space by a factor R (reduction factor), while keeping the spatial resolution fixed, reduces the acquisition time by the same factor. This also decreases the FOV, resulting in aliasing or wraparound artifacts. In PI, the spatial dependence of the RF Coil array elements is used to remove or prevent aliasing.

As parallel imaging is dependent on the combination of the individual coil signals, several techniques for the optimal combination and reconstruction of multiple loops were developed, like the sum‐of‐squares (SoS),60, 61 or the SENSE62 and GRAPPA63 reconstruction techniques, and many more which are the topics of other publications.64 Theoretical and practical studies on ultimate SNR in parallel MRI65, 66 and in hardware67 pushed the development of phased‐array RF coils even further in subsequent years.

The important breakthrough came 9 years after the introduction of the phased array by Pruesmann et al,62 when they managed to use the spatial heterogeneity in receiver sensitivity to unfold aliased images in order to speed up MRI data acquisitions. The performance in extracting the aliased image from the non‐aliased part is expressed as a g‐factor. The SNR in parallel imaging is described as:

$$SN{R}_{Accelerated}=\frac{SN{R}_{unaccelerated}}{g\sqrt{R}}$$

where SNR_{unaccelerated} describes the baseline performance of the coil system, R is the Reduction/Acceleration factor, and g is the geometry factor, which is related to coil geometry, the location of the imaging plane, and the FOV.68

The use of array coils increases the SNR. Combined with improved image reconstruction schemes that incorporate (compressed) SENSE, CAIPIRINHA, multiband imaging, finger printing, and deep learning, a higher channel count can increase image acquisition speed substantially.

The feasibility of higher channel counts has already been proven several times.69 Not only the SNR increase, but also the noise amplification for parallel imaging (g‐factor) decreases, which allows for higher acceleration factors compared to low‐channel count arrays.70 In order to gain the proposed SNR with array coils, it is necessary that each element of the array is properly decoupled from each other. If two coils with the same resonance frequency are shifted towards each other, they start to “see” or “talk” to each other, and none of the loops will be an efficient receiver. The closer the antennas get to each other, the worse this problem becomes. This breakdown of frequencies leads to a reduction of sensitivity at the resonance frequency and an unwanted transmission of signal to other coils. This effect is known as passive or geometrical coupling and is characterized by the existence of a mutual impedance in the equivalent circuit of the two coils71 (Fig. 11).

Figure 11.

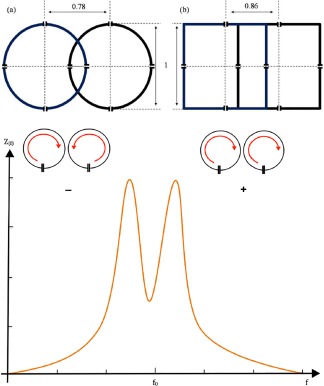
The behavior of two loops with resonance frequency f ₁ = 1/[2π√(L ₁ C ₁)] and f ₂ = 1/[2π√(L ₂ C ₂)] can be described with the impedance curve. The mutual inductance increases as the distance between the coils decrease, meaning that moving the loops further the two peaks will fuse to one. If the coupling between two coils gets stronger, they over‐couple and the resonance frequency splits into two current modes: a co‐rotating (+) and a counter‐rotating (–) mode. The optimal distance for geometrical decoupling depends on the loop dimensions. The ideal distances for maximal passive/inductive decoupling depend on the loop shape and size (a), (b).

At one certain overlap position, depending on the shape and size of the loops, the mutual inductance between adjacent coils becomes ideally zero, meaning these loops are electromagnetically “isolated” from each other. The degree of isolation or amplification of a signal is measured in dB.

A further way to reduce the mutual coupling between next neighbors in array coils is to make use of the already mentioned preamplifier decoupling. Reykowski et al72 showed that it is possible to build MRI arrays without preamplifier decoupling even in the presence of significant intercoil coupling. The suggested method simplified the tuning and matching procedure. Several further methods like the combination of a conventional but robust overlap decoupling, regarding coil loading and resonance frequency, with the extended FOV of nonoverlapped coils73 or a wideband decoupling network58 represent only a few new approaches.

Part C: New Developments and Outlook

New Developments

Since Purcell et al's74 re‐entrant cavity resonator and Bloch et al's75 crossed transmit and receive coil pair, MRI RF coils have evolved from the simple wire‐wound solenoids, and copper‐tape resonators of chemistry laboratories to the complex multichannel transmitters and receivers of modern clinical and research MRI systems.

Current clinical use of high‐field and ultrahigh‐field MRI scanners is constrained by the lack of homogeneity of the resulting image and by constraints related to the SAR of the RF field. Using independent transmit channels enables shimming of the uniformity of the transmit field using constructive and destructive interferences of the RF waves radiated from multiple antennas. Particularly when combined with multidimensional gradient pulses, uniform flip angles can be obtained within the human body at ultrahigh frequencies. Since at ultrahigh fields local SAR restricts the use of a high‐duty cycle of RF pulses, dynamic RF shimming over the RF pulse trains can reduce local SAR, as the hotspot can be shifted during the train of RF pulses.

Moreover, to benefit from image acceleration the number of receiver elements in an array can be increased. At higher fields the element size can be very small, while still remaining in tissue load dominance. Adding more channels introduces decoupling issues, which are the topic of novel decoupling methods. The aim is to position more receiver channels closely around the imaging target (eg, brain, heart) and to increase the spatial variance in reception profiles of the receivers to maximize the ability to decode spatial information from the MR signals.

Metamaterials

Another novel decoupling technology, which makes use of so‐called metamaterials, is presented in Ref. 76. Metamaterial coils have the goal to find new materials or technologies in order to tackle the high SAR levels and image inhomogeneity.77 They influence the RF field through their effective material properties, which define the electromagnetic properties like permeability. Based on this idea, new coils for ultrahigh field using newest approaches from antenna theory research have been designed and are still under development by consortia.

Big Data and Digitization

Besides the design and construction challenges of array RF coils, another challenge is to interface the RF coils with the MR scanner system. The hard‐ and software of any MRI machine from any vendor is not capable of accepting more than 128 channels at the time of writing. A recently introduced digital MRI system architecture basically presents a digitization of the MR machine that is meant to reduce the control‐ and transceive‐chain to a digital network architecture. This digital MR system is in theory scalable in any dimension (eg, receiver‐transmitter channels). The biggest issue there is the embedded system design handling the vast amounts of data produced, versus the cost factor. Using parallelization technologies like field programmable gate arrays (FPGA), which are integrated circuits for digitization, used, for example, in mobile communications, makes the data handling in the range of Gbs possible,78 which reduces the cost per RF channel. The digitization starts right after the detection of the MR signal by the RF coils, and therefore possibly overcomes analog transmission issues.

Wireless Technology

Optical or even wireless technology used in signal transmission simplifies coil handling by the operator. As the amount of receivers keeps increasing, the issue of cabling is a challenge on its own. The more cables, the higher the interactions between the cables and coil elements (coupling), and more cables also introduce physical design limits like space and weight. As wireless coils may advance safety by eliminating baluns, digitizing the picked‐up signal very close to the loop and before transmission, and offering convenience and ease of operation, they introduce challenges in maintaining the phase information of individual signals, or powering the active parts of the RF coil.79, 80

Flexible and Adaptive RF Coils

A more patient‐centered approach is represented by flexible or stretchable RF coil elements. Especially in the receive domain, the RF coil has to closely fit various shapes and sizes of the patient population. Almost for every region of the body, a special local RF coil exists. This results in many RF coils in the clinic, which need space and training for their appropriate use. Therefore, the goal is to have a “one‐size‐fits‐all” RF receive coil. Ultra‐flexible screen‐printed RF coils offer the ability of a low‐cost highly flexible RF receive coil, which allows a close fit to the subject, especially in pediatric subjects.81, 82 Stretchable coil arrays 83 and adaptive coils 84 increase SNR significantly, while enabling imaging of a wide range of patient sizes and shapes at the same time. Adaptive coils face the issue of changing tuning and matching because the loops adapt to size and shape, which results in a change of electromagnetic properties. Therefore, automatic tuning and matching strategies have already been developed.85, 86 The latest approach to ultra‐flexible and adaptive RF coils claims the use of special conductive material (INCA conductor) to allow a very high flexibility and maintain the electromechanical properties at the same time.87

As SNR scales roughly with the field strength of the main magnetic field, the boost in sensitivity (increase in SNR) can yield higher spatial resolution or scanning speeds. As the field strength increases, so does the resonance frequency required to excite the protons. At 7T, the Larmor frequency reaches 300 MHz, which corresponds to a wavelength of about 12 cm in tissue. At such short wavelength, head or body resonators form standing‐wave field patterns, resulting in a degradation of SNR by causing regional signal losses. Using a cylindrical lining in an MRI cavity as a waveguide with a simple antenna placed at one end of the MRI, replaces the RF coils entirely, and is referred as traveling wave imaging. The patient or sample inside the MRI is exposed to a traveling RF wave, emitted and received by the same antenna.88

Multituned RF Coils

The last development that merits discussion are multituned coils.89 These RF coils are tuned to several resonance frequencies to detect signals from nuclei other than hydrogen. Having a multituned RF coil system allows the examiner to do metabolic investigations without changing the RF coils and replacing the subject of interest, which also eliminates registration issues. MRI observable nuclei other than hydrogen are not as abundant and, thereby, the image SNR is much lower.

Discussion

In conclusion, RF coils are an essential part of the MRI process, functioning as transmitters or receivers of RF signals. In over four decades of RF coil design, the technology has evolved from a single transceiver to multidimensional arrays used in daily routine in clinic as well in research. The movement towards multi‐purpose applications and clinical efficiency is added to the engineering challenges of achieving maximal SNR at low cost, and improved patient comfort.