Population Pharmacokinetics and Pharmacodynamics of Oral Propranolol in Pediatric Patients With Infantile Hemangioma

Abstract

This study aimed to characterize the population pharmacokinetics and exposure‐response relationship of propranolol (Hemangiol^® Syrup for Pediatric) in infants with infantile hemangioma. Using nonlinear mixed‐effects modeling with 63 pooled sets of plasma concentration‐time data from 32 Japanese patients aged 35‐150 days, we described the disposition of propranolol adequately by a 1‐compartment model with first‐order absorption. The estimated population mean apparent clearance and apparent central volume of distribution were 9.34 L/h and 146 L, respectively. Body weight and postnatal age influenced the population pharmacokinetic model. The clinical end points—success (complete or nearly complete resolution of the target hemangioma) and failure—at weeks 12 and 24 were characterized by logistic regression using the area under the concentration‐time curve (AUC), estimated from the final population pharmacokinetic model, as an exposure predictor. The logistic regression showed that a higher AUC was associated with a higher probability of successful treatment. At each exposure level, probability of successful treatment was correlated with gestational age and treatment duration. Model‐predicted probabilities of successful treatment were consistent with actual results in the clinical trial. Simulations using several dosing regimens indicated that oral propranolol at 3 mg/kg per day was effective and would be appropriate for treating Japanese infants. These simulation results can support optimization of dosing regimens, such as selecting amounts, treatment durations, and dosing intervals, for clinical use.

Infantile hemangioma is the most common soft‐tissue tumor in infants. When there is a risk of its being life threatening, causing functional impairment, or causing scarring and disfigurement, infantile hemangioma should be treated immediately after onset. Oral propranolol is the first‐line therapy for treating infantile hemangioma.1 The mechanism of action of propranolol on infantile hemangioma is not well understood, but the drug was proposed to regulate hemangioma cell proliferation through catecholamine production or the vascular endothelial growth factor pathway.2 The dose of propranolol used for treating infantile hemangioma ranges from 0.5 to 3 mg/kg daily, and many studies have used 2 mg/kg daily.1 In a multicenter clinical trial, 3 mg/kg daily was superior to 1 mg/kg daily.3 Therefore, the approved dose for the propranolol‐based pharmaceutical product “Hemangiol® Syrup for Pediatric 0.375%” is 3 mg/kg daily. A phase 3 clinical trial of propranolol syrup in Japanese pediatric patients with infantile hemangioma confirmed the efficacy of 3 mg/kg daily administered for 24 weeks.4 The trial also evaluated plasma propranolol concentrations. There is little information on the therapeutic effects of different doses and treatment durations in Japanese infantile hemangioma patients. Moreover, no reports have described the relationship between plasma propranolol exposure and therapeutic effects on infantile hemangioma in any ethnic group. In adults, the pharmacokinetic properties of propranolol hydrochloride are well known.5, 6, 7, 8 However, in children, especially infants, such information is limited.9, 10 In a previous study, body weight–normalized oral clearance was similar in infants as in adults.11

In this retrospective post hoc analysis we developed a population pharmacokinetic model to describe propranolol pharmacokinetics in infantile hemangioma patients and identified potential sources of pharmacokinetics variability. We also established a pharmacodynamic (PD) model to describe the relationship between propranolol exposure and its therapeutic effects in infantile hemangioma.

Methods

Study Design and Patients

The study protocol and informed consent form were approved by the Pediatric Clinical Trials Network Central Institutional Review Board for 8 institutions or the respective Institutional Review Boards of the remaining 5 institutions.4 The parent(s) of all patients provided written informed consent before enrollment. The study was conducted in accordance with the Declaration of Helsinki and Japanese Good Clinical Practice Guidelines. Data were obtained from a multicenter, open‐label, phase 3 study in infantile hemangioma patients conducted at 13 sites in Japan.4 Infantile hemangioma patients meeting all the following criteria were eligible for this study: age 35‐150 days at enrollment and proliferating infantile hemangioma (target hemangioma) with a minimum diameter of 1.5 cm.

Drug Administration, Blood Sampling, and Bioanalysis

Propranolol solution 3.75 mg/mL (propranolol base) was orally administered for 24 weeks. Treatment with each daily dose divided into 2 administrations was initially 1 mg/kg propranolol solution daily and then was increased at 1 mg/kg daily increments to 3 mg/kg daily every other day (titration period). All patients were treated with 3 mg/kg daily propranolol solution after the titration period. Propranolol solution was administered during or immediately after meals.

For pharmacokinetics measurements, 2 blood samples (250 μL each) were obtained from each patient. The first data point was selected from the following schedule: 1, 2, 3, 4, or 6 hours after administration of the study drug (morning) at 1 day after the start of propranolol administration at 3 mg/kg daily. The second point was at 2 hours after morning intake in week 12. Plasma propranolol concentrations were measured, after methanol extraction, by liquid chromatography with tandem mass spectrometry, with results validated over the concentration range 0.5‐250 ng/mL in accordance with Food and Drug Administration guidelines for bioanalytical method validation.12 The calibration curve had good linearity (correlation coefficient > 0.9994) with a back‐calculated accuracy of 94.4% to 105.1%. The intra‐ and interassay precision values were 4.7% to 6.3% and 2.8% to 9.3%, respectively. The intra‐ and interassay accuracy values were 93.4% to 101.6% and 97.1% to 103.7%, respectively. Propranolol in the plasma was stable for 3 months during storage at −20°C, and all samples were analyzed within that storage period.

Efficacy Assessments

The efficacy in the target infantile hemangioma was evaluated by 2 independent, trained, and validated readers using standardized digital photographs taken at weeks 12 and 24 and was expressed as the success rate. Treatment success was defined as centralized assessment of complete or nearly complete resolution of the target infantile hemangioma at week 24. Nearly complete resolution was defined as a minimum degree of telangiectasia, erythema, skin thickening, soft‐tissue swelling, and/or distortion of anatomical landmarks.4

Data Analyses

Population pharmacokinetic/PD analysis was performed using nonlinear mixed‐effects modeling (NONMEM version 7.3; ICON Development Solutions, North Wales, Pennsylvania) with first‐order conditional estimation with interaction method. Graphics and data‐set creation were performed using R version 3.2.2 (R Foundation, Vienna, Austria), Xpose4 version 4.5.3 for the statistical package R, and SAS version 9.3 (SAS Institute Inc, Cary, North Carolina). The population pharmacokinetic/PD model was built sequentially. First, the population pharmacokinetic model was developed, and next, the probability of successful treatment was modeled with each individual area under the concentration‐time curve (AUC) calculated as (dose)/(estimated population mean apparent clearance [CL/F]), based on each patient's dose and empirical Bayesian estimated CL/F.

Population Pharmacokinetic Modeling

A 1‐compartment model was used for pharmacokinetic modeling. The first‐order absorption rate constant (k_a) was fixed at the value calculated according to the equation t_max  =  Ln(k_a / k_el)/(k_a − k_el), using previously reported pharmacokinetic parameters11 because of a lack of sampling points. Interindividual variability on each parameter assumed a log‐normal distribution and was estimated with an exponential error model. An additive error model, a proportional error model, and a combination of additive and proportional error models were investigated to describe the residual variability. A basic model was selected using the Akaike information criterion. Body weight, postnatal age, postmenstrual age, height, serum creatinine, aspartate aminotransferase, alanine aminotransferase, and sex were examined as candidates for pharmacokinetic covariates. As a structural covariate, a model using fixed theoretical exponents (0.75 for CL/F and 1 for apparent central volume of distribution [V/F]) with body weight was included in the basic model to account for the dose calculation (in mg/kg) and growth and development of the infants. The selection of covariates to be included in the model was conducted using stepwise forward selection (P < .05), followed by backward elimination (P < .01), based on changes in objective function value (OFV). Continuous covariates were modeled with a power function centered on a median value. A categorical covariate was incorporated as a discrete indicator variable. The adequacy of the constructed population pharmacokinetic model was assessed using goodness‐of‐fit plots. Goodness‐of‐fit was investigated using plots of observations versus population prediction (PRED) and individual prediction (IPRED), conditional weighted residuals13 versus time after the first administration and time after the last administration, conditional weighted residuals versus PRED and absolute individual weighted residuals versus IPRED. Shrinkage in random effects was computed to guide the appropriateness of using ETA (η, empirical Bayes estimate of the interindividual random effect) and IPRED values in the goodness‐of‐fit assessment.14 The ability of the final population pharmacokinetic model to describe observed concentration data was evaluated by visual predictive check. A total of 1000 simulations were performed with the final population pharmacokinetic model, and the 90% prediction interval (PI) was calculated and used to overlay the observed data for visual predictive check. Evaluation of model robustness was performed using the nonparametric bootstrap approach with Perl speaks NONMEM version 4.4.8.15 The median values and 95%CIs for the parameter estimates obtained from 1000 bootstrap replicates of the original dataset were compared with the original population parameters.

Population Pharmacokinetic/PD Modeling

Exposure‐response analysis was performed in a total of 32 infants with infantile hemangioma for whom propranolol concentration data and clinically relevant measurements were available. Comparisons of exposures estimated from individual post hoc parameters between the efficacy determination results—success (complete or nearly complete resolution of the target hemangioma) and failure—were performed. Each patient's exposure at week 24 was obtained as an extrapolated value, using the final population pharmacokinetic model. In addition, the exposure‐response relationship was evaluated using a logistic regression analysis. The probability of achieving treatment success that occurred by the final evaluation time was used as the dependent variable, and each AUC estimated from the final population pharmacokinetic model was used as the independent variable. The probability that the event (treatment success versus failure) occurred as a function of independent variables was described as follows:

$$\begin{array}{c}\hfill \mathrm{Ln}(\mathrm{odds})=\mathrm{Ln}[P_{\mathrm{i}}/(1-P_{\mathrm{i}})]=\alpha +{\beta }_1{\mathrm{X}}_1+\cdots +\\ \hfill {\beta }_{\mathrm{n}}{\mathrm{X}}_{\mathrm{n}}+\eta \end{array}$$

where P _i is the probability of the event in the i‐th patient and α is the baseline Ln(odds) of the event; β₁···β_n denotes regression coefficients; X₁···X_n denotes unit changes in the independent variables; and η is an individual random effect in the logit transformation of P. The value of η was fixed at 0 because the precision of estimated interindividual variability was not high. The covariates tested and the exploration of covariates in the logistic regression analyses were according to methods described in the population pharmacokinetic modeling section. To assess robustness of each estimated parameter, a bootstrap analysis was performed. The logistic analysis was conducted using NONMEM with the first‐order conditional estimation method with likelihood options.

Model‐Based Simulation

Using the developed model, efficacy of 24 week repeated oral administration of propranolol at 3 mg/kg daily, divided into 2 doses, was simulated in patients whose ages were 1‐2, 2‐3, 3‐4, 4‐5, and 5‐6 months at the beginning of treatment. Body weight for the age was set to the median weight based on a general survey of Japanese people and a hospital survey,16 and the gestation period was set to 240 or 280 days. Furthermore, for an age of 3‐4 months at the beginning of treatment, efficacy for exposure at a dose of 3 mg/kg and efficacy at daily doses of 1 and 2 mg/kg were examined. In all cases the number of simulations was 1000. To divide 3 mg/kg into 2 doses per day, the interval between 2 doses in the same day was set to 6, 9, or 12 hours, and this approach was repeated for 7 days. Subsequently, trough and peak levels were simulated (number of trials = 100 000). To execute the simulation, NONMEM and R were used.

Statistical Analysis

Statistical analyses were conducted with R (version 3.2.2; https://www.R-project.org/). The Mann‐Whitney U‐test was applied to exposure levels, stratified according to efficacy determination results. Differences were considered to be significant at P < .05.

Results

Patient Baseline Characteristics

For population pharmacokinetic/PD analysis, 63 propranolol plasma concentration‐time records were obtained in 32 patients for 12 weeks from the beginning of treatment. The PD analysis data set consisted of 64 measurements, taken at 12 and 24 weeks after the beginning of treatment. Patient demographics and characteristics are shown in Table 1. Ages at the beginning of treatment were 53‐150 (median 113) days and weights were 3.15‐8.71 (median 6.12) kg. Of the 32 patients, 23 were female. The highest observed individual plasma propranolol concentration was 299 ng/mL at 3 hours after administration, on day 1 of the maintenance dose. Plasma concentrations (minimum to maximum) at 2 hours after the administration at 12 weeks of treatment were 15.4‐177 ng/mL (Supplemental Figure S1). According to the centralized assessments, the success rates at weeks 12 and 24, from baseline, were 43.8% (14/32 patients) and 78.1% (25/32 patients), respectively.

Table 1.

Demographic and Baseline Characteristics and Efficacy Assessment Data of 32 Patients Included in the Population Pharmacokinetic/Pharmacodynamic Analyses

Parameter	Median (Range)
Body weight (kg)	6.115 (3.15‐8.71)
Postnatal age (days)	113 (53‐150)
Postmenstrual age (days)	374 (317‐437)
Gestational age (days)	272 (213‐293)
Height (cm)	60.6 (49‐67.5)
Aspartate aminotransferase (U/L)	40.5 (29‐97)
Alanine aminotransferase (U/L)	32 (13‐71)
Serum creatinine (mg/dL)	0.2 (0.1‐0.28)
Sex (male/female)	9/23

Centralized assessment of target infantile hemangioma at week 12 (success/failure), 14/18; centralized assessment of target infantile hemangioma at week 24 (success/failure) 25/7; IH, Infantile hemangioma.

Population Pharmacokinetic Analysis

The plasma propranolol concentration profile was described using a 1‐compartment model with a first‐order absorption and elimination process (Supplemental Figure S2). Residual variability was modeled as a proportional error, and interindividual variability was modeled using an exponential error term on CL/F. Interoccasional variability in CL/F and covariance between CL/F and V/F were examined, but the model was not improved. For CL/F and V/F, effects of body weight were included with fixed theoretical exponents (0.75 for CL/F and 1 for V/F). Furthermore, analysis of covariates affecting propranolol pharmacokinetics confirmed the effects of postnatal age on CL/F.

The adequacy of the developed final population pharmacokinetic model was evaluated using goodness‐of‐fit plots. Goodness‐of‐fit plots revealed the high predictive performance of the final population pharmacokinetic model (Figures 1A and 1B), and there was little bias in prediction dependent on concentration and time (Figures 1C, D and E). There was a slight trend in the relationship between individual weighted residuals and IPRED (Figure 1F), which could be due to a limited sample size in this study. In all cases there was improvement of goodness‐of‐fit in the final model, compared with in the base model, the latter being the same structural model without the effects of postnatal age on CL/F (Supplemental Figure S3). Table 2 shows the estimated parameters of the final population pharmacokinetic model and results of the bootstrap analysis. Regression equations for each parameter in the final population pharmacokinetic model were:

$$\begin{array}{c}\hfill \mathrm{CL}/\mathrm{F}\left(\mathrm{L}/\mathrm{h}\right)=9.34\times {\left(\mathrm{body}\mathrm{weight}/6.115\right)}^{0.75}\times \\ \hfill \left(\mathrm{postnatal}\mathrm{age}/113\right)\times \exp ({\eta }_{\mathrm{CL}})\end{array}$$

$$\mathrm{V}/\mathrm{F}\left(\mathrm{L}\right)=146\times \left(\mathrm{body}\mathrm{weight}/6.115\right)$$

$${\mathrm{k}}_{\mathrm{a}}\left({\mathrm{h}}^{-1}\right)=1.03$$

Figure 1.

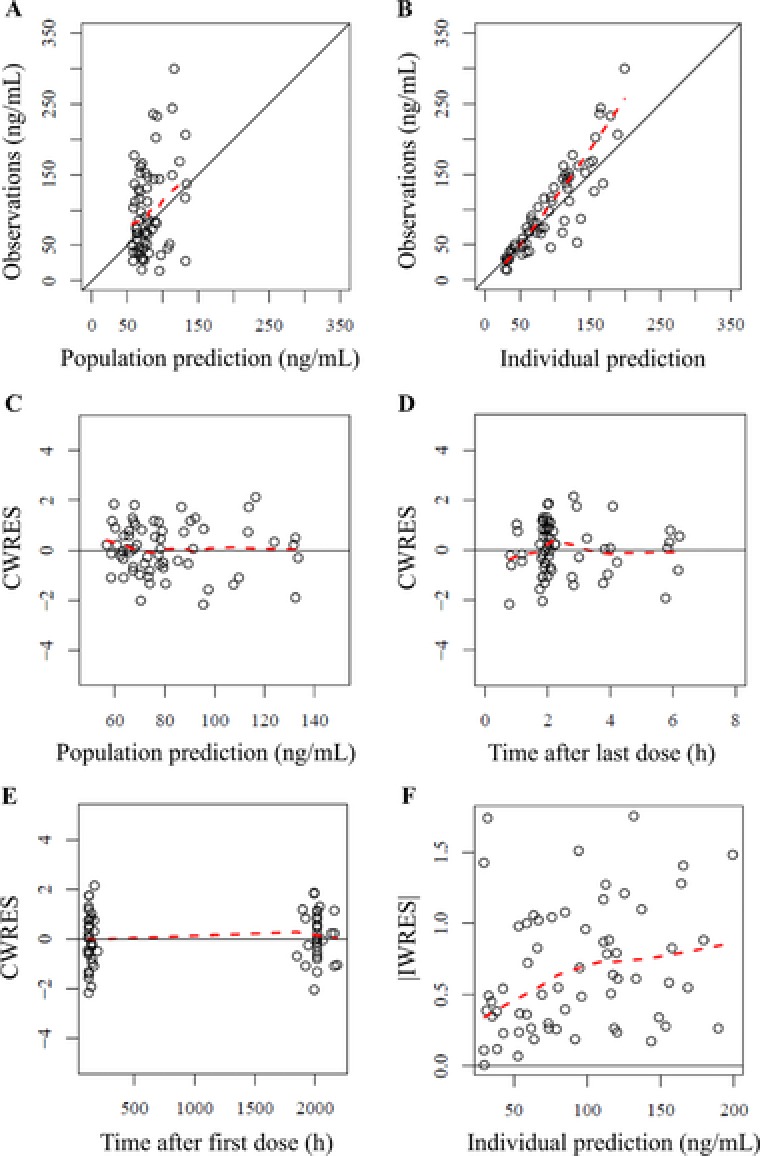
Goodness‐of‐fit plots of the final population pharmacokinetics model. A, Population prediction (PRED) vs observations. B, Individual predictions (IPRED) vs observations. C, PRED vs conditional weighted residuals (CWRES). D, Time after the last dose vs CWRES. E, Time after the first dose vs CWRES. F, IPRED vs absolute individual weighted residuals (|IWRES|). Population predictions were performed using population mean parameters. Individual predictions were obtained using individual empirical Bayesian estimated parameters. The solid black lines represent the lines of identity (A and B) and y = 0 (C, D, and E). The dashed red lines represent lowess curves.

Table 2.

Final Population Pharmacokinetic and Pharmacodynamic Parameters and Results of Bootstrap Replicates for Propranolol

	Original Data		1000 Bootstrap Sample Data
Parameter	Estimate (%RSE)	Shrinkage (%)	Median	95%CI
Pharmacokinetics
CL/F (L/h)	9.34 (13.7)	NA	9.67	7.32‐13.0
V/F (L)	146 (26.8)	NA	141	64.8‐228
ka (h–1)	1.03 fixed	NA	1.03 fixed	NA
PowerAGE for CL/F	1 fixed	NA	1 fixed	NA
IIV CL/F (%)	76.9 (29.3)	5.9	75.5	50.7‐99.3
Proportional error (%)	34.0 (11.9)	20.0	33.5	25.2‐42.8
Pharmacodynamics
Baseline	–4.64 (12.6)	NA	–5.02	–8.20 to –3.89
Slope	2.64 (36.6)	NA	2.84	0.909‐5.85
Treatment duration (weeks) on baseline	0.215 (14.4)	NA	0.234	0.175‐0.373
Gestational age (days) on baseline	0.0583 (44.4)	NA	0.0637	0.0223‐0.252

Baseline indicates intercept coefficient of logistic regression; CL/F, apparent oral clearance; IIV, interindividual variability; k_a, absorption rate constant; NA, not applicable; Power_{AGE for CL/F}, power exponent of AGE for CL/F; RSE, relative standard error; slope, slope of drug effect; V/F, apparent volume of distribution.

For precision of estimated parameters, in the final population pharmacokinetic model, all relative standard errors were within 30%, indicating high precision (Table 2). A sensitivity analysis for k_a fixed at a value calculated using published parameters11 demonstrated that fixing the k_a value had minimal effect on estimation of the remaining parameters (Supplemental Table S1). The effect of postnatal age on CL/F was fixed at 1 through a backward elimination step (ΔOFV = 0.265). Each estimated parameter calculated with the bootstrap samples (median and 95%CI) agreed well with estimated parameters obtained with the final population pharmacokinetic model, confirming the robustness of the model. Furthermore, examination of the median and 5% and 95% PIs of the 1000 simulated data in VPC, compared with the actual values, confirmed that the final population pharmacokinetic model described actual values well (Figure 2).

Figure 2.

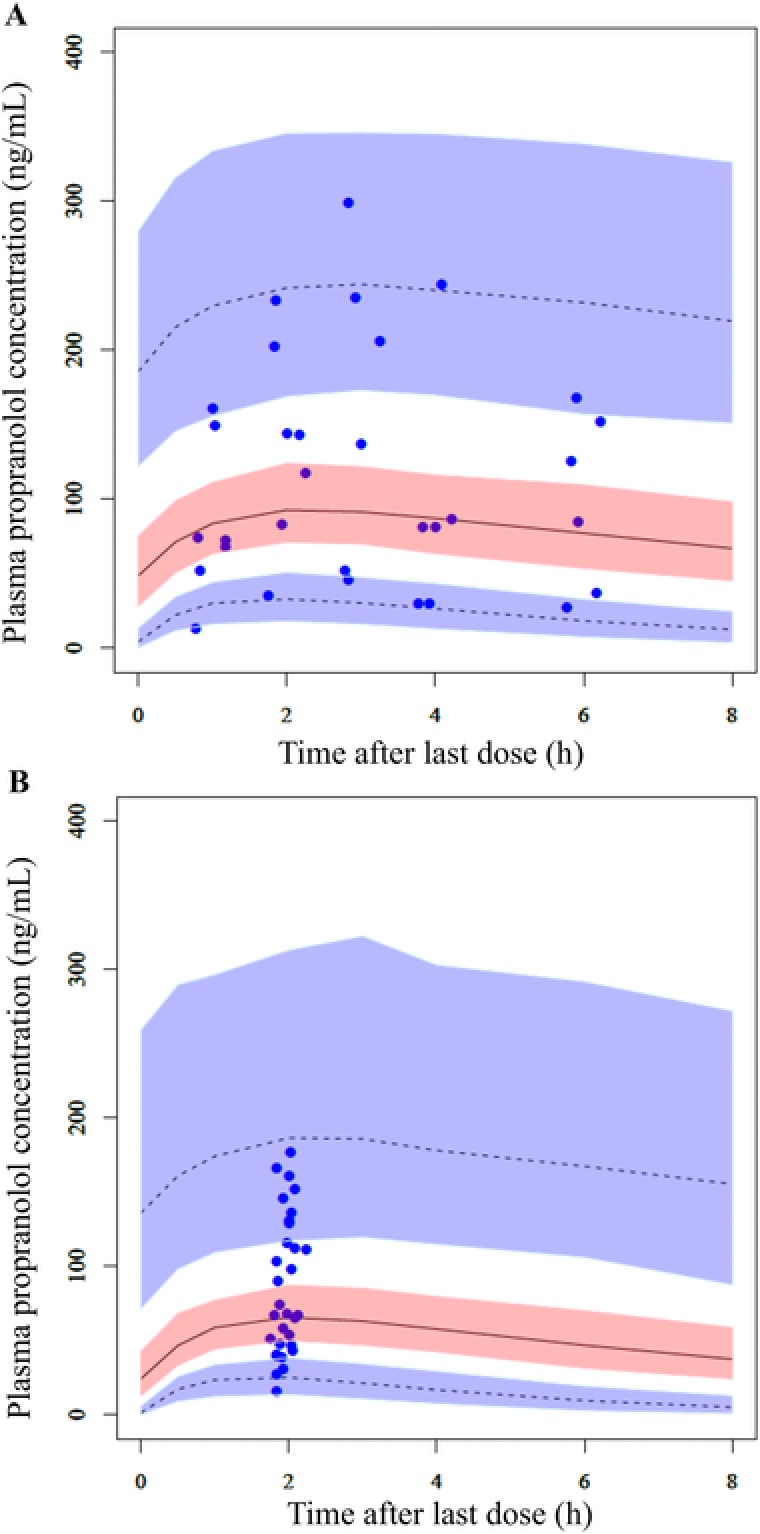
Visual predictive check of propranolol plasma concentrations at (A) 1 day and (B) steady state (week 12) after administration of the maintenance dose of 3 mg/kg daily. The 5th, 50th, and 95th percentiles (lower dashed, middle, and upper dashed lines, respectively) and corresponding simulated 95% confidence intervals (shaded area) obtained from 1000 simulations are shown, along with observed propranolol concentrations (closed circles).

Population Pharmacokinetic/PD Analysis

Each patient's exposure levels (trough, peak, and AUC) at 12 and 24 weeks after the beginning of treatment, as estimated based on individual post hoc predictions from the final population pharmacokinetic model, were compared with efficacy determinations (Figure 3). At 12 weeks after the beginning of treatment, the exposure indexes showed no differences between patients reaching success and those reaching failure end points. However, at 24 weeks, exposures were significantly lower in patients reaching the failure end point than in those reaching the success end point. Subsequently, the exposure‐response relationship was assessed using a logistic regression model. In the analyses, a significant relationship between the increase in odds and the AUC was identified (ΔOFV > 6.63, P < .01). In addition, factors that influence success rates, treatment duration (weeks), and gestation period (days) were included in the model. Table 2 shows median and 95%CI values calculated from the estimated parameters and bootstrap analyses. The model equation of population success rate P in which “treatment success” occurred was:

$$\begin{array}{c}\hfill \mathrm{Ln}\left(\mathrm{odds}\right)=-4.64+0.215\times \mathrm{treatment}\mathrm{duration}\left(\mathrm{weeks}\right)\\ \hfill +0.0583\times (\mathrm{gestational}\mathrm{age}\left[\mathrm{days}\right]-272)\\ \hfill +2.64\times \mathrm{AUC}/1000\end{array}$$

Figure 3.

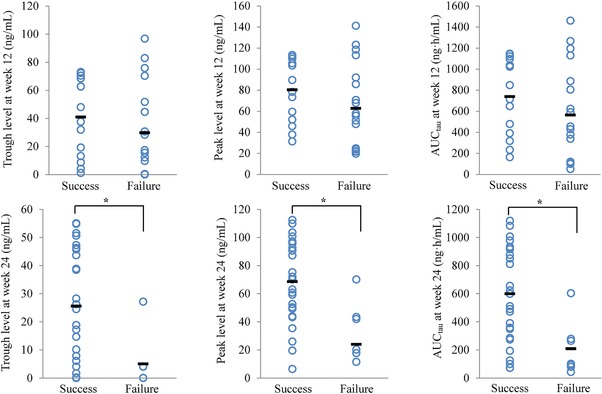
Relationship between exposure and efficacy determinations at weeks 12 and 24. Trough, peak, and area under the concentration‐time curve (AUC_tau) were obtained from individual empirical Bayesian estimated parameters, based on the final population pharmacokinetics model. The horizontal bar for each group is the mean value. Statistical comparisons were performed using the Mann‐Whitney U test (^* P < .05).

The model‐predicted percentage of patients achieving treatment success adequately described the observed values (success rates, Figure 4). In addition, the observed values calculated for patients stratified based on AUC levels were well contained within 95% PIs at both week 12 and week 24 (Supplemental Figure S4). The median values of the estimates from bootstrapping were similar to the population estimates in the final population pharmacokinetic/PD model, and the significance of covariates was verified by the finding that 95%CI values of all parameters did not include 0.

Figure 4.

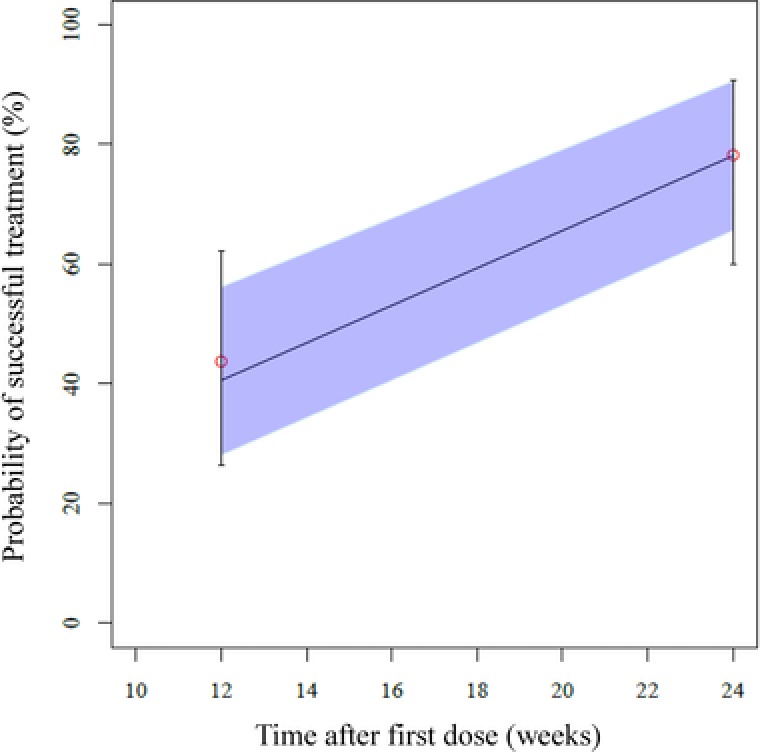
Visual predictive check representing probability of successful treatment vs time. The median (line) and 95% confidence intervals (shaded area) obtained from 1000 simulations are shown. Also shown are the actual observations with 95% confidence intervals.

Model‐Based Simulation

Using the developed model, for each age group and gestation period at the beginning of the treatment, the success rate was simulated for an administered dose of 3 mg/kg daily. The results showed that, for patients at younger ages at the beginning of the treatment, success rates were higher. However, success rates increased with treatment duration and converged to similar levels at 24 weeks (Figure 5A). In addition, success rates were lower in premature infants than in full‐term infants (Figure 5B). Similarly, for each exposure (20th, 50th, and 80th percentiles) and administered dose (1, 2, and 3 mg/kg), the success rate was simulated and visualized (Figure 5C, Supplemental Table S2 and Figure 5D).

Figure 5.

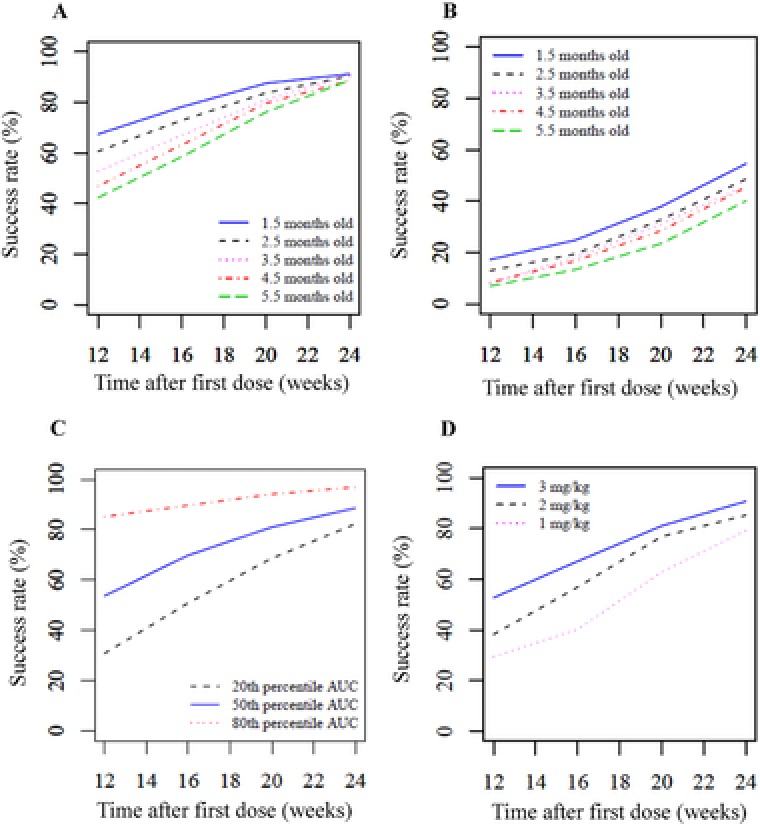
Simulation of success rates with propranolol for treating infantile hemangioma in each population. Success rates represent the percentages (median) of patients achieving successful treatment after 12, 16, 20, and 24 weeks of treatment. A, 3 mg/kg daily; age 1.5‐5.5 months at first dose; gestation period 280 days. B, 3 mg/kg daily; age 1.5‐5.5 months at first dose; gestation period 240 days. C, 3 mg/kg daily; 20th, 50th, or 80th percentile area under the concentration‐time curve; age 3.5 months at first dose; gestation period 280 days. D, 1, 2, or 3 mg/kg daily; age 3.5 months at first dose; gestation period 280 days.

Furthermore, trough and peak levels were simulated with the dose of 3 mg/kg daily, divided into 2 administrations, and the intervals between these 2 oral administrations were set at 6, 9 and 12 hours for 7 days. The results showed that the 90% PI values of the peak level at steady state, at 7 days after administration were 28.3‐234 (median, 84.3), 25.6‐225 (median, 75.4), and 23.9‐214 (median, 69.3) ng/mL for administration intervals of 6, 9, and 12 hours, respectively (Table 3 and Supplemental Figure S5). The rate of change in peak level at the administration interval of 9 hours was ±15% for all administration intervals, thus indicating similar plasma levels.

Table 3.

Simulated Trough and Peak Propranolol Concentrations After 7 Days of Repeated Administrations of 3 mg/kg Daily, With Each Daily Dose Divided Into 2 Administrations

	Trough (ng/mL)b		Peak (ng/mL)
Dosing Intervala	Median	90% PI	Median	95% PI
6 hours	16.7	0.119‐142	84.3	28.3‐234
9 hours	20.8	0.335‐150	75.4	25.6‐225
12 hours	26.4	0.981‐159	69.3	23.9‐214

PI indicates prediction interval.

^aDosing intervals between first and second administrations within the same day.

^b168 hours after the first dose.

Discussion

This study reported, for the first time, an analysis of propranolol exposure‐response relationship in infantile hemangioma patients. The success rate for infantile hemangioma was expressed as a function of exposure (AUC), confirming that treatment duration and gestation period affect infantile hemangioma.

The pharmacokinetics of propranolol in Japanese infantile hemangioma patients was well described by a 1‐compartment model with first‐order absorption and elimination. In these trial data focused on infants, a 1‐compartment model was used because of limitations in how many blood samples per patient could be collected. This was considered valid because propranolol pharmacokinetics in adults17 and non‐Japanese infants,11 with 6 blood‐sampling points per patient (trough, 1, 2, 4, 6, and 9 hours postdosing), more than in this trial, were also well described by a 1‐compartment model. In addition to the favorable results of a sensitivity analysis of fixing the k_a value, we believe that this fixed value was acceptable because it had been reported under the same meal conditions as those in this study. In covariate modeling, body weight, postnatal age, postmenstrual age, and serum creatinine, which reflect developmental characteristics of infancy while also having high versatility in clinical applications, were selected as candidates. Because of the effects of body size and maturation, as well as the fact that the dose of propranolol is normally set based on body weight, effects of body weight were included through a model using fixed theoretical exponents.18 In addition, the effect of postnatal age on CL/F was incorporated in the final model. This was interpreted to enable modeling of growth effects that cannot be expressed by body weight. It was reported that postmenstrual age is superior as a descriptor of maturation.18 However, in our analysis, we selected postnatal age because of its association with a greater decrease in objective function and high clinical versatility. Including effects of postnatal age on CL/F in the model was also considered justifiable because renal and metabolic functions, which mature after birth, remained immature in these subjects. It is known that the activity of enzymes involved in metabolizing propranolol differs in ontogeny. CYP2D6 has almost no activity at birth and remains low until 2 weeks of age, developing after 3 weeks and reaching adult levels by 10 years of age.19 CYP2C19 expression is low at birth and increases linearly over the first 5 postnatal months, varying 21‐fold from ages 5 months to 10 years.20 There is little CYP1A2 expression at birth, and it develops from 1 to 3 months after birth.21 Interindividual differences in plasma concentrations obtained in the clinical trial were high, and the estimate for interindividual variability of CL/F was also relatively high, at 76.9%. This may have been caused by the contribution of interindividual differences in expression and/or activities of CYP1A2, 2D6, 2C19, and UGT, all relevant to propranolol elimination. However, because genotype data were not acquired, it was difficult to further identify covariates, leaving the cause unknown. Additional studies will be required to identify further factors associated with variations in propranolol pharmacokinetics. Plasma concentrations obtained in this study were nearly consistent with previous results in preterm neonates and 2‐ to 13‐year‐old children.22, 23

To analyze the relationship between exposure and efficacy, we used the exposure index of each subject estimated based on empirical Bayesian estimated parameter obtained in the final population pharmacokinetic model. In the logistic regression analysis a model was examined with a particular focus on AUC. This was because AUC describes mean exposure and can be calculated from CL/F and dose, which include interindividual variability with good estimate precision. In our trial, blood sampling was not performed at 24 weeks after the beginning of treatment. Therefore, values at 24 weeks were extrapolated from the model, but this was considered to be acceptable because:

• Post hoc CL/F values at 24 weeks (median, 3.4 L/[h·kg]) were within ranges previously reported in adults5, 24, 25, 26 (2.16‐5.2 L/[h·kg]) and infants11 (3.3 ± 1.7 L/[h·kg]).

• The final population pharmacokinetic model incorporated effects of body weight and postnatal age, and growth beyond 12 weeks was also considered.

A model describing the efficacy of propranolol in infantile hemangioma was developed as a function of AUC, with treatment duration and gestation period incorporated as factors affecting success rate. The observed increased success rate with treatment duration and higher efficacy with higher dose (exposure) were consistent with randomized controlled trial results3 and trends, as described in many previous clinical reports. Also, the lower limit of the CI values of success rates determined in this study did not overlap with success rates of the placebo group in the controlled trial3 using the same efficacy assessment criteria. Therefore, a drug effect was clearly demonstrated in this study. Although it is known that efficacy increases with gestation period, there have been few reports of therapeutic effects in premature infantile hemangioma patients, so there is not yet consensus on this issue. The number of infantile hemangioma lesions in premature infants is high, and infantile hemangioma is reportedly more severe in such patients.27, 28, 29 In addition, infantile hemangioma exhibits a characteristic sequence of growth and spontaneous involution.2 Thus, including effects of treatment duration and gestational age on the baseline was justifiable because pathology and disease progression of infantile hemangioma may influence placebo effects. Because the number of premature infants included in this study was low (4/32), a larger study would be needed for more detailed and definitive conclusions.

Through various simulations executed using our model, the success rate of propranolol on infantile hemangioma was visualized for postnatal age, gestation period, and dosage. Simulation results showed that oral propranolol at 3 mg/kg daily was effective and would be an appropriate amount for clinical use. These results also suggested that its efficacy would be improved by optimization of dosing regimens, in accordance with patient characteristics. Further studies are needed to clarify the effects on efficacy of adjusting dosages and prolonging treatment durations. A pharmacokinetics simulation showed that, even when the dosing interval between the first (morning) dose and the second (evening) dose on the same day was between 6 and 12 hours, the peak concentration of plasma propranolol remained approximately the same. This indicated that flexible administration of drugs, corresponding to the varied schedules of each infant, would be feasible.

Some genetic polymorphisms in CYP2D6 mainly associated with propranolol metabolism were shown to alter the metabolic function of the enzyme.30 Furthermore, ethnic differences in the frequency of the variant CYP2D6 alleles were reported.31, 32 The contribution of CYP2D6 genetic polymorphisms to propranolol metabolism might be different in infants than in adults. However, propranolol pharmacokinetics (post hoc CL/F) in Japanese infants (mean ± SD = 22.4 ± 17.5 L/h) was similar to that observed in non‐Japanese infants (∼23 L/h).11 In addition, the dosing regimens of propranolol treatment for infantile hemangioma are the same in Japan, North America, and Europe, with no notable ethnic differences in efficacy. Therefore, although further research is necessary, the relationship between exposure and efficacy shown in our study may be generalizable to other ethnic groups.

Finally, our study has several limitations. We performed exposure‐response analysis with a limited sample size, using nonserial sample collection. Therefore, it will be important to update the model in future studies. In addition, to clarify exposure‐response relationships for other treatment durations shorter than 12 or longer than 24 weeks, additional studies will be needed.

Conclusions

Propranolol pharmacokinetics in infantile hemangioma patients can be well described using a 1‐compartment model with first‐order absorption and elimination and is affected by body weight and postnatal age. Analysis of the relationship between exposure and efficacy indicated that the therapeutic effect of propranolol in infantile hemangioma was greater when exposure was increased, and the probability of successful treatment was positively correlated with increasing treatment duration and gestation age. These results suggested that oral propranolol at 3 mg/kg daily was effective and would be an appropriate dose for clinical use. The results of each simulation are potentially useful for optimization of dosing regimens, such as selecting dose levels, treatment durations, and dosing intervals, in accordance with patient characteristics.

Supporting information

Population pharmacokinetics and pharmacodynamics of oral propranolol in pediatric patients with infantile hemangioma