Gradient nonlinearity effects on upper cervical spinal cord area measurement from 3D T1-weighted brain MRI acquisitions

Abstract

Purpose

To explore: (1) the variability of upper cervical cord area (UCCA) measurements from volumetric brain 3D T1-weighted scans related to gradient nonlinearity (GNL) and subject positioning; (2) the effect of vendor-implemented GNL-corrections; and (3) easily applicable methods that can be used to retrospectively correct data.

Methods

A multiple sclerosis patient was scanned at 7 sites using 3T MRI scanners with the same 3D T1-weighted protocol without GNL-distortion correction. Two healthy subjects and a phantom were additionally scanned at a single site with varying table positions. 2D and 3D vendor-implemented GNL-correction algorithms and retrospective methods based on: (1) phantom data fit; (2) normalization with C2 vertebral body diameters; and (3) the Jacobian determinant of non-linear registrations to a template, were tested.

Results

Depending on positioning of the subject, GNL introduced up to 15% variability in UCCA measurements from volumetric brain T1-weighted scans when no distortion corrections were utilized. 3D vendor-implemented correction methods and the three proposed methods reduced this variability to less than 3%.

Conclusion

Our results raise awareness of the significant impact that GNL can have on quantitative UCCA studies and point the way to prospectively and retrospectively managing GNL-distortions in a variety of settings, including clinical environments.

INTRODUCTION

Quantifying spinal cord atrophy in neurologic conditions from various etiologies, including trauma, inflammation, or neurodegeneration, has gained increasing attention in the neuroimaging field, particularly with the development of dedicated spinal cord imaging techniques (1–5). In multiple sclerosis (MS), upper cervical cord area (UCCA) is a surrogate of atrophy, and has been shown to be associated with physical disability, particularly in progressive stages of the disease (6–11). Spinal cord magnetic resonance imaging (MRI) remains technically challenging and adds substantial time to a scanning session, therefore many clinical sites do not routinely acquire dedicated spinal cord MRI that can provide reliable measures of UCCA. However, standard brain high-resolution 3D T1-weighted acquisitions that include the upper cervical cord can be used to provide estimates of UCCA (12,13).

Gradient nonlinearity (GNL) distortions in MRI are a consequence of technical challenges in the design of gradient coils, and an important source of systematic error interfering with the integrity of imaging metrics in longitudinal and multi-site studies. These challenges are particularly important in modern whole-body MRI scanners designed with shorter bores for increased patient comfort and reduced footprint, and fast gradient rise times for faster imaging. Moreover, a recent head-only, compact gradient design was reported to provide increased peripheral nerve stimulation thresholds (14) and very high slew rates (up to 700 T/m/s) that provide significantly improved echo-planar imaging performance (15). However, such systems have significantly increased GNL effects over standard whole-body scanners, including terms associated with asymmetric transverse gradients. Large, multisite initiatives have investigated the effect of GNL-distortions on brain tissue volume quantification (16–19); however, the effect of GNL on UCCA measurements extracted from standard brain T1-weighted acquisitions has not yet been assessed. This is extremely important, as the spinal cord is located in the periphery of the field of view, where GNL effects are expected to introduce maximal errors.

In the present work, we explored: (1) the variability of the UCCA measurements from brain 3D T1-weighted scans related to GNL and subject positioning; (2) the effect of correction algorithms implemented on commercial scanners; and (3) easily applicable methods that can be used to retrospectively correct data acquired without optimal distortion correction.

METHODS

Image data acquisition

All human MRI acquisitions reported in the present study were conducted with the approval of Ethics Boards of the involved institutions.

MS patient acquisition:

A 45-year-old male with stable relapsing-remitting MS was scanned at 7 North American Imaging in Multiple Sclerosis (NAIMS) Cooperative sites within a period of four months using Siemens 3T MRI scanners equipped with different hardware and software versions (4 Skyra, 2 Trio, 1 Verio), with the same uncorrected sagittal 3D T1-weighted MPRAGE protocol extended to the upper cervical spinal cord: voxel size=1×1×1mm³, FOV=256×256×176mm³, TR/TE/TI/FA=1900/2.52/900ms/9°, parallel imaging acceleration factor=2, acquisition time=4:17min. Multi-channel coils were used, with either head-neck elements (64, 20 or 12) or only head elements (32) with good sensitivity in the upper cervical cord region. The acquisition was repeated twice at each site, with repositioning.

Table position variation and distortion correction tests:

To test for table position variation and distortion correction effects on UCCA measurements, two healthy controls (HC, both men, 25 and 40 years old, named HC-A and HC-B) were scanned at a single site using a Siemens 3T Skyra scanner (bore length=173cm) with the same T1-weighted protocol used for the MS patient, with a variety of table positions. Uncorrected and distortion-corrected data (using Siemens’s 2D and 3D methods) were exported. Siemens methods calculate the geometric displacements from the spherical harmonic expansion of the magnetic field generated by the specific gradient coils model (17,20).

Phantom acquisition:

To validate the HC acquisitions performing area measurements without confounding patient motion, a phantom manufactured in-house (a 13mm diameter cylindrical test tube filled with oil) was scanned with varying table positions using the above-mentioned T1-weighted protocol without distortion correction. The phantom was placed on the posterior elements of the head-neck coil with the main axis along the head-foot direction. A vitamin pill was placed on the side of the tube at about the position of the upper cervical cord of subjects laying in the scanner, and a water sphere was placed on top to correctly load the coil.

Healthy control acquisition on a different scanner type:

To test for variability between scanners of different models, HC-B was additionally scanned twice on three Siemens 3T scanners of the same model (Trio, bore length=213cm, 40 cm longer than the Skyra) with T1-weighted brain protocols extended to the upper cervical cord without distortion correction.

Data analysis

UCCA measurements:

UCCA was measured on the brain T1-weighted acquisitions by extracting five consecutive 1mm thick axial slices perpendicular to the long axis of the cord at the C2-C3 disc level, and measuring the average area of the cord(13) using the semi-automated “cord finder toolbox” of the software JIM (version 6.0) (21) with fixed settings(22): nominal cord diameter 8mm, number of shape coefficients 24, order of longitudinal variation 12. The markers requested by the toolkit were placed at the center of the spinal cord in each of the five slices.

After having evaluated the reliability of the method on ten HC (Supporting Information), UCCA of the MS patient, HC-A and HC-B was measured by a single operator (NP)

Determination of distance between scanner isocenter and C2-C3 disc level:

The C2-C3 disc distance from the scanner isocenter (Z_CI) was measured by determining the Z coordinate of the central slice that was extracted for the UCCA measurement for each individual (information provided by the JIM Multi-planar Reconstruction tool). If the scanner table was moved after patient positioning, the actual table position was extracted from the DICOM header and added to the Z coordinate.

Retrospective correction methods:

Phantom fit:

On uncorrected acquisitions of the cylindrical phantom test tube, axial areas (A(Z_CI)) were measured at the vitamin pill level as a function of Z_CI. A(Z_CI) was normalized to the area measured at the scanner isocenter position (A₀), and fitted to a quadratic model (least squares regression, ε(Z_CI) indicates the residual):

$$\mathrm{A}({\mathrm{Z}}_{\text{Cl}})∕{\mathrm{A}}_0=1+\mathrm{a}\times {\mathrm{Z}}_{\text{Cl}}+\mathrm{b}\times {{\mathrm{Z}}_{\text{Cl}}}^2+\epsilon ({\mathrm{Z}}_{\text{Cl}}).$$ [1]

The estimated parameters (a,b) were used to extrapolate the UCCA measured from the uncorrected images of HC-A and HC-B to the scanner isocenter position (obtaining UCCA₀ for each UCCA(Z_CI)).

Normalization using C2 vertebral body diameters:

For all uncorrected acquisitions of HC-A, HC-B and the MS patient, the anterior-posterior and right-left diameters of the C2 vertebral body were measured with the software JIM on a single slice. UCCA(Z_CI) was divided by the product of the two diameters (Vert(Z_CI)) for each acquisition.

For visual comparison with uncorrected data, a further normalization to the value measured in the acquisition with the table positioned closest to the scanner isocenter (Z_CImin) was performed using the equation:

$$\text{UCCA}{({\mathrm{Z}}_{\text{Cl}})}^{,}=[\text{UCCA}({\mathrm{Z}}_{\text{Cl}})∕\text{Vert}({\mathrm{Z}}_{\text{Cl}})]\times \text{Vert}({\mathrm{Z}}_{\text{Clmin}}),$$ [2]

where UCCA(Z_CI)’ indicates the normalized value.

Normalization using the Jacobian determinant of non-linear registrations:

Single-subject templates were created for HC-A and the MS patient as described by Avants et al (23) using the Advanced Normalization Tools (ANTs) software package (http://stnava.github.io/ANTs). Briefly, this approach employs a non-linear, symmetric, and group-wise registration procedure that builds an optimal template representing the average shape of all images. For this step, “antsMultivariateTemplateConstruction2.sh” was run with default parameters, combining rigid (6 parameters), affine (12 parameters) and deformable registrations. Degrees of freedom in the deformable registration were equal to the number of voxels in the image times 3 (for three dimensional displacement vectors). Four levels of spatial resolution were used for each registration step. After template creation, all images were nonlinearly registered to the respective single-subject template using the SyN algorithm(24) and a cross-correlation similarity metric. The deformation field for each transformation was computed. To serve as a measure of in-plane area change, the deformation field in the Z-direction was ignored (substituting values with zeroes). The determinant of the modified Jacobian (representing the in-plane area shrinkage or expansion) was computed voxel-by-voxel. An ROI over 3 slices was drawn on the C2 vertebra on each template, and the average Jacobian of voxels within the ROI was extracted for each image. The UCCA was divided by this latter value for each image. A variant of the method can be found in Supporting Information and Supporting Figures S1 and S2.

RESULTS

Inter-site measurement variability in a single MS patient:

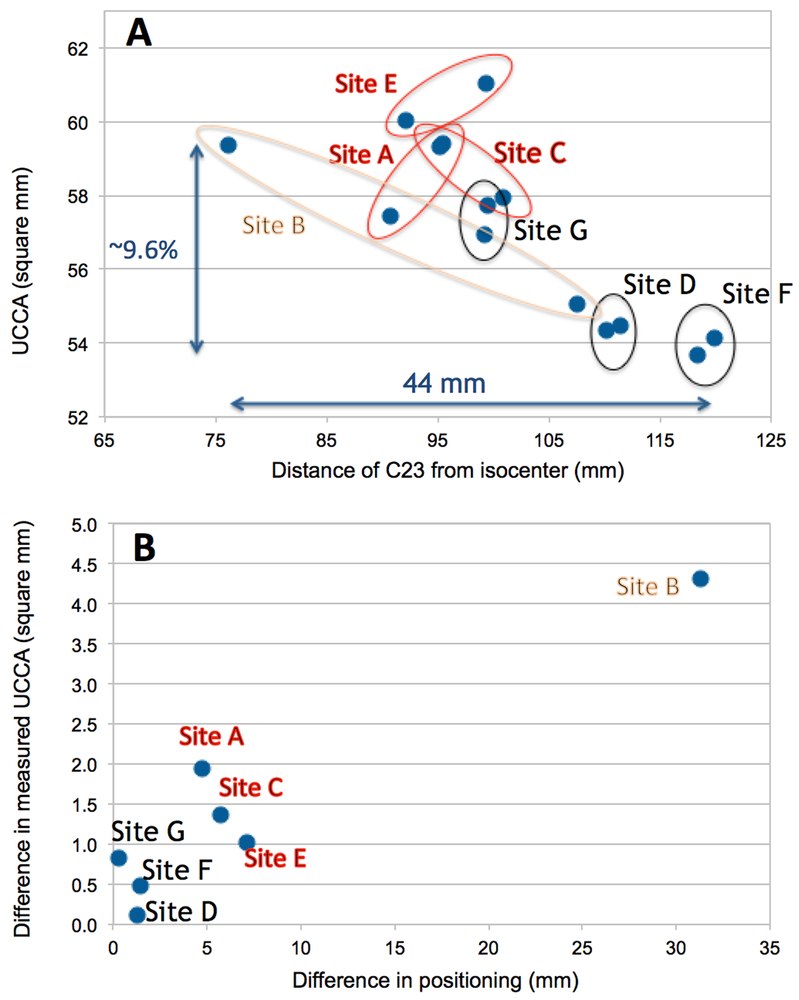
Across sites, the relative Z_CI ranged from 76mm (Z_CImin) to 120mm (Z_CImax), which corresponded to a 9.6% difference in UCCA (59.4 to 53.7mm²) (Figure 1A). The average UCCA measured at the 7 sites was 57.2mm² with 2.5mm² standard deviation (SD). Within sites, variability in Z_CI with repositioning resulted in poorer rescan reproducibility (Figure 1B).

Figure 1.

A: UCCA of the multiple sclerosis patient measured at the 7 NAIMS sites as a function of the distance between the C2-C3 disc and the scanner isocenter (Z_CI). B: Within sites variability in Z_CI with repositioning was associated with poorer rescan reproducibility.

Table position variation and effect of vendor-implemented distortion correction:

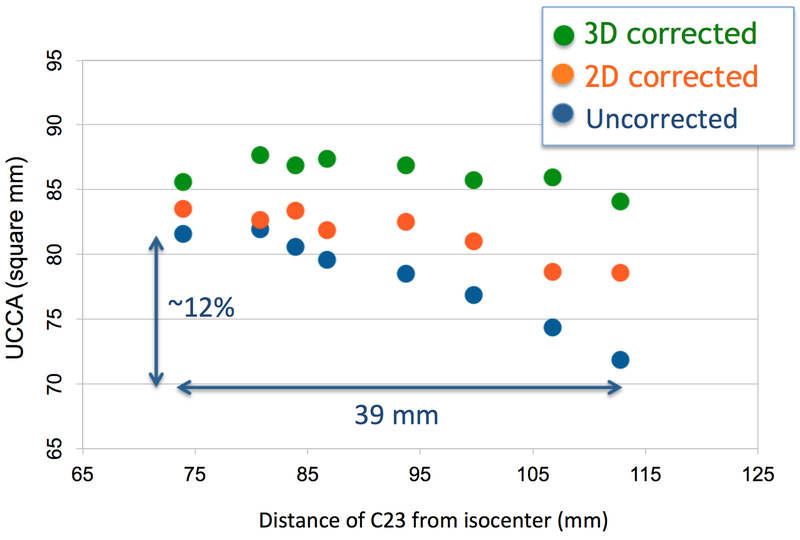
A quadratic decrease in UCCA as a function of Z_CI was found in HC-A and HC-B scanned without distortion correction at a single site. For HC-A, the relative Z_CI ranged from 67 to 121mm, which corresponded to a 15.2% difference in UCCA (81.2–68.9mm², mean(SD)=76.1(4.2)mm²). For HC-B (Figure 2), the relative Z_CI ranged from 74 to 113mm, which corresponded to a 12% difference in UCCA (81.6–71.8mm², mean(SD)=78.2(3.6)mm²). The range of Z_CI (Z_CImax-Z_CImin) was very similar to what was observed with the single MS patient scanned across the 7 scanners, with similar corresponding relative reduction in measured UCCA.

Figure 2.

UCCA as a function of the distance of the C2–3 disc from scanner isocenter for a healthy control: uncorrected and distortion-corrected data.

For HC-A, vendor-implemented 2D correction decreased the difference of UCCA for extreme table positions from 15.2% to 6.8% (SD was reduced from 4.2mm² to 2.0mm²). 3D correction further improved the results, reducing the difference of UCCA for extreme table positions to 2.1% (SD was reduced to 1.0mm²). For HC-B, 2D correction decreased the difference of UCCA for extreme table positions from 12% to 5.9% (SD was reduced from 3.6mm² to 2.0mm²). 3D correction reduced the difference of UCCA for extreme table positions to 1.8% (SD was reduced to 1.2mm²) (Figure 2).

Table 1 summarizes the effect of vendor-implemented corrections together with the effect of the retrospective methods, which will be described in the subsequent sections.

Table 1. Effect of the different correction methods on UCCA measures.

Top row: percent difference of measured UCCA at the extreme table positions (Z_CImin and Z_CImax). Bottom row: standard deviation of the group of measures performed with different table positions or at the different sites.

Correction method:	None	Scanner 2D	Scanner 3D	Phantom fit	Vertebral diameters	Jacobian
Healthy Control A (single site)	15.2% 4.2mm2	6.8% 2.0mm2	2.1% 1.0mm2	2.9% 0.9mm2	1.9% 1.1mm2	0.7% 1.1mm2
Healthy Control B (single site)	12.0% 3.6mm2	5.9% 2.0mm2	1.8% 1.2mm2	3.2% 1.3mm2	1.0% 1.9mm2	–
MS patient (across 7 sites)	9.6% 2.5mm2	–	–	–	1.1% 1.6mm2	1.2% 1.7mm2

Between-scanner variability for a healthy control:

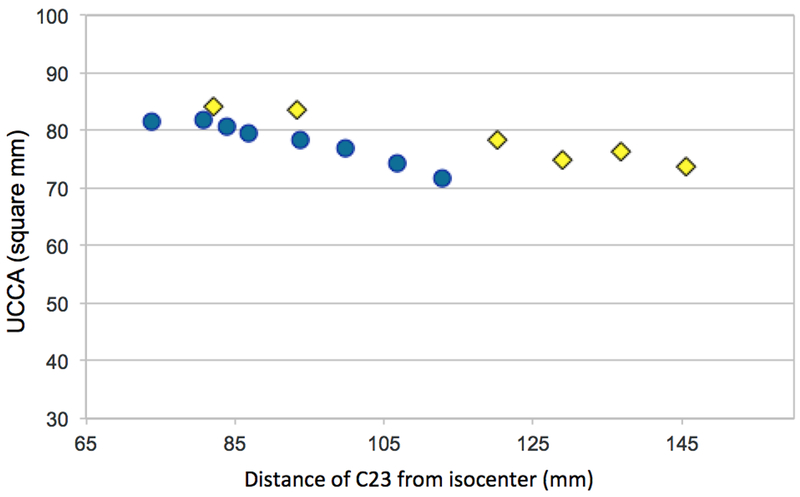
HC-B was also scanned twice on 3 scanners with the longer bore. The Z_CI of the 6 measurements ranged from 81 to 146mm (65mm difference), which corresponded to a 9.9% difference in UCCA (82.0–73.9mm²). For the shorter bore scanner, the Z_CI range was 39mm and the UCCA difference 12%. Therefore, for the longer bore scanners, a larger Z_CI variation was reflected in a smaller relative difference in the measured UCCA (Figure 3).

Figure 3.

UCCA measured in the same healthy control scanned on a Skyra (bore length=173cm, blue dots) and on 3 different Trio scanners (bore length=213cm, yellow diamonds), as a function of the distance of the C2–3 disc from scanner isocenter.

Retrospective correction methods:

Phantom fit:

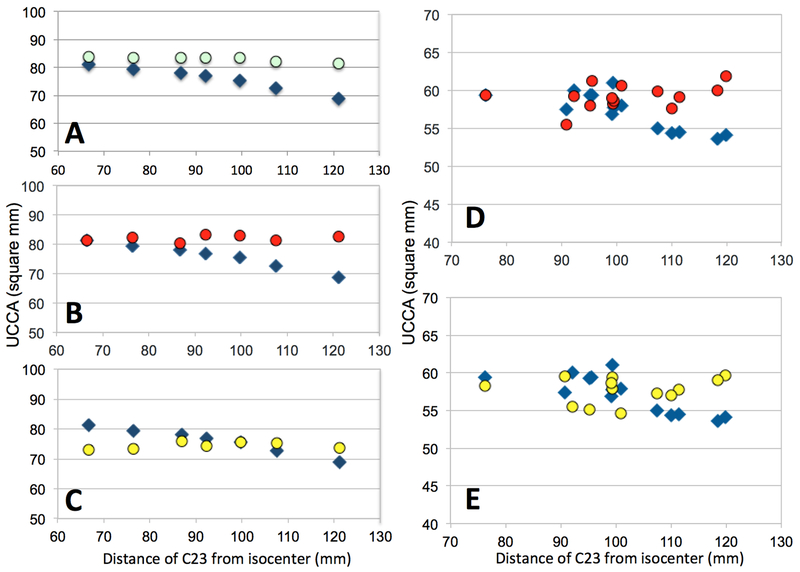
The fit of the phantom data was used to retrospectively correct the HC data. For HC-A (Figure 4A) the difference between UCCA measurements at extreme table positions was reduced from 15.2% to 2.9% (SD from 4.2mm² to 0.9mm²) and for HC-B from 12% to 3.2% (SD from 3.6mm² to 1.3mm²).

Figure 4.

UCCA as a function of the distance of the C2–3 disc from scanner isocenter: uncorrected data (blue diamonds), retrospectively corrected using the fit of phantom data (emerald circles), normalized using C2 vertebral body diameters (red circles) and normalized using the Jacobian determinant (yellow circles). A, B, C: Healthy control scanned at one site; D, E: multiple sclerosis patient scanned at the 7 NAIMS sites.

Normalization using C2 vertebral body diameters:

Dividing the UCCA measurements for Vert(Z_CI) substantially reduced the variability with Z_CI, for both the HC (SD for HC-A decreased from 4.2mm² to 1.1mm² (Figure 4B), for HC-B from 3.6mm² to 1.9mm²) as well as for the MS patient (from 9.6% to 1.1% for the extreme table positions, SD from 2.5mm² to 1.6mm², Figure 4D).

Normalization using the Jacobian determinant:

The Jacobian normalization reduced the SD of all the UCCA measures from 4.2mm² to 1.1mm² for the HC-A (Figure 4C) and from 2.5mm² to 1.7mm² for the MS patient (Figure 4E).

DISCUSSION

In the present study, we explored the effect of GNL and subject positioning on the variability of UCCA measurements from high-resolution brain 3D T1-weighted scans.

The method used here to measure UCCA from brain scans was previously described by Liu et al (13) and applied with small variations in other spinal cord quantitative imaging studies. Although Liu and colleagues also showed that cord area measurements in a 5 mm segment, 2.5 cm below the pons, can offer a surrogate measurement for spinal cord UCCA, a measurement at the C2-C3 disc level remains the gold standard. Intra-session (test/retest) COV and inter-operator ICC of the UCCA measurements showed excellent reliability (Supporting Information), indicating that the method was appropriate for the aims of the study. Other software to measure UCCA is available and could have been used as an alternative.

Our data showed that varying the distance from the scanner isocenter is potentially a major source of variability for UCCA estimation when using uncorrected brain 3D T1-weighted acquisitions. We found that GNL can introduce up to 15% variability in UCCA measurements, depending on subject positioning. The magnitude of the error in our study is in accordance with what was previously reported by Jovicich et al, who concluded that up to 8% error in measuring a diameter is possible at the periphery of the field of view, where GNL-distortions are strongest(17). The measure of UCCA from brain images is particularly prone to this effect, as the spinal cord is located toward the periphery of the field of view. Correctly dealing with such variability is critical for longitudinal patient monitoring studies, since it dwarfs typical clinical changes in UCCA over relevant time spans (1–2 years) (9). Defining consistent positioning with respect to the isocenter seems warranted for single-site and multi-site studies.

A quadratic decrease in UCCA as a function of Z_CI was found in the two HC and the phantom scanned without distortion correction at one site. We acquired data from a HC on two different 3T scanners. The effect of GNL was more pronounced for the shorter bore scanner (bore length=173cm) than for the longer bore scanner (bore length=213cm). This is consistent with the idea that stronger distortions are present in short bore scanners where technological challenges increase the difficulty in obtaining linearity in gradient performance (19).

The decrease in UCCA with Z_CI observed for the MS patient scanned at the 7 sites presumably reflected the combination of site-specific quadratic dependencies related to GNL, superimposed on other sources of variance in the measurement, such as subject movement and heterogeneity of hardware/software platforms reflected in different contrast-to-noise-ratio/blurring at tissue interfaces. Sites E and C used a longer bore scanner. The offset towards higher values for the UCCA measured at these sites is therefore consistent with the results obtained scanning a HC with different scanner models (Supporting Figure S3).

Even though an exhaustive exploration of correction methods available on different scanner models and vendors was beyond the scope of the present study, our data suggest that when planning to measure UCCA from standard brain high-resolution 3D T1-weighted acquisitions, 2D correction methods are suboptimal. At least for the vendor tested here, the use of 3D correction methods – introduced by this vendor about a decade ago (16,17) – is preferred. If such correction is not applied during acquisition, methods based on spherical harmonic expansion of the magnetic field could be applied off-line (17). Since this information may not be readily available from the vendors, mapping the distortion field using phantoms with fiducial markers or other complex structures is also an option to consider (19,25,26), in particular when planning a new study. However, these methods can be difficult to implement in clinical environments.

Here, we explored three different easily applicable methods that can be used to retrospectively correct data acquired with no (or suboptimal) distortion correction. The first approach was based on a quadratic fit of phantom-scan data obtained over a range of table positions. Once Eq.1 is determined from the fit, it can be applied to correct the UCCA estimated from the uncorrected images without requiring any further post-processing. Although we used a simple in-house made phantom, larger phantoms with other structures could also be used (19,25). This method is straightforward to apply, but it is not always possible to acquire phantom data with various table positions in identical hardware/software conditions used for the human data acquisitions. This is particularly true in large multi-center studies or longitudinal studies started several years in the past. As a second approach, normalization using diameters of a structure expected to be relatively stable with time and pathology (here, the C2 vertebral body) was tested. This is a powerful method for calculating % year changes in long-running longitudinal studies, as it doesn’t require knowledge about distortion correction, hardware changes, or the positioning of the subject in the scanner across time points. This method gave good results for both the HC who underwent MRI at one single site and for the MS patient who was scanned at the 7 NAIMS sites. Nevertheless, this normalization can be difficult to implement and may lack precision. The C2 vertebral body, for example, is not a perfect cylinder at any level, and defining anatomical references to measure its diameters on the same plane at different time points can be challenging. Therefore this method needs to be further explored in larger datasets. We proposed a third method, based on the Jacobian determinant of non-linear registrations. This method was the most effective in reducing the GNL-related variability and it does not require further acquisitions or difficult measurements, therefore it is likely the most interesting to be implemented in typical clinical studies.

The present study has a number of limitations. First, we tested 3T scanners from a single vendor. The goal of the study was not to perform an exhaustive exploration of the extent of distortions on all possible platforms, and the results here reported would need to be extended to scanners of other manufacturers and to other magnetic field strengths. Second, the vendor-implemented correction algorithms were not exhaustively tested. Further tests are necessary to confirm our preliminary results suggesting that 3D methods are reliable, while 2D methods are suboptimal. Third, this study did not assess intensity variability due to receiver coils non-uniform sensitivity (as done by Losseff et al. (27)) that can be indirectly affected by gradient nonlinearity. Finally, solution of the problem using off-line corrections based on spherical harmonic expansion of the magnetic field was not tested. Instead, we preferred to study three practical methods that could be used in a variety of settings, including clinical environments.

CONCLUSIONS

The main goal of this technical note is to raise awareness of the significant impact that gradient nonlinearity can have in quantitative UCCA studies. While this problem is well described in the brain tissue volume quantification literature, it has not yet been addressed in spinal cord quantitative imaging. Our results point the way to managing gradient nonlinearity distortions when measuring UCCA from brain scans, taking into account the aims and the specific conditions of each study.

Supplementary Material

Supporting Figures S1-S3

Supporting Figure S1. Correlation between normalization values extracted with the two different methods that use the Jacobian of non-rigid transformations to a template. Acquisitions of the multiple sclerosis patient at the 7 NAIMS sites.

Supporting Figure S2. UCCA as a function of the distance of the C2–3 disc from scanner isocenter: uncorrected data (blue diamonds) and retrospectively corrected using the cubic root of the squared value of the volume Jacobian determinant (yellow circles). A: Healthy control scanned at one site; B: multiple sclerosis patient scanned at the 7 NAIMS sites.

Supporting Figure1 S3. UCCA of the multiple sclerosis patient measured at the 7 NAIMS sites as a function of the distance between the C2-C3 disc and the scanner isocenter (Z_CI). The same data of Figure 1 are here reported with a different scale, and symbols colored according to the scanner model: blue for Skyra (bore length=173cm), light blue for Verio (bore length=173cm) and red for Trio (bore length=213cm). Notice how, in accordance with the results of the healthy control acquisition test on different scanner types, the UCCA measurements for the longer bore scanners, for similar distances from scanner isocenter, are biased towards higher values.