Cell-types for our sense of location: where we are and where we are going

Abstract

Technological advances in profiling cells along genetic, anatomical and physiological axes have fomented interest in identifying all neuronal cell-types. This goal nears completion in specialized circuits like the retina, while remaining more elusive in higher-order cortical regions. We propose this differential success of cell-type identification may not simply reflect technological gaps in co-registering genetic, anatomical and physiological features in the cortex. Rather, we hypothesize it reflects evolutionarily-driven differences in the computational principles governing specialized circuits versus more general-purpose learning machines. In this framework, we consider the question of cell-types in medial entorhinal cortex (MEC), a region likely involved in memory and navigation. While MEC contains subsets of identifiable functionally-defined cell-types, recent work employing unbiased statistical methods and more diverse tasks revealed unsuspected heterogeneity and adaptivity in MEC firing patterns. This suggests MEC may operate more as a generalist circuit, obeying computational design principles resembling those governing other higher cortical regions.

Main Text

“That of dividing things again by classes, where the natural joints are, and not trying to break any part, after the manner of a bad carver” Plato, Pheadrus 265e, translated by Harold Fowler.

As we try to make sense of our world, our mind attempts to ‘carve nature at its joints’ to find meaningful categories, or clusters of sensory data, which then form the basis of our thoughts and actions¹. Similarly, when faced with the complexity of neuroscientific data, our mind attempts to ‘carve neural data at its joints’ to find meaningful, recurring patterns. One such dominant pattern is the notion of a cell-type. Fundamentally, cell-types can be thought of as clusters of co-occurring, neurobiological features that arise more often than chance. Researchers have defined these features genetically, in terms of recurring gene expression patterns, morphologically, in terms of repeated neural shapes, anatomically, in terms of organized connectivity patterns, or physiologically, in terms of recurring firing rate patterns across stimuli or behavior.

Recently, the goal of identifying all neuronal cell-types has taken on prominence in science, as evidenced by the cell atlas project at the Chan Zuckerberg Biohub (https://czbiohub.org/projects/cell-atlas/), the cell-types database at the Allen Brain Institute (http://celltypes.brain-map.org/) and the BRAIN Initiative call to identify neural cell-types (https://braininitiative.nih.gov/pdf/BRAIN2025_508C.pdf). In part, this push to classify cell-types reflects recent technological developments that facilitate the identification and manipulation of genetically defined cell-types. In contrast, at the level of systems neuroscience, the quest to understand how the moment-by-moment dynamics of neural circuits gives rise to cognition and behavior has led scientists to focus on physiological firing patterns and search for functionally defined cell-types. However, within many brain regions, correspondences between genetically and functionally defined cell-types remain unclear. Notable exceptions include specialized circuits at the sensory and motor periphery^{2, 3}. The retina, for example, possesses clearly defined functional cell-types that co-register with genetic and anatomical cell-type definitions^4–9. In contrast, many studies of higher-order cortical regions do not report well-defined functional cell-types^10–15. Instead, individual neurons show dissimilar firing patterns that lack a simple relationship to sensory or behavioral correlates, thereby potentially obscuring our understanding of higher-level circuit organization. However, such organization frequently becomes clear when the collective dynamics of a large neural population are considered^{10, 11}.

One explanation for the development of such radically different perspectives might simply involve the limitations of some experimental methods. For example, extracellular recordings alone do not offer access to the genetic or connectivity profile of a cell. Thus, if we could observe multiple cellular features simultaneously, across a range of tasks, then we might discover lawful relationships between a neuron’s functional firing patterns and its genetic or anatomical features. However, any such relationship must also be consistent with the lack of clustering in the physiological firing patterns of cortical cells observed in many tasks^{12, 16}. Such a lack of clustering remains difficult to reconcile with the idea that a cortical neuron’s functional firing pattern is completely determined by its genetic or anatomical cell-type.

A potentially deeper reason for the diverging views about cell-types in the retina versus cortical areas is that these regions lie at the extremes of an axis of teleological evolutionary origin ranging from specialist circuits to generalist circuits. We define specialist circuits as those that solve a set of well-defined tasks that do not fundamentally change over evolutionary time-scales. For such tasks, evolutionary processes have had time to bake solutions into relatively hard-wired circuits in which genetic identity, connectivity, and physiology are tightly correlated. In contrast, generalist circuits may be designed to be general purpose learning machines that can solve new tasks evolution could never have anticipated. When faced with a fundamentally new situation, generalist circuits must wire up a new circuit solution that never previously existed. In such a new and often recurrent circuit, any individual cell’s physiological firing pattern cannot be ascribed to that cell alone, but rather is an emergent property of the entire learned circuit connectivity. In this situation, tight clustering of physiological properties may be more difficult to find, and instead, emergent, dynamical population patterns may provide a more satisfactory conceptual description of learned circuit function^{17, 18}.

Here, we discuss the implications of this proposal in the context of cell-types in the medial entorhinal cortex (MEC), a region with coding principles that may fall between the extremes of specialized circuits like the retina and generalized circuits like the prefrontal cortex. Many MEC neurons recorded as rodents forage in open arenas show firing patterns with clear correlates to the animal’s location^19–22 (Fig.1A). A subset of MEC neurons, classified as grid cells, fire in periodic locations that tile the environment^{19, 20} (Fig.1A). The crystalline structure of the grid pattern lent support to using tuning curve features to classify MEC neurons into functionally-defined cell-types, and thus implicitly suggested that MEC may act as a more specialist circuit. In addition to grid cells, these cell-types include: border cells that fire maximally near environmental boundaries^21–23, head direction cells that fire when the animal faces a particular direction^{24, 25} and speed cells that change their firing rate with running speed^{26, 27} (Fig.1A). However, recent evidence suggests MEC may play a more generalist role. Such evidence includes deficiencies in the current classification of functional cell-types in MEC, and striking flexibility in entorhinal firing patterns in navigational and non-navigational tasks^{16, 28, 29}. Here, we begin by discussing the difficulties of quantitatively defining cell-types, and then present extremal examples of specialist versus generalist circuits. With this theoretical framing in mind, we revisit the issue of cell-types in MEC and provide a new proposal for the general function of MEC.

Figure 1.

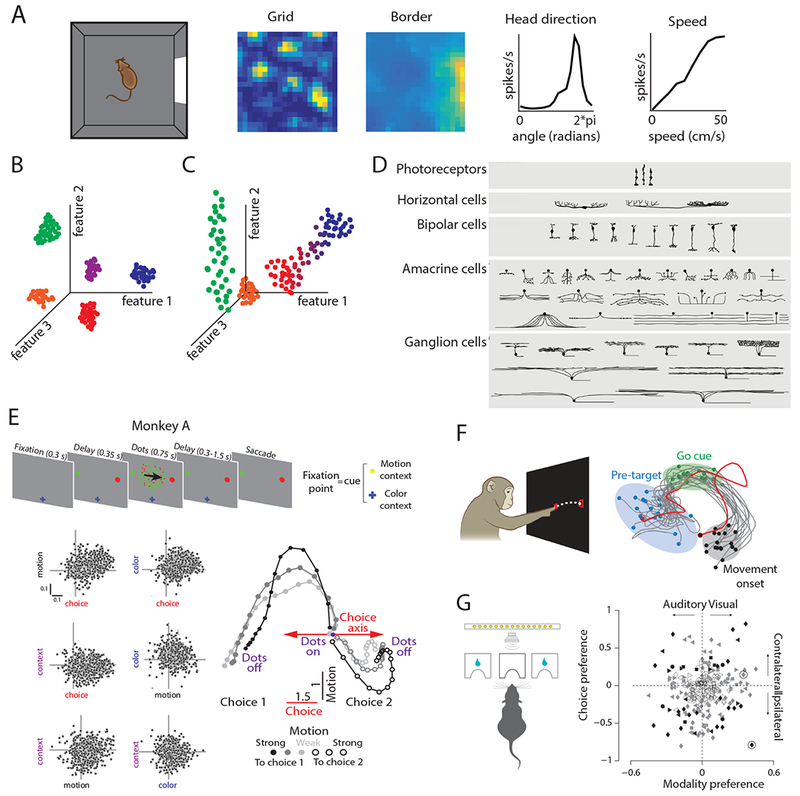
The range at which clear cell-type clustering emerges varies across neural circuits. A. Left-most panel: schematic of the open field foraging paradigm often used to identify MEC neurons in rodents. Right panels: example tuning curves of grid, border, head direction, and speed cells. Spatial tuning curves are color coded for minimum (blue) and maximum (yellow) values. [Reproduced from Hardcastle et al., 2017¹⁶]. B. Schematic of cell-type clusters in an arbitrary feature space. Each point represents a cell, and is colored by the cluster to which it belongs. In this example, all cell-types cluster along each feature independently. C. Schematic of challenges to clustering cell-types in an arbitrary feature space. The green cells only cluster along one axis, the red and blue cells exist along a continuum, and the orange cells do not exhibit significant values for these features. D. Schematic of retinal ganglion cell-types. [Reproduced with permission from Masland 2001⁷⁷]. E. Schematic of task employed in Mante et al., 2013¹³ and observed cell responses along task parameters. Top: schematic of task, in which a monkey must choose the correct target that corresponds with the dominant motion or color of the presented dots. Bottom left: cell responses along motion, choice, color, and context axes. Responses are the de-noised regression coefficients from a multivariate linear regression model. Bottom right: Schematic of the dimensionality-reduced population level response during the motion context, projected onto the axes of choice and motion. [Reproduced with permission from Mante et al., 2013¹³]. F. Left: schematic of reaching task to assess preparatory activity in motor cortex. Right: Example motor neural activity, projected into a 2-dimensional latent space, during reaching. Blue dots indicate 100 ms before target onset, green dots indicate time of go cue (when the reach could commence), and the black dots denote the neural activity at the time of movement onset. [Reproduced with permission from Shenoy et al., 2013³⁴]. G. Left: schematic of task used in Raposo et al., 2014¹². In this task, the rat chose the left or right port based on the visual, auditory or combined visual-auditory stimulus. Right: Modality (visual or auditory) versus choice (left or right) preference for cells recorded in posterior parietal cortex during this task. Preference for the task variables was computed from the area under the receiver operating characteristic curve; for example, a value of +1 for choice preference indicates the neuron always firing more during trials with a contralateral choice. The absence of clustering in this space indicates a lack of functional cell-types. [Reproduced from Raposo et al., 2014¹²].

The search for cell-types as a statistical problem

Any data-driven approach that asserts the existence of well-defined cell-types must solve an essential statistical problem: it must demonstrate the existence of distinct subpopulations, such that neurons within a subpopulation are significantly more similar than neurons across subpopulations. Thus, critical to the notion of cell-type is the quantitative definition of similarity. A simple approach to defining similarity is to select a set of neurobiological features and consider each cell as a point in this feature space (Fig. 1B). For example, in genetically defined cell-types, each axis in this feature space would represent the expression level of a single gene. The similarity between cells is then inversely related to the distance between cells for an appropriately chosen distance metric in this space. A collection of cell-types would then constitute tight clusters of cells that occupy a specific location in feature space, with relatively large empty spaces separating the tight clusters.

This view, while appealing, has limitations. The gold-standard outcome of this approach would reveal that every cell-type forms a tight cluster along multiple genetic, anatomical and physiological axes (Fig. 1B). While this gold-standard may be feasible in specialized circuits, generalist circuits may show more diverse profiles. For example, cells may cluster along one subset of axes and spread out along other axes (green dots in Fig. 1C). More generally, cells may spread out uniformly along a continuum. Intermediate cases between a continuum and tight clustering can also occur, resulting in a non-uniform density of cells in feature space (blue and red dots in Fig. 1C). This could result in a focus on the extreme ends of higher density, potentially yielding an incomplete view of circuit function. Finally, perhaps the most serious pitfall is that we do not choose the right axes, or we cannot measure them. This causes large populations of cells to lie at the origin of the feature space, essentially invisible to any cell-type analysis (orange dots in Fig. 1C). Below, we review how cells cluster in feature space for hypothesized specialized and generalist circuits, and then review the situation for functionally-defined MEC cell-types.

Examples of specialist versus generalist circuits

The retina serves as an ideal example of a specialist circuit (Fig. 1D). The retina must transform complex spatiotemporal light patterns from a large number of photoreceptors into firing patterns in a limited number of retinal ganglion cell nerve fibers. Given the bottleneck presented by the optic nerve, the retina must perform this transformation efficiently, taking into account the statistical properties of natural images³⁰. These statistical properties have likely remained invariant across hundreds of millions of years, allowing cell-types with consistent genetic, anatomical and physiological definitions to evolve^{31, 32}, with each cell-type dedicated to specific aspects of this transformation⁴ (Fig. 1D). For example, unbiased clustering of genetic, immunohistochemical, electrical and physiological response features led to a general consensus that the mouse retina contains ~50 distinct cell-types⁹. In this fashion, the retina is moving towards becoming a gold-standard example of a specialist circuit where physiological function can be ascribed to individual cells, in a manner that is correlated with each cell’s genetic identity, connectivity pattern, and morphology.

In contrast to the efficient coding of natural scenes, a problem defined by image statistics that have remained invariant over evolutionary time-scales, many higher-order cortical regions must support cognitive processes in which input statistics can change rapidly. For example, autobiographical memory requires rapid associations between vast numbers of highly processed neural representations, such as different individuals, emotions or spatial locations³³. Evolution could not have anticipated the full breadth of these combinations and instead, brain regions that support this type of flexible coding, like the hippocampus, may have evolved to operate as general purpose learning circuits.

A recent example of this principle in prefrontal cortex involves a decision making task in which different fractions of colored dots move left or right¹³ (Fig. 1E). Depending on a visual context signal, the monkey must use an eye movement to report either the majority color, or the majority direction of motion of the dots (Fig. 1E). Over the course of evolution, no monkey has encountered this specific task, yet the monkey can learn this task and recordings from prefrontal cortex reveal striking neural correlates of the solution. However, these neural correlates do not exhibit any discernible functional cell-types, as each neuron encodes different degrees of sensory, motor, and cognitive aspects of the task. In contrast, emergent neural population dynamics, obtained through dimensionality reduction methods, reveal highly organized neural state space dynamics¹⁸ (Fig. 1E). These dimensionality reduction methods yield linear combinations of cells, or population firing patterns, that provide essential clues to the mechanism for context dependent gating of sensory evidence¹³. Thus, at least for this study, carving neural circuits at the joint of single cells was not as conceptually informative as carving them at the higher level of population dynamics.

The essential nature of this example has been replicated in recordings from other cortical regions. For example, in motor cortex during reaching movements, the identification of a neural preparatory state – a population level activity pattern that occurs immediately prior to motion – could only be achieved when the notion of cell-types was set aside and the collective activity of many neurons was considered^{14, 15, 34} (Fig. 1F). Also, in a sequence memory task, prefrontal cortex neurons exhibited a high degree of ‘mixed selectivity’ for various task parameters, which can be an advantageous coding scheme for learning arbitrary rules^{10, 11, 35}. Finally, recent studies posit that neurons in mouse posterior parietal cortex are ‘category free’, reflecting random combinations of task parameters and hence inherently defy the notion of functionally-defined cell-types¹² (Fig. 1G). Thus, an emerging body of work is raising the possibility that well-defined physiological cell-types, especially in higher cortical regions, may not constitute a fundamental organizing principle for understanding network function.

Defining cell-types in medial entorhinal cortex

With the precise cell-type identification in the retina and the category-free approach in prefrontal cortex serving as bookends, where does the idea of cell-types in MEC fit? A high-order cortical region that supports memory and navigation^36–38, MEC contains neurons that have been classified morphologically^39–41, biophysically^{42, 43} and genetically^44–46. However, as alluded to previously, one of the prominent cell-type classifications in MEC has been along functional axes (Fig. 1A). These MEC cell-types are often identified from neural activity recorded as rodents explore open arenas and include grid, border, head direction and speed cells^{19, 21, 22, 24, 26} (Fig. 2A). To classify these neurons, researchers often calculate a ‘score’ (e.g. grid score), which quantifies specific features of a neuron’s tuning curve (e.g. 60° symmetry). This score is then compared to that expected by chance, which is determined from a null distribution of scores generated by randomly time-shifting spike trains of a single cell and re-computing the score. This null distribution can be generated from shuffles pooled across the entire population^{47, 48} or within the same cell²⁸ (Fig. 2A).

Figure 2.

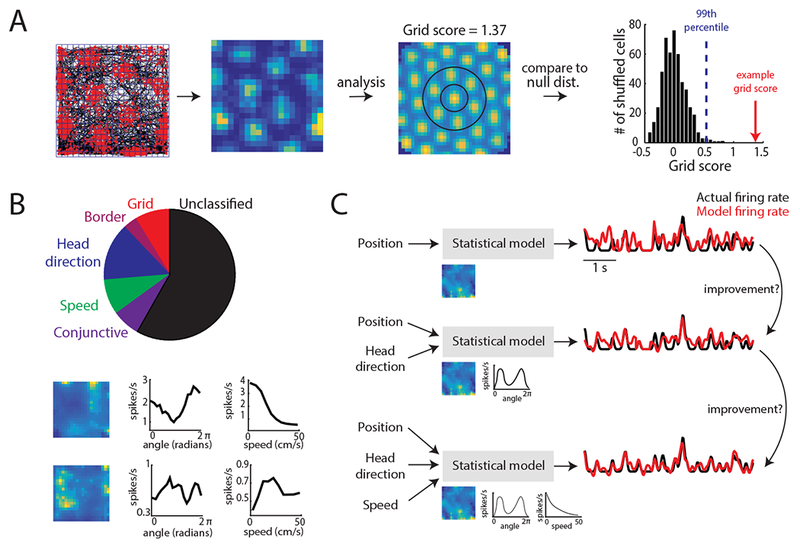
Capturing coding in MEC using a tuning curve score versus model-based method. A. Schematic of the tuning curve and score method conventionally used to characterize grid cells and other functionally-defined MEC neurons^{47, 78}. Far-left: Spatial tuning of a grid cell in a 1 × 1 m open arena. Red dots denote neural spikes and black lines indicates the animal’s trajectory. Blue lines denote the spatial bins used to generate firing rate tuning curves. Middle-left: firing rate tuning curve. Each pixel corresponds to the average spikes/second of the grid cell at that binned spatial position and is color coded for minimum (blue) and maximum (yellow) values. Middle-right: spatial autocorrelation of the tuning curve. To generate a grid score, the inner ring of fields (circled in black) is first rotated 30, 60, 90, 120, and 150 degrees and correlated to the original ring. The grid score is the minimum correlation at 60 or 120 degrees minus the maximum correlation at 30, 90, or 150 degrees. Right: distribution of 500 grid scores generated by adding a random amount to the spike train (modulo the length of the session) of the given cell, and re-computing the grid score. The blue line denotes the 99^th percentile of the shuffled distribution, while the red arrow indicates the actual grid score for this example cell. B. Top: Pie chart of MEC cell classifications based on the score method. Based on dataset used in Hardcastle et al., 2017¹⁶. Bottom: Examples of position (left), head direction (middle), and speed (right) tuning curves that are not characterized by the score method. C. Schematic of a model-based approach using the forward-search method to identify the set of navigational variables encoded by the cell. In this approach, position, head direction, and speed information are used to predict neural spikes (black and red lines). The model uses this information by learning a set of parameters (images under ‘Statistical model’) that transform the animal’s position, head direction, or speed to firing rate. Single-variable contribution to neural spiking can be assessed by analyzing the performance of the simplest model (top of diagram) and continually adding variables to this model to see if performance improves.

This approach has pushed forward our understanding of how MEC encodes behaviorally-relevant information and, in the process, built a framework for hypotheses about the mechanisms generating MEC cell-types and their function in navigational behavior⁴⁹. For example, the classification of grid, head direction, and speed cells as functionally-dedicated cell-types led to the hypothesis that MEC is responsible, at least in part, for path-integration based navigation^{19, 50}. In addition, studies leveraged the common tuning curve structure of grid cells along the dorsal-ventral MEC axis to demonstrate that grid spatial scale increases discretely along the same axis^{19, 51}, which provided guidance for the type of network architecture computational models could use generate grid cell responses^52–55.

Another benefit of a functionally-defined classification approach in MEC is that it captures common computational principles in a neural population where the links between functional and genetic or anatomical features remains unclear. In other words, MEC neurons are like the green dots in Figure 1C: cells can be classified by their functional properties (features 1 and 3) but remain difficult to classify based on other features (feature 2). For example, grid cell firing patterns occur in approximately equal numbers of CalbindinD-28K-positive pyramidal cells and Reelin-positive cells, two classes of cells that differ in their biophysics, morphology, projections and microcircuit organization^{43, 44, 54–58}. Furthermore, while the biophysical, molecular, and morphological features of MEC neurons vary along the dorsal-ventral MEC axis^{46, 59, 60}, grid cells have been identified across this entire axis, although this dorsal-ventral organization likely contributes to the dorsal-ventral expansion of grid spatial scale^{55, 59, 61, 62}. Finally, classification of speed cells by genetic or morphological features remains challenging, as speed coding is observed in both interneurons and excitatory principal neurons^{26, 27, 56}. Thus, functional definitions currently remain the primary modus for MEC cell-type classification, as the functional axis remains the only known coordinate frame in which subsets of MEC neurons show clear correlates to behavior.

However, despite the insights gained from using tuning curves to classify MEC cell-types, this approach carries limitations. One disadvantage is that classified neurons must exhibit a tuning curve that follows an experimenter-defined shape. The number of classified MEC cells then relies on the heterogeneity of experimenter-defined shapes, rather than the true heterogeneity of tuning. This can result in an incomplete picture of the coding principles neurons might follow for a given behavior (Fig. 2B). In MEC, for example, many papers utilize tuning curve scores that result in narrowly defined MEC cell-types (Fig. 2B), leaving the features encoded by the majority of MEC cells unclassified²⁶ (i.e. orange dots, Fig. 1C). A second issue arises from classifying cell-types by requiring scores to surpass a threshold (Fig. 2A). This could result in the discretization of a population of neurons that possess an underlying continuous representation of navigational variables. Indeed, recent data indicated the strength with which conjunctive MEC cells encode multiple navigational variables falls along a continuum¹⁶, generating a distribution similar to the red and blue dots in Figure 1C. Finally, tuning curves assume a static relationship between an external sensory stimulus and the neural response. Thus, this framework will miss behavior or state-dependent coding properties.

An alternative way to advance the field is to apply more unbiased methods – analysis techniques that can better confront cell-type diversity and do not rely on assumptions regarding tuning curve shapes. One example of such an approach is the use of statistical models that learn the relationship between a set of variables and a single-neuron spike train^63–68 (Fig. 2C). These models can be built to have the flexibility to learn any tuning curve shape for a given variable (e.g. position), while maintaining the power to determine whether that variable significantly explains neural spiking. This latter aspect of the framework is critical, as it offers an explicit report as to whether knowing a variable significantly explains spiking variability, resulting in an approach more robust to heterogeneity in behavior compared to the score-based approach. While the model-based method still requires the researcher to identify the variables to which a neuron might respond, this framework allows considerable freedom in the mapping from external variables to neural spike trains. Although information about tuning curve shape is inherently absent, tuning curve features can be quantified from the learned mappings and cells such as grid cells, still identified. However, as we discuss in the following section, the flexibility of this framework provides a more inclusive, and richer, view of MEC coding properties than previously suspected.

The axes for defining entorhinal coding

Indeed, recent works employing statistical models have revealed high degrees of heterogeneity and multiplexing in MEC neurons. First, by fitting models of speed-dependent firing, researchers demonstrated that speed tuning is heterogeneous, as the sign of this relationship can be positive or negative and the shape can take linear, saturating or non-monotonic forms^{16, 26, 27}. Expanding upon this result, the application of a statistical model in which position, head direction and running speed were used as variables to explain neural spiking empirically demonstrated that a high degree of heterogeneity exists for the encoding of all navigational variables in MEC (Fig. 2C, 3A)¹⁶. In this approach, the position, head direction, and/or running speed of a mouse over time were fed as inputs to a linear-nonlinear-Poisson (LN) model. This information was then used to try to produce a spike train matching, as close as possible, that observed from an MEC neuron. This approach detected navigational-encoding in 71% of MEC neurons, a higher number than the 41% detected from the score approach used by the majority of published papers¹⁶ (Fig. 2B, 3A). Further, this model identified a higher degree of multiplexing than the tuning curve score approach (37% versus 7%). Along a similar vein, recent work using spatial information captured spatial coding in the vast majority of MEC neurons, with grid and border cells composing only a small minority of these position encoding cells²⁸. As spatial information quantifies the degree of positional information carried by a single spike and does not make strict assumptions about tuning curve shape, this approach is similar in spirit to model-based approaches. However, unlike model-based approaches, the use of spatial information does not provide a model capable of predicting spiking in novel navigational settings¹⁶. Taken together, these studies support the idea that MEC coding is highly heterogeneous and contains many cells with unconventional, yet meaningful coding features^{16, 28}.

Figure 3.

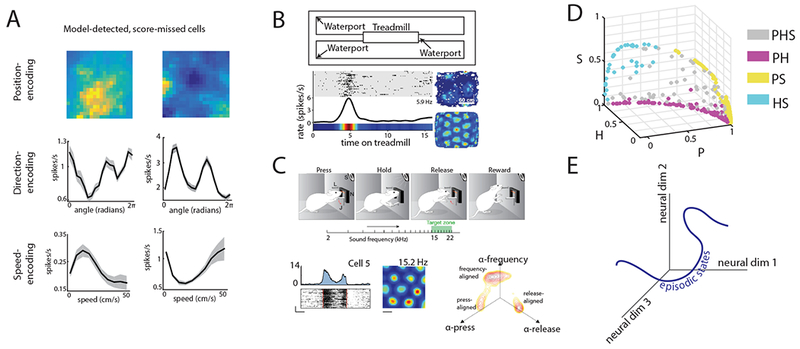
Entorhinal neurons represent multiple task variables in heterogeneous ways. A. Cells with low grid, border, head direction, and speed score that were detected as encoding position (top), head direction (middle), or speed (bottom) by a model-based method. [Reproduced from Hardcastle et al., 2017¹⁶]. B. Schematic of task used in Kraus et al., 2015⁷⁰ and example results. In this task, animals ran in place on a treadmill that varied in speed and running duration (top). A subset of grid cells encodes time on the treadmill, in addition to location in 2-dimensional space (bottom) [Reproduced with permission from Kraus et al., 2015⁷⁰]. C. Schematic of an auditory frequency task, in which rats pressed a bar to play sequentially higher auditory frequencies, releasing the bar when a learned frequency was played. A subset of grid cells, as assessed in a 2-dimensional environment, responded to the initial press, the release, or a given frequency (example in bottom left). When plotted in a space defined by linear model coefficients that capture tuning to frequency, lever pressing, or lever releasing, MEC neurons cluster along these three axes (bottom right) [Reproduced with permission from Aronov et al., 2017⁷²]. D. MEC neurons detected as encoding combinations of position (P), head direction (H), and speed (S) plotted in a variable-contribution space. This space represents the normalized contribution of each variable to spike prediction, which is computed from differences in the performance of models of varying complexity. In this space, MEC neurons lack significant clustering. [Reproduced from Hardcastle et al. 2017¹⁶]. E. Schematic of the episodic state hypothesis. The axes denote a dimensionality-reduced space in which neural data is projected onto, while the blue line illustrates the potential trajectory of population-level neural data in this space during a behavioral task.

Multiplexing in MEC also extends to coding non-spatial stimuli. In rats required to associate odors with reward, a subset of grid cells encoded information about the context of the reward rather than just the spatial location of the animal⁶⁹. Moreover, tasks with more complex behavioral demands than open field foraging have revealed significant heterogeneity in the repertoire of variables MEC cells encode. For example, using a treadmill to force rats to run in place for a specific amount of time, a model-based analysis revealed that subsets of MEC cells encode time elapsed, distance traveled or a combination of both variables⁷⁰ (Fig. 3B). This hints at the idea that while MEC circuit computations may have evolved to support the traversal of trajectories through physical space, they can also generalize to encode variables necessary to support spatiotemporal trajectories through mental space, such as an episodic memory⁷¹. Extending this idea, recent work examined MEC coding as rats navigated through a one-dimensional auditory space⁷² (Fig. 3C). In this task, rats pressed a bar to increase the frequency of an auditory tone, which took a variable amount of time, and then released the bar once the tone reached a learned frequency. Subsets of classically defined grid, border and head direction cells encoded different task variables, with their activity aligning to the initial bar press, a specific auditory frequency, or the bar release⁷² (Fig. 3C). Interestingly, MEC neurons did not respond during passive playback of the auditory stimulus, consistent with the idea that MEC neural responses reflect navigation through a behaviorally relevant stimulus space regardless of the coordinate frame of that space. Future work using such complex tasks combined with neural recording will further answer to what extent MEC is a generalist circuit that can encode any set of variables relating to real or imagined navigation. Combined, these studies also raise the idea that at least in certain tasks, functionally-defined cell-types can be found in MEC. Whether these task-specific functional cell-types map to genetic or anatomical features, or how they behave across many tasks, remain intriguing questions.

In contrast, recent analyses employing the LN model demonstrate that MEC neurons likely encode navigational variables along a continuum and that subsets of MEC neurons change their coding across behavioral states, which is more consistent with a generalist circuit¹⁶. For example, the strength with which MEC neurons encode multiple navigational variables (e.g. position and head direction) exhibited a continuous distribution¹⁶ (Fig. 3D), and therefore defied classification into highly discrete functionally-defined cell-types. In addition, this approach revealed state-dependent changes in the encoding of navigational variables by MEC neurons. In particular, many MEC neurons dynamically altered the variables they encoded during fast versus slow running speeds. For example, some MEC neurons that encoded head direction at slow running speeds encoded both position and head direction at high speeds¹⁶. Such dynamic codes could extend to variables beyond speed, such as time or attentional state, ideas future work could aim to address. Combined, the above studies raise the possibility that MEC is a highly adaptive and flexible brain circuit, whose distribution of responses recorded in any experiment will depend strongly on the task used to probe MEC function. Moreover, unbiased statistical methods may be required to reveal the richness of this function.

A generalist role for medial entorhinal cortex

Recent results, as reviewed above, demonstrate more heterogeneity and state-dependence in MEC firing patterns than previously suspected²⁷. In addition, by moving to tasks with relevant non-spatial variables, MEC neurons have been shown to play roles in representing navigation along more diverse trajectories than through physical space alone. Taken together, these results suggest that MEC behaves more like a generalist than specialist circuit. If so, what is the general computational principle governing MEC codes?

One possibility is that the MEC, potentially in conjunction with the hippocampus, computes what we call the episodic state of the animal (Fig. 3E). The episodic state is the minimal function of the past stream of sensory and motor experience that is required to predict either future sensory experience or future actions that lead to reward. For example, during spatial navigation, knowledge of the position and velocity of the animal is sufficient to predict its future sensory experience over short time-scales. It is important to note that position and velocity are abstract variables, meaning they are not directly accessible to the animal via a set of dedicated primary sensory receptors. Instead, they must be computed from multiple lower-level sensory and motor variables that are directly accessible in the sensorimotor periphery. The presence of high-level position and velocity coding in MEC during spatial navigation suggests that MEC plays a role in the computation of episodic state by extracting these abstract variables from the peripheral sensorimotor stream. If this is the case, then MEC circuitry could contribute to the computation of episodic state in diverse scenarios beyond just spatial navigation.

Data currently at least supports the idea that MEC can improve the computation of episodic state in the context of spatial navigation. For example, application of the LN model to different speed bins revealed that MEC neurons encode more information about spatial location at high compared to low running speeds, an example of improved computation of episodic state for navigation¹⁶. However, the power, and limits, of MEC to compute general episodic states could be more broadly tested by examining MEC neural responses as animals perform tasks in environments that set up novel contingencies between past motor actions, past sensory experience, and future sensory experience and reward. This could be achieved, in rodents for example, by leveraging virtual reality technology^{73, 74}. Moreover, if episodic state computation really is the generalist role that MEC plays, then at what joints might we best carve function out of data from entorhinal cortex? Taking cues from previous successful analyses in other generalist brain regions^10–15, we may wish to analyze MEC data at the level of population patterns rather than single cells. In essence, the minimal goal of any circuitry that computes episodic state is to assign different neural population patterns to different states, thereby tracing out a neural manifold of firing patterns as a function of the episodic state. There may be higher order emergent structure in this neural manifold that is not apparent at the level of highly heterogeneous single cells, and this higher order structure may provide clues into the mechanisms of episodic state computation in MEC. Indeed, theoretical work has shown that across many neural networks trained to solve the same complex task, correspondences in neural representations at the level of single neurons can be rare, while correspondences at the level of population patterns can be common⁷⁵. This theory, in addition to prior empirical work^10–15, motivates the search for relationships between neural activity and behavior at the level of population patterns rather than single cells, not only in MEC, but also in other generalist circuits solving complex tasks.

Discussion

In this Perspective, we present a new way of thinking about MEC functional cell-types, born of unbiased statistical approaches for defining how MEC cells encode information. Moreover, we posit a potentially useful specialist-generalist conceptual axis for thinking about the relationship between cell-types and network function across diverse brain regions. We propose that, given the high degree of heterogeneity and adaptivity of MEC firing patterns, the circuit may behave more like generalist circuits like the prefrontal cortex, rather than specialist circuits like the retina. As a result, it may be more useful to conceptualize MEC function in terms of higher-level population patterns, rather than in terms of single neuron functional cell-types.

Overall, our discussion of generalist circuits raises a central issue: if functionally defined cell-type clusters are not prevalent in recordings from higher-order cortical regions^12–16, then what role do genetically and anatomically defined cell-types play in generalist network function? In specialist circuits, genetically and anatomically defined cell-types have been extremely useful to identify, because of the tight correlation between such defined cell-types and single cell physiology. We propose that in contrast, in generalist circuits, the diversity of genetically and anatomically defined cell-types exist not to determine single-cell physiological firing patterns but rather to implement a general purpose learning circuit in which plasticity enables the circuit to learn new population patterns relevant for a task. Then the critical question to ask is, how do different cell-type features, like layer specificity, subcellular localization of connectivity, and plasticity rules conspire to sub-serve general purpose learning? While it may not be the case that the conjunction of these cell-type features determine the final learned single-cell physiological firing patterns, they certainly must define the path whereby the generalist circuit translates new problems into new network solutions.

Another interesting possibility is that brain regions we consider to be generalist circuits still implement canonical computations that are largely invariant across multiple regions⁷⁶. In this case, differences in physiological responses across such circuits could simply reflect differences in their upstream inputs, even though the underlying transformation from input to output is similar across circuits. Understanding such circuits then necessitates a shift in perspective from understanding neural representations to understanding neural transformations, which would require simultaneous measurements of circuit inputs and outputs. With such measurements in hand, one may be able to discover specific functional roles for genetically identified cell-types in implementing different aspects of the transformations, if not the representations, underlying canonical circuit computations. Whether a single or a small set of canonical computations repeated across the brain would be powerful enough to solve a great diversity of generalist tasks that evolution could not anticipate is an intriguing open question.

In summary, while there is a strong drive to identify cell-types, it remains unclear whether a conceptual understanding of how our cognitive capabilities arise from the on-going dynamics of circuits in our brain will be found at the level of single cells and cell-types. After all, it is highly likely that a virtuoso musician has the same complement of genetically identifiable cell-types as any other human, but not all humans can generate such beautiful music. Thus, to understand the neural dynamics underlying our greatest achievements, we may have to conceptually carve neural function at some higher level of organization beyond individual cells and their types.