A simple developmental model recapitulates complex insect wing venation patterns

Significance

The wing veins of the fruit fly Drosophila melanogaster have long been studied as an example of how signaling gradients in a growing tissue can generate precise, reproducible patterns. However, fruit fly wings represent only a small slice of wing diversity. In many insect species, wings are like human fingerprints: even the left and right wings of the same individual have unique vein patterns. We analyze wing geometry in many species and then present a minimal developmental model for how vein patterns can be formed. This model will serve as a hypothesis for future empirical work.

Abstract

Insect wings are typically supported by thickened struts called veins. These veins form diverse geometric patterns across insects. For many insect species, even the left and right wings from the same individual have veins with unique topological arrangements, and little is known about how these patterns form. We present a large-scale quantitative study of the fingerprint-like “secondary veins.” We compile a dataset of wings from 232 species and 17 families from the order Odonata (dragonflies and damselflies), a group with particularly elaborate vein patterns. We characterize the geometric arrangements of veins and develop a simple model of secondary vein patterning. We show that our model is capable of recapitulating the vein geometries of species from other, distantly related winged insect clades.

Insect wings are a marvel of evolution and biological engineering. They are lightweight, strong, durable, and flexible—traits made possible by “wing veins,” the thickened, strut-like structures embedded in the wing surface. The density and spatial arrangement of wing veins vary tremendously among insects (1–3), wherein they serve many functions: stiffening the wing (4), resisting crack propagation (5–7), forming the vertices of corrugation (8–10), conducting hemolymph (11, 12), supporting sensory structures (13, 14), and contributing to an architecture that undergoes useful passive deformation in response to aerodynamic forces (4, 9, 15, 16).

The study of wing veins has mostly focused on “primary veins”—those whose relative positions are shared between left and right wings of the same individual and among individuals of the same species. The morphology of primary veins has served as essential evidence in the effort to place long-extinct insects into a comprehensive insect phylogeny (17, 18). Likewise, subtle shifts in the positions of homologous primary veins, quantified with the tools of comparative morphometrics, have provided insight into evolutionary patterns (19, 20) and fluctuating asymmetry—deviations from perfect symmetry that indicate developmental noise (21, 22).

In addition to primary veins, many insect species also have “secondary veins.” These veins, sometimes referred to as “cross-veins,” cannot be matched one-to-one on the left and right wings of the same individual (2) (see labels on Fig. 1A). In some taxa, secondary veins comprise a large majority of wing veins yet remain poorly described. For species that have them, secondary veins form a unique pattern on every wing, which suggests that a stochastic patterning mechanism is responsible for their formation. To our knowledge, the geometric arrangement of secondary veins has not been quantitatively characterized for any species. It is not known whether a universal developmental process generates the diverse secondary vein arrangements found among insects. In fact, because the best-studied model species (e.g., Drosophila melanogaster) do not have secondary veins, the developmental basis of their patterning remains a mystery.

Fig. 1.

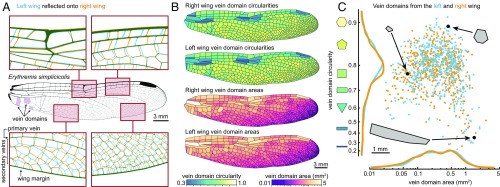
Secondary veins form a unique pattern on every wing. (A) Overlay of the left (blue) and right (orange) forewing of the same individual of Erythremis simplicicolis. (B) Left and right wings of the same individual, with domains colored by circularity and area. Left wings have been reflected for display. (C) Area and circularity of each vein domain. Each point represents a single domain (blue points, left wing; orange points, right wing).

We collected original high-resolution micrographs and combined them with published wing tracings, resulting in vein patterns of 468 wings from 232 insect species. This dataset is composed of wings that span a 36-fold range in area, and it includes representatives from three taxonomic orders. We developed computational tools to segment images of wings and used them to calculate geometric traits for each digitized wing image, including vein lengths, connectivities, angles, and densities.

With the resulting data, we describe clade-specific distributions of secondary vein arrangements; we also show that these distributions scale with wing size. Then, we synthesize our work with published developmental data to create a minimal geometric model of secondary vein development based on evenly spaced inhibitory signaling centers. This model is able to recapitulate the vast majority of secondary vein arrangements that are observed in our dataset. Furthermore, our model allows us to make specific, testable hypotheses about wing development for all insects with stochastically patterned secondary veins, a group that collectively spans ∼400 My of evolution (23).

Results

We initially focus on dragonflies and damselflies (order: Odonata), a group of aerial predators whose wings have especially complex venation patterns. An overlapping projection of the left and right wings of an example dragonfly, Erythremis simplicicolis, allows us to identify the primary and secondary veins, as defined above (Fig. 1A; see SI Appendix for details). This categorization of veins is similar to those used in previous studies (24, 25).

In many insect species, wing veins form tens to thousands of closed polygonal shapes called “vein domains” (Fig. 1A, examples highlighted in purple). Characterizing the areas and shapes of vein domains is a tractable way to study the geometric properties of veins. We present a custom method to segment wing images based on level sets (SI Appendix). This approach is well-suited to studying the morphologies of diverse wing vein patterns, robust to variations in image resolution, and it requires minimal parameter adjustment. This allows us to precisely calculate attributes—such as area and circularity—of every vein domain in a wing. Circularity is defined as the ratio of a domain’s area to the area of a circle whose perimeter is equal to that of the domain. The left and right wings of E. simplicicolis are shown, with each domain colored according to its area and circularity (Fig. 1B). When vein domain area is plotted against circularity for left and right wings (Fig. 1C), it is clear that each wing’s set of domain shapes is a unique fingerprint, yet the marginal distributions of each trait are strikingly similar.

Our dataset includes published wing tracings from 215 odonate species, including representatives from 17 families, whose wings range from 20 to 725 mm² in area (Fig. 2A). We took high-resolution micrographs of example species to verify that the wing tracings accurately capture the geometric arrangement of veins (SI Appendix, Figs. S1 and S4–S6). We segmented the vein domains on all wings in the dataset, finding that the number of vein domains scales allometrically with wing size: species with larger wings have larger and more numerous vein domains (Fig. 2B). The full segmented dataset contains 150,000+ vein domains, from <0.01 to >5 mm² in area (SI Appendix, Fig. S13A).

Fig. 2.

Comparing vein domains across species. (A) Forewings of the smallest, median, and largest dragonfly (Right) and damselfly (Left) species included in our dataset. Vein domains are colored by area on the same scale. (B) Area of the entire wing (in square millimeters) versus the total number of wing domains on a log scale for each dragonfly (green; n = 343) and damselfly (purple; n = 119). Best fits are shown as solid lines, with an identity line in dashed gray. For both dragonflies and damselflies, the exponent on the fit is less than 1. (C) Schematic of the process used to create P–D morphology traces. The wing is divided into a series of rectangular bins. For a given bin, mean area and circularity are computed; the value for each domain is weighted by its overlap with the rectangular bin. P–D traces are smoothed with a Gaussian of width 3. (D) P–D traces of all damselflies in the dataset. (E) Distribution of P–D morphology traces for damselflies (purple) and dragonflies (green).

These data enable us to explore how vein domain area and circularity vary along the proximal to distal (P–D) axis (i.e., from a wing’s base to its tip) for each forewing and hindwing. We divide wings into 21 equally spaced rectangular bins along the P–D axis. For a given bin, we determine the area and circularity of each vein domain within it, and then calculate an area-weighted mean for the entire bin. For each wing, we plot the P–D morphology trace of its vein domains in a 2D space determined by circularity and area (Fig. 2C). By plotting P–D traces of many species, we show that damselflies and dragonflies exhibit distinct, clade-specific patterns (Fig. 2 D and E), and within each group, P–D morphology traces are related to wing size (SI Appendix, Fig. S13 B and C).

In nature, there are many developing structures that can be approximated as a flat tissue that is stochastically partitioned. Examples include leaf vascularization (26, 27), reptile scale formation (28), and a variety of pigmentation patterns (29). Theoretical and empirical work has shown that such patterns can form in different ways—as a bifurcating process in which branches grow toward secreted signal sources (26), a mechanism wherein stresses in the growing tissue trigger localized differentiation (27, 28), or diffusion-based systems with feedback loops that generate evenly spaced domains from a noisy precursor signal (29). Each class of processes produces characteristic geometric patterns.

Secondary veins in odonate wings have several features that are consistent with a simultaneous, diffusion-based patterning mechanism: (i) secondary veins that terminate in space are extraordinarily rare (SI Appendix, Table S1), (ii) 180° joints rarely occur among secondary veins (SI Appendix, Fig. S15), and (iii) domains made of secondary veins tend to be approximately the same size as their immediate neighbors (SI Appendix, Fig. S16). Last, rectangles tend to form between closely spaced parallel primary veins while pentagons and hexagons predominate in regions where primary veins are distantly spaced. Collectively, these features are conspicuously similar to those of a Voronoi tessellation of evenly spaced seeds in a 2D region (SI Appendix, Fig. S29) (30). A Voronoi tessellation is produced by taking a set of seed locations on a plane, and then partitioning every seed into its own region in space. The shape of each region is given by the set of all points that are closer to its seed than to any other. Voronoi tessellations are mathematically tractable, and they appear in nature in different contexts (31–33); we use them as the basis for a minimal model of secondary vein patterning.

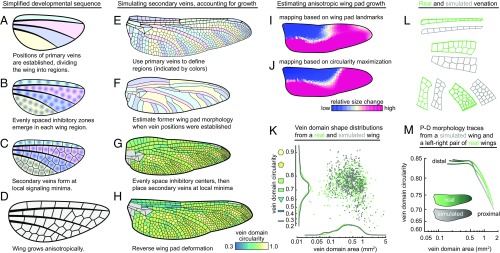
We hypothesized that, to a first approximation, the development of secondary veins proceeds as follows. First, the positions of primary veins are established on the wing pad (Fig. 3A) (34–42). Second, an as-yet-undescribed stochastic patterning mechanism generates evenly spaced inhibitory centers within the regions bound by the primary veins (Fig. 3B) [see, for example, mammalian hair follicle patterning (43) and avian feather bud patterning (44)]. Third, secondary veins arise at the inhibitory signal’s local minima, which can be well approximated by Voronoi cells (Fig. 3C). Finally, during subsequent nymphal development and wing eclosion, the wing undergoes anisotropic growth (41, 45) (Fig. 3D). This simplified sequence of steps serves as a tool to generate testable hypotheses about the mechanisms of wing vein patterning.

Fig. 3.

A model for simulating secondary vein patterning. (A–D) A simplified schematic of secondary vein development. (E–H) Process for simulating secondary veins while taking tissue growth into account. Gray domains in G and H are bounded on all sides by primary wing veins; these are not simulated in the model. (I and J) Mapping an example dragonfly (Anax junius) wing pad to the adult wing shows that the tissue grows heterogenously; two methods of calculating local growth produce similar spatial distributions of relative size changes: (I) map generated using landmarks on a nymphal wing pad; (J) map based on a wing pad morphology that was estimated by maximizing vein domain circularities. (K) The area and circularity distributions of the simulated wing (in gray) compared with the real P–D morphology trace (in green). (L) Simulated vein patterns for a hindwing of D. spinosus next to real vein patterns. (M) The P–D traces of the true left and right wings (green) compared with the P–D trace of a simulated wing (gray).

We use the developmental sequence described above to simulate the formation of secondary veins in an example wing, the hindwing of the dragonfly Dromogomphus spinosus. To start with the simplest possible model, we ignore wing growth altogether by simulating secondary veins as though they emerge on a fully formed adult wing (SI Appendix, Fig. S21 A–C). First, we manually divide the wing into regions that are bounded by primary veins and the wing margin. Next, we use the following procedure to generate a set of evenly spaced inhibitory centers for each wing region: we randomly place “inhibitory centers” equal in number to the number of vein domains in the matching region of the real wing, and then use Voronoi iteration as a method to evenly space the inhibitory centers (46). Finally, we position secondary veins at local minima of the inhibitory signal. When we compare the simulated wing to a left–right pair of real wings, we find that this model recovers some natural vein features, yet it systematically overestimates vein domain circularity (SI Appendix, Fig. S21D).

Next, we modified the model to include wing pad growth and shape change. As above, we use primary veins to define wing regions (Fig. 3E), and then estimate the former morphology of the wing pad (Fig. 3F; described below). We evenly space inhibitory centers on the wing pad and place secondary veins at local minima (Fig. 3G). Last, we simulate anisotropic growth by reforming the wing pad into the shape of the mature wing (Fig. 3H).

To estimate the shape of a wing pad, we make two assumptions about wing development based on earlier literature (34–41): the wing pad develops as a roughly convex shape, and the pattern of secondary veins that forms on the wing pad is composed of well-spaced polygons, which tend to maximize the circularity of vein domains. We use the mature wing to calculate a corresponding wing pad shape via a coordinate transformation that maximizes the circularity of all vein domains, while constraining the wing pad to be approximately convex (an example transformation for D. spinosus is shown in Fig. 3 E and F; see SI Appendix for further details).

To assess the effectiveness of our wing pad shape estimation, we use a published micrograph of the hindwing pad from the dragonfly Anax junius, which was dissected from the nymph before secondary veins had formed (47). We use primary veins as landmarks to map the adult wing onto the wing pad, and then color each vein domain according to its relative size change (Fig. 3I and SI Appendix, Fig. S23). This shows that the nymphal wing pad-based map produces a coordinate transformation that is strikingly similar to the map we independently calculate using the circularity maximization procedure described in the previous paragraph (Fig. 3J).

When we employ this computational model to simulate secondary veins for the hindwing of D. spinosus, it results in the secondary-venation pattern shown in Fig. 3H. Real and simulated veins from different parts of the wing are shown side-by-side in Fig. 3L. The simulated wing has a vein domain area distribution, circularity distribution, and P–D morphology trace that closely match those of the true wing (Fig. 3 K and M; left and right wings of the same individual shown for comparison). We simulated secondary veins for odonates from several different families, and in each case the same simple model recapitulates the observed geometric rearrangements of veins (e.g., SI Appendix, Fig. S30); conversely, the model does not generate any arrangements that are not seen in true wings.

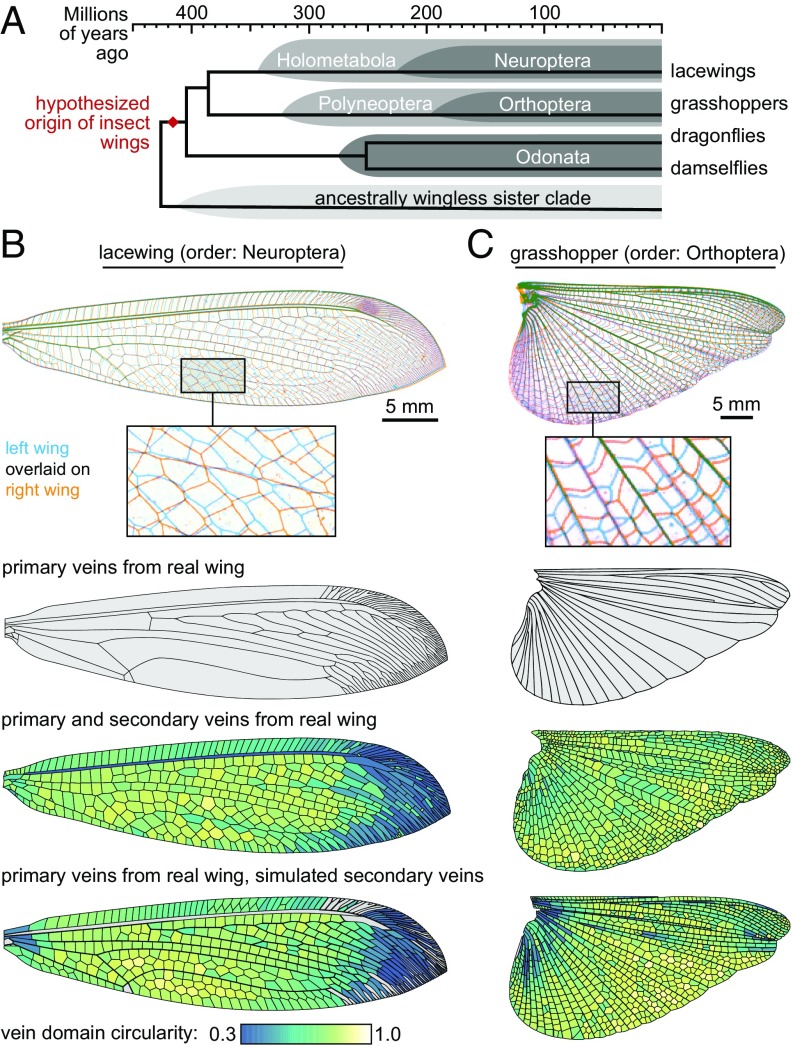
Next, we apply the secondary vein simulation model to representatives from orders Orthoptera and Neuroptera. With respect to Odonata, these orders are drawn from distantly related parts of the insect phylogeny (Fig. 4A)—the last common ancestor of the three orders may have been the shared ancestor of all extant winged insects (23). As above, we treat primary veins as boundaries and simulate secondary veins within them. Likewise, the model recapitulates most of the secondary vein patterns in each example species (Fig. 4 B and C), producing distributions of vein domain size and circularity that are broadly similar to those of the true wings. However, there are a few subregions in the wing of each species where the model does not capture vein domain geometry as accurately. For instance, in lacewing and grasshopper, vein domains along the trailing wing margin in the real wings have a systematically lower circularity than the analogous vein domains in simulations. A possible explanation for this mismatch is considered in Discussion.

Fig. 4.

Modeling the secondary veins of distantly related species. (A) The evolutionary relationships among the insects considered in this study. (B and C) The model applied to a (B) lacewing (order: Neuroptera) and (C) grasshopper (order: Orthoptera). Gray vein domains in B are bounded on all sides by primary wing veins; these are not simulated in the model.

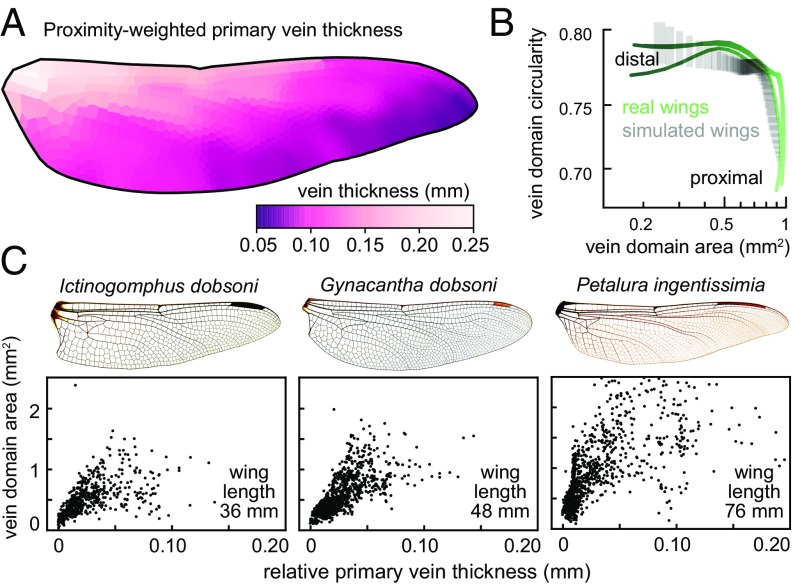
We assess model sensitivity to variation in the density of inhibitory centers by resimulating secondary venation at a range of densities. The resulting venation patterns have substantial changes to their vein domain area and circularity distributions (SI Appendix, Fig. S27D), demonstrating that it is essential for the model to include an accurate estimate of the number of inhibitory centers in each region. With the model described so far, the density of inhibitory centers in each region is drawn directly from real wings, effectively “baking it” into the model. Therefore, we ask whether it is possible to accurately model the secondary vein pattern using primary vein morphology as the only input. The thickness of primary veins varies substantially across a wing (10, 48). We hypothesized that if primary veins are the source of a morphogen that affects inhibitory centers in nearby tissue, primary vein thickness on the wing pad could indicate the strength or concentration of that signal. This, in turn, would determine the length scale of the pattern generator. We show in an example wing that the relative thicknesses of primary veins are correlated with the thicknesses of the corresponding veins on the adult wing (SI Appendix, Fig. S26). Therefore, we use primary vein thickness on the adult wing as a proxy for relative thickness on the wing pad. We inquire how the thickness of primary veins is related to the area of nearby vein domains. We do so by measuring the thickness of each primary vein segment in an adult wing. Then, we calculate the shortest distance from each vein domain to every primary vein and compute a proximity-weighted primary vein thickness (Fig. 5A; see SI Appendix for details). Across multiple species, we find a positive relationship between primary vein thickness and vein domain area (Fig. 5C and SI Appendix, Fig. S28). We use this relationship to simulate secondary veins without predetermining the number of inhibitory centers in each wing region. Using high-resolution micrographs of wings from the dragonflies Libellula cyanea and Sympetrum vicinum, we measure primary vein thickness to produce a distribution of thicknesses and domain areas. We use this distribution to simulate a wing from E. simplicicolis—a species that was not used to generate the sample distribution. We stochastically simulate an E. simplicicolis wing repeatedly, computing the P–D morphology trace each time. The variation between simulated wings is comparable to the disparity we observe between left and right real wings of the same individual (Fig. 5B). Therefore, knowing only the thickness and arrangement of primary veins on a wing, we are able to simulate secondary veins whose pattern is comparable to that of a real wing.

Fig. 5.

Primary vein thickness correlates with the length scale of secondary vein spacing. (A) An example wing from the dragonfly Petalura gigantean, with vein domains colored by proximity-weighted primary vein thickness (see text for details). (B) P–D morphology traces of many simulated wings, generated by drawing from the distribution of primary vein thickness vs. vein domain density. Gray boxes show 25th to 75th percentiles for bins along the P–D axis of simulated wings. Green traces represent the real left and right wings of a single individual. (C) In dragonflies, there is a relationship between the thickness of nearby long veins and the size of domains. The x axis shows the thickness of the nearby long veins; the y axis shows the size of wing domains. Wing images courtesy of Wikimedia Commons/John Tann.

Discussion

The molecular basis of primary wing vein patterning has been studied extensively in Drosophila melanogaster (49), but because fruit flies do not have secondary veins, the developmental basis of these “fingerprint” veins is still unknown. Some previous researchers have qualitatively described secondary veins and speculated about how their curious geometric patterns are formed. K. G. Andrew Hamilton (2) described the patterns from diverse species and attempted to place them in broad morphological categories. D’Arcy Thompson (50) likened them to the shapes formed by interfaces equilibrating under tension, as one can observe in clusters of soap bubbles. However, only with the advent of high-throughput digital image quantification tools has it become possible for us to chart the geometric attributes of secondary veins in detail and test a model to explain their patterning.

The model we present is not molecularly specific, but it allows us to make falsifiable hypotheses about the development of secondary veins: first, the position of a primary vein is established before the positions of neighboring secondary veins. Second, there exists an inhibitory signal that restricts secondary vein formation to certain locations in the developing wing. Third, there is a stochastic input to the process that evenly spaces inhibitory centers. These are probably generated by a reaction–diffusion process (29), a simple feedback system that is able to generate diverse patterns, including pigmentation patterns that are observed on insect wings (51). Similarly, a reaction–diffusion-based hypothesis for wing vein patterning has been proposed for the wings of Orosanga japonicus (52). Finally, we hypothesize that once secondary vein locations have been established, vein morphogenesis itself is deterministic. Our model is consistent with empirical observations, but we have not proven that the model captures a specific molecular mechanism. Further testing of the model would entail a mechanistic investigation into the abovementioned hypotheses that form its foundation. This will require detailed developmental description, as well as functional genetic and developmental experiments on developing wings of species that have reticulate secondary veins.

Our model is largely effective in recapitulating secondary vein arrangements in three orders of insect wings. However, there are two features of real wings for which the model is systematically inaccurate: (i) wing regions in which there is a pronounced gradient in the size of domains, and (ii) wing regions in which secondary vein segments are arranged in an atypically collinear manner (SI Appendix, Figs. S31 and S32). The existence of the latter case suggests that a strict dichotomy of primary veins and secondary veins cannot fully describe wing vein identities. We hypothesize that after primary vein positions are established, secondary veins can take on primary vein–like function and morphology in wing regions that are sufficiently distant from an inhibitory signal that emanates from primary veins [for further discussion of vein identity, see other authors (53, 54) who have reviewed the evolution and development of diverse wing veins in closer detail].

To discern the functional ramifications of a given arrangement of wing veins, it is necessary to consider additional aspects of wing morphology beyond the topology and thickness of veins (3). In odonates, for instance, wing veins are tubular struts composed of several different layers of cuticle (48) that are joined together in a variety of mechanically complex ways (9, 55–58). It will be instructive to integrate large-scale vein arrangement data with functional manipulations of wings. The biomechanical effects of venation patterns can be assessed from another perspective as well: recent work on miniature winged robots has used natural veined insect wings as models for biomimetic wings (59, 60). The present study, by illuminating principles of geometric wing design, could guide efforts to generate life-like, synthetic vein patterns, and in turn be used to examine how vein patterns affect the mechanical properties of a wing.

A variety of open questions in morphological evolution could be addressed using the approach we take in the present study. Phenotypic description is typically the most expensive aspect of a project and usually requires a great deal of expertise (61, 62). The centuries-long documented history of life science scholarship is rich with observations that were recorded as images, but they remain mostly untapped for large-scale investigations, partly because phenotypes have not been recorded in a precise, machine-parsable manner (63). We suggest that the method used here could be applied to many biological questions that are answerable with existing image-based data. To demonstrate the possibilities of this approach, we apply our quantification tools to diverse patterned tissues (SI Appendix, Fig. S3), finding that it enables us to effectively characterize each of them. This offers a fruitful avenue for future research.

Methods

Microscopy and Collecting Published Images.

Wings were dissected from specimens and imaged with a flat-mount scanner, macroscopic photography, or dissection microscope. Each technique produces a 2D image of the 3D wing. Since some wings are corrugated (10, 64, 65), capturing them in 2D introduces a slight distortion to vein domain shapes. For typical vein domains, this distortion results in an underestimate of vein domain area and circularity by 1–5% (SI Appendix, Figs. S8–S10). When measuring the thicknesses of primary veins, we found that lighting conditions could affect the measured lengths by altering the apparent thickness of a vein. To compare the data from multiple species, we plotted relative vein thickness, calculated by subtracting the smallest vein thickness from every measured thickness on that wing. Images in electronic publications were extracted digitally; images in printed publications were digitally scanned (40, 45, 66–68).

Segmenting Wing Images and Calculating Vein Domain Attributes.

Segmentation of wing images was accomplished with a code based on the fast marching method with a variable background velocity field (69, 70). The segmented images were used to make a polygonal representation of each vein domain, which provided two advantages over the segmented image: (i) domain perimeter was a more rigorously defined quantity, and (ii) geometric computations were less sensitive to segmentation-related noise. Segmented wing images are available for all wings examined in this paper. See https://github.com/hoffmannjordan/insect-wing-venation-patterns.

Full methods are available in SI Appendix. This includes mathematical details on calculating wing attributes, simulating secondary veins, measuring primary vein thickness, and validating the use of wing tracings from published sources.