Leak potassium channels regulate sleep duration

Significance

To address molecular mechanisms regulating sleep duration, a simple computational model of a cortical neuron [simplified averaged neuron (SAN) model], which recapitulates the electrophysiological characteristics of slow-wave sleep (SWS) and wakefulness, is developed in this study. Comprehensive bifurcation and detailed mathematical analyses predicted that leak K⁺ channels play a role in generating the cortical electrophysiological characteristics of SWS, leading to a hypothesis that leak K⁺ channels play a role in the regulation of sleep duration. We comprehensively generated and analyzed 14 knockout mice of the leak K⁺ channel family, which demonstrated that impairment of the leak K⁺ channel (Kcnk9) decreases sleep duration. The results confirm the validity of the SAN model and suggest a molecular mechanism regulating sleep duration.

Abstract

A primary goal of sleep research is to understand the molecular basis of sleep. Although some sleep/wake-promoting circuits and secreted substances have been identified, the detailed molecular mechanisms underlying the regulation of sleep duration have been elusive. Here, to address these mechanisms, we developed a simple computational model of a cortical neuron with five channels and a pump, which recapitulates the cortical electrophysiological characteristics of slow-wave sleep (SWS) and wakefulness. Comprehensive bifurcation and detailed mathematical analyses predicted that leak K⁺ channels play a role in generating the electrophysiological characteristics of SWS, leading to a hypothesis that leak K⁺ channels play a role in the regulation of sleep duration. To test this hypothesis experimentally, we comprehensively generated and analyzed 14 KO mice, and found that impairment of the leak K⁺ channel (Kcnk9) decreased sleep duration. Based on these results, we hypothesize that leak K⁺ channels regulate sleep duration in mammals.

Sleep is a physiological phenomenon widely conserved among species (e.g., nematodes, jellyfish, flies, and mammals). The sleep/wake cycle occurs with a time scale of hours in primates and one of minutes in rodents. Although the daily sleep duration varies among species, it is conserved within a species (1), suggesting that a genetic mechanism is involved in its regulation. Studies on the cellular and molecular nature of sleep/wake cycle regulation have revealed some sleep/wake-promoting circuits and secreted molecules (2, 3). Indeed, the synaptic projection from sleep/wake-promoting nuclei in the brainstem to the cerebral cortex has been found to regulate the sleep/wake cycle (3). However, it is still elusive how the daily sleep duration and the sleep/wake cycle are genetically regulated.

Whereas the regulation of sleep duration has relatively slow dynamics (i.e., from minutes to hours), the EEG during each state of the sleep/wake cycle exhibits faster dynamics (i.e., from milliseconds to seconds). For example, nonrapid eye movement (NREM) sleep is accompanied by a high-amplitude, low-frequency (0.5–4 Hz) pattern of EEG, whereas other states (wakefulness or REM sleep) are associated with low-amplitude high frequencies, which are respectively generated by the synchronous or irregular firing of cortical neurons (4–7). The membrane potential of cortical neurons exhibits a depolarized bursting pattern (awake firing pattern) during wakefulness or REM sleep, whereas it alternates between depolarized “up” states and hyperpolarized “down” states during NREM sleep. This firing pattern during NREM sleep is represented as the slow-wave sleep (SWS) firing pattern in this study. Several computational studies have attempted to reveal the mechanism underlying these firing patterns (8–12). These studies led to the idea that the transition from the up state to the down state occurs in cortical neurons as a result of their regulation by neural networks (e.g., the thalamocortical network). However, although the role of synaptic connections in the sleep/wake cycle has been revealed, the intracellular mechanisms of sleep/wake cycle regulation are still elusive.

A recent study proposed a new mechanism for the sleep/wake cycle regulation by focusing on intracellular mechanisms of the SWS firing pattern (13). The study succeeded in computationally recapitulating the SWS firing pattern in an averaged-neuron (AN) model, whereby a cortical neuron transmitted its output to equivalent neurons (i.e., its output returns to itself as input), suggesting that an intrinsic mechanism, the regulation of a Ca²⁺-dependent hyperpolarization pathway, is involved in generating the SWS firing pattern (13). Notably, the components of the Ca²⁺-dependent hyperpolarization pathway, which are predicted to be important for generating the SWS firing pattern, are also involved in regulating sleep duration (13), suggesting that the regulation of the SWS firing pattern (fast dynamics) and sleep duration (slow dynamics) could share a common mechanism (13, 14). In other words, the changes in cortical firing patterns might not just accompany the sleep/wake cycle but rather cause it. Therefore, determining the mechanism by which the SWS firing pattern is generated could reveal clues about the regulation mechanism of the sleep/wake cycle.

Although the AN model succeeded in revealing the role of the Ca²⁺-dependent hyperpolarization pathway in generating the SWS firing pattern, its detailed mathematical structure was still unknown. Because the major difference between the SWS and awake firing patterns is the presence or absence of the down state, it is important to elucidate how the transition from the up to the down state occurs. This question can be addressed by mathematical analyses, for example, to analyze the currents responsible for the transition from the up to the down state, but the AN model, which contains 13 components, is too complicated to conduct such analyses. Studies of other rhythmic bursting patterns that are also characterized by up and down states (e.g., the pre-Bötzinger complex or hippocampal pyramidal neurons) have indicated that approximately four to nine channels are sufficient to generate them (15–17), raising the possibility that some of the 13 components in the AN model are redundant for generating the SWS firing pattern. Indeed, another study indicated that NMDA receptors and voltage-gated Ca²⁺ channels have redundant roles and that GABA receptors are minimally involved in generating the SWS firing pattern (13). These reports suggest that the AN model might be simplified to conduct mathematical analyses. Therefore, to reveal the mechanism for generating the down state and the SWS firing pattern, here we developed a simplified model and used it to perform detailed mathematical analyses.

Results

Construction of the Simplified AN Model, Which Recapitulates the SWS Firing Pattern.

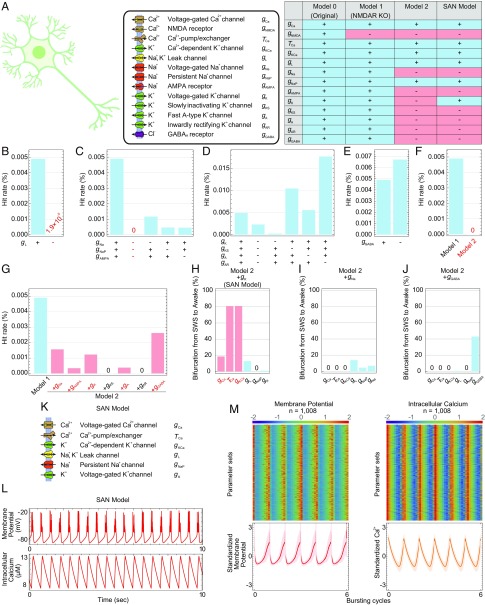
To analyze the SWS firing pattern occurring in the cortical neurons during SWS (6), we simplified the AN model (13) by eliminating its components: channels, receptors, and pump (Fig. 1A). We first sought to identify which components were redundant for generating the SWS firing pattern by conducting random parameter searches and calculating the hit rates (i.e., the percentage of parameter sets that showed the SWS firing pattern among all randomly generated parameter sets) under KO of the components (i.e., setting the conductance to zero). We compared the hit rate of each model, and when the hit rate of a model is more than 100 times lower than the other, we assumed that the model is highly unlikely and inappropriate. If eliminating components had only a minor effect on the hit rate, those components were considered redundant for the generation of the SWS firing pattern and were eliminated to simplify the model.

Fig. 1.

Construction of the SAN model by simplifying the AN model. (A) Schematic illustration of the AN model (Left). Table shows the channels included in each model (Right). (B–E) Hit rates of model 1 or model 1 under the KO of leak channels (B), Na⁺ channels (C), K⁺ channels (D), or GABA receptors (E). (F and G) Hit rates of model 1 or model 2 (F) or model 1 or model 2 plus each ion channel condition (G). (H–J) Summary of the bifurcation analysis in each condition: model 2 plus g_K (H), model 2 plus g_Na (I), or model 2 plus g_GABA model (J). Conductance and time constants related to the Ca²⁺-dependent hyperpolarization pathway are in red. (K) Schematic illustration of the SAN model. (L) Typical patterns of the membrane potential and intracellular Ca²⁺ concentration in the SAN model. (M) The standardized membrane potential and intercellular Ca²⁺ concentration of the 1,008 parameter sets obtained by parameter searches in the SAN model. The line and shadow (Lower) indicate the mean and SD, respectively.

Because the voltage-gated Ca²⁺ channels and the NMDA receptors play redundant roles, the elimination of the NMDA receptors was reported to only slightly affect the hit rate (13). Therefore, the NMDA receptors were eliminated first from model 0 to generate model 1. We then classified the channels in model 1 into five categories: Ca²⁺-related channels (g_Ca, g_KCa), leak channels (g_L), Na⁺ channels (g_Na, g_NaP, g_AMPA), K⁺ channels (g_K, g_KS, g_A, g_AR), and Cl⁻ channels (g_GABA). Because both of the Ca²⁺-related channels (g_Ca, g_KCa) are reported to be essential for generating the SWS firing pattern under NMDA receptor KO (13), we conducted the random parameter searches and compared the hit rates under the KO of each category except for the Ca²⁺-related channels. The parameter searches under KO of leak channels exhibited a much lower hit rate (∼1.9 × 10⁻⁵%) than model 1 (∼4.9 × 10⁻³%; Fig. 1B), indicating that the leak channels are considered essential for generating the SWS firing pattern and should therefore be preserved in the model. The hit rate under KO of all three Na⁺ channels was zero (Fig. 1C), indicating that at least one of the Na⁺ channels is necessary for generating the SWS firing pattern. Among the three Na⁺ channels, the parameter searches under KO of voltage-gated Na⁺ channels exhibited a higher hit rate (∼1.2 × 10⁻³%) than those under KO of persistent Na⁺ channels (∼4.6 × 10⁻⁴%) or of AMPA receptors (∼4.5 × 10⁻⁴%; Fig. 1C), indicating that the voltage-gated Na⁺ channels are less important for generating the SWS firing pattern than the other two. Because the persistent Na⁺ channel is an intrinsic channel that was found to be important for generating the rhythmic bursting in other studies (15, 16, 18, 19), the persistent Na⁺ channels were chosen to be preserved in the model. In addition, the parameter searches under KO of all four K⁺ channels (g_K, g_KS, g_A, g_AR) or the GABA receptors exhibited hit rates (∼2.3 × 10⁻³% or ∼6.7 × 10⁻³%, respectively) in the same range as model 1 (Fig. 1 D and E), indicating that the K⁺ channels and the GABA receptors play limited roles in generating the SWS firing pattern. Based on these results, the voltage-gated Na⁺ channels, AMPA receptors, four K⁺ channels, and GABA receptors were considered candidates for elimination from model 1.

However, the hit rate under KO of the voltage-gated Na⁺ channels, AMPA receptors, four K⁺ channels (g_K, g_KS, g_A, g_AR), and GABA receptors (model 2) was zero (Fig. 1F), indicating that model 2 lacks some components needed to generate the SWS firing pattern. To find the sufficient model, we generated seven models by adding each eliminated component back to model 2 and conducted the random parameter searches. The models consisting of model 2 plus g_Na, model 2 plus g_AMPA, model 2 plus g_K, model 2 plus g_A, and model 2 plus g_GABA exhibited nearly normal hit rates (∼1.6 × 10⁻³%, ∼3.5 × 10⁻⁴%, ∼1.2 × 10⁻³%, ∼3.9 × 10⁻⁴%, and ∼2.6 × 10⁻³%, respectively; Fig. 1G); hence, these five models were further considered as candidates for the simplified model.

As the simplified model should exhibit the important characteristics of model 1, in which down-regulation of the Ca²⁺-dependent hyperpolarization pathway causes the transition from the SWS to awake firing pattern (SI Appendix, Fig. S1A), we conducted a bifurcation analysis (i.e., a gradual change in parameter values) in the five models. In the bifurcation analysis of 1,008 parameter sets in the model 2 plus g_K model, the Ca²⁺-dependent hyperpolarization pathway was preserved, whereby down-regulating the conductance of voltage-gated Ca²⁺ channels or Ca²⁺-dependent K⁺ channels or reducing the time constant of Ca²⁺ efflux caused the transition from the SWS to awake firing pattern in 188 (18.7%), 816 (81.0%), and 815 (80.9%) parameter sets, respectively (Fig. 1H). However, this transition derived from the Ca²⁺-dependent hyperpolarization pathway was not observed in the other four models (Fig. 1 I and J and SI Appendix, Fig. S1 B and C). These results indicated that the model 2 plus g_K model preserved more of the characteristics of model 1 than the other four models. Therefore, we chose the model 2 plus g_K model as the simplified AN (SAN) model (Fig. 1K and SI Appendix, SI Materials and Methods, SAN Model), which contains six components and three variables in differential equations, as opposed to the 13 components and 10 variables in differential equations in the AN model. The SAN model exhibited a similar membrane potential and intracellular Ca²⁺ concentration as model 1 (Fig. 1 L and M and SI Appendix, Fig. S1 D–H), suggesting that the SAN model preserved the characteristics of model 1.

Leak K⁺ Channels Play a Role in Generating the SWS Firing Pattern Based on the SAN Model.

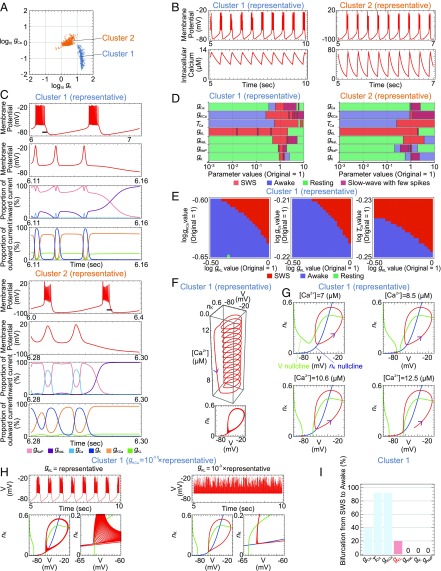
The histogram of the 1,008 parameter sets with the SWS firing patterns in the SAN model showed bimodality of the g_K and g_Ca values, implying that these parameter sets could be divided into two clusters (SI Appendix, Fig. S2A). In fact, the logarithmic plot of g_K against g_Ca exhibited two clusters (Fig. 2A): cluster 1 with 480 parameter sets and cluster 2 with 528 parameter sets. These clusters were also obtained by principal component analysis (SI Appendix, Fig. S2B), supporting their validity. We then determined the representative parameter set in each cluster by performing the density estimation (SI Appendix, Table S2). The representative parameter set exhibited the SWS firing pattern in each cluster (Fig. 2B). We analyzed cluster 1 and then confirmed that cluster 1 and cluster 2 represent the same results. As the major difference between the SWS and awake firing patterns is whether the down state exists, we focused on the currents of channels during the down state of the SWS firing pattern. The analysis of current with the representative parameter sets revealed that the leak K⁺ channels and Ca²⁺-dependent K⁺ channels were two major sources of outward current in the down state (Fig. 2C and SI Appendix, Fig. S2C). These results suggested that the leak K⁺ channels, in addition to the Ca²⁺-dependent K⁺ channels, which were previously studied (13), are important for generating the down state in the SWS firing pattern. To investigate the role of the leak K⁺ channels in generating the SWS firing pattern, we conducted the bifurcation analysis with the representative parameter sets. However, down-regulating the conductance of the leak K⁺ channels alone did not cause a transition between the SWS and awake firing patterns (Fig. 2D and SI Appendix, Fig. S2 D and E). Considering that the leak K⁺ channels and the Ca²⁺-dependent K⁺ channels play redundant roles in the down state (Fig. 2C and SI Appendix, Fig. S2C), the leak K⁺ channels might regulate the threshold of the transition derived from the Ca²⁺-dependent hyperpolarization pathway. Therefore, we next conducted a 2D bifurcation analysis, in which two of four parameters (the conductance of the leak K⁺ channels, Ca²⁺-dependent K⁺ channels, and voltage-gated Ca²⁺ channels; and the time constant of Ca²⁺ efflux) were changed gradually and simultaneously. This analysis showed that down-regulating the conductance of leak K⁺ channels caused a transition from SWS to awake firing patterns under the down-regulated conductance of Ca²⁺-dependent K⁺ channels or voltage-gated Ca²⁺ channels or the reduced time constant of Ca²⁺ efflux (Fig. 2E and SI Appendix, Fig. S3A). These results suggested that the leak K⁺ channels change the threshold for the transition induced by the Ca²⁺-dependent hyperpolarization pathway and are therefore important for generating the SWS firing pattern. Notably, the current and bifurcation analyses against the representative parameter set in cluster 2 also supported this scenario (Fig. 2 C and D and SI Appendix, Figs. S2 C and D and S3B).

Fig. 2.

Leak K⁺ channels play a role in generating the SWS firing pattern based on the SAN model. (A) Scatter plot of the g_K and g_Ca values for all 1,008 parameter sets obtained by the parameter searches. All parameter sets were divided into two clusters, cluster 1 (blue) and cluster 2 (orange), according to the g_K and g_Ca values. (B) Membrane potential and intracellular Ca²⁺ concentration of the representative parameter set in each cluster over time. (C) Membrane potential, proportion of each channel’s inward current, and proportion of each channel’s outward current of the representative parameter set in each cluster over time. (D) Bifurcation analysis of the representative parameter set in each cluster. The definitions and examples of SWS, awake, resting, and slow-wave with few spikes are described in SI Appendix, Fig. S2E and Table S5, respectively. (E) Two-dimensional bifurcation analysis of the representative parameter set in cluster 1. (F) Three- (Upper) and two-dimensional (Lower) plots of the trajectory of the representative parameter set in cluster 1. (G) Phase planes of the representative parameter set in cluster 1 in cases in which the Ca²⁺ concentration is fixed at 7 μM, 8.5 μM, 10.6 μM, or 12.5 μM. The red, green, and blue lines indicate the trajectory of the differential equation, V nullcline, and n_K nullcline, respectively. (H) Membrane potential and phase plane of the parameter set whose g_KCa was lower (Left) or whose g_KCa and g_KL were lower (Right) than the representative parameter set in cluster 1. (I) Summary of the bifurcation analysis in cluster 1. Conductance of the leak K⁺ channels is in red.

Leak K⁺ Channels Play a Role in Generating the Down State of the SWS Firing Pattern Based on Detailed Mathematical Analyses.

To reveal the role of the leak K⁺ channels in generating the SWS firing pattern, we focused on their role in the transition from the up to the down state during the SWS firing pattern by analyzing cluster 1 and then confirmed that cluster 1 and cluster 2 represent the same results. First, we plotted the trajectory of the SWS firing pattern in the phase space. Whereas the AN model has 10 variables, the SAN model has only three variables (V, the membrane potential; n_K, the dimensionless quantity associated with the activation of the voltage-gated K⁺ channels; and [Ca²⁺], the intracellular calcium concentration) in the differential equation. Therefore, the trajectory of the SAN model could be represented in the 3D space (Fig. 2F). The coiled part and the straight part of the trajectory correspond to the up state and the down state, respectively (Fig. 2F). The Ca²⁺ concentration gradually increased or decreased in the up or down state, respectively (Fig. 2F). To understand how this trajectory was generated, we plotted the V nullcline, n_K nullcline, and [Ca²⁺] nullcline with the trajectory (SI Appendix, Fig. S3C). As the nullcline is a set of the points whose differential of a certain direction is zero, its position describes which direction each point in the space moves. Therefore, the nullcline enables us to understand the approximate dynamics of the differential equation. To analyze this phase space in more detail, we then plotted the nullclines and the trajectory at four fixed Ca²⁺ concentrations (Fig. 2G). At the low Ca²⁺ concentration (7 µM in cluster 1), the trajectory converged to the stable limit cycle (Fig. 2G), which corresponded to the up state of the SWS firing pattern. At the middle Ca²⁺ concentrations (8.5 and 10.6 µM in cluster 1), there were at least two stable states: a stable point (Fig. 2G, orange point) and a stable limit cycle, which correspond to the down state and the up state, respectively (Fig. 2G). At these Ca²⁺ concentrations, the stable limit cycle was not able to reach the orange point, and therefore still existed (Fig. 2G). At the high Ca²⁺ concentration (12.5 µM in cluster 1), the stable limit cycle disappeared, and the trajectory converged to the orange point (Fig. 2G). In summary, the phase planes of the SAN model revealed that the transition between the up and the down state is controlled by a calcium-dependent bistable system, which is understood by the regulation of two nullclines, the V nullcline and the n_K nullcline. In other words, the bistability at the middle Ca²⁺ concentrations enabled oscillation between the up and down states.

To demonstrate the role of the leak K⁺ channels in regulating the nullclines, and hence the transition from the up to the down state, we down-regulated the conductance of leak K⁺ channels and plotted the nullclines and the trajectory. This analysis showed that down-regulating the conductance of leak K⁺ channels caused the V nullcline to shift in a positive direction on the n_K axis, which prevented the transition from the up to the down state and generated the awake firing patterns (Fig. 2H). Interestingly, down-regulating the conductance of Ca²⁺-dependent K⁺ channels, the other major source of outward current during the down state (Fig. 2C), also caused the V nullcline to shift in a positive direction on the n_K axis, preventing the transition from the up to the down state, and generated the awake firing pattern (SI Appendix, Fig. S3G). These results indicated that the leak K⁺ channels and the Ca²⁺-dependent K⁺ channels cooperatively control the shift of the V nullcline and hence the intersection point of the V nullcline and the n_K nullcline, thereby determining the transition from the SWS to awake firing pattern by regulating the transition from the up to the down state. Furthermore, the additive control of the V nullcline by the leak K⁺ channels and Ca²⁺-dependent K⁺ channels could explain the results of the 2D bifurcation analysis against these channels (Fig. 2E).

The voltage-gated Ca²⁺ channels and the time constant of Ca²⁺ efflux cooperatively regulate the Ca²⁺ concentration, which also controls the transition from the SWS to awake firing pattern. This can also be elucidated by the control of the V nullcline by the Ca²⁺-dependent K⁺ channels. Because the Ca²⁺-dependent K⁺ channels are regulated by the Ca²⁺ concentration, the voltage-gated Ca²⁺ channels and the time constant of Ca²⁺ efflux could affect the transition from the up to the down state by regulating the Ca²⁺-dependent K⁺ channels and thus the V nullcline (Fig. 2G). Therefore, the voltage-gated Ca²⁺ channels, the time constant of Ca²⁺ efflux, and the leak K⁺ channels could cooperatively control the transition from the up to the down state and hence from the SWS to awake firing pattern.

To investigate the generality of these findings, we conducted a bifurcation analysis of 480 parameter sets in cluster 1 of the SAN model, in which the leak channels are divided into the leak K⁺ and Na⁺ channels. Down-regulating the conductance of leak K⁺ channels caused the transition from the SWS to awake firing patterns in 96 parameter sets (20.0%) of cluster 1 (Fig. 2I), indicating that the leak K⁺ channels are involved in generating the SWS firing pattern. Notably, phase plane analyses against the representative parameter set and bifurcation analyses in cluster 2 also supported this finding (SI Appendix, Fig. S3 C–J).

Leak K⁺ Channels Play a Role in Generating the Down State of the SWS Firing Pattern Based on the AN Model.

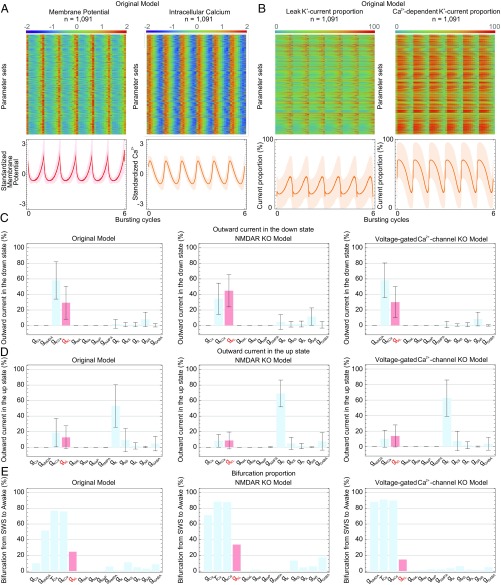
To evaluate the role of the leak K⁺ channels in generating the SWS firing pattern under synaptic connections (i.e., a model containing the AMPA receptors, the NMDA receptors, and the GABA receptors), we conducted the current and bifurcation analyses in the AN model, which contains 13 components including synaptic currents. In the previous study, the leak K⁺ channels and the leak Na⁺ channels were represented as one type of leak channels (13). To elucidate the role of the leak K⁺ channels, we analyzed currents of the leak K⁺ and Na⁺ channels together with the other channels in the original AN model, the KO of NMDA receptors (i.e., setting the conductance of the NMDA receptors to zero in the original AN model) model, and the KO of voltage-gated Ca²⁺ channels (i.e., setting the conductance of the voltage-gated Ca²⁺ channels to zero in the original AN model) model. The percentages of the current of the leak K⁺ channels and the Ca²⁺-dependent K⁺ channels were high in the original AN model (Fig. 3 A and B and SI Appendix, Fig. S4 A–C), as with the SAN model (Fig. 2C and SI Appendix, Fig. S2C). Interestingly, the percentages of the current of the leak K⁺ channels and Ca²⁺-dependent K⁺ channels in the down state were relatively high: 29.4% and 58.0%, respectively, in the original AN model, 44.8% and 34.5% in the KO of NMDA receptors model, and 30.2% and 58.2% in the KO of voltage-gated Ca²⁺ channels model (Fig. 3C and SI Appendix, Fig. S4D). On the contrary, the percentages of the current of the leak K⁺ channels and Ca²⁺-dependent K⁺ channels in the up state were relatively low: 12.7% and 18.6%, respectively, in the original AN model, 8.7% and 8.2% in the KO of NMDA receptors model, and 13.8% and 10.2% in the KO of voltage-gated Ca²⁺ channels model (Fig. 3D and SI Appendix, Fig. S4E). These results suggested that the leak K⁺ channels and the Ca²⁺-dependent K⁺ channels are involved in the down state rather than the up state. To elucidate the role of the leak K⁺ channels in the transition between the SWS and awake firing patterns, we conducted the bifurcation analysis in the original AN model, the KO of NMDA receptors model, and the KO of voltage-gated Ca²⁺ channels model. The result showed that down-regulating the conductance of leak K⁺ channels and Ca²⁺-dependent K⁺ channels led to the transition from SWS to awake firing patterns in 270 parameter sets (24.7%) and 828 parameter sets (75.9%) of the original AN model, 395 parameter sets (33.8%) and 1,024 parameter sets (87.7%) of the KO of NMDA receptors model, and 140 parameter sets (14.8%) and 851 parameter sets (89.8%) of the KO of voltage-gated Ca²⁺ channels model (Fig. 3E). These results indicated that the Ca²⁺-dependent K⁺ channels are important (13) and that the leak K⁺ channels are also involved in generating the SWS firing pattern. These results from the AN model also suggest that the currents of the leak K⁺ channels and Ca²⁺-dependent K⁺ channels cause the transition from the up to the down state, and hence the transition between the SWS and awake firing patterns. In support of these findings, the KO of NMDA receptors model, which showed a higher proportion of the leak K⁺ channels in the down state (44.8%; Fig. 3C), exhibited a higher proportion of the transition from the SWS to awake firing patterns (33.8%; Fig. 3E) in down-regulating the conductance of the leak K⁺ channels than the other two models. These results indicated that the leak K⁺ channels are especially involved in the down state and generated the SWS firing pattern in the SAN and AN models.

Fig. 3.

Leak K⁺ channels play a role in generating the SWS firing pattern based on the AN model. (A) Standardized membrane potential and intracellular Ca²⁺ concentration of 1,091 parameter sets obtained by the parameter searches in the original AN model. The line and shadow (Lower) indicate the mean and SD, respectively. (B) Normalized proportion of the current of leak K⁺ channels or Ca²⁺-dependent K⁺ channels of 1,091 parameter sets obtained by the parameter searches in the original AN model. (C and D) Proportion of each channel’s outward current in the down state (C) or the up state (D) under the original AN model, the NMDAR KO model, or the voltage-gated Ca²⁺-channel KO model. The leak K⁺ channel data are in red. (E) Summary of the bifurcation analysis under the original AN model, the NMDAR KO model, and the voltage-gated Ca²⁺ channel KO model. The leak K⁺ channel data are in red. Error bars indicate SD.

Impairment of Leak K⁺ Channels Decreases Sleep Duration in Mice.

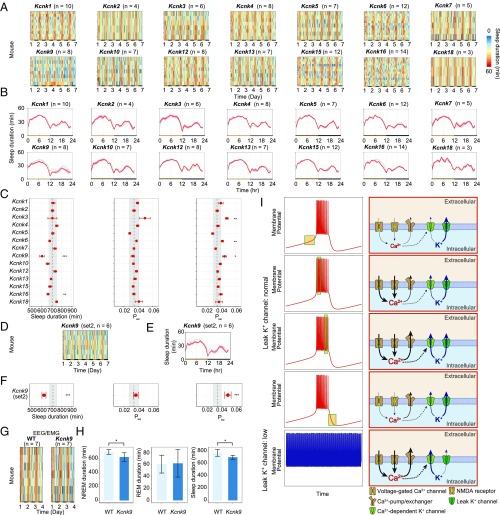
Analyses of the SAN and AN models indicated that down-regulating the leak K⁺ channels led to the transition from the SWS to awake firing patterns. This also suggested the possibility that a mouse whose leak K⁺ channel is down-regulated might have a stronger tendency to generate the awake firing patterns than the SWS firing patterns and exhibit decreased sleep duration. Therefore, we tested the hypothesis that an impairment of leak K⁺ channels would decrease the sleep duration. In the mouse genomes, 14 genes [K_2p1.1 (Kcnk1), K_2p2.1 (Kcnk2), K_2p3.1 (Kcnk3), K_2p4.1 (Kcnk4), K_2p5.1 (Kcnk5), K_2p6.1 (Kcnk6), K_2p7.1 (Kcnk7), K_2p9.1 (Kcnk9), K_2p10.1 (Kcnk10), K_2p12.1 (Kcnk12), K_2p13.1 (Kcnk13), K_2p15.1 (Kcnk15), K_2p16.1 (Kcnk16), and K_2p18.1 (Kcnk18)] are categorized into the K_2p channel family, which is composed of the two-pore-domain potassium channels and is also known as the leak K⁺ channels according to their sequence similarity.

To knock out all of the K_2p channel family members, we used the “triple-target CRISPR” method, which achieved almost perfect efficiency in producing whole-body KO mice in a single generation by using three guide RNAs targeting a single gene (SI Appendix, Fig. S5 A–N and Table S8) (20), and also used the highly accurate sleep/wake recording system called the Snappy Sleep Stager (SSS) (20). Sleep/wake phenotyping was performed for animals with the KO genotype, which was confirmed by quantitative PCR (qPCR; SI Appendix, Fig. S5 P–AC and Table S9). The Kcnk9 and Kcnk16-KO mice exhibited significantly decreased sleep duration (Fig. 4 A and C). Because the Kcnk9-KO mice exhibited the greatest decrease in sleep duration among the K_2p channel family members, i.e., 606.2 ± 22.8 min (mean ± SEM; n = 8), which was 106.3 min (∼2.6 SD) shorter than that of WT mice (P < 0.001), we focused on these mice. The Kcnk9-KO mice exhibited shorter sleep durations than WT mice over most times of the day (Fig. 4B). The Kcnk9-KO mice also exhibited a higher P_sw (the transition probability from a sleep state to an awake one) but a normal P_ws (the transition probability from an awake state to a sleep one) compared with WT mice (Fig. 4C), suggesting that a decrease in sleep-state stabilization, but not an increase in awake-state stabilization, underlies their short-sleeper phenotype (i.e., shorter episode durations of a sleep state). Although Kcnk9-KO mice were reported to have a (not-significant) tendency to have decreased sleep duration (21, 22), our noninvasive sleep phenotyping clearly revealed a significant short-sleeper phenotype in the Kcnk9-KO mice. As further validation, we generated another group of Kcnk9-KO mice by using an independent CRISPR/Cas9 probe set (set 2; SI Appendix, Fig. S5 O and AD and Tables S8 and S9), and confirmed the observed short-sleeper phenotypes (Fig. 4 D–F). These results indicated that the observed short-sleeper phenotype of the Kcnk9-KO mice was not caused by an off-target effect of the CRISPR, but rather by common genomic defects in the Kcnk9 gene. We also note that the Kcnk9, Kcnk10, and Kcnk16-KO mice exhibited increased relative amplitude, which suggested that the variation of sleep duration within the daily sleep/wake cycle would increase in these mice and the KO of these genes may have an effect on the regulation of daily sleep patterns (SI Appendix, Fig. S6A).

Fig. 4.

Impairment of the leak K⁺ channels decreases sleep duration in mice. (A) Sleep duration (per hour) over 6 d for mice knocked out for the 14 leak K⁺ channels. Each row indicates the data from one KO mouse. (B) Sleep duration (per hour) over 24 h, averaged over 6 d in mice knocked out for leak K⁺ channels. Red lines indicate mean sleep duration at each time of day for each strain. Gray, WT (n = 101). Shaded area, SEM for each time point. (C) Distributions of sleep/wake parameters of the mice knocked out for leak K⁺ channels. The definition of each parameter (P_sw and P_ws) is described in SI Appendix, SI Materials and Methods. Red dots and lines indicate the mean and SEM, respectively. Black dashed line and gray shading indicate the mean and 1 SD range from the WT data. (D–F) Sleep-duration phenotype for another group of Kcnk9-KO mice (set 2). Sleep duration (per hour) over 6 d (D), sleep duration (per hour) over 24 h averaged over 6 d (E), and distributions of sleep/wake parameters (F). (G and H) Sleep-duration phenotype based on the EEG/EMG for WT (n = 7) and Kcnk9-KO mice (set 1; n = 7). Sleep duration (per hour) over 6 d (G). NREM sleep duration, REM sleep duration, and sleep duration for 1 d are shown in a bar graph (H). (I) Schematic of the mechanisms generating the SWS firing pattern. Toward the end of the down state, the Ca²⁺ concentration is low and the Ca²⁺-dependent K⁺ channels are inactivated, which initiates the up state. After initiation of the up state, Ca²⁺ enters through voltage-gated Ca²⁺ channels and NMDA receptors, raising the intracellular Ca²⁺ concentration. Toward the end of the up state, the high Ca²⁺ concentration activates the Ca²⁺-dependent K⁺ channels, which causes the transition from the up to the down state in cooperation with the leak K⁺ channels. After initiation of the down state, the intracellular Ca²⁺ concentration decreases as a result of low Ca²⁺ entry. When the conductance of leak K⁺ channels is down-regulated, the up state does not transition to the down state because the leak K⁺ channels regulate the threshold for the transition from the up to the down state. WT, C57BL/6N male mice. Error bars indicate SEM (*P < 0.05, **P < 0.01, and ***P < 0.001; SI Appendix, SI Materials and Methods).

To exclude the possibility that the gene KO affected the respiration of the mice, causing the SSS system to miscalculate their sleep duration, we performed EEG/electromyography (EMG) recordings of the Kcnk9-KO mice. The observed short-sleep phenotype of Kcnk9-KO mice was confirmed by this EEG/EMG recording, which revealed that the Kcnk9-KO mice exhibited significant decreases in NREM sleep (i.e., SWS) duration and in total sleep duration (Fig. 4 G and H). The differences in the transition probabilities between Kcnk9-KO mice and WT mice were not significant (SI Appendix, Fig. S6B). Of particular note, the significant difference of P_sw observed in the SSS recording was not confirmed in the EEG/EMG recording (SI Appendix, Fig. S6B). This might be because the ages of mice used in each measurement were different (i.e., 8-wk-old mice were used in the SSS system and 10–14-wk-old mice were used in the EEG/EMG recording) or because the surgery required for the EEG/EMG recording might have a slight effect on the detailed structure of sleep/wake transition. Further study will be needed to clarify which transition between NREM, REM, and awake state causes the decreased NREM sleep duration in Kcnk9-KO mice. Notably, the Kcnk9-KO mice exhibited a tendency of decreased delta power, suggesting that Kcnk9 may play a role in the regulation of sleep homeostasis (SI Appendix, Fig. S6 C and D). However, as the difference of delta power between Kcnk9-KO mice and WT mice is not significant, further studies will be needed to validate the role of Kcnk9 in the regulation of sleep homeostasis. These results validated the hypothesis that leak K⁺ channels regulate sleep duration in mammals.

Discussion

Putative Mechanism for Generating the SWS Firing Pattern.

In this study, we developed the SAN model, which recapitulates the SWS firing pattern using five channels and a pump. The SAN model enabled us to conduct detailed mathematical analyses (i.e., current and phase plane analyses) against the SWS firing pattern, which revealed that the leak K⁺ channels and Ca²⁺-dependent K⁺ channels cooperatively induce the down state, and hence the SWS firing pattern. According to the AN model (13, 14, 23, 24), the putative intracellular mechanism for generating the SWS firing pattern is as follows (Fig. 4I). (i) During the up state, Ca²⁺ enters mainly through NMDA receptors and voltage-gated Ca²⁺ channels to increase the intracellular Ca²⁺ concentration. (ii) The transition from the up to the down state occurs when the intracellular Ca²⁺ concentration reaches a certain threshold, which activates Ca²⁺-dependent K⁺ channels. (iii) In the down state, Ca²⁺ exits through Ca²⁺-pump/exchangers to decrease the intracellular Ca²⁺ concentration. (iv) The transition from the down to the up state occurs when the intracellular Ca²⁺ concentration decreases, which inactivates the Ca²⁺-dependent K⁺ channels. The SAN model further indicated that the conductance of leak K⁺ channels alters the threshold for the transition from the up to the down state mediated by the Ca²⁺-dependent K⁺ channels. When the conductance of the leak K⁺ channels is relatively high, a relatively lower conductance of the Ca²⁺-dependent K⁺ channels is sufficient to induce the down state.

Notably, this putative mechanism for generating the SWS firing pattern is consistent with the reported extracellular K⁺ bias between sleep and wakefulness: the extracellular K⁺ concentration is relatively low during sleep and high during wakefulness in vivo (25). Because an extracellular K⁺ bias will alter the tendency of the K⁺ flux, the relatively low extracellular K⁺ concentration during sleep could drive K⁺ efflux through the leak K⁺ channels and Ca²⁺-dependent K⁺ channels, thereby generating the down state. Consistent with this scenario, the extracellular Ca²⁺ concentration is relatively high during sleep (25), which could drive Ca²⁺ influx through the voltage-dependent Ca²⁺ channels and NMDA receptors, thereby generating the down state by activating the Ca²⁺-dependent K⁺ channels during sleep. Indeed, by implementing ion concentration dependency in the AN model, a recent computational study indicated that the extracellular ion concentration and the conductance of the Ca²⁺-dependent K⁺ channels could coordinately regulate the transition between the SWS and awake firing patterns (26). The SAN model also predicted that persistent Na⁺ channels are involved in initiating the up state (SI Appendix, Fig. S2C), which is a proposed mechanism for rhythmic bursting patterns in the pre-Bötzinger complex or hippocampal pyramidal neurons (15, 16, 18, 19). These results show that the common mechanisms may underlie the generation of the SWS firing pattern and other rhythmic bursting patterns. Collectively, we hypothesize that the Ca²⁺-dependent hyperpolarization pathway and leak K⁺ channels are involved in generating the SWS firing pattern. A remaining challenge will be to combine this putative intracellular mechanism with the accumulated knowledge of intercellular mechanisms in sleep/wake cycle regulation.

The SAN Model as a Tool for Elucidating the Mechanisms of Generating the SWS Firing Pattern and Regulating Sleep Duration.

In this study, the SAN model predicted that the leak K⁺ channels are involved in generating the SWS firing pattern, which led to the hypothesis that a mouse whose leak K⁺ channel is down-regulated might have a stronger tendency to generate the awake firing patterns than the SWS firing patterns and exhibit decreased sleep duration. This hypothesis was validated by a comprehensive sleep phenotyping of mice knocked out for leak K⁺ channel family members such as Kcnk9. Together with the results of a previous study (13), five components—the leak K⁺ channel (Kcnk9), Ca²⁺-dependent K⁺ channels (Kcnn2 and Kcnn3), voltage-gated Ca²⁺ channels (Cacna1g and Cacna1h), NMDA receptors (probably Nr1/Nr2b), and Ca²⁺-exchanger/pump (Atp2b3)—might be involved in generating the SWS firing pattern and in the regulation of sleep duration. These results suggested that generating the SWS firing patterns and regulating sleep duration could share common molecular mechanisms. Therefore, elucidating the mechanism of generating the SWS firing pattern with mathematical models might provide a clue about the mechanism of regulating sleep duration.

Mathematical analyses using the phase plane method indicated that the intersection of the V nullcline and the n_K nullcline at approximately −65 mV regulates the transition from the up to the down state (Fig. 2G and SI Appendix, Fig. S3E). Because the current of each channel around −65 mV determines the position of this intersection, these currents might be essential for the transition from the up to the down state. Thus, the balance between the outward currents through leak K⁺ channels and Ca²⁺-dependent K⁺ channels and the inward currents through leak Na⁺ channels could regulate the transition between the SWS and awake firing patterns. Interestingly, these channels are also thought to regulate the resting membrane potential, suggesting that common mechanisms are involved in controlling the SWS firing pattern and the resting membrane potential. This is consistent with the previous report that the resting membrane potential might affect the SWS firing pattern (10). In this sense, other components that regulate the resting membrane potential (e.g., Na⁺-K⁺ ATPase) are candidates for molecular components generating the SWS firing pattern and possibly regulating sleep duration. Indeed, mice carrying an inactivating mutation in the neuron-specific Na⁺-K⁺ ATPase α3 subunit exhibit decreased sleep duration (27). Thus, other components that regulate the resting membrane potential are possible molecular candidates for regulating sleep duration. To assess the association of these components with the generation of SWS firing patterns, it might be possible to add each of them to the SAN model and to analyze its role mathematically in detail. Taken together, the SAN model predicts that common mechanisms are involved in regulating the SWS firing pattern and the resting membrane potential and could be a versatile model for investigating the role of other ion channels in generating the SWS firing pattern and regulating sleep duration.

The Role of Leak K⁺ Channels in Generating the SWS Firing Pattern and Regulating Sleep Duration.

Although mathematical approaches predicted that the leak K⁺ channels play a role in generating the up and down states of the SWS firing pattern, its underlying mechanism is still a mystery. It would be a promising approach to clarify the mechanism of generating the up and down states in cortical neurons electrophysiologically. In fact, the cortex has numerous types of neurons, and it is still difficult to measure and perturb an activity of a specific neuron, such as the SWS firing pattern, in vivo. If such technical limitations can be overcome, the mechanism of generating the SWS firing pattern as well as its relationship with the regulation of sleep duration will be uncovered. Given the current difficulty of in vivo validation, the next step will be conducting an electrophysiological experiment to evaluate the role of leak K⁺ channels in a cortical slice. It would be a good surrogate to measure the membrane potential of a cortical slice under Kcnk9-KO or Kcnk9 knock-down conditions.

One interesting question rising from this study is why Kcnk9-KO mice exhibited a severe decrease in sleep duration whereas the other KO mice of the K_2p channel family members did not. One possible reason for this result is a difference in neuronal expression between the K_2p channel family members. Although Kcnk9 has expression in various brain regions including cerebral cortex, other members have different expression patterns in mice (28), which implies that some members might have weak expression in cerebral cortex. In addition, cell-type specificity of Kcnk9 expression could be also related to the sleep phenotype of its KO mice. Investigating where and in what type of neuron Kcnk9 has strong expression could be an interesting future direction to validate the role of Kcnk9 in the regulation of sleep duration. Another possible reason is the compensation of the role of a K_2p channel family member by other members. The KO effect of a K_2p channel family member could be reduced if the other members have stronger expression than WT mice and compensate the gene’s role. Further study such as investigating the expression of other K_2p channel family members in KO mice or measuring sleep duration in double-KO mice of K_2p channel family members will be needed to examine this possibility.

Materials and Methods

Details of the study materials and methods are supplied in the SI Appendix, SI Materials and Methods.

SAN Model.

The SAN model was constructed by simplifying the AN model. The full system of equations is presented in SI Appendix, SI Materials and Methods. Parameter searches for the SWS firing patterns were conducted, and the SAN model was determined by comparing the hit rates of various models, which are shown in SI Appendix, Table S7, and conducting the bifurcation analyses.

Analysis of the SAN Model.

We divided all of the parameter sets with the SWS firing patterns into two clusters according to the conductance of the voltage-gated K⁺ channels and voltage-gated Ca²⁺ channels. The representative parameter set was determined by using kernel density estimation in each cluster. First, the proportion of the current of each channel was analyzed. Second, in normal bifurcation and 2D analyses, each channel’s conductance was gradually changed from the representative parameter sets. Third, the trajectory of these differential equations was analyzed by the phase plane. The changes in the trajectory and the nullclines caused by down-regulating the conductance of leak K⁺ channels or Ca²⁺-dependent K⁺ channels were analyzed. Fourth, bifurcation analysis of all of the parameter sets was conducted, in which the transitions from the SWS to awake firing patterns were counted.

Further Analysis of the AN Model.

The currents in the down and up states were calculated with all of the parameter sets in the original AN model, the KO of NMDA receptors model, and the KO of voltage-gated Ca²⁺ channels model. The bifurcation analyses were conducted with all of the parameter sets in the original AN model, the KO of NMDA receptors model, and the KO of voltage-gated Ca²⁺ channels model, in all of which the leak channels were divided into the leak K⁺ channels and the leak Na⁺ channels.

Animals and Sleep Phenotyping.

All experimental procedures and housing conditions involving animals and their care were approved by the institutional animal care and use committee. Sleep phenotyping was performed noninvasively by SSS. KO mice were generated and subjected to sleep phenotyping at the University of Tokyo, and C57BL/6N mice (n = 101) were used as controls (Fig. 4 B, C, E, and F and SI Appendix, Fig. S6A). The EEG/EMG recording for Kcnk9-KO mice was performed at the University of Tokyo. CRISPR-KO animals were generated by one-cell embryo microinjection of synthesized Cas9 mRNA and gRNAs (mix of three targeting sequences; template sequences are shown in SI Appendix, Table S8) into C57BL/6N fertilized eggs. KO genotypes were confirmed by qPCR.