Collimated ultrabright gamma rays from electron wiggling along a petawatt laser-irradiated wire in the QED regime

Significance

Even though bright X-rays below mega-electron volt photon energy can be obtained from X-ray free electron lasers and synchrotron radiation facilities, it remains a great challenge to generate collimated bright gamma-ray beams over 10 mega-electron volts. We propose a scheme to efficiently generate such beams from submicron wires irradiated by petawatt lasers, where electron accelerating and wiggling are achieved simultaneously. With significant quantum electrodynamics effects existing even with petawatt lasers, our full 3D simulations show that directional gamma rays can be generated with thousand-fold higher brilliance and thousand-fold higher photon energy than those from synchrotron radiation facilities. In addition, the photon yield efficiency approaches 10%, 100,000-fold higher than those typical from betatron radiation and Compton scattering based on laser-wakefield accelerators.

Abstract

Even though high-quality X- and gamma rays with photon energy below mega-electron volt (MeV) are available from large-scale X-ray free electron lasers and synchrotron radiation facilities, it remains a great challenge to generate bright gamma rays over 10 MeV. Recently, gamma rays with energies up to the MeV level were observed in Compton scattering experiments based on laser wakefield accelerators, but the yield efficiency was as low as $10^{-6}$, owing to low charge of the electron beam. Here, we propose a scheme to efficiently generate gamma rays of hundreds of MeV from submicrometer wires irradiated by petawatt lasers, where electron accelerating and wiggling are achieved simultaneously. The wiggling is caused by the quasistatic electric and magnetic fields induced around the wire surface, and these are so high that even quantum electrodynamics (QED) effects become significant for gamma-ray generation, although the driving lasers are only at the petawatt level. Our full 3D simulations show that directional, ultrabright gamma rays are generated, containing $10^{12}$ photons between 5 and 500 MeV within a 10-fs duration. The brilliance, up to $10^{27}$ photons $s^{-1}\hspace{0.17em}mra{d}^{-2}\hspace{0.17em}m{m}^{-2}$ per 0.1% bandwidth at an average photon energy of 20 MeV, is second only to X-ray free electron lasers, while the photon energy is 3 orders of magnitude higher than the latter. In addition, the gamma ray yield efficiency approaches 10%—that is, 5 orders of magnitude higher than the Compton scattering based on laser wakefield accelerators. Such high-energy, ultrabright, femtosecond-duration gamma rays may find applications in nuclear photonics, radiotherapy, and laboratory astrophysics.

Bright gamma rays with energy above mega-electron volt (MeV) are highly demanded in broad applications ranging from laboratory astrophysics (1), emerging nuclear photonics (2), photon–photon colliders (3), fine measurement of atomic nuclei (4), to radiotherapy (5). Even though diverse X- and gamma-ray sources below MeV are available from large-scale X-ray free electron lasers (XFELs) (6) and synchrotron radiation facilities (7, 8) as well as laser-driven compact synchrotron light sources (9) and high harmonic generation (10), it remains a great challenge to generate gamma rays of 10 MeV and beyond. These applications can potentially benefit from gamma-ray sources based upon laser wakefield acceleration (LWFA) (11). Via LWFA, giga-electron volt (GeV) electron beams typically with a duration of tens of femtoseconds (fs), transverse size of micrometers, and divergence of a few mrad are generated from gas plasma. Through betatron radiation (12–15) or Compton scattering (16–22), the beams are wiggled by electrostatic and/or laser fields and then emit gamma rays basically with similar duration, size, and divergence to the beams. These cause high-peak brilliance $10^{19}-10^{23}$ photons ${\mathrm{s}}^{-1}\hspace{0.17em}{\mathrm{m}\mathrm{r}\mathrm{a}\mathrm{d}}^{-2}\hspace{0.17em}{\mathrm{m}\mathrm{m}}^{-2}$ per 0.1% bandwidth. Mainly limited by wiggling field strengths, most gamma-ray photons are distributed in sub-MeV range. By increasing the scattering laser strength (19, 22) or frequency (18), the Compton photon energy can be enhanced to multi-MeV. However, both the energy conversion efficiency from the pulse to the gamma rays and the resulting photon number are not high, typically around $10^{-6}$ for the conversion efficiency (17) and $10^6-10^8$ photons (14, 15, 19), respectively, due to low charges of $\sim$pico-coulombs (pC) in LWFA beams and limited wiggling strengths.

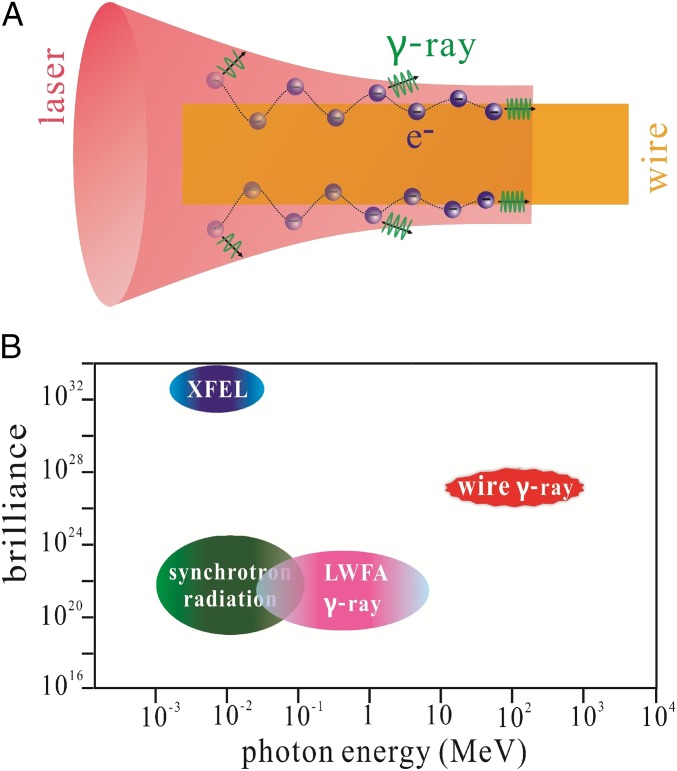
To overcome these limits and further enhance the photon energy to the GeV range, we propose a scheme in which a currently available petawatt (PW) laser pulse (23, 24) propagates along a wire of subwavelength in transverse dimension, as shown in the schematic diagram in Fig. 1A. Note that such a target can be fabricated easily now by 3D laser writing (25). Making use of the high density of the wire, a directional GeV electron beam with tens of nano-coulombs (nC) charge is generated along the wire surface. Meanwhile, electrostatic and magnetostatic fields induced at the surface are strong, which intensively wiggles the beam electrons. This leads to significant quantum electrodynamics (QED) parameters of electrons (26) given by $\chi ={\gamma }_e\sqrt{{{\left(\mathbf{E}+{\mathbf{v}}_{\mathbf{e}}\times \mathbf{B}\right)}^2-\left({\mathbf{v}}_{\mathbf{e}}\cdot \mathbf{E}\right)}^2}/E_{Sch}$, where ${\gamma }_e$ and ${\mathbf{v}}_{\mathbf{e}}$ represent the electron relativistic factor and velocity normalized by the light speed $c$, respectively, and $E_{Sch}=1.32\times 10^{18}V/m$ is the Schwinger field strength. By QED synchrotron radiation from the GeV, nC beam, near 10% laser energy ($10^5$ higher than that based upon LWFA) is converted to directional gamma rays, containing $10^{12}$ photons with energy near GeV according to our 3D particle-in-cell (PIC) simulations. With the laser power $P_0$ ranging from 0.5 to 5 PW available currently, this scheme can robustly produce gamma rays peaked at $1^{○}$ with the photon energy and number roughly scaling with $P_0$ and $P_0^{3/2}$, respectively. Due to inheriting the femtosecond-laser duration and wire width of submicron, the gamma rays have a high brilliance second only to XFEL, while the average photon energy of 20 MeV is 3 orders of magnitude higher than XFEL, as shown in the chart of photon energy and brilliance of gamma rays in Fig. 1B and refs. 6–8.

Fig. 1.

Schematic of the wire scheme. (A) Schematic: As a laser pulse propagates along a subwavelength wire and approaches its focusing plane (a distance behind the wire front to allow the electron to guide and accelerate), electrons along the wire surface are gradually accelerated with reduced divergent angles; meanwhile, the electrons are wiggled perpendicularly to the surface, which causes gamma rays emitted with increased photon energies and decreased divergent angles. (B) Chart of photon energy and brilliance (photons ${\mathrm{s}}^{-1}\hspace{0.17em}{\mathrm{m}\mathrm{r}\mathrm{a}\mathrm{d}}^{-2}\hspace{0.17em}{\mathrm{m}\mathrm{m}}^{-2}$ per 0.1% bandwidth) of gamma rays generated from our wire scheme, XFEL, synchrotron radiation facilities, and betatron radiation and Compton scattering based on LWFA.

We show that the PW laser-irradiated subwavelength wire drives both wiggling and accelerating of collimated electron beams of nC. Our scheme embraces both the merits of high directionality comparable to those based upon LWFA and high charge comparable to those based upon laser–solid interaction. Note that the wire accelerator has been studied (27, 28) and its application for terahertz radiation considered (29). Here, we show unique electron wiggling in the QED regime caused by the electrostatic and magnetostatic fields. This is different from nonlinear Compton scattering (30–32) or resonance acceleration (33) in the QED regime, which is driven directly by laser fields with powers above 10 PW. In a previous channel-like target scheme with a PW laser pulse (34), the wiggling electrons are across the whole channel with the transverse size near the laser spot diameter, and therefore, the generated photons have emission angles of $40^{○}$, which doe not result in high brilliance. In our scheme, the wiggling electrons are restricted around the wire surface, which enables the emitted photons to be peaked at small angles around $1^{○}$ and thereby leads to extremely high brilliance. Very recently a scheme to generate GeV photons was proposed (35), where 12 laser pulses totally at 40 PW with proper pulse duration are required to reach the brilliance of $9\times 10^{24}$ photons ${\mathrm{s}}^{-1}\hspace{0.17em}{\mathrm{m}\mathrm{r}\mathrm{a}\mathrm{d}}^{-2}\hspace{0.17em}{\mathrm{m}\mathrm{m}}^{-2}$ per 0.1% bandwidth

Directional Gamma Rays Emitted from a Submicron Wire

We first demonstrate the scheme sketched above (Figs. 1 and 2A) through 3D particle-in-cell (PIC) simulations with the $KLAPS$ code (36) including photon and pair generation via QED processes (32). The pulse propagates along the $+x$ direction with $y$-direction polarization, wavelength ${\lambda }_0=1\hspace{0.17em}\mathrm{\mu }\mathrm{m}$ (laser period ${\tau }_0=2\pi /{\omega }_0=3.33\hspace{0.17em}\mathrm{f}\mathrm{s}$), peak power 2.5 PW, and duration 20 fs in full width at half maximum (FWHM). With an initial spot radius $r_{ini}=6.12\hspace{0.17em}\mathrm{\mu }\mathrm{m}$ and amplitude $a_{ini}=56$ normalized by $m_{e}c{\omega }_0/e$ (the corresponding intensity $4.3\times 10^{21}\hspace{0.17em}{\mathrm{W}\mathrm{c}\mathrm{m}}^{-2}$), the pulse is located at 5 Rayleigh lengths ($22.6\hspace{0.17em}\mathrm{\mu }\mathrm{m}$) ahead of the focusing plane. The spot radius at the focusing plane is expected to be $r_0=1.2\hspace{0.17em}\mathrm{\mu }\mathrm{m}$ with $a_0=285$ in the vacuum. An aluminum wire of cuboid is taken with 50 $\mathrm{\mu }\mathrm{m}$ long in the x direction and 0.6 $\mathrm{\mu }\mathrm{m}$ wide, which is placed 2.4 $\mathrm{\mu }\mathrm{m}$ behind the pulse initial wavefront. Note that when aluminum is fully ionized to be plasma, it has a density of $690n_c$ ($n_c=1.1\times 10^{21}\hspace{0.17em}{\mathrm{c}\mathrm{m}}^{-3}$).

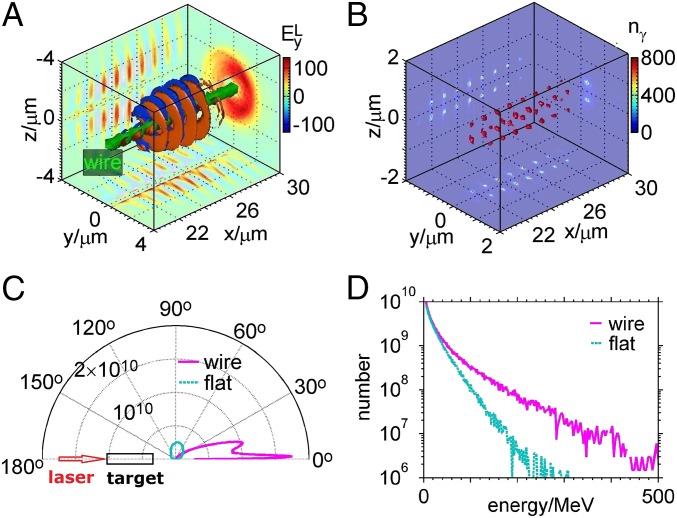
Fig. 2.

Generated gamma rays. 3D isosurfaces of (A) the laser field ($mc{\omega }_0/e$) and (B) gamma-ray photon density ($n_c$) at the time of 30 ${\tau }_0$ as well as the slices at the planes with respective peak values, where a $0.6\hspace{0.17em}\mathrm{\mu }\mathrm{m}$-wide wire is taken. Note that the laser pulse peak arrives at the focusing plane at about 30 ${\tau }_0$. (C) Angular distributions and (D) energy spectra of gamma rays emitted from the wire and a flat slab target, respectively.

Fig. 2 shows the gamma rays emitted from the aluminum wire as well as from a flat slab aluminum target with a large enough transverse size of 24 $\mathrm{\mu }\mathrm{m}$ for comparison. With the wire, the gamma rays have a sharp peak angle nearly along the wire surface, as shown in Fig. 2C (the angular distributions of beam electrons are shown in Fig. 6). However, large divergence gamma rays are generated with the flat target, as obtained in previous reports (30, 31). The photon number in the peak angle is one order of magnitude higher in the wire case. Fig. 2B shows that the gamma rays have a FWHM duration of about 10 fs and a transverse size near the wire width of 0.6 $\mathrm{\mu }\mathrm{m}$ because they are generated around the wire surface. The brilliance in the peak angle of $1^{○}$ is found to be $1.2\times 10^{27}$, $8\times 10^{26}$, and $1.5\times 10^{26}$ photons ${\mathrm{s}}^{-1}\hspace{0.17em}{\mathrm{m}\mathrm{r}\mathrm{a}\mathrm{d}}^{-2}\hspace{0.17em}{\mathrm{m}\mathrm{m}}^{-2}$ per 0.1% bandwidth at 5 MeV, 20 MeV, and 100 MeV, respectively. The gamma rays have $1.75\times 10^{10}$ photons in the angle $1^{○}$ with the divergence of $3.49\times 3.49\hspace{0.17em}{\mathrm{m}\mathrm{r}\mathrm{a}\mathrm{d}}^2$ (we count the photon number with an angle displacement of $0.2^{○}$). As a comparison with the flat slab target, the source size is increased to a few microns, determined by the plasma area of laser hole boring. The increased size and decreased photon number at the peak angle cause the peak brilliance to be reduced by 3 orders of magnitude. Fig. 2D shows the photon energy spectra. With the wire target, the photons distributed from 5 MeV to 500 MeV have an average energy of about 20 MeV. Note that there are some beam electrons with energy above 1 GeV that can emit photons of 500 MeV since the electron QED parameters (26) $\chi >0.2$ as shown in our following simulation results. With the flat target, both the photon energy and number in the higher energy part are significantly reduced. This suggests that the wire geometry is more favorable to bring a larger $\chi$ for higher photon energy.

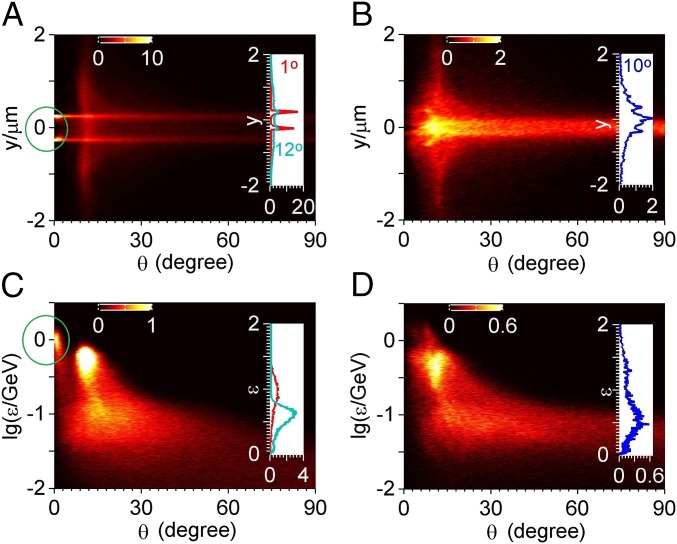
Fig. 6.

Generated electron beams. The number (units of $10^8$) of electrons with energies above 10 MeV as a function of ($\theta$, $y$, $\epsilon$) at 30 ${\tau }_0$, where Insets in each plot show number distributions at angles of $1^{○}$, $10^{○}$, and $12^{○}$ corresponding to curves in different colors. The left (A and C) and right columns (B and D) correspond to 0.6 $\mathrm{\mu }\mathrm{m}$ and 0.3 $\mathrm{\mu }\mathrm{m}$ wires, respectively. In A and C, the electron beam at the angle about $1^{○}$ is circled.

Wiggling Fields Formed at the Wire Surface

We examine the wiggling fields in detail. The fields composed of electrostatic and magnetostatic components are perpendicular to velocities of the beam electrons moving along the $+x$ direction. First, the laser field strips a large number of electrons away from the wire surface (Figs. 2A and 3B), which induces electrostatic fields $E_y^S$ (see Fig. 3A) and $E_z^S$ around the surfaces $y\simeq \pm 0.3\hspace{0.17em}\mathrm{\mu }\mathrm{m}$ and $z\simeq \pm 0.3\hspace{0.17em}\mathrm{\mu }\mathrm{m}$, respectively. In turn, the laser field becomes hollow, as observed in Fig. 2A. Due to its transverse ponderomotive force, the hollow laser pulse together with the electrostatic fields tends to confine electrons within the wire. To compensate for the beam-electron flux along the $+x$ direction, a return current is formed around the wire surface (Fig. 3D), which induces magnetostatic fields $B_z^S$ (Fig. 3C) around $y\simeq \pm 0.3\hspace{0.17em}\mathrm{\mu }\mathrm{m}$ and $B_y^S$ around $z\simeq \pm 0.3\mathrm{\mu }\mathrm{m}$. According to Fig. 3 A and C, $E_y^S$ and $B_z^S$ basically have similar strengths and the same signs, positive at $y>0$ and negative at $y<0$. For the electrons along the $+x$ direction, the magnetic force is opposite to the electric force, which can result in electron wiggling along the $y$ direction with the force $-e\left(E_y^S-v_{e,x}{B}_z^S\right)$. With $v_{e,x}\simeq 1$, the wiggling field around the surfaces $y\simeq \pm 0.3\mathrm{\mu }\mathrm{m}$ can be written by $F_y^{wig}\simeq E_y^S-B_z^S$. Note that contributions of laser electric and magnetic fields to $F_y^{wig}$ and resulting $\chi$ are counteracted (37) when $v_{e,x}\simeq 1$. Therefore, the radiation is not caused directly by the laser fields. Similarly one can write $F_z^{wig}\simeq E_z^S+B_y^S$ around the surfaces $z\simeq \pm 0.3\mathrm{\mu }\mathrm{m}$.

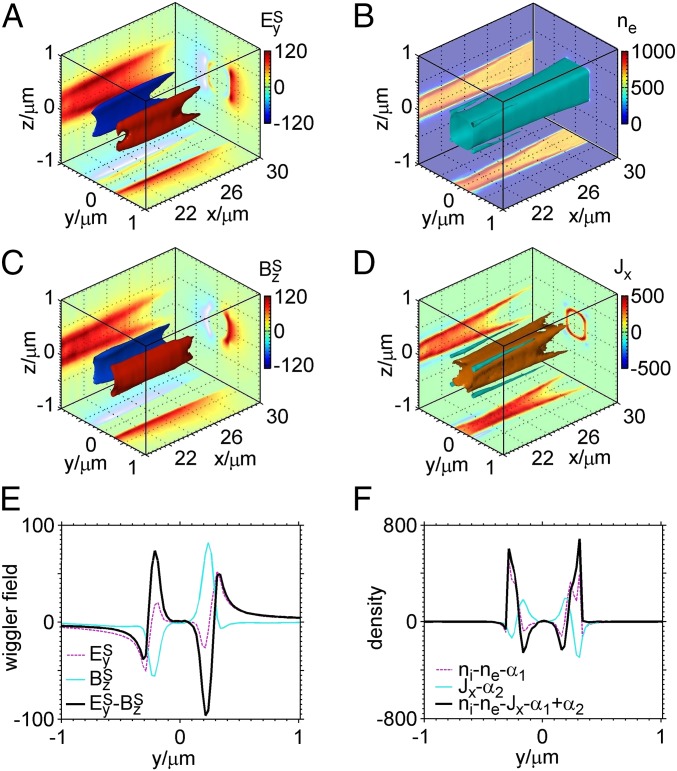
Fig. 3.

Wiggling fields. 3D isosurfaces of (A) electrostatic and (C) magnetostatic fields ($mc{\omega }_0/e$), (B) electron density ($n_c$), and (D) current density ($ec{n}_c$) at the time of 30 ${\tau }_0$ as well as the slices at the planes with respective peak values, where they are obtained by temporally averaging $E_y$, $B_z$, $n_e$, and $J_x$, respectively, over one laser cycle. The corresponding one-dimensional distributions of these fields and densities at $x=21\hspace{0.17em}\mathrm{\mu }\mathrm{m}$ and $z=0.26\hspace{0.17em}\mathrm{\mu }\mathrm{m}$ are shown in E and F.

To clarify further whether $F_y^{wig}$ can lead to an effective wiggling motion, we analyze its distribution across the wire. Formation of the electrostatic and magnetostatic fields can be described by $\partial E_y^S/\partial y+\partial E_z^S/\partial z=2\pi \left(n_i-n_e\right)$ and $\partial B_z^S/\partial y-\partial B_y^S/\partial z=2\pi J_x$, where $E_x^S$, $B_x^S$, static $J_y$, and $J_z$ are relatively weak, as observed in our PIC simulation. Here, $n_i$ and $n_e$ are normalized by $n_c$, $J_x$ by $ec{n}_c$, and fields by $m_{e}c{\omega }_0/e$. According to our PIC simulation, we find that $E_z^S$, $B_y^S$, $\partial E_z^S/\partial z$, and $\partial B_y^S/\partial z$ are roughly constant at the surface with a given $z$ since the wire width is much smaller than the laser spot diameter (similarly, one can see in Fig. 3 A and C that $E_y^S$, $B_z^S$, $\partial E_y^S/\partial y$, and $\partial B_z^S/\partial y$ are roughly constant at the surface with a given $y$). Then, $\partial E_y^S/\partial y\simeq 2\pi \left(n_i-n_e-{\alpha }_1\right)$ and $\partial B_z^S/\partial y=2\pi \left(J_x-{\alpha }_2\right)$ at a given $z_0$, where ${\alpha }_1$ and ${\alpha }_2$ satisfy $\partial E_z^S/\partial z{|}_{z_0}\simeq 2\pi {\alpha }_1$ and $\partial B_y^S/\partial z{|}_{z_0}=-2\pi {\alpha }_2$. One can obtain

$$\partial F_y^{wig}/\partial y\simeq 2\pi \left(n_i-n_e-J_x-{\alpha }_1+{\alpha }_2\right)=2\pi {\rho }^{e\mathit{ff}}.$$ [1]

According to this equation, one can understand Fig. 3 E and F, where we simply take ${\alpha }_1=40$ and ${\alpha }_2=30$ to satisfy neutrality at $y=0$ (at the wire center). Note that basically $|{\alpha }_1-{\alpha }_2|$ is far smaller than $|n_i-n_e|$ and $\left|J_x\right|$, so that the effective charge density ${\rho }^{e\mathit{ff}}$ is mainly determined by $n_i-n_e-J_x$. Around the wire center, ${\rho }^{e\mathit{ff}}\simeq 0$; increasing $\left|y\right|$, electrons are piled up by laser radiation pressure with $n_e>n_i$ and return currents are mainly located in this region with $J_x>0$, and consequently ${\rho }^{e\mathit{ff}}<0$. Further increasing $\left|y\right|$ and close to the surface, wire electrons are stripped with $n_e\sim 0$, there are well-guided beams in the ion channel with $J_x<0$, and thus ${\rho }^{e\mathit{ff}}\simeq n_i-J_x>0$ (Fig. 3F).

Such ${\rho }^{e\mathit{ff}}$ generates effective wiggling fields $F_y^{wig}$ shown in Fig. 3E. There are two zero-field points close to the surfaces $y\simeq \pm 0.3\hspace{0.17em}\mathrm{\mu }\mathrm{m}$, respectively. Around these points, the fields are bipolar, which naturally causes electron wiggling. Note that the peak field strength inside the wire is higher than that outside, which prevents the beam electrons from crossing the wire center and keeps them wiggling at one side of the wire (see Fig. 4A). One can also see in Fig. 3E that change of $F_y^{wig}$ with $y$ is sharp at the zero-field points due to large ${\rho }^{e\mathit{ff}}\simeq n_i$. This causes small spatial displacement of the electron wiggling and small angles of photon emission (see Fig. 4 A and C).

Fig. 4.

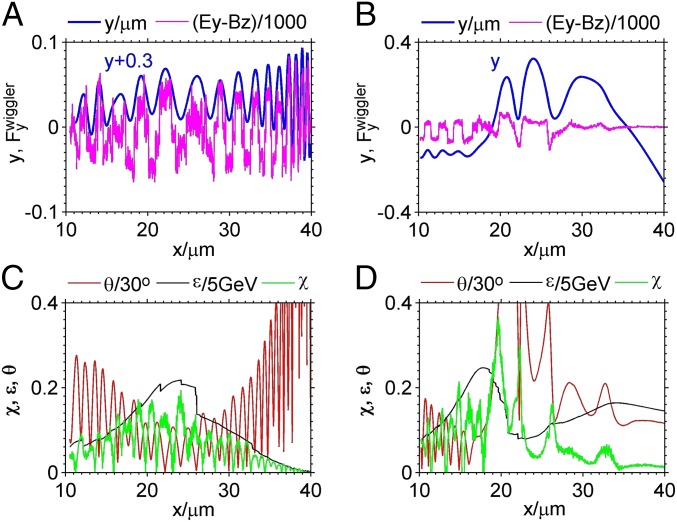
Trace of typical electrons. Evolution for an electron from the 0.6 $\mathrm{\mu }\mathrm{m}$ (A and C) and 0.3 $\mathrm{\mu }\mathrm{m}$ wires (B and D), respectively, is shown for the transverse position y ($\mathrm{\mu }m$), $E_y-B_z$ (units of $1000m_{e}c{\omega }_0/e$), divergence angle $\theta$ (units of $30^{○}$), energy $\epsilon$ (units of 5 GeV), and QED parameter $\chi$, where we plot $y+0.3$ in A, since the electron wiggles around $-0.3\hspace{0.17em}\mathrm{\mu }\mathrm{m}$.

Electron Wiggling Motion Around the Wire Surface

The trajectory and energy evolution for an electron located around the wire surface $y\simeq -0.3\mathrm{\mu }\mathrm{m}$ are plotted in Fig. 4 A and C. One can see in Fig. 4A that the field $E_y-B_z$ experienced by the electron significantly varies as $y$ slightly changes. Note that the electron moves along with the laser pulse at $v_{e,x}\simeq 1$. Therefore, its wiggling motion is driven by the static fields rather than the laser fields. As the pulse moves to the focusing plane around $x=26\hspace{0.17em}\mathrm{\mu }\mathrm{m}$, the electron energy $\epsilon$ grows gradually to $>$1 GeV with increasing QED parameter $\chi$ and decreasing emission angles $\theta$ (Fig. 4C). Around the focusing plane, the strongest emission arises with the largest $\chi \simeq 0.2$ accompanied with the smallest $\theta \simeq 1^{○}$, and therefore, the gamma rays have the angle peak around $1^{○}$ (see Fig. 2C and angular distributions of beam electrons in Fig. 6 A and C). One can notice that $\epsilon$ significantly jumps down around $x=26\hspace{0.17em}\mathrm{\mu }\mathrm{m}$ when high-energy photons are emitted. Later, both $\epsilon$ and $\chi$ decrease, while $\theta$ increases. From Fig. 4C, one can also calculate the effective wiggler strength: $K=61$ around $x=10\hspace{0.17em}\mathrm{\mu }\mathrm{m}$; it increases to 123 as the energy is enhanced to 1 GeV around $x=26\hspace{0.17em}\mathrm{\mu }\mathrm{m}$; then, it decreases.

To optimize the gamma-ray emission for efficient yield and directionality, we take the laser-focusing plane a distance behind the wire front end. This allows a distance to accelerate and generate a well-guided GeV beam before reaching the highest laser intensity, where the largest $\chi$ is achieved and a small emission angle $\theta$ maintained. The QED parameter $\chi ={\gamma }_e\sqrt{{\left(\mathbf{E}+{\mathbf{v}}_{\mathbf{e}}\times \mathbf{B}\right)}^2-{\left({\mathbf{v}}_{\mathbf{e}}\cdot \mathbf{E}\right)}^2}/E_{Sch}$ (26) of an electron with $v_{e,x}\simeq 1$ can be simplified as

$$\chi \simeq {\gamma }_e|E_y^S-B_z^S|/E_{Sch},$$ [2]

for the wiggling along the y direction. According to Eq. 2 with $|E_y^S-B_z^S|\simeq 50$, ${\gamma }_e\simeq 1957$ read from Fig. 4 A and C, one can calculate $\chi =0.23$ in agreement with the value $\chi$ shown in Fig. 4C.

Scaling Laws of Photon Energy and Number

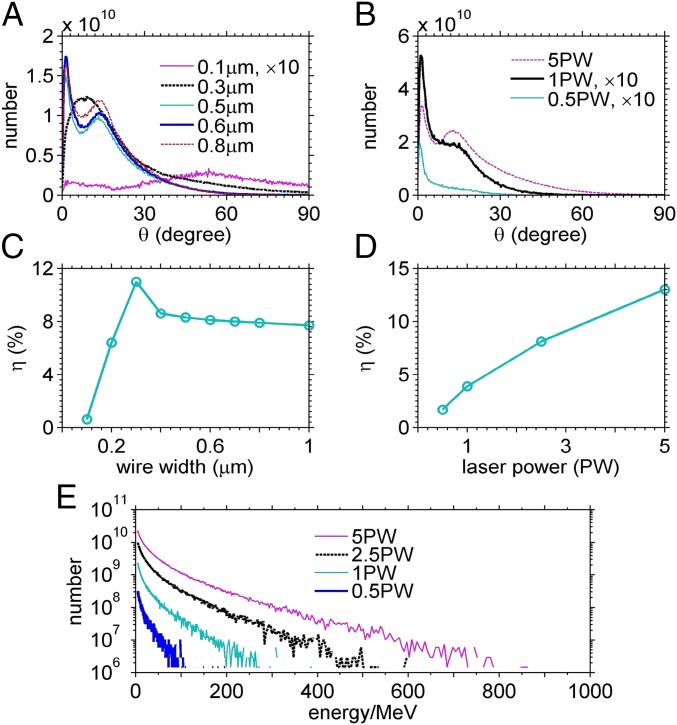
We examine the dependence of photon emission on the wire width and laser power. Fig. 5 indicates that our scheme works well with the width ranging from 0.4 $\mathrm{\mu }\mathrm{m}$ to 1 $\mathrm{\mu }\mathrm{m}$ and the power from 0.5 PW to 5 PW available currently (23, 24) (note that the angular distributions in the 0.4 $\mathrm{\mu }\mathrm{m}$ and 1 $\mathrm{\mu }\mathrm{m}$ cases are similar to 0.5 $\mathrm{\mu }\mathrm{m}$ and 0.8 $\mathrm{\mu }\mathrm{m}$, respectively). In particular, even at 0.5 PW the gamma-ray brilliance can reach $1.2\times 10^{26}$ photons ${\mathrm{s}}^{-1}\hspace{0.17em}{\mathrm{m}\mathrm{r}\mathrm{a}\mathrm{d}}^{-2}\hspace{0.17em}{\mathrm{m}\mathrm{m}}^{-2}$ per 0.1% bandwidth at 6 MeV. The conversion efficiency is decreased to 1.6%, and photon energy is lowered in this case (Fig. 5E) because $\chi$ is decreased. Besides, when the wire width is changed from 0.5 $\mathrm{\mu }\mathrm{m}$ to 0.8 $\mathrm{\mu }\mathrm{m}$, very similar angular distributions and conversion efficiency are achieved, suggesting that this scheme is robust.

Fig. 5.

Dependency of gamma-ray generation on laser powers and wire widths. Angular distributions of gamma rays with different wire widths (A) and under different laser powers (B), where “$\times 10$” in the legend means the photon number multiplied by a factor of 10. Energy conversion efficiency of the gamma rays versus wire widths (C) and laser powers (D). (E) Energy spectra of gamma rays at 50 ${\tau }_0$ under different laser powers. In A and C, the laser power is fixed at 2.5 PW. In B, D, and E, the wire width is fixed at 0.6 $\mathrm{\mu }\mathrm{m}$.

While the width is too small (e.g., 0.1 $\mathrm{\mu }\mathrm{m}$), the wire is completely destructed by the laser fields and electrons move like in the vacuum. Hence, the gamma rays have high divergence and low conversion efficiency. When increasing the width to 0.3 $\mathrm{\mu }\mathrm{m}$, the wire structure can be kept before the pulse approaches its focusing plane, and therefore, electrons are first wiggled around the wire surface (Fig. 4B). Later, electrons cross the wire center with large angles when the strongest radiation occurs due to $\epsilon$ and $\chi$ at the maximums (Fig. 4 B and D). This causes the gamma rays peaked at a larger angle than the 0.6 $\mathrm{\mu }\mathrm{m}$ wire case (Fig. 5A). These can be seen more clearly in Fig. 6, where spatial, angular, energy distributions of electrons are plotted. In the 0.6 $\mathrm{\mu }\mathrm{m}$ case (Fig. 6 A and C), the higher energy electrons are distributed around the wire surface and peaked at $1^{○}$, which have an nC charge (we circle these electrons in Fig. 6 A and C). They are wiggled on one side of the surface and then strongly emit gamma rays around $1^{○}$. In the 0.3 $\mathrm{\mu }\mathrm{m}$ case (Fig. 6 B and D), however, the electrons are peaked around $10^{○}$ and mainly located at the wire center.

Fig. 5C shows that the conversion efficiency decreases with the wire width when it is larger than 0.3 $\mathrm{\mu }\mathrm{m}$. With the wire width above 0.3 $\mathrm{\mu }\mathrm{m}$, the wire structure can be kept even at the laser-focusing plane. However, the laser pulse can be considerably blocked by the wire since it cannot enter the wire interior, which becomes more significant with the increasing width. This leads to the decrease of the laser absorption and conversion efficiency.

To further understand Fig. 5 D and E, we analyze the scaling of the photon energy and number with the laser intensity or amplitude $a_0$. The electron beam energy can roughly be $⟨{\gamma }_e⟩\simeq 3.13a_0\exp \left(-{\lambda }_0^2/16r_0^2\right)$, according to ref. 28, which predicts the value 437 MeV close to the peak energy 650 MeV shown in Fig. 6C. Then, Eq. 2 can be rewritten by $⟨\chi ⟩\simeq 3.13a_0\exp \left(-{\lambda }_0^2/16r_0^2\right)\left|F_y^{wig}\right|/E_{Sch}$. In our case, with the peak intensity around $10^{22}-10^{23}\hspace{0.17em}{\mathrm{W}\mathrm{c}\mathrm{m}}^{-2}$ and the wire width below ${\lambda }_0$, the electrons on the wire surface are completely stripped, and therefore, the static field strength or $\left|F_y^{wig}\right|$ depends strongly upon the wire charge density and weakly upon the laser intensity. When the wire parameter is fixed and the laser power $P_0$ is adopted within 0.5 to 5 PW, one can roughly take $\left|F_y^{wig}\right|$ as a value about 50 according to our simulations and then $⟨\chi ⟩\simeq 0.00037a_0$. To obtain photon data, one can use the theory of synchrotron radiation (30, 37), which is general when the acceleration field of an electron is given in its rest frame—that is, $\chi$. The emitted photons have an average energy $⟨{\epsilon }_{ph}⟩\simeq 0.44⟨\chi ⟩⟨{\gamma }_e⟩m_e{c}^2\simeq 0.000245a_0^2\hspace{0.17em}\left[\mathrm{M}\mathrm{e}\mathrm{V}\right]$, and the photon generation rate per electron is $1.4\times 10^{13}⟨{\gamma }_e⟩\simeq 4.2\times 10^{13}{a}_0$. With $P_0=$ 5, 2.5, 1, and 0.5 PW, $⟨{\epsilon }_{ph}⟩$ is calculated as 40, 20, 8, and 4 MeV, respectively, which reasonably agrees with our simulation results: 31, 20, 13, and 6 MeV. To obtain the photon number, we count the number $N_e$ of electrons above 10 MeV in our simulations and find a rough scaling $Ne\propto a_0^2$. We assume that beam electrons have nearly the same efficient radiation time with $P_0$ ranging from 0.5 to 5 PW. This is because the laser spot size is much larger than the wire width; therefore, the wire slightly affects the evolution of the pulses with different high powers. Then, the photon number follows $N_{ph}\propto a_0^3$, which agrees with our simulation results: $2.8\times 10^{12}$, $1.24\times 10^{12}$, $3.6\times 10^{11}$, and $1.6\times 10^{11}$ photons with 5, 2.5, 1, and 0.5 PW, respectively. Then, one can obtain the conversion efficiency $\eta \propto a_0^3$, which is in reasonable agreement with the results shown in Fig. 5D.

Discussion

We propose a scheme to provide a compact ultrabright gamma-ray source with photon energy ranging to GeV. This is achieved with a PW laser-irradiated subwavelength solid wire, which can drive both acceleration of nC, GeV electron beams, and their wiggling in the QED regime. The electrostatic and magnetostatic fields induced by the incident laser pulse around the wire surface are responsible for the wiggling of energetic beam electrons. Due to the high density of the wire, the quasistatic fields are so high that the GeV electrons are with QED parameters $\chi \sim 0.1$ even with a laser power of 0.5 PW. Therefore, the synchrotron radiation is produced uniquely in the QED regime, leading to ultrabright, high-energy gamma rays peaked at $1^{○}$. The average photon energy scales with $a_0^2$ as well as the photon number and conversion efficiency scale with $a_0^3$. The results are supported by 3D PIC simulations and theoretical analysis. Our scheme embraces the merits of high directivity, high charge, small transverse size, and short duration in generated electron beams, which are inherited by the gamma rays.

We have taken the laser-focusing plane behind the wire fore-end, allowing an acceleration distance to generate a well-guided GeV beam before the largest $\chi$ appears at the focusing plane. This puts forward a requirement on proper alignment between the wire and the laser in the experiments (see SI Appendix). To fully apply this scheme and generate gamma rays with energy ranging to 100 MeV, the laser intensity on the focusing plane needs to reach $10^{22}\hspace{0.17em}{\mathrm{W}\mathrm{c}\mathrm{m}}^{-2}$. Therefore, we have taken a spot radius of $1.2\mathrm{\mu }\mathrm{m}$. Although such tight focusing can be achieved in experiments (38), it is a challenge for most PW-class laser systems. With a larger spot radius, our scheme still works, even though the photon energy will be reduced (see SI Appendix). Another possible challenge is the laser contrast. If the contrast ratio is low, the laser prepulses may damage the wire front. Since our scheme requires the pulse to be focused behind the front end, one could take a relatively long wire and shift backward the focusing plane along the wire according to the contrast condition.

Note that our scheme is different from the betatron radiation in a gas target (12–14). Our scheme involves a solid target with much higher density, which causes the effective wiggling field to be several orders of magnitude higher and the generated beam charge to also be much higher. Then, the radiation can enter the QED regime, which is not the case with the normal betatron scheme. Therefore, both energies and yield efficiency of photons are much higher in our scheme. Besides, in the betatron scheme, the electrons are wiggled mainly by an electrostatic field, and they cross the target center. In our scheme, the electrons are wiggled by electrostatic and magnetostatic fields within a small space around the target surface and do not cross the target center.

Methods

Numerical Simulation Design.

To guide electron beams, the laser pulse propagates along a subwavelength wire (along the $+x$ direction), and the laser spot center coincides with the wire section center. We take a cuboid wire to reduce the computation. The laser-focusing plane is located $22\hspace{0.17em}\mathrm{\mu }\mathrm{m}$ behind the front end of the wire. When the laser approaches its focusing plane, the electrons are gradually accelerated and their divergent angles are reduced. Around the focusing plane, the electron energies become the highest and the angles turn the smallest; meanwhile, these electrons gain the largest QED parameters $\chi$. At this time, the strongest radiation occurs, which ensures the gamma-ray photons emitted with smallest divergence angles. We take the laser pulses with powers between 0.5 and 5 PW; therefore, the wire target can be considered as fully ionized plasma of density 690 $n_c$. Since the high-energy electrons and gamma rays move nearly along +x together with the laser, we adopt a moving window at the light speed $c$. The window has a simulation box $16\hspace{0.17em}\mathrm{\mu }\mathrm{m}\times 24\hspace{0.17em}\mathrm{\mu }\mathrm{m}\times 24\hspace{0.17em}\mathrm{\mu }\mathrm{m}$ in $x\times y\times z$ directions. We take the cell sizes in the three directions as 0.02 $\mathrm{\mu }\mathrm{m}$, the time step as 0.033 fs, and 8 quasi-particles per cell. The simulations are finished at 50 ${\tau }_0$. All photons generated are recorded, although some of them have left the simulation box before 50 ${\tau }_0$.

PIC Simulation Code.

We carry out 3D PIC simulations with the KLAPS code (36), including gamma-ray photon and pair generation via QED effects (32), fourth order zigzag current calculation (36), and so forth. With the fourth algorithm, the numerical noise in our simulations is well controlled. An adjustable time step (32) is taken to calculate photon and pair generation with enough accuracy.