Relation between single-molecule properties and phase behavior of intrinsically disordered proteins

Significance

Some proteins can undergo phase separation in vivo to form membraneless organelles with distinct physiological functions. In many cases, the driving force is believed to be the intrinsically disordered domains that lack regular structural features and can phase separate in vitro. Relating protein sequences to phase-separation propensity is the goal of this work. Toward this goal, we highlight the connection between the temperature where a single chain collapses, the temperature where interactions within a dilute solution favor self-association, and the critical temperature of phase separation. Our results show that these characteristic temperatures are highly correlated, suggesting that experiments performed in dilute conditions may be used to predict phase separation.

Abstract

Proteins that undergo liquid–liquid phase separation (LLPS) have been shown to play a critical role in many physiological functions through formation of condensed liquid-like assemblies that function as membraneless organelles within biological systems. To understand how different proteins may contribute differently to these assemblies and their functions, it is important to understand the molecular driving forces of phase separation and characterize their phase boundaries and material properties. Experimental studies have shown that intrinsically disordered regions of these proteins are a major driving force, as many of them undergo LLPS in isolation. Previous work on polymer solution phase behavior suggests a potential correspondence between intramolecular and intermolecular interactions that can be leveraged to discover relationships between single-molecule properties and phase boundaries. Here, we take advantage of a recently developed coarse-grained framework to calculate the $\theta$ temperature $T_{\theta }$, the Boyle temperature $T_B$, and the critical temperature $T_c$ for 20 diverse protein sequences, and we show that these three properties are highly correlated. We also highlight that these correlations are not specific to our model or simulation methodology by comparing between different pairwise potentials and with data from other work. We, therefore, suggest that smaller simulations or experiments to determine $T_{\theta }$ or $T_B$ can provide useful insights into the corresponding phase behavior.

Liquid–liquid phase separation (LLPS) of proteins and nucleic acids has recently drawn significant attention due to its relevance to physiological functions (1–4), disease pathology (5–7), and design of self-assembling materials with tunable properties (8–10). One major reason for this interest in LLPS is its relation to intracellular compartmentalization via the formation of membraneless organelles (11–14). Experimental studies suggest that the main driving force of LLPS for many of the proteins involved comes from their intrinsically disordered domains (i.e., those that lack a stable folded structure) (11, 12). A working hypothesis is that the disordered domains drive LLPS under physiological conditions, thus increasing the effective concentration of other (folded) domains (e.g., RNA binding domains) that carry out additional functions by recruiting other biomolecules, such as RNA (11, 14–17). Many proteins that are known to form dynamic liquid-like assemblies through LLPS can also form pathological aggregates. It has been suggested that this high-density phase might help overcome nucleation barriers and promote aggregation (6, 7). The effects of known disease-related mutations, which promote both LLPS and formation of solid-like aggregates, provide evidence in support of this hypothesis (7, 17). LLPS-susceptible protein sequences are also promising for the design of materials for a variety of applications (8, 9).

Relating sequence to phase-separation properties is a major goal in this work; it will allow for the exploration of the proteome to identify sequences which may participate in LLPS and will aid in directed design of peptide sequences having desired assembly and material properties. An excellent study by Quiroz and Chilkoti (8) has already provided much evidence on the relationship between amino acid composition and phase behavior by measuring the demixing temperature for a large number of sequences. Several studies have also addressed the relation between the degree of collapse of an intrinsically disordered protein (IDP) in dilute conditions and the phase boundaries. Lin and coworkers (18, 19) observed a correlation between the radius of gyration ($R_g$) of an isolated protein and the LLPS critical temperature ($T_c$) for a collection of polyampholytic sequences. Riback et al. (20) found a similar correlation between the single-chain $R_g$ and the demixing temperature ($T_{\mathrm{d}\mathrm{e}\mathrm{m}\mathrm{i}\mathrm{x}}$) for sequences of differing hydrophobicity. Both of these studies, despite focusing on different aspects of protein sequence properties, suggest that the $R_g$ of a single chain in dilute solution is linked to its ability to phase separate. However, such a correspondence is not expected to hold well for proteins of different lengths due to the differences in the scaling of $R_g$ and $T_c$ as a function of chain length.

LLPS of IDPs shares common features with the well-established field of polymer solution phase behavior, suggesting that existing polymer-physics principles might be a good starting point toward a better understanding of the underlying phenomenon (8, 21–23). For example, the collapse of a single isolated homopolymer chain and polymer solution phase separation are related via the effective monomer–monomer interaction strengths in the Flory–Huggins theory (24, 25). Panagiotopoulos et al. (26) have shown that the temperature of the coil-to-globule transition ($T_{\theta }$) and $T_c$ are equal in the limit of infinite chain length. Wang and Wang (27) applied self-consistent field theory to also show the correspondence between $T_{\theta }$, the Boyle temperature ($T_B$) at which the second virial coefficient ($B_{22}$), is equal to 0, and $T_c$. We investigate whether these theories in polymer physics can also be applied to understand LLPS of finite-length heteropolymeric IDPs.

Our goal is to find a general relationship between $T_{\theta }$, $T_B$, and $T_c$ for a variety of IDP sequences. To accomplish this, we use a recently developed coarse-grained (CG) computational framework that is capable of obtaining all three of these properties (28). We have shown previously that this approach is sufficient to capture qualitative trends in phase behavior as induced by sequence mutations or by inclusion of a folded domain (28–30). We calculate these three characteristic temperatures for 20 different IDP sequences and mutants with diverse hydropathy, charge, patterning, and sequence length from experimental and theoretical studies on IDP phase separation (12, 17, 28, 30, 31). We further calculate $T_{\theta }$ for a set of 30 synthetic polyampholyte sequences and compare with $T_c$ determined from theoretical methods to show that this correlation is not specific to our CG framework (18). We observe a strong linear correlation among $T_{\theta }$, $T_B$, and $T_c$. This highlights the utility of polymer-physics principles in discovering predictive models of protein LLPS. Moreover, since it may be easier to obtain $T_{\theta }$ and $T_B$ via simulations or some experimental methods, they can serve as proxy descriptors of LLPS and allow for high-throughput screening of sequences.

Results and Discussion

Obtaining Phase Diagrams from Molecular Simulations.

To obtain the phase coexistence envelope for an IDP sequence, we use a recently proposed CG modeling framework (28) that has already been applied to understand the sequence determinants of specific IDPs (29, 30). The sequences that we consider include the low-complexity (LC) domain of FUS and four different phosphomimetic variants (7, 12, 29), the multivalent repetitive FUS sequences (${\left[\mathrm{F}\mathrm{U}\mathrm{S}\mathrm{40}\right]}_n$) (28), the LC domain of hnRNPA2 and two disease-related mutants (30, 32, 33), the N-terminal intrinsically disordered region of LAF-1 (11) and five designed variants having similar or identical sequence composition, and the disordered C-terminal domain of TDP-43 (17). We obtain the phase coexistence using two different CG potentials for several of the sequences to check whether the results presented here are model-dependent.

For efficient sampling of the phase diagram, we use the slab method (28, 34), in which the simulations are initiated from a high-density protein slab that is continuous in the $x,y$ plane of a simulation cell with an elongated $z$ axis, allowing for efficient equilibration between the low- and high-density phases (Fig. 1C and Movie S1). This geometry has been widely used to study liquid–liquid (35), solid–liquid (36), and liquid–vapor (37) phase coexistence, and the results are highly consistent with conventional grand canonical approaches (34, 38) (SI Appendix, Fig. S1). Standard chemical potential routes are computationally prohibitive for longer chains that we study here. This challenge can be overcome by the use of lattice models (26) or by simplifying the protein chains as patchy particles as done recently by Nguemaha and Zhou (39). We instead prefer an approach that can faithfully capture the polymeric nature of IDPs and their interactions leading to the formation of a dense phase with concentration that is dependent on the protein sequence.

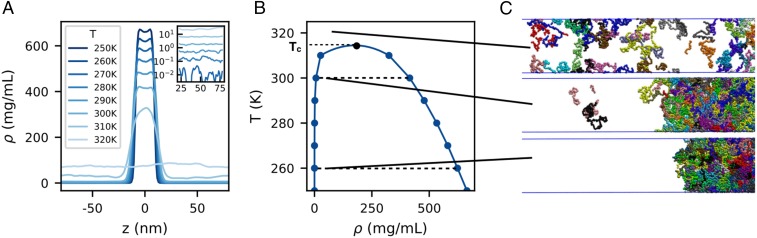
Fig. 1.

Determining phase diagrams via slab simulations. (A) Density profiles become flat at temperatures higher than $T_c$. Inset shows low-density phase in log scale to highlight that the density converges well and is nonzero. (B) From the density profile, we generate the coexistence curve of the sequence. (C) Snapshots of slab simulations at supercritical (Top), near-critical (Middle), and below-critical (Bottom) conditions.

We show in SI Appendix, Fig. S2 that simulations of phase coexistence using a cubic box with a spherical “droplet” of chains (Movie S2) and using slab geometry produce very similar phase diagrams. By simulating the droplet geometry at different system sizes, we also find that the coexistence densities approach the values determined using slab geometry as the system size increases, even past the number of chains used for the slab simulations themselves (SI Appendix, Fig. S3). We conclude that the slab geometry provides an advantage over simulations using droplet geometry in that it reduces finite-size effects.

For WT hnRNPA2 at temperatures where we observe phase coexistence, we calculate concentrations in the low-density phase to be in the range of 0.017–23.8 mg/mL (1.2–1,870 $\mathrm{\mu }$M) and the high-density phase to be within 324.0–664.3 mg/mL (22.6–43.4 mM). These densities are in excellent agreement with experimental measurements by Ryan et al. (30), who observed micromolar concentration of the aqueous phase at low temperatures and estimated the concentration in the condensed phase to be between 30 and 40 mM. Brady et al. (14) also find the coexistence concentrations to be within the ranges of 0–50 and 150–400 mg/mL for the low- and high-density phases, respectively, for Ddx4, a sequence similar to LAF-1. We see good agreement of coexistence densities with many other experimental studies as well that show proteins having saturation concentrations in the $\sim$1-mg/mL range and high-density concentration in the hundreds of milligrams per milliliter range (12, 17, 29, 40).

As the nonbonded interactions between amino acid residues in our models are temperature independent, we only observe the upper critical solution temperature, hereafter referred to as $T_c$. We calculate $T_c$ from the coexistence densities as detailed in SI Appendix. We note that the $T_c$ estimated in this way is rather insensitive to the range of temperatures fitted (SI Appendix, Fig. S4). We have also directly verified $T_c$ estimated by this method in several cases by running simulations near $T_c$: just 5 K above $T_c$, the slab is observed to disintegrate, while below $T_c$, it is stable and will spontaneously form even when the simulation is initiated from a fully dispersed initial condition (SI Appendix, Fig. S5 and Movie S3). Representative coexistence density profiles and the phase diagram are shown in Fig. 1 A and B for WT hnRNPA2 along with snapshots of simulations at different temperatures (Fig. 1C). Phase diagrams for all sequences are presented in SI Appendix, Fig. S6.

The Relation Between Single-Chain Properties and Protein LLPS.

We further determine $R_g$ as a function of temperature from replica exchange molecular dynamics (REMD) simulations of a single CG protein chain (Movie S4). We note that the models used here provide chain dimensions and asphericity values similar to an all-atom implicit solvent model (41), which has been applied extensively to IDPs involved in LLPS (42–45) (SI Appendix, Fig. S7). We also note that, using the Kim–Hummer (KH) variant of our coarse-grained potential, the $R_g$ values of the two sequences, hnRNPA2 and FUS, are 2.2 and 3.4 nm, respectively, at 300 K, which are comparable with experimental measurements of the hydrodynamic radius by Ryan et al. (30) of 2.89 and 3.32 nm, respectively. When comparing WT and phosphomimetic variants of FUS, we see the expected increase of chain dimensions as also reported by Ryan et al. (30). This increase in chain dimensions being accompanied by lower propensity for phase separation has been observed by several other studies (18, 20, 29) and should hold for sequences of similar length and composition.

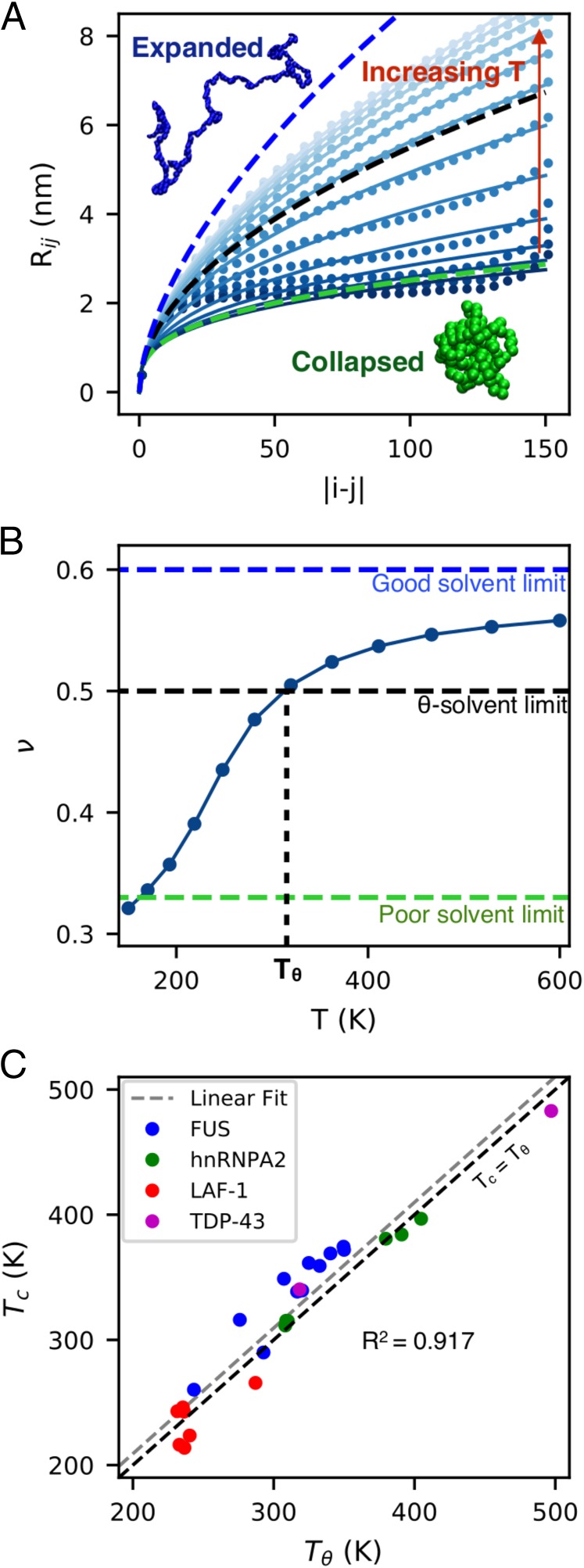
For IDPs of different lengths, $R_g$ scales with respect to chain length as $R_g\propto N^{\nu }$, where $N$ is the number of peptide bonds and $\nu$ is the Flory scaling exponent (46). Since $R_g$ by itself is not expected to correlate well with $T_c$ for IDPs of different length (SI Appendix, Fig. S8), we use $\nu$, which we believe should scale more similarly to $T_c$ with changes in chain length. $\nu$ can be determined directly from single-chain simulations by fitting average interresidue distance $R_{ij}$ between the $i$th and $j$th residues as a function of chain separation $|i-j|$ (47) as follows, $R_{ij}=b|i-j{|}^{\nu }$, where $b$ is the Kuhn length, which is set to be 0.55 nm as suggested for disordered proteins (48–50) (Fig. 2A). It should be noted that, for collapsed proteins, $R_{ij}$ can deviate from the power law scaling (low-temperature data in Fig. 2A) due to intramolecular interactions resulting in the formation of nonspecific structures. We observe good fits for data near and above $T_{\theta }$ for most sequences as shown in Fig. 2A. For each protein, $\nu$ is estimated as a function of the temperature to determine $T_{\theta }$ as the temperature where $\nu =1/2$. An example is shown in Fig. 2B for WT hnRNPA2 (32, 33); results for all other proteins are given in SI Appendix, Fig. S9. At $T_{\theta }$, the protein chain behaves like an ideal chain, as attractive intraprotein interactions are canceled by repulsive excluded volume interactions (46).

Fig. 2.

Comparison between $T_{\theta }$ obtained from single-chain simulations and $T_c$ obtained from slab simulations. (A) Scaling of average intramolecular distances, $R_{ij}$, with sequence separation $|i-j|$, as a function of temperature. The dashed green, black, and blue curves correspond to scaling exponents of $1/3$, $1/2$, and $3/5$, respectively. Snapshots in Insets show an expanded conformation under good solvent conditions and a collapsed configuration under poor solvent conditions. (B) $\nu$ crosses 0.5 at the $\mathrm{\Theta }$ point and defines $T_{\theta }$. (C) Correlation between $T_c$ and $T_{\theta }$. The error bars of both quantities are smaller than the symbols.

Previous studies have shown that $T_{\theta }$ of a homopolymer coincides with $T_c$ in the limit of infinite chain length (26, 27). We are interested in determining whether finite-length chains of heteropolymers, such as IDPs, may still show such a correspondence between the two temperatures. We test if solvent quality characterized by $\nu$ at a single temperature (300 K) can provide useful information about $T_c$. The overall correlation between $T_c$ and $\nu$ (SI Appendix, Fig. S10) is quite reasonable ($R^2=0.760$). We observe an even stronger correlation ($R^2$ = 0.925) between $T_{\theta }$ and $T_c$ as shown in Fig. 2C for all sequences with temperatures varying over a broad range from $\approx$200 to 500 K. The correlation between $T_{\theta }$ and $T_c$ is found to be approximately linear with a slope of one and intercept near the origin, which suggests that the temperature at which intramolecular attraction and repulsion are balanced is roughly the same as the temperature at which intermolecular interactions in a protein solution are also canceled out. Thus, we expect that this correlation should not change significantly for experimental data on similar protein sequences and hope that our results will motivate future experimental work in this direction. It is also notable that the correlation is independent of the computational model used, as we include data from two very different CG models of interresidue interactions (Figs. 2C and 4C and SI Appendix, Fig. S11), further suggesting that these correlations could be universal, regardless of technique or protein.

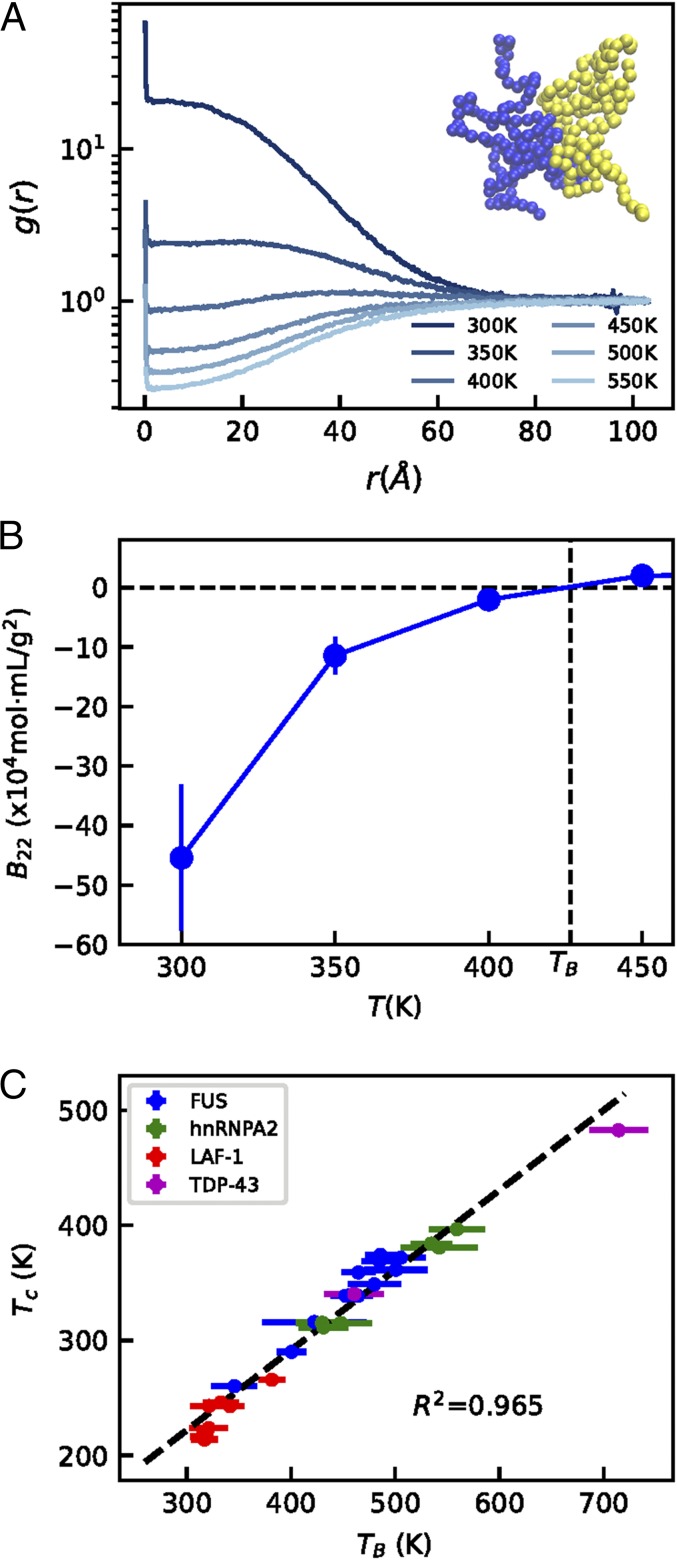
Fig. 4.

Comparison between Boyle temperature $T_B$ obtained from the temperature dependence of $B_{22}$ and $T_c$. (A) Radial distribution function between the two isolated chains with increasing temperature. The snapshot in Inset shows typical configurations in the simulation. (B) The temperature at which $B_{22}=0$ defines $T_B$. (C) Correlation between $T_c$ and $T_B$. The errors of $T_B$ are shown as bars, whereas the errors of $T_c$ are smaller than the symbols.

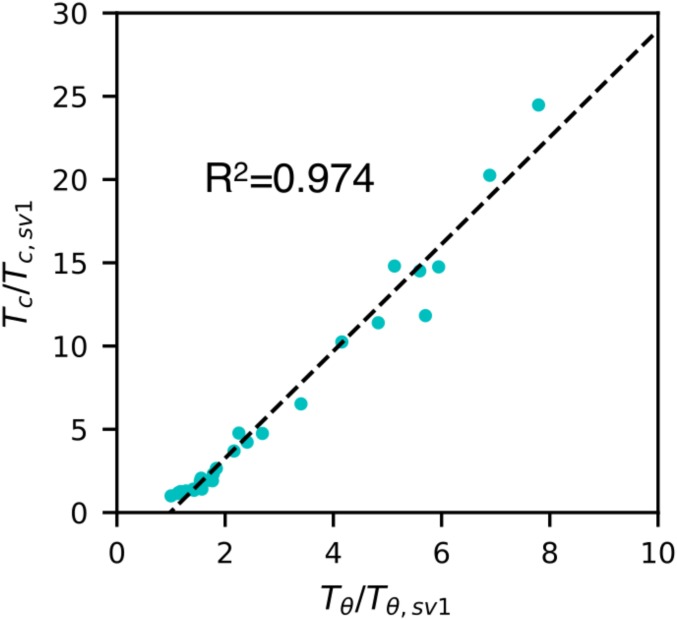
The protein sequences considered so far do not account for additional factors that are important for the IDP behavior, such as charge patterning (47). To check if the correlation between $T_c$ and $T_{\theta }$ can also be useful for capturing changes in the protein LLPS due to sequence patterning, we consider a set of 30 polyampholytic sequences with the same amino acid composition but differently arranged, ranging from perfectly mixed to block copolymer (51, 52). Lin and coworkers (18, 22) recently investigated the LLPS behavior of these protein sequences (termed SV series) via Flory–Huggins theory combined with a random phase approximation method. We take advantage of the available $T_c$ data from this study by comparing with $T_{\theta }$ from our model using REMD simulations. We find the correlation to be quite strong ($R^2$ = 0.974) for the SV series as shown in Fig. 3. We note that, for sequences having a high degree of charge segregation, the intrachain distances do not fit the polymer scaling law well (SI Appendix, Fig. S12). Therefore, we have also applied an alternative method to obtain $\nu$ (50) (SI Appendix) and shown that $T_{\theta }$, when calculated by this method, also correlates very well with the $T_c$ results from Lin and coworkers (18, 22) (SI Appendix, Fig. S13). The correlation is better than those seen for the previous 20 IDP sequences, mainly due to the balanced charge and identical sequence composition. These results suggest that well-established polymer-physics principles can be used to understand and predict the LLPS of IDPs. In general, when considering intramolecular interactions, as in the case of $T_{\theta }$, each individual residue’s self-interactions are ignored. Such interactions may be quite relevant for intermolecular interactions when estimating $T_c$, especially for sequences that are not well-mixed or charged sequences with long-range electrostatic interactions. In the case of LAF-1, we had previously identified a short eight-residue region that has high propensity for interactions with itself in other chains. Moreover, LAF-1 also has a higher fraction of charged residues that will further make it difficult to capture information on such interactions purely based on a single-chain property, such as $T_{\theta }$. We expect that such interactions will be better captured with measures, such as second virial coefficient.

Fig. 3.

Test on designed sequences with different charge patterns (51). $T_c$, as calculated by Lin and Chan (18), and $T_{\theta }$, as determined from our monomer simulations and normalized to the sequence with the lowest temperature (sv1), are plotted against each other and show good correlation.

The Relation Between Protein Affinities in Dilute Solutions and LLPS.

The observed correlation between $T_{\theta }$ and $T_c$ suggests a strong similarity between the intrachain interactions of an isolated protein and the interchain interactions among proteins in a liquid-like phase. Interchain interactions can also be quantified by the osmotic second virial coefficient ($B_{22}$). Previously, $B_{22}$ was shown to be related to the growth rates of protein crystals (53) and the temperature at which protein solutions become turbid (54). As discussed in the Introduction, $T_{\theta }$ of a homopolymer chain coincides with $T_B$ in the limit of infinite chain length (26, 27). Therefore, as in the previous section, we would like to test if such a correlation applies to finite-length IDPs that are involved in LLPS.

In molecular simulations, $B_{22}$ can be calculated from the radial distribution function, $g\left(r\right)$, between two protein chains (55) as follows:

$$B_{22}=2\pi \underset{0}{\overset{\infty }{\int }}\left[1-g\left(r\right)\right]\hspace{0.17em}{r}^{2}dr.$$ [1]

It is somewhat cumbersome to estimate $B_{22}$ from simulation for disordered proteins, as the $g\left(r\right)$ sampling involves conformational changes as well as distance and orientational degrees of freedom. However, it is still considerably less computationally demanding than sampling phase coexistence using slab geometry. Following previous work (56), we are able to determine $B_{22}$ with excellent statistical certainty (especially near the $T_B$) using a combination of Monte Carlo and umbrella sampling methods (Movie S5). The $g\left(r\right)$ for WT hnRNPA2 is shown in Fig. 4A. We determine $T_B$ by interpolating the temperature at which $B_{22}=0$ in Fig. 4B for WT hnRNPA2 and in SI Appendix, Fig. S14 for all of the proteins (details are in SI Appendix,). We observe a strong correlation between $T_B$ and $T_c$ ($R^2$ = 0.965) as shown in Fig. 4C (the correlation between $T_B$ and $T_{\theta }$ is shown in SI Appendix, Fig. S15). The correlation between $T_c$ and $T_B$ seems to be statistically stronger than between $T_c$ and $T_{\theta }$, which suggests that, for finite-length proteins, intermolecular interactions captured by $B_{22}$ may be a better metric than $\nu$ that is based on intrachain interactions. Of course, the two temperatures differ from each other for the finite-length proteins considered here compared with the infinitely long homopolymers. The slope of the correlation is not one and its intercept is not zero as with $T_c$ and $T_{\theta }$. Considering that the results from different models fall on the same correlation, it would be tempting to conclude that the slope and intercept of the fit to the data will remain unchanged if experimental data were also included here. However, given the lack of suitable theories that can be used to assess this issue further, we reserve such judgment for future work.

Conclusions

We have shown in this work that theories originally intended for use with homopolymers of infinite chain length (26, 57) can also be applied to heteropolymeric, finite-length IDPs to relate the characteristics of dilute and condensed phase interactions. Specifically, we have observed strong correlations between $T_c$, $T_{\theta }$, and $T_B$. This general correlation is encouraging for several reasons. (i) The correlation suggests that our knowledge of homopolymers and the variety of tools from polymer physics are applicable to the study of LLPS of IDPs. (ii) The correlation can advance the simulation prediction of $T_c$ by using either more detailed or faster models. All-atom explicit solvent simulations, which predict single-chain dimensions with high accuracy (58–60) but are also more computationally demanding, can be applied to the study of phase behavior by taking advantage of the correlation between $T_c$ and $T_{\theta }$. Rapid screening of IDP sequences for their phase behavior might be also possible if $T_{\theta }$ can be predicted by sequence composition (e.g., mean hydrophobicity or net charge) or by efficient CG simulations. More work is clearly needed to reach this ambitious goal. (iii) This relation allows a variety of alternative experimental techniques, such as single-molecule FRET (61, 62) and small-angle X-ray scattering (SAXS) (20, 63), to be used to infer the relative propensity of different protein sequences to undergo LLPS. It is possible to estimate $\nu$ using single-molecule FRET, as previously done by Schuler and coworkers (48) with multiple FRET dye labeling positions. In addition, recently developed methods for analysis of SAXS (50, 64) and FRET (65) allow a value of $\nu$ to be estimated more easily from a single variant of any protein with the same experimental burden as would be needed to obtain $R_g$. In SI Appendix, Figs. S10 and S11, we present correlations of $T_c$ with alternative experimental observables that may be easier to determine, depending on the context.

One can, in principle, also extend this beyond critical temperature and estimate critical salt concentration, critical pH, and other solution conditions just from the response of $\nu$ and $B_{22}$ to perturbations. An additional advantage of using $T_B$ as an indicator of phase separation is that it has the potential to be extended to characterize coassembly of mixtures of different proteins and of protein and RNA mixtures, which is of great biological interest (13, 66). However, there are going to be examples where interactions are more complicated than what can be captured at the level of one or two chains using $T_{\theta }$ or $T_B$, such as systems driven by higher-order oligomerization of folded domains (13, 67). Despite these caveats, we trust that our results here will promote rigorous characterization of IDPs at different conditions and allow the field to progress toward solving the problem of sequence-encoded phase behavior. Such a high-throughput method would allow for rapid design of sequences, such as those designed by Quiroz and Chilkoti (8), and would aid in the development of protein models and techniques that can be used to more accurately predict the properties of IDP LLPS (13, 28, 68).

Materials and Methods

CG Model.

We use our recently developed $C_{\alpha }$-based model, where proteins are represented as flexible chains and each amino acid residue is considered as a single particle. Bonds are modeled using harmonic springs, long-range electrostatics are modeled using a Coulombic term with Debye–Hückel electrostatic screening (69), and nonbonded pairwise interactions are modeled using one of two knowledge-based potentials that we have previously applied to these systems (28, 56, 70) (SI Appendix).

Simulation Methods.

An initial configuration for slab simulations was generated via simulations at constant pressure and temperature, starting from a dispersed phase of protein chains and collapsed to a dense phase. Production simulations were conducted for $\sim$5 $\mathrm{\mu }$s at constant temperature and volume using the HOOMD-Blue v2.1.5 software package (71). Monomer simulations were conducted at a range of temperatures using REMD (72) in cubic boxes using the LAMMPS software package (73). Umbrella-sampling Monte Carlo simulations were used for simulations of two protein chains using in-house simulation software. Errors for $T_c$ and $T_{\theta }$ are estimated using block averages with five blocks, and for $T_B$, we follow a bootstrapping strategy. Additional details are in SI Appendix.