A formal model of fuzzy-trace theory: Variations on framing effects and the Allais paradox

Abstract

Fuzzy-trace theory assumes that decision-makers process qualitative “gist” representations and quantitative “verbatim” representations in parallel. We develop a lattice model of fuzzy-trace theory that explains both processes. Specifically, the model provides a novel formalization of how: 1) decision-makers encode multiple representations of options in parallel; 2) representations compete or combine so that choices often turn on the simplest representation of encoded gists; and 3) choices between representations are made based on positive vs. negative valences associated with social and moral principles stored in long-term memory (e.g., saving lives is good). The model integrates effects of individual differences in numeracy, metacognitive monitoring and editing, and sensation seeking. We conducted a systematic review of variations on framing effects and the Allais Paradox, both core phenomena of risky decision-making, and tested whether our model could predict observed choices: The model successfully predicted 82 out of 88 (93%) pairs of studies (comparing gain to loss conditions) demonstrating 16 variations on effects, theoretically critical manipulations that eliminate or exaggerate framing effects. When examining these conditions individually, the model successfully predicted 153 (90%) out of 170 eligible studies. Parameters of the model varied in theoretically meaningful ways with differences in numeracy, metacognitive monitoring, and sensation seeking, accounting for risk preferences at the group level. New experiments show similar results at the individual level. The model is also shown to be scientifically parsimonious using standard measures. Relations to current theories, such as Cumulative Prospect Theory, and potential extensions are discussed.

Risk preferences are fundamental to psychological and economic theory, and to decision neuroscience (Fischhoff, 2013; Reyna & Huettel, 2014). We propose a new model of risk preferences that integrates theoretical principles relevant to mental representations with individual differences in metacognitive monitoring and reward sensitivity. Our model is based on fuzzy-trace theory (FTT), an account of decision-making under risk. Our tests focus on 16 variations on phenomena that adjudicate among theories regarding variations of gain-loss “framing” biases and the Allais paradox.

Section 1: Overview

FTT’s central tenet is that people encode, store, retrieve, and forget multiple mental representations in parallel. These mental representations are characterized by different levels of detail and meaningfulness (e.g., Brainerd, Reyna, & Howe, 2009). By “mental representation,” we mean the way a stimulus is encoded into a subject’s memory, referred to as “gist” and “verbatim” per their usage in psycholinguistics (e.g., Clark & Clark, 1977). FTT posits that decision-makers use qualitative, categorical “gist” representations that capture the meaning of decision information, in parallel with (encoded simultaneously with, rather than derived from) precise “verbatim” representations that capture the exact words and numbers in that information (Reyna, 2012). Decision makers operate on these representations.

By modeling these mental representations, we can account for core phenomena in decision theory such as framing effects (i.e., shifts in risk preference when logically equivalent gambles are described in terms of gains rather than losses). We also extend our model beyond these phenomena to encompass manipulations designed as critical tests of leading theories of risky choice. Specifically, our parsimonious model of choice provides an explicit formalism for gist and verbatim mental representations in decision-making, showing how risk preferences are determined by multiple representations of decision options. The ultimate preference is determined by applying “voting” rules that adjudicate among representations. Like other models of category learning, such as COVIS (Ashby, Alfonso-Reese, Turken & Waldron, 1998) and ATRIUM (Erickson & Kruschke, 1998), our model incorporates competition between multiple levels of representation. However, our formalization is the first to use a unified mathematical framework to account for these different levels of representation in risky decision-making.

Our model also accounts for relevant individual differences and cognitive abilities. Specifically, we account for prior work showing that some individuals are more likely to notice that two versions of the same decision problem are related (e.g., that one decision problem can be derived from another mathematically) and to reconcile their answers to these problems, diminishing framing effects and other cognitive biases (e.g., Kahneman, 2003; Stanovich, West, & Toplak, 2011). These people, who exhibit need for cognition (NFC; Cacioppo, Feinstein, & Jarvis, 1996) and numeracy (mathematical ability), edit their preferences when decision problems that are mathematically related to one another are presented within-subjects (when subjects answer more than one such problem sequentially, e.g., Peters et al., 2006; Stanovich & West, 2008). The magnitude of effects due to these individual differences depends on the mix of individuals in a given sample of subjects. Our model accounts for the effects of individual differences by incorporating a mechanism for modifying preferences based on metacognitive monitoring and editing that is triggered by NFC and numeracy.

We test the model using different approaches to determine whether there is converging evidence for its assumptions. We focus our analysis on risky choice tasks, specifically variations on framing effects and the Allais Paradox, accounting for experimental evidence from several important types of decision problems and experimental manipulations of these problems (e.g., Allais, 1953; Kühberger & Tanner, 2010; Peters & Levin, 2008; Reyna, 2012; Tversky & Kahneman, 1986). We reviewed the literature and found 88 replications of important decision problems (e.g., the so-called Asian Disease Problem). Each of these replications consists of a pair of conditions, such as a gain and loss condition. For each problem, we used a jackknife/leave-one-out (JLOO) estimator derived from the remaining problems to calibrate our model’s parameters. We then used those parameter estimates to predict differences in log-odds ratios for 82 (93%) gain-loss pairs from our sample of 88. A second approach, tested on each gain or loss condition separately, yielded a successful fit for 153 (90%) of 170 comparisons (the JLOO procedure did not allow testing of three pairs of problems using our second approach).

Using the parameters estimated by Tversky and Kahneman (1992), we examined predictions of a major standard theory, namely Prospect Theory (PT). We found that, under these assumptions, PT could not account for all of the 16 variations that we discuss; indeed, some effects seem to contradict PT’s predictions. Although no definitive conclusion can be reached about PT’s predictions because it has multiple free parameters, the same parameter values cannot account for both the presence and absence of framing effects for numerically identical problems presented to the same subjects, as observed (see below). In contrast, our model successfully accounts for such effects as (a) reversals of preferences for objectively identical gambles, namely, risk aversion for gains and risk seeking for losses, which together are framing effects; (b) effects of truncating (or deleting parts of) risky gambles in different ways that attenuate or exaggerate framing effects; (c) reduction of within-subjects framing as compared to between-subjects framing, which reflects metacognitive monitoring and editing; and (d) differences across individuals in reward-related approach motivation (often assessed as sensation seeking and related constructs; Duckworth, Tsukayama & Kirby, 2013). Thus, we explain how effects of internal representation, external representation (wording of gambles), cognitive style and ability, and personality (i.e., reward-related approach motivation) combine to produce predicted variations in risk taking for both gains and losses.

The outline of this paper is as follows: Section 2 provides an overview of the key tenets of FTT, and motivates the need for a formal account of the theory. Section 3 provides the full mathematical formulation of our model. In Section 4, we use this formulation to explain a range of phenomena associated with variations on framing effects and the Allais Paradox drawn from a systematic search of the literature. We use two techniques to do so: First, we calculate odds ratios between pairs of gain-loss conditions (or Allais-paradox problems) to test our model’s predictions in a manner that is independent of subjects’ reward sensitivity. Next, we introduce, and estimate, a parameter accounting for this reward sensitivity, enabling us to make predictions for these problems separately. We show how our model’s parameters vary with measures of metacognitive monitoring and editing, and with reward sensitivity, at the aggregate and at the individual levels. We also test our model’s parsimony using standard measures of goodness-of-fit. Finally, in Section 5, we discuss alternative models and outline directions for future work, including extensions of our model.

Section 2: Key Tenets of Fuzzy Trace Theory

FTT is motivated by the insight that mental representations drive decisions. For example, consider the following decision:

1. Winning $180 for sure; versus

2. .90 chance of winning $250 and .10 chance of no money.

One might represent this decision as a simple choice between the following two options:

1. Some chance of winning some money

2. Some chance of winning some money and some chance of winning no money.

Given this representation, most decision makers would favor option 1 because it promises some money without the chance of no money. Alternatively, one could represent the choice as:

1. More chance of winning less money

2. Less chance of winning more money and some chance of winning no money.

This representation, although more precise, does not allow for a clear decision to be made because most people would prefer winning more money to winning less money, but they would also prefer more chance of winning to less chance of winning. Finally, one may choose a precise representation of the problem whereby one calculates the expected value of each option by multiplying its respective outcomes by their probabilities, as follows:

1. Expected value of $180 (i.e., $180 * 1)

2. Expected value of $225 (i.e., $250 * 0.90 + $0 * 0.10)

This representation seems to favor option 2, since it promises more money on average. FTT, the tenets of which are described below, explains how these representations are encoded, and how decisions are made based on these representations.

Gist Representations Are Qualitative

Experimental evidence from many tasks in cognitive psychology (e.g., in memory, psycholinguistics, and cognitive development) suggests that gist representations, even of numbers, are simple and qualitative rather than precise (e.g., Kintsch & Mangalath, 2011; Reyna, 2008; Thompson & Siegler, 2010). Gists do not depend on verbatim representations of exact words, precise numbers, eidetic images, or other detailed information. Despite their simplicity, gists are grounded in experience and are more likely to be relied on by adults, compared to children (though the categories may have their roots in childhood; Cimpian & Erikson, 2012), and by experts compared to novices (Reyna & Lloyd, 2006).

Verbatim Representations Are Precise

A verbatim representation of a stimulus captures its surface form – exact words, numbers, and pictures (Clark & Clark, 1977). Even though verbatim representations reproduce the details of a given stimulus, they, too, are symbolic mental representations. Verbatim representations are sufficiently precise to support rote analytical processing. For example, many elementary schoolers retrieve multiplication facts from verbatim memory by rote, as opposed to processing such problems conceptually (Ashcraft & Rudig, 2012). Novices and younger children are more likely to rely on verbatim-level representations, compared to experts and older children/adults (Brainerd & Reyna, 1993; Reyna & Ellis, 1994).

Preference for Simple “Fuzzy” Processing

Moving beyond traditional psycholinguistic definitions, research on FTT has shown that gist and verbatim representations are encoded separately and roughly in parallel, as demonstrated by double dissociations, non-monotonic trends, and crossover interactions (Reyna & Brainerd, 1995; Reyna, 2012). When making risky decisions, people process the gist of risky choices in parallel with verbatim processes in which precise magnitudes of probabilities and outcomes trade off (Kühberger & Tanner, 2010; Reyna & Brainerd, 1995).

Although multiple representations are encoded, a core tenet of FTT is that decision-makers prefer to operate on the simplest meaningful gist that distinguishes decision options. For numerical information, the simplest level is often categorical (or nominal) because this level is the least fine-grained (e.g., Reyna 2012). Categorical gist entails representing decision outcomes as members of different categories, such as “no” money versus “some” money (e.g., Mills, Reyna, & Estrada, 2008). This fuzzy-processing preference increases with experience in a domain (e.g., Reyna, Chick, Corbin, & Hsia, 2014; Reyna & Lloyd, 2006). More precise, yet still qualitative, representations are also generated simultaneously, such as ordinal representations (e.g., small vs. large amount of money). At the most precise level, interval verbatim representations are encoded. Thus, FTT posits a hierarchy of gist that is, in the domain of numbers, analogous to scales of measurement (Reyna, 2008; Stevens, 1946).

Categorical comparisons

When two decision outcomes are represented as members of different qualitative categories (e.g., “some money” vs. “no money”), the gist representation compares these two categories rather than the specific details. As we discuss below, each of these categories has a valence; the category that is more highly valued will be chosen. (These valences compare between categories, not between points within the same category.)

Ordinal comparisons

Ordinal comparisons are made between points within the same categories (e.g., some to some or none to none) per the categorical gist. Thus, ordinal levels of precision are representative of a form of gist that is intermediate between categorical and interval, and becomes evident when two decision options’ outcomes fall into the same category, and, thus, cannot be discriminated. The ordinal representation differs from the categorical in that ordinal representations are internally ordered along dimensions, such as outcome, probability, or time. Specifically, affective values (e.g., positive valences for money, health, kin, and so on) enable ordered comparison among points possessing the same categorical representation.

For example, if one medical treatment is described as having a 20% chance of death and another treatment as having a 5% chance of death, both treatments can be categorized as having “some” risk of death (e.g., Fagerlin, Zikmund-Fisher, & Ubel, 2005; Reyna, 2008). To discriminate between treatment options, a more fine-grained ordinal distinction needs to be made: the first treatment has a high risk relative to the second treatment. FTT (e.g., Reyna & Brainerd, 1995; Rivers et al., 2008) and other theories (e.g., Stewart, Chater, & Brown, 2006; Stewart, Reimers, & Harris, 2014; Ungemach, Stewart, & Reimers, 2011) have suggested – and associated research has supported – that people mentally represent such ordinal comparisons. (These other theories are wholly ordinal in nature. The novel contribution of our approach is that it combines ordinal decision making with categorical and interval level representations.) In contrast, categorical representations have no such internal ordering along these dimensions – that is, decision complements that fall within the same category are represented as if they were equivalent. We will see that the mathematical formalizations of these two constructs are also quite different.

Although ordinal representations are more precise than categorical ones, they might still yield indifference between decision options. For example, one could imagine a choice between:

1. 90% chance of winning $200 and a 10% chance of no money – interpreted as “less₁ money is more₂ likely, and no money is less₃ likely”

2. 60% chance of winning $300 and a 40% chance of no money – interpreted as “more₁ money is less₂ likely, and no money is more₃ likely”

We use subscripts to clearly indicate which parts of each complement are being compared. Consistent with our prior discussion, such a representation only compares outcomes that have the same categorical gist. For example, we compare “Less₁ money is more₂ likely” with “More₁ money is less₂ likely” because both have the categorical gist of “some money with some chance.” Similarly, we compare “no money is less₃ likely” to “no money is more₃ likely” because both have the categorical gist of “no money with some chance.” If any of these comparisons favors different choices, the ordinal level of comparison is treated as indeterminate in our model. Thus, since the first comparison, with subscripts 1 and 2, favors neither option, the decision outcome for the example above is indeterminate.

Interval comparisons

When categorical and ordinal comparisons lead to an indeterminate decision outcome, even more precise representations such as interval-level values become evident. For example, classical expected value (i.e., the product of outcomes and probabilities) is an interval representation that may be favored by more numerate individuals¹ (Schley & Peters, 2014). For simplicity, we assume a literal interpretation for the verbatim representation, which can be processed using rote mathematical operations (e.g., addition and multiplication; Ashcraft & Battaglia, 1978; Geary, 1994; Holmes & McGregor, 2007; LeFevre et al., 1996). This level of representation makes no assumptions regarding additional parameters, such as decision weighting functions, as are commonly used in expected utility theories (but it accounts for observed effects without such assumptions; see below).

To illustrate, using interval-level numbers, the expected value of the first decision option in the example above is 0.90 multiplied by $200 (plus 0.10 times no money): $180. The second decision option has an expected value of $300 times 0.60 (plus 0.40 times no money): again $180. Human memory can store exact interval-level information such as this, but these verbatim representations are fragile and subject to interference (e.g., Brainerd & Reyna, 1993; Gallo, 2006; Frank, Fedorenko, Lai, Saxe, & Gibson, 2012; Kintsch & Mangalath, 2011).

Comparing Valenced Affects (Values) and Combining Representations

According to FTT, decisions are made on the basis of simple valenced (i.e., positive or negative) affect (Peters & Levin 2008; Slovic, Finucane, Peters, & MacGregor, 2004). Thus, once options are represented in a categorical, ordinal, or interval fashion, the more positively valenced option within a given representation is chosen (e.g., winning some money is preferred to winning no money because money is positively valenced; losing no lives is preferred to losing some lives because losing lives is negatively valenced).

Recall the decision between winning $180 for sure versus a .90 chance of winning $250 and .10 chance of no money discussed at the beginning of this section. Here, multiple representations prefer different options, and so different, simultaneously encoded, representations will compete with one another. In general, the fuzzy-processing preference dictates that decisions are unlikely to be driven only by the verbatim representation, and will additionally be influenced by the simplest gist that distinguishes between outcomes. Therefore, when gist and verbatim representations make different predictions, subjects may choose an outcome that is intermediate between these two, and when they make the same prediction, the proportion of subjects choosing the predicted option will be higher.

Why Formalize Fuzzy-Trace Theory?

FTT has been successfully applied to research on memory, development, and decision-making. However, its assumptions about how gist representations are generated and combined with values to make choices have never been modeled; nor have they been evaluated for goodness-of-fit to empirical data. The proposed mathematical model provides explicit quantitative predictions that address several important questions: For example, how does one know which gists are encoded? When multiple possible gists are encoded, which is relied on in decision-making? How are categorical, ordinal, and interval representations combined to make a decision? How are conflicting values resolved? The answers to these questions have not yet been explicitly formalized.

Several mathematical models of FTT have been proffered (e.g., Brainerd, Aydin, & Reyna, 2012; Reyna & Brainerd, 2011; Levine, 2012), but none of these assign a mathematical structure to the central concepts of gist and verbatim representations, the fuzzy-processing preference, or affective values (in the sense of valenced affect). Our formalization of these concepts answers the questions posed above, enabling us to explain several risky choices (e.g., for options with equal and unequal expected values), including framing effects, and experimental manipulations that test predictions of alternative theories. The theory, as we discuss below, also makes predictions, supported by data, that are not made by alternative decision theories (e.g., Reyna et al., 2014). Thus, with some straightforward assumptions about representations of options (as categorical, ordinal, and interval), outcomes that vary along positively- or negatively-valenced dimensions, and decision rules that turn on affective values for those dimensions, the new model accounts for a variety of risky choice problems.

Section 3: The Model

In what follows, we flesh out the qualitative predictions described above with the mathematical machinery underlying our model. To do so, we draw on algebraic tools originally developed to explain visual object perception and human concept learning (Feldman, 1997). In this section, we use the example above (i.e., a certain $180 versus .90 chance of winning $250) to illustrate our approach to modeling multiple levels of representation.

The Decision Space: Formalizing Categorical Decision Making

We represent the complements in these options as points in a 2-dimensional space (see Figure 1a), representing all possible combinations of amounts of money (or, generally, some outcome) and probability that a decision-maker could encounter. Since we are studying risky decision problems with complements containing orthogonal numerical values (such as probability and outcome values; also see Stewart et al., 2006, who include temporal values), we assume a Euclidean space with Cartesian coordinates (i.e., it contains an origin point and remaining points are described relative to the origin). Our formalizations of categorical, ordinal, and interval representations (and resulting decisions) are all defined relative to such a space.

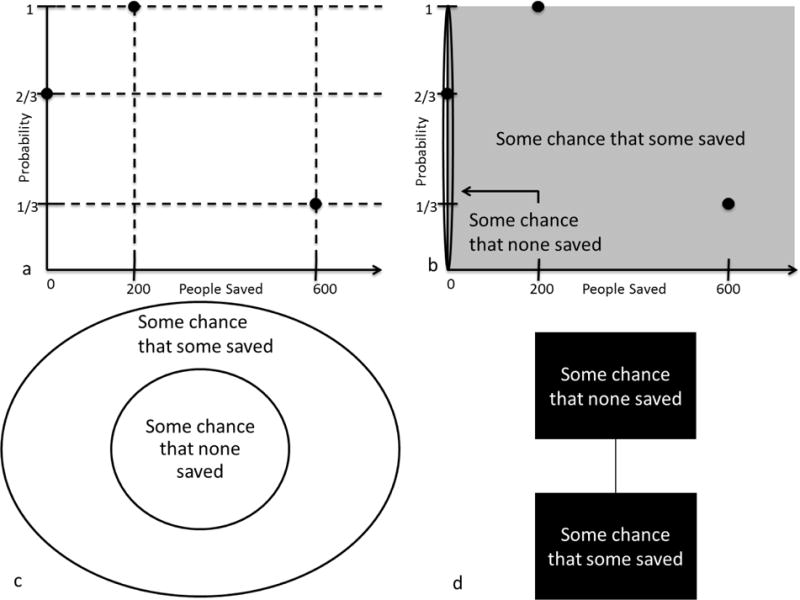
Figure 1.

a) visual representation of the choice faced by a hypothetical decision-maker. Each point in this space represents a decision outcome (i.e., a fixed amount of money with a fixed probability). b) The gist representation of the decision problem. All points in the grey box are interpreted as “some chance of some money,” all points in the horizontal oval are interpreted as “some money with no chance,” and all points in the vertical oval are interpreted as “some chance of no money.” Note that there are portions of the space where the ovals and grey box overlap each other. c) Venn diagram representing overlapping gists for the problem. d) A lattice representation of the gists in the decision problem. Higher elements in the lattice are preferred interpretations. Links indicate that all of the points in the higher gist category are contained within the lower gist category., and b

Identifying Categories in the Decision Space

Gist representations consist of categories distinguishing certain primitive concepts – such as, “no money” and “no chance” (i.e., probability of 0). Such categories determine the gist with which each decision complement is represented, and whether pairs of complements are interpreted differently. How do we know that these values form separate gist categories? For example, why doesn’t an arbitrarily different value of probability, such as 42.613%, form a separate category? Although our mathematical framework could accommodate a range of possible gists, certain categories are qualitatively and psychologically distinguishable, such as the difference between “some” and “none” of a quantity. Common categories are found in the literature on numerical cognition (e.g., Thompson & Siegler, 2010). For example, “no money” is psychologically special because it represents a qualitatively different outcome that is perceived as distinct from (and generally worse than) “some money.” Similarly, very small probabilities are interpreted as essentially nil (i.e., no chance) by many subjects (Stone, Yates, & Parker, 1994). According to FTT, decision-makers’ gists are also driven by their prior knowledge and expertise (e.g., Reyna & Lloyd, 2006). For example, people may rely on knowledge about safe versus unsafe levels of a toxin to distinguish gist categories (e.g., Schulze & Wansink, 2012).

“Some” and “none” are psychologically meaningful categories

Several independent findings support a distinction between the categories “some” and “none” when processing numbers. Beyond the relevant FTT findings (e.g., Reyna & Brainerd, 1991; Reyna, 2012; Reyna et al., 2014), experimental data have shown that subjects prefer to avoid winning nothing in a risky gamble, even if doing so lowers their overall expected value (e.g., the “P_max” strategy of avoiding winning nothing as in Venkatraman & Huettel, 2012; Venkatraman, Payne, Bettman, Luce, & Huettel, 2009). In addition, recent findings show that zero may be encoded into an “end stimulus” category that is separate from how other numbers are encoded (Goldman, Tzelgov, Ben-Shalom, & Berger, 2013; Pinhas & Tzelgov, 2012; Wellman & Miller, 1986), leading Pinhas and Tzelgov (2012) to hypothesize that “0…representing a null quantity triggers the emergence of an additional level of mental representation.” Thus, we assume that the categorical distinction between “some” and “none” of a quantity is primitive. The mapping between several stimuli from classical framing problems and their categorical representations is shown in Supplemental Material (Table S1).

For parsimony, we assume that the same “some” vs. “none” distinction in the domain of outcomes also applies to the domain of probability. This is consistent with the mathematical formulation of our model as a Euclidean decision space with Cartesian coordinates (i.e., a unique origin point from which orthogonal rays extend to infinity).

Categorical representation of the decision space

Recall that the gist representation of the choice is:

1. Some chance of winning some money

2. Some chance of winning some money and some chance of winning no money.

These gists are represented in a 2-dimensional Euclidean space, as shown in Figure 1b. All points in Figure 1b are interpreted according to the part of the diagram in which they are located. However, these gist representations can overlap. For example, a point that falls into the part of the space marked as “some chance of no money” also falls into the part marked as “some chance of some money.” Thus, multiple gist representations are possible for some points. Our gists are related as shown in the Venn diagram in Figure 1c. A full mathematical treatment of categorical representation is presented in Supplemental Material.

Selecting a preferred interpretation

We extend the fuzzy-processing preference to help us differentiate between overlapping gists, such as those indicated in Figure 1c. If each circle in the Venn diagram in Figure 1c is a possible interpretation, then we can select a preferred interpretation by representing our Venn diagram as a lattice (shown in Figure 1d) – a hierarchy in which higher elements are preferred interpretations when compared to lower elements. Since each decision complement is a point in our space, we can determine each complement’s possible gist representations as the set of overlapping gist categories into which the point corresponding to the decision complement falls. The highest such category in the associated lattice diagram stipulates how that decision complement is interpreted. A full mathematical treatment of category lattices is presented in Supplemental Material.

Values map mental representations to preferences

The preferred (likely) interpretation, or mental representation, is not the same thing as the preferred option. For example, a decision-maker will prefer to interpret “2/3 probability that 0 live” as “some chance that none live” as opposed to “some chance that some live.” However, given a choice between this option, interpreted as “some chance that none live” and another option, interpreted as “some chance that some live,” most decision-makers would choose the latter. Thus, once options are mentally represented (interpreted), we must define preferences over the options themselves.

Decision makers choose between options based on which has the higher-valued affect. The affect assigned to a given option is a function of how that option is represented. For example, “no money with some chance” is a preferred interpretation for the point ($0, 0.10) – a 10% chance of no money – when compared to “some money with some chance.” However, a prospect that is interpreted as “some money with some chance” has a higher valence when compared to one that is interpreted as “no money with some chance.” Thus, a decision-maker would choose the option with the higher valence. To formalize this prediction, we again use a partial order – i.e., every pair of elements within the category lattice may be less than, greater than, equal to, or unrelated to one another in the domain of values. Full mathematical details of this partial order are presented in Supplemental Material.

Formalizing Ordinal Decision-Making

Mapping problem information to ordinal mental representations

FTT predicts that decision-makers use ordinal representations (e.g., “more” vs. “less”) in parallel with categorical and interval representations. When mapping problem information to ordinal mental representation, points are compared such that “more” is always in the direction away from zero and “less” is always in the direction toward zero for each dimension in the decision space. Importantly, points may only be compared at the ordinal level if they exist within a common category. For example, one may compare “0 live with 2/3 chance” to “200 live with certainty” because both may be represented as “some chance that some live” (even if this is not the preferred interpretation for both options, it is an admissible interpretation for both). Since 0 is less than 200 and 2/3 is less than certainty, the corresponding ordinal representations are “less₁ live with less₂ chance” and “more₁ live with more₂ chance.”

Mapping ordinal mental representations to preference

Ordinal decision-makers also compare between options based on which has the higher-valued affect. In practice, this means that each dimension in the decision space has a preferred direction (e.g., more money is better than less money). When comparing two decision options, if the ordinal representation of one option is preferred along all dimensions of the decision space, and is strictly preferred along at least one dimension, then that decision option is preferred overall. For example, “more live with more chance” is preferred when compared to “less live with less chance.” Otherwise, a decision cannot be made and the ordinal representation is indifferent, such as when “more₁ live with less₂ chance” is compared to “less₁ live with more₂ chance”. A full mathematical treatment of ordinal representation and partial orders over decision options is presented in Supplemental Material.

Formalizing How Each Representation Chooses Among Decision Options

A “gist hierarchy” is a set of mental representations ranging in precision from a categorical gist representation up to an interval verbatim representation, and sets of rules for making decisions that are unique to each of these representations. We formalize the gist hierarchy as follows: At the categorical level, each point is represented according to the extended fuzzy-processing preference (i.e., preference for the least generic category – the one highest on the lattice). At the ordinal level, a point is chosen if it is weakly preferred along all dimensions and strongly preferred along at least one such dimension. Points in disjoint categories cannot be compared. At the interval level, decisions options are evaluated according to their expected values (i.e., the sum of each outcome multiplied by its probability).

Combining Information Across Representations

Our formalization thus far has described how each of three representations – categorical, ordinal, and interval – represents and chooses between decision options. If all representations prefer a given decision option, the decision maker will choose that option. However, if the preferences of each representation conflict, we require a way to aggregate information from across these representations. Indeed, up until this point, our model has not explicitly provided an account of conflicts between representations (e.g., if the categorical representation prefers one option whereas the interval representation prefers a different option). Since these representations are encoded in parallel, a rule is needed to select a decision option. In other words, these representations must be aggregated so that the decision-maker may ultimately choose one option.

We address such conflicts in our model by assuming that each representation casts a “vote” for its preferred decision option. For example, given a choice between two decision options, each of the categorical, ordinal, and interval representations “votes” (−1 for the less risky option, +1 for the riskier option, or 0 if indifferent) for a preferred option according to its own particular representational logic. A weighted sum across these votes, explained below, determines the final decision. We chose summation because it is the simplest combination rule for this sort of aggregation.

An Error Theory for Risky Decision Problems

Thus far, given decision weights and votes, our model makes strict predictions regarding the modal decision outcome. However, it does not indicate what proportion of decision makers might choose that outcome. In this section, we indicate how to account for “error” – i.e., effect sizes – that encompass deviations from the modal prediction. The need for such an error theory in the domain of risky decision-making has long been recognized (e.g., Kühberger, 1995).

Consistent with the literature on qualitative discrete choice models, we represent error using a standard multinomial logistic distribution (e.g., McFadden, 2001). For decisions with two options, effect size typically follows a standard logistic distribution – a functional form that is commonly used in signal detection theory (e.g., MacMillan, 2002; McNicol, 2005) when the range of a function is between 0 and 1. Logistic distributions are used because of their computational tractability, ease of interpretation, and similarity in shape to the cumulative normal distribution. For our specific application, we model the probability, P, that a subject will choose a given decision option in a risky choice gamble by the logistic function:

$$P(\overrightarrow{x})=\frac{1}{1+e^{-(\overrightarrow{a}\cdot \overrightarrow{x}+b)}}$$ (1)

Although this function has long been used to model discrete choices (e.g., Luce, 1956/2005, Peirce & Jastrow, 1884), the novel contribution of our approach lies in the interpretation of the logistic function’s parameters and application of lattice theory. Specifically, $\overrightarrow{x}$ is a three-element vector containing an entry for each representation (categorical, ordinal, and interval), and $\overrightarrow{a}$ is a three-element vector containing an entry for each corresponding decision weight. We also introduce a factor, b, capturing the reward sensitivity of a given set of subjects. Thus, we account for conflict between representations by adding weighted votes from each representation and constrain the values that $\overrightarrow{a}$ and b can take by assuming that subjects with similar psychological characteristics (e.g., those with similar values of reward sensitivity) will have similar parameter values.

Factors affecting the decision weight vector

In the domain of decision making, two major individual difference factors associated with metacognitive monitoring and editing have been proposed – numeracy (e.g., Peters et al., 2006; Liberali et al., 2012) and NFC (Cacioppo, et al.,1996; Stanovich & West, 2008). People who are higher in numeracy and/or NFC are more likely to spontaneously compare and convert alternative “framings” of a problem (see below), reducing cognitive biases. We model the effects of numeracy and NFC using the decision weight vector $\overrightarrow{a}$. Furthermore, if we make the simplifying assumption that all of these decision weights are equal, we may replace $\overrightarrow{a}$ by a scalar factor, a, which captures the “strength” of a given set of votes. When a is large, preferences from individual mental representations will lead subjects to strongly favor one option over another, presuming that different representations do not conflict with one another. In contrast, when a is small, decision makers’ choices tend towards indifference when representations do not conflict. (Individual differences in conjunction with conflicting representations should make preferences diverge, as discussed below.)

Numeracy

For typical framing experiments, in which subjects receive only one frame of a given problem, differences in numeracy are a source of individual differences in biases. Peters and colleagues (2006) defined numeracy as “the ability to process basic probability and numerical concepts” and found that more numerate subjects were less susceptible to attribute framing effects. For example, subjects were more likely to rate a hypothetical psychology student’s work more highly if their exam scores were framed positively (e.g., “74% correct”) versus negatively (“26% incorrect”), even though the two representations are equivalent. This framing effect – the average distance in rating between the frames – was larger for low numeracy subjects than it was for high numeracy subjects. In the domain of risky decision framing, Peters and Levin (2008) found that more numerate subjects were less likely to show risky choice framing. They argued that highly numerate individuals are more likely to notice that decision problems are related (that a loss decision problem can be derived mathematically from the gain version of that problem) diminishing cognitive biases such as framing by reconciling their answers to the problems. Finally, Schley and Peters (2014) found that more numerate individuals treated numbers as more linear when making a risky decision, suggesting that they rely more on interval (linear) representations of probabilities and outcomes.

Need for cognition

Prior work suggests that subjects reconcile answers to oppositely framed versions of the same problem when both frames or obviously factorial design manipulations are presented within-subjects, or when subjects respond to multiple presentations of the same problem. Kahneman and Frederick (2002) have argued that such designs can lead subjects to focus on the variables that are being manipulated, and to compare different versions of the same underlying problem instead of treating each independently. Thus, the magnitude of framing effects varies systematically with experimental design (e.g., Stanovich & West, 2008).

The tendency to reconcile responses to different versions (or related problems) when they are presented within-subjects is greater for those higher in NFC. Subjects with high NFC tend to edit their choices more than those with low NFC, presumably because they are more likely to notice the common structures underlying these problems (i.e., high NFC subjects display “analytic override;” Kahneman, 2003; LeBoeuf & Shafir, 2003; Stanovich & West, 2008). When frame was manipulated within subjects, Smith and Levin (1996) found that framing effects were only found among low-NFC subjects and LeBoeuf and Shafir (2003) found that high-NFC were more likely to respond consistently across frames. Similarly, Simon, Fagley, and Halleran (2004) and Curseu (2006) found that framing effects were absent among high NFC subjects when these subjects were exposed to several framing problems with similar structures, although frame was manipulated between subjects. In these cases, high-NFC subjects presumably compare structurally similar risky choice problems and edit their preferences to align them.

Numeracy, a cognitive skill, and NFC, a cognitive or thinking disposition, are distinct sources of individual differences and their relationship has been studied extensively especially in the domain of risky decision-making (Liberali et al., 2012; Peters & Levin, 2008; Simon et al., 2004; Stanovich & West, 2008). For numerical decision problems such as those we analyze, they each have been found to relate to the tendency to actively (metacognitively) process and transform given information. One may understand the difference between numeracy and NFC in terms of ability and willingness to engage in metacognitive monitoring and editing of responses. Subjects who are highly numerate can easily reconcile two options that are mathematically equivalent. Subjects who are low in numeracy may need to exert more effort to perform mathematical computations, but if they are high in NFC, they may have the desire to do so (for a review, see Reyna, Nelson, Han, & Dieckmann, 2009). Finally, subjects with low NFC may appear less numerate because they are less motivated to perform mathematical computations (Bruine de Bruin, McNair, Taylor, Summers, & Strough, 2015). When framing problems are presented within-subjects, or when subjects are exposed to multiple problems with the same structure, subjects who have high numeracy or NFC are cued to directly compare two versions of the same problem (e.g., gaining $200 out of a possible $600 vs. losing $400 from an initial endowment of $600), leading them to conclude that these are equivalent.

Reward sensitivity

Our model also incorporates personality differences associated with willingness to pursue reward despite risk (e.g., Caspi et al., 1997; Zuckerman, 2007), including sensation seeking or reward-related approach (Lauriola, Panno, Levin, & Lejuez, 2014; Lejeuz et al., 2002; Reyna et al., 2011; Zuckerman, 2007; Zuckerman & Kuhlman, 2000) and factors related to cross-cultural differences (e.g., Du et al., 2002; the “cushion hypothesis” of Weber & Hsee, 1999). We represent this in our model by a linear additive risk preference, b, which, when positive, is used to indicate a predisposition toward the higher rewards available in a gamble despite the risk (gambles are typically constructed in studies so that the risky option offers more uncertain but higher rewards relative to the sure option; Romer & Hennessy, 2007; Zuckerman, 2007). The linear additive nature of this factor is based on Reyna et al. (2011) who found evidence supporting distinct additive effects (i.e., beyond verbatim and gist processing) of subjects’ sensation seeking on risk taking.

Summary of the psychological content of our model’s parameters

This model is the first to unpack the processes inside gist and verbatim representations by simultaneously mapping a stimulus to decision categories using lattice theory; to a partially-ordered ordinal representation of the stimulus using a Cartesian product of total orders; and to a linear expected value representation. This aspect of the model spells out the psychological processes that transform decision stimuli into mental representations. The model then links these representational processes with individual differences in the tendency to be an active processor of information, for example, the tendency for highly numerate people to spontaneously convert numbers (e.g., 200 people saved out of 600 affect yields 400 people died, thus attenuating the effect of any one frame) and for those high in NFC to spontaneously notice and compare different versions of the same decision problem (e.g., having seen a problem about 200 people saved, noticing that a second problem about 400 died is that same problem, just worded differently). These kinds of processes have been referred to as “cognitive reflection,” “thinking dispositions,” and “metacognitive intercession” (e.g., Amsel et al., 2008; Stanovich & West, 2008). Finally, the model integrates all of these processes with individual differences in the reward system, linking motivational with metacognitive and cognitive representational processes. Thus, the model integrates psychological processes from widely disparate literatures, showing how they combine to influence risky choices, as illustrated in Figure 2.

Figure 2.

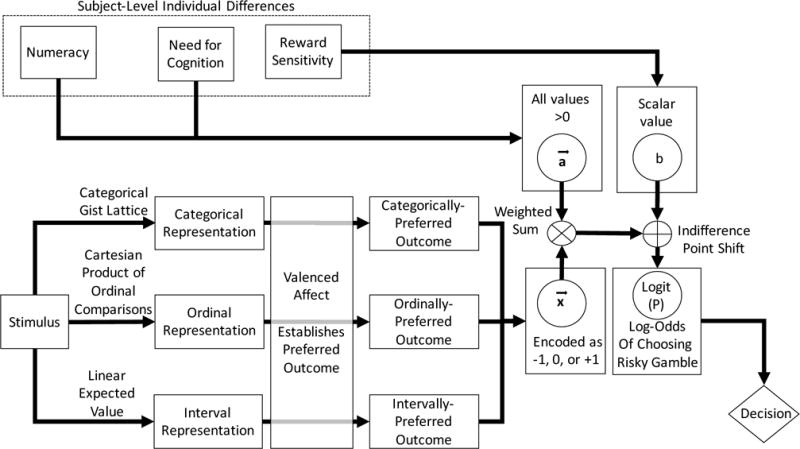
Flow diagram illustrating the specific processes by which values of $\overrightarrow{x}$, $\overrightarrow{a}$, and b are derived.

In sum, our model consists of one variable, $\overrightarrow{x}$, capturing mental representation, and two parameters, $\overrightarrow{a}$, capturing metacognitive monitoring and editing, and b, capturing reward sensitivity. These parameters summarize the interpretations of the model (for examples of evidence regarding related process assumptions, see Brainerd, Reyna, Wright, & Mojardin, 2003; Reyna, 2012), and the mechanics of how these different factors combine to account for behavior.

A worked example

Consider the decision between a certain gain of $180 versus a 0.90 chance of winning $250 and a 0.10 chance of no money discussed above. Recall that the categorical representation prefers the certain option (−1), the ordinal representation is indifferent (0), and the interval representation prefers the risky gamble (+1). Thus, $\overrightarrow{x}=[-1,0,1]$ in our model. For the sake of illustration, suppose we use prior data to estimate our sample’s metacognitive monitoring and editing parameters as $\overrightarrow{a}=[1,1,1]$ for each of the three levels of mental representation posited by our model. Therefore, $\overrightarrow{a}\cdot \overrightarrow{x}=-1+0+1=0$ (indicating that the categorical and interval representations compete). Finally, suppose we estimate our sample’s reward sensitivity from prior data to be b = 0.25, indicating a slight preference for the riskier, but more rewarding, option. Then, the probability that a randomly chosen subject from our sample will choose the risky gamble option is $P(\overrightarrow{x})=1/(1+{\mathrm{e}}^{-\mathrm{0..25}})=56\%$.

JLOO: An approach to estimating parameters

One approach to determining parameter values, that avoids overfitting, is to use a jackknife/leave-one-out technique (JLOO; e.g., Miller, 1974) to estimate the a and b parameters. This approach imposes constraints on the values that these parameters can take by ensuring that all experiments for which subjects exhibit similar values of metacognitive monitoring must have similar values of a and that all experiments for which subjects have similar values of reward sensitivity must have similar values of b.

Estimating a with JLOO

In order to determine the value of a for a given problem, we calculate the maximum likelihood estimate (MLE) of a, $\widehat{a}$, for all experiments in the same “analytic category” as the value of a that we are trying to estimate (e.g., all replications of framing problems with a single presentation for which framing is manipulated between subjects). The JLOO estimator is given by the average value of $\widehat{a}$ (weighted by the total number of subjects in each study); however, to avoid overfitting, we exclude the value of $\widehat{a}$ that is associated with the specific problem that we are trying to predict from our average (we “leave one out”). Thus, this approach never uses the data from a given experiment to test that same experiment, and is therefore a form of calibration, rather than post hoc estimation (Busemeyer & Wang, 2000). A worked example of the JLOO procedure is found in the Supplemental Material.

Choice of analytic categories for a

We have discussed how the effect of NFC varies with experimental design. In addition, numeracy has been shown to vary with nationality (Galesic & Garcia-Retamero, 2010; Garcia-Retamero & Galesic, 2009). Thus, when estimating a, we distinguish experimental design and nationality of participants. Since numeracy is mathematical literacy (Reyna et al., 2009), studies may be grouped into two categories representing participants from nations in the top and bottom halves of Program for International Student Assessment (PISA) mathematical literacy scores (Stacey, 2012). Samples with subjects from both high- and low-PISA countries (e.g., Kühberger & Tanner, 2010) make up a third category.

Estimating b with JLOO

In order to avoid overfitting, the JLOO procedure is applied to estimate values of b given analytic categories. As above, we calculate the MLE estimate of b, $\widehat{b}$, for all experiments in the same category as the value of b that we are trying to determine.

Choice of analytic categories for b

Prior work has indicated that risk-taking varies by national culture. For example, Chinese subjects tend to be more risk seeking than equivalent American and European samples when faced with financial decisions (e.g., Bontempo et al., 1997; Du, Green, & Myerson, 2002; Hsee & Weber, 1999; Weber & Hsee, 1998). In contrast, Japanese subjects are not statistically distinguishable from Americans in the domain of risk-taking (Du et al., 2002). Thus, categories are associated with nationality of participants (North American, European, and Japanese vs. Chinese). Similarly, prior training and experience, such as whether subjects were civilians or members of the military, may affect risk taking (both Haerem, Kuvaas, Bakken, & Karlsen, 2012, and Zhang, Xiao, Ma, & Miao, 2008 found that military decision makers differed significantly from civilians in attitudes towards risk). In addition, age (after adolescence) and female gender are associated with decreased sensation seeking (e.g., Romer & Hennessy, 2007; Zuckerman, Eysenck, & Eysenck, 1978), suggesting separate categories for these factors as well. Finally, reward sensitivity would be expected to influence choices more when reward magnitudes are high rather than low.

Section 4: Model Application

Below, we show how our formalization explains the outcomes of risky choice problems (e.g., Gonzalez et al., 2005), such as Tversky and Kahneman’s (1981) Asian Disease Problem (ADP), and the Allais Paradox problems (Allais, 1953). Next, we show how our model explains the results of experimental manipulations of the ADP and other framing problems, known as truncation and disambiguation problems, in which parts of gambles are deleted or added. Truncation and disambiguation problems are interesting because expected utility theory, PT (Kahneman & Tversky, 1979), and cumulative prospect theory (CPT; Tversky & Kahneman, 1992) predict that these changes would not alter outcomes, whereas experimental data indicate that decision-makers do indeed choose different outcomes than in corresponding standard framing problems. Truncation problems were initially constructed to test FTT (e.g., Reyna & Brainerd, 1991; Kühberger & Tanner, 2010; Reyna et al., 2014). Therefore, they enable us to test the extent to which our formalization captures key FTT results. Additionally, as we discuss in detail below, our model correctly predicts the outcomes of disambiguation problems (e.g., Kühberger & Tanner, 2010). Next, we test our model at the level of individual subjects, showing that parameters $\overrightarrow{a}$ and b vary in meaningful ways with individual difference factors associated with metacognitive monitoring (and editing) and reward sensitivity. Finally, we discuss our model’s predictions in light of assumptions of PT.

Validating Our Model with Theoretically Important Effects

In this section, we use our model to explain effects that are central to major theories of risky choice framing. We begin by applying our model to the standard Asian Disease Problem (ADP; Tversky and Kahneman, 1981; 1986). The ADP is one of the literature’s most widely replicated demonstrations of framing effects, providing a good test of our model across many studies. The classic framing effect is that people avoid risks when options are framed as gains, but are risk seeking when those same options are described as losses. Framing effects challenge a fundamental axiom of economic theory (that preferences are coherent across different descriptions of the same options; Kühberger 1998). Many experiments have confirmed framing effects across domains (e.g., Druckman 2001a; Druckman 2001b; Kiene, Barta, Zelenski, & Cothran, 2005; Levin, Gaeth, Schreiber, & Lauriola, 2002; Levin, Hart, Weller, & Harshman, 2007; Mahoney, Buboltz, Levin, Doverspike, & Svyantek, 2011; Miller, Fagley, & Casella, 2009). We test our model by comparing its predictions to results of experiments derived from a systematic review of the literature.

Next, we apply our model to explain the Allais Paradox problems (Allais, 1953). The Allais Paradox demonstrates a violation of another one of expected utility theory’s core assumptions, known as the independence axiom, which states that adding an independent outcome to decision options should not change decision preferences. The Allais Paradox problems demonstrate that the addition of some outcomes can lead to a preference reversal.

The Asian Disease Problem

Replications of the ADP published in peer-reviewed scientific journals were gathered from Google Scholar, using the search term “Asian Disease Problem,” for all years between 1981 and 2015. Experiments were excluded from our analysis if they did not provide sufficient information to determine the raw counts of subjects choosing each option in each framing condition, or if they deviated significantly from Tversky and Kahneman’s original (1981) protocol (e.g., by changing the numbers in the original problem, requiring that subjects provide rationales for their choices before answering, or by requiring subjects to answer in a specified time period). Studies were also excluded if they were conducted using online marketplaces such as Amazon’s Mechanical Turk (e.g., Paolacci, Chandler, & Ipeirotis, 2010; Horton, Rand & Zeckhauser, 2011; Berinsky, Huber, & Lenz, 2012) because some proportion of subjects on these platforms may be “bad workers,” who answer questions randomly (Berinsky, Margolis, & Sances, 2014). In addition, many workers in online labor markets are much more highly experienced than equivalent laboratory samples (Rand et al., 2014), who may exhibit reduced effect sizes due to prior exposure to similar framing problems. Using these criteria, we identified 27 separate experimental replications of the Asian Disease Problem for which framing was manipulated between subjects. In addition, we identified two experimental replications of the ADP and one replication of related framing problems for which framing was manipulated within subjects. We identified ten experiments for which framing was manipulated between subjects but the ADP was one of several framing problems with a similar structure answered in a random order. These different types of problems were analyzed separately, as will be described below. The text of the gain-framed standard ADP is:

Imagine that the U.S. is preparing for the outbreak of an unusual Asian disease, which is expected to kill 600 people. Two alternative programs to combat the disease have been proposed. Assume that the exact scientific estimates of the consequences of the program are as follows:

• 1If Program A is adopted, 200 people will be saved
• 2If Program B is adopted, there is a 1/3 probability that 600 people will be saved and a 2/3 probability that no people will be saved. (Tversky & Kahneman, 1981)

The loss-framed version of the problem uses the same preamble but presents the options as:

• 3If Program C is adopted 400 people will die.
• 4If Program D is adopted there is a 1/3 probability that nobody will die, and a 2/3 probability that 600 people will die. (Tversky & Kahneman, 1981)

Options 1 and 3 are typically referred to as the “certain option,” whereas options 2 and 4 are the “gamble option.” The typical result (i.e., the framing effect) is that most people prefer the certain option in the gain frame, but they prefer the risky gamble option in the loss frame.

Although the ADP was initially explained with PT (Tversky & Kahneman, 1981), subsequent tests supported a FTT-based interpretation of framing effects (e.g., Kühberger & Tanner, 2010; McElroy & Seta 2003; Reyna & Brainerd, 1991, 1995). The clearest of these tests include truncation effects (reviewed below) and removal of numerical information in whole or part from choice problems, which increases framing effects, as predicted, due to greater reliance on the simplest (categorical) gist. Other illustrations of the role of gist in framing effects include the finding that subjects are more likely to be susceptible to framing effects when they are primed with a meaningful (gist) stimulus as opposed to a “statistical” (verbatim) stimulus (Bless, Betsch, & Franzen, 1998; Igou & Bless 2007). Furthermore, FTT predicts that gist-level processing will be less common in children and adolescents and more common in older adults, consistent with empirical findings (e.g., Chien, Lin, & Worthley, 1996; Kim, Goldstein, Hasher, & Zacks, 2005; Reyna et al., 2011; Reyna & Farley, 2006). Finally, FTT predicts more gist-level processing and, hence, stronger framing effects among experts, as compared to novices, when they are faced with risky choices in their field of expertise (e.g., Christensen, Heckerling, Mackesy, Bernstein, & Elstein, 1991; Miller et al., 2009, Reyna et al., 2014).

Determining each representation’s vote

There are two types of numbers that a decision-maker is required to understand in the ADP. The first represents the number of people who are saved (or who die), and the second number represents the probability with which this outcome occurs. We represent these numbers in a 2-dimensional space, with the horizontal axis capturing outcomes (e.g., lives saved or lost), and the vertical axis capturing probability. The certain option is located at (200, 1) because there is a 100% chance that 200 people will be saved. The first (non-zero) complement of the gamble option is located at (600, 1/3) since there is a 1/3 probability that 600 people will be saved; the second (zero) complement of the gamble option is located at (0, 2/3) since there is a 2/3 probability that 0 people will be saved (Figure 3a).

Figure 3.

a) An example of a 2-dimensional decision space for the Asian Disease Problem. b) a representation of the gist categories associated with the gain frame of the standard ADP. c) Venn diagram representing overlapping gists for the Asian Disease problem. d) The lattice for the gain-framed Asian Disease Problem where there is only one subcategory {none live}.

Once this space is established, the next step is to determine which gist categories apply to the problem’s formulation. “No chance” is omitted for brevity because there are no points on the horizontal axis. Thus, only the following subcategory is used: {none saved}. In other words, an option in which no one is saved is qualitatively different than an option in which some are saved (Reyna, 2012). The resulting categories are shown in Figure 3b. Figures 3c and 3d show the associated Venn diagram and lattice, respectively. Interpretations associated with higher levels on the lattice are preferred to those on lower levels. The decision-maker therefore faces the choice shown in Table 1 corresponding to the categorical representation. Furthermore, most decision-makers value human life; thus, relevant values are retrieved from long-term memory indicating that “some lives saved is better than no lives saved.” Option 1 therefore dominates option 2. Finally, the ordinal and interval representations are indifferent between these decision options, as shown in Table 1. Thus, $\overrightarrow{x}=[-1,0,0]$ for the gain-framed ADP.

Table 1.

Categorical, Ordinal, and Interval Level Representations for Each of the 16 Effects Tested in this Paper

Effect Predicted	Problem Statement	Categorical Representation	Ordinal Representation	Interval Representation
Standard Framing Problem
Gain Frame	200 people will be saved	some chance that some are saved	more chance that fewer are saved	200 are saved
	there is a 1/3 probability that 600 people will be saved and a 2/3 probability that no people will be saved	some chance that some are saved and some chance that none are saved	less chance that more are saved and some chance that none are saved	200 are saved
Loss Frame	400 people will die	some chance that some die	more chance that fewer die	400 die
	there is a 1/3 probability that nobody will die, and a 2/3 probability that 600 people will die	some chance that some die, and some chance that none die	less chance that more die and some chance that none die	400 die
Allais Gambles
Gamble 1	1 million dollars with certainty	some money with some chance	more chance that some are saved	1 million dollars
	89% chance of 1 million dollars, 10% chance of 5 million dollars, and a 1% chance of 0 dollars	some chance of some money, some chance of some money, or some chance of no money	some chance of some money, less chance of more money, some chance of no money	1.39 million dollars
Gamble 2	1 million dollars with 11% probability and $0 with 89% probability	some chance of some money and some chance of no money	less money with a large chance, and no money with a small chance	0.11 million dollars
	5 million dollars with 10% probability and $0 with 90% probability	some chance of some money and some chance of no money	more money with a large chance, and no money with a small chance	0.50 million dollars
Zero-complement truncated framing problems
Gain Frame	200 people will be saved	some chance that some are saved	more chance that fewer are saved	200 are saved
	there is a 1/3 probability that 600 people will be saved	some chance that some are saved	less chance that more are saved	200 are saved
Loss Frame	400 people will die	some chance that some die	more chance that fewer die	400 die
	there is a 2/3 probability that 600 people will die	some chance that some die	less chance that more die	400 die
Nonzero-complement truncated framing problems
Gain Frame	200 people will be saved	some chance that some are saved	more chance that fewer are saved	200 are saved
	there is a 2/3 probability that no people will be saved	some chance that none are saved	some chance that none are saved	200 are saved
Loss Frame	400 people will die	some chance that some die	more chance that fewer die	400 die
	there is a 1/3 probability that nobody will die	some chance that none die	some chance that none die	400 die
Certain-option disambiguated problems
Gain Frame	200 people will be saved and 400 people will not be saved	some chance that some are saved and some chance that some are not saved	more chance that fewer are saved and some chance that some are not saved	200 are saved
	there is a 1/3 probability that 600 people will be saved and a 2/3 probability that no people will be saved	some chance that some are saved and some chance that none are saved	less chance that more are saved and some chance that none are saved	200 are saved
Loss Frame	400 people will die and 200 people will not die	some chance that some die and some chance that some do not die	more chance that fewer die and some chance that some do not die	400 die
	there is a 1/3 probability that nobody will die, and a 2/3 probability that 600 people will die	some chance that some die, and some chance that none die	less chance that more die and some chance that none die	400 die
“400 not saved” certain-option disambiguated and truncated problems
Gain Frame	400 people will not be saved	some chance that some are not saved	some chance that some are not saved	200 are saved
	there is a 1/3 probability that 600 people will be saved and a 2/3 probability that no people will be saved	some chance that some are saved and some chance that none are saved	less chance that more are saved and some chance that none are saved	200 are saved
	200 people will not die	some chance that some do not die	some chance that some do not die	400 die
Loss Frame	there is a 1/3 probability that nobody will die, and a 2/3 probability that 600 people will die	some chance that some die, and some chance that none die	less chance that more die and some chance that none die	400 die
Certain-option disambiguated, zero-complement truncated problems
Gain Frame	200 people will be saved and 400 people will not be saved	some chance that some are saved and some chance that some are not saved	more chance that fewer are saved and some chance that some are not saved	200 are saved
	there is a 1/3 probability that 600 people will be saved	some chance that some are saved	less chance that more are saved	200 are saved
Loss Frame	400 people will die and 200 people will not die	some chance that some die and some chance that some do not die	more chance that fewer die and some chance that some do not die	400 die
	there is a 2/3 probability that 600 people will die	some chance that some die	less chance that more die	400 die
“400 not saved vs. 2/3 chance that 600 not saved” truncation problem
Gain Frame	400 people will not be saved	some chance that some are not saved	more chance that fewer are not saved	200 are saved
	there is a 2/3 probability that 600 people will not be saved	some chance that some are not saved	less chance that more are not saved	200 are saved
Loss Frame	200 people will not die	some chance that some do not die	more chance that fewer do not die	400 die
	there is a 1/3 probability that 600 people will not die	some chance that some do not die	less chance that more do not die	400 die

Note. Text in bold indicates a given representation’s preferred option. If no option is bolded, the corresponding representation is indifferent. The overall preferred outcome is indicated in bold and, if the preference is strong (preferred by more than one mental representation), it is also underlined.

Similar logic applies to the loss framing of the ADP, where option 4 (the gamble) dominates option 3 (the certain option), prompting the decision-maker to choose the gamble. This produces the framing effect typically found in the standard ADP (e.g., Kühberger & Tanner, 2010; Reyna, 2012). Thus, $\overrightarrow{x}=[1,0,0]$ for the standard loss-framed ADP.

Comparison with experimental data

Rearranging terms, our model is $\mathit{\text{logit}}(P)=\overrightarrow{a}\cdot \overrightarrow{x}+b$, where, in the ADP, P is the probability that a given experimental subject will choose the risky gamble. Our model makes specific predictions regarding the values of $\overrightarrow{x}$ – specifically, ${\overrightarrow{x}}_{\mathit{\text{gain}}}=[-1,0,0]$ in the gain frame and ${\overrightarrow{x}}_{\mathit{\text{loss}}}=[1,0,0]$ in the loss frame. Given our prior assumption that $\overrightarrow{a}=[a,a,a]$, and if P_gain is the probability of choosing the risky gamble in the gain frame and P_loss is the corresponding probability in the loss frame, then

$$\text{logit}(P_{\mathit{\text{gain}}})-\text{logit}(P_{\mathit{\text{loss}}})=2a$$ (2)

for the ADP, a quantity that does not require estimating b. Furthermore, the difference of two logit quantities is interpretable as a log-odds ratio,

$$\text{logit}(P_{\mathit{\text{gain}}})-\text{logit}(P_{\mathit{\text{loss}}})=\text{ln}\left(\frac{P_{\mathit{\text{gain}}}(1-P_{\mathit{\text{loss}}})}{P_{\mathit{\text{loss}}}(1-P_{\mathit{\text{gain}}})}\right).$$ (3)

The standard error for an odds ratio is given by,

$$SE=\sqrt{\frac{1}{n_{\mathit{\text{certain,gain}}}}+\frac{1}{n_{\mathit{\text{certain,loss}}}}+\frac{1}{n_{\mathit{\text{gamble,gain}}}}+\frac{1}{n_{\mathit{\text{gamble,loss}}}}}$$ (4)

where n_certain,gain is the number of subjects choosing the certain option in the gain frame, n_risky,loss is the number of subjects choosing the risky gamble in the loss frame, and so on. For sufficiently large n, this standard error asymptotically approaches a normal distribution. Equivalently, the associated Wald statistic, ${\left(\frac{\mathit{\text{logit}}({\widehat{P}}_{\mathit{\text{gain}}})-\mathit{\text{logit}}({\widehat{P}}_{\mathit{\text{loss}}})-2a}{SE}\right)}^2$ follows a chi-square distribution with one degree of freedom, where ${\widehat{P}}_{\mathit{\text{gain}}}$ and ${\widehat{P}}_{\mathit{\text{loss}}}$ are the empirical probabilities with which a given experimental sample chooses the risky gamble in the gain and loss frames, respectively (i.e., their maximum likelihood estimates, MLE). Thus, given a value for a, we may use the Wald statistic to test the goodness-of-fit of our model.

ADP with framing manipulated between-subjects

The a parameter was estimated using the JLOO procedure, where the MLE value of a is given by $\widehat{a}=\frac{\mathit{\text{logit}}({\widehat{P}}_{\mathit{\text{gain}}})-\mathit{\text{logit}}({\widehat{P}}_{\mathit{\text{loss}}})}{2\sum \overrightarrow{x}}$ and where $\sum \overrightarrow{x}$ is the sum of all of the elements in the $\overrightarrow{x}$ vector (−1 for the gain frame and 1 for the loss frame). Using this approach, our model’s predicted log-odds ratios differed from those reported for only one (4%) out of 27 experimental replications of the ADP in which framing was manipulated between-subjects (Table 2). The outlier, Tversky and Kahneman’s (1981) test of the ADP, is known to have a larger effect (Kühberger, 1998). Consistent with expected differences in numeracy, we found that â values differed for samples from low-PISA countries when compared to high-PISA samples in experiments for which framing was manipulated between subjects, and in which subjects were exposed to a single framing problem, t(30) = 2.06, p = 0.048. Samples from low-PISA countries had higher values of â, indicating stronger framing effects.

Table 2.

88 Sampled Experimental Replications of Decisions Under Risk and Our Model’s Predictions

Reference	1st Choice		2nd Choice		Log-Odds Ratio		SE	χ2
	n	$\widehat{P}(\%)$	n	$\widehat{P}(\%)$	Actual	Predicted
Standard ADP; one presentation, between-subjects, low PISA, $\overrightarrow{x}=[\pm 1,0,0]$
Tversky & Kahneman, 1981	152	28	155	78	2.20	1.65	0.26	4.34*
Reyna & Brainerd 1991	36	53	36	81	1.31	1.72	0.54	0.57
Tindale, Sheffey, Scott 1993	144	42	144	79	1.63	1.71	0.26	0.10
Wang & Johnston, 1995	50	40	50	68	1.16	1.73	0.42	1.83
Highhouse & Yuce, 1996	122	29	122	74	1.94	1.68	0.29	0.82
Wang, 1996	31	42	34	77	1.50	1.71	0.54	0.14
Stanovich & West, 1998	148	32	144	65	1.37	1.74	0.25	2.34
Druckman, 2001a	50	32	55	77	1.93	1.70	0.44	0.27
Druckman, 2001b	69	32	79	76	1.91	1.70	0.37	0.34
Mayhorn, Fisk, & Whittle, 2002 (young adults)	29	24	29	86	2.98	1.68	0.69	3.52
Mayhorn, Fisk, & Whittle, 2002 (older adults)	29	21	29	69	2.14	1.70	0.61	0.53
LeBoeuf & Shafir, 2003 #1, no justification required condition	48	49	55	56	1.40	1.74	0.25	1.77
LeBoeuf & Shafir, 2003 #2	147	25	146	57	1.47	1.71	0.43	0.32
Stein, 2012	47	40	57	68	1.16	1.73	0.41	1.89
TOTAL of 14 predicted							13 (93%)
Standard ADP; one presentation, between-subjects, high PISA, $\overrightarrow{x}=[\pm 1,0,0]$
Takemura, 1994	45	20	45	69	2.18	1.39	0.49	2.56
Mandel, 2001	26	54	26	85	1.55	1.44	0.67	0.03
Fischer, Jonas, Frey, & Kastenmüller, 2008	17	36	17	77	1.78	1.43	0.76	0.21
Zhang & Miao, 2008 #1	65	66	68	87	1.21	1.47	0.44	0.34
Zhang & Miao, 2008 #2	45	67	48	88	1.25	1.46	0.54	0.14
Zhang, Xiao, Ma, & Miao, 2008, military	134	54	130	83	1.44	1.44	0.29	0.00
Zhang, Xiao, Ma, & Miao, 2008, civilian	60	65	58	90	1.54	1.43	0.51	0.04
Haerem, Kuvaas, Bakken, & Karlsen, 2011	29	59	26	73	0.65	1.48	0.58	2.02
Okder, 2012	52	37	53	76	1.68	1.42	0.43	0.34
Kühberger & Gradl, 2013, Experiment #1	63	32	63	68	1.53	1.43	0.38	0.06
Kühberger & Gradl, 2013, Experiment #2	14	57	15	73	0.72	1.46	0.80	0.85
Mandel, 2014, Experiment #2	38	42	38	74	1.35	1.45	0.49	0.04
Mandel, 2014, Experiment #3	25	32	25	80	2.14	1.42	0.66	1.20
TOTAL of 13 predicted							13 (100%)
Standard ADP; within-subjects, low PISA, $\overrightarrow{x}=[\pm 1,0,0]$
Stanovich & West, 1998	292	32	292	54	0.9	0.94	0.24	1.58
Levin, Gaeth, Schrieber, & Lauriola, 2002 (other framing problems)	102	28	102	56	1.2	0.92	0.30	0.94
LeBoeuf & Shafir, 2003 Experiment #2	287	25	287	46	0.57	1.05	0.17	7.86*
TOTAL of 3 predicted							2 (67%)
Standard ADP; multiple presentations, between-subjects, low PISA, $\overrightarrow{x}=[\pm 1,0,0]$
Fagley & Miller, 1990, experiment #1	94	51	96	70	0.79	0.95	0.30	0.27
Fagley & Miller, 1990, experiment #2	54	39	55	73	1.43	0.92	0.41	1.55
Miller & Fagley, 1991	23	43	23	67	0.89	0.94	0.61	0.01
Jou, Shanteau, & Harris, 1996	80	35	80	80	2.01	0.87	0.36	9.66*
Rönnlund, Karlsson, Laggnäs, Larsson, & Lindström, 2005, younger adults	32	41	32	69	1.19	0.93	0.53	0.23
Rönnlund, Karlsson, Laggnäs, Larsson, & Lindström, 2005, older adults	32	28	32	56	1.17	0.94	0.52	0.20
TOTAL of 6 predicted							5 (83%)
Standard ADP; multiple presentations, between-subjects, low PISA, $\overrightarrow{x}=[\pm 1,0,0]$
Kühberger, 1995, Experiment #1	25	48	23	78	1.36	0.73	0.64	1.31
Kühberger, 1995, Experiment #2	16	56	14	57	0.04	0.81	0.74	0.81
Druckman & McDermott, 2008	101	45	113	67	0.94	0.71	0.28	1.84
TOTAL of 3 predicted							3 (100%)
Allais Paradox gambles; low PISA, $\overrightarrow{x}=[-1,0,1]$ for first gamble and [1,1,0] for second gamble
Conlisk, 1989	236	49	236	86	1.83	1.68	0.23	0.44
Carlin, 1990	65	40	65	78	1.7	1.71	0.39	0
TOTAL of 2 predicted							2 (100%)
Allais Paradox gambles; low PISA, $\overrightarrow{x}=[-1,0,1]$ for first gamble and [1,1,0] for second gamble
Huck & Müller, 2012, laboratory	70	66	70	87	1.26	1.73	0.44	1.14
TOTAL of 1 predicted							1 (100%)
Other framing problems; multiple presentations, between-subjects, low PISA, $\overrightarrow{x}=[\pm 1,0,0]$
Reyna et al., 2014, College students	63	35	63	55	0.85	0.95	0.37	0.02
Reyna et al., 2014, Adults	54	40	54	60	0.8	0.95	0.39	0.01
Reyna et al., 2014, Experts	36	38	36	71	1.37	0.93	0.5	0.18
TOTAL of 3 predicted							3 (100%)
Other framing problems; multiple presentations, between-subjects, high PISA, $\overrightarrow{x}=[\pm 1,0,0]$
Kühberger, 1995, Plant Problem #1	25	52	23	83	1.48	0.73	0.68	1.61
Kühberger, 1995, Cancer Problem #1	24	38	25	48	0.43	0.8	0.58	0.2
Kühberger, 1995, Plant Problem #2	16	19	17	71	2.34	0.7	0.83	4.43*
Kühberger, 1995, Cancer Problem #2	16	69	14	64	−0.2	0.82	0.78	1.39
TOTAL of 4 predicted							3 (75%)
Other framing problems; multiple presentations, between-subjects, mixed PISA, $\overrightarrow{x}=[\pm 1,0,0]$
Kühberger & Tanner, 2010, Drinking Water Contamination	93	33	93	73	1.69	1.27	0.32	1.78
Kühberger & Tanner, 2010, Genetically engineered crops	93	33	93	59	1.06	1.36	0.3	0.92
Kühberger & Tanner, 2010, Fish kidney disease	93	28	93	59	1.32	1.32	0.31	0
Kühberger & Tanner, 2010, Endangered forest	93	24	93	55	1.37	1.31	0.32	0.03
TOTAL of 4 predicted							4 (100%)
Zero-complement truncated framing problems, one presentation; framing manipulated between-subjects, $\overrightarrow{x}=[0,0,0]$
Reyna & Brainerd, 1991	35	51	36	58	0.28	0	0.48	0.34
Mandel, 2001, #1	23	48	25	72	1.03	0	0.61	2.86
Mandel, 2001, #2	36	64	38	63	−0.03	0	0.48	0
TOTAL of 3 predicted							3 (100%)
Zero-complement truncated framing problems; multiple presentations, framing manipulated between-subjects, $\overrightarrow{x}=[0,0,0]$
Kühberger & Tanner, 2010, Drinking Water Contamination	93	54	93	65	0.45	0	0.3	2.21
Kühberger & Tanner, 2010, Genetically engineered crops	93	54	93	43	−0.43	0	0.3	2.14
Kühberger & Tanner, 2010, Fish kidney disease	93	63	93	43	−0.83	0	0.3	7.68*
Kühberger & Tanner, 2010, Endangered forest	93	40	93	43	0.13	0	0.3	0.2
Reyna et al., 2014, College students	63	43	63	49	0.25	0	0.36	0.47
Reyna et al., 2014, Adults	54	51	54	55	0.18	0	0.39	0.23
Reyna et al., 2014, Experts	36	52	36	62	0.41	0	0.48	0.74
TOTAL of 7 predicted							6 (86%)
Nonzero-complement truncated framing problems; one presentation, between-subjects, low PISA, $\overrightarrow{x}=[1,1,0]$
Reyna & Brainerd, 1991	35	26	37	81	2.52	3.44	0.57	2.59
TOTAL of 1 predicted							1 (100%)
Nonzero-complement truncated framing problems; multiple presentations, between-subjects, low PISA, $\overrightarrow{x}=[1,1,0]$
Reyna et al., 2014, College students	63	23	63	60	1.61	1.9	0.4	0.51
Reyna et al., 2014, Adults	54	26	54	73	2.05	1.87	0.44	0.15
Reyna et al., 2014, Experts	36	20	36	81	2.84	1.85	0.59	2.72
TOTAL of 3 predicted							3 (100%)
Nonzero-complement truncated framing problems; one presentation, between-subjects, low PISA, $\overrightarrow{x}=[1,1,0]$
Kühberger & Tanner, 2010, Drinking Water Contamination	93	25	93	85	2.84	2.61	0.38	0.39
Kühberger & Tanner, 2010, Genetically engineered crops	93	29	93	78	2.19	2.7	0.34	2.28
Kühberger & Tanner, 2010, Fish kidney disease	93	22	93	83	2.87	2.61	0.37	0.49
Kühberger & Tanner, 2010, Endangered forest	93	15	93	65	2.33	2.68	0.36	0.96
TOTAL of 4 predicted							4 (100%)
Certain-option disambiguated problems; single presentation, between-subjects, $\overrightarrow{x}=[0,0,0]$
Mandel, 2001, #1	23	52	22	50	−0.09	0	0.6	0.02
Mandel, 2014, #3	22	41	24	50	0.37	0	0.6	0.38
TOTAL of 2 predicted							2 (100%)
Certain-option disambiguated problems; multiple presentations, between-subjects, $\overrightarrow{x}=[0,0,0]$
Kühberger, 1995, Asian Disease Problem #1	26	62	23	57	−0.21 0	0	0.58	0.13
Kühberger, 1995, Plant Problem #1	26	46	23	52	0.24 0	0	0.57	0.18
Kühberger, 1995, Cancer Problem #1	24	50	23	35	−0.63	0	0.6	1.1
Kühberger, 1995, Asian Disease Problem #2	22	41	19	37	−0.17	0	0.64	0.07
Kühberger, 1995, Plant Problem #2	13	31	19	37	0.27	0	0.77	0.13
Kühberger, 1995, Cancer Problem #2	7	71	13	62	−0.45	0	1.01	0.19
TOTAL of 6 predicted							6 (100%)
“400 not saved” certain-option disambiguated and truncated problems; multiple presentations, between-subjects, high PISA, $\overrightarrow{x}=[\mp 1,0,0]$
Kühberger, 1995, Asian Disease Problem #1	25	60	23	43	−0.67	−0.79	0.59	0.04
Kühberger, 1995, Plant Problem #1	27	44	23	57	0.49	−0.88	0.57	5.68*
Kühberger, 1995, Cancer Problem #1	24	75	23	43	−1.36	−0.74	0.63	0.98
Kühberger, 1995, Asian Disease Problem #2	16	50	19	37	−0.54	−0.79	0.69	0.13
Kühberger, 1995, Plant Problem #2	14	57	14	50	−0.29	−0.8	0.76	0.45
Kühberger, 1995, Cancer Problem #2	14	50	16	44	−0.25	−0.8	0.73	0.56
TOTAL of 6 predicted							5 (83%)
Certain-option disambiguated, zero-complement truncated problems; single presentation, between-subjects, high PISA, $\overrightarrow{x}=[\mp 1,0,0]$
Mandel, 2014, Experiment #3	26	58	25	32	−1.06	−1.46	0.58	0.45
TOTAL of 1 predicted							1 (100%)
“400 not saved vs. 2/3 chance that 600 not saved” truncation problem; single presentation, framing manipulated between-subjects, $\overrightarrow{x}=[0,0,0]$
Mandel, 2001, #1	23	57	24	58	0.07	0	0.59	0.02
Mandel, 2001, #2	36	64	37	59	−0.19	0	0.48	0.15
TOTAL of 2 predicted							2 (100%)
TOTAL of 88 predicted							82 (93%)

Note.

^*= p < 0.05, $\widehat{P}$ = Proportion of subjects selecting the riskier option; SE = Standard Error. Actual Log-Odds Ratio is given by $\mathit{\text{logit}}\left({\widehat{P}}_2\right)-\mathit{\text{logit}}\left({\widehat{P}}_1\right)$ and the Predicted Log-Odds Ratio is given by $2{\widehat{a}}_{-i}{\displaystyle \sum \overrightarrow{x}}$ where ${\widehat{a}}_{-i}$ is the JLOO estimate of the a parameter; 1^st (2^nd) Choice is the certain (risky gamble) option in framing problems and the first (second) gamble in the Allais gambles; ADP = Asian Disease Problem; low (high) PISA = study conducted in nation scoring below (above) the median mathematics score in the OECD Programme for International Assessment; mixed PISA = study conducted on an international sample combining subjects from across OECD PISA scores; between-subjects = framing manipulated between subjects; within-subjects = framing manipulated within subjects; χ² is the Wald statistic comparing our model’s predictions to the actual data, given by ${\left(\frac{\mathit{\text{logit}}\left({\widehat{P}}_{\mathit{\text{gain}}}\right)-\mathit{\text{logit}}\left({\widehat{P}}_{\mathit{\text{loss}}}\right)-2{\widehat{a}}_{-i}}{SE}\right)}^2$, which is distributed according to a chi-square distribution with one degree of freedom.

Framing problems with metacognitive monitoring and editing

Next, we examined three problems in which framing was manipulated within-subjects. JLOO estimates of $\widehat{a}$ enable us to correctly predict two of the associated three experimental effects (reported in Table 2; two of these were replications of the ADP). The small number of replications is due to the absence of raw frequency count data reported in many within-subjects framing studies. We also included the “cholesterol problem,” which has an ADP-like structure, but a different description, reported by Levin, Gaeth, Schrieber, and Lauriola, 2002, in order to test how our model generalizes to other within-subjects framing problems, which our model correctly predicted. Overall, within-subjects framing problems had significantly smaller $\widehat{a}$ values (i.e., they elicited larger effects of individual differences) when compared to problems manipulating framing between subjects with similar PISA scores, t(15) = 2.84, p = 0.01.

Finally, we examined nine ADP replications in which subjects answered several framing problems with the same structure, but frame was manipulated between-subjects. Using JLOO estimates of $\widehat{a}$ for these problems, results differed significantly from model predictions in one out of nine replications (11%; reported in Table 2). These problems have significantly smaller $\widehat{a}$ values than the experiments for which subjects answered only one question: t(18) = 3.83, p = 0.001 for low PISA scores and t(14) = 2.18, p = 0.047 for high PISA scores. In contrast, these experiments did not yield significantly different $\widehat{a}$ values when compared to within-subjects framing problems: t(7) = 1.37, p = 0.21 for low PISA scores (there are no within-subjects framing problems in our sample from nations with high PISA scores). As noted by Kahneman and Frederick (2002), the similar structure of repeated problems leads some subjects to compare problems, in a manner similar to within-subjects framing. Following Kahneman and Frederick (2002), we therefore consider within-subjects framing problems and problems with multiple presentations as representative of a common class of problems in which metacognitive monitoring is more likely to be engaged. In the case of subjects exposed to multiple framing problems, samples from low-PISA countries once again had higher $\widehat{a}$ values when compared to samples from high-PISA countries, t(23) = 2.35, p = 0.03. There were no within-subjects replications with subjects from high-PISA countries (our results for low-PISA countries do not change when within-subjects replications are combined with between-subjects problems in which subjects were exposed to multiple framing problems, t(26) = 2.32. p = 0.03).

Discussion

Using the JLOO estimates of these parameters, our model matches the data for 36 of 39 eligible experiments (92%; see all sections marked as “Standard ADP” in Table 2). Our model does not just estimate these effects, but is also able to explain choices in terms of central constructs, such as levels of representation. These experiments, and the associated effects, demonstrate that our model is capable of accounting for theoretically important results in the decision-making literature.

The Allais Paradox gambles: When gist and verbatim compete

In this section, we report our model’s results for the Allais Paradox problems, which are also pivotal for theory. The options offered subjects in the first Allais Paradox problem, and their associated categorical, ordinal, and interval representations, are shown in Table 1 (translated from French; Allais, 1953). The subcategory associated with this problem is: {No money}. The resulting space and categories are similar to Figures 3a and 3b and the associated lattice is similar to Figure 3d.

The first Allais gamble

Most decision makers value some money over no money. The categorical level of representation thus prefers choosing option 1 in the first Allais gamble (this is also the outcome predicted by Allais, 1953, although no data are provided). In contrast, option 2 has the higher expected value (the expected value of option 1 is 1 million dollars, whereas that of option 2 is 1.39 million dollars) and the ordinal representation is indifferent. According to our theory, the gist and verbatim representations will compete, i.e., $\overrightarrow{x}=[-1,0,1]$. Thus, our prediction differs from Allais’ (1953), who claimed that the certain option 1 would be clearly preferred. Our predictions for the Allais paradox turn on a categorical representation of money. At the simplest gist level, 1 million dollars and 5 million dollars are in the same category: “some” money. One might object that a subjective value of a difference of 4 million dollars is larger than zero. According to FTT, decision-makers encode the numbers as different, but simultaneously also interpret both of these numbers as “some.” These gist and verbatim representations are encoded in parallel and compete if they identify different preferences.

The second Allais gamble

The second Allais decision problem, and corresponding interpretations, are also shown in Table 1. Here, the category set contains the subcategory {No $}. This yields a lattice similar to that shown in Figure 3d. This problem is indeterminate at the categorical level: both options are interpreted as “Some money with some chance and no money with some chance.” At the ordinal level, the very close probability values of 10% and 11% are assigned similar meaning as are their complements, 90% and 89% (Leland, 1994; Stevens, 2016; Reyna, 2012). Thus, the ordinal representation boils down to a decision between “less money” and “more money,” favoring option 4. Option 4 also has a higher expected value. In total, our model predicts a strong preference for option 4: $\overrightarrow{x}=[0,1,1]$.

When testing our model, we included only studies with problems that replicate Allais’ initial numbers. We identified three such studies, shown in Table 2. (Some studies, such as by Kahneman & Tversky, 1979, used smaller numbers that are closer in expected value, which does not provide as strong a test of our model). As with the ADP, we excluded studies that used online samples who repeatedly answered similar surveys (e.g., Huck & Müller’s 2012 online panel). Our model did not differ from the data in any of the three cases.

Discussion

Using the JLOO estimates of these parameters, our model explains all three of the eligible experiments (100%). These results extend our model to predict choices between gambles (instead of just a certain option and a gamble) and problems with unequal expected values, providing a fit to the Allais Paradox problem data.

Explaining Truncation and Disambiguation Problems

The concept of gist representations is central to our theory of how decision-makers perceive options. Manipulations of these gists can result in larger framing effects, reversal of framing effects, or the absence of effects altogether. In this section, we use our model to explain the outcomes of several manipulations (including manipulations of the ADP but also other problems) reported in the literature on risky choice framing. Specifically, by emphasizing or removing certain parts of a problem in such a way that its expected value does not change, one can still change the gist of a decision option. For example, one might remove redundant parts of the gamble that mention a zero outcome (i.e., deleting 2/3 probability of saving no one in the ADP), leaving the 1/3 probability of saving 600 people (and similarly for the loss problem). PT and its successor, CPT, predict that these manipulations do not change choices. Thus, these “truncation” experiments were initially performed as critical tests of such theories and of FTT by Reyna and Brainerd (1991) and later replicated by others (e.g., Kühberger & Tanner, 2010; Reyna et al., 2014). As predicted by FTT, all of these investigators determined that framing effects did not persist when the zero-complement in the gamble option (e.g., 2/3 probability of saving no one) was removed (a selective attention effect; Reyna, 2008; Reyna & Brainerd, 1995). Conversely, also as predicted, focusing attention on the zero-complement in the gamble option, and deleting the non-zero complement, augments framing effects. These effects do not depend on ambiguity; they persist when all of the truncated information is supplied in the preamble (but attention is focused selectively). Also, subjects who are later tested for truncated information are aware of it, arguing against an ambiguity explanation for truncation effects (Chick, Reyna, & Corbin, 2015).

For each manipulation (e.g., truncation), we tested our model by comparing its predictions against all of the identified experimental replications of framing problems, including the ADP and others, derived from a systematic search of the literature on risky choice framing. Experiments were included in this analysis if they tested both risky choice framing problems and the truncation and disambiguation manipulations of those problems. Our model successfully predicts the outcomes of 10 (91%) out of 11 standard risky-choice framing problems in our sample (“Other risky-choice framing problems” in Table 2). Effects of truncation and disambiguation are discussed below.

Zero-complement truncated framing problems

Framing problems in which the zero-complement is truncated (the outcome of this complement is zero, e.g., “2/3 probability that no people will be saved,” shown in Table 1) form the primary critical test of FTT, PT and CPT. This version of the ADP has the same expected value as the standard ADP (Kühberger, 1995). In this formulation of our problem, none of the points in our space lies on the “none saved with some chance” line (or any other subcategory), and the associated lattice has only one node and no links – i.e., every point is interpreted as part of the same category. Both options have the same categorical representation, and the ordinal representation is indifferent because the it falls into the part of the product order that is undefined due to the conflicting less/more amounts. The more precise interval representation is also indifferent because both options have the same expected value – i.e., $\overrightarrow{x}=[0,0,0]$ – resulting in the absence of a framing effect as reported by Reyna and Brainerd (see discussion in 2011) and others. The loss-framed version of the problem yields similar results (400 die vs. 600 die with 2/3 probability). Table 2 shows that, consistent with our model’s prediction, 9 (90%) of 10 experimental replications found no framing effects in the zero-truncated problem.

Nonzero-complement truncated framing problems

The opposite truncation effect, which retains the zero complement, yields a framing effect that is stronger than that found in the standard ADP. Here, the contributions of the categorical and the ordinal representations, both of which support the certain option are combined – i.e., $\overrightarrow{x}=[-1,-1,0]$ in the gain frame, as described in Table 1. Like the standard ADP, the subcategory {none saved} applies. The associated lattice is identical to that shown in Figure 3d because this truncation problem includes the gist “none are saved.” Recall that, in our theory, even though the zero complement does not contain the words “nobody will be saved,” the numerical value of 0 has the same effect. That is, the verbatim elements of “nobody” and “0” differ, but both convey the gist of the stark difference between “nothing” and “not nothing” (i.e., something). Similar principles apply to the loss frame. We correctly predict all eight replications (100%) using the JLOO estimator (Table 2).

Certain-option disambiguated problems

Disambiguated problems, and their truncated variants, occur when the certain decision option is presented along with its logical complement. Kühberger and Tanner (2010) use the terminology “completely described frames” to describe these problems because they argue that standard framing problems are ambiguous. Although we call these problems “disambiguated,” we contend that the standard framing problems’ certain option is not incompletely described; rather, the subject’s attention is selectively focused on what is explicitly presented in the problem’s formulation. For example, the certain option in a certain-option disambiguated, gain-framed ADP might read, “200 saved and 400 are not saved” instead of the standard “200 saved.” Linguistically, this is a gain-frame problem; psychologically, positive and negative outcomes are combined. Thus, we translate the positive and negative valences exactly as we did earlier for positive and negative outcomes. This leads to an “on the one hand…on the other hand” type of effect (i.e., the decision-maker perceives a simultaneous gain and loss), as will be shown below. Our mathematical model explains the outcomes reported for “certain-option disambiguated problems,” shown in Table 1, which have not been modeled by previous theories such as PT and CPT.

The space for this problem differs from that for the standard ADP – “not saved” is a possible outcome that is interpreted as a loss. We model this by extending the “saved” axis into the negative numbers. “Saved” and “not saved” are disjoint categories in the decision space, separated by the category “none saved,” i.e., the origin (see Figure 4), consistent with the interpretation of Kahneman and Tversky (1979), who understood the value functions for gains and losses to be interpreted separately and yet meet at the origin.

Figure 4.

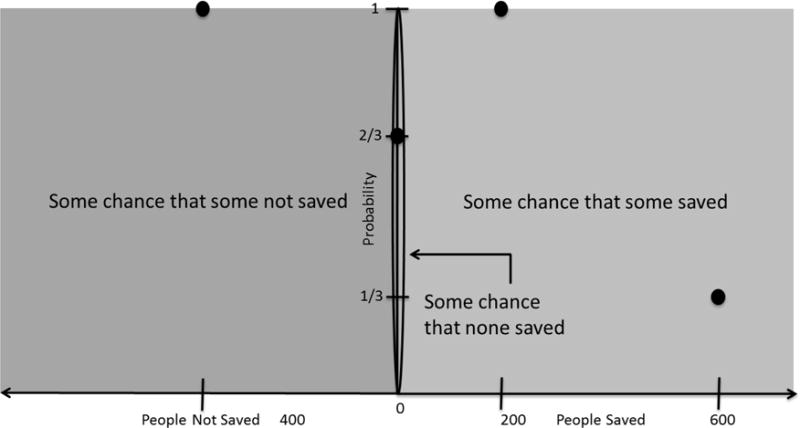
A representation of the gist categories associated with the certain-option disambiguated gain-framed ADP.

Here, the category set is {none saved}. “None saved” is not equivalent to “all are not saved.” Instead, it connotes the absence of a gain (but also no loss). Neither is it explicit that “some saved” implies that “some are not saved.” These statements, although implied pragmatically, are interpreted separately – the first in the domain of gains, and the second in the domain of losses. Since saved and not saved are both components on the same axis, we represent them on the same lattice structure for brevity. The associated regularity lattice is therefore similar to that found in Figure 3d.

Table 1 shows the options preferred by each representation. Note that the ordinal representation is indifferent because of the comparison across two disjoint categories – elements in “some not saved” and “some saved” cannot be directly compared at the ordinal level because there is no category of which they are both members. This is a subtle point. Points within “none saved” and points within “some saved” may be compared at the ordinal level because “none saved” is a subset of “some saved,” and points within “none saved” still exist within “some saved.” In contrast, points within “some not saved” and “some saved” are entirely distinct and therefore cannot be considered comparable except at the categorical level. Results did not differ significantly from our model, which predicts no framing effect – i.e., $\overrightarrow{x}=[0,0,0]$. The same applies to the loss-framed version of this problem (pivoting on some die vs. some do not die). We correctly predicted all eight replications of this problem (Table 2).

“400 not saved” certain-option disambiguated and truncated problems

We next address a truncated version of the certain-option disambiguated problems that can be explained using similar logic, shown in Table 1. As above, “not saved” (a loss) is a possible outcome. We henceforth refer to this problem as the “‘400 not saved’ certain-option disambiguated and truncated problem.” Our space is the same as that shown in Figure 4 only the point at (200,1) is not present. Here, the category set contains {none saved}, similar to the lattice shown in Figure 3d. Some saved (a gain) is better than both none saved (neither gain nor loss) and some are not saved (a loss), and the ordinal and interval representations are indifferent: $\overrightarrow{x}=[1,0,0]$ in the gain frame. This leads to a reversal of the classic framing effect consistent with Kühberger’s (1995) findings and our model’s predictions. The loss frame yields similar results. We correctly predict five of six (83%) replications of these problems reported in the literature (Table 2).

Certain-option disambiguated, zero-complement truncated problems

This type of problem has a disambiguated gain-framed certain option and a zero-truncated gamble option shown in Table 1. Our space is similar to that shown in Figure 4 only with no point at (0, 2/3). In this framing of the problem, the category set is empty and $\overrightarrow{x}=[1,0,0]$ in the gain frame. Table 2 shows no significant difference between our model and the one replication of the certain-option disambiguated, zero-complement truncated problem in our sample.

“400 not saved vs. 2/3 chance that 600 not saved” truncation problem

In this problem, shown in Table 1, both the certain and gamble options contain the phrase “not saved” instead of “saved”. Our space is similar to that shown in Figure 4 only with points at (−400,1) and (−600, 2/3) and $\overrightarrow{x}=[0,0,0]$. We correctly predict both replications of this problem (Table 2).

Discussion

Using the JLOO estimates of these parameters, our model explains 43 of 46 eligible experiments (93%; Table 2). Our model does not just estimate these effects, but is also able to explain choices in terms of central constructs, such as levels of representation. This set of results demonstrates that our model provides a formal framework to explain a variety of effects in the decision-making literature, predicting novel effects that have not been formally evaluated in the past. Over these manipulations, our model differed significantly from results for only six (7%) out of 88 different experiments. Overall, we predicted 16 variations of experimental effects within one mathematical framework by formalizing and extending the three major tenets of FTT – the gist vs. verbatim distinction, the hierarchy of gist and associated extended fuzzy-processing preference, and value-based decision-making. These effects are listed in Table 1.

Estimating Reward Sensitivity

Thus far, we have been able to predict differences between pairs of conditions in risky choice problems, such as differences between gains and losses in framing problems. However, it is desirable to predict exact numbers of subjects who might choose a given option for individual conditions. Such predictions require the use of the risk-taking parameter, b, that, until now we have not used. In this section, we compare values of b to known sources of variance in sensitivity to reward-despite-risk, and use the JLOO technique to estimate values of b to further test our model. To begin, we estimated the MLE values of the risk parameter, b, for each of the experiments in our sample. For framing problems, the MLE of b is given by

$$\widehat{b}=\frac{\mathit{\text{logit}}({\widehat{P}}_{\mathit{\text{gain}}})+\mathit{\text{logit}}({\widehat{P}}_{\mathit{\text{loss}}})}{2}$$ (5)

For the Allais gambles, in which gist and verbatim representations compete, $\mathit{\text{logit}}\left({\widehat{P}}_{\mathit{\text{gamble}}1}\right)=\left(\widehat{a}+0-\widehat{a}\right)+\widehat{b}=\widehat{b}$. Thus, our model predicts that the outcome of the first Allais gamble is a function of individual differences in reward sensitivity. Expected value predicts choice of the risky gamble. Our theory predicts indifference (modulated by individuals’ reward sensitivity) because of a competition between gist and verbatim representations.

Prior research has indicated that preferences for reward-despite-risk may vary systematically with national culture. Thus, for each ADP civilian undergraduate sample replication (and associated variants) we compared $\widehat{b}$ to the value of Hofstede’s Uncertainty Avoidance Index (UAI; Hofstede, 2001), the degree to which the members of a society feel uncomfortable with uncertainty and ambiguity that has been linked to seeking reward despite risk (Hofstede, 1985; Li, Griffin, Yue, & Zhao, 2013), corresponding to the country in which the study was conducted. Thus, we expect UAI to be associated with reward sensitivity (see also Bontempo, Bottom, & Weber, 1997). We found that $\widehat{b}$ was significantly negatively correlated with UAI, r(36) = −0.40, p = 0.01. Consistent with Du et al. (2002), our data also show that Chinese samples have higher $\widehat{b}$ values, indicating more risk taking behavior when faced with higher rewards (Table 3), although North American, Japanese, and European subjects did not differ significantly from one another.

Table 3.

t-Statistics (Degrees of Freedom) for Bivariate Comparisons of $\widehat{b}$ Across Civilian Undergraduate Samples of the ADP and Associated Truncated and Disambiguated Variants.

	Chinese	European	Japanese
European	5.54 (11)***
Japanese	6.03 (4)**	0.64 (10)
North American	7.33 (23)***	0.06 (30)	0.27 (22)

Note.

^***=p<0.001,

^**=p<0.01. All values remain significant at the p<0.05 level after controlling for multiple comparisons. ADP = Asian Disease Problem

Consistent with the literature on sensation seeking, mean age of the sample was significantly negatively correlated with $\widehat{b}$ for those replications of the ADP reporting it r(6) = −0.87, p = 0.01². Among American and European replications of the ADP, samples of undergraduate students were significantly more risk-taking when compared to the two studies in our sample containing middle-aged and older adults (Mayhorn, Fisk & Whittle, 2002; Rönnlund, Karlsson, Laggnäs, Larsson, & Lindström, 2005), t(32) = 2.27, p = 0.03. In contrast, undergraduate students in Reyna et al.’s (2014) study testing 30 different risky-choice framing problems were significantly less risk-seeking than middle-aged adults and experts given the same problems, t(7) = 4.15, p = 0.004.

In order to more fully test our model, we once again used the JLOO procedure to estimate values of b for each experiment in our sample. Three studies (i.e., European military students, Chinese military students, and the “cholesterol problem” of Levin et al., 2002) were excluded because it was not possible to apply the JLOO procedure to categories with only one member. JLOO estimator values were then used, together with JLOO estimates of a, to predict the probability with which subjects in each experiment would choose the risky gamble. These probabilities were multiplied by the total number of subjects in each framing condition, and then compared to actual experimental counts using distribution-free chi-square goodness-of-fit tests. Table 4 shows that findings match our model in 153 out of 170 eligible cases (90%). Four (24%) of these deviations from our predictions are associated with inaccurate JLOO estimators for a.

Table 4.

170 Experimental Replications of Decisions Under Risk and Our Model’s Predictions

Reference	Model Inputs			1st Choice					2nd Choice
	$\overrightarrow{x}$	${\widehat{a}}_{-i}$	${\widehat{b}}_{-i}$	nrisky		nsafe		χ2	nrisky		nsafe		χ2
				Actl.	Pred.	Actl.	Pred.		Actl.	Pred.	Actl.	Pred.
Asian Disease Problem, North American, Japanese, and European Undergraduate Students
Tversky & Kahneman, 1981	[±1,0,0]	0.82	0.08	43	49.01	109	102.99	1.09	121	110.37	34	44.63	3.55
Fagley & Miller, 1990, #1	[±1,0,0]	0.48	0.07	48	37.64	46	56.36	4.75*	67	60.86	29	35.14	1.69
Fagley & Miller, 1990, #2	[±1,0,0]	0.46	0.08	21	21.97	33	32.03	0.07	40	34.78	15	20.22	2.13
Miller & Fagley, 1991	[±1,0,0]	0.86	0.08	19	11.31	17	24.69	7.63*	29	25.85	7	10.15	1.36
Reyna & Brainerd, 1991, standard	[±1,0,0]	1.72	0.09	9	5.72	26	29.28	2.24	30	31.77	7	5.23	0.69
Reyna & Brainerd, 1991, ZCT	[0,0,0]	0.00	0.09	18	18.25	17	16.75	0.01	21	18.77	15	17.23	0.55
Reyna & Brainerd, 1991, NCT	[±1, ±1,0]	0.47	0.09	10	9.31	13	13.69	0.08	15	14.62	8	8.38	0.03
Tindale, Sheffey & Scott, 1993	[±1,0,0]	0.86	0.06	60	44.80	84	99.20	7.48*	113	102.96	31	41.04	3.43
Takemura, 1994	[±1,0,0]	0.70	0.09	9	15.92	36	29.08	4.66*	31	30.96	14	14.04	0.00
Kühberger, 1995, #1	[±1,0,0]	0.00	0.08	16	13.55	10	12.45	0.93	13	11.98	10	11.02	0.18
Kühberger, 1995, #2	[±1,0,0]	0.37	0.08	12	10.73	13	14.27	0.26	18	14.04	5	8.96	2.87
Kühberger, 1995, COD, #1	[0,0,0]	−0.39	0.09	15	15.45	10	9.55	0.03	10	9.75	13	13.25	0.01
Kühberger, 1995, COD; problem, #2	[0,0,0]	0.00	0.09	9	11.50	13	10.50	1.14	7	9.93	12	9.07	1.82
Kühberger, 1995, 4NSCODT, #1	[∓1,0,0]	0.41	0.09	9	6.73	7	9.27	1.32	8	8.69	6	5.31	0.14
Kühberger, 1995, 4NSCODT, #2	[∓1,0,0]	−0.40	0.09	8	9.90	8	6.10	0.96	7	8.06	12	10.94	0.24
Wang & Johnston, 1995	[±1,0,0]	0.86	0.09	20	15.74	30	34.26	1.68	34	36.04	16	13.96	0.41
Highhouse & Yüce, 1996	[±1,0,0]	0.84	0.09	35	39.04	87	82.96	0.61	90	87.50	32	34.50	0.25
Jou, Shanteau, & Harris, 1996	[±1,0,0]	0.44	0.08	28	32.90	52	47.10	1.24	64	50.04	16	29.96	10.41*
Wang, 1996	[±1,0,0]	0.86	0.08	13	9.79	18	21.21	1.54	26	24.44	8	9.56	0.36
Stanovich & West, 1998 (between subjects)	[±1,0,0]	0.87	0.10	48	46.63	100	101.37	0.06	94	104.36	50	39.64	3.74
Stanovich & West, 1998 (within subjects)	[±1,0,0]	0.49	0.10	118	117.50	173	174.50	0.01	174	188.06	118	103.94	2.96
Druckman, 2001a	[±1,0,0]	0.85	0.08	22	21.93	47	47.07	0	60	56.67	19	22.33	0.69
Druckman, 2001b	[±1,0,0]	0.85	0.08	16	15.88	34	34.12	0	42	39.48	13	15.52	0.57
Mayhorn, Fisk, & Whittle, young adults, 2002	[±1,0,0]	0.84	0.08	7	9.26	22	19.74	0.81	25	20.76	4	8.24	3.05
LeBoeuf & Shafir, 2003, #1, no justification	[±1,0,0]	0.86	0.09	13	15.26	35	32.74	0.49	34	39.68	21	15.32	2.92
LeBoeuf & Shafir, 2003, #2 (between subjects)	[±1,0,0]	0.52	0.13	106	115.79	184	171.21	1.78	146	188.86	141	98.14	28.45*
LeBoeuf & Shafir, 2003, #2 (within subjects)	[±1,0,0]	0.87	0.12	36	47.14	111	99.86	3.88*	83	106.44	63	39.56	19.05*
Rönnlund, Karlsson, Laggnäs, & Lindström, 2005	[±1,0,0]	0.47	0.09	13	12.98	19	19.02	0	22	20.32	10	11.68	0.38
Druckman & McDermott, 2008	[±1,0,0]	0.72	0.09	6	5.90	11	11.10	0	13	11.74	4	5.26	0.44
Fischer, Jonas, Frey, & Kastenmüller, 2008	[±1,0,0]	0.35	0.08	45	43.64	56	57.36	0.07	76	68.53	37	44.47	2.07
Okder, 2012	[±1,0,0]	0.71	0.08	19	18.07	33	33.93	0.07	40	36.51	13	16.49	1.07
Stein, 2012	[±1,0,0]	0.86	0.08	19	14.79	28	32.21	1.75	39	41.08	18	15.92	0.38
Kühberger & Gradl, 2013, #1	[±1,0,0]	0.72	0.09	20	21.92	43	41.08	0.26	43	43.56	20	19.44	0.02
Kühberger & Gradi, 2013, #2	[±1,0,0]	0.73	0.08	8	4.82	6	9.18	3.21	11	10.39	4	4.61	0.12
TOTAL of 68 predicted												60 (88%)
Asian Disease Problem, North American and European Adults
Mayhorn, Fisk, & Whittle, 2002	[±1,0,0]	0.85	−0.34	6	6.75	23	22.25	0.11	20	18.09	9	10.91	0.54
Rönnlund, Karlsson, Laggnäs, Larsson, & Lindström, 2005	[±1,0,0]	0.47	−0.27	9	10.34	23	21.66	0.26	18	17.55	14	14.45	0.03
TOTAL of 4 predicted												4 (100%)
Asian Disease Problem, Chinese Undergraduate Students
Zhang & Miao, 2008, #1	[±1,0,0]	0.73	1.36	43	42.34	22	22.66	0.03	59	60.53	9	7.47	0.35
Zhang & Miao, 2008, #2	[±1,0,0]	0.73	1.33	30	29.06	15	15.94	0.09	42	42.56	6	5.44	0.07
Zhang, Xiao, Ma, & Miao, 2008, civilians	[±1,0,0]	0.72	1.29	39	38.35	21	21.65	0.03	52	51.18	6	6.82	0.11
TOTAL of 6 predicted												6 (100%)
Allais Paradox Problems, North American and European Undergraduate Students
Conlisk, 1989	[−1,0,1] & [1,1,0]	1.68	0.14	121	109.63	115	126.37	0.49	34	32.79	202	203.21	0.05
Carlin, 1990	[−1,0,1] & [1,1,0]	1.71	0.11	39	30.72	26	34.28	4.23*	14	9.09	51	55.91	3.08
Huck & Müller, 2012	[−1,0,1] & [1,1,0]	1.46	−0.13	24	37.23	46	32.77	10.04*	9	14.58	61	55.42	2.69
TOTAL of 6 predicted												4 (67%)
Average of 30 assorted framing problems, North American Undergraduate Students
Reyna et al., 2014	[±1,0,0]	0.47	−0.29	21.80	20.03	41.20	42.97	0.23	34.84	34.36	28.16	28.64	0.01
Reyna et al., 2014, ZCT	[±1,0,0]	0.00	−0.32	27.03	26.58	35.97	36.42	0.01	30.87	26.58	32.13	36.42	1.20
Reyna et al., 2014, NCT	[±1,0,0]	0.95	−0.19	14.30	15.32	48.70	47.68	0.09	37.55	42.93	25.45	20.07	2.12
TOTAL of 6 predicted												6 (100%)
Average of 30 assorted framing problems, North American Undergraduate Students
Reyna et al., 2014	[±1,0,0]	0.47	0.10	21.71	22.03	32.29	31.97	0.01	32.35	34.55	21.65	19.45	0.39
Reyna et al., 2014, experts	[±1,0,0]	0.46	0.06	13.61	14.45	22.39	21.55	0.08	25.38	22.66	10.62	13.34	0.88
Reyna et al., 2014, ZCT	[±1,0,0]	0.00	0.07	27.32	27.98	26.68	26.02	0.03	29.81	27.98	24.19	26.02	0.25
Reyna et al., 2014, experts, ZCT	[±1,0,0]	0.00	0.05	18.54	18.47	17.46	17.53	0	22.18	18.47	13.82	17.53	1.52
Reyna et al., 2014, NCT	[±1,0,0]	0.94	0.11	14.04	16.39	39.96	37.61	0.49	39.47	39.95	14.53	14.05	0.02
Reyna et al., 2014, experts, NCT	[±1,0,0]	0.93	0.09	7.09	10.89	28.91	25.11	1.90	29.05	26.45	6.95	9.55	0.96
TOTAL of 12 predicted												12 (100%)
Refugee Problem, North American and European Undergraduate Students
Mandel, 2001, COD	[0,0,0]	0.00	0.35	12	13.50	11	9.50	0.40	11	12.92	11	9.08	0.69
Mandel, 2001, #1, 4NS6NST	[0,0,0]	0.00	0.33	13	13.38	10	9.62	0.03	14	13.96	10	10.04	0.00
Mandel, 2001, #2, 4NS6NST	[0,0,0]	0.00	0.30	23	20.72	13	15.28	0.59	22	21.30	15	15.70	0.05
Mandel, 2014, #2	[±1,0,0]	0.72	0.32	16	15.24	22	22.76	0.06	28	28.13	10	9.87	0.00
Mandel, 2014, #3	[±1,0,0]	0.71	0.33	8	10.15	17	14.85	0.77	20	18.46	5	6.54	0.49
Mandel, 2014, COD, #3	[0,0,0]	0.00	0.37	9	13.03	13	8.97	3.05	12	14.21	12	9.79	0.84
Mandel, 2014, COD ZCT #3	[∓1,0,0]	−0.73	0.38	15	19.56	11	6.44	4.29*	8	10.35	17	14.65	0.91
TOTAL of 20 predicted												19 (95%)
Plant Problem, European Undergraduate Students
Kühberger, 1995, #1	[±1,0,0]	0.36	−0.15	13	9.39	12	15.61	2.22	19	12.74	4	10.26	6.89*
Kühberger, 1995, #2	[±1,0,0]	0.35	0.10	3	7.01	13	8.99	4.09*	12	10.39	5	6.61	0.64
Kühberger, 1995, COD, #1	[0,0,0]	0.00	0.07	12	13.44	14	12.56	0.32	12	11.89	11	11.11	0.00
Kühberger, 1995, COD, #2	[0,0,0]	0.00	0.16	4	7.01	9	5.99	2.81	7	10.25	12	8.75	2.24
Kühberger, 1995, 4NSCODT, #1	[+1,0,0]	−0.44	0.05	12	16.76	15	10.24	3.57	13	9.32	10	13.68	2.44
Kühberger, 1995, 4NSCODT, #2	[+1,0,0]	−0.40	0.03	8	8.49	6	5.51	0.07	7	5.74	7	8.26	0.47
TOTAL of 12 predicted												10 (83%)
Cancer Problem, European Undergraduate Students
Kühberger, 1995, #1	[±1,0,0]	0.40	0.20	9	10.82	15	13.18	0.56	12	16.18	13	8.82	3.06
Kühberger, 1995, #2	[±1,0,0]	0.41	0	11	6.39	5	9.61	5.54*	9	8.43	5	5.57	0.10
Kühberger, 1995, COD, #1	[0,0,0]	0.00	0.20	12	13.22	12	10.78	0.25	8	12.67	15	10.33	3.83
Kühberger, 1995, COD, #2	[0,0,0]	0.00	0.04	5	3.56	2	3.44	1.18	8	6.62	5	6.38	0.59
Kühberger, 1995, 4NSCODT, #1	[+1,0,0]	−0.37	0.01	18	14.23	6	9.77	2.45	10	9.46	13	13.54	0.05
Kühberger, 1995, 4NSCODT, #2	[+1,0,0]	−0.40	0.13	7	8.81	7	5.19	1.01	7	6.92	9	9.08	0
TOTAL of 12 predicted												11 (92%)
Drinking Water Contamination Problem, Mixed North American and European Sample
Kühberger & Tanner, 2010	[±1,0,0]	0.63	0.34	31	39.78	62	53.22	3.38	68	67.51	25	25.49	0.01
Kühberger & Tanner, 2010, ZCT	[0,0,0]	0.00	0.23	50	51.85	43	41.15	0.15	60	51.85	33	41.15	2.89
Kühberger & Tanner, 2010, NCT	[±1, ±1,0]	1.30	0.26	23	24.28	70	68.72	0.09	79	76.96	14	16.04	0.31
TOTAL of 6 predicted												6 (100%)
Genetically Engineered Crops Problem, Mixed North American and European Sample
Kühberger & Tanner, 2010	[±1,0,0]	0.68	0.07	31	32.74	62	60.26	0.14	55	63.07	38	29.93	3.21
Kühberger & Tanner, 2010, ZCT	[0,0,0]	0.00	0.02	50	46.95	43	46.05	0.40	40	46.95	53	46.05	2.08
Kühberger & Tanner, 2010, NCT	[±1, ±1,0]	1.35	−0.11	27	17.46	66	75.54	6.41*	73	72.09	20	20.91	0.05
TOTAL of 6 predicted												5 (83%)
Fish Kidney Disease Problem, Mixed North American and European Sample
Kühberger & Tanner, 2010	[±1,0,0]	0.66	0.14	26	34.61	67	58.39	3.41	55	64.09	38	28.91	4.15*
Kühberger & Tanner, 2010, ZCT	[0,0,0]	0.00	−0.08	59	44.75	34	48.25	8.74*	40	44.75	53	48.25	0.97
Kühberger & Tanner, 2010, NCT	[±1, ±1,0]	1.30	−0.08	20	18.70	73	74.30	0.11	77	71.90	16	21.10	1.60
TOTAL of 6 predicted												4 (67%)
Endangered Forest Problem, Mixed North American and European Sample
Kühberger & Tanner, 2010	[±1,0,0]	−0.46	0.66	22	23	71	70	0.06	51	51.11	42	41.89	0.00
Kühberger & Tanner, 2010, ZCT	[0,0,0]	−0.53	0	37	34.51	56	58.49	0.29	40	34.51	53	58.49	1.39
Kuhberger & Tanner, 2010, NCT	[±1, ±1,0]	−0.42	1.34	14	13.66	79	79.34	0.01	60	66.55	33	26.45	2.27
TOTAL of 6 predicted												6 (100%)
TOTAL of 170 predicted												153 (90%)

Note.

^*= p < 0.05, Actl. = Actual, Pred. = Predicted, ${\widehat{a}}_{-i}$ is the JLOO estimate of the a parameter and ${\widehat{b}}_{-i}$ is the JLOO estimate of the b parameter. 1^st (2^nd) Choice is the certain (risky gamble) option in framing problems and the first (second) gamble in the Allais gambles. ZCT = zero complement truncated; NCT = nonzero complement truncated; COD = certain-option disambiguated; 4NSCODT = “400 not saved” certain-option disambiguated and truncated; 4NS6NST = “400 not saved vs. 2/3 chance that 600 not saved” truncation problem; The model in Table 2 differed significantly from the data for references in italics. Per Table 3, Japanese, European, and North American samples did not differ from one another and were therefore combined.

Estimating $\overrightarrow{a}$ and b for individual subjects

Up to this point, our model has only been applied to aggregate samples of subjects; however, scholars such as Estes and Maddox (2005) have cautioned against drawing conclusions about individual subjects from aggregate data. We therefore conducted three experiments that were designed to elicit individual-level estimates of $\overrightarrow{a}$ and b. In addition, we examined individual-level data recently published by White, Gummerum, and Hanoch (2016). Specifically, we examined how estimates of $\overrightarrow{a}$ and b vary with measures of metacognitive monitoring and reward sensitivity, respectively.

Participants

Demographics for all three experiments from Cornell are shown in Table 5. Participants for the White et al. (2016) study were 296 English students who were split into adolescent and adult age groups. Full details are reported in the corresponding paper.

Table 5.

Demographics of Participants in the Three Experiments Conducted at Cornell University

Experiment	N	% female	Mean age (SD)	% White	% African-American	% Asian	% Mixed/Other	% Hispanic
1	745	65	20.30 (3.60)	63	5	30	2	11
2	124	79	19.94 (3.02)	60	4	29	7	9
3	389	70	19.50 (3.55)	64	5	23	8	8

Note. SD = Standard Deviation.

Materials

In Cornell Experiment 1, participants were presented with a total of 32 framing problems. The study was a 2 (gain or loss) × 2 (candy or alcohol) × 2 (certain option magnitude 1 or 6 candy bars/drinks) × 2 (probability in risky option 1/3 or 2/3) × 2 (equal or unequal expected value) repeated factors design. All problems were true framing problems, meaning that they described endowments in the loss frame. When expected values were unequal, the option that opposed the framing effect was the more attractive option. Participants also completed several indicators of individual differences including the Cognitive Reflection Test (CRT, a measure of metacognitive monitoring and numeracy; Frederick, 2005) and reward seeking despite risk, namely the Hoyle Brief Sensation Seeking Scale (BSSS; Hoyle, Stephenson, Palmgreen, Lorch, & Donohew, 2002). Cornell Experiment 2 used the same design as Experiment 1 except that all problems were reflection problems, meaning that they described no endowments in the loss frame. Finally, in Cornell Experiment 3, the study was a 2 (gain or loss) × 3 (candy, alcohol, or money) × 2 (certain option magnitude 1 or 6) × 2 (probability in risky option 1/3 or 2/3) × 2 (equal or unequal expected value) repeated factors design for a total of 48 problems. All problems in Experiment 3 were reflection problems.

Participants in the White et al. (2016) study completed an online music quiz in which they were faced with 12 online gambling problems (six loss framed and six gain framed) of equal expected value with an initial endowment (a music voucher). The study used a 3 (£5, £20, or £150 reward) × 2 (gain or loss frame) × 2 (probability in risky option 1/2 or 3/4) repeated factors design. Adolescent vs. young adult status, gender, and BSSS score were collected.

Statistics

For the Cornell experiments, the existence of problems with unequal expected values enabled us to independently estimate, for each subject, separate values for the categorical and interval components of $\overrightarrow{a}$ (we could not estimate the ordinal component of $\overrightarrow{a}$ since our theory predicted no contribution from the ordinal representation), which we denote ${\widehat{a}}_{\mathit{\text{categorical}}}$ and ${\widehat{a}}_{\mathit{\text{interval}}}$, respectively. In addition, we estimated values of $\widehat{b}$ for each subject independently. Since all problems had equal expected values in the White et al. (2016) study, we assumed a single scalar value, a, for the categorical, ordinal, and interval components of $\overrightarrow{a}$. All values of ${\widehat{a}}_{\mathit{\text{categorical}}}$ were estimated using within-subjects values of ${\widehat{P}}_{\mathit{\text{gain}}}$ and ${\widehat{P}}_{\mathit{\text{loss}}}$ for problems with equal expected value; ${\widehat{a}}_{\mathit{\text{interval}}}$ was then estimated as the arithmetic difference between the observed value of $\widehat{a}$ and ${\widehat{a}}_{\mathit{\text{categorical}}}$ for problems with unequal expected value. Values of ${\widehat{P}}_{\mathit{\text{gain}}}$ and ${\widehat{P}}_{\mathit{\text{loss}}}$ equal to zero or one were smoothed to $\frac{1}{N}$ and $1-\frac{1}{N}$ respectively, where N is the total number of problems in each experiment, to allow calculation of logit values for subjects that consistently chose the risky or safe option.

Results

After controlling for demographic variables (age, gender, race, and ethnicity), we found that CRT significantly predicted ${\widehat{a}}_{\mathit{\text{interval}}}$ across all three experiments in the Cornell studies (see Table 6). Consistent with FTT’s predictions, White et al. (2016) report that adults were significantly more likely to frame than adolescents, as measured by total selection of risky gambles in the loss frame and safe options in the gain frame. (In our logit-transformed analysis, the relationship between adult status and â barely missed significance, β = 0.21, t(291) = 1.95, p = 0.053.)

Table 6.

Results of Linear Regression Analyses for the Three Cornell Experiments and the White et al. (2016) Sample

	acategorical		ainterval		b1		b6
	β (SE)	t	β (SE)	t	β (SE)	t	β (SE)	t
Cornell Experiment 1
Age	0.01 (0.01)	1.19	−0.01 (0.02)	−0.32	−0.01 (0.01)	−0.81	−0.01 (0.01)	−0.73
Male Gender	−0.09 (0.08)	−1.14	0.30 (0.16)	1.92	0.14 (0.09)	1.59	0.21 (0.10)	2.13*
Hispanic Ethnicity	−0.17 (0.09)	−1.81	0.23 (0.19)	1.23	0.16 (0.10)	1.51	0.12 (0.11)	1.07
Asian	0.00 (0.08)	0.01	−0.13 (0.16)	−0.81	0.19 (0.09)	2.13*	0.24 (0.10)	2.46*
African-American	0.07 (0.18)	0.41	0.42 (0.36)	1.17	-0.13 (0.20)	−0.65	−0.22 (0.22)	−1.01
Mixed/Other	−1.03 (0.96)	−1.08	1.72 (1.89)	0.91	1.15 (1.06)	1.09	2.08 (1.17)	1.78
CRT	−0.03 (0.03)	−0.76	0.29 (0.07)	4.34***	0.03 (0.04)	0.92	−0.06 (0.04)	−1.52
BSSS	−0.01 (0.01)	−0.90	0.01 (0.01)	0.91	0.01 (0.01)	1.14	0.01 (0.01)	0.87
Intercept	0.40 (0.29)	1.36	0.61 (0.57)	1.07	−1.18 (0.32)	−3.68***	−1.29 (0.35)	−3.64***
Cornell Experiment 2
Age	0.09 (0.04)	2.56*	−0.05 (0.07)	−0.61	−0.01 (0.04)	−0.33	0.02 (0.05)	0.45
Male Gender	0.19 (0.21)	0.91	0.25 (0.43)	0.59	0.07 (0.22)	0.33	0.13 (0.30)	0.43
Hispanic Ethnicity	−0.22 (0.33)	−0.65	1.03 (0.68)	1.52	0.08 (0.36)	0.22	−0.13 (0.47)	−0.27
Asian	0.08 (0.19)	0.43	−0.63 (0.38)	−1.64	−0.20 (0.20)	−0.99	0.14 (0.27)	0.51
African-American	−0.82 (0.45)	−1.82	−0.33 (0.92)	−0.36	0.06 (0.48)	0.13	0.48 (0.64)	0.74
Mixed/Other	−0.04 (0.40)	−0.10	0.23 (0.81)	0.28	−0.51 (0.42)	−1.21	−0.26 (0.56)	−0.47
CRT	0.02 (0.08)	0.30	0.70 (0.16)	4.31***	−0.06 (0.09)	−0.76	−0.15 (0.11)	−1.34
BSSS	−0.01 (0.02)	−0.59	0.05 (0.03)	1.52	0.04 (0.02)	2.65**	0.01 (0.02)	0.54
Intercept	−0.93 (0.89)	−1.05	0.34 (1.81)	0.19	−1.22 (0.95)	−1.28	−1.30 (1.26)	−1.04
Cornell Experiment 3
Age	0.01 (0.01)	1.07	−0.02 (0.03)	−0.67	0.00 (0.02)	−0.20	0.01 (0.02)	0.34
Male Gender	−0.06 (0.11)	−0.51	0.52 (0.25)	2.10*	0.12 (0.12)	0.94	0.26 (0.12)	2.12*
Hispanic Ethnicity	0.20 (0.21)	0.93	0.74 (0.46)	1.59	−0.01 (0.23)	−0.06	0.32 (0.23)	1.36
Asian	−0.08 (0.22)	−0.36	0.49 (0.48)	1.01	−0.25 (0.24)	−1.02	−0.20 (0.24)	−0.82
African-American	0.00 (0.23)	−0.01	−0.41 (0.50)	−0.83	0.02 (0.25)	0.06	−0.12 (0.25)	−0.45
Mixed/Other	0.20 (0.12)	1.61	0.09 (0.27)	0.34	−0.01 (0.13)	−0.10	−0.03 (0.13)	−0.22
CRT	0.13 (0.05)	2.62**	0.47 (0.11)	4.41	0.03 (0.05)	0.60	−0.04 (0.05)	−0.76
BSSS	−0.01 (0.01)	−1.35	0.01 (0.02)	0.56	0.00 (0.01)	−0.30	0.00 (0.01)	0.18
Intercept	0.44 (0.37)	1.20	1.16 (0.80)	1.46	−0.19 (0.40)	−0.48	−0.55 (0.41)	−1.35
White, Gummerum, and Hanoch (2016) Sample
	a		b5		b20		b150
Male Gender	−0.22 (0.12)	−1.79	0.24 (0.33)	0.72	−0.22 (0.32)	−0.67	−0.08 (0.32)	−0.26
Adult	0.21 (0.11)	1.95	0.16 (0.29)	0.55	−0.20 (0.28)	−0.70	−0.25 (0.28)	−0.90
BSSS	−0.01 (0.01)	−0.85	0.04 (0.02)	1.59	0.05 (0.02)	1.98*	0.06 (0.02)	2.64**
Intercept	0.66 (0.27)	2.45*	−3.02 (0.73)	−4.15***	−3.57 (0.70)	−5.08	−4.42 (0.70)	−6.31***

Note.

^***= p<0.001;

^**= p<0.01;

^*= p<0.05. β = Linear regression coefficient. SE = Standard Error. BSSS = score on Hoyle’s Brief Sensation-Seeking Scale. CRT = score on Cognitive Reflection Test. b_x indicates the value of b for reward level x. 53, 13, and 39 observations were dropped from Cornell Experiments 1, 2, and 3 respectively, and 1 observation was dropped from the White et al. (2016) sample because of incomplete demographic data.

Consistent with the definition of b as seeking reward-despite-risk, we found that BSSS significantly predicted $\widehat{b}$ for large (£150) and medium (£20) rewards, but not for small (£5) rewards (Table 6), as expected (Reyna et al., 2011). Furthermore, there was a significant effect of sensation seeking on $\widehat{b}$ for Cornell Experiment 2, but not for Experiments 1 or 3. In all Cornell samples, reward magnitudes were smaller (1 and 6 in the certain option and a maximum of 21 in the risky gamble); however, null results are, of course, not determinative either way. As is well known, adolescents are more sensation seeking than adults and, hence, there is more opportunity to observe the effects of sensation seeking in the White et al. (2016) sample.

Discussion

Results are generally consistent with FTT’s predictions. CRT, a measure of metacognitive monitoring and numeracy, consistently predicts ${\widehat{a}}_{\mathit{\text{interval}}}$, indicating that more weight is placed on the interval representation by those individuals who display stronger metacognitive abilities. Furthermore, ${\widehat{a}}_{\mathit{\text{categorical}}}$ is insensitive to metacognitive intercession (although ${\widehat{a}}_{\mathit{\text{categorical}}}$ was significantly associated with CRT in Cornell Experiment 3), suggesting that the categorical representation is encoded distinctly, rather than derived, from the interval representation. This finding also suggests that even those individuals possessing the ability and the desire to convert between (or compare) frames are influenced by the categorical gist of the stimulus. Thus, it lends credence to our model’s description of competition between gist and verbatim representations for problems with unequal expected value. Results from the White et al. (2016) study provide additional support for our model, showing the effect of reward sensitivity on risk taking as measured by b. Furthermore, these data show that adolescents are less likely to be susceptible to framing when compared to adults, as the theory expects. These results provide some support for our model’s predictions at the individual level.

Test of our Model’s Parsimony

In order to further demonstrate the adequacy and parsimony of this model, we adapted a technique used by Busemeyer, Wang, and Shiffrin (2015), where we compare our model’s fit to a “null” model (in which each decision option is equally likely); a “saturated” model (in which maximum-likelihood parameter values are separately estimated for each experiment in our sample); and a model that estimates parameters based on the same theoretically motivated analytic categories used in the JLOO procedure. Specifically, the 88 studies in our sample were each associated with a stimulus type (e.g., ADP, Allais paradox problems, etc.), nationality of participants, age (undergraduate students and older adults), occupation of participants (civilian or military), and experimental design (framing manipulated between subjects with single presentation, framing manipulated between subjects with multiple problems, and framing manipulated within subjects). The Akaike Information Criterion (AIC) and Bayesian Information Criterion (BIC) of our model, AIC = 13409, BIC = 13510, outperformed several candidates, including the “null” model, AIC = 14982, BIC = 14987, the “saturated” model, AIC = 13491, BIC = 14049, a model accounting for variation in individual differences but not mental representation, AIC = 14808, BIC = 14878, and others (Supplemental Material), indicating our model’s parsimony.

Comparisons to Cumulative Prospect Theory

Many leading theories of decision under risk, such as CPT (Tversky & Kahneman, 1992), make predictions regarding modal choice outcomes. Although such theories make predictions for individual decision makers given a set of parameter values, they do not specify how error is distributed (see also Birnbaum, 1999; 2010). Therefore, to conduct a preliminary analysis, we used the parameter values reported by Tversky and Kahneman (1992; similar parameter values, used by Erev, Roth, Slonim, & Barron, 2002, and cited in Glöckner & Betsch, 2008, yielded the same qualitative choice predictions for all problems in our sample⁴) to compare the individual-level predictions of CPT to FTT’s qualitative predictions, given by the unweighted sum of the elements in the $\overrightarrow{x}$ vector (1: standard framing, 2: strong preference for the option predicted by CPT, 0: attenuated preference for the option predicted by CPT, and -1: reverse framing). Following Glöckner and Betsch, we compared the proportion of subjects that made the decision predicted by CPT using these standard parameter values. Results of our preliminary analysis, shown in Figure 5, support the qualitative predictions of FTT over those of CPT under these assumptions. A more detailed analysis, analyzing problems by analytic category for a, yielded similar results (see Supplemental Material). However, we acknowledge that, because CPT has multiple free parameters, the theory can cover a rather large range of possible choice patterns.

Figure 5.

Comparison of Fuzzy Trace Theory’s (FTT) predictions to those of Cumulative Prospect Theory (CPT). Error bars represent one standard error.

Section 5: General Discussion

In this paper, we integrated memory and decision-making research to formalize FTT’s core tenets: 1) the gist/verbatim distinction (formalized by theoretically motivated subcategories); 2) the hierarchy of gist (formalized by our extended fuzzy-processing preference and associated lattices); and 3) preferences over these gists based on valenced affect associated with social and moral principles (e.g., saving lives is good). These three formalized tenets are used to predict 16 variations of experimental effects (Table 1) concerning risky choice.

The results we have discussed show how truncation, disambiguation, and other changes to decision problems can greatly change risky choices—and we bring these effects together with standard framing and Allais effects under the same formal model for the first time. These truncation and disambiguation changes are often treated as equivalent to standard framing effects, despite producing results that sharply diverge from those effects. The effects the model encompasses are not just restricted to the ADP; we also account for ten variations on the framing effect (Table 2), the Allais problems, a study (Reyna et al., 2014) that demonstrated truncation and disambiguation effects for 30 separate framing problems, within-subjects framing problems presented by Levin and colleagues (2002), the candy, drinks, and money problems (with equal and unequal expected values) tested in the Cornell experiments, and the online risk-taking study of White et al. (2016). Although we did not test several framing problems in the literature because they did not meet our inclusion criteria, they yield similar results (e.g., other framing problems in papers from which we extracted ADP replications: Fagley & Miller, 1990; Wang & Johnnston 1995; Wang, 1996; Jou, Shanteau & Harris, 1996, and others). Thus, our results are consistent with effects obtained from a wide range of experimental stimuli reported in meta-analyses of framing effects (e.g., Kühberger, 1998). The model describes mechanisms motivated by research on memory, reasoning, and psycholinguistics, uniting classic and divergent results under a coherent and explicit theoretical umbrella.

Our model includes a parameter, a, accounting for individual differences, such as numeracy and NFC, that allow people to inhibit biases. We have shown that values of a are smaller when subjects are more numerate and when factors associated with experimental design, such as a within-subjects framing manipulation, encourage individuals with high NFC to compare different (e.g., oppositely-framed) versions of the same problem. Thus, task features and individual differences combine to facilitate metacognitive monitoring of the outputs of cognition and inhibition of biases when those outputs are inconsistent.

Our model also includes a parameter, b, accounting for reward sensitivity (i.e., reward seeking despite risks), which varies systematically with national culture and factors associated with sensation seeking, such as age. As b moves further away from zero, subjects become increasingly risk-taking (increasing b) or risk-averse (decreasing b). Due to the nature of the logistic function, larger absolute values of b lead to smaller absolute differences in framing (when differences in rewards oppose framing effects). By separating effects of mental representation (categorical, ordinal, and interval) from individual differences in metacognitive monitoring (and inhibition) and in reward sensitivity, we can account for differences among educational, cultural, and age groups. Thus, our model provides a needed formal mechanism explaining how risky choices reflect these factors (e.g., Reyna & Brainerd, 2011).

Using the JLOO estimation technique to account for differences in numeracy and differences in metacognitive monitoring associated with experimental design, our model successfully predicted results for a total of 82 (93%) of 88 theoretically central decision effects (Table 2), each associated with a pair of problems (4 of these 88 would be expected to differ from the model’s prediction by chance alone). Novel variants of these pairs of problems were also used to make, and test, new predictions. The model explained problems with equal and unequal expected values (where gist and verbatim representations compete), choices between pairs of gambles, and choices between sure options and gambles. By separating effects of representation (categorical, ordinal, and interval) from reward sensitivity, we account for differences among cultural and age groups in 153 (90%) out of 170 eligible experiments. Finally, our model is scientifically parsimonious when compared to alternatives.

Comparisons to Other Models and Theory

Several other models of decision making assume representations of reward value and cognitive control, which predict preferences at a process level (see Johnson, 2013; Hare, Camerer, & Rangel, 2009). Our approach incorporates some of these ideas. However, unlike most models of decision-making, our approach unpacks levels of cognitive representations, ranging from a qualitative categorical gist-based process (nevertheless quantifiable in the model) to a metric verbatim representation. Process tests of these representations have been conducted in research on memory and on numerical cognition (e.g., Brainerd et al., 2003: Reyna & Brainerd, 1994).

To our knowledge, no prior mathematical model explains how gist representations of decision options are derived and processed. Although lexicographic rules (e.g., Tversky, 1969), such as the priority heuristic (Brandstätter, Gigerenzer, & Hertwig, 2006), bear some resemblance to gist there are also important differences. These other approaches are mainly about processing less information as opposed to processing essential meaning, producing distinct predictions (see also Birnbaum 2008; 2010; Birnbaum & Guiterrez, 2007, who found evidence against the priority heuristic). These other approaches are also not grounded in research on memory for, and development of, gist and verbatim representations, psycholinguistics, or gestalt theory, as FTT is.

Although there have been some efforts to model standard dual-process-models (e.g., Loewenstein, O’Donoghue, & Bhatia, 2015; Mukherjee, 2010), these prior dual-process models have not been evaluated for fit to actual subjects’ data. Moreover, our proposed model goes beyond standard dual-process theory in adding an explicit formalism for representations to individual differences in cognitive control (e.g., using numeracy to detect and inhibit cognitive biases) and reward sensitivity, bringing to bear theories of personality, cognitive ability, and decision-making in a unified model.

Our approach builds on Tversky and Kahneman’s PT (e.g., 1992) in that we hold losses and gains, rather than final assets, as the carriers of value. Unlike PT, we do not represent different degrees of these quantities with a traditional value or decision-weight function. Instead, verbatim representations of decision options capture numerical distinctions (Reyna, 2013; see also Yechiam & Hochman, 2013, whose emphasis on selective attention is broadly consistent with our framework). In addition, decision options are perceived as gists that may be categorically or ordinally distinct. Categorical comparisons made between two numerical quantities with the same gist would be perceived as qualitatively similar (based on their gist representations), yielding lower levels of quantitative sensitivity.

Several scholars have found that decision-makers can be insensitive to quantity when making valuations (e.g., Dickert, Västfjäll, Kleber, & Slovic, 2015; Fetherstonhaugh, Slovic, Johnson, & Friedrich, 1997; Kogut & Ritov, 2005). Some theorists argue that such scope insensitivity is associated with strong emotion (e.g., Hsee & Rottenstreich, 2004). Our theory implies that scope insensitivity need not require emotion; rather, it only requires a categorical representation associated with valenced affect, which is routinely extracted under predictable conditions. Although emotion may cause scope insensitivity, our model suggests that it is not necessarily required.

Several alternative approaches have used mathematical functions that warp decision weights to characterize effects related to those we have reviewed. For example, Gonzales and Wu (1999) used a log-odds transform to capture the generalized inverse s-shape of probability-weighting functions. They found that the parameters associated with these log-odds transforms varied widely both between subjects and across domains for a given subject. For some domains, the curve resembled a “step function” – i.e., could be best described by the categories “certainty will,” “certainly will not,” or “maybe.” In other examples from their data, curves drop sharply near zero. Both of these patterns of findings are consistent with the presence of categorical thinking, as in our model, which may be more pronounced in subgroups of subjects. Gonzales and Wu (1999) also report a small number of subjects for whom subjective probability scales in a roughly linear fashion, consistent with interval thinking. Although Gonzalez and Wu (1999) suggested that “…decision theorists may also want to consider individual differences in the weighting function,” (p. 160) they did not include these in their analyses.

Similarly, Zhang and Maloney (2012) observed that a log-odds transform could account for decision outcomes across several domains, but did not test specific a priori hypotheses associated with the underlying parameters. Our model offers an explanation for the distortions related to choice probabilities that Zhang and Maloney observed, also by operating on a log-odds transform, but transforming objective probabilities using a weighted sum of votes from three different mental representations posited by FTT: categorical-, ordinal-, and interval-level thinking. Adding differential weights to accommodate individual or domain differences in the use of representations can be accomplished easily in our framework.

Results of several additional experiments may also be explained using our framework. For example, the sacred values research program (e.g., Ginges & Atran, 2011; Tanner, Medin, & Iliev, 2008) has found that subjects who use deontological modes of reasoning are more likely to draw categorical decisions consistent with these valences, compared to consequentialist decision-makers (Reyna & Casillas, 2009). Similarly, Mishra and Fiddick (2012) found that subjects’ framing effects disappeared when they were told that at least 300 people (or 100 people) had to be saved in the ADP, creating novel categories (see also Schulze & Wansink, 2012). In such cases, the experimental manipulation induces the formation of new categories; the category set changes to include “success” (i.e., at least 300 saved) instead of failure (“none saved”). This becomes the boundary of a category that may be interpreted as distinguishing between whether this need is or is not met. The absence of a difference between gain and loss frames reported by Mishra and Fiddick (2012) is explained by the fact that, regardless of frame, the certain option is interpreted as a categorical failure (or categorical success).

Accounting for Additional Gist Categories

One might object that our approach requires a complete theory for converting scenarios described in natural language into specific gist categories (but see Table S1). Leading theories of decision-making under risk currently lack such an explicit mechanism and generally do not have natural language primitives. In contrast, our model treats “none” and “some” as analogous to logical primitives (McCawley, 1980). An elaborate natural language interpretation beyond this for categorical gist is not necessary: zero maps to none and any other amount maps to some. Interpretation of these primitives is consistent with basic abilities of numerical cognition (Goldman et al., 2013; Pinhas & Tzelgov, 2012), including research on representations of quantities such as probabilities (e.g., Reyna & Brainerd, 1994; Spelke & Kinzler, 2007). Although an explicit theory of natural language interpretation is not necessary here to make these predictions, such a mechanism would expand our knowledge of gist.

For example, “all” is also a logical primitive, which, if included, would attenuate the framing effect as shown in Figure 6. Indeed, one might think that “all” and “certainty should constitute separate categories. Although FTT predicts that such end stimulus categories are encoded (along with interval and ordinal representations), the fuzzy-processing preference indicates that they are not relied upon if they do not help the decision-maker to differentiate between two options³. Importantly, our model is capable of including categories consistent with the presence of gist subcategories such as “all” and “certainty,” should future research determine conditions under which they are interpreted as separate gists.

Figure 6.

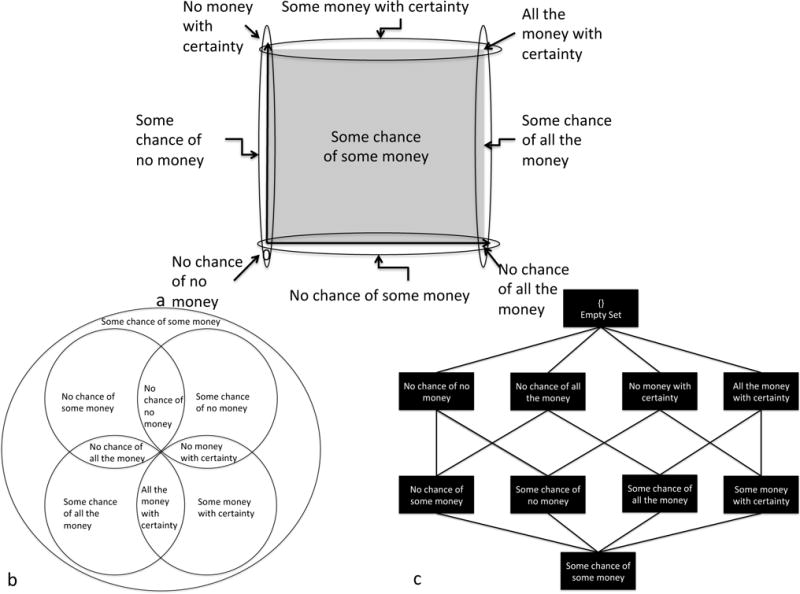
a) The gist representation of the decision problem when we include “all” and “certainty” as categories. b) Venn diagram representing overlapping gists for the same problem. d) A lattice representation of the gists in this problem. The highest element in the lattice is the empty set because the categories in the next level lower do not overlap.

Further Individual-Level Tests of our Model

Beyond the individual-level tests presented in this paper, there are a number of counterintuitive implications of this model that can be tested in future research. We have already shown that the greater reward sensitivity of risk-taking adolescents (compared to adults) can be modeled (Galván et al., 2013; Steinberg et al., 2008; White et al., 2016). Beyond these findings, and controlling for numeracy, adolescents should be more likely than adults to make “advantageous” choices in the sense that they will choose options with higher expected value. Even more surprising, these effects of choosing a higher expected value option should be greater for those who are more sensation seeking. A key aspect of the model is that one must control for countervailing effects of numeracy and NFC on such risky choices. Additionally, our model applies to populations that rely especially heavily on categorical gist representations (e.g., experts and older adults) or verbatim representations (e.g., children and autistic individuals; Reyna & Brainerd, 2011). Although, throughout most of this paper, we have assumed that all components of the $\overrightarrow{a}$ vector are constant, this simplifying assumption may not apply in these populations.

Epilogue

In this article, we proposed a mathematical formalization and extension of an evidence-based theory of decision-making under risk – FTT. We focused on risky choice tasks, especially framing problems, variants of those problems, and the Allais Paradox problems (e.g., Kühberger & Tanner, 2010; Peters & Levin, 2008). Our work is based on Feldman’s (1997) formalization of the perception of visual categories. Therefore, to the extent that our framework is successful, it demonstrates a potential theoretical unification of elements of risky decision-making with elements of visual perception. Indeed, in their seminal paper on framing Tversky and Kahneman (1981) compared different frames with perspectives on a visual scene. Our work extends this analogy, demonstrating that related mathematical formalisms can be fruitfully applied to both domains. Furthermore, Feldman’s (2009) work suggests the possibility that one might use FTT to structure priors for Bayesian inference.

We formalize mental representations of decision outcomes and probabilities, integrating memory and decision-making research (Reyna, 2012). Our model explains both gist and verbatim processing, providing a novel formalization of how decision-makers encode multiple (potentially competing) representations of decision options in parallel, how these representations are combined, and how choices between these representations are made based on valenced affect. In so doing, we integrate effects of individual differences in numeracy, metacognitive monitoring and editing, and reward seeking despite risk. Like some other contemporary memory-based approaches (e.g., Busemeyer, Pothos, Franco, & Trueblood, 2011; Pleskac 2007), we show how characteristics of memory shape decision-making, and especially how the abstract, yet robust, characteristics of gist memory shape risk preferences (Weber & Johnson, 2009). Parameters of the model varied in theoretically meaningful ways with differences in numeracy, monitoring, and sensation seeking, accounting for risk preferences.

This model is the first, to our knowledge, to explicitly formalize the key concepts of gist encoding, a gist hierarchy of multiple representations, and qualitative decision-making. Our mathematical model provides a novel extension to FTT by explaining gist selection in terms of category boundaries driven by qualitative distinctions that impose interpretive structure on the space of possible decisions. We extended FTT to explain problems with multiple gambles and unequal expected values. Our formalized theory, therefore, explains a variety of phenomena, integrating known effects and novel predictions.