Identification of Hostile Hemodynamics and Geometries of Cerebral Aneurysms: A Case-Control Study

Abstract

BACKGROUND AND PURPOSE:

Hostile hemodynamic conditions and geometries are thought to predispose aneurysms for instability and rupture. This study compares stable, unstable, and ruptured aneurysms while controlling for location and patient characteristics.

MATERIALS AND METHODS:

The hemodynamics and geometries of 165 stable, 65 unstable, and 554 ruptured aneurysms were compared. Hemodynamics was modeled using image-based computational fluid dynamics. Case-control pairs were selected matching aneurysm location, patient age, and sex. Paired Wilcoxon tests were used to compare hemodynamic and geometric variables among different aneurysm groups. The pairing was repeated 100 times, and the combined P values were calculated and adjusted for multiple testing.

RESULTS:

Ruptured aneurysms had lower minimum wall shear stress (P = .03), higher maximum wall shear stress (P = .03), more concentrated (P = .03) and mean oscillatory shear stress (P = .03), higher maximum velocity (P = .03), and more complex flows (vortex core-line length, P = .03) than stable aneurysms. Similarly, unstable aneurysms had more concentrated shear stress (P = .04) and more complex flows (vortex core-line length, P = .04) than stable aneurysms. Compared with stable aneurysms, ruptured aneurysms were larger (size ratio, aneurysm size/vessel size, P = .03), more elongated (aspect ratio, P = .03), and irregular (nonsphericity index, P = .03). Similarly, unstable aneurysms were larger (size ratio, P = .04), more elongated (aspect ratio, P = .04), and irregular (bulge location, P = .04; area-weighted Gaussian curvature; P = .04) than stable aneurysms. No significant differences were found between unstable and ruptured aneurysms.

CONCLUSIONS:

Unstable and ruptured aneurysms have more complex flows with concentrated wall shear stress and are larger, more elongated, and irregular than stable aneurysms, independent of aneurysm location and patient sex and age.

Many factors appear to be related to aneurysm rupture risk: location, size, morphology, hemodynamics, perianeurysmal environment, and patient history, among others.¹ It is well-understood that aneurysm rupture-risk estimation is based on the combination of such factors and is a complex process.² The American Heart Association and American Stroke Association guidelines for intracranial aneurysm management recommend that in addition to the size and location of the aneurysm and patient's age and health status, it may be reasonable to consider the morphologic and hemodynamic characteristics of the aneurysm when discussing its rupture risk.³ Thus, identification of “hostile” hemodynamic conditions and geometries that predispose aneurysms to instability and rupture is important to discriminate high- and low-risk aneurysms and guide the management strategy for each individual patient.⁴ Additionally, understanding adverse conditions and their connections to the underlying mechanisms of aneurysm progression, instability, and rupture is valuable for designing new therapeutic strategies targeting those mechanisms.⁵

Several previous studies have analyzed possible associations between hemodynamics and rupture^6–9 and between aneurysm morphology and rupture.^1,10 One of the most important limitations of most cross-sectional studies comparing ruptured and unruptured aneurysms is the inability to discriminate stable and unstable unruptured aneurysms.^8,9 On the other hand, the most important limitation of most longitudinal studies is the small sample size drawn from a highly selected population.^11–13 Additionally, only a few studies control for aneurysm location and/or patient characteristics.¹⁴ These limitations may cause confusion and apparent conflicts among the results of different studies.¹⁵

The goal of this study was to compare the hemodynamics and geometries of stable, unstable, and ruptured aneurysms while controlling for location and patient characteristics.

Materials and Methods

Data

Our data base contains >2000 cerebral aneurysms imaged with 3D rotational angiography and basic information including aneurysm status, location, size, patient age, and sex. The main contributors have been Inova Fairfax Hospital (Virginia), Mt. Sinai Medical Center (New York), and the Mayo Clinic (Minnesota). Age was divided into 3 groups: young (younger than 40 years), middle age (40–60 years), and old (older than 60 years). The images and data have been anonymized, and the study has been approved by the institutional review board of George Mason University. In the present study, a subset of 784 aneurysms was included, subdivided into the following subgroups (the distribution of aneurysms by location is presented in On-line Table 1):

1) Stable Aneurysms.

Untreated unruptured aneurysms followed longitudinally without noticeable enlargement, shape change, new symptoms, or rupture for at least 1 year were considered stable. A total of 165 stable aneurysms in 85 patients were considered.

2) Unstable Aneurysms.

Unruptured aneurysms were considered unstable if they either enlarged during follow-up (as determined by Sforza et al¹¹) or presented with symptoms such as cranial nerve palsy indicative of aneurysm instability. A total of 65 aneurysms in 55 patients were classified as unstable, with 53 aneurysms classified as growing and 12 with instabilities related to symptoms.

3) Ruptured Aneurysms.

The ruptured aneurysms group included all aneurysms confirmed as the source of subarachnoid hemorrhage. A total of 554 ruptured aneurysms in 501 patients were considered.

Models

Computational fluid dynamics models of all 2000 aneurysms in our data base have been created from the corresponding 3D rotational angiography images (at baseline for longitudinally followed aneurysms) using previously described methods.¹⁶ These models include the patient-specific vascular geometry, but because patient-specific flow conditions were not available, typical pulsatile flow conditions were derived from phase-contrast MR imaging measurements in healthy subjects and scaled with the area of the inflow vessel.¹⁷ Outflow boundary conditions consistent with flow splits given by the principle of minimal work (Murray law) were prescribed at the outlets. Vessel walls were approximated as rigid, and blood viscosity was approximated as Newtonian. The unsteady incompressible Navier-Stokes equations were numerically solved with a finite-element code developed in-house.¹⁸ All simulations were run in parallel shared-memory computers for 2 cardiac cycles. Data from the second cycle were used to quantitatively characterize the aneurysm hemodynamic environment by computing several flow variables over the aneurysm cavity, the aneurysm orifice, and the aneurysm surface.¹⁹ Additionally, several geometric variables were also computed to characterize the aneurysm morphology.²⁰ A list of the variables considered is provided in On-line Table 2.

Analysis

Case-control studies are a common and efficient means of studying rare diseases with long latency periods, such as ruptured/unruptured aneurysms.²¹ Matching of cases and controls is frequently used to control the effects of known potential confounding variables. The analysis of matched data requires specific statistical methods. The nonparametric Wilcoxon signed rank test for measured outcomes with 1:1 matching was used in the following 4 case-control studies: 1) stable-versus-ruptured aneurysms, 2) stable-versus-unstable aneurysms, 3) unstable-versus-ruptured aneurysms, and 4) unruptured-versus-ruptured aneurysms. In each study, case-control pairs were created and the mean values of hemodynamic and geometric variables of the 2 groups were statistically compared using a paired Wilcoxon test. The matching of cases and controls in each study was performed as detailed below:

1) Stable-versus-Ruptured Aneurysms.

In this case, the controls (stable aneurysms) were fewer than the cases (ruptured aneurysms); therefore, the matching was performed as follows: For each stable aneurysm, a list of ruptured aneurysms with matching location, sex, and age groups was created, and one of these matching aneurysms was randomly selected. A total of 134 aneurysm pairs were thus created.

2) Stable-versus-Unstable Aneurysms.

In this study, the cases (unstable aneurysms) were fewer than the controls (stable aneurysms); therefore, for each unstable aneurysm, a stable one was randomly selected from the list of stable aneurysms at the same location with matching sex and age groups. Sixty-five aneurysm pairs were created.

3) Unstable-versus-Ruptured Aneurysms.

In this study, for each unstable aneurysm, a ruptured one was randomly selected from the list of ruptured aneurysms matching location, sex, and age. Sixty pairs were created.

4) Unruptured-versus-Ruptured Aneurysms.

In this study, the controls (unruptured aneurysms) were fewer than the cases (ruptured aneurysms). Thus, for each unruptured aneurysm, a ruptured one was randomly selected from the list of unruptured aneurysms at the same location with matching sex and age groups. A total of 180 pairs were created.

Once the case-control pairs were created, the mean values of the hemodynamic and geometric variables of the 2 groups were statistically compared using a paired Wilcoxon test. Because the pairing processes described above involve random selection of a case-control pair from the list of available matches, a bootstrapping or random sampling with a replacement approach was used²² to improve the robustness of the analysis. Specifically, the pairing and tests were repeated 100 times, and the P values were combined with the Wilkinson method.²³ A difference was then considered statistically significant if the combined P value was <.05. The combined P values were then adjusted for multiple testing using the false discovery rate method.²⁴ It was verified that 100 pairings were enough by performing 200 pairings and verifying that the significance of the comparisons did not change. All statistical analyses were performed by using R scripts (R statistical and computing software; http://www.r-project.org).

Results

The general hemodynamic and geometric characteristics of the aneurysm groups considered in this study are summarized in the Table. This Table lists the mean values and SDs of each variable over each group.

Values of hemodynamic and geometric variables in stable, unstable, and ruptured aneurysms^a

Variable	Unruptured			Ruptured
	Stable	Unstable
		Symptoms	Growing
WSSmin	0.8 ± 1.9	0.3 ± 0.5	1.0 ± 4.5	0.4 ± 1.3
WSSmax	223.7 ± 187.5	235.0 ± 101.8	253.7 ± 170.2	377.5 ± 948.8
WSSmean	21.4 ± 18.5	16.6 ± 13.8	22.0 ± 22.1	23.2 ± 28.9
WSSnorm	0.6 ± 0.3	0.4 ± 0.3	0.5 ± 0.3	0.4 ± 0.3
SCI	3.78 ± 4.76	8.52 ± 9.44	5.52 ± 4.53	6.23 ± 6.88
LSA	45.8 ± 33.6	62.9 ± 29.7	58.8 ± 30.9	51.6 ± 33.0
OSImax	0.259 ± 0.137	0.358 ± 0.089	0.303 ± 0.125	0.317 ± 0.114
OSImean	0.012 ± 0.011	0.014 ± 0.008	0.017 ± 0.016	0.017 ± 0.017
Q	0.746 ± 0.805	1.360 ± 1.368	1.081 ± 0.957	0.730 ± 0.807
ICI	0.716 ± 0.763	1.193 ± 1.309	1.088 ± 0.941	0.791 ± 0.764
Vmax	62.9 ± 31.8	70.8 ± 19.6	80.4 ± 50.0	88.8 ± 62.6
VE	9.7 ± 6.4	8.7 ± 5.7	10.1 ± 6.1	9.8 ± 8.1
SR	226.2 ± 176.1	155.0 ± 131.4	202.9 ± 221.2	231.5 ± 260.7
VO	307.7 ± 241.1	218.0 ± 183.7	278.9 ± 279.0	317.4 ± 344.4
CORELEN	1.753 ± 3.313	2.726 ± 1.827	2.504 ± 3.043	2.378 ± 2.593
PODENT	0.176 ± 0.125	0.227 ± 0.115	0.228 ± 0.155	0.207 ± 0.137
Asize	0.687 ± 0.524	1.109 ± 0.603	0.933 ± 0.550	0.770 ± 0.398
Nsize	0.482 ± 0.309	0.690 ± 0.461	0.577 ± 0.311	0.429 ± 0.172
SizeR	1.834 ± 1.395	2.440 ± 1.127	2.533 ± 1.487	2.492 ± 1.373
AR	0.879 ± 0.607	1.308 ± 0.828	1.200 ± 0.831	1.304 ± 0.691
VOR	0.894 ± 3.355	1.220 ± 1.310	1.460 ± 2.906	0.919 ± 1.559
EI	0.273 ± 0.036	0.268 ± 0.021	0.263 ± 0.026	0.273 ± 0.025
NSI	0.202 ± 0.051	0.229 ± 0.080	0.211 ± 0.041	0.246 ± 0.054
BF	1.167 ± 0.465	1.414 ± 0.478	1.377 ± 0.574	1.322 ± 0.441
BL	0.290 ± 0.161	0.431 ± 0.170	0.361 ± 0.144	0.355 ± 0.163
CR	0.762 ± 0.144	0.793 ± 0.083	0.816 ± 0.118	0.785 ± 0.100
CP	0.210 ± 0.161	0.069 ± 0.170	0.139 ± 0.144	0.145 ± 0.163
UI	0.238 ± 0.144	0.207 ± 0.083	0.184 ± 0.118	0.215 ± 0.100
GAA	16.339 ± 17.905	5.861 ± 4.444	7.893 ± 8.034	12.763 ± 13.717

Note:—Q indicates aneurysm flow rate; ICI, inflow concentration index; VE, mean aneurysm velocity; SR, mean aneurysm shear rate; VO, mean aneurysm velocity; PODENT, POD entropy, flow instability; POD, proper orthogonal decomposition; Nsize, neck maximum size; EI, ellipticity index; BF, bottleneck factor; CR, convexity ratio; UI, undulation index; WSSnorm, normalized wall shear stress.

^aValues are given as mean ± SD.

Stable-versus-Ruptured Aneurysms

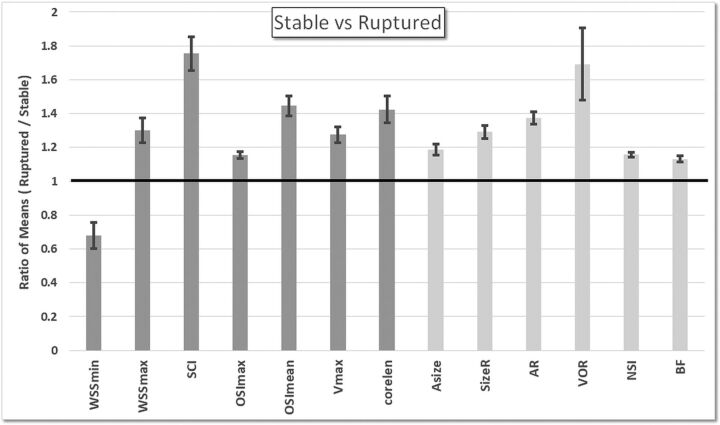
The statistically significant differences (P < .05 before correcting for multiple testing) between stable and ruptured aneurysms are summarized in Fig 1. The bars represent the ratio of the mean values of the ruptured aneurysm group over the mean values of the stable aneurysm group, and the error bars represent the variability of these ratios over the 100 random pairings. The mean and SDs of all variables over the 2 groups, along with the corresponding P values, are listed in On-line Table 3.

Fig 1.

Ratios of the mean values of the ruptured aneurysm group over mean values of the stable aneurysm group. Only hemodynamic (dark gray) and geometric (light gray) variables that were significantly different between these groups (P < .05 before adjusting for multiple testing) are included.

These results indicate that compared with stable aneurysms, after adjustment for multiple testing, ruptured aneurysms tend to have hemodynamic environments characterized by lower minimum wall shear stress (WSSmin, P = .03), higher maximum WSS (WSSmax, P = .03), more concentrated shear stress distributions (SCI, P = .03), more mean oscillatory shear stress (OSImean, P = .03), higher maximum velocity (Vmax, P = .03), and more complex flow patterns (vortex core-line length [CORELEN], P = .03). Additionally, ruptured aneurysms had geometries characterized by larger size (size ratio, aneurysm size/vessel size [SizeR], P = .03), more elongated shapes (aspect ratio [AR], P = .03), and more irregular shapes (nonsphericity index [NSI], P = .03).

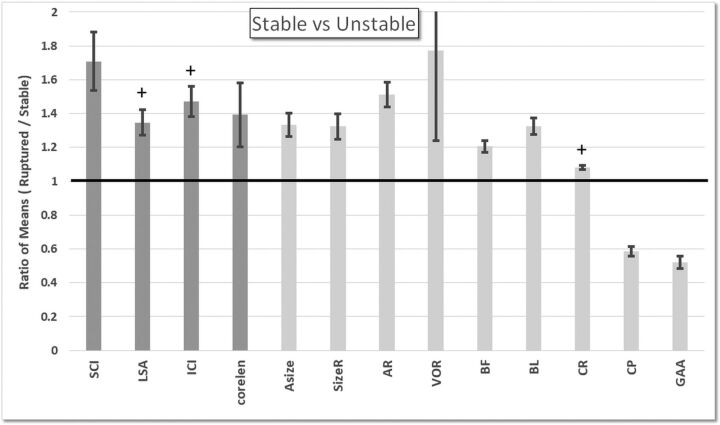
Stable-versus-Unstable Unruptured Aneurysms

Comparisons of hemodynamic and geometric variables between stable and unstable unruptured aneurysms are presented in On-line Table 4 and are summarized in Fig 2. These results indicate that unstable aneurysms tend to have more SCI (P = .04) and more complex flow patterns (CORELEN, P = .04) than stable aneurysms. Unstable aneurysms also tend to have larger areas under low WSS (percentage area under low WSS [LSA], P = .10 before adjustment) and more concentrated inflow jets (inflow concentration index, P = .07 before adjustment), but these associations did not reach statistical significance. Geometrically, unstable aneurysms are larger (aneurysm maximum size [Asize], P = .04; SizeR, P = .04), more elongated (AR, P = .04; volume-to-ostium ratio [VOR], P = .04), and more irregular in shape (bulge location [BL], P = .04; conicity parameter [CP], P = .04; area-weighted Gaussian curvature; [GAA], P = .04) than stable aneurysms.

Fig 2.

Ratios of mean values of the unstable aneurysm group over mean values of the stable aneurysm group. Only hemodynamic (dark gray) and geometric (light gray) variables that were significantly different (P < .05 before adjusting for multiple testing) or marginally significant (P < .1 before adjusting for multiple testing; marked with a plus sign) are included. ICI indicates inflow concentration index; BF, bottleneck factor; CR, convexity ratio.

Unstable-versus-Ruptured Aneurysms

No significant differences between unstable unruptured aneurysms and matched ruptured aneurysms were found, including both hemodynamic and geometric variables (see the results in On-line Table 5).

Unruptured-versus-Ruptured Aneurysms

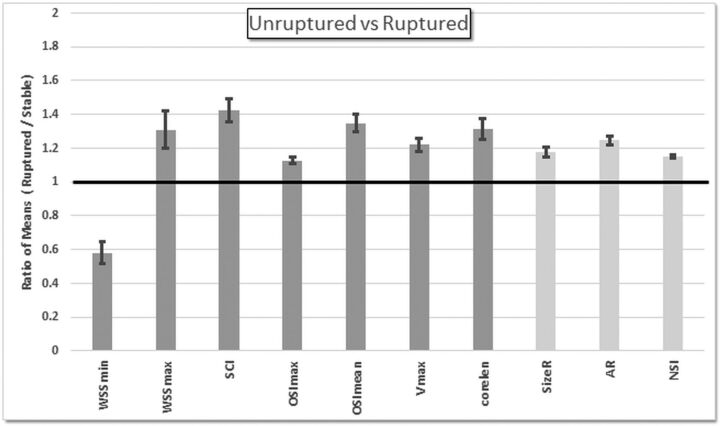
Results of the comparison of all unruptured aneurysms included in this study (stable and unstable combined) against matching ruptured aneurysms are presented in On-line Table 6 and summarized in Fig 3. Again, ruptured aneurysms had more SCI (P = .04) and more complex flow patterns (CORELEN, P = .04) with higher Vmax (P = .04) compared with unruptured aneurysms. They also tended to have lower WSSmin (P = .02 before adjustment) and larger WSSmax (P = .02 before adjustment), as well as more maximum oscillatory shear stress (OSImax, P = .02; OSImean, P = .02 before adjustment), but these associations became only marginally significant (P = .06) after adjusting for multiple testing. Geometrically, ruptured aneurysms were more elongated (AR, P = .04) and more irregular (NSI, P = .04) and tended to be larger (SizeR, P = .02 before adjustment), but the latter association became marginally significant (P = .06) after adjusting for multiple testing.

Fig 3.

Ratios of mean values of the ruptured aneurysm group over mean values of the unruptured aneurysm group. Only hemodynamic (dark gray) and geometric (light gray) variables that were significantly different between these groups (P < .05 before adjusting for multiple testing) are included.

Discussion

The current study attempts to characterize hostile aneurysm hemodynamics and geometry that could predispose aneurysms to instability and rupture while controlling for location, sex, and age. This knowledge is important for improved understanding of the mechanisms of wall degeneration and aneurysm progression.

The differences observed between stable and ruptured aneurysm pairs allow us to identify hemodynamic and geometric characteristics that are more prevalent in ruptured aneurysms. Our results indicate that these hostile hemodynamic characteristics include extreme values of wall shear stress (low and high), concentrated and oscillatory shear stress distributions, and complex intrasaccular flow patterns. Adverse aneurysm geometries include large, elongated, and irregular shapes. These characteristics are illustrated with 3 examples presented in Fig 4. Additionally, a simple correlation analysis was performed to identify variables correlated to one another. Groups of correlated variables (whose pair-wise regression coefficient was greater than 0.80) are presented in On-line Tables 7–9. Most interesting, no correlations were found between hemodynamic and geometric variables in this sample.

Fig 4.

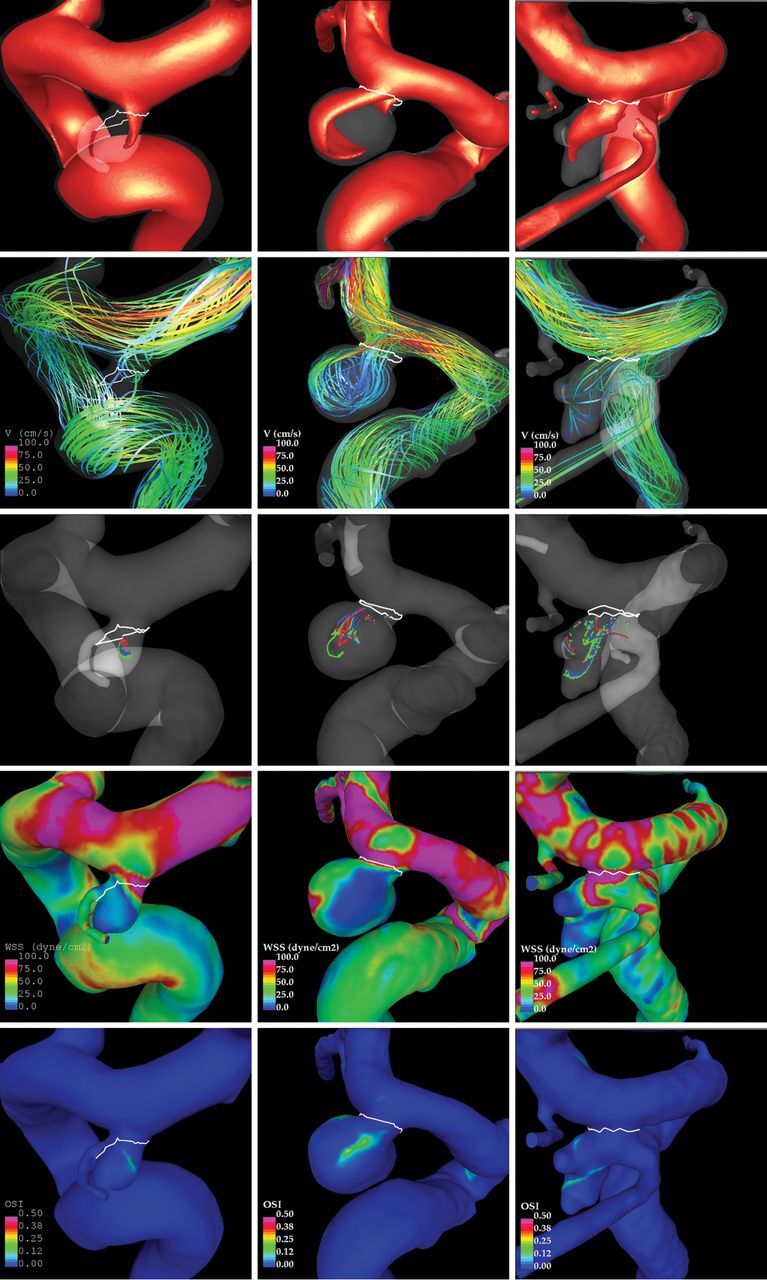
Examples of stable (left), unstable (middle), and ruptured (right) aneurysms at a single location (posterior communicating artery). Visualizations show, from upper to lower: inflow jet, flow pattern, vortex core lines at 4 instants during the cardiac cycle, wall shear stress, and oscillatory shear index.

Differences between stable and unstable aneurysms were less pronounced but in the same general direction as those between stable and ruptured aneurysms. Specifically, unstable aneurysms had more complex flow patterns with concentrated wall shear stress than stable aneurysms, and they were larger and more elongated and irregular. These features suggest that unstable and ruptured aneurysms differ from stable aneurysms in similar ways. Furthermore, no significant differences were found between unstable and ruptured aneurysms. These observations are consistent with a study²⁵ that found differences between symptomatic and asymptomatic posterior communicating artery aneurysms that were similar to the differences between symptomatic and ruptured aneurysms at this location. This finding suggests that hemodynamic environments and shapes of unstable aneurysms may resemble those of ruptured aneurysms, but further studies with larger samples are needed to confirm this conjecture. Finally, when comparing all unruptured aneurysms (stable and unstable combined) against ruptured aneurysms, differences similar to those observed between stable and ruptured aneurysms were observed. This is likely due to the larger proportion of stable aneurysms in the unruptured group.

Several studies have compared stable and unstable unruptured aneurysms, but without controlling for location or patient characteristics. One such study did not find significant geometric or hemodynamic differences (149 stable, 20 unstable),²⁶ while 2 other studies found differences in geometric (70 stable, 23 unstable)²⁷ and hemodynamic (17 stable, 16 unstable) characteristics.¹¹ Our findings agree with these latter studies. Two other studies found larger LSAs in unstable aneurysms compared with stable aneurysms after matching location and size (12 stable, 12 unstable)¹⁴ as well as sex and age (12 stable, 12 unstable).²⁸ In general, our results show similar trends, but LSA did not reach statistical significance.

In summary, the results of our study suggest that hostile hemodynamic environments (ie, more prevalent in ruptured and unstable aneurysms than in stable aneurysms) are characterized by complex flows and concentrated wall shear stress distributions, while adverse geometries include larger and more elongated and irregular shapes. This finding leads us to propose that through geometric and flow analysis, there are ways to a priori identify unruptured aneurysms that will evolve toward instability and will therefore be at a higher risk of rupture. Additionally, our study suggests that lumping stable and unstable aneurysms into a single group of unruptured aneurysms (as in most cross-sectional studies) still allows characterization of adverse conditions likely because of the higher prevalence of stable aneurysms in the unruptured population.

Our study has several limitations. Computational fluid dynamics models are based on several assumptions and approximations.¹⁹ Our sample size and available data were not large enough to allow us to match and control for more patient characteristics or to obtain more statistical significance. The unstable group contained growing and cerebral palsy cases, which should be studied separately with larger samples. This study identified several trends that suggest that hostile hemodynamics and geometries could help identify aneurysms at higher risk of instability and rupture and should be considered in studies aiming at further understanding the underlying mechanisms that contribute to the evolution of a cerebral aneurysm from stable to unstable and ultimately ruptured status.

Conclusions

Unstable and ruptured aneurysms have more complex flows with concentrated wall shear stress and are larger, more elongated, and irregular than stable aneurysms, independent of aneurysm location, sex, and age. These adverse conditions could be used to identify unruptured aneurysms at higher risk of rupture and should be taken into account in studies of the mechanisms responsible for aneurysm wall degradation and progression to instability and rupture.

ABBREVIATIONS:

AR

aspect ratio

Asize

aneurysm maximum size

BL

bulge location

CORELEN

vortex core-line length, flow complexity

CP

conicity parameter

GAA

area-weighted Gaussian curvature

LSA

percentage area under low WSS

max

maximum

min

minimum

NSI

nonsphericity index

OSI

oscillatory shear stress

SCI

concentrated shear stress

SizeR

size ratio (aneurysm size/vessel size)

Vmax

maximum velocity

VOR

volume-to-ostium ratio

WSS

wall shear stress