Model‐based assessment of the benefits and risks of recombinant tissue plasminogen activator treatment in acute ischaemic stroke

Abstract

Aims

Recombinant tissue plasminogen activator (rt‐PA) is the only first‐line agent approved by the US Food and Drug Administration to treat acute ischaemic stroke. However, it often causes the serious adverse event (AE) of haemorrhagic transformation. The present study developed a pharmacometric model for the rt‐PA treatment effect and AE and, using the developed model, proposed a benefit‐to‐risk ratio assessment scheme as a supportive tool to optimize treatment outcome.

Methods

The data from 336 acute ischaemic stroke patients were used. The treatment effect was assessed based on an improvement in National Institutes of Health Stroke Scale (NIHSS) scores, which were described using an item response theory (IRT)‐based disease progression model. Treatment failure and AE probabilities, and their occurrence times, were described by incidence and time‐to‐event models. Using the developed model, benefit‐to‐risk ratios were simulated under various scenarios using the global benefit‐to‐risk trade‐off ratio (GBR).

Results

High initial NIHSS score and middle cerebral artery (MCA) stroke were risk factors for treatment failure, where the failure rate with MCA stroke was 2.87‐fold higher than with non‐MCA stroke. The haemorrhagic transformation time was associated with longitudinal changes in NIHSS scores. The benefit‐to‐risk ratio simulated was highest in minor stroke severity, with GBR >1 in all scenarios, and the ratio with non‐MCA stroke was 2–3 fold higher than with MCA stroke.

Conclusions

The study demonstrated the feasibility of applying an IRT model to describing the time course of the rt‐PA treatment effect and AE. Benefit‐to‐risk ratio analyses showed that the treatment was optimal in non‐MCA stroke with minor stroke severity.

What is Already Known about this Subject

• In assessments of the recombinant tissue plasminogen activator (rt‐PA) treatment effect in acute ischaemic stroke, approaches using categorized National Institutes of Health Stroke Scale scores have yielded contradictory results.

• There have been no previous studies that have quantitatively analysed rt‐PA effects and adverse events (AEs) together, from the perspective of a benefit‐to‐risk ratio assessment.

What this Study Adds

• Our study demonstrated the feasibility of using an item response theory model to predict rt‐PA treatment effects and the AE of haemorrhagic incidence, and to assess benefit‐to‐risk ratios for the treatment.

• Benefit‐to‐risk ratio analyses showed that the treatment was optimal in non‐MCA stroke with minor stroke severity.

Introduction

Acute ischaemic stroke is defined as an episode of neurological dysfunction caused by focal cerebral, spinal or retinal infarction, and accounts for approximately 80% of strokes 1, 2. When a stroke occurs, blood flow to the brain tissue is interrupted, cerebral metabolism can be altered and primary neuronal injury can occur in the centre of the infarcted tissue, which can ultimately result in cell death 3. In this respect, rapidly resolving blood clots and achieving revascularization have been regarded as a primary goal of the management of acute ischaemic stroke.

To date, however, http://www.guidetopharmacology.org/GRAC/ObjectDisplayForward?objectId=2392 (rt‐PA) has been the only first‐line agent available for the treatment of early detected stroke 4.

A variety of scoring systems have been proposed to evaluate the effect of treatment on disease severity, which is not measurable in nature for many types of disease, including neurological diseases. The National Institutes of Health Stroke Scale (NIHSS) scoring system, consisting of 13 tests, is widely used in assessing neurological deficit in stroke patients 5. For simplicity and convenience, the NIHSS score is often transformed into a categorical scale using cut‐off points selected to define different levels of disease severity from a clinical significance point of view 6.

However, approaches using categorized NIHSS scores based on cut‐off points have yielded contradictory results. For example, it has previously been shown that when clinical improvement was defined as a decrease of more than four points in the NIHSS score, the NIHSS score decrease at 24 h after the treatment was not statistically significant in the treatment group compared with the placebo group 7. However, when the assessment was made at 90 days after the treatment, the improvement was significantly better in the rt‐PA treatment group than in the placebo group. By contrast, a reanalysis of the data presented in the above‐cited study, where a cut‐off point was defined differently, as a decrease of more than five points in the NIHSS score, showed that clinical improvement when using rt‐PA was statistically significant even at 24 h after treatment 8. This clearly shows the limitation of using categorical scoring systems in analyses, and indicates the importance of establishing an appropriate criterion for accurately assessing clinical improvement. In general, the categorization of data is not recommended, not only because of the loss of information, but also because of potential increases in type I errors 9.

In addition, given the potential adverse event (AE) of haemorrhagic transformation associated with rt‐PA treatment, researchers have proposed scoring systems to evaluate the risk factors associated with the occurrence of haemorrhagic events 10, 11, 12, 13 and to distinguish those patients who are vulnerable to such AEs 10, 13, 14. However, to date, there have been no studies that have quantitatively analysed the rt‐PA effect and AE together, from the perspective of a benefit‐to‐risk ratio assessment.

Using noncategorized NIHSS scores, the primary aims of the present study were to develop an integrative quantitative model for rt‐PA treatment that could predict: (i) the longitudinal change in stroke progression and (ii) the incidence and occurrence time of dropouts (i.e. treatment failure) and haemorrhagic transformation. The secondary aim was to apply the developed model to propose a benefit‐to‐risk ratio assessment scheme for patient subpopulations. The model was developed within the framework of item response theory (IRT), which has been increasingly used in the analysis of clinical outcome based on a scoring system composed of multiple tests. It was anticipated that the developed approach could be used as a supportive tool for better evaluation and management of revascularization treatment in acute ischaemic stroke.

Methods

Data

Data were retrospectively collected from the electronic medical records of patients who had received intravenous rt‐PA treatment at Yonsei University Severance Hospital, Seoul, Korea, during the period 2006–2014. A total of 336 patients were eligible for the analysis. The inclusion criterion was being an acute ischaemic stroke patient who had been treated with rt‐PA as first‐line therapy and had NIHSS scores available before and after rt‐PA treatment.

The NIHSS score, which represents the total score derived from 13 items (or 13 tests), measures neurological deficits for the following items: ʻlevel of consciousness (LOC): responsivenessʼ (Test 1); ʻ LOC: questionsʼ (Test 2); ʻ LOC: commandsʼ (Test 3); ʻhorizontal eye movementʼ (Test 4), ʻvisual field testʼ (Test 5); ʻfacial palsyʼ (Test 6); ʻmotor armʼ (Test 7); ʻmotor legʼ (Test 8); ʻlimb ataxiaʼ (Test 9); ʻsensoryʼ (Test 10); ʻlanguageʼ (Test 11); ʻspeechʼ (Test 12) and ʻextinction and inattentionʼ (Test 13). Each test was scored from 0 to its maximum value, where the maximum varied from 2 to 4, depending on the given test. Accordingly, the NIHSS score per patient ranged from 0 to 42, with a higher NIHSS score indicating more severe neurological impairment.

Data inspection revealed that most of the patients received anticoagulant or antiplatelet agents the day after rt‐PA treatment, even if revascularization was successfully achieved using rt‐PA treatment, indicating that receiving rt‐PA treatment alone was not sufficient to promote a full recovery from neurological damage. Accordingly, only NIHSS scores up to 24 h after the onset of stroke were used in the analysis to avoid confounding the effect of rt‐PA with that of other agents, as illustrated in the literature 2. Consequently, the number of NIHSS scores per patients used in the analysis was limited to between one and eight.

This retrospective study was approved by the Institutional Review Board of Yonsei University Severance Hospital.

IRT

IRT has been developed for the analysis and scoring of tests, questionnaires and similar tools used to assess a subject's ability, attitude or other variables. Assuming a test consisting of multiple items, where each item is not equally difficult, this theory focuses on the item itself, whereas other approaches focus on a test level assuming equal difficulty among items. In this context, the term item represents any informative item measured on a discrete scale, such as multiple‐choice questions, questionnaires to indicate rating, or symptoms scored as present/absent.

IRT‐based models, often referred to as latent trait models, can be classified by the type of data they are used to analyse, and if the data is polychotomous, they can be further classified into nominal response models for nominal data and graded response models (GRM) or partial credit models (PCM) for ordered data 15. In the present study, both the GRM and PCM were tested.

Baseline model for NIHSS scores

The first step in IRT modelling is to characterize the probability distribution of the latent severity of each item comprising NIHSS scores at baseline (t = 0) using an item characteristic curve (ICC), which is described in terms of a logistic model.

For the GRM approach, the ICC is formulated as follows 16:

$$P\left(Y_{\mathit{ij}}\ge k+1\right)=\frac{e^{{\alpha }_j\left(D_i-{\beta }_{\mathit{jk}}\right)}}{1+e^{{\alpha }_j\left(D_i-{\beta }_{\mathit{jk}}\right)}},k=1,..,m_j-1$$ (1)

$$P\left(Y_{\mathit{ij}}=k+1\right)=P\left(Y_{\mathit{ij}}\ge k+1\right)-P\left(Y_{\mathit{ij}}\ge k+2\right)$$ (2)

where P is the probability, Y _ij the i‐th subject's response to the j‐th item, k the category and m_j the number of categories of the j‐th item, with P(Y_ij = 1) = 1 − P(Y_ij ≥ 2) and P(Y_ij = m_j) = P(Y_ij ≥ m_j). In Equation (1), α_j is the slope or scale parameter denoting the discrimination power of the j‐th item, quantifying the capability to discern patients' ability (α_j > 0), β_jk is the location or threshold parameter denoting the item difficulty (β_jk > 0) and D_i is the patient‐specific ability common to all items, denoting latent trait or unobserved disease severity, which is assumed to follow a standard normal distribution. β_jk is the point on the latent scale where the probability that a patient would respond to category k or higher in the j‐th item is 0.5.

For the PCM approach, the ICC is formulated as follows:

$$P\left(Y_{\mathit{ij}}=1\right)=\frac{1}{1+{\sum }_{c=1}^{m_j-1}\mathit{exp}\left[{\sum }_{v=1}^c{a}_j\left(D_i-b_{\mathit{jv}}\right)\right]}$$ (3)

$$P\left(Y_{\mathit{ij}}=k+1\right)=\frac{\mathit{exp}\left[{\sum }_{v=1}^k{a}_j\left(D_i-b_{\mathit{jv}}\right)\right]}{1+{\sum }_{c=1}^{m_j-1}\mathit{exp}\left[{\sum }_{v=1}^c{a}_j\left(D_i-b_{\mathit{jv}}\right)\right]},k=1,..,m_j-1$$ (4)

In the above parameterization, a_j is the slope parameter, similar to α_j in the GRM model. However, b_jv has a different meaning, in that it is defined as the item step or intersection parameter denoting the points on the latent trait scale where the plots of P(Y_ij = k) and P(Y_ij = k + 1) intersect 17. b_jv is not sequentially ordered with increasing v because it represents the relative difficulty in transiting from category k to k + 1.

Disease progression model for NIHSS scores

After the ICC has been characterized, the rt‐PA treatment effect was assessed based on disease progression or longitudinal change in NIHSS score over the first 24 h, which was described as being driven by the corresponding longitudinal change of latent disease severity D_i(t) as follows:

$$D_i\left(\mathrm{t}\right)=D{0}_i+{\mathit{AMP}}_i·\left(1-e^{-{\mathit{SLO}}_i·t}\right)$$ (5)

where D0_i, AMP_i and SLO_i are, respectively, the initial value, the amplitude and the slope of D(t) for the i‐th subject. D_i(t) in Equation (5) was then substituted as D_i(t) in Equations (1), (3) and (4) to estimate D0_i, AMP_i and SLO_i, with α_j and β_jv being fixed at their estimates obtained in the previous step of characterizing the ICC for baseline NIHSS scores.

In modelling disease progression in Equation (5), the natural course of severity progression could not be incorporated because placebo treatment data were unavailable for the patients due to ethical considerations. Using the parameter estimates thus obtained, the NIHSS score was predicted as the sum of Y_ij, the value of which was determined by comparing P(Y_ij = k) with a generated random number from the uniform distribution (0, 1).

Incidence model for dropout

The dropout from rt‐PA monotherapy due to no treatment effect and receiving additional treatment during the first 24 h after rt‐PA treatment was described using a logistic model as shown in Equation (6), where θ₀ is the baseline logit, COV_i is a set of covariates and θ_i is a set of associated covariate coefficients.

$$P\left(\mathrm{Y}=1\right)=\frac{exp\left({\theta }_0+\sum {\theta }_i·{\mathrm{COV}}_i\right)}{1+exp\left({\theta }_0+\sum {\theta }_i·{\mathrm{COV}}_i\right)},\text{where}\mathrm{Y}=1\text{for dropout}$$ (6)

Time to event (TTE) model for dropout

To assess the probability of dropout from rt‐PA monotherapy with time, a TTE model was used to describe the time to dropout, where various hazard functions were tested, including constant, Weibull, log‐logistic and Gompertz hazard functions, as shown below.

$$\begin{array}{cc}\mathrm{S}\left(\mathrm{t}\right)=exp\left(-{\int }_0^{t}h\left(\tau \right)\mathit{d\tau }\right)& \\ \mathrm{h}\left(\mathrm{t}\right)=\mathrm{\lambda }& \left(\text{Constant}\right)\\ =\mathrm{\lambda }\cdot \mathrm{\gamma }\cdot t^{\mathrm{\gamma }-1}& \left(\text{Weibull}\right)\\ =\frac{\mathrm{\lambda }\cdot \mathrm{p}\cdot {\left(\mathrm{\lambda }\cdot \mathrm{t}\right)}^{\left(p-1\right)}}{1+{\left(\mathrm{\lambda }\cdot \mathrm{t}\right)}^p}& \left(\mathrm{Log}-\text{logistic}\right)\\ =\mathrm{\lambda }\cdot exp\left(\mathrm{\gamma }\cdot \mathrm{t}\right)& \left(\text{Gompertz}\right)\end{array}$$ (7)

S(t) denotes survival probability and h(t) hazard. The predicted hazard h(t) was then compared with the observed hazard h(t)_obs for goodness of fit, where h(t)_obs was obtained as a conditional probability, as shown in Equation (8):

$$h{\left(t\right)}_{\mathit{obs}}=\frac{N{\left(t\right)}_{\mathit{new}}}{N\left(t\right)}$$ (8)

where N(t)_new is the number of patients who dropped out between t‐Δt and t, and N(t) is the number of patients who did not drop out until t‐Δt 18, with ∆t chosen to be 0.01 h.

Incidence model for haemorrhagic transformation

Haemorrhagic transformation was defined as clinical deterioration verified by computed tomography (CT) or magnetic resonance imaging within 36 h after rt‐PA administration 19, 20. The incidence model was described using a logistic model similar to that shown in Equation (6).

TTE model for haemorrhagic transformation

As the exact time for haemorrhagic transformation was not known, where time was defined as the time from treatment initiation, the haemorrhagic event was conjectured to have occurred between the last observation time of the NIHSS score and the time of the CT scan. This was based on the emergency management guidelines for rt‐PA treatment in acute ischaemic stroke, which require that CT scans should be obtained 24 h before the beginning of anticoagulant or antiplatelet treatment 21 and additionally require that scans should be performed when patients develop symptoms of deterioration such as headache, nausea or vomiting 14, 21. Accordingly, the TTE model for haemorrhagic transformation was built using the interval censored time between the last observation and the time of the CT scan. Similarly to the TTE model for dropout, constant, Weibull and log‐logistic functions were examined for the hazard model.

Covariate effects

At each modelling stage, a step‐wise covariate modelling approach was used based on the criteria of P < 0.01 [which corresponds to an objective function value (OFV) difference of 6.63 at a degree of freedom of 1] for forward selection and P < 0.001 (which corresponds to an OFV difference of 10.83 at a degree of freedom of 1) for backward deletion. Covariate effects were tested for demographics; past/present medical and disease history, including hypertension, stroke, diabetes and cardiovascular diseases; and baseline status, including NIHSS score, location of infarction, platelet count, blood glucose, international normalized ratio (INR) and blood pressure. Furthermore, time to treatment (TTT) and weight‐normalized dose (ʻdoseʼ) were tested. Histories of hypertension, stroke and diabetes were treated as dichotomous variables of ʻpresenceʼ vs. ʻabsenceʼ, and cardiovascular disease as a categorical variable ranging from 0 to 4 associated with the number of cardiovascular diseases that patients have. Location of infarction was assessed for middle cerebral artery (MCA) stroke vs. non‐MCA stroke. NIHSS score, platelet count, glucose, INR, blood glucose, TTT and dose were treated as continuous variables. For TTE models, a covariate search was performed using two different approaches, one by incorporating covariates directly into parameters of hazard function, and the other by implementing them using a proportional hazard modelling framework, where NIHSS score change with time was included in potential covariates to check for the influence of time‐varying severity of disease progression.

Benefit‐to‐risk ratio analysis

In this analysis, benefit was defined as a reduction of four points in NIHSS score or latent disease severity [D_i(t) in Equation (5)] at 24 h after rt‐PA administration, and risk was defined as an occurrence of haemorrhage transformation within 36 h after rt‐PA administration.

Assuming 10 scenarios (five for MCA infarction and five for non‐MCA infarction), 100 simulated datasets, each with 1000 subjects, were generated using the developed models: disease progression, drop‐out incidence and TTE haemorrhage models. Simulated subjects were classified into minor (NIHSS score 1–5), moderate (NIHSS score 5–15), moderate‐to‐severe (NIHSS 16–20) and severe (NIHSS 21–42) groups [6]. Then, for each dataset, the benefit‐to‐risk ratio was estimated using the global benefit–risk trade‐off ratio (GBR) 22, 23, which is defined in Equation (9) (see Supporting Information for the derivation):

$$\mathrm{R}=\frac{P_1+\alpha ·P_2}{\left(1-\alpha \right)·P_4+P_5}$$ (9)

P₁:

Probability for benefit without risk

P₂:

Probability for benefit with risk

P₄:

Probability for no benefit with risk

P₅:

Probability for drop‐out.

P₅:

Probability for drop‐out.

α:

Constant (0 < α < 1)

Software and model evaluation

All models were built using NONMEM 7.3.0 (ICON Development Solutions, Hanover, MD, USA) and the Laplacian method. Perl‐Speaks‐NONMEM 3.6.2 and R (3.2.2) were used for graphical representation of the data 24, 25. Model selection was performed on the basis of OFV, the Akaike information criterion and the precision of parameter estimates. For model evaluation, goodness‐of‐fit plots, such as a logistic plot for the IRT model, a bar plot for the incidence model and a hazard plot for TTE models, were examined. A visual predicted check (VPC) was then performed by simulating 1000 data sets and checking that the 95% confidence interval of simulated values includes observed values, and a Kaplan–Meier mean covariate plot was additionally investigated when the model included time‐varying covariates 26.

Nomenclature of targets and ligands

The key protein target in this article is hyperlinked to the corresponding entry in http://www.guidetopharmacology.org, the common portal for data from the IUPHAR/BPS Guide to PHARMACOLOGY 27, and is permanently archived in the Concise Guide to PHARMACOLOGY 2017/18 28.

Results

Data

Table 1 summarizes patient characteristics, including basic demographics, disease history, baseline status and treatment factors related to intravenous rt‐PA treatment. The median age of patients (59.8% of whom were male) was 69 years and the median weight was 61 kg. In terms of medical and disease history, 34.2% of patients had taken an antiplatelet agent or an anticoagulant, 67.3% had been diagnosed with hypertension, 22.3% had cerebrovascular events and 56.5% had cardiovascular diseases other than hypertension. For baseline status, the median NIHSS score was 14, and 73.2% of patients had MCA stroke. For treatment factors, the median time to treatment from symptom onset was 1.63 h, additional therapy for revascularization such as intra‐arterial thrombolysis and endovascular treatment was conducted in 31.8% of patients, and haemorrhagic transformation within 36 h after treatment was observed in 16.2% of patients receiving rt‐PA monotherapy.

Table 1.

Patients’ characteristics

Demographics
Gender, no. (%)	Male: 201 (59.8)
	Female: 135 (40.2)
Age (years), median (range)	69 (26–90)
Weight (kg), median (range)	61 (37–130)

Medical and disease history
Premedication, no. (%)	No: 221 (65.8)
	Yes: 115 (34.2)
Hypertension, no. (%)	No: 110 (32.7)
	Yes: 226 (67.3)
Previous stroke, no. (%)	No: 261 (77.7)
	Yes: 75 (22.3)
Diabetes, no. (%)	No: 248 (73.8)
	Yes: 88 (26.2)
Cardiovascular diseases, no. (%)	No: 146 (43.5)
	Yes: 190 (56.5)
	(1:130, 2:47, 3:11, 4:2)a

Baseline status
NIHSS score, median (range)	14 (2–36)
Location of infarction, no. (%)	MCA: 246 (73.2)
	PCA: 12 (3.6)
	Basilar: 18 (5.4)
	Multiple: 33 (9.8)
	Others: 27 (8.0)
Creatinine (mg dl –1 ), median (range)	0.95 (0.4–14.9)
Platelet count (× 10 3 μl), median (range)	233 (107–568)
Glucose (mg dl –1 ), median (range)	124.5 (67–580)
INR, median (range)	0.97 (0.78–3.32)
Systolic blood pressure (mmHg), median (range)	150 (93–270)
Diastolic blood pressure (mmHg), median (range)	81 (46–210)

Treatment factors
Time to treatment (h), median (range)	1.63 (0.23–3.82)
Dose (mg kg –1 ), median (range)	0.9 (0.36–1.45)
Additional therapy, no. (%)	No: 229 (68.2)
	Yes: 107 (31.8)
Haemorrhage in rt‐PA treatment only, no. (%)	No: 192 (83.8) Yes: 37 (16.2)

INR, international normalized ratio; MCA, middle cerebral artery; NIHSS, National Institutes of Health Stroke Scale; PCA, posterior cerebral artery; rt‐PA, recombinant tissue plasminogen activator

^aIn A:B, A means the number of cardiovascular diseases each patient had and B the number of patients

Baseline model for NIHSS scores

The GRM described baseline NIHSS scores better than the PCM (7613.71 vs. 7776.01 in OFV, respectively), yielding model parameter estimates for 13 tests, as shown in Table 2, and ICCs, as displayed in Figure 1. Among the 13 tests, Test 7 for dysarthria was found to have the highest discrimination power for neurological deficit (α₇ = 2.864) and Test 10 for limb ataxia had the lowest discrimination power (α₁₀ = 0.001). The discrimination power is also reflected in Figure 1, in which the slope of the ICC of Test 7 was the steepest and that of Test 10 was almost flat. Estimation of α₁₀was not successful because the majority of patients received a score of 0 in this test, so that α₁₀ was fixed to 0.001. β _10,2 was also fixed to zero as its estimate was almost zero with a large relative standard error (RSE, %).

Table 2.

Item characteristic curve parameter estimates (% relative standard error) for baseline National Institutes of Health Stroke Scale scores

j	αj	βj1	βj2	βj3	βj4
1	0.443 (46.5)	4.051 (45.6)	3.075 (38.5)	3.851 (42.8)
2	0.183 (97.5)	11.44 (98.4)	−10.4 (98.8)
3	0.337 (62.3)	5.313 (63.6)	−3.064 (70.9)
4	0.710 (19.0)	0.172 (123.7)	0.695 (31.1)
5	0.454 (23.7)	3.293 (31.1)	−4.215 (27.6)	8.39 (25.9)
6	0.991 (20.6)	−1.44 (15.6)	0.351 (40.6)	4.367 (19.1)
7	2.864 (49.8)	−1.117 (10.3)	−0.320 (36.9)	−0.493 (59.1)	0.995 (13.0)
8	2.131 (25.3)	−0.918 (13.3)	−0.272 (44.1)	−0.038 (383.6)	1.656 (10.4)
9	0.739 (20.8)	−0.671 (29.5)	2.928 (16.9)
10	0.001 FIX	3989 (7.37)	0 FIX
11	0.184 (73.1)	11.28 (75.4)	−3.935 (88.4)	−3.349 (75.1)
12	0.629 (37.8)	−3.312 (29.6)	−0.104 (200.4)
13	0.140 (97.2)	17.51 (98.2)	−10.02 (100.9)

α_j, slope or scale parameter denoting the discrimination power of test j; β_jv, test step or intersection parameter denoting the points on the latent trait scale, where the plots of P(Y_ij = k) and P(Y_ij = k + 1) intersect, with Y_ij being a test score; j, test number (j = 1, 2, ... 13), v, category number (v = 1, 2, 3, 4)

Figure 1.

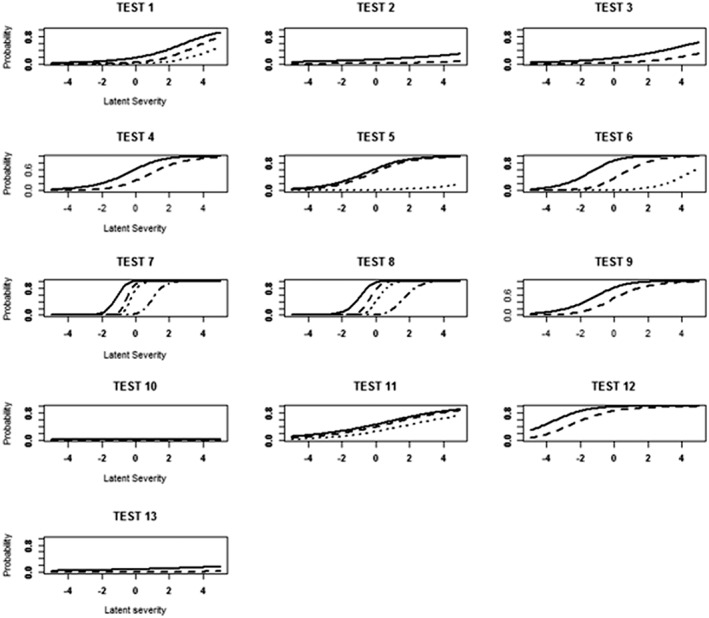
Item characteristic curves estimated for each test. The x‐axis shows severity, and the y‐axis the predicted probability of getting a score greater than 1 (solid line), 2 (dashed line), 3 (dotted line) and 4 (dot–dash line), respectively

To check the reliability of the ICC, the VPC for the predicted probability of receiving a specific score for each test based on the ICC was compared with the corresponding observed probability, as displayed in Figure 2. Apart from a few tests (e.g. Tests 7 and 8), the overall observed probability was satisfactorily included in the 95% confidence interval of the predicted probability.

Figure 2.

Visual predictive check for item characteristic curve. The x‐axis shows latent severity, and the y‐axis the probability of getting a specific score for each test. Solid lines are observed probability and shaded areas mean 95% confidence interval of predicted probability

Disease progression model for NIHSS scores

The estimates of D0, AMP and SLO, and the typical or population median values of D0_i, AMP_i and SLO_i, are shown in Table 3. Attempts to estimate the interindividual variability for SLO were unsuccessful. Despite the high interindividual variability of model parameters, no significant covariate was found. The VPC for each test indicates that almost all the observed probability was well covered by the 95% confidence interval of the model prediction (Figure 3A). The VPC for total NIHSS scores displayed in Figure 3B shows that overestimation occurred after about 5 h, and the degree of overestimation increased with time.

Table 3.

Parameter estimates for disease progression model for National Institutes of Health Stroke Scale (NIHSS) scores, incidence and time‐to‐event models for dropout and haemorrhagic transformation

Model	Parameter	Estimate (% relative standard error )
DIS	D0	−0.074 (81.1)
	AMP	−1.245 (17.4)
	SLO (h−1)	0.536 (27.6)
	ω2 D0 [CV (%)]	105.3 (6.26)
	ω2 AMP [CV (%)]	164.7 (19.6)
DROP INC	θ 0	−3.468 (13.4)
	θ NIHSS0	0.127 (18.4)
	θ INF	1.115 (31.9)
DROP TTE	γ	1.325 (25.2)
	λ	0.205 (30.6)
	θ CNIHSS0	0.469 (25.2)
HEM	γ	0.0915 (24.3)
	λ	7.19 *10−6 (36.1)
	θ NIHSS	0.056 (34.6)

AMP, amplitude; CV, coefficient of variation; DIS, disease progression model for NIHSS scores; DROP_INC, incidence model for dropout; DROP_TTE, TTE model for dropout; D(t), longitudinal change of latent disease severity; HEM, TTE model for haemorrhagic transformation; NIHSS0, initial NIHSS score; SLO, slope of D(t); TTE, time to event

For DIS, the model is as follows: D(t) = D0 + AMP · (1 − e^{−SLO · t})

For DROP_INC, DROP_TTE and HEM, the models are as follows:

P(Y = 1) = $\frac{exp\left({\theta }_0+{\mathrm{\theta }}_{\text{NIHSS}0}·\text{NIHSS}0+{\mathrm{\theta }}_{\mathrm{INF}}·\mathrm{INF}\right)}{1+exp\left({\theta }_0+{\mathrm{\theta }}_{\text{NIHSS}0}·\text{NIHSS}0+{\mathrm{\theta }}_{\mathrm{INF}}·\mathrm{INF}\right)}$ for DROP_INC

h(t) = λ ·  exp (γ · t) ·  exp (θ_CNIHSS0 · CNIHSS0) for DROP_TTE

h(t) = λ · γ · t^γ − 1 ·  exp (θ_PNIHSS · PNIHSS) for HEM

where INF denotes location of infarction, NIHSS0 denotes observed initial NIHSS score; CNIHSS0 denotes categorized NIHSS0, defined as CNIHSS0 = 1 for NIHSS0 ≤ 15, CNIHSS0 = 2 for 16 ≤ NIHSS0 ≤ 20 and CNIHSS0 = 3 for NIHSS0 ≥ 21; and PNIHSS denotes predicted NIHSS score

Figure 3.

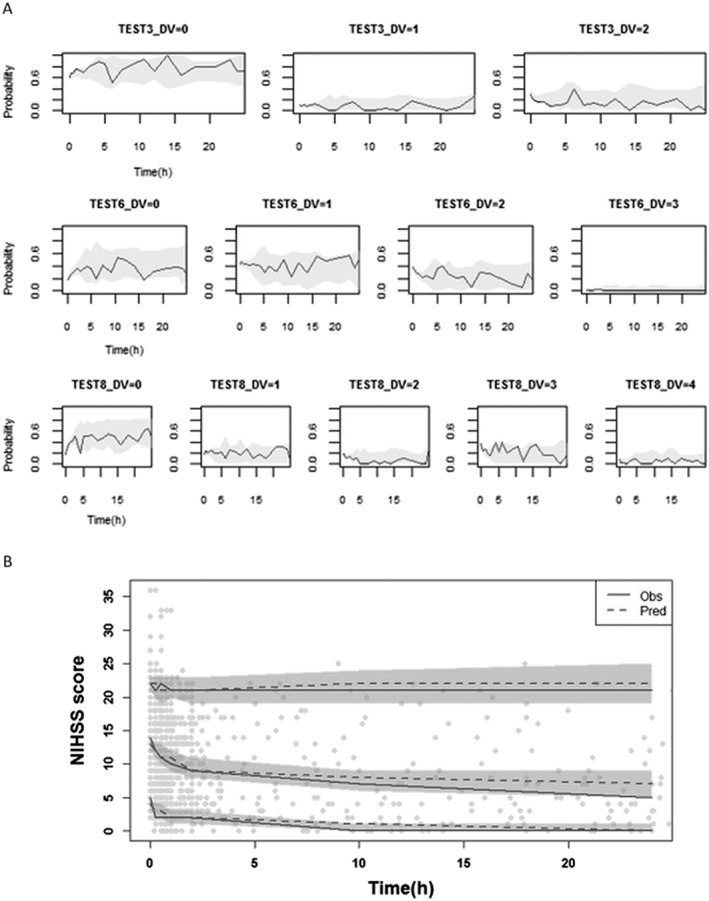
(A) Visual predictive check for disease progression model for National Institutes of Health Stroke Scale (NIHSS) scores of individual test for first 24 h after intravenous recombinant tissue plasminogen activator (rt‐PA) for three selected tests with m _j = 3 (Test 3: upper), 4 (Test 6: middle) and 5 (Test 8: lower), with m _j being the number of category of j‐th item [see Equation (1)]. Solid lines stand for observed probability and grey areas are the 95% confidence interval of the predicted probability. (B) Visual predictive check for the disease progression model for total NIHSS scores for the first 24 h after intravenous rt‐PA. Obs, observation; Pred, prediction

Incidence model for dropout

The observed initial NIHSS score, denoted as NIHSS0, and location of infarction were significant covariates for the incidence of dropout from rt‐PA monotherapy due to treatment failure and requiring an additional therapy during the hyperacute phase (Table 3). This result indicates that patients with MCA stroke are 2.87 times [= 0.0868/0.0303 from θ₀= −3.468 and θ_i= 1.115 substituted in Equation (6)] more likely to need additional therapy. The interaction between NIHSS0 and location of infarction was not significant, and neither TTT nor dose was significant either. Figures 3B and 4A display goodness‐of‐fit plots for the incidence model. The NHISS score producing 50% of population dropout was approximately 18–19 for MCA stroke and 27–28 for non‐MCA stroke. Although the overall prediction followed the observation, misfits were observed for some NIHSS scores, particularly for non‐MCA stroke, which was probably the result of the imbalanced distribution of observed NIHSS scores.

Figure 4.

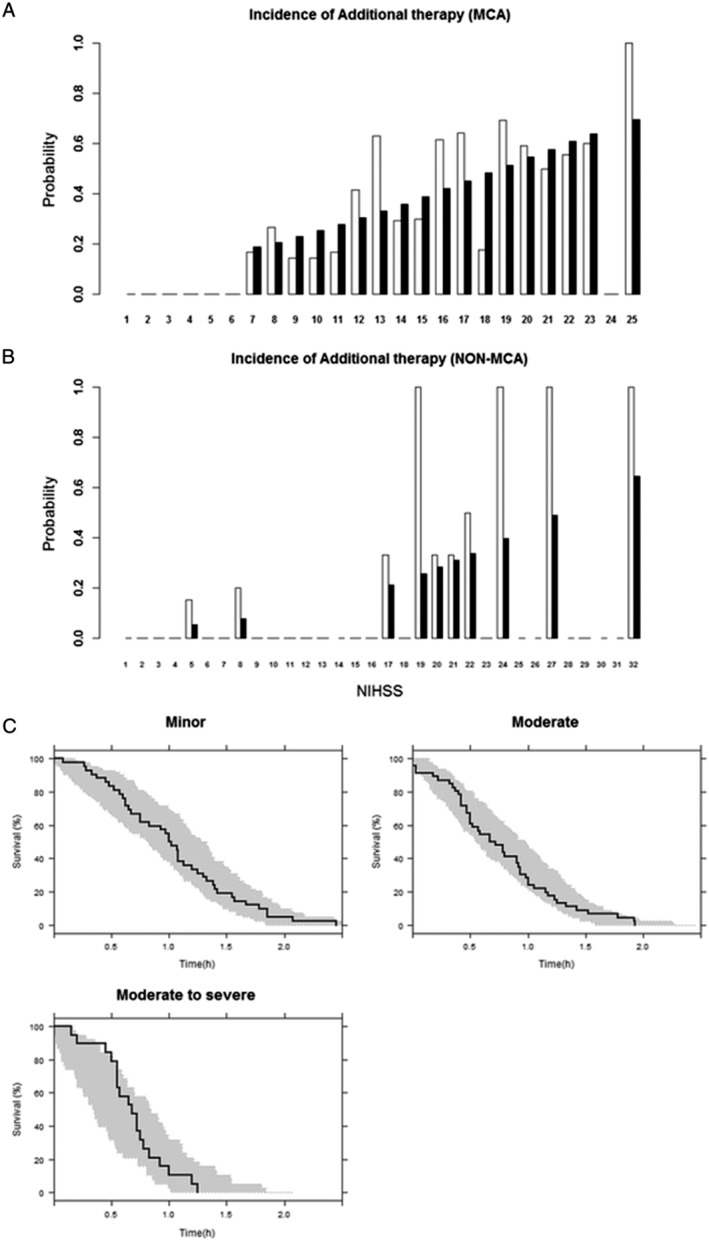
(A) Goodness of fit plot for the incidence model for dropout for the middle cerebral artery (MCA) group. The x‐axis shows the observed initial National Institutes of Health Stroke Scale (NIHSS) score, and the y‐axis the probability of dropout following the recombinant tissue plasminogen activator treatment (black bar: prediction, white bar: observation). (B) Goodness‐of‐fit plot for incidence model for dropout for non‐MCA group. (C) Visual predictive check for survival predicted by time‐to‐event model for dropout, obtained using the Gompertz hazard. Survival curves denote Kaplan–Meier survival probability, and the shaded areas represent the 95% confidence interval of predicted values

TTE model for dropout

All dropouts occurred within 3 h after rt‐PA treatment. For a basic hazard model, a Gompertz model was selected, yielding an OFV of 141.85, compared with 177.99 for a constant model and 159.32 for a Weibull model (not shown). For covariate analyses, baseline categorized NIHSS0, denoted as CNIHSS0, was found to be significant for hazard, with a coefficient estimate of 0.469, as shown in Table 3, where CNIHSS0 represents categorized NIHSS0, defined as CNIHSS0 = 1 for NIHSS0 ≤ 15, CNIHSS0 = 2 for 16 ≤ NIHSS0 ≤ 20 and CNIHSS0 = 3 for NIHSS0 ≥ 21 based on clinical significance 6. Other covariates, including time‐varying disease severity, TTT and dose, were found to be non‐significant (Table 3).

Although categorization causes a loss of information, this approach was used in the present study because NIHSS scores at dropout times were not evenly distributed, with very low incidences at high NIHSS scores, causing numerical problems. Covariate analysis was conducted within the proportional hazard modelling framework, as it better described the model than incorporating the covariate directly into the hazard model parameters. The goodness‐of‐fit plot for the selected model showed that the predicted hazard corresponded well to the observed hazard (not shown). The resulting VPC plot stratified by CNIHSS0 category is shown in Figure 4C, indicating that, overall, the observed survival is satisfactorily included in the range of the 95% prediction interval.

Incidence model for haemorrhagic transformation

For the incidence model for haemorrhagic event, no covariate was found to be significant.

TTE model for haemorrhagic transformation

Time to haemorrhagic event was best described by the Weibull hazard model. The predicted NIHSS score change with time was found to improve the model fit significantly, with an OFV decrease of 11.16 (P < 0.001). TTT and dose, however, were not significant. Similarly to the TTE model for dropout, the covariate effect was better explained when incorporated using the proportional hazard modelling framework. The resulting VPC plot is shown in Figure 5A, and the associated Kaplan–Meier mean covariate plot for predicted NIHSS score is shown in Figure 5B, which confirms the adequacy of modelling the time‐varying nature of this covariate. Although the survival curve in the VPC plot was satisfactorily included in the 95% confidence interval of predictions, the mean covariate plot was somewhat overestimated at later time points. A partial explanation for such misfits is the sparseness of data at later time points.

Figure 5.

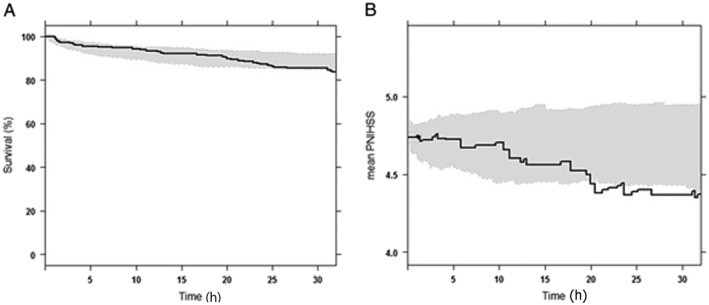
Visual predictive check for time‐to‐event (TTE) model for haemorrhagic transformation obtained using Weibull hazard (A) and the associated Kaplan–Meier mean covariate plot for predicted NIHSS score (B). Survival curve in (A) denotes Kaplan–Meier survival probability, and PNIHSS in (B) denotes predicted National Institutes of Health Stroke Scale score. In both panels, shaded areas represent the 95% confidence interval of the predicted value

Benefit‐to‐risk ratio analysis

Table 4 summarizes 10 scenarios used in the simulation and Table 5 reports the mean and standard deviation (SD) of the 100 GBR values obtained from the 100 simulated datasets for a set of scenarios, subjects group and alpha. The mean proportion of each severity group was 0.26, 0.44, 0.21 and 0.10 for minor, moderate, moderate‐to‐severe and severe severity, respectively. The key results were as follows.

1. For patients with minor and moderate severity, the benefit‐to‐risk ratio was greater than 1 in all simulation scenarios, with the ratio decreasing with NIHSS severity; patients with minor severity showed the highest, and those with the highest severity the lowest, benefit‐to‐risk ratio.

2. For moderate‐to‐severe and severe patients, a ratio of less than 1 was noted for MCA stroke patients in all scenarios, whereas a ratio greater than 1 was noted in non‐MCA stroke patients with moderate‐to‐severe severity in some selected scenarios.

3. The benefit‐to‐risk ratio of non‐MCA stroke patients was nearly two‐ or three‐fold higher than that of MCA stroke patients.

Table 4.

Summary of scenarios

Scenario number	Definition of benefit
1	More than 4‐point decrease in NIHSS score or the zero NIHSS score at 24 h
2	0.5‐fold decrease in disease severity or the zero NIHSS score at 24 h
3	1.0‐fold decrease in disease severity or the zero NIHSS score at 24 h
4	1.5‐fold decrease in disease severity or the zero NIHSS score at 24 h
5	2.0‐fold decrease in disease severity or the zero NIHSS score at 24 h
6	More than 4‐point decrease in the NIHSS or the zero NIHSS score at 24 h
7	0.5‐fold decrease in disease severity or the zero NIHSS score at 24 h
8	1.0‐fold decrease in disease severity or the zero NIHSS score at 24 h
9	1.5‐fold decrease in disease severity or the zero NIHSS score at 24 h
10	2.0‐fold decrease in disease severity or the zero NIHSS score at 24 h

MCA, middle cerebral artery; NIHSS, National Institutes of Health Stroke Scale

Scenario number 1, 2, 3, 4, 5: non‐MCA infarction

Scenario number 6, 7, 8, 9, 10: MCA infarction

Table 5.

Summary of global benefit‐to‐risk trade‐off ratio statistics, obtained from 100 simulated datasets

Scenario	Groupa	R value
		α = 0.5		α = 0.6		α = 0.7		α = 0.8		α = 0.9
		Mean	SD	Mean	SD	Mean	SD	Mean	SD	Mean	SD
1	1	6.617	0.653	6.911	0.670	7.229	0.687	7.576	0.704	7.956	0.722
	2	5.096	0.200	5.171	0.199	5.247	0.198	5.325	0.197	5.405	0.196
	3	2.223	0.113	2.248	0.112	2.274	0.112	2.299	0.111	2.325	0.111
	4	1.000	0.084	1.010	0.084	1.021	0.084	1.032	0.084	1.043	0.084
2	1	13.153	0.762	13.514	0.755	13.893	0.746	14.292	0.735	14.711	0.721
	2	5.699	0.198	5.770	0.197	5.842	0.195	5.916	0.194	5.990	0.192
	3	2.266	0.111	2.291	0.111	2.317	0.110	2.343	0.110	2.369	0.110
	4	0.885	0.082	0.895	0.082	0.906	0.083	0.916	0.083	0.927	0.083
3	1	10.543	0.743	10.903	0.747	11.285	0.749	11.693	0.750	12.129	0.749
	2	5.438	0.198	5.511	0.197	5.585	0.196	5.661	0.194	5.738	0.193
	3	1.922	0.116	1.947	0.116	1.972	0.115	1.997	0.115	2.023	0.115
	4	0.554	0.084	0.562	0.085	0.570	0.085	0.577	0.086	0.585	0.087
4	1	8.741	0.701	9.080	0.711	9.444	0.721	9.836	0.729	10.259	0.737
	2	5.178	0.191	5.252	0.190	5.328	0.189	5.406	0.188	5.485	0.187
	3	1.556	0.115	1.579	0.115	1.602	0.115	1.626	0.116	1.650	0.116
	4	0.299	0.064	0.304	0.065	0.309	0.066	0.313	0.067	0.318	0.067
5	1	7.644	0.650	7.963	0.663	8.307	0.676	8.679	0.689	9.084	0.701
	2	4.906	0.174	4.981	0.173	5.059	0.172	5.137	0.171	5.218	0.171
	3	1.228	0.116	1.248	0.117	1.268	0.118	1.289	0.118	1.310	0.119
	4	0.141	0.048	0.144	0.048	0.146	0.049	0.149	0.050	0.151	0.050
6	1	2.504	0.231	2.550	0.233	2.598	0.236	2.647	0.238	2.698	0.240
	2	1.763	0.065	1.777	0.065	1.791	0.065	1.805	0.065	1.819	0.065
	3	0.749	0.036	0.755	0.036	0.760	0.036	0.766	0.036	0.772	0.036
	4	0.332	0.027	0.335	0.027	0.338	0.027	0.341	0.027	0.343	0.027
7	1	4.690	0.238	4.746	0.237	4.802	0.236	4.859	0.234	4.918	0.233
	2	1.958	0.064	1.971	0.064	1.985	0.064	1.999	0.064	2.013	0.064
	3	0.763	0.036	0.769	0.036	0.774	0.036	0.780	0.036	0.786	0.036
	4	0.295	0.027	0.298	0.027	0.300	0.027	0.303	0.027	0.305	0.027
8	1	3.848	0.244	3.903	0.244	3.960	0.245	4.017	0.245	4.077	0.245
	2	1.874	0.065	1.888	0.065	1.901	0.065	1.915	0.064	1.930	0.064
	3	0.651	0.038	0.656	0.038	0.661	0.038	0.667	0.038	0.672	0.038
	4	0.186	0.028	0.188	0.028	0.190	0.028	0.191	0.028	0.193	0.028
9	1	3.243	0.238	3.296	0.239	3.350	0.241	3.405	0.242	3.462	0.243
	2	1.790	0.063	1.804	0.063	1.818	0.063	1.832	0.063	1.846	0.062
	3	0.530	0.038	0.535	0.038	0.540	0.038	0.544	0.038	0.549	0.038
	4	0.101	0.021	0.102	0.022	0.103	0.022	0.104	0.022	0.105	0.022
10	1	2.865	0.225	2.915	0.227	2.966	0.229	3.019	0.231	3.073	0.233
	2	1.702	0.057	1.715	0.057	1.729	0.057	1.743	0.057	1.757	0.057
	3	0.421	0.039	0.425	0.039	0.428	0.039	0.432	0.039	0.436	0.039
	4	0.048	0.016	0.048	0.016	0.049	0.016	0.049	0.017	0.050	0.017

NIHSS, National Institutes of Health Stroke Scale; SD, standard deviation

^aGroup: 1 (minor, NIHSS score 1–5), 2 (moderate, NIHSS score 5–15), 3 (moderate‐to‐severe, NIHSS 16–20), 4 (severe, NIHSS 21–42)

Discussion

The present study proposed a pharmacometric approach that can be used quantitatively to assess and predict clinical outcomes (i.e. treatment effect and failure) and accompanying risk (i.e. haemorrhagic transformation) in rt‐PA treatment using acute ischaemic stroke data collected retrospectively. To describe treatment effects, the IRT model was used in this work. This model was initially applied in Alzheimer's disease 29, where, by using the IRT approach to model the latent variable corresponding to disease severity underlying Alzheimer's Disease Assessment Scale–cognitive subscale test scores, the work demonstrated that the power to detect drug effects can be improved.

When continuous data obtained from multiple tests are used in analyses without being categorized, the IRT model can produce results that are more reliable than those obtained using other models. This was well illustrated in the present work, where all NIHSS scores between 0 and 35 were analysed without being categorized by applying the IRT model to 13 individual test scores comprising the total NIHSS score. In addition, the work intended to demonstrate how a population model‐based pharmacometric approach can be used in analysing routine clinical data with an application to acute ischaemic stroke patients. With a growing need for efficient utilization of patient records obtained from routine clinical practice, a population modelling approach has become increasingly important because of its advantages in the analysis of observational data such as routine clinical data.

For the ICC of baseline NIHSS scores, the PCM was selected for the following reasons. Firstly, the GRM yielded a large estimate of 42.75 for α₇, the scale parameter for Test 7. This large value of α₇ was regarded as unrealistic because a scale parameter larger than 8 generally yields an ICC whose shape is close to a step function. Moreover, the PCM is more appropriate for describing NIHSS scores 30. In the disease progression model, the between‐subject variability of AMP was very large, but no significant covariates were selected, suggesting that this variability might be attributable to other sources, including inaccurate medical records, such as incorrect infarction volume or radiological diagnosis. Unfortunately, these types of data were not available. Regarding the misfits in Figure 3B, we inspected the data and found that seven patients with an NIHSS score >23 had observation records only up to 3 h, which we suggest might have caused overestimation. Nevertheless, dropout was not incorporated as it did not statistically improve the model when included, probably because these patients represented only 2% (7/336) of the entire patient group.

In the incidence model for dropout, patients with MCA stroke and higher NIHSS0 are more unlikely to respond to rt‐PA treatment and need additional therapy afterwards. This result might be expected from the pathophysiological point of view, that NIHSS scores reflect a neurological deficit in stroke and thus a higher score would indicate a more severe disease state requiring additional intervention. In the TTE model for dropout, CNIHSS0 was a significant covariate, which is consistent with a literature report indicating that patients with MCA stroke tend to have a relatively low revascularization rate after rt‐PA treatment 31. The longitudinal change in NIHSS scores showed no significant association with the time to dropout. Alternatively, CNIHSS0 was adopted to represent partially patients’ severity, and it was found to be significant. This might have been because additional therapies, which are supposed to be decided on by clinicians, were all given within 3 h after rt‐PA treatment, leading to no likelihood of NIHSS scores beyond 3 h being used in deciding the time to dropout for additional treatment.

With regard to the TTE model for haemorrhagic event, the predicted NIHSS score change with time was selected as an important covariate capable of predicting the probability of haemorrhage risk at a particular time over the course of treatment. The reason for the misfit observed in Figure 5B is that the disease progression model used to predict NIHSS scores was developed using NIHSS scores only up to 24 h, and therefore could not accurately predict these scores beyond 24 h. None of the covariates reported in the literature as being significant, including age, blood glucose level, platelet count and blood pressure 10, 14, 32, 33, were found to be statistically significant. This discrepancy might have been due to differences in the analytical method and the definition of haemorrhagic event between our study and previous studies.

In the present work, TTT and dose were not found to have a significant influence on clinical outcomes following rt‐PA treatment. We suggest that the reason is as follows: for TTT, the interquartile range was 1.27–2.25 h (data not shown), indicating that the majority of the patients received rt‐PA treatment within 3 h of symptom onset, which is known to be the ʻgolden hourʼ for successful functional outcomes with rt‐PA treatment 34, and therefore treatment effect and AE were not significantly affected by TTT. For dose, the interquartile range was 0.89–0.90 mg kg^–1 (data not shown), indicating that almost the same dose was given to most of the patients, resulting in no significant influence on clinical outcomes.

Despite the severe AE of haemorrhagic transformation with rt‐PA treatment, few attempts have been made to take into account both the benefits and risks in treatment outcome analysis, except for one example found in the ischaemic stroke risk score 35. Furthermore, no study has described a quantitative approach for assessing the benefits and risks of rt‐PA treatment in the hyperacute phase of ischaemic stroke. In this regard, we conducted a simulation study using the developed model to investigate the benefit‐to‐risk ratio using GBR by classifying patients into minor, moderate, moderate‐to‐severe and severe patients based on NIHSS score in each simulated dataset. Our results indicating that minor stroke patients showed the highest benefit‐to‐risk ratio appear to be contradictory to the rt‐PA guidelines 2, in which rt‐PA treatment is not recommended for patients with minor neurological deficit. However, the criteria used for excluding patients with minor stroke from rt‐PA treatment were not based on clear evidence 36. Moreover, according to recent research, the rate of rt‐PA related side effects was relatively low in minor stroke patients, and benefits even outweighed the risks 36, 37, which is consistent with our results.

In summary, based on the IRT‐based pharmacometric model describing the time course of rt‐PA treatment effect and AE in stroke patients, the present work revealed that rt‐PA treatment would be best recommended for minor and moderate severity patients, with the expected benefit‐to‐risk ratio being greater than 1, and the ratio decreased with NIHSS severity, being nearly two‐ or threefold higher in non‐MCA than in MCA stroke patients as compared with at the same disease severity. Despite a limitation that very severe patients with an NIHSS score >36 were not included in the analysis and thus caution should be made when extrapolating the modelling results to very severe patients, this work has demonstrated the feasibility of applying a model‐based approach in optimizing the rt‐PA treatment effect in stroke patients.

Competing Interests

There are no competing interests to declare.

This work was supported by a grant from the Brain Korea 21 PLUS Project for Medical Science, Yonsei University.

Contributors

In this work, J.G. and K.P. contributed to data interpretation, literature search, figure creation and writing; D.C. and H.S. contributed to data interpretation and writing; J.Y. contributed to data collection and writing; and J.H.H. contributed to study design, study conduct, data collection and writing.

Supporting information

Figure S1 Visual predictive check for disease progression model for National Institutes of Health Stroke Scale (NIHSS) scores of individual test for first 24 h after intravenous recombinant tissue plasminogen activator (rt‐PA) for all 13 tests. Solid lines stand for observed probability and grey areas are the 95% confidence interval of predicted probability

Guk, J. , Chae, D. , Son, H. , Yoo, J. , Heo, J. H. , and Park, K. (2018) Model‐based assessment of the benefits and risks of recombinant tissue plasminogen activator treatment in acute ischaemic stroke. Br J Clin Pharmacol, 84: 2586–2599. 10.1111/bcp.13715.