Meta‐analysis: Key features, potentials and misunderstandings

Abstract

A meta‐analysis consists of a systematic approach to combine different studies in one design. Preferably, a protocol is written and published spelling out the research question, eligibility criteria, risk of bias assessment, and statistical approach. Included studies are likely to display some diversity regarding populations, calendar period, or treatment settings. Such diversity should be considered when deciding whether to combine (some) studies in a formal meta‐analysis. Statistically, the fixed effect model assumes that all studies estimate the same underlying true effect. This assumption is relaxed in a random effects model and given the expected study diversity a random effects approach will often be more realistic. In the absence of statistical heterogeneity, fixed and random effects models give identical estimates. Meta‐analyses are especially useful to provide a broader scope of the literature; they should carefully explore sources of between study heterogeneity and may show a treatment effect or an exposure–outcome association where individual studies are not powered. However, its validity largely depends on the validity of included studies.

Essentials.

• A systematic review aims to appraise and synthesize the available evidence addressing a specific research question; a meta‐analysis is a statistical summary of the results from relevant studies.

• A meta‐analysis will provide a non‐valid answer if included studies are not valid. Judgment of validity of individual studies is thus crucial.

• When deciding whether to perform a formal meta‐analysis, study diversity and statistical heterogeneity should be considered.

1. INTRODUCTION

In 2007, a meta‐analysis showed an increased cardiovascular risk in patients using rosiglitazone, an anti‐diabetic drug.1 Here, a meta‐analytic approach displayed its full potential: to show a side‐effect for which individual studies were not powered. Similarly, the increased cardiovascular risk for rofecoxib was shown in a meta‐analysis.2

The rosiglitazone paper was firmly debated; for example, the statistical approach was criticized.3 This highlights that meta‐analyses are not immune to criticism, despite being conceived as high‐level evidence. Choices in design or analysis of a review can be debated or criticized by readers, underlining the need for transparent reporting.

This tutorial discusses central features of meta‐analyses, including potential misconceptions. A glossary (Table 1) provides an explanation of the methodological terms used; displayed terms are shown in the main text in italics. In Table 2, ten potential misunderstandings in meta‐analyses are shown.

Table 1.

Glossary with short explanation of technical terms used in meta‐analyses

Term	Explanation
Cochrane's Q‐test	Statistical test that examines the null‐hypothesis that all studies have the same true effect.13 A significant P value provides evidence of statistical heterogeneity. The test is based on the deviations of study estimates from the overall mean
Fixed effect model	Statistical method to obtain a weighted average of study estimates. Studies are weighted according the inverse of the variance, meaning that larger studies bear more weight. The fixed effect model assumes that included studies estimate the same underlying true effect
Forest plot	Graphical display of effect estimates of individual studies, often presented with a weighted estimate. Forest plots display studies’ effect estimates and 95% confidence intervals, the weight the studies get in the meta‐analysis (shown as box and/or percentage) and the overall weighted estimate with a 95% confidence interval
Funnel plot	A funnel plot is a graphical display plotting effect estimates against sample size or inverse of the variance. The idea behind a funnel plot is that study effects scatter around a mean effect, but that smaller studies can deviate more from this mean. Publication bias may be considered if smaller studies show on average a more positive effect than larger studies. Smaller studies are more prone to only getting published if the result is positive, large trials tend to get published anyway. There are statistical techniques to judge whether these small studies show a different effect compared to larger studies18
I2 statistic	Measure to quantify the amount of heterogeneity between studies that cannot be explained by chance. It is quantified as a percentage between 0 and 100; as a general rule low, moderate, and high heterogeneity can be assigned to I2 values of 25%, 50%, and 75%13
Individual Patient Data (IPD) meta‐Analysis	In standard meta‐analyses the individual study is the unit of analysis. In an IPD meta‐analysis the researchers have access to data at the level of individual patients from different studies. This is especially useful to harmonize endpoints and perform analyses in prespecified subgroups
Meta‐regression	Statistical technique to relate study characteristics to effect estimates.19 For example the association between treatment duration and treatment effect for depression was studied in a meta‐regression framework20
Network meta‐analysis	A network meta‐analysis allows the comparison of more than two groups.21 This can be a useful approach when more than two treatment options exist for the same indication. An example is a comparison of the thrombosis risk of different oral contraceptives22
Random effects model	Statistical method to obtain a weighted average of study estimates. In contrast to a fixed effect model, a random effects model assumes that studies have different underlying true effects. The combined effect in a random analysis is an estimation of the mean of these underlying true effects. Technically, the random effects model takes the between‐study variation into account
Subgroup analysis	Restricting the statistical analysis to a group of studies based on a specific characteristic. For example, an analysis can restricted to randomized studies, studies with low risk of bias, or studies performed in children. Subgroup analyses can be used as a way to explore heterogeneity

Table 2.

Ten potential misunderstandings in meta‐analyses

Potential misunderstanding	Background
A meta‐analysis is an objective procedure	Every meta‐analysis is characterized by decisions regarding research question, eligibility criteria, risk of bias analysis, and statistical approach. These decisions should be reasonable and transparently reported. Probably, no single best and ultimately objective procedure exists. For this reason, different meta‐analyses on the same topic may come to different conclusions
A meta‐analysis provides the highest level of evidence	A meta‐analysis is generally considered to provide high‐level evidence. However, the validity of a meta‐analysis depends largely on the validity of included studies (“garbage in—garbage out”); a meta‐analytic design is thus not a guarantee for highest level evidence
Study quality is synonymous with risk of bias	Study quality is about the question whether a study has been optimally performed; risk of bias relates to threats of validity. A study can be high quality but still have a high risk of bias for certain bias domains. An example is a comparison between two surgical techniques; even if the study is optimally performed, it cannot, by design, be blinded
A risk of bias analysis resolves the bias	A risk of bias analysis mainly displays this bias risk; such a display does not resolve it, although a sensitivity analysis restricted to low risk of bias studies can be considered
Random effects models solve heterogeneity	Random effects models allow that different studies have a different underlying true effect; the random effects model thus does not explain, solve, or even remove heterogeneity
Assuming homogeneity between studies when the statistical test fails to show heterogeneity	In the presence of few studies only, tests for heterogeneity have low power; the presence of a nonsignificant test does thus not provide strong evidence for true homogeneity between studies. This is especially the case if the review includes <10 studies
Present the I2 statistic as if it was a test	The I2 statistic is formally not a test that can reject a null hypothesis. It provides a quantitative measure of the heterogeneity between studies beyond chance13
Assuming funnel plot symmetry when the statistical test fails to show heterogeneity	In the presence of few studies only, the test for heterogeneity has low power; the absence of a nonsignificant test does thus not provide strong evidence for symmetry
Funnel plot asymmetry proves publication bias	Funnel plot asymmetry means that smaller studies show on average a different effect compared to larger studies; one explanation is publication bias, other explanations are effect modification and chance
Meta‐analyses “speak for themselves”	Even meta‐analyses need an interpretation.16 Such an interpretation pertains to questions on validity, heterogeneity, and clinical relevance. For example, a recent review concluded that low‐molecular‐weight heparin lowered the risk of venous thromboembolism in patients with lower‐limb immobilization.18 The translation of this review to clinical practice requires a discussion whether it is clinically relevant to reduce thrombosis found by routine ultrasound screening, which was the way to assess the endpoint in most included papers

2. RESEARCH QUESTION AND STUDY PROTOCOL

Similarly to other study designs, systematic reviews start with a research question to be specified in terms of population, intervention or risk factor, or control group and outcome(s). Defining the research question is a balancing act: if very narrow, the review may end up with few studies only (for example: effect of 40 mg simvastatin on recurrent thromboembolism in 60‐ to 70‐year‐old males); if too broad, a meaningful overview may be cumbersome (for example: effect of inflammation on coagulation). A rough idea on the number of publications on a particular topic may guide framing of the research question.

A related point is that within a systematic review framework, researchers are dependent on how studies are performed and reported. If the effect of wine on coagulation is assessed in a review, some studies may report on the association between coagulation and alcohol in general, without providing data for wine‐drinkers only. Such considerations should be taken into account up front when deciding on inclusion criteria. For the wine‐coagulation example, no formal rule will decide whether broad alcohol categories provide meaningful information to the review. This decision is up to the researchers, but arguments should be provided in the protocol and the paper that clarify decisions made.

It is advised to write and publish a protocol specifying details of design and analyses.4 The advantage prespecifying a protocol is that decisions will be made independently of study results.

3. SEARCHING STUDIES AND EXTRACTING DATA

Many electronic databases can be used for searching studies; Embase, Medline, and Cochrane Library are the most well‐known. More than one database should be searched, given the incomplete coverage of single databases.5 As writing database‐specific search strings requires specific bibliographical knowledge, a search should be developed in collaboration with an information specialist. To optimize the search process, key articles should be provided to the information specialist, as they may contain clues to keywords and indexing. Additionally, references of key papers can be checked.

Inclusion of papers follows from the eligibility criteria. Data extraction should be done by two researchers independently. This reduces the error rate, but it also may help to discuss choices to be made.6 For example, a paper may present effects of wine drinking on coagulation factors using different sets of adjusted confounders. Researchers have to decide which effect estimate to extract for a formal meta‐analysis.

4. RISK OF BIAS ANALYSIS

A meta‐analysis will provide a nonvalid answer if included studies are not valid. The judgment of validity of individual studies is referred to as risk of bias assessment. For randomized trials risk of bias assessment is standardized, and elements to be judged are concealment of allocation, blinding (participants, personnel and outcome assessors), selective outcome reporting, and incomplete outcome data.7 For these domains, researchers judge included studies for their risk of bias, which is reported at the study level. For example, an unblinded study is judged “high risk of bias” with respect to blinding. The full risk of bias analysis is preferably tabulated to facilitate an overview and to provide an overall idea on the validity of included studies. Although we are actually judging risk of bias, there is evidence that risk of bias is related to actual bias. For example, unblinded studies show on average a more positive effect than adequately blinded studies.8 This was shown in detail for a study assessing the effect of rosiglitazone on cardiovascular endpoints, where the unblinded design was the likely cause of case‐forms being filled in more often in favor of the study drug.9 As risk of bias depends on reporting, some elements cannot always be judged; for example, loss‐to‐follow up (potentially introducing selection bias10) is often poorly reported, especially in observational studies.

The crucial distinction between randomized and observational studies is the potential for confounding and judging the risk of confounding is key for reviews of observational studies. Confounding means that compared groups are different with respect to important prognostic factors. In the context of interventions, this is called confounding by indication. It is a decision of the researchers what is considered a sufficient set of confounders to be adjusted for, and what statistical techniques are considered adequate. The mere statement that a study suffers from confounding because it is observational is too simplified. Moreover, confounding is a matter of degree. For the association between a vegetarian diet and thrombosis, the confounding will be almost intractable, whereas it has been shown that side effects can reliably be assessed in observational studies, as confounding is only marginally an issue.11, 12 Importantly, standard statistical techniques (including propensity scores) cannot fully adjust for unmeasured confounding.

For observational studies, two other bias domains are also important. Misclassification can be of either risk factor or intervention under study, the outcome, or both. Selection bias refers to the bias introduced by selection mechanisms in studies. This type of bias requires methodological expertise and is often difficult to detect. Guidance exists for risk of bias assessment for observational studies on therapeutic interventions.10

Three approaches can be considered to incorporate results from a risk of bias analysis.

1. Researchers can restrict their meta‐analysis to studies with low risk of bias. This is the approach for many meta‐analyses on therapeutic interventions where observational studies are not eligible.

2. If risk of bias is considered too high, researchers may want to abstain from statistical combining the results.

3. Exploration (by meta‐regression or subgroup analyses), this approach tries to answer the question whether risk of bias influences reported effect estimates.

5. DIVERSITY AND HETEROGENEITY

By design, a systematic review includes studies from different patient populations. Likely, these different populations will display diversity, for example with regard to clinical characteristics, study period, or health care facilities. Some diversity is thus inevitable. Researchers should display such between‐diversity as it will facilitate a judgment whether included papers “tell a similar story.”

Statistical assessment of heterogeneity only considers the heterogeneity of the quantitative estimates. Such statistical measures (Cochrane's Q‐test and I ² statistic) approach the question of whether differences in effect estimates are beyond chance. Statistical tests are not powered to detect heterogeneity when the review includes fewer than 10 papers.13 Study diversity may translate into statistical heterogeneity, but this does not need to be the case. Researchers should thus, when thinking about heterogeneity and deciding whether to perform a formal meta‐analysis, take into account both the clinical judgment and the statistical verdict.

6. STATISTICAL ANALYSES

From a statistical point of view, meta‐analyses are fairly simple: the pooled estimate is a weighted average of effect estimates of individual studies. The weighting is according to the inverse of the variance, which means that larger studies get more weight. A forest plot is a graphical display of a meta‐analysis’ results.

Researchers have two basic statistical options to perform a meta‐analysis: a fixed and a random effects model. The fixed effect model assumes that all studies have the same underlying true effect; this assumption is rigid (Do we really have certainty that all studies only differ due to chance?). A random effects model relaxes this assumption and does not assume that all studies have the same underlying true effect.

When comparing the two models, smaller studies get relatively more weight in a random model, and the confidence intervals are wider in a random effects model. This is shown in Figure 1, a graphical display of both models. What is the correct model? There is no final answer,14 although it is often realistic to assume some underlying heterogeneity and start with a random model. In case of absence of statistical heterogeneity, the two models give identical results.

Figure 1.

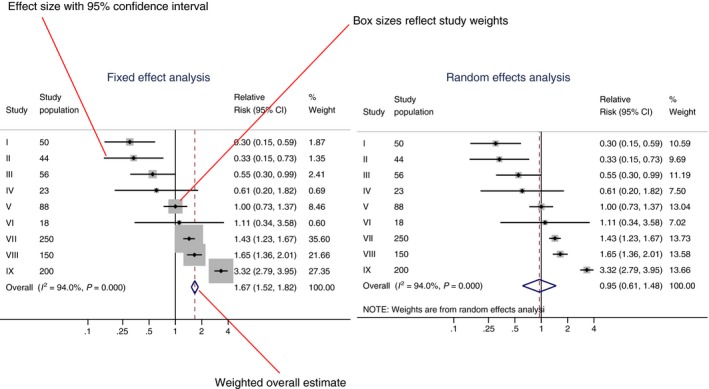
Graphical display of a fixed and random effects model. Forest plot showing two different statistical meta‐analytic approaches for the same set of (fictional) studies: a fixed effect model (left) and a random effects model (right). In the forest plot effect estimates of individual studies, the study weights, a weighted overall effect and measures of heterogeneity (I ² statistic and a P value for the heterogeneity test) are shown. CI, confidence interval

Mostly, fixed and random effects models give very similar pooled estimates, the main difference being the wider confidence interval for the random model. There is an exception to this rule, when on average effects from smaller studies are different from effects in larger studies, as in Figure 1. As expected, the confidence interval from the fixed effect model is smaller, but there is also clear difference in pooled estimate.

7. PUBLICATION BIAS

Risk of bias refers to bias at the level of individual studies; publication bias distorts the overall picture. Publication bias occurs when studies with statistically significant positive effects are more likely to get published. There are many reasons for negative studies remaining unpublished, such as lower motivation of authors to finalize or submit negative studies, and unwillingness of journals to publish “uninteresting results.” Publication bias will often result in a too‐positive picture of an intervention. This was shown for antidepressants, where published papers showed a 50% greater treatment effect, compared to unpublished papers on the same drug.15 Although often publication bias is considered a problem of meta‐analyses, it is clearly a broader problem the moment a systematic overview is used to inform doctors, patients, and policymakers.

A funnel plot can facilitate the judgment whether publication bias is an issue. Publication bias may be considered if smaller studies show on average a more positive effect than larger studies.

8. ANSWERING THE RESEARCH QUESTION

A systematic review provides an optimal opportunity to place studies in a broader context.16 Sometimes the interpretation of a meta‐analysis is straightforward, when all studies give the same picture. This was the case in studies on the association between acromegaly and mortality, where all studies showed a slightly increased risk, which became significant in a meta‐analysis.17

But in other cases the interpretation is more difficult, for example when one or two large trials show effects not directly comparable to the weighted average of a much larger number of trials. Researchers should than carefully balance the arguments for a decision: are the two large trials less likely to be biased, or is the weighted estimate closer to the truth?

In summary, meta‐analyses are especially useful to provide a broader scope of the literature; they should carefully explore sources of between study heterogeneity, and may show a treatment effect or an exposure–outcome association where individual studies are not powered. However, its validity largely depends on validity of included studies.

Dekkers OM. Meta‐analysis: Key features, potentials and misunderstandings. Res Pract Thromb Haemost. 2018;2:658–663. 10.1002/rth2.12153