Psychometric properties of a short form of the Center for Epidemiologic Studies Depression (CES-D-10) scale for screening depressive symptoms in healthy community dwelling older adults

Abstract

Background:

The 10-item Center for the Epidemiological Studies of Depression Short Form (CES-D-10) is a widely used self-report measure of depression symptomatology. The aim of this study is to investigate the psychometric properties of the CES-D-10 in healthy community dwelling older adults.

Methods:

The sample consists of 19,114 community-based individuals residing in Australia and the United States who participated in the ASPREE trial baseline assessment. All individuals were free of any major illness at the time. We evaluated construct validity by performing confirmatory factor analysis, examined measurement invariance across country and gender followed by evaluating item discrimination bias in age, gender, race, ethnicity and education level, and assessing internal consistency.

Results:

High item–total correlations and Cronbach’s alpha indicated high internal consistency. The factor analyses suggested a unidimensional factor structure. Construct validity was supported in the overall sample, and by country and gender sub-groups. The CES-D-10 was invariant across countries, and although evidence of marginal gender non-invariance was observed there was no evidence of notable gender specific item discrimination bias. No notable differences in discrimination parameters or group membership measurement non-invariance were detected by gender, age, race, ethnicity, and education level.

Conclusion:

These findings suggest the CES-D-10 is a reliable and valid measure of depression in a volunteer sample. No noteworthy evidence of invariance and/or item discrimination bias is observed across gender, age, race, language and ethnic groups.

1. Introduction

A systematic review of depression prevalence in elderly populations showed that the prevalence of major depression ranges from 0.9% to 9.4% in private households and from 14% to 42% in institutional living; and the prevalence of clinically relevant depressive symptoms in similar settings varies between 7.2% and 49% [1]. Another systematic review on depression prevalence in later life (≥ 75 years) illustrated that the prevalence of major depression ranged from 4.6% to 9.3%, and that of depressive disorders from 4.5% to 37.4% [2]. Depression is a major contributor to healthcare costs in older populations, and is projected to be the leading cause of disease burden in older populations by the year 2020 [3,4]. The prevalence of depression in patients aged ≥ 65 years may be as high as 40% in hospitalised and nursing home patients, and 8–15% in community settings [5]. Depression in the elderly is associated with an increased risk of mortality, dementia and substantial psychosocial disability [6], resulting in an economic burden of $15 billion in Australia [7] and $83 billion in the United States [8].

The Center for Epidemiologic Studies Depression Scale (CES-D) has been widely used to assess depressive symptoms in community and population-based epidemiological studies [9]. The scale’s validity and internal consistency in the detection of both clinical and non-clinical depressive symptoms have been established. It has however been suggested that the length of the 20-item CES-D could be halved without appreciable loss to reliability and validity. Various short and/or simplified forms of the 20-item CES-D have been evaluated [10–14]. The Boston form (10 dichotomously scored items), the Iowa form (11 items with three response options) developed by Kohout et al. [15] and the four-category response 10-item form (CES-D-10) developed by Andresen et al. [10] are most commonly used. The Andresen version, CES-D-10, has strong reliability and excellent sensitivity and specificity in screening for major depression in older adults [14]. Construct validity of the short form of the CES-D has been examined in Singaporean older adults in community settings [16], Chinese elderly in community dwelling [17] and older Chinese in social centres [18]. While the published validity studies of the CES-D-10 illustrated acceptable factorial validity there were indications that the factorial structure has not been consistently determined. For example while studies among adults in Zulu, Xhosa and Afrikaans in South Africa [19] and the USA Hispanics population [20] concluded a one factor solution had the best model fit, studies in Canadian adolescents [21] and Singaporian elderly [16] resulted in a two-factor model and validation studies in older Chinese populations [17,18] reported two-factor and three-factor models of the CES-D-10 respectively. These contradictory findings may be due in part to the use of: i) individuals with different cultural background; ii) differences in study sample age ranges; iii) participant characteristics (e.g. a psychiatric sample as compared with community-based participants) or; iv) small sample size (sample size in the studies with factorial validation in elderly populations was 231, 742 and 1013 respectively (16–18)). In such situations, performing confirmatory factor analyses (CFA), a commonly approach for the evaluation of the construct validity of psychometric inventories, on a large sample of community-based elderly individuals with diverse ethnic and cultural backgrounds [22], is a unique opportunity to clarify this issue.

Reise, Widaman and Pugh [23] further recommend the use of measurement invariance tests within the CFA framework to examine the invariance of the instrument’s psychometric properties across different groups. The goal of the present study was to investigate the internal consistency and construct validity of the CES-D-10, relying on a CFA approach in healthy community-dwelling older Australian and American adults who participated in the ASPirin in Reducing Events in the Elderly (ASPREE) trial [24]. ASPREE is a placebo-controlled trial of low-dose aspirin to determine whether 5 years of daily 100-mg enteric-coated aspirin extends disability-free and dementia-free life in a healthy elderly population and whether these potential benefits outweigh the risks. We also aimed to evaluate measurement invariance across the two countries and sexes and examine item-response bias analyses of the exogenous variables: age, gender, ethnicity, race and education.

2. Methods

2.1. Participants

This study included all 19,114 community-based individuals who participated in the baseline measurements of the ASPREE trial and were subsequently randomised. The participants were recruited from general practice services in Australia and community-based centres in the United States (U.S.). Recruitment ended in December 2014 with 16,703 Australian and 2411 American participants. Readers are referred to the work of the ASPREE Investigator Group [24] and Berk et al. [25] for details regarding the research settings, recruitment strategies, inclusion and exclusion criteria and ethical aspects of the study. In short, participants aged from 70 years old (Australians and U.S. non-(racial) minorities) or 65 years (U.S. - (racial) minorities) and were free of cardiovascular disease, dementia and physical disability. There were no exclusion criteria based on depressive symptoms. CES-D-10 overall score ranged from 0 (4277 cases) to 30 (2 cases) and 1906 (9.9%) of participants had CES-D-10 of 8 or above. Recruitment by age group was 65–74 years 11,163 (58%), 75–84 years 7219 (38%) and 85+ years 732 (4%), with 10,782 (56%) female. There were 1664 (9% of total cohort) US minority participants, of whom 54% (901) were African American and 29% (488) from the U.S. Latino/Hispanic population. A total of 10,477 (55%) had 12 years or more of formal education and 856 (4%) spoke a first language other than English. Further details on demographics and other baseline characteristics can be found in McNeil et al. [26].

2.2. Measures

The 10-item version of the Center for Epidemiologic Studies Short Depression Scale (CES-D-10) was used [10]. All items included four response categories indicating the frequency of depressive symptoms. Of the ten, eight items focussed on positive symptoms while the other two (items 5 and 8) assessed negative symptoms of depression. In brief, subjects responded to each item of the scale by rating the frequency of each mood or symptom ‘during the past week’ on a four-point scale. A score is assigned by totalling all items (after reversing the positive mood items).

2.3. Data analysis and results

We hypothesised a priori that representing depression by CES-D-10 score (depression score) can be explained by a single first-order factor. This model was compared with various alternative models. The single factor CFA was first estimated on all participants. Hu and Bentler’s [27] and Hair et al.’s (2010) guidelines for model fit indices’ cut-offs were used. In particular, Comparative Fit Index (CFI), Tucker-Lewis Index (TLI) and Goodness of Fit Index (GFI) above 0.95 were taken to manifest a good level of model fit. A Root Mean Squared Error of Approximation (RMSEA) value of 0.06 or lower and Standardised Root Mean Squared Residual (SRMR) < 0.09 were considered to indicate a satisfactory fit.

The CES-D-10’s internal consistency was assessed using both Cronbach’s alpha and composite reliability. Cronbach’s alphas were obtained from factor analysis. Composite reliability was calculated from the squared sum of standardised factor loadings divided by the total of the squared sum of standardised factor loadings and the sum of error variance for a factor [28]. A threshold of 0.7 for both reliability coefficients was used to indicate the consistency of all items to measure a factor [28,29].

Measurement invariance tests were utilised to examine the invariance of the CES-D-10 between male and female participants, and between Australia and America. A series of nested hierarchies of hypotheses within the CFA framework was tested to address the cross-group invariance of the CES-D-10. As suggested by Meade et al. [30] a cut off of 0.002 or lower for absolute differences in CFI (|ΔCFI|, i.e. differences in CFI obtained when an unconstrained model was compared with a model with measurement invariance constraints) was used as an indicator that the null hypothesis of invariance should not be rejected. Change in the CFI statistic is independent of both model complexity and sample size, and it is not correlated with the CFA overall goodness of fit measures.

In additional analyses, in order to examine gender-specific item discrimination, we applied multiple indicators, multiple causes models (MIMICs) using generalised structural equations. The MIMIC model consisted of three components: a measurement model (it is assumed that observed responses on each item relate to the unobserved latent variable of depression); a regression model (analogous to multiple regression of the latent variable on several covariates); and a ‘direct effect’ estimate to detect measurement non-invariance in item response associated with membership of a particular group (a path that relates the covariate of interest, e.g. age of the respondent, to an item of interest, such as ‘item 1. Bothered’- see Fig. 1 for a graphical illustration). MIMIC models with full maximum likelihood estimation on ordered categorical CES-D-10 items based on ordered probit regressions were implemented. When item discrimination exists due to the presence of group membership invariance, individuals from two different groups but with the same underlying level of the latent trait being measured will nevertheless have different probabilities of endorsing specific items [31]. For example, if item discrimination due to gender invariance exists, males and females with the same total CES-D-10 score will have different tendencies in endorsing some or all of the CES-D-10 items. Further, MIMIC models keeping gender and adding one additional exogenous covariate to identify the presence of measurement non-invariance with age (as ordinal categories: 65–74, 75–84 and 85 + years), race (White vs else and African American vs else), ethnicity (Hispanic vs else), education (dichotomised; ≤ 12 years vs > 12 years) or language (English vs else) were employed. The MIMIC model was used for each item; one item at the time (a total of 7 models per covariate that repeated 10 times per each CES-D-10 item), and we then determined if there was meaningful non-invariance in each item by considering the rule [32], an odds ratio > 2.0 (equivalent to an absolute value of > 0.7, i.e. | direct loading | > 0.7) or, conversely, < 0.5. An odds ratio of 2.0 translates to those in the comparative group being at twice the odds of responding higher to the individual item than those in the reference group, after being adjusted for overall depressive score.

Fig. 1.

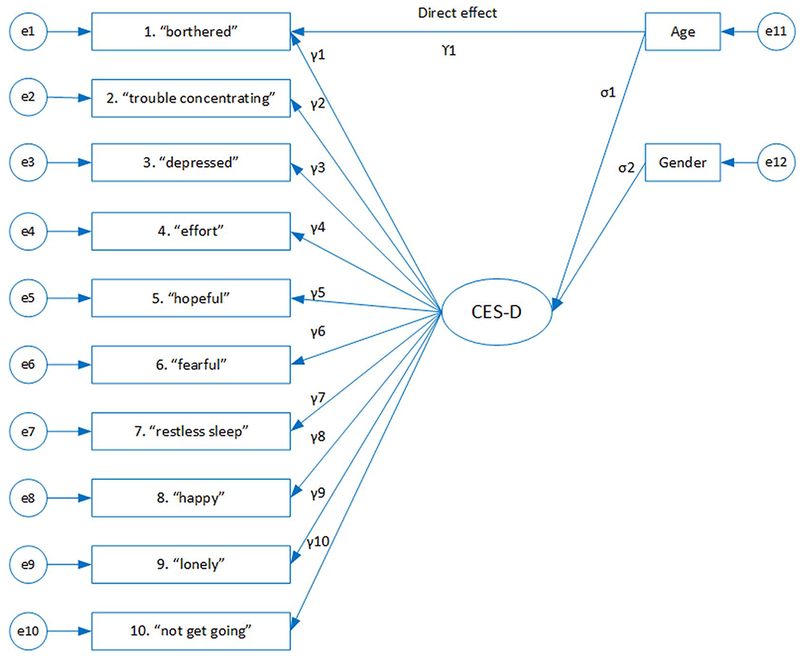
The MIMIC model consists of three components: a measurement model, a regression model and a direct effect estimate. In the measurement model, a continuous latent variable underlies the item responses. The latent variable is linked to a number of covariates in the regression part of the model. Finally, the direct effect is an indicator of measurement invariance and evaluates whether the response to the item “bothered” is associated with age group other than through its relationship to depression. Note: ‘e’ represents error term, γ represents factor loading, λ represents direct effect, and σ represents indirect effect.

Convergent validity was assessed by examining the CES-D-10 indirect link with gender and age variables through the MIMIC models, with the expectation that there should be a positive association between depression score and older age and being female [2,33].

Data were analysed using IBM SPSS AMOS version 24.0 and Stata version 14.2.

2.4. Model specification

The one-factor model of the CES-D-10 is specified in Fig. 2a. Each item was labelled with a key phrase, mirroring Bradley et al.’s [21] presentation of items (except for item 10). The model was over-identified with 35 degrees of freedom in the model.

Fig. 2.

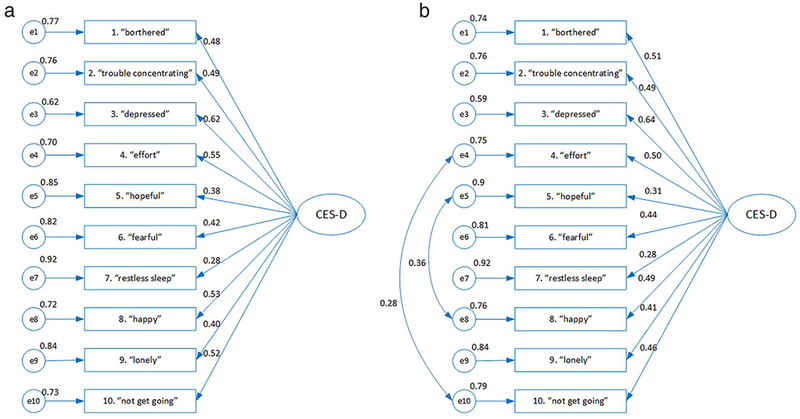
Confirmatory factor analysis. Fig. 2a. Initial covariance model for one-factor CES-D-10. Fig. 2b. Final covariance model for one-factor CES-D-10. The ovals represent the latent factor, the rectangles represent ten measured items of the CES-D-10 and the circles represent error terms (e1–e10). Numbers above arrows are standardised factor loadings and numbers above error terms are error variances.

2.5. Sample size justification

Four participants were not included due to missing CES-D-10 item responses. Summary statistics (mean and standard deviation) of the items are given in Table 1. There was no zero frequency in any item’s response distribution, with frequencies ranging from 0.5% (89) for the ‘Most or all of the time’ category of item 6 ‘Fearful’ to 92% (17,528) for the ‘Rarely or none of the time’ category of item 6 ‘Fearful’. The fact that none of the item means and/or SDs were zero, and all item frequencies were non-zero made the available sample suitable for further analyses. According to Hair et al. [28] to enhance robust structural equation models for non-normal distribution, the ratio of respondents to parameters needs to be > 15:1, to which this study’s ratio of 955.5:1 compares favourably.

Table 1.

Factor loadings and internal consistency coefficients.

Item		Mean (SD)	Unstandardized loadings	Standard errors	Standardised loadings	Composite reliabilityc	Composite reliability if item deleted	αd if item deleted
1. I was bothered by things that usually don’t bother me.	‘Bothered’	0.24 (0.58)	1.09	0.03	0.51	0.26	0.69	0.68
2. I had trouble keeping my mind on what I was doing.	‘Trouble concentrating’	0.25 (0.54)	0.97	0.02	0.49	0.24	0.70	0.68
3. I felt depressed.	‘Depressed’	0.17 (0.48)	1.13	0.02	0.64	0.41	0.68	0.66
4. I felt like everything I did was an effort.	‘Effort’	0.25 (0.56)	1.03	0.02	0.50	0.25	0.70	0.67
5. I felt hopeful about the future.a	‘Hopeful’	0.46 (0.80)	0.92	0.03	0.31	0.10	0.72	0.69
6. I felt fearful.	‘Fearful’	0.11 (0.40)	0.65	0.16	0.44	0.19	0.70	0.69
7. My sleep was restless.	‘Restless sleep’	0.82 (0.96)	0.99	0.03	0.28	0.10	0.72	0.72
8. I was happy.a	‘happy’	0.38 (0.66)	1.18	0.03	0.49	0.24	0.70	0.66
9. I felt lonely.	‘Lonely’	0.22 (0.57)	0.86	0.02	0.41	0.17	0.71	0.69
10. I could not get going.	‘Not get going’	0.30 (0.59)	1.00b		0.46	0.21	0.70	0.67
	Total	3.19 (3.30)				0.72		0.70

^aItems 5 and 8 are reverse-scored.

^bNot tested for statistical significance. All other unstandardized loadings are statistically significant (p < 0.01).

^cThe estimated extracted variance was 21%. Extracted variance assesses the amount of variance captured by the latent factor in relation to the variance attributable to measurement error [49].

^dα: Cronbach’s alpha.

3. Results

3.1. CFA model evaluation

Model fit indices indicated poor fit for a single factor structure with uncorrelated errors: df = 35, χ²/df = 131.51, GFI = 0.950, AGFI = 0.926, RMSEA = 0.083, SRMR = 0.051, CFI = 0.836 and TLI = 0.789. In an attempt to improve model fit, two pairs of error terms (e4–el0, e5–e8) were correlated based on modification indices and the CFA re-computed. The fit of this model was excellent with df = 33, χ²/df = 30.44, GFI = 0.989, AGFI = 0.982, RMSEA = 0.039, SRMR = 0.024, CFI = 0.965 and TLI = 0.952. This final model is illustrated in Fig. 2b.

All factor loadings were statistically significant (except p-value for item 10 as being constrained to 1). Standardised factor loadings were low, ranging from 0.28 to 0.64 (Table 1). Items 5 (‘hopeful’) and 7 (‘restless sleep’) had the lowest loadings (0.31 and 0.28 respectively), indicating that < 10% of response variance on each of the two items was explained by the latent factor. Items 3 (‘depressed’) and 1 (‘bothered’) had the highest loadings (0.64 and 0.51 respectively), which reflected 41% and 26% of variance respectively explained by the latent factor. The change in the composite reliability and Cronbach’s alpha when an item was deleted also shed light on the meaning of each item to the overall scale’s internal consistency. In general, the Cronbach’s alpha of 0.70 and composite reliability of 0.72 manifested good internal consistency of all ten items in measuring the latent factor (Table 1).

3.2. Measurement Invariance Test

Multi-group CFA was calculated by implementing Sequential CFA in each sub-group (Table 2) to compare the performance of the CES-D-10 by gender and country. The model fit in all these four sub-groups was excellent. As Table 2 illustrates, the invariance assumption was not rejected for country (Australia versus US). The Measurement Invariance Test for gender showed slight evidence of invariance as ΔCFI was just above 0.002 (Table 2). Despite the differences, model fit of the one factor CES-D-10 remained excellent across the groups, indicating that the scale performs equally well in males and females.

Table 2.

Multi-group analysis using confirmatory factor analysis.

Overall model		Model fit indices
		χ2	df	χ2/df	GFI	RMSEA	CFI	ΔCFI
		1004.37	33	30.44	0.982	0.039	0.965
Multi-group analysis by gender
Sequential	Male (n = 8331)	412.25	33	12.49	0.990	0.037	0.966
	Female (n = 10,779)	660.40	33	20.01	0.988	0.042	0.961
Simultaneous	Configural invariancea	1072.65	66	16.25	0.989	0.028	0.963
	Metric invarianceb	1159.68	75	15.46	0.988	0.028	0.960	0.003
Multi-group analysis by country
Sequential	Australia (n = 16,699)	909.71	33	27.57	0.989	0.040	0.964
	America (n = 2411)	174.37	33	5.25	0.985	0.042	0.961
Simultaneous	Configural invariancea	1084.09	66	16.43	0.989	0.028	0.964
	Metric invarianceb	1130.39	75	15.07	0.988	0.027	0.962	0.002

^aUnconstrained model.

^bFactor loadings constrained, df: degree of freedom, GFI: Goodness of Fit Index, RMSEA: Root Mean Square of Approximation, CFI: Comparative Fit Index, ΔCFI: differences in CFI between configural model and metric model.

3.3. The MIMIC models

Parameter estimates for the MIMIC model are shown in Table 3. The factor loadings were very similar to those from the CFA model, a confirmation of the CFA model validity and an indication that the impact of gender and other covariates on the CFA one-factor solution were limited. Both age and gender had a moderate impact on the depression latent trait. There was a negative indirect effect for Male vs Female (estimated beta coefficient from Model 1 in Table 3: −0.21), and a positive indirect effect older age (estimated beta coefficient from Model 2 in Table 3: 0.03) indicating that higher depression score is positively associated with being Female and older. The expected direction of these associations illustrated convergent validity. Implementing the Cole et al. guidelines [32], we concluded there is no gender invariance that could be associated with any of the 10 CES-D-10 items. Further analysis was performed to evaluate item discrimination in age group, ethnicity, education level and racial group by implementing gender-adjusted MIMIC models for each factor separately. The direct effect was estimated one item at a time. The results are summarised in Table 3; we concluded that CES-D-10 was relatively free of item bias for age group, ethnicity, education level and racial group as none of the item preference odds ratios (i.e. exponentiated value of direct effect estimations) was larger than 2 or < 0.5.

Table 3.

Parameter estimates (with standard errors) for MIMIC models; Model 1 adjusted for indirect gender effect and examining each item’s direct effect (invariance) impact one item at a time; Model 2–7 adjusted for indirect effect of gender and age, ethnicity, race, education or language respectively and examined each item’s direct effect impact one item at a time for age, ethnicity, race, education or language.

Item	Model1			Model2	Model3	Model 4	Model 5	Model 6	Model 7
	Unstandardised loadings	Standardised loadings	Direct effect	Direct effect	Direct effect	Direct effect	Direct effect	Direct effect	Direct effect
Item loading
1. ‘Bothered’	1 (constrained)	0.21	−0.00 (0.02)	−0.05 (0.02)	−0.02 (0.07)	−0.12 (0.04)	0.09 (0.05)	0.03 (0.02)	0.02 (0.06)
2. ‘Trouble concentrating’	0.98 (0.03)	0.21	−0.10 (0.02)	−0.03 (0.02)	0.15 (0.07)	−0.11 (0.04)	0.20 (0.05)	−0.02 (0.02)	0.00(0.05)
3. ‘Depressed’	1.56 (0.05)	0.33	0.04 (0.03)	0.00 (0.02)	0.31 (0.08)	−0.06 (0.05)	0.00 (0.06)	0.07 (0.03)	0.18 (0.07)
4. ‘Effort’	1.17 (0.04)	0.25	−0.06 (0.2)	0.07 (0.02)	−0.22 (0.07)	−0.04 (0.05)	0.03 (0.05)	0.07 (0.02)	−0.13 (0.06)
5. ‘Hopeful’	0.83 (0.03)	0.17	0.17 0(0.02)	0.00 (0.02)	−0.02 (0.06)	0.15 (0.04)	−0.21 (0.05)	−0.02 (0.02)	−0.02 (0.05)
6. ‘Fearful’	1.04 (0.04)	0.22	−0.20 (0.03)	−0.07 (0.03)	0.15 (0.09)	−0.13 (0.05)	0.10 (0.06)	−0.02 (0.03)	0.19 (0.07)
7. ‘Restless sleep’	0.48 (0.02)	0.10	−0.09 (0.02)	−0.07 (0.01)	−0.26 (0.05)	0.26 (0.04)	−0.26 (0.04)	0.06 (0.02)	−0.24 (0.04)
8. ‘Happy’	1.17 (0.04)	0.25	0.20 (0.02)	−0.06 (0.02)	0.06 (0.07)	−0.00 (0.04)	0.00 (0.05)	−0.17 (0.02)	0.10 (0.05)
9. ‘Lonely’	0.85 (0.03)	0.18	−0.14 (0.02)	0.15 (0.02)	0.17 (0.07)	−0.16 (0.04)	0.20 (0.05)	0.11 (0.02)	0.19 (0.05)
10. ‘Not get going’	1.10 (0.04)	0.23	−0.01 (0.02)	0.03 (0.02)	−0.17(0.07)	0.19 (0.05)	−0.15 (0.05)	−0.02 (0.02)	−0.26 (0.06)
Indirect effect
Gender (male)			−0.21 (0.01)	−0.21 (0.01)	−0.21 (0.01)	−0.21 (0.01)	−0.20 (0.01)	−0.21 (0.01)	−0.12 (0.01)
Age			–	0.03 (0.01)	–	–	–	–	–
Ethnicity (Hispanic)			–	–	0.09 (0.04)	–	–	–	–
Race (White)			–	–	–	−0.18 (0.03)	–	–	–
Race (African American)			–	–	–	–	0.20 (0.03)	–	–
Education (≤ 12 yrs)			–	–	–	–	–	0.02 (0.01)	–
Language (English)			–	–	–	–	–	–	0.05 (0.03)

4. Discussion

The purpose of this study was to explore the psychometric properties, and validate the factor structure, of the CES-D-10. We found that a one-factor CFA model of the CES-D-10 was appropriate in healthy Australian and American elderly community dwelling people. Overall, the analysis suggested a satisfactory fit of the specified model to participant responses, indicating that the CES-D-10 is a psychometrically sound self-report depression scale suitable for use in an otherwise healthy elderly population.

According to a rule of thumb [28] a minimum sample of 300 is needed for robust structural equation models with 20 parameters (i.e. 10 items, one factor solution). Models with weaker factor loadings require dramatically larger samples relative to models with strong factor loadings. For example, Monte Carlo data simulation techniques showed that in a one factor CFA model with 4 items, decreasing the strength of the factor loadings from 0.80 to 0.50 necessitated a threefold increase in the sample size and on average, factor loadings of 0.50 were associated with nearly 2.5-fold increases in required sample size relative to an identical model with loadings of 0.80 [34]. Within the CFA setting, increasing the number of latent variables also resulted in a significant increase in the minimum sample size. For example, minimum sample size requirements at least doubled when moving from one to two factors CFA [34]. A review of the literature of published CES-D-10 validation studies revealed that except for one study with over 16,000 participants [20], sample sizes for one factor solution varied from as low as 47 to 755 [11,18,19,21,35–39]. Also, two studies with sample sizes of 1013 and 742 reported a two factor solution [16,17]. Considering generally low factor loadings, and/or more than one latent variable in SEMs, this suggests that most published studies to date have been underpowered and at risk of inappropriate conclusions. The present study is the largest published CES-D-10 validation study. In addition, the fact that data were collected from two countries across various States and locations under the same protocol adds to generalisability of the findings [40]. This is also the first study that investigated validity of CES-D-10 across gender, age, race, language and ethnic groups.

4.1. Internal consistency

This study suggests the CES-D-10 is a reliable tool for measuring depression. The value of the reliability coefficient (Cronbach’s alpha of 0.70 and composite reliability of 0.72) in this study is similar to Cronbach’s alphas reported in other population-based CES-D validation studies. In Singaporean settings, α = 0.71 was reported in 1013 people over 65 years of age [16]. Similarly, internal consistency for the CES-D-10 was found at α = 0.71 in 468 women who lived in rural Mexico [41]. The level of internal consistency of the CES-D 10 in these community-dwelling individuals is satisfactory yet substantially lower than that in clinically diagnosed populations. Cronbach’s alphas reported in patients with HIV-positive [39], post traumatic spinal cord injuries [37] or with psychiatric problems [38] were 0.88, 0.86 and 0.90 respectively. Perhaps, higher Cronbach’s alphas could be expected in clinical situations where populations are selected on the basis of target symptomatology and are therefore much more homogeneous than population cohorts.

4.2. Factor loadings and model fit

In the present study, the fit of the one-factor model of the CES-D-10 was examined. Fit indices indicated a commendable level of fitness of the model to Australian and American elderly in community settings. This model has previously been found variously to have poor [16,21], acceptable [35], good [36] and excellent fit [20]. Our finding was in line with a large scale validation study on English and Spanish speaking U.S. resident Hispanic adults that confirmed the validity of a one-factor model [20].

The CFA factor loadings of the CES-D-10’s ten items ranged from 0.28 to 0.64 in this study. In other papers, loadings were as low as 0.088 [21] or as high as 0.87 [36,39]. Similar to the results reported by Bradley et al. [21], Lee and Chokkanathan [16], Cheng et al. [18] and Amtmann et al. [35], items with loadings less than the threshold of 0.4 existed in this study. Specifically, items 5 ‘hopeful’ and 7 ‘restless sleep’ had loadings of 0.31 and 0.28 respectively. Amtmann et al. [35] also reported a lowest item-total correlation coefficient of 0.33 in 455 people diagnosed with multiple sclerosis and living in the community. A smaller correlation coefficient of item 5 (‘hopeful’) compared with the remaining items has been commonly identified in the literature [16–18,21]. Lee and Chokkanathan [16] additionaly identified a very low loading of item 8 ‘happy’ in a one-factor model (0.17). This was however not the case in the present study (loading = 0.49). Our results suggest that the previously identified ‘positive affect’ factor [16,18] can be accounted for by method variance and no distinct factor is necessary. This addresses previous concerns about problems with factors consisting of only two items, given that factors with fewer than three items are generally weak and unstable [42].

The method of Maximum likelihood was used for estimating structural equation models in CFAs [43]. This means the likelihood function being maximized formally assumes the full joint normality of all the variables, including the observed variables. While large sample size in our study warranted robust estimation of factor loadings and standard errors [44] an asymptotic distribution free (ADF) estimation methods was used as a sensitivity analysis. The implemented ADF method is a form of weighted least squares estimation approach [45]. It makes no assumption of joint normality or even symmetry, whether for observed or latent variables. The results from both methods were fairly similar and the ADF method did not change the conclusions.

While the initial CFA model (Fig. 1.a) showed acceptable model fit in an attempt to improve model fit two pairs of error terms were correlated (Fig. 1b). According to Brown [46], a good justification to add correlated errors between indicators of the construct is needed and error correlations should not be added only to reach better model fit. Item 5 (‘hopeful’) and 8 (‘happy’) are both positively worded and items 4 and 10 (‘I felt like everything I did was an effort.’ and ‘I could not get going.’) could have similar interpretation. Specific item content (i.e. positively worded) for item 4 and 10 and shared method variance due to similar wording compared to other indicators (i.e. ‘effort’ and ‘get going’) are potential reasons why these correlated errors has occurred. While the justification for correlated errors is reasonable we would like to emphasis the exploratory nature of the proposed model.

4.3. Measurement invariance evaluation

A strange feature of measurement invariance evaluation is that non-invariance is typically seen as undesirable, and as such it has been treated as a statistical hurdle that must be overcome before progressing to other research questions [47]. As a consequence, testing invariance assumption is performed even under poor study conditions such as low sample size, few indicators per factor, or relatively low communality in items. This is an undesirable psychometric situation. It has been shown that favourable settings such as large sample sizes and well-developed psychometric instruments can lead to a greater chance of detecting non-invariance [48]. To offset this, we have not viewed invariance as an either/or proposition. Instead, for the instance in which there was evidence of gender non-invariance, we implemented MIMIC models to estimate effect sizes for the factor loading differences and avoided sub-group CFAs in race, language and ethnicity.

The result of multi-group CFAs and measurement invariance tests showed that across countries, full invariance of the CES-D-10 was supported, indicating that the scale performs equally well in Australian and American populations. There was evidence of measurement invariance across gender sub-groups. Further analysis was performed to locate the difference by using MIMIC models. We found no evidence that any of the CES-D-10 items tend to be differentially rated by women compared with men, after adjusting for total depression score. This is consistent with the conclusion of Lee and Chokkanathan [16], who found a gender non-invariance assumption acceptable. We found no evidence of item bias by age when comparing 65–74, 75–84 and 85+ year age groups. The absence of an age bias might reflect reality or might be due to the restricted age range in our sample. No previous work has simultaneously addressed racial, ethnicity and level of education item discrimination measurement invariance in the CES-D-10. Our novel finding, that there was no item preference bias in African American, non-White and Hispanic minorities as well as in dichotomised education-level groups suggests that the CES-D-10 was an effective instrument across the cultural and ethnic groups included in this study.

We purposefully selected an effect size cut-point to define a meaningful level of item bias through the MIMIC models. We did so to take the emphasis off the p-value and focus on the measure of association. In total, we made 70 direct effect comparisons. Had we used the Bonferroni correction for multiple comparisons, the p-value of a statistically significant association would have been < 0.0004.

4.4. Limitations

Criterion related validity was not assessed in this study. Further studies of the psychometric properties of the CES-D-10 could include the assessment of the scale compared with psychiatric diagnosis.

The ASPREE participants were a volunteer sample from a healthy elderly population across both countries, so study population might not be representative of the broader population. The fact that data came from a cross-sectional sample with no alternative methods to evaluate true status and/or severity of depression limited the scale validation to construct validity, convergent validity and internal consistency aspects. Alternative study design, such as a cohort study with multiple CES-D-10 measurements and alternative evaluation of depression such as clinical diagnostics etc. will provide an opportunity to evaluate other aspects of instrument validation such as its sensitivity, specificity and predictive values.

5. Conclusion

Data from a healthy elderly population across Australia and the United States suggested enhanced construct validity and internal consistency of the CES-D-10, making the scale summary score a useful tool for assessing depressive symptoms in this population. CFA results indicated good model fit of a one-factor model in the overall sample, Australia and U.S. sub-samples and gender sub-groups. Although there are no a-priori assumptions on proposed potential correlations between Item 5 (‘hopeful’) and 8 (‘happy’) and between items 4 (‘effort’) and 10 (‘not get going’) needs further confirmation through examining construct validity in similar settings. Establishing item invariance is of prime importance for drawing unbiased inferences in research using multi-item measurement scales. Our results supported measurement invariance in gender, race, ethnicity, language and level of education. In comparison with cohorts included in other published studies on validation of the CES-D-10, ASPREE participants were broadly representative of an older, healthy population [26]. They were independent living, community dwelling, lived in city and regional areas across Australia and the U.S. and, although they were predominantly White, they included representation from a number of ethnic groups. As such, this study could serve as a useful validation reference for older community-dwelling populations with diverse racial, ethnicity and language backgrounds. Future studies should specifically focus on benefits and limitations of CES-D-10 as a screening tool by evaluating its sensitivity, specificity and predictive values in community dwelling adults in general and in elderly population.