Abstract
Multiple scattering is a major barrier that limits the optical imaging depth in scattering media. In order to alleviate this effect, we demonstrate aberration-diverse optical coherence tomography (AD-OCT), which exploits the phase correlation between the deterministic signals from single-scattered photons to suppress the random background caused by multiple scattering and speckle. AD-OCT illuminates the sample volume with diverse aberrated point spread functions, and computationally removes these intentionally applied aberrations. After accumulating 12 astigmatism-diverse OCT volumes, we show a 10 dB enhancement in signal-to-background ratio via a coherent average of reconstructed signals from a USAF target located 7.2 scattering mean free paths below a thick scattering layer, and a 3× speckle contrast reduction from an incoherent average of reconstructed signals inside the scattering layer. This AD-OCT method, when implemented using astigmatic illumination, is a promising approach for ultra-deep volumetric optical coherence microscopy.
1. Introduction
Deep imaging inside scattering biological media is desirable for many applications. Such a capability could extend the investigation of biological systems into new regimes. It can be beneficial for both fundamental in vitro studies in engineered cell cultures or animal models of disease in vivo, as well as for clinical diagnostics or monitoring of therapies. However, current optical imaging technologies experience severe limitations in these studies because multiple scattering (MS) photons corrupt the sample information carried by single scattering (SS) or so-called ‘ballistic’ photons. In label-free coherent imaging at optical frequencies, e.g. with optical coherence tomography (OCT), the imaging depth within scattering tissues is limited to ~1-2 mm [1–3].
Various approaches have been demonstrated to overcome MS [4, 5]. Traditional approaches include the use of a confocal gate to suppress or reject multiply scattered light [6–8]. The level of MS rejection can be further enhanced through the combination of a confocal and coherence gate, which is particularly beneficial for higher numerical aperture (NA) optical coherence tomography/microscopy (OCT/OCM) [9]. Longer wavelengths that have a lower scattering coefficient in tissue have been shown to provide increased imaging depth in coherent imaging [10–12], as well as nonlinear microscopy [13, 14].
Recently, several ‘non-traditional’ approaches for deep optical microscopy have generated significant excitement [5]. A major class of methods is time reversal wavefront shaping [15–19], which ‘pre-scrambles’ the phase of incident light with hardware wavefront shaping to conjugate the effect of sample induced MS and wavefront distortion. These techniques can form a tight focal spot within a turbid medium, but they require spatially-variant wavefront shaping to account for region-dependent phase distortions across a wide field-of-view (FOV). This adds complexities in live imaging environments where dynamic sample fluctuations can occur. Another class of techniques for MS suppression exploits different correlation characteristics between SS and MS photons [20–22], in which the MS signal becomes decorrelated across multiple acquisitions, while the SS signal maintains its correlation. Other related methods have been demonstrated to produce decorrelated speckle patterns [23, 24]. This class of techniques for MS/speckle reduction is usually accompanied by confocal and/or coherence gating for further MS suppression.
Previously, we demonstrated OCT with hybrid adaptive optics (hyAO) [25] to enhance the volumetric imaging throughput of optical coherence microscopy (OCM), by splitting the work of image formation between both hardware and computation. In [25], we utilized an astigmatic illumination beam produced via hardware adaptive optics (HAO) to enhance signal collection compared to a standard Gaussian beam, and the resolution penalty of this intentionally applied aberration was mitigated in post-processing via computational adaptive optics (CAO) [26]. However, hyAO relies on single scattered photons to achieve a good CAO reconstruction, and imaging performance can be degraded in highly scattering samples [25].
In this paper, we use aberration-diverse OCT (AD-OCT) to extend this astigmatic imaging into the MS regime, by exploiting phase correlation behaviors (similar with [20, 22]) to distinguish SS from MS photons in volumetric reconstructions. AD-OCT takes advantage of the principle that a diversified illumination point spread function (PSF) passes through different spatial regions of a scattering medium, and therefore generates differing realizations of MS signal. By using various aberrated illumination PSFs (such as a rotating astigmatic PSF in this paper), the patterns formed by multiple realizations of the MS field decorrelate between acquisitions, while the SS field remains deterministically correlated. A coherent accumulation of multiple volumes then extracts the SS signal while suppressing the MS components. Meanwhile, since the aberration diversity also generates multiple decorrelated realizations of speckle, an incoherent accumulation can reduce the speckle contrast. By using AD-OCT, we achieved a 10 dB enhancement in signal-to-background ratio (SBR) when imaging a USAF target hidden beneath a scattering layer consisting of TiO2 beads with 7.2 scattering mean free paths (MFP), and a 3× reduction in speckle contrast within this layer.
2. Theory
When imaging inside a scattering medium, the complex signal reconstructed from a spectral domain OCT (SD-OCT) system can be described by the superposition of the following components:
| (1) |
In Eq. (1), is the detected OCT signal at a particular depthimaged with certain orientation angle , defined as the orientation of the first astigmatic line focus in the transverse (xy-) plane. is the single-scattered signal from the sample after CAO reconstruction, and in theory it does not depend on astigmatism rotation angleafter the aberration has been removed. The background (which is not related to the self-interference signal from the OCT reference arm) includes the MS contributionand OCT system noise (e.g. optical shot/intensity noise or thermal/electronic noise), that is
| (2) |
The OCT system noiseis assumed to be circularly Gaussian distributed in the shot noise limit and can be reduced by temporal averaging [27–29]. However, the MS contributionis not inherently randomized in time. Suppressingrequires inducing a decorrelation of the MS signal (e.g. by rotating the astigmatic angle ) across multiple acquisitions and can be accomplished via imaging with a diverse set of aberrated PSFs in AD-OCT.
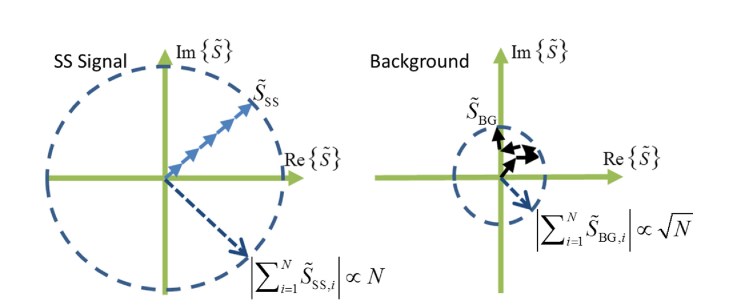
In this paper, AD-OCT utilizes astigmatism as the aberration and rotates the astigmatic angle across volumetric acquisitions. Since the optical illumination and collection paths in the scattering medium are altered by this rotation, the patterns formed by MS photons at the detector become decorrelated. However, the SS signals, as acquired with different astigmatic PSFs, still converge to the same correlated signal after CAO reconstruction. Therefore, as illustrated in Fig. 1, assuminganddoes not change appreciably across aberration states, by coherently summing the complex field from AD-OCT acquisitions, the SS signal grows with the number of states, while the background from uncorrelated phasor sums increases with .
Fig. 1.
The summation of complex signals from SS and background contributions. A complex SS signal which maintains a stable phase grows proportionally with N (left), while a background exhibiting a random phase grows analogous to a random walk, proportional to(right).
We can then define the SBR of a coherent averageas the SS signal magnitude over the background magnitude, as
| (3) |
whereandrepresent the single-scattered and background contributions respectively, from the ith aberration state.
Although the coherent average is able to suppress the background, it cannot reduce the speckle contrast (in the context of this paper, speckle refers to the interference pattern formed by both sub-resolution SS scatterers and MS photons), because this coherent process generates a new speckle pattern that has the same statistics as the old one. However, since AD-OCT acquires decorrelated speckle patterns resulting from aberration diversity, an incoherent magnitude-based average can achieve speckle reduction, with the speckle contrast reduced by a factor of [24, 30–32], that is
| (4) |
In Eq. (4),represents the contrast ratio from incoherently averaged speckle patterns having a mean signal magnitudewith standard deviation, where. The individual speckle patterns are assumed to follow a Rayleigh distribution with mean magnitudeand standard deviation.
In summary, since AD-OCT decorrelates the interference pattern formed by MS waves, it can suppress the MS contribution using a coherent complex average and/or reduce speckle using an incoherent magnitude average of decorrelated speckle patterns.
3. Methods
3.1 Experimental setup
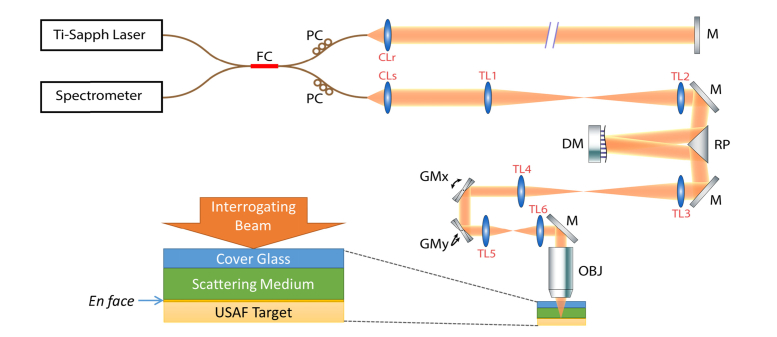
The AD-OCT setup is based on SD-OCT with adaptive optics, as illustrated in Fig. 2. The system was illuminated by a Ti:Sapph broadband laser source (Femtolasers, Integral Element) with 810 nm central wavelength and 150 nm bandwidth. In the sample arm, the plane of the deformable mirror (Alpao, DM 97-15) was conjugate to the entrance pupil of the objective lens (Olympus, UMPlanFl 20XW) to shape the wavefront. The deformable mirror was operated in open loop (i.e. without feedback from a wavefront sensor) for this study. After the sample arm signal was superimposed with a reference arm signal at a 50:50 coupler, the net signal was collected by a spectrometer (Wasatch Photonics, Cobra 800) with a 12-bit line scan camera (e2v, Octopus). The entire system offered a 2 μm full-width-at-half-maximum (FWHM) isotropic resolution in air. For the experiments in this work, a 75 kHz line scan rate was used to acquire volumes with a transverse size of 256 × 256 voxels (resulting in an acquisition time of 0.9 seconds per volume). The total incident power on the sample was measured to be 23 mW, yielding a peak imaging sensitivity of 94 dB (at the Gaussian beam focus) at 300 μm below zero optical path delay (with a 5 dB/mm sensitivity fall-off). The sensitivity is limited by the reflection loss from the mirrors and telescopes lenses in the sample arm optics (~50% single-pass loss) and/or residual misalignment/higher order aberrations/fiber coupling losses of the overall optical system.
Fig. 2.
System diagram for AD-OCT setup and sample configuration. FC: 50-50 Fiber Coupler, PC: Polarization Controller, M: Mirror, DM: Deformable Mirror, RP: Right-angle Prism, GMx and GMy: Galvanometer mirror along x and y directions, OBJ: Objective Lens, CLr: Reference arm collimating lens, CLs: Sample arm collimating lens (f = 50 mm), TL1 and TL2: Telescope lens 1 and 2 (f1 = f2 = 400 mm), TL3 and TL4: Telescope lens 3 and 4 (f3 = 400 mm, f4 = 250 mm), TL5 and TL6: Telescope lens 5 and 6 (f5 = f6 = 100 mm). All the telescope lenses are AR-coated achromatic doublets. Folding mirrors in the system are not shown.
The sample consisted of a cover glass, scattering medium (optical thickness of 7.2 scattering MFP), and USAF target. The cover glass served as a reference surface for phase registration across multiple volumes. The scattering layer was made with 1% w/w TiO2 particles inside a silicone medium, which consisted of 1:10:100 w/w/w of RTVb, RTVa (Momentive, RTV615) and silicone oil, respectively. The scattering MFP was measured from the exponential decaying confocal responses fused with multiple focal depths inside the layer, as described in [33], with the sensitivity fall-off removed by simultaneously adjusting the sample and reference arm. The USAF target helped to characterize the improvement of SBR and speckle reduction, and was placed at the second line foci of the astigmatic beam. The DM in the sample arm was used to rotate the astigmatism across acquisition volumes. In the experiment, the astigmatism induced by the deformable mirror resulted in a line foci separation of 100 μm (in air), and a complete rotation (180°) was covered by 100 volumes (corresponding to 100 astigmatic states). As shown and discussed later in the paper, using only 12 states (equally spaced over the 100 astigmatic states; 15° angular separation between volumes) was adequate to observe significant improvements. The purpose of acquiring more states than necessary was to demonstrate a saturation effect when finer angular separation was applied.
3.2 Data processing
The workflow in AD-OCT post-processing involves standard OCT reconstruction, phase registration across volumes, and CAO aberration compensation.
Standard OCT reconstruction corrects for dispersion mismatch between the sample and reference arms, resamples the wavenumber to a linear spacing, and performs a Fourier transforms along wavenumber to convert the signal into the space domain.
Phase registration corrects phase drifting which takes place across multiple volumes and is essential for a coherent average of sequentially acquired volumes. The first step is to utilize the upper surface of the cover glass as a phase reference, which is then used to conjugate the phase across the entire A-scan. The details of this phase stabilizing approach can be found in [34, 35].
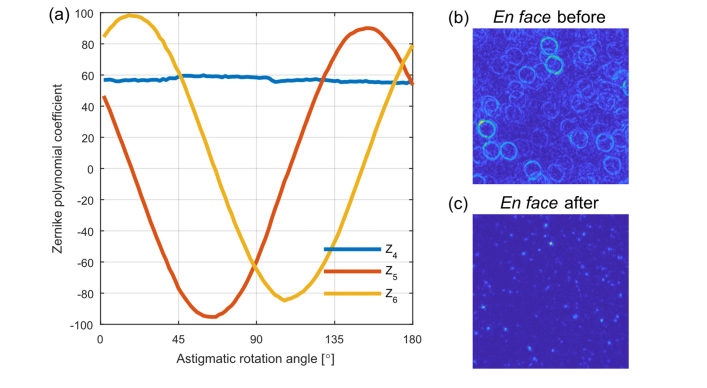
The second step is to account for any tilt in the optical system alignment or sample, which produces an offset in the Fourier-domain OCT signal with respect to the center of the computed pupil coordinate system. If the Fourier-domain OCT signal bandwidth is not centered in the computed pupil coordinate system, the application of CAO defocus or astigmatic correction centered about the pupil origin will lead to a residual 2D phase ramp in the CAO-corrected Fourier-domain signal. For a given Fourier-domain signal offset, the magnitude and orientation of the residual 2D phase ramp depends on the magnitude and orientation of the astigmatic correction. Therefore, application of different astigmatic CAO correction kernels, corresponding to the rotating astigmatic line foci, will produce a residual 2D linear phase ramp in the CAO-corrected Fourier domain signal whose orientation rotates with the orientation of the astigmatic line foci. This 2D linear phase ramp with rotating orientation in the CAO-corrected Fourier domain signal leads to an astigmatic-state-dependent shift of the spatial-domain image, resulting in a ‘wobbling’ FOV, as shown in Fig. 3b. Assuming the Fourier domain offset is constant across data sets, one solution to this FOV wobble is to correct the residual astigmatic-state-dependent phase ramp, or alternatively (as we implemented in this paper), to remove the offset of the Fourier-domain OCT signal before applying the CAO correction. The final step is to fix small, bulk space-domain offsets using cross correlation, and adjust the constant phase offsets (i.e. piston aberration), across the acquired volumetric data sets.
Fig. 3.
Illustration of wobble correction during AD-OCT. (a) Variation of the Zernike polynomial coefficients with rotating astigmatic angle for a sparsely scattering sample. Z4: Defocus, Z5: Oblique astigmatism, Z6: Vertical astigmatism. (b) AD-OCT of en face plane from 100 volumes in a resolution phantom, before wobble correction. (c) The same plane as in (b) after wobble correction.
CAO reconstruction removes the aberration and defocus, restores the SS signal to its aberration-free phase, and recovers focal-plane resolution throughout the volume. The detailed procedure of CAO is explained in [26]. In order to find the proper CAO parameters for astigmatism correction, a calibration step was conducted in a sparse resolution phantom (made with the same procedure as the scattering layer except that the TiO2 concentration was 0.1%) to map the hardware pupil (controlled by DM) to a computational virtual pupil (controlled by CAO). Assuming the refractive index is not altered in the scattering layer, CAO is able to mitigate astigmatism with the calibrated parameters and correct defocus with the maximum intensity metric [36] (we refer to ‘intensity’ as the magnitude squared of the complex OCT signal).
4. Results
4.1 AD-OCT with diverse astigmatism
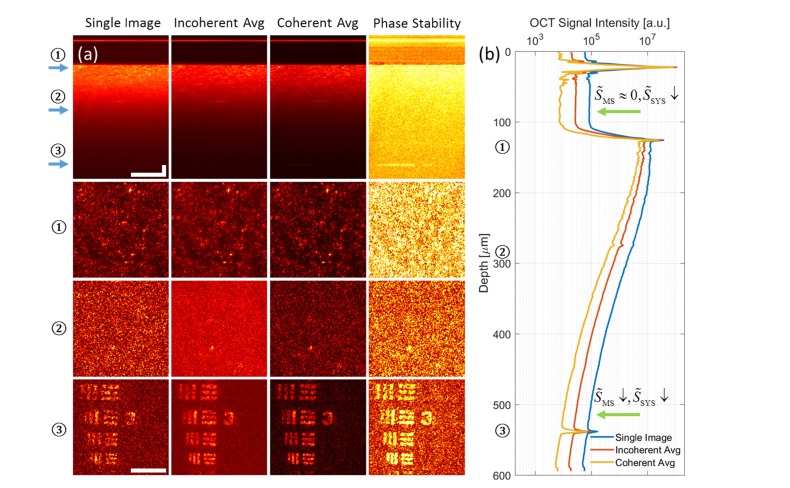
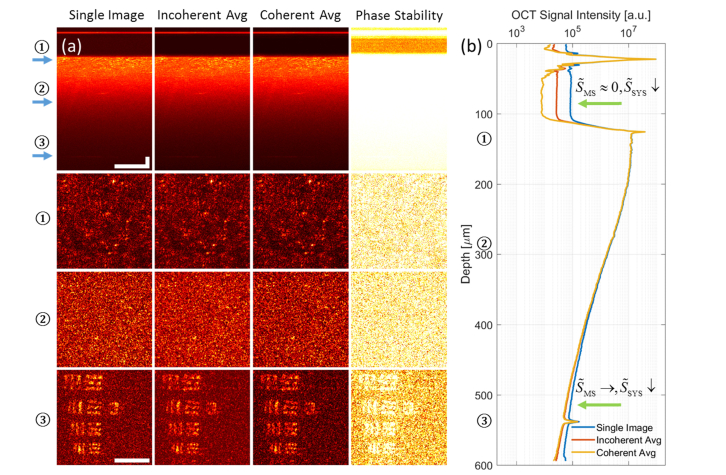
Using the methods described in the previous sections, we demonstrated background suppression from AD-OCT (using 12 equally spaced aberration states) compared to a single image, as shown in Fig. 4. We note that the colormap of Fig. 4(a) has a fixed range (i.e. without normalization) at each depth for the en face comparison, so that the level of background suppression can be interpreted directly. This colormap will be consistent throughout the paper and in supplementary visualizations, for any en face plane at a particular depth.
Fig. 4.
Volumetric AD-OCT reconstruction results, showing a USAF target hidden beneath a scattering layer with an optical thickness of 7.2 scattering MFP. (a) Comparison of cross section (first row, γ = 0.7) and en face (3 bottom rows) among single image, incoherent average, and coherent average, from 12 volumes reconstructed with AD-OCT (15° angular separation). The depth of each en face plane is indicated by the arrows in the cross section view. The last column shows the phase stability measurements for AD-OCT. Scale bars indicate 40 μm for all images. The colormap has a fixed range at each depth for the first three columns, and from 0 to 1 for the last column. (b) Plot of OCT signal magnitude (99th percentile at each depth) versus depth for single image, incoherent average, and coherent average, from 12 volumes reconstructed with AD-OCT (15° angular separation). The depths of the 3 en face planes in (a) are labelled on the axis. The upper green arrow indicates a region where AD-OCT reduces the system noise floor by time averaging, and the bottom green arrow points to a region where AD-OCT reduces MS contribution by aberration diversity and the system noise floor by time averaging.
Comparing the first and third columns of Fig. 4(a), the en face plane inside the scattering layer and on the USAF target shows an improvement in SBR after a coherent average of AD-OCT volumes. From the signal versus depth plot in Fig. 4(b), since the deep region near the bottom of the scattering layer (bottom green arrow) can be considered as containing a significant fraction of MS contributions, the reduction in signal magnitude indicates a suppression of MS components. On the other hand, the region between the cover glass surfaces (upper green arrow) contains mostly the system noise, where the background reduction is due to time averaging. The slight reduction in peak signal at the USAF target plane can be attributed to signal variations from different PSFs passing through the scattering medium, and fluctuations in the system (such as laser power, DM surface shape, etc).
Comparing the first and second columns of Fig. 4(a), the en face plane inside the scattering layer and on the USAF target shows an improvement in the level of speckle after an incoherent average of AD-OCT volumes. This is evident from the more homogeneous (less speckled) appearance of the image (when away from isolated bright scatterers or USAF target bars). Further quantitative analysis of the speckle reduction is given in Section 4.3.
In Supplementary Visualization 1 (17.6MB, mp4) (SV1), the background suppression from AD-OCT can be tracked while averaging over varying numbers of astigmatism rotations (equally spaced across the 100 astigmatic states). As can be seen in SV1(b), when the first few aberration states are applied, the MS contribution and system noise are reduced at a similar rate simultaneously. However, as more states are included, the MS suppression starts to saturate, while the system noise keeps decreasing. This saturation effect indicates a diminishing return from using finer angles of astigmatic rotation.
The phase stability metric shown in the fourth column of Fig. 4(a) is calculated as the ratio of the coherent and incoherent averages, ranging from 0 (total phase instability) to 1 (perfect phase stability). The rationale for this metric is that the coherent average with phase-stable complex phasors converges to an incoherent magnitude average (giving a value close to 1), whereas the coherent average with random phasors sums to a smaller value compared to an incoherent average (giving a value closer to 0). Therefore, phase stable regions will be highlighted with this metric.
4.2 Single astigmatic state control
In order to verify that MS/speckle suppression originates from aberration diversity, as opposed to temporal averaging, we compared the AD-OCT reconstruction with a single-state control, in which a single aberration state was applied across multiple volumes. From the results shown in Fig. 5, the resulting single-state control does not achieve the level of improvement demonstrated by AD-OCT with diverse aberration states.
Fig. 5.
Single-state control experiment for AD-OCT, showing a USAF target hidden beneath a scattering layer with an optical thickness of 7.2 scattering MFP. (a) Comparison of cross section (first row, γ = 0.7) and en face (3 bottom rows) among single image, incoherent average, and coherent average, from 12 volumes with a single aberration state. The depth of each en face plane is indicated by the arrows in the cross section view. The last column shows the phase stability measurements for the single-state control. Scale bars indicate 40 μm for all images. The colormap has a fixed range at each depth for the first three columns, and from 0 to 1 for the last column. (b) Plot of OCT signal magnitude (99th percentile at each depth) versus depth for single image, incoherent average, and coherent average from 12 volumes with a single aberration state. The depths of the 3 en face planes in (a) are labelled on the axis. The upper green arrow indicates a region where the single-state control reduces the system noise floor by time averaging, and the bottom green arrow points to a region where the background cannot be reduced purely with time averaging.
Comparing the first and third columns of Fig. 5(a), the en face views from all depths show little improvement using a single-state control. From the signal versus depth plot, the reduction in the system noise floor was at the same level as with AD-OCT, but there is almost no MS suppression deep in the scattering layer.
From Supplementary Visualization 2 (14.4MB, mp4) , we can confirm this trend when increasing the number of a fixed astigmatic state. Therefore, purely reducing the system noise with temporal averaging does not improve the image quality as effectively as AD-OCT.
Comparing the first and second columns of Fig. 5(a), the en face view after the incoherent average shows little difference compared to the single image. Moreover, unlike the results in Fig. 4(a), the level of speckle after either a coherent or incoherent average appears similar to the single image. Further quantification of these trends is presented in Section 4.3.
4.3 Quantitative comparison between AD-OCT and single-state control
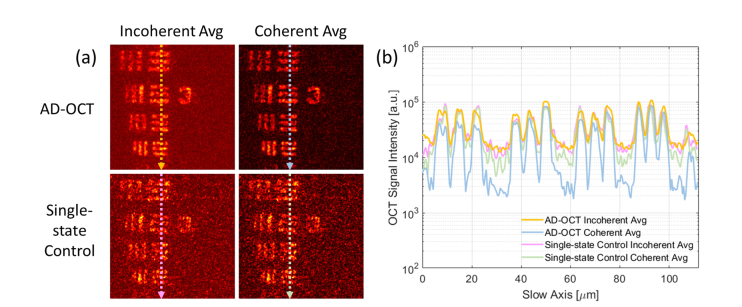
In this subsection, a more quantitative result from the comparison of AD-OCT reconstruction and single-state control is shown. Figure 6 shows reconstructed images of the USAF target plane, and selected intensity profiles along the slow axis of the raster-scanned spectral-domain OCT acquisition. From these results, background suppression is apparent in the coherent AD-OCT data. By comparison, the coherent average of the single-state control does not show a similar level of background suppression. The slightly lower background in the single-state coherent average can be attributed to a reduction in OCT system noise (e.g. optical shot/intensity noise or thermal/electronic noise) or fluctuations in the deformable mirror shape.
Fig. 6.
Intensity profile of the USAF target beneath MS layer for N = 12. (a) En face plane of the target, extracted from Fig. 4 and Fig. 5. (b) Intensity plot along the arrow indicated at each en face plane, averaged from 30 pixels along the fast axis. The colormap has the same range as Fig. 4.
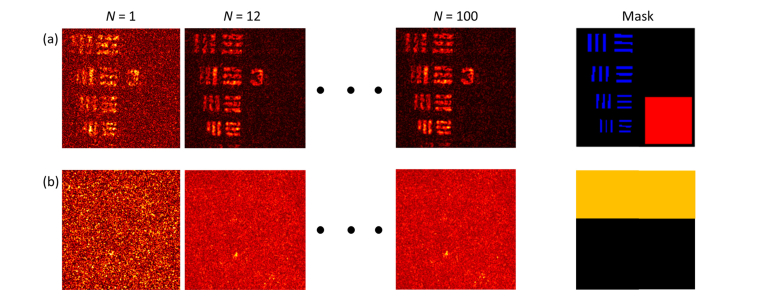
The level of enhancement from AD-OCT is related to the number of aberration states. In order to quantify this effect, we adopted the following approach for measuring SBR and speckle contrast. As shown in Fig. 7(a), for SBR measurements at the USAF target plane (plane ③ in Fig. 4, at a depth of 7.2 scattering MFP, located at the second astigmatic line focus), the signal was taken as the average magnitude inside the blue region where the USAF target bar is expected to appear, and the background was taken as the average magnitude of the red region where no SS event is expected to exist (this assumes that the back-reflection from the glass surface of the USAF target falls below the noise floor of the OCT system at the depth of the USAF plane). In Fig. 7(b), for speckle contrast measurement, a plane was chosen inside the scattering layer (plane ② in Fig. 4, at a depth of 3.1 scattering MFP), located 100 μm above the first astigmatic line focus. In this plane, the mean signal magnitude and its standard deviation was calculated from the yellow region, which encloses the interference pattern from the thick layer of scattering beads, but avoids some of the bright, isolated scatterers at that depth.
Fig. 7.
Images and masks used for the SBR and speckle contrast calculations. (a) Examples of USAF target en face view, and the SBR mask used to define the areas of expected signal and background. Any voxel within the blue regions are defined to be the signal, while the red region is defined to be the background. (b) Examples of en face view inside the scattering layer, and the speckle mask used to define the area of interest. Any voxel within the yellow region is considered as the speckle.
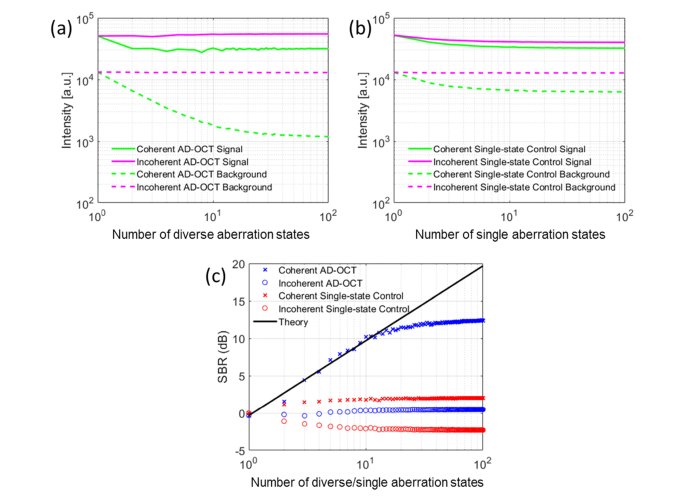
The SBR enhancement from coherent AD-OCT increases as more states are utilized, resulting in a ~10 dB improvement at 12 aberration states. Meanwhile, the speckle contrast from incoherent AD-OCT reduces with an increasing number of aberration states, yielding a 3× reduction at 12 states. The SBR and speckle contrast ratio are plotted in Figs. 8 and 9. By comparing the AD-OCT performance over the single-state control, we can conclude that the SBR improvement and speckle reduction does not originate from system noise reduction.
Fig. 8.
Quantitative measurement of SBR at the USAF target plane. (a) Intensity versus number of states from AD-OCT reconstruction, (b) Intensity versus number of states from single-state control, (c) SBR enhancement of coherent AD-OCT as more aberration states are applied.
Fig. 9.
Quantitative measurement of speckle reduction inside scattering layer. (a) Distribution of signal magnitude in speckle region from incoherent AD-OCT reconstruction, (b) Distribution of signal magnitude in speckle region from incoherent single-state control, (c) Speckle contrast reduction of incoherent AD-OCT as more aberration states are applied.
Note that for a given number of astigmatic states, these states are chosen to be equally spaced across a 180° rotation, which was sampled by a total of 100 states. The rotation of astigmatism in each volume is subsampled from these 100 states (1.8° angular separation), resulting an under-sampling (insufficient angular separation) when selecting 51 to 99 states, and hence the astigmatic rotation in these reconstructions is not exactly equally-spaced.
In Fig. 8(a) and Fig. 8(b), the average intensity from the signal region experiences a decay. One contributing factor could be OCT system fluctuations and imperfect phase registration. Another factor is related to MS suppression. Since the signal voxel contains a superposition of both SS and MS components, a MS suppression from AD-OCT reduces the voxel intensity. This effect has been accounted for in the definition of SBR in Eq. (3) (derivation not shown), and when calculating the SBR curve in Fig. 8(c). Meanwhile, the background is suppressed by a factor of 8 in AD-OCT relative to the single-state control, due to the aberration diversity of imaging PSFs, leading to a net increase in SBR with AD-OCT.
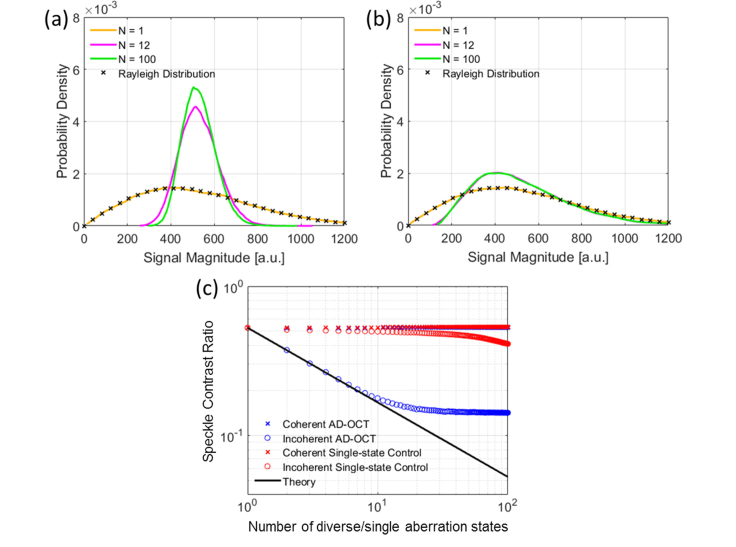
In Fig. 9(a), we observe a Gaussian distribution with a narrower standard deviation after incoherently accumulating speckle patterns from AD-OCT. This trend is consistent with the central limit theorem, suggesting a narrower Gaussian-like shape after the addition of decorrelated speckle patterns, where each individual pattern is described by a Rayleigh distribution. Since the signal distribution from the single-state control (Fig. 9(b)) does not change as much as for AD-OCT, we attribute the speckle reduction to the utilization of aberration diversity.
From Section 2, we expect the SBR enhancement and speckle reduction to scale with. However, Figs. 8(c) and 9(c) show that this relation only held for a small values of N, and that the benefit of AD-OCT began to saturate for >12 astigmatic rotation states. This may have been caused by a more significant overlap between the astigmatic PSFs. Further discussion on the underlying reasons behind this issue can be found in Section 5.
4.4 Combined suppression of both multiple scattering and speckle
We have seen the capability of coherent AD-OCT for MS suppression, and incoherent AD-OCT for speckle reduction. Given that the MS and speckle suppression saturates after ~12 states, can the remaining 88 AD-OCT volumes that were acquired be leveraged in some way to achieve simultaneous MS suppression and speckle reduction?
In Fig. 10, the SBR and speckle contrast ratio is calculated the same way as in Section 4.3, except that the background mask is chosen to be the region of speckle. Thesplit means that separate groups ofcoherent AD-OCT reconstructions were incoherently averaged to achieve the final result. For example, with the N = 100 diverse aberration states (giving an angular separation of 1.8°), the 5 × 20 split first performs a coherent average of 20 states with uniform spacing of astigmatism rotation (9° angular separation). Then an incoherent average is performed to accumulate the available 5 different realizations (9°/1.8° = 5) of the coherently averaged signal. This process gives a combined suppression in MS and speckle.
Fig. 10.
En face view of USAF target showing joint suppression of MS and speckle. From total MS suppression with no speckle reduction (left) to no MS suppression with total speckle reduction (right). The colormap has the same range as Fig. 4.
Our results show that it is indeed possible to achieve joint suppression of both MS and speckle by performingcoherent averages (< N), followed by an incoherent average of the resultingrealizations. However, given a fixed number of astigmatic states, the total diversity of astigmatism rotation that we can use for MS suppression or speckle reduction appears to be conserved. In other words, the ‘aberration diversity budget’ (level of decorrelation provided by the acquired AD-OCT volumes) cannot be simultaneously used to achieve the full performance of both MS and speckle suppression (i.e. the performance obtainable when all aberration diverse volumes are devoted entirely to a coherent vs. incoherent average).
5. Discussion
In this paper, we have presented AD-OCT, which is an approach that exploits the advantages of hyAO, namely the ability to combine physical wavefront manipulation with computational image formation. This method is capable of reducing MS or speckle when imaging with an aberration-diverse astigmatic beam.
In principle, the type of aberration-diverse PSF used in AD-OCT can be arbitrary, as long as the MS field can be decorrelated and the applied aberration can be adequately compensated with CAO before the final averaging step. However, using lower order aberrations (such as rotating astigmatism) to achieve aberration diversity can have some special advantages. First, in the case of a double-pass imaging configuration, CAO reconstruction for higher order aberrations may negatively impact the final transverse resolution, due to attenuation in the pass-band of the optical transfer function. In addition, since an astigmatic beam has a more equalized illumination and collection across depth compared to a Gaussian beam, astigmatic imaging inherently has a larger depth coverage [25]. Therefore, using astigmatism in AD-OCT maintains the advantages of astigmatic imaging and further extends its application into the MS regime. On the other hand, we should note that the confocal gate associated with a standard Gaussian beam OCT imaging configuration helps to reduce MS as well [9]. However, this paper focuses on imaging with an astigmatic beam, as this configuration has been shown to provide a crucial benefit for high throughput imaging [25]. A thorough analysis on the performance of astigmatic beams versus Gaussian beams in MS environments will be the focus of future work.
The performance of AD-OCT experienced a saturation effect, and we attribute this phenomenon to the overlap of rotational astigmatic PSFs causing a reduction in decorrelation between MS patterns. This may be resolved by increasing the astigmatism magnitude or utilizing higher-order aberrations. The former is more practical to implement, but it requires the sample arm power to be increased accordingly so as to not sacrifice the signal-to-noise ratio. The latter will provide additional diversity in MS patterns, but it can induce attenuation in the pass-band of the imaging aperture, and is thus more difficult to correct with CAO even with the forward model [37], as attenuated portions of the signal aperture may be fall below the noise floor.
For in vivo/vitro live imaging, sample motion may cause phase instabilities that degrade the CAO reconstruction of each volume and the coherent average across multiple volumetric acquisitions. Nevertheless, achieving the necessary phase stability for AD-OCT of live samples may still be feasible through increased acquisition speed and/or the use of additional phase registration algorithms [38]. For example, the use of swept-source FDML lasers can support video-rate volumetric acquisition [39–41]. On our current SD-OCT system, AD-OCT may still be feasible for ultra-deep cross-sectional imaging. A potentially feasible acquisition scheme would involve the acquisition of smaller, aberration diverse volumetric data sets, with the length of the slow-axis dimension being just long enough to enclose the full transverse width of the aberrated PSFs (this will typically be much smaller than the length of the fast-axis dimension). The fast refresh rate of the DM (~1 ms in open loop) can be leveraged to rapidly switch aberration states between the acquisition of each small volume, and a cross-sectional AD-OCT image can be reconstructed at the central slice position along the slow axis. In our SD-OCT system, assuming the use of a comparable level of astigmatism to that used in this study, we estimate a total acquisition time of less than 25 seconds for a 12 state AD-OCT cross-sectional image with FOV 1 × 1 mm2 (depth × fast axis, 1024 × 1500 × 100 voxels per aberration state, at 75 kHz line scan rate) at 2 μm isotropic FWHM resolution. For in vivo AD-OCT applications, even though saturation can be a potential concern for absolute performance in MS suppression, sample motion may not allow for the acquisition of a sufficient number of stable volumes to reach the saturation limit. When compared to other methods for ultra-deep or speckle-reduced imaging [20–22, 24], even though AD-OCT may encounter an earlier saturation at the current level of astigmatism, it offers a larger depth coverage than similar approaches using SD-OCT [22, 24] (due to the use of hyAO [25]), and can serve as a cross-sectional complement to the en face techniques [20, 21].
In this paper, we placed the USAF target plane at the second line focus of the astigmatic beam, in order to obtain a good illumination intensity. One question that remains open is how sample placement will affect the decorrelation level of MS or speckle provided by the aberration diversity. For example, it is worthwhile to investigate whether there is any difference to place the USAF target at the first line focus, plane of least confusion, or second line focus, given the same scattering layer thickness that the imaging beam passes through. This depth dependency with respect to the astigmatic beam structure needs to be studied in future work, as it may lead to the development of alternative PSF conventions for volumetric AD-OCT.
The functionality of the DM in AD-OCT could in principle be performed with other alternatives, such as a cylindrical lens, a liquid-crystal-on-silicon spatial light modulator (LCoS SLM), or a digital micro-mirror device (DMD). For example, a cylindrical lens in conjunction with a mechanical rotation stage would be able to support a comparable data acquisition scheme. However, the use of wavefront shaping devices may provide more precise wavefront control and better high-speed phase stability due to a lack of bulk moving parts during astigmatism rotation, and offer greater flexibility to enable a wide range of applications in the future, including simultaneous realization of AD-OCT and HAO correction of sample-induced aberrations [42–45]. An SLM or DMD can also provide real-time wavefront shaping capabilities. However, compared to a DM, an SLM has a slower refresh rate that may impose limitations for high speed imaging and can only impart a group delay to the optical wavefront when the required peak-to-valley correction is less than a wavelength, and a DMD has a poorer diffraction efficiency that degrades the quality of the wavefront [46]. Therefore, a DM with high-speed, precise aberration control is an attractive choice for AD-OCT.
6. Conclusion
We have presented AD-OCT as a novel approach for MS suppression and speckle reduction. AD-OCT uses aberration diversity to randomize the MS field and obtain decorrelated speckle realizations across CAO-reconstructed volumes. A coherent average of these reconstructed aberration-diverse volumes provides suppression of MS, and an incoherent average leads to speckle reduction. We utilized AD-OCT to demonstrate a 10 dB SBR improvement of a USAF target hidden beneath a scattering layer via coherent accumulation, and a 3× speckle contrast reduction inside the scattering layer via incoherent accumulation. The total level of aberration diversity can also be split between a partial MS suppression and partial speckle reduction. AD-OCT extends astigmatic beam imaging into the MS regime, and thus is potentially beneficial for various biomedical applications that require volumetric imaging inside a scattering medium. Future work will investigate the ultimate imaging depth limits of AD-OCT, compare its performance to Gaussian confocal gating, and explore additional or alternative options for aberration diversity.
Acknowledgments
The authors would like to thank Dr. Jerome Mertz for helpful discussions and Dr. Warren Zipfel for loaning the objective lens used in this work. Additional information can be found at http://adie.research.engineering.cornell.edu.
Funding
This research was supported in part by a Cornell Discovery and Innovation Research Seed Award; National Institutes of Health (1R21EY028389, NIBIB-R21EB022927); National Science Foundation (CAREER: CBET-1752405).
Disclosures
The authors declare a conflict of interest. S.L., M.R.E.L., and S.G.A. are listed as inventors on a patent application related to the work presented in this manuscript.
References
- 1.Schmitt J. M., “Optical coherence tomography (OCT): a review,” IEEE J. Sel. Top. Quantum Electron. 5(4), 1205–1215 (1999). 10.1109/2944.796348 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Fercher A. F., Drexler W., Hitzenberger C. K., Lasser T., “Optical coherence tomography - principles and applications,” Rep. Prog. Phys. 66(2), 239–303 (2003). 10.1088/0034-4885/66/2/204 [DOI] [Google Scholar]
- 3.Drexler W., Liu M., Kumar A., Kamali T., Unterhuber A., Leitgeb R. A., “Optical coherence tomography today: speed, contrast, and multimodality,” J. Biomed. Opt. 19(7), 071412 (2014). 10.1117/1.JBO.19.7.071412 [DOI] [PubMed] [Google Scholar]
- 4.Dunsby C., French P. M. W., “Techniques for depth-resolved imaging through turbid media including coherence-gated imaging,” J. Phys. D Appl. Phys. 36(14), R207–R227 (2003). 10.1088/0022-3727/36/14/201 [DOI] [Google Scholar]
- 5.Gigan S., “Optical microscopy aims deep,” Nat. Photonics 11(1), 14–16 (2017). 10.1038/nphoton.2016.257 [DOI] [Google Scholar]
- 6.Wilson T., Shepparu C. J. R., Löschke K., Theory and Practice of Scanning Optical Microscopy, Crystal Research and Technology (Academic Press, 1984). [Google Scholar]
- 7.Pawley J., Handbook of Biological Confocal Microscopy (Springer, 2006). [Google Scholar]
- 8.Iftimia N., Ferguson R. D., Mujat M., Patel A. H., Zhang E. Z., Fox W., Rajadhyaksha M., “Combined reflectance confocal microscopy/optical coherence tomography imaging for skin burn assessment,” Biomed. Opt. Express 4(5), 680–695 (2013). 10.1364/BOE.4.000680 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Izatt J. A., Hee M. R., Owen G. M., Swanson E. A., Fujimoto J. G., “Optical coherence microscopy in scattering media,” Opt. Lett. 19(8), 590–592 (1994). 10.1364/OL.19.000590 [DOI] [PubMed] [Google Scholar]
- 10.Drexler W., “Ultrahigh-resolution optical coherence tomography,” J. Biomed. Opt. 9(1), 47–74 (2004). 10.1117/1.1629679 [DOI] [PubMed] [Google Scholar]
- 11.Srinivasan V. J., Radhakrishnan H., Jiang J. Y., Barry S., Cable A. E., “Optical coherence microscopy for deep tissue imaging of the cerebral cortex with intrinsic contrast,” Opt. Express 20(3), 2220–2239 (2012). 10.1364/OE.20.002220 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Chong S. P., Merkle C. W., Cooke D. F., Zhang T., Radhakrishnan H., Krubitzer L., Srinivasan V. J., “Noninvasive, in vivo imaging of subcortical mouse brain regions with 1.7 μm optical coherence tomography,” Opt. Lett. 40(21), 4911–4914 (2015). 10.1364/OL.40.004911 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Kobat D., Durst M. E., Nishimura N., Wong A. W., Schaffer C. B., Xu C., “Deep tissue multiphoton microscopy using longer wavelength excitation,” Opt. Express 17(16), 13354–13364 (2009). 10.1364/OE.17.013354 [DOI] [PubMed] [Google Scholar]
- 14.Horton N. G., Wang K., Kobat D., Clark C. G., Wise F. W., Schaffer C. B., Xu C., “In vivo three-photon microscopy of subcortical structures within an intact mouse brain,” Nat. Photonics 7(3), 205–209 (2013). 10.1038/nphoton.2012.336 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Vellekoop I. M., Mosk A. P., “Focusing coherent light through opaque strongly scattering media,” Opt. Lett. 32(16), 2309–2311 (2007). 10.1364/OL.32.002309 [DOI] [PubMed] [Google Scholar]
- 16.Popoff S., Lerosey G., Fink M., Boccara A. C., Gigan S., “Image transmission through an opaque material,” Nat. Commun. 1(6), 81 (2010). 10.1038/ncomms1078 [DOI] [PubMed] [Google Scholar]
- 17.Xu X., Liu H., Wang L. V., “Time-reversed ultrasonically encoded optical focusing into scattering media,” Nat. Photonics 5(3), 154–157 (2011). 10.1038/nphoton.2010.306 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Mosk A. P., Lagendijk A., Lerosey G., Fink M., “Controlling waves in space and time for imaging and focusing in complex media,” Nat. Photonics 6(5), 283–292 (2012). 10.1038/nphoton.2012.88 [DOI] [Google Scholar]
- 19.Hillman T. R., Yamauchi T., Choi W., Dasari R. R., Feld M. S., Park Y., Yaqoob Z., “Digital optical phase conjugation for delivering two-dimensional images through turbid media,” Sci. Rep. 3(1), 1909 (2013). 10.1038/srep01909 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Kang S., Jeong S., Choi W., Ko H., Yang T. D., Joo J. H., Lee J.-S., Lim Y.-S., Park Q. H., Choi W., “Imaging deep within a scattering medium using collective accumulation of single-scattered waves,” Nat. Photonics 9(4), 253–258 (2015). 10.1038/nphoton.2015.24 [DOI] [Google Scholar]
- 21.Badon A., Li D., Lerosey G., Boccara A. C., Fink M., Aubry A., “Smart optical coherence tomography for ultra-deep imaging through highly scattering media,” Sci. Adv. 2(11), e1600370 (2016). 10.1126/sciadv.1600370 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Thrane L., Gu S., Blackburn B. J., Damodaran K. V., Rollins A. M., Jenkins M. W., “Complex decorrelation averaging in optical coherence tomography: a way to reduce the effect of multiple scattering and improve image contrast in a dynamic scattering medium,” Opt. Lett. 42(14), 2738–2741 (2017). 10.1364/OL.42.002738 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Desjardins A. E., Vakoc B. J., Oh W. Y., Motaghiannezam S. M. R., Tearney G. J., Bouma B. E., “Angle-resolved Optical Coherence Tomography with sequential angular selectivity for speckle reduction,” Opt. Express 15(10), 6200–6209 (2007). 10.1364/OE.15.006200 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Liba O., Lew M. D., SoRelle E. D., Dutta R., Sen D., Moshfeghi D. M., Chu S., de la Zerda A., “Speckle-modulating optical coherence tomography in living mice and humans,” Nat. Commun. 8, 15845 (2017). 10.1038/ncomms15845 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Liu S., Mulligan J. A., Adie S. G., “Volumetric optical coherence microscopy with a high space-bandwidth-time product enabled by hybrid adaptive optics,” Biomed. Opt. Express 9(7), 3137–3152 (2018). 10.1364/BOE.9.003137 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Adie S. G., Graf B. W., Ahmad A., Carney P. S., Boppart S. A., “Computational adaptive optics for broadband optical interferometric tomography of biological tissue,” Proc. Natl. Acad. Sci. U.S.A. 109(19), 7175–7180 (2012). 10.1073/pnas.1121193109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Park B., Pierce M. C., Cense B., Yun S.-H., Mujat M., Tearney G., Bouma B., de Boer J., “Real-time fiber-based multi-functional spectral-domain optical coherence tomography at 1.3 µm,” Opt. Express 13(11), 3931–3944 (2005). 10.1364/OPEX.13.003931 [DOI] [PubMed] [Google Scholar]
- 28.Goodman J. W., Statistical Optics (John Wiley & Sons, 2015). [Google Scholar]
- 29.Leitgeb R. A., Wojtkowski M., “Complex and coherence-noise free Fourier domain optical coherence tomography,” in Optical Coherence Tomography: Technology and Applications (Springer, 2015), 195–224. [Google Scholar]
- 30.Bashkansky M., Reintjes J., “Statistics and reduction of speckle in optical coherence tomography,” Opt. Lett. 25(8), 545–547 (2000). 10.1364/OL.25.000545 [DOI] [PubMed] [Google Scholar]
- 31.Karamata B., Hassler K., Laubscher M., Lasser T., “Speckle statistics in optical coherence tomography,” J. Opt. Soc. Am. A 22(4), 593–596 (2005). 10.1364/JOSAA.22.000593 [DOI] [PubMed] [Google Scholar]
- 32.Hillman T. R., Adie S. G., Seemann V., Armstrong J. J., Jacques S. L., Sampson D. D., “Correlation of static speckle with sample properties in optical coherence tomography,” Opt. Lett. 31(2), 190–192 (2006). 10.1364/OL.31.000190 [DOI] [PubMed] [Google Scholar]
- 33.Jacques S. L., Wang B., Samatham R., “Reflectance confocal microscopy of optical phantoms,” Biomed. Opt. Express 3(6), 1162–1172 (2012). 10.1364/BOE.3.001162 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Ralston T. S., Marks D. L., Carney P. S., Boppart S. A., “Phase stability technique for inverse scattering in optical coherence tomography,” in 3rd IEEE International Symposium on Biomedical Imaging: Nano to Macro , 2006., 2006), 578–581. 10.1109/ISBI.2006.1624982 [DOI] [Google Scholar]
- 35.Ralston T. S., Marks D. L., Carney P. S., Boppart S. A., “Interferometric synthetic aperture microscopy,” Nat. Phys. 3(2), 129–134 (2007). 10.1038/nphys514 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Xu Y., Liu Y.-Z., Boppart S. A., Carney P. S., “Automated interferometric synthetic aperture microscopy and computational adaptive optics for improved optical coherence tomography,” Appl. Opt. 55(8), 2034–2041 (2016). 10.1364/AO.55.002034 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.South F. A., Liu Y.-Z., Bower A. J., Xu Y., Carney P. S., Boppart S. A., “Wavefront measurement using computational adaptive optics,” J. Opt. Soc. Am. A 35(3), 466–473 (2018). 10.1364/JOSAA.35.000466 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Shemonski N. D., South F. A., Liu Y.-Z., Adie S. G., Carney P. S., Boppart S. A., “Computational high-resolution optical imaging of the living human retina,” Nat. Photonics 9(7), 440–443 (2015). 10.1038/nphoton.2015.102 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Wieser W., Biedermann B. R., Klein T., Eigenwillig C. M., Huber R., “Multi-megahertz OCT: High quality 3D imaging at 20 million A-scans and 4.5 GVoxels per second,” Opt. Express 18(14), 14685–14704 (2010). 10.1364/OE.18.014685 [DOI] [PubMed] [Google Scholar]
- 40.Klein T., Wieser W., Reznicek L., Neubauer A., Kampik A., Huber R., “Multi-MHz retinal OCT,” Biomed. Opt. Express 4(10), 1890–1908 (2013). 10.1364/BOE.4.001890 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Tozburun S., Blatter C., Siddiqui M., Meijer E. F. J., Vakoc B. J., “Phase-stable Doppler OCT at 19 MHz using a stretched-pulse mode-locked laser,” Biomed. Opt. Express 9(3), 952–961 (2018). 10.1364/BOE.9.000952 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Kocaoglu O. P., Lee S., Jonnal R. S., Wang Q., Herde A. E., Derby J. C., Gao W., Miller D. T., “Imaging cone photoreceptors in three dimensions and in time using ultrahigh resolution optical coherence tomography with adaptive optics,” Biomed. Opt. Express 2(4), 748–763 (2011). 10.1364/BOE.2.000748 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Jang J., Lim J., Yu H., Choi H., Ha J., Park J.-H., Oh W.-Y., Jang W., Lee S., Park Y., “Complex wavefront shaping for optimal depth-selective focusing in optical coherence tomography,” Opt. Express 21(3), 2890–2902 (2013). 10.1364/OE.21.002890 [DOI] [PubMed] [Google Scholar]
- 44.Yu H., Jang J., Lim J., Park J.-H., Jang W., Kim J.-Y., Park Y., “Depth-enhanced 2-D optical coherence tomography using complex wavefront shaping,” Opt. Express 22(7), 7514–7523 (2014). 10.1364/OE.22.007514 [DOI] [PubMed] [Google Scholar]
- 45.Jian Y., Xu J., Gradowski M. A., Bonora S., Zawadzki R. J., Sarunic M. V., “Wavefront sensorless adaptive optics optical coherence tomography for in vivo retinal imaging in mice,” Biomed. Opt. Express 5(2), 547–559 (2014). 10.1364/BOE.5.000547 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Yu H., Park J., Lee K., Yoon J., Kim K., Lee S., Park Y., “Recent advances in wavefront shaping techniques for biomedical applications,” Curr. Appl. Phys. 15(5), 632–641 (2015). 10.1016/j.cap.2015.02.015 [DOI] [Google Scholar]