Components of Water Use Efficiency Have Unique Genetic Signatures in the Model C₄ Grass Setaria^,

Both water-dependent and water-independent processes controlled by unique genetic components regulate plant growth in the model C₄ grass Setaria.

Abstract

Plant growth and water use are interrelated processes influenced by genetically controlled morphological and biochemical characteristics. Improving plant water use efficiency (WUE) to sustain growth in different environments is an important breeding objective that can improve crop yields and enhance agricultural sustainability. However, genetic improvement of WUE using traditional methods has proven difficult due to the low throughput and environmental heterogeneity of field settings. To overcome these limitations, this study utilizes a high-throughput phenotyping platform to quantify plant size and water use of an interspecific Setaria italica × Setaria viridis recombinant inbred line population at daily intervals in both well-watered and water-limited conditions. Our findings indicate that measurements of plant size and water use are correlated strongly in this system; therefore, a linear modeling approach was used to partition this relationship into predicted values of plant size given water use and deviations from this relationship at the genotype level. The resulting traits describing plant size, water use, and WUE all were heritable and responsive to soil water availability, allowing for a genetic dissection of the components of plant WUE under different watering treatments. Linkage mapping identified major loci underlying two different pleiotropic components of WUE. This study indicates that alleles controlling WUE derived from both wild and domesticated accessions can be utilized to predictably modulate trait values given a specified precipitation regime in the model C₄ genus Setaria.

Improving crop productivity while simultaneously reducing agricultural water input is essential to ensure the security of our global food supply and protect our diminishing freshwater resources. The irrigation requirements needed to mitigate the productivity loss associated with drought stress makes agriculture the largest industrial consumer of fresh water (Boyer, 1982; Hamdy et al., 2003). Addressing these challenges will require an integrated approach that combines irrigation practices that minimize water loss and the deployment of crop plants with superior water use efficiency (WUE; Stanhill, 1986; Evans and Sadler, 2008; Morison et al., 2008; Boutraa, 2010; Gregory and George, 2011; Davies and Bennett, 2015).

Plant WUE can be defined broadly as the ratio of biomass produced to total water lost (Monteith, 1993; Condon et al., 2004; Evans and Sadler, 2008; Morison et al., 2008; Bacon, 2009; Blum, 2009; Tardieu, 2013). This complex trait is determined by many factors, including photosynthetic carbon assimilated per unit of water transpired (Farquhar et al., 1989; Condon et al., 2002; Morison et al., 2008; Seibt et al., 2008), leaf architecture (Sack and Holbrook, 2006; Brodribb et al., 2007), stomata characteristics (Franks and Farquhar, 2007; Lawson and Blatt, 2014), epidermal wax content (Premachandra et al., 1994), canopy and root architecture (Martre et al., 2001; White and Snow, 2012), stomatal dynamics (Blatt, 2000; Hetherington and Woodward, 2003; Lawson et al., 2010, 2012; Flood et al., 2011), hydraulic transport (Holloway-Phillips and Brodribb, 2011; Edwards et al., 2012), portion of carbon lost from respiration (Escalona et al., 2012; Tomás et al., 2014), and partitioning of photoassimilates (Chaves, 1991; Carmo-Silva et al., 2009). Given that plant species (Stewart et al., 1995; Winter et al., 2005; Zegada-Lizarazu and Iijima, 2005; Zhou et al., 2012) and ecotypes within species (Xu et al., 2009; Kenney et al., 2014; Lopez et al., 2015; Nakhforoosh et al., 2016; Ryan et al., 2016; Pater et al., 2017) exhibit variation in WUE, it is likely that the characteristics that determine this trait are under genetic control and have evolved in response to different environmental conditions such as water availability (Huxman et al., 2004; Brodribb et al., 2009; Assouline and Or, 2013). Therefore, WUE is likely influenced by both genetically encoded developmental programs and changes in growth environments throughout the plant life cycle (Fleury et al., 2010).

The technical challenges associated with measuring plant size and transpiration in large, structured genetic populations have historically limited experimental efforts to identify genetic components associated with WUE. This task is particularly difficult in field settings, due to year-to-year climate fluctuation and microenvironmental variation within agricultural fields. The advent of controlled-environment, high-throughput phenotyping instruments (Granier et al., 2006; Reuzeau et al., 2006; Sadok et al., 2007; Walter et al., 2007; Pereyra-Irujo et al., 2012; Tisné et al., 2013; Chen et al., 2014; Fahlgren et al., 2015) alleviates many of these challenges through stringent control of climatic variables and automated, high-resolution measurement of plant size and evapotranspiration across large populations.

Evidence from studies conducted on both crop and model plants indicates that the traits associated with WUE are heritable and largely polygenic. However, identifying the causal loci associated with differential performance in crop plants has proven difficult due to plant size and genome complexity (Xu et al., 2009; Chen et al., 2012; Adiredjo et al., 2014; Honsdorf et al., 2014; Aparna et al., 2015; Parent et al., 2015; Coupel-Ledru et al., 2016; Schoppach et al., 2016). The utilization of model plants (the C₃ annuals Arabidopsis [Arabidopsis thaliana] and purple false brome [Brachypodium distachyon]) that possess tractable genetic and experimental properties has enabled scientists to identify quantitative trait loci (QTL) that contribute to WUE (Lowry et al., 2013; Easlon et al., 2014; Vasseur et al., 2014; Des Marais et al., 2016; Mojica et al., 2016), a few of which have been mapped to causal genes (Ruggiero et al., 2017). Species in the genus Setaria (green foxtail [Setaria viridis] and foxtail millet [Setaria italica]) also possess many of these desirable qualities and can be used as experimental models to identify genetic components associated with WUE in a C₄ plant that is closely related evolutionarily to C₄ crops like maize (Zea mays), sorghum (Sorghum bicolor), and bioenergy grasses (Brutnell et al., 2010; Li and Brutnell, 2011; Bennetzen et al., 2012; Huang et al., 2016; Zhu et al., 2017). However, to study the diversity of resource utilization tactics present in natural and mapping populations of Setaria (Saha et al., 2016) or other C₄ plant species, methods to quantify plant performance and WUE in different environments must be developed.

The objectives of this study were to use a controlled-environment, high-throughput phenotyping system to characterize the genetic architecture of plant size, water use, and WUE in an interspecific Setaria recombinant inbred line (RIL) population under two different watering regimes. Our findings indicate that plant size, water use, and WUE are polygenic traits influenced by soil water content and over 10 pleiotropic loci, whose effect size changes differentially throughout development. In addition, we identify and discuss several aspects of experimental design that should be considered when performing high-throughput phenotyping experiments to study plant WUE.

RESULTS

Measuring Plant Size and Water Use throughout the Plant Life Cycle

Plant size and water use over time were measured in individuals of a Setaria RIL population (Devos et al., 1998) grown at two soil water content levels (Fahlgren et al., 2015). Plant size was estimated through the calculation of relative side-view pixel area, which exhibits a strong correlation with fresh and dry weight (Fig. 1; Supplemental Fig. S1). The ratio of biomass accumulation in the water-limited environment relative to the well-watered one suggests that the growth of the parental line B100 is less responsive to water limitation or less able to use all the water in the well-watered treatment (Supplemental Fig. S2). Transgressive segregation for this trait was observed, with RIL_099 and RIL_010 occupying the tails of this distribution (Supplemental Fig. S2).

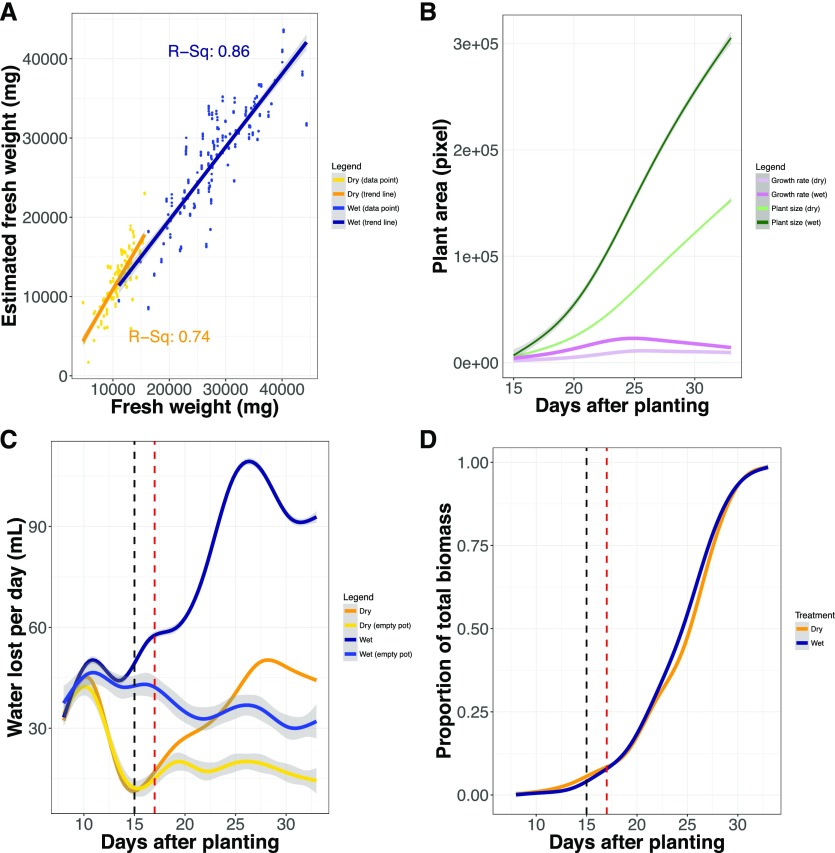
Figure 1.

Plant size and water use can be inferred accurately throughout a majority of the plant life cycle. A, Correlation between plant fresh weight biomass estimated from side-view pixel area and actual plant fresh weight biomass measured gravimetrically. B, Estimates of plant size and growth rate based on pixel area are plotted across the duration of the experiment. Green lines reflect absolute average size, whereas purple lines report on growth rate. Dark and lighter shaded lines report the well-watered and water-limited treatment blocks, respectively. C, Daily water loss is plotted throughout the duration of the experiment. Dark blue and orange lines correspond to average daily water lost from pots, whereas the lines with lighter shades of similar colors report the average water loss of empty pots. The dashed black line denotes the day at which dry down within the water-limited treatment block is complete, whereas the dashed red line demarks when water use can be measured accurately. D, Proportion of total biomass accumulated throughout the duration of the experiment. The dashed black line denotes the day at which dry down within the water-limited treatment block is complete, whereas the dashed red line demarks when water use can be measured accurately.

Daily plant water use was inferred through gravimetric measurement of pot weight performed two to three times daily. By 15 d after planting (DAP), the dry-down phase for the water-limited treatment group was complete, and pots containing plants lost substantially more water than their empty pot counterparts in the well-watered treatment group (Fig. 1; Ge et al., 2016). Beginning the analysis at day 17 enabled us to minimize the artifacts of evaporation, which were stronger early in the experiment, while still capturing growth attributes over a large proportion (∼92%) of the plant growth (Fig. 1). Another potential confounding issue was the use of a fixed set point for the pot weight, which neglected the increasing weight of the plant when calculating the amount of water needed to return the pot weight to the set point during watering jobs. This factor decreased the volume of water present within each pot after watering by approximately 12.5% (well watered) and 17.5% (water limited), on average, by the end of the experiment (Supplemental Fig. S3).

Plant Size and Water Use Are Correlated

Over the course of this experiment, cumulative plant size and water use were highly correlated. The correlation was highest between 21 and 27 DAP in the well-watered treatment group (greater than 0.94), followed by the water-limited treatment group between 20 and 27 DAP (greater than 0.87; Fig. 2). In both treatments, correlations between these traits were lowest at the beginning and end of the experiment but never dropped below 0.67. The correlation of the daily rate-of-change values associated with these traits appeared qualitatively different. The correlation between plant growth rate and the rate of water use was initially substantial (greater than 0.79) but decreased rapidly at about 26 DAP, as the rate of growth slowed (ultimately approaching zero) by the end of the experiment (Fig. 2) while transpiration remained high.

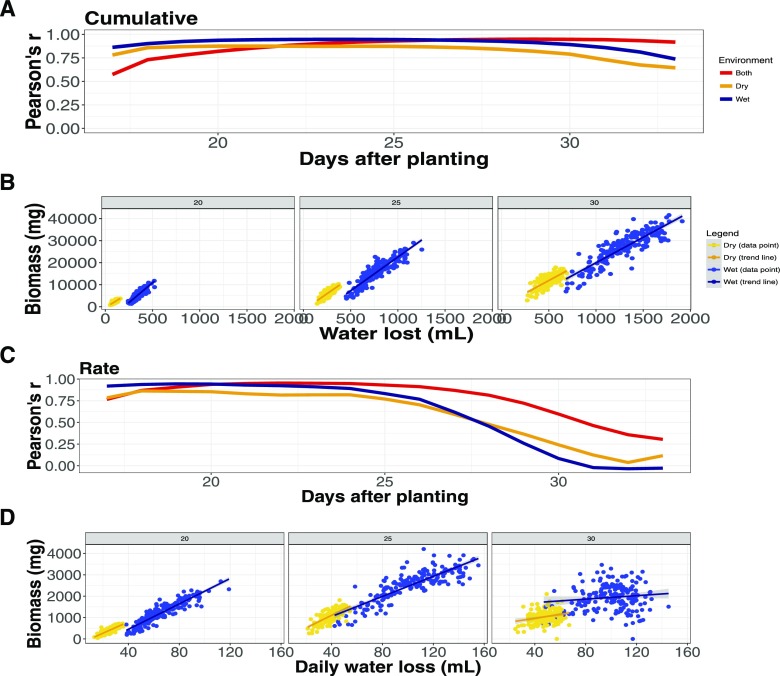
Figure 2.

Plant size and water use are tightly correlated. Pearson correlation coefficient is shown between plant size and water use both within and between treatment groups throughout the experiment. A, Correlation between cumulative plant size and water use. B, Relationship between plant size and water use at 20, 25, and 30 DAP. C, Correlation between the rate of plant growth and daily water use. D, Relationship between plant growth rate and daily water use at 20, 25, and 30 DAP.

We implemented two numerical approaches to characterize the genetic architecture of the relationship between these traits. The first method, hereafter referred to as the water use efficiency ratio (WUE_ratio), calculated the ratio of biomass relative to the volume of water lost from the pot.

Values of cumulative WUE_ratio calculated during this experiment were comparable to those from other experiments where plant size and water use were measured manually at lower throughput (25–29 g fresh weight L⁻¹ water and 7–9 g dry weight L⁻¹ water). On average, the cumulative and daily WUE_ratio were greater in the water-limited treatment than in well-watered conditions. In principle, the WUE_ratio should attenuate the relationship between biomass and water use, but a substantial correlation was still observed between these two variables, particularly within the rate statistic over the last week of the experiment (Supplemental Figs. S4 and S5).

The high correlation between plant size and water use suggests that these were not independent traits in this experimental setup. Therefore, as a second approach, ordinary least squares linear regression was used to model the relationship between plant biomass and water use. For each day of the experiment, a WUE_model was used to predict plant size (dependent/response variable) based upon water loss (independent/explanatory variable) within each treatment group (Fig. 3). The residual of this model fit was distributed evenly around zero across the entire distribution of the predicted values, suggesting that this approach is only minimally biased (Supplemental Fig. S6).

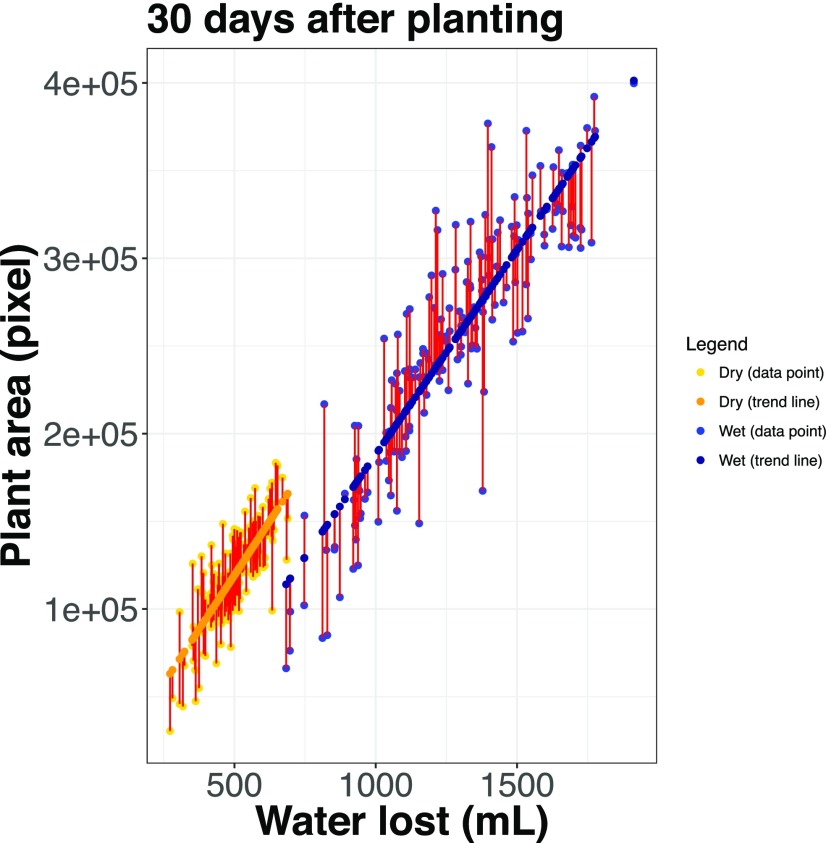
Figure 3.

Modeling the relationship between plant size and water use results in two traits: the predicted value of water use given size (WUE_fit), colored in dark blue, and deviations from this relationship (WUE_residual), plotted in red. This plot illustrates this relationship at 30 DAP.

This approach resulted in two traits. The first is WUE_fit, which described the sum of squares relationship between biomass and water use. The second is WUE_residual, a genotype-specific deviation from this relationship combined with measurement error. As expected, the fit values derived from the WUE_model were highly correlated with plant size (Supplemental Fig. S7). A slight correlation between cumulative plant biomass and the residual of the WUE_model was observed, particularly later in the experiment, demonstrating that biomass had components that were not accounted for by the linear model fit (Supplemental Fig. S8). Using a major axis regression framework (Legendre, 2014) had little effect on downstream analysis, whereas reversing the dependence structure resulted in no significant qualitative genetic signature.

Each trait (biomass, water loss, WUE_ratio, WUE_fit, and WUE_residual) exhibited high average heritability at all experimental time points within and across water treatments (0.28–0.77; Supplemental Fig. S9). Heritability was highest in the middle of the experiment. Proportionally, the treatment effect of water limitation explained the largest percentage of the variance within biomass, water loss, and the WUE_fit, although genotype and genotype × treatment interaction also explain a substantial portion of the variance (Supplemental Fig. S10). The heritability of the rate traits was, on average, 5% lower than the heritability of the cumulative traits. In all cases, the average heritability of each trait was higher within the well-watered environment relative to the water-limited environment.

The Genetic Architecture of Plant Size and Water Use Traits

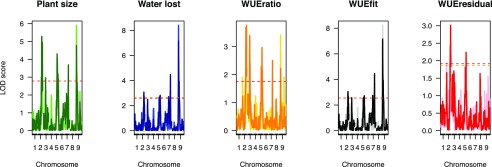
For each day of the experiment, a best-fit multiple QTL model was selected for each trait (plant size, water use, WUE_ratio, WUE_fit, and WUE_residual) and the daily rate of change of the trait within each treatment group based upon penalized log of the odds (LOD) score using a standard stepwise forward/backward selection procedure (Broman et al., 2003). This approach identified 86 (Fig. 4; Supplemental Table S1) and 106 (Supplemental Fig. S11; Supplemental Table S1) unique single-nucleotide polymorphisms (SNPs) associated with at least one of the five traits. Many of these SNPs group into clusters that are likely representative of a single QTL location. These local clusters of SNPs (10-cm radius) were then condensed into the most significant marker within each cluster to simplify comparisons of genetic architecture between traits (Supplemental Figs. S12 and S13). Collapsing these SNP positions yielded 23 unique QTL locations associated with cumulative trait values (Fig. 5) and 27 unique rate QTL locations (Supplemental Table S2). QTL will henceforth be referred to by their location within a chromosome (for instance, a QTL detected on chromosome 7 at position 99.1 will be reported as 7@99).

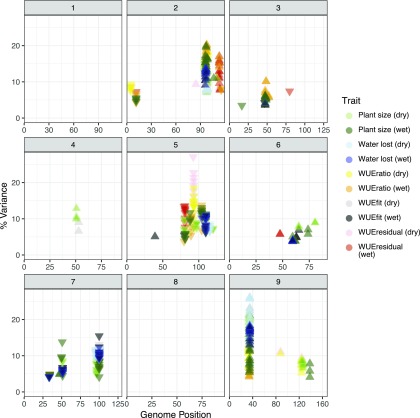
Figure 4.

Eighty-six unique QTL locations were detected across all traits in this experiment. Each box corresponds to an individual chromosome, where the values along the x axis are chromosome position and values along the y axis denote the proportion of genetic variance explained by the QTL. Each triangle represents a single QTL detected, where the color indicates the trait each QTL is associated with. The darkness of color shading is indicative of the treatment group, where darker represents the well-watered group and lighter corresponds to the water-limited group. The direction of the triangle indicates the directional effect of the B100 parental allele.

Figure 5.

The genetic components that contribute to subsets of traits largely overlap. The QTL locations identified are plotted on the x axis, and the traits are plotted on the y axis. Colored matrix entries denote at least one significant association within this experiment. A, Genetic architecture of cumulative traits. B, Genetic loci associated with trait rate of change. C, Genetic components associated with genotype × environment traits.

Of the 23 unique QTL identified, plant biomass contributes the highest number of QTL (18), followed by WUE_ratio (12), WUE_fit (11), WUE_residual (10), and water loss (eight; Fig. 5; Supplemental Fig. S14). Even though only one QTL location (2@96) was common across all traits and environments, the genetic architecture that contributes to each of these characteristics was related. The strong correlation between plant size, water loss, and the predicted value of plant size given water loss (WUE_fit) is reflected in the genetic architecture associated with these traits. Plant size, water loss, and WUE_fit all shared eight QTL (2@96, 3@48, 5@109, 6@65, 7@34, 7@51, 7@99, and 9@34) within either the well-watered or water-limited treatment group (Fig. 5; Supplemental Fig. S14). Plant size, WUE_ratio, and deviations from the relationship between plant size and water use (WUE_residual) shared five QTL unique to this subset (2@11, 2@113, 5@79, 5@92, and 9@127), which diverge from the fundamental relationship between plant size and water loss (Fig. 5; Supplemental Fig. S14). Several QTL were associated uniquely with plant size (3@21, 5@119, 6@80, and 9@138), WUE_residual (2@82, 3@77, and 6@47), and WUE_fit (5@39), whereas no QTL was associated uniquely with water loss or WUE_ratio (Fig. 5; Supplemental Fig. S14).

The genetic architecture of all five traits appears to be influenced by water availability. All traits other than water loss exhibited QTL unique to each treatment (Fig. 5; Supplemental Fig.S15). Biomass, water loss, and WUE_fit all shared four QTL in common across environments (2@96, 5@109, 7@99, and 9@34), whereas WUE_ratio and WUE_residual shared a single QTL (2@11) between treatments, which was not associated with other traits. Two QTL (3@48 and 7@34) were found specifically within the well-watered treatment group for all traits other than WUE_residual, whereas QTL specific to the water-limited environment were associated with biomass and WUE_fit (4@52) or WUE_ratio and WUE_residual (9@87 and 9@127). Inheriting the B100 allele of QTL identified specifically in the water-limited environment (4@52, 9@87, and 9@127) increased the value of all traits, particularly later in development.

The identities of QTL associated with the daily rate values suggest that the genetic architectures were largely cognate with the QTL associated with the traits themselves, in both identity and response to treatment. The relative value of mapping the rate-of-change QTL relative to traits measured as cumulative values is an open area of inquiry, so we took both approaches. In total, 28 QTL comprised the union of all unique QTL associated with both the trait value and the daily rate of change calculated from the trait value. Of these QTL, 22 were common between both the trait value and the rate statistic associated with the trait, whereas five were only found associated with the rate (1@54, 2@58, 3@4, 3@61, and 8@35), and only one QTL was associated uniquely with the cumulative trait values alone (6@47; Supplemental Fig. S16).

Genotype × Environment Interactions

To assess the genetic architecture of trait plasticity (Lynch and Walsh, 1998; Des Marais et al., 2013), linkage mapping was performed on the numerical difference, relative difference, and trait ratio between the phenotypic values observed within each treatment group. In total, 148 unique SNP locations were associated significantly with at least one of the difference trait formulations across all standard and derived plant size and water use traits (Supplemental Table S3; for discussion of the significance criteria, see “Materials and Methods”). The substantial overlap between these categories of genotype × interaction traits indicates that each formulation detects similar genetic signals (Supplemental Fig. S17), although the large number of SNPs found associated uniquely with the trait ratio may indicate that some of these associations are spurious. As such, these QTL (trait ratio genotype × environment QTL) were removed from further analysis. The numerical difference and relative difference traits exhibited an association with 43 and 40 unique SNP positions, which were representative of 20 and 18 QTL, respectively (Supplemental Table S4; Supplemental Figs. S18–S20).

A majority of the QTL (10 of 15) associated with the trait difference between treatments also were found associated with the cumulative trait in both treatment groups (Fig. 5). The exceptions to this were QTL located on 3@21, 3@48, 5@39, 7@34, and 9@127, associated significantly with the difference between treatments but only identified in either well-watered (3@21, 3@48, 5@39, and 7@34) or water-limited (9@127) conditions. Interestingly, the QTL located on 3@48, 7@34, and 9@127 were associated with more than one trait in a single treatment, which may indicate that these QTL impart pleiotropic phenotypic effects that were dependent upon soil water content (Fig. 5).

The Temporal Genetic Architecture of Plant Growth and Water Usage

To account for the time dependence of the five plant traits, we used a function-valued approach based upon the average log of the odds score across the experiment (SLOD) for each trait (Kwak et al., 2016). This analysis parallels the individual time point analysis, although the reduction of complexity (fewer, higher confidence QTL) provides an opportunity for simplification and a better understanding of the major loci that influence plant WUE.

SLOD-based function-valued QTL models indicate that several major QTL (2@96, 5@109, 7@99, and 9@36) influenced both plant size- and water use-related traits, although the magnitude of statistical significance attributed to each locus varied by trait and throughout plant development (Fig. 6; Supplemental Fig. S21). Using the SLOD approach, we were able to partition combinations of QTL unique to related traits (Fig. 6). For several QTL (those around 2@96 and 5@109), the location at which the maximal LOD score was observed changed noticeably in a trait- and environment-dependent manner, due to either multiple closely linked loci or noise in our measurements. Because the confidence intervals of the QTL generally overlap, our reporting in this section will hereafter refer to these loci by their approximate chromosomal locations.

Figure 6.

Significant associations identified using single-marker-scan functional QTL mapping. Chromosomal position is plotted on the x axis, whereas the LOD score of trait association across the genome is plotted on the y axis. Treatment block is indicated by color intensity (darker is well watered and lighter is water limited). Significance thresholds (based on 1,000 permutations) are plotted as dashed yellow (water limited) and red (well watered) lines.

Both plant biomass and cumulative water use exhibited almost a complete overlap of QTL within the well-watered environment, whereas the predicted plant size given water use (WUE_fit) and the deviation of plant size from this fundamental relationship (WUE_residual) each exhibits a unique genetic signature (Fig. 6). As observed when trait values at individual time points were treated as independent traits, a single QTL on 2@96 is the only genetic component shared across all five traits. The linear modeling approach successfully partitions out QTL associated with WUE_fit (2@96, 7@99, and 9@36) from the genetic components that contribute to WUE_residual (2@96 and 5@109). The QTL associated with WUE_ratio (2@96, 3@52, and 5@109) also likely reflects deviations from the relationship between biomass given water loss associated with WUE_residual. Overall, the identities of QTL associated with each trait were similar between the two treatments (Fig. 6; Supplemental Fig. S21), as were the QTL associated with the values of rate statistics derived from these measurements (Supplemental Figs. S22 and S23).

A Temporal Model of the Genetic Architecture That Influences Plant WUE

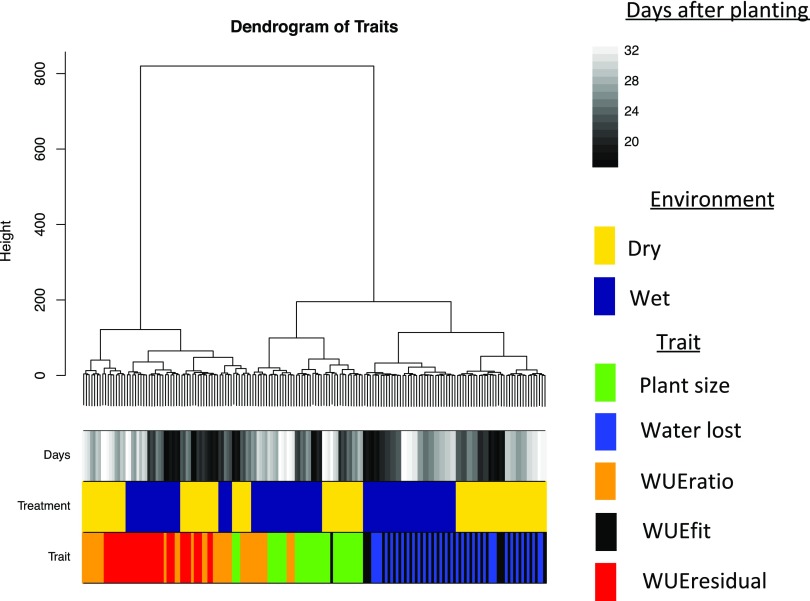
Our QTL results suggest at least two components of WUE with distinct genetic architectures. To compare the genetic architecture across all traits, treatments, and time points in a common framework, we analyzed how each trait was influenced by a common set of loci. Fourteen QTL were selected based upon their association with multiple traits, robust linkage with a single trait, or having a differential contribution to traits across treatments (Supplemental Table S5). The proportional contribution of each locus to the additive genetic variance was calculated using drop-one-term, type III ANOVA performed for all experimental traits, time points, and treatment. Agglomerative hierarchical clustering of the signed proportion of additive genetic variance explained by each locus was performed to identify modules of traits and loci that define plant phenotypes. Examination of scree plots of the within-group sum of squares suggested that the variance within traits could be attributed to approximately six groupings, although a majority of this variance could be captured within the largest two to three partitions (Supplemental Fig. S24). These partitions represented the major relationships between trait classes. WUE_ratio and WUE_residual generally were grouped separately from a larger cluster of traits that included cumulative plant size, water use, and WUE_fit (Fig. 7). The genetic architecture of plant water use and WUE_fit were more related to each other than they were to plant size, which formed the third group. The influence of water availability on these traits was apparent from the grouping of clusters, whereas the effects of time were distributed within the treatment groups. The genetic architecture of WUE_ratio in the well-watered treatment at early time points was more similar to the architecture of plant area than itself later in development, whereas plant area in the water-limited treatment group exhibited a genetic architecture similar to WUE_ratio late at the end of the experiment.

Figure 7.

Agglomerative hierarchical clustering defines the relationship between plant size, water use, and derived WUE traits. The additive effect size of 14 common QTL was calculated across all traits, treatments, and developmental time points through hierarchical clustering using Ward’s method. Color bars on the bottom indicate trait, treatment group, and DAP.

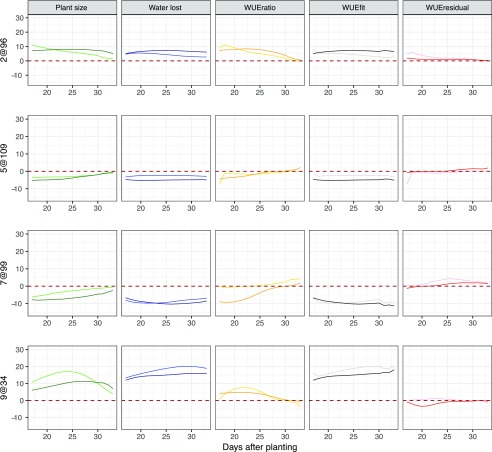
Examination of the signed, proportional allelic effects within the greater fixed QTL model indicated that QTL on 2@96, 5@109, 7@99, and 9@34 contribute medium to large effects to a majority of the traits examined in both treatments (Fig. 8). The B100 alleles associated with QTL on 2@96 and 9@34 both contributed to increased plant size, water loss, WUE_fit, and WUE_ratio. The QTL on 2@96 exhibited its greatest influence in the well-watered treatment, whereas the contribution of 9@34 was greater on average in the water-limited treatment group. Both QTL exhibited similar temporal patterns, showing an earlier effect on plant size and WUE_ratio but a consistent effect across water loss. The contribution of the B100 allele on 7@99 and 5@109 decreased plant size, water use, and WUE_fit traits, the effect of which was greater in well-watered conditions. The magnitude of effects contributed by the QTL on 7@99 on plant size decreased over time, whereas the effects on water loss and WUE_fit peaked at 20 d. The 5@109 locus showed little temporal variation in plant water use and WUE_fit. A majority of the other QTL contributed minor effects that became more prominent in one of the two treatment groups or at a particular developmental time point. Inheriting the B100 allele at QTL on 2@113, 3@48, 4@52, 6@65, and 9@127 increased plant size, water use, and WUE, while the B100 allele at the remaining loci (2@11, 5@79, 5@95, 7@34, and 7@53) decreased the values of these traits (Supplemental Fig. S25).

Figure 8.

Additive relative effect size of the four major pleiotropic QTL plotted throughout the course of the experiment. A model containing 14 QTL was fit across traits, treatment blocks, and days. The developmental time point (DAP) is indicated by the x axis, whereas the proportional additive genetic effect size of the B100 allele is plotted along the y axis. Columns are representative of traits, while rows correspond to individual QTL. Shading within the colors denotes treatment block (darker = well watered and lighter = water limited).

A majority of the QTL exhibit unidirectional effects across both the well-watered and water-limited environments, although the direction of the effect was largely dependent on the trait (Supplemental Fig. S26). The exceptions to this trend represent short experimental periods at which the relative effect size is near zero within one or both treatment groups (Fig. 8; Supplemental Fig. S25).

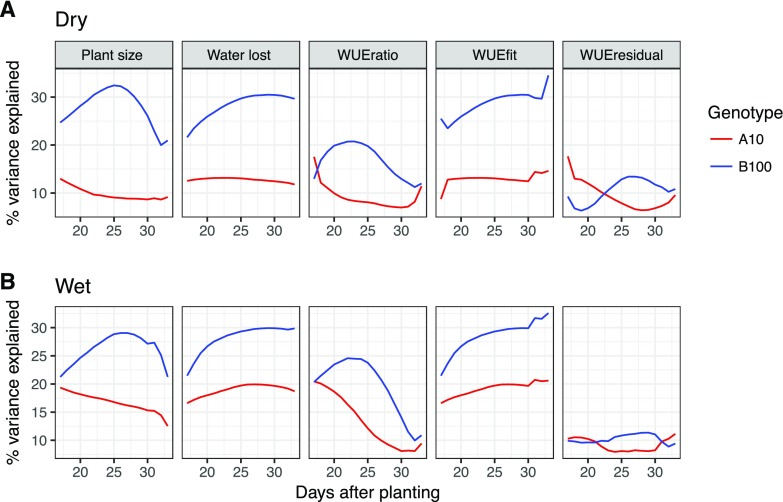
The proportional contribution of parental alleles toward increased trait values varied between traits, within treatment groups, and throughout plant development. For example, B100 alleles contributed to increased trait values for all traits other than WUE_ratio in the water-limited environment and WUE_residual across both treatment groups (Fig. 9). Alternatively, the contributions of the A10 alleles proportionally increased the WUE_residual value early and then again late in plant development relative to those inherited from the B100 parent. The influence of A10 alleles on WUE_ratio also was greater than that of their B100 counterpart under water-limited conditions early in plant development.

Figure 9.

The proportional contributions of parental alleles to increased trait values depend upon trait, environmental water content, and plant developmental stage. Alleles derived from the B100 parent contribute a greater proportion of additive genetic variance to plant size, water use, an WUE model fit in both well-watered and water-limited conditions than their A10 allelic counterparts. Both the WUE ratio and WUE model residual traits exhibit dynamic behavior, where A10 alleles contribute either greater or close to equal proportions of additive genetic variance early and late in plant development. A, Contribution of parental alleles in the water-limited treatment block. B, Contribution of parental alleles in the well-watered treatment block.

DISCUSSION

The objectives of this study were to utilize technological advances in high-throughput phenotyping (Granier et al., 2006; Reuzeau et al., 2006; Sadok et al., 2007; Walter et al., 2007; Pereyra-Irujo et al., 2012; Tisné et al., 2013; Chen et al., 2014; Fahlgren et al., 2015) to characterize the genetic architecture of WUE and how this architecture responds to water limitation in an experimental C₄ grass model system. Although considerable efforts have been made to characterize these processes in Arabidopsis, C₃ grass crops, and other species (Ruggiero et al., 2017), few studies have used high-throughput phenotyping tools to examine an annual C₄ grass RIL population. These efforts enabled us to identify genetic loci that contribute to differential biomass accumulation given water use in well-watered and water-limited environments. Our findings suggest that the major genetic components associated with plant size, water use, and WUE exhibit pleiotropic behavior and that the magnitude of their allelic effects is dependent upon the environment and developmental stage. We used two complementary approaches to define traits, and our analysis confirmed that the genetic architecture was similar with both approaches. We demonstrate that the loci controlling biomass accumulation can be divided roughly into two groups: those that control the amount of water used to create biomass (WUE_fit) and those that control how efficiently that water is used (WUE_residual). The results from this study indicate that alleles from both domesticated foxtail millet and a species representative of its wild progenitor contribute to maximal vegetative biomass yield or WUE grown in environments with different watering regimes. In addition, we highlight aspects of our experimental design and analysis that could be improved in future studies.

The Genetic Architecture of Plant Size, Water Use, WUE, and the Relationship between These Traits

Within the A10 × B100 Setaria RIL population, plant size, water use, and the relationship between these two variables are unique polygenic traits whose values all are likely influenced by greater than 10 loci. Four QTL located on 2@96, 5@106, 7@99, and 9@36 exhibit strong pleiotropic influence across this suite of traits, and the relative magnitude of each is dependent upon growth environment and developmental time point. Despite the strong correlation between plant size and water use, we successfully identified genetic architectures distinct to each trait. This was achieved by modeling plant size as a function of water use and examining the resulting values of the model fit (plant size given water use) and deviations from this relationship (residual of plant size given water use). This linear modeling approach has been used less frequently in the literature (Lopez et al., 2015; Nakhforoosh et al., 2016) than WUE_ratio (Adiredjo et al., 2014; Honsdorf et al., 2014; Aparna et al., 2015; Fahlgren et al., 2015; Lopez et al., 2015). While the genetic architectures associated with WUE_ratio and WUE_residual in this population are closely related (Fig. 7), WUE_residual exhibits substantial heritability and is less correlated with plant size than WUE_ratio (Supplemental Figs. S7 and S11), making it a more desirable metric.

By examining the model-based components of WUE with function-valued single-marker-scan QTL analysis, which accounts for multiple hypothesis testing across time points (Kwak et al., 2016), we were able to partition the four major pleiotropic QTL into the genetic components on 2@96, 7@99, and 9@36 and those on 2@96 and 5@109. The former control plant size given water use (WUE_fit), while the latter contribute to deviations from this relationship (WUE_residual). Inheriting alleles from the B100 parent at 2@96 and 9@36 has the effect of increasing biomass, whereas inheriting the A10 allele at 5@109 and 7@99 has the effect of decreasing biomass production. This result suggests that QTL associated with WUE_fit (7@99 and 9@36) potentially control the development of transpiring plant biomass, whereas the QTL associated with WUE_residual and WUE_ratio (2@96 and 5@109) influence the production of nontranspiring tissues or biological processes not related directly to transpiration. This conclusion is in accordance with the results of other studies performed on this population, which demonstrate that these loci are largely pleiotropic (Mauro-Herrera and Doust, 2016), although the loci on 2@96 and 5@109 substantially influence plant height (Feldman et al., 2017) and stem biomass, whereas those on 7@99 and 9@36 are not associated with the accumulation of stem material (Banan et al., 2017).

Our study also identified many small-effect QTL that influence biomass, water use, and WUE traits. The B100 parental allele contributes substantial positive (3@48, 4@52, 6@65, and 9@127) and negative (7@34 and 7@53) effects on all traits, whereas QTL on 2@11, 2@113, 5@79, and 5@95 contribute either to plant size/WUE_ratio/WUE_residual ratio to a greater degree than on plant size/water loss/WUE_fit ratio. The B100 alleles of QTL located at positions 4@52 and 9@127 are associated with increased plant size and WUE in water-limited conditions and, thus, could be resources for drought improvement.

Roughly two-thirds of the QTL associated with trait plasticity as a response to water availability (difference or relative difference between treatment groups) also were associated with the cumulative traits within both treatments. This observation indicates that, in many cases, soil water content influences the temporal dynamics of the allelic effects by differential progression through developmental processes that share similar genetic components (Feldman et al., 2017). This study identifies several QTL (3@48, 7@34, and 9@127) associated with genotype × environment traits that also exhibit a significant influence on multiple plant traits within a single treatment group. This result suggests that these QTL have a pleiotropic influence on size- and water use-related traits in an environment-specific manner. In contrast, QTL identified only by mapping the difference or relative difference of the traits between each environment are largely specific to individual traits.

Our results support an evolutionary genetic model where the majority of QTL associated with the measured traits exhibit conditional neutrality across both soil water potentials examined. Although all traits other than plant size sometimes exhibit opposite directional effects across treatments, the evidence supporting a model of antagonistic pleiotropy is weak. When identified, QTL exhibiting opposite directional effects within individual treatment groups were limited to short experimental periods and are characterized by negligible relative effects during these time points. Alleles from both parental lines contribute to increased WUE irrespective of soil water potential, suggesting that neither parent is optimized for WUE. For example, alleles from the A10 parent contribute a greater proportion of additive genetic variance to increased WUE during early development in both well-watered and water-limited environments, whereas B100 alleles have a greater effect on a majority of the measured traits throughout the time course. The contribution of alleles from both parents to WUE is expected, given that an earlier study performed on the same platform showed that the parental lines have similar WUE under water-limited conditions (Fahlgren et al., 2015).

Considerations When Measuring Plant Size, Water Use, and WUE

As observed in other studies (Golzarian et al., 2011; Chen et al., 2012; Honsdorf et al., 2014; Fahlgren et al., 2015; Lopez et al., 2015; Parent et al., 2015; Ge et al., 2016), relative plant side-view pixel area provided a robust and accurate measurement of plant biomass. Although the incorporation of additional plant architectural features can improve estimates of this relationship (Parent et al., 2015), our results indicate that caution should be taken not to overfit models on data collected exclusively at the end of the experiment, as was performed in this study (Supplemental Fig. S27).

Automated or manual gravimetric measurement of pot weight has proven to be a reliable estimator of plant transpiration, but only if it accounts for the evaporative loss of moisture from the soil. Our results indicate that the inclusion of empty pots (or pots that contain plastic plants [Parent et al., 2015] or fabric wicks [Halperin et al., 2017]) is an appropriate empirical method to estimate the experimental time point at which transpiration contributes meaningfully to total pot evapotranspiration (Pereyra-Irujo et al., 2012; Lopez et al., 2015; Coupel-Ledru et al., 2016). Estimation of evapotranspiration after this critical time point has been used effectively by several other groups to identify and eliminate confounding data points collected early during similar experiments (Vasseur et al., 2014; Coupel-Ledru et al., 2016; Ge et al., 2016). Our findings indicate that the subtraction of empty pot weight, as performed previously (Pereyra-Irujo et al., 2012; Parent et al., 2015; Coupel-Ledru et al., 2016), may overcorrect for evaporation at early experimental time points even after the point at which plant transpiration contributes substantially to total pot water loss. Although not utilized during this experiment, plastic covering to shield pots from evaporative moisture loss, in combination with the approaches discussed above, may improve the quantification of plant transpiration (Granier et al., 2006; Vasseur et al., 2014; Aparna et al., 2015; Coupel-Ledru et al., 2016; Ellsworth et al., 2017; Halperin et al., 2017). In this study, the contribution of plant biomass to overall pot weight was not accounted for during the estimation of plant water use. Although the contribution of plant biomass to pot weight in most experiments performed using Arabidopsis is negligible (Tisné et al., 2010), plant biomass within this Setaria RIL population accounted for 12% to 18% of total average pot water content by the end of the experiment (Supplemental Fig. S3). Our inability to account for this growth has the undesirable effect of systematically decreasing the soil water content of larger genotypes, although, in practice, this small change in soil water potential likely has a minimal impact on the transpiration dynamics of the plants.

A strong correlation between plant size and water use was observed despite the fact that these traits can potentially be controlled by different physiological mechanisms. A similar trend also has been described in experiments designed to study WUE in Arabidopsis, apple (Malus domestica), and wheat (Triticum aestivum; Vasseur et al., 2014; Lopez et al., 2015; Parent et al., 2015; Nakhforoosh et al., 2016; Schoppach et al., 2016). The magnitude of this correlation is likely inflated in this study due to the large differences in size between parental lines and segregants within the A10 × B100 RIL population. Future studies aimed at investigating the genetic basis of WUE can attenuate this correlation by selecting parental lines of similar size and flowering times that differ in their rates of transpiration within environments of interest.

CONCLUSION

This study leverages recent advances in high-throughput phenotyping and quantitative genetics to identify the genetic loci associated with plant size, water use, and WUE in an interspecific RIL population of the model C₄ grass Setaria. Our findings indicate that these traits are highly heritable and largely polygenic, although the effects of four major pleiotropic QTL account for a substantial proportion of the variance observed within each trait. Parental alleles from both the domesticated and wild progenitor lines contribute to the maximization of these characteristics. Overall, the underlying genetic architecture of each of these processes is distinct and influenced substantially by soil water content as well as plant developmental stage. In addition, several aspects of our experimental design could be improved to obtain a better understanding of the genetic components that underlie plant size, water use, and WUE in future high-throughput phenotyping studies.

MATERIALS AND METHODS

Plant Material and Growth Conditions

The experimental procedure used here was first described in an earlier study (Feldman et al., 2017) that focused on plant height, and the details are repeated here for clarity. An interspecific Setaria F7 RIL population composed of 189 genotypes (1,138 individuals) was used for genetic mapping. The RIL population was generated through a cross between the wild-type green foxtail (Setaria viridis) accession A10 and the domesticated, partially male-sterile foxtail millet (Setaria italica) accession B100 (Devos et al., 1998; Wang et al., 1998; Bennetzen et al., 2012). Despite the fact that this cross was generated to study domestication (seedling color and tillering) and herbicide tolerance (Wang et al., 1998), evidence suggests that these parental lines may segregate for traits that influence WUE, with the B100 parent being less water use efficient than A10 under well-watered conditions (Fahlgren et al., 2015). As presented in “Results,” the biomass production of the B100 parental line was less sensitive to water limitation than that of the A10 parent (Supplemental Fig. S2). After a 6-week stratification in moist long-fiber sphagnum moss (Luster Leaf Products) at 4°C, Setaria seeds were planted in 10-cm-diameter white pots prefilled with ∼470 cm³ of Metro-Mix 360 soil (Hummert) and 0.5 g of Osmocote Classic 14-14-14 fertilizer (Everris). After planting, seeds were given 7 d to germinate in a Conviron growth chamber with a long-day photoperiod (16-h day/8-h night, light intensity of 230 μmol m⁻² s⁻¹) at 31°C day/21°C night before being loaded onto the Bellwether Phenotyping System using an α-lattice design replicating each genotype and treatment combination in triplicate (Supplemental Table S6). For each replicate, individual plants of the same genotype were grown side by side, with one individual receiving unlimited water supply while the other individual was subjected to water limitation. The growth chamber location of each of these paired replicates was assigned randomly and did not vary during the experiment. The effect of the positional location of these paired replicates was negligible. Including metadata that encoded the paired nature of the replicates did not significantly improve the estimation of plant side-view area relative to a model without this descriptor (Akaike’s Information Criterion [AIC], 254605.1 and degrees of freedom, 185 versus AIC, 254598.0 and degrees of freedom, 186) based upon AIC (Bozdogan, 1987). Plants were grown on the system for 25 d under a long-day photoperiod (16-h day/8-h night, light intensity of 500 μmol m⁻² s⁻¹) with the same temperature regime used during germination. Relative humidity was maintained between 40% and 80%. This large range of variation within the atmospheric water content was observed due to incomplete installation of dehumidifying equipment. Gravimetric estimation of pot weight was performed two to three times per day, and water was added to maintain soil volumetric water content at either 33% full capacity (FC; water limited) or 100% FC (well watered), as determined by Fahlgren et al. (2015). The prescribed soil water content across both treatment groups was achieved by 15 DAP.

The volume of water transpired by individual plants at each pot weighing was calculated as the difference between the measured pot weight and the weight of the prefilled pot at pot capacity (100% FC) or the difference between current pot weight and the previous weight measurement if no water was added. At the conclusion of each weighing, if the pot weight was below the set point, water was added to the pot to return soil water content to its target weight. This strategy effectively maintains soil moisture content at a consistent level within both treatment groups. To evenly establish seedlings before the water limitation treatment began, equal volumes of water (100% FC) were added to all pots for 2 d after transfer to the system. At 10 DAP, a dry-down phase was initiated (no watering) to establish the water-limited treatment group (40% FC) while continuing to maintain a soil water content of 100% FC within the well-watered treatment group.

Image Acquisition and Derived Measurements

RGB images of individual plants were acquired using top-view and side-view cameras at four different angular rotations (0°, 90° 180°, and 270°) every other day at the Bellwether Phenotyping Facility (Fahlgren et al., 2015). Optical zoom was adjusted throughout the experiment to ensure the accurate quantification of traits throughout plant development. The unprocessed images and the details of the configuration settings can be found at https://plantcv.danforthcenter.org/pages/data-sets/setaria_height.html.

Plant objects were extracted from images and analyzed using custom PlantCV Python scripts specific to each camera (side view or top view), zoom level, and lifter height (https://github.com/maxjfeldman/Feldman_Elsworth_Setaria_WUE_2017). Scaling factors relating pixel area and distance to ground truth measurements calculated by Fahlgren et al. (2015) were used to translate pixels to relative area (pixels cm⁻²) and relative distance (pixels cm⁻¹).

Biomass Estimation

At the conclusion of the experiment, 176 individual plants (91 from the 100% FC group and 85 from the 40% FC group) were selected randomly and harvested to measure aboveground biomass. Gravimetric measurement of fresh weight and saturated fresh weight were taken directly upon tissue harvest, after which plant tissue was placed into polypropylene microperforated bags (PJP MarketPlace #361001), dried for 3 d at 60°C, and weighed subsequently to determine dry weight biomass. Multivariate linear regression was used to evaluate, select, and calibrate a predictive model to estimate both fresh and dry weight plant biomass.

Regressing plant fresh weight biomass as a function of side-view area, perimeter length, height, object solidity, and width indicated that each of these terms is a significant predictor of fresh weight biomass after stepwise model selection using AIC (Bozdogan, 1987; multiple R² = 0.89). Unlike fresh weight biomass, side-view area, width, and height were the only significant terms used for the prediction of dry weight biomass after using the AIC stepwise model selection correction procedure (multiple R² = 0.76). Models containing all significant terms and their interaction achieved a greater model fit, but they introduced artifacts at earlier developmental time points due to model overfitting (Supplemental Fig. S27). Generally, models constructed to estimate fresh weight biomass in the well-watered treatment group exhibited greater explanatory power than those constructed to predict dry weight biomass or those in the water-limited treatment group (Fig. 1).

A minimal model containing only the most significant term (side-view area) in both fresh and dry weight models produced a goodness of fit similar to more complex models (fresh weight R² = 0.86, dry weight R² = 0.74). To avoid the propagation of error, values that incorporated plant fresh weight biomass were calculated based on adjusted side-view pixel area and translated to fresh weight biomass after analysis. Cumulative biomass values calculated on a genotype-within-treatment basis were interpolated using loess smoothing using the loess function (default parameters) within the R stats library (Chambers and Hastie, 1992). Plant size accumulation on a per day basis was calculated as the difference between the loess fit values on a given day and the estimates from the previous day. Plots illustrate the mean and variance of traits (Supplemental Fig. S28).

Water Loss Tabulation

The LemnaTec instrument at the Bellwether Phenotyping Facility provided measurements of water use based upon the gravimetric weight of each pot before watering, the volume of water applied, and the resulting weight after watering. On days when water was added, the daily volume of water added was the sum of water volumes added over a single calendar day. On days when water was not added (e.g. during the dry-down period), the water volume was calculated as the minimum gravimetric weight of the pot on the day in question subtracted from the minimum weight value from the previous day. The cumulative volume of water used on a specific day was the sum of all water used prior to that day. Examination of the ratio between fresh weight biomass accumulated relative to the amount of water used and mathematical prediction of the amount of water used per day over this period suggests that the amount of water used between days 15 and 17 can be used as an approximation of cumulative water transpired by the plant throughout this experiment up to this point (Supplemental Fig. S29). These data and the observation that, at day 17, the plants are still relatively small (less than 8% of their maximum size on average) support the rationale of starting the analysis on this day (Fig. 1). Volumes of water use on a genotype-within-treatment basis were estimated using loess smoothing, whereas the rate of water use was calculated as the difference between the loess fit values on a given day and the estimates from the previous day.

Calculation of WUE

WUE was calculated using two different approaches. The ratio between loess estimates of plant size (relative pixel area) and evapotranspiration (mL) calculated on a genotype-within-treatment basis is referred to as WUE_ratio:

WUE_model was constructed by predicting plant size (relative pixel area) given the independent variable evapotranspiration (mL). This formulation results in two traits: WUE_fit and WUE_residual:

To ensure that these results were not an artifact of the variable dependence structure, we also performed the analysis using major axis regression (Legendre, 2014) and using the reciprocal variable dependence designation (water use ? plant size). The rate-of-change traits were calculated by subtracting the loess estimate on the current day from the loess estimate of the previous day and dividing this quantity by the number of days that have passed (1 d).

Heritability and Trait Variance Partitioning

We used the same approach as described (Feldman et al., 2017), and the details are repeated here for clarity. During this experiment, plant area was measured every other day, so the number of replicates per treatment to calculate broad sense heritability on any given day was limited. To alleviate this technical shortcoming, trait values for each individual were interpolated across missing days using loess smoothing.

Variance components corresponding to broad sense heritability and total variance explained were estimated using a mixed linear model using the R package lme4 (Bates et al., 2015). Broad sense heritability was calculated using two methods. Within an individual experiment, broad sense heritability on a line-estimate basis was calculated using the following formula:

in which n_treatment is the harmonic mean of the number of treatment groups in which each line was observed and n_replicates is the harmonic mean of the number of replicates of each genotype in the experiment. Heritability within treatment groups was calculated by fitting a linear model with genotype as the only explanatory factor within each treatment group:

The proportion of variance attributed to genotype divided by the total variance within each treatment group is reported as broad sense heritability within a treatment (Eq. 4). The total variance explained was calculated by fitting a linear model including factors, genotype, treatment, plot, and genotype × treatment effects across all phenotypic values in all treatments. The proportion of variance that is incorporated into these factors divided by the total variance in the experiment is reported as the total variance explained for each factor.

QTL Analysis

We used the same approach as described (Feldman et al., 2017), and the details are repeated here for clarity. QTL mapping was performed at each time point within treatment groups and on the numerical difference, relative difference, and trait ratio calculated between treatments using functions encoded within the R/qtl and funqtl packages (Broman et al., 2003; Kwak et al., 2016). The functions were called by a set of custom Python and R scripts (https://github.com/maxjfeldman/foxy_qtl_pipeline). Two complementary analysis methods were utilized. First, a single QTL model genome scan using Haley-Knott regression was performed to identify QTL exhibiting LOD score peaks greater than a permutation-based significance threshold (α = 0.05, n = 1,000). Next, a stepwise forward/backward selection procedure was used to identify an additive, multiple QTL model based upon the maximization of penalized LOD score. Both procedures were performed at each time point, within treatment groups, and on the numerical difference, relative difference, and trait ratio calculated between phenotypic values measured in treatment groups at each time point. QTL associated with difference or ratio composite traits may identify loci associated with genotype × environment interaction (Des Marais et al., 2013).

The function-valued approach described by Kwak et al. (2016) was used to identify QTL associated with the average (SLOD) and maximum (MLOD) scores at each locus throughout the experiment. Each genotypic mean trait within treatments was estimated using loess smoothing, and the QTL significance threshold was determined based upon the permutation-based likelihood of observing the empirical SLOD or MLOD test statistic. Separate, independent linkage mapping analysis performed at each time point identified a larger number of QTL locations relative to similar function-valued analysis based on the SLOD and MLOD statistics calculated at each marker throughout the experimental time course.

After the refinement of QTL position estimates, the significance of fit for the full multiple QTL model was assessed using type III ANOVA. The contribution of individual loci was assessed using drop-one-term, type III ANOVA. The absolute and relative allelic effect sizes were determined by comparing the fit of the full model with a submodel with one of the terms removed. All putative protein-coding genes (S. viridis genome version 1.1) found within a 1.5-LOD confidence interval were reported for each QTL.

Accession Numbers

The accession number for A10.1 is PI669942. All scripts and data for this article can be found at https://doi.org/10.5281/zenodo.1340752.

Supplemental Data

The following supplemental materials are available.

• Supplemental Figure S1. A plot of the residual versus predicted values indicates a minor systemic bias.

• Supplemental Figure S2. The ratio of plant size in a water-limited environment given plant size in a well-watered environment for parental lines.

• Supplemental Figure S3. The proportional decrease in pot water content.

• Supplemental Figure S4. WUE ratio is not a quantity that is orthogonal to plant size.

• Supplemental Figure S5. The WUE ratio rate of change and plant size rate of change are not orthogonal to the rate of change to plant size.

• Supplemental Figure S6. The relationship between the WUE_residual and predicted plant sizes given water use indicates that this quantity is orthogonal to plant size given water use.

• Supplemental Figure S7. The relationship between WUE_fit and plant sizes.

• Supplemental Figure S8. The relationship between WUE_residual and plant size.

• Supplemental Figure S9. The broad sense heritability of each trait through plant development.

• Supplemental Figure S10. The proportion of variance contributed by each factor of each trait throughout plant development.

• Supplemental Figure S11. One hundred six unique QTL locations were detected across all rate-of-change traits.

• Supplemental Figure S12. Twenty-three unique QTL locations detected across all traits in this experiment were found after combining SNP markers that fell within a 10-cm radius.

• Supplemental Figure S13. Twenty-seven unique QTL locations detected across all traits in this experiment were found after combining SNP markers that fell within a 10-cm radius.

• Supplemental Figure S14. Venn diagram illustrating the overlap of QTL detected within trait classes.

• Supplemental Figure S15. Venn diagrams illustrating the overlap of QTL detected within treatment blocks for each trait class.

• Supplemental Figure S16. Venn diagrams illustrating the overlap of QTL detected as common or unique to cumulative or rate statistic traits.

• Supplemental Figure S17. Venn diagram illustrating the overlap of QTL detected within genotype × environment trait classes.

• Supplemental Figure S18. Venn diagrams illustrating the overlap of QTL detected as cumulative and cumulative genotype × environment traits.

• Supplemental Figure S19. Venn diagram illustrating the overlap between trait classes of QTL shared between cumulative traits and the genotype × environment traits.

• Supplemental Figure S20. Venn diagram illustrating the overlap between trait classes of QTL unique to the genotype × environment traits.

• Supplemental Figure S21. Significant associations identified by using a stepwise multiple QTL mapping approach based on interpolated functional traits.

• Supplemental Figure S22. Significant associations identified by using a stepwise multiple QTL mapping approach based on interpolated functional rate-of-change traits.

• Supplemental Figure S23. Significant associations identified using single-marker-scan functional QTL mapping of cumulative rate-of-change traits.

• Supplemental Figure S24. Screen plot illustrating the decrease of within-group sum of squares.

• Supplemental Figure S25. Additive relative size of minor QTL plotted throughout the course of the experiment.

• Supplemental Figure S26. Ratio of the percentage variance explained by each QTL.

• Supplemental Figure S27. Distribution of fresh weight biomass values with a predictive model across time points for plant biomass.

• Supplemental Figure S28. Summary statistics describing the mean, cumulative variance, rate of change, and variance within the rate of change of each trait.

• Supplemental Figure S29. Both convergence and predicted values indicate that data collected before 17 DAP may result in measurement artifacts.

• Supplemental Table S1. SNPs associated with cumulative and rate-of-change traits.

• Supplemental Table S2. Unique QTL locations associated with cumulative and rate-of-change traits.

• Supplemental Table S3. SNPs associated with cumulative and rate-of-change genotype × environment traits.

• Supplemental Table S4. Unique QTL locations associated with cumulative and rate-of-change genotype × environment traits.

• Supplemental Table S5. QTL included when fitting the fixed QTL model.

• Supplemental Table S6. Summary of parental line and RIL replication within the experiment.

Dive Curated Terms

The following phenotypic, genotypic, and functional terms are of significance to the work described in this paper:

• water CHEBI: CHEBI:15377