Abstract
C-arm cone-beam computed tomography (CBCT) has been used increasingly as an imaging tool for yielding 3D anatomical information about the subjects in surgical and interventional procedures. In the clinical applications, the limited field-of-view (FOV) of C-arm CBCT can lead to significant data truncation, resulting in image artifacts that can obscure low contrast tumor embedded within soft-tissue background, thus limiting the utility of C-arm CBCT. The truncation issue can become serious as most of the surgical and interventional procedures would involve devices and tubes that are placed outside the FOV of C-arm CBCT and thus can engender angularly-varying-data truncation. Existing methods may not be adequately applicable to dealing with the angularly-varying truncation. In this work, we seek to reduce truncation artifacts by tailoring optimization-based reconstruction directly from truncated data, without performing pre-reconstruction data compensation, collected from physical phantoms and human subjects. The reconstruction problem is formulated as a constrained optimization program in which a data-derivative-ℓ2-norm fidelity is included for effectively suppressing image artifacts caused by the angularly-varying-data truncation, and the generic Chambolle–Pock algorithm is tailored to solve the optimization program. The results of the study suggest that an appropriately designed optimization-based reconstruction can be exploited for yielding images with reduced artifacts caused by angularly-varying-data truncation.
Keywords: Computed tomography, Image reconstruction, Optimization program, Primal-dual algorithm, Angularly-varying-data truncation, Data derivative
1 Introduction
C-arm cone-beam computed tomography (CBCT) is used frequently as a tomographic imaging tool for providing 3D anatomical information about the subjects in surgical and interventional procedures [1–9]. While it is of utility for revealing high contrast anatomic structures, there exist increased needs for localizing soft-tissue tumors in images of C-arm CBCT procedure guidance and possible complication detection. In current clinical C-arm CBCT, the flat-panel detector forms only a field of view (FOV) of limited size, thus resulting in significant data truncation. Image artifacts caused by data truncation can obscure the identification of low-contrast tumors in surgical and interventional procedures. This truncation issue becomes increasingly serious as the surgical and interventional procedures often involve devices and tubes that are placed outside the FOV of C-arm CBCT, thus engendering angularly-varying-data truncation at different projection views.
Ad hoc methods such as pre-reconstruction data compensation [10–17] have been investigated for reducing truncation artifacts in C-arm CBCT imaging. While these methods have some success in a limited number of situations, they may not be adequately applicable to the angularly-varying-data truncation considered. More importantly, these methods may introduce additional artifacts as a result of their inadequate data compensation, especially for clinically relevant situations in which some high-contrast interventional devices/tubes are present outsides of the FOV.
Optimization-based reconstruction methods may be exploited for reducing image artifacts as a result of data truncation. In particular, evidence exists suggesting that optimization-based reconstruction incorporating a data-derivative divergence term appears to be effective in minimizing image artifacts caused by angularly-varying-data truncation [18, 19]. The resulting reconstruction appears to behave analogously to images reconstructed with analytic methods referred to as the Λ- or local-tomography [20–23], and the data-derivative divergence term helps the recovery of detailed structures relative to standard optimization-based reconstruction and improves reconstruction robustness against angularly-varying truncated projection data. In this work, we seek to reduce image artifacts observed in the reconstructions obtained with the current clinical algorithm by applying an optimization-based reconstruction method [18, 19] directly to angularly-varying-truncation data collected from physical phantoms and human subjects in neurological interventional procedures.
As mentioned above, the image reconstruction is designed specifically as a constrained optimization program, which contains a data fidelity of ℓ2-norm form and a constraint on the image total-variation (TV), thus forming a non-smooth, convex program [24–26]. We show that the appropriate design of the overall data fidelity is a key to effectively reduce the angularly-varying-truncation artifacts in C-arm CBCT. Specifically, we demonstrate that a data-derivative-ℓ2-norm fidelity can be included in the overall data fidelity for effectively suppressing the image artifacts caused by the angularly-varying-data truncation. The optimization program is designed as a convex program, and thus algorithms exist that can be used for solving the program. In the work, the generic CP algorithm that can solve mathematically non-smooth, convex program is tailored to solve our designed optimization program [18, 19, 24, 25]. The results of the study suggest that an appropriately designed optimization-based reconstruction with a data-derivative fidelity and the corresponding CP algorithm can be exploited for yielding image reconstruction with reduced artifacts directly from truncated data collected in CBCT imaging in neurological interventional procedures.
We organize the paper as follow. Data acquisition from a physical head phantom and a patient by use of a clinical C-arm CBCT system is described in Sect. 2. An image-TV-constrained, weighted ℓ2-norm data-fidelity-minimization reconstruction is proposed for the C-arm CBCT imaging and the tailored CP reconstruction algorithm along with the convergence conditions are presented in Sect. 3. Image-reconstruction results from physical phantom data and patient data are presented in Sect. 4, followed by discussion and remarks about our study in Sect. 5.
2 Data Acquisition
In this work, we collected projection data by using a C-arm system (Canon Medical System Infinix™-i, Japan) in which the X-ray source has distances of 700 mm and 1100 mm to the rotation center and to the detector. The flat-panel detector consists of a 1024 × 1024 array of detector bins with a size of 0.29 × 0.29 mm2, which is rebinned often to a 512 × 512 array with a bin size of 0.58 × 0.58 mm2, and thus forms a circular FOV of diameter 18.7 cm, as shown in Fig. 1. With this system, C-arm CBCT data were collected from a physical head phantom and a patient subject at 247 views over a short-scan angular range of ~194°. Therefore, the dataarray sizes for both the phantom and patient studies are 512 × 512 × 247. The standard calibration scheme of the clinical C-arm system was performed on data prior to the image reconstruction.
Fig. 1.
a The scanning configuration in which the dashed circle indicates the field of view (FOV) formed by the planar detector of the C-arm imaging system and a metal tube is placed outside of the FOV. The dashed lines pointed by arrows indicate the projection loci of the tube at b the 0°- and c the 90°-view. Clearly, projection data is truncated at the 90°-view as the tube projection is beyond the detector
While the FOV may be sufficient to cover the scanned subject, some interventional devices, which may or may not touch directly the subject, are presented often outside the FOV during the intra-operative imaging process. For example, as shown in Fig. 1, a metal tube placed outside the FOV is projected onto the detector at 0°view without any truncation, whereas its projection is outside the detector at 90°-view, thus resulting in data truncation. Clearly, the degree of the tube truncation depends upon the projection views, i.e., it varies as a function of projection views and is thus referred to as the angularly-varying truncation. It is this type of truncations that causes the prominent streak artifacts observed in clinical reconstructions, as demonstrated in Sect. 4 below.
3 Optimization-Based Reconstruction
We summarize below the optimization program, reconstruction algorithm, and practical convergence conditions that form the necessary components of the optimization-based reconstruction [18, 19].
3.1 Optimization Program
The problem of image reconstruction considered is formulated as a constrained optimization program [19, 27]:
| (1) |
where f and gm denote image vector of size N and measured-data vector of size M, respectively; ℋ the system matrix of size M × N ; ||f||TV the image total-variation (TV); t1 > 0 a constraint parameter on the image TV, and fj entry j of image vector f; and DW (gm, ℋf) the data divergence. In the work, in an attempt to reduce the angularly-varying truncation, we consider [18]
| (2) |
where weighting matrix Wc is given by
| (3) |
and ℐ denotes the identity matrix of size M × M, and matrix 𝒟u of size M × M represents a two-point-difference operation (i.e., an approximation of the derivative) carried out along the horizontal axis of the detector, and c a parameter that weights the contributions of (ℋf − gm) and its derivative to the data divergence. It can be observed that DW (gm, ℋf) becomes the standard data ℓ2-norm when c = 1, and the data-derivative ℓ2-norm when c = 0. The derivative operation is analogous to the derivative operation involved in local tomography that enhances the structural boundaries in an image [20–23]. It has been shown [18, 19] that the appropriate incorporation of data derivative 𝒟u can suppress effectively truncation artifacts in reconstructed images.
While the form of the optimization program is given by Eq. (1), the complete specification of the program depends also upon ℋ, c, and t1, which are referred to as program parameters. Clearly, program parameters can significantly impact the program and thus its solution (i.e., the reconstruction). In each of phantom- and patient-data studies below, we discuss the selection of the program parameters specific to the study.
3.2 Reconstruction Algorithm
The problem of image reconstruction is thus tantamount to solving Eq. (1), which is a convex but non-smooth problem. Therefore, we will use a primal-dual algorithm by tailoring the generic CP algorithm to solve the non-smooth convex problem in our reconstruction, and summarize below the tailored CP algorithm for which the detailed derivation can be found in Refs. [18, 19].
Using two positive parameters λ and ν, we change the form of Eq. (1) to
| (4) |
which specifies a feasible solution set identical to that defined by optimization problem in Eq. (1). It can readily be shown that the constrained optimization program in Eq. (4) can be recast into an unconstrained problem as
| (5) |
where ∇ depicts a gradient matrix of size 3N × N with its transpose given by ; superscript “⊤” indicates a transpose operation; ∇x, ∇y, and ∇z are matrices of size N × N representing two-point differences along x-, y-, and z-axis, respectively, yielding vectors ∇xf, ∇yf, and ∇zf of size N, which in turn form vector ∇f of size 3N in a concatenated form in the order of x, y, and z; |∇f|MAG denotes a vector of size N in which entry i is given by ; and indicator functions δP(x) and δDiamond(νt1)(x) are defined as
| (6) |
Now, our problem of image reconstruction becomes to solve the unconstrained problem in Eq. (5). As discussed above, since the objective function in Eq. (5) includes non-smooth functions such as the image-TV term, we use a specific primal-dual algorithm tailored from the generic CP algorithm [24, 25] to solve the optimization program in Eq. (5).
The generic CP algorithm solves a primal minimization problem of the form
| (7) |
where K denotes a linear transform, and functions F and G are convex. The pseudo codes of the preconditioned generic CP algorithm [24, 25, 28] that solves the primal minimization problem in Eq. (7) are given in Table 1:
Table 1.
| 1: Σ ← 1Y/(|K|1X) ; 𝒯 ← 1X/(|K|1Y ) |
| 2: θ ← 1 ; n ← 0 |
| 3: INITIALIZE x0 and y0 to zero |
| 4: x̄0 ← x0 |
| 5: REPEAT |
| 6: yn+1 ← proxΣ[F*](yn + ΣKx̄n) |
| 7: xn+1 ← prox𝒯 [G](xn − 𝒯 K⊤yn+1] |
| 8: x̄n+1 ← xn+1 + θ(xn+1 − xn) |
| 9: n ← n + 1 |
| 10: UNTIL the convergence conditions are satisfied |
| 11: OUTPUT: image fconv ← fn+1 |
where |·| takes the absolute value of each entry of a matrix, vectors 1X and 1Y of the sizes identical to that of x and y have all components set to 1.
In attempt to tailor the generic CP algorithm to solve our optimization problem in Eq. (5) [or, equivalently, Eq. (1)], we need to carry out two key steps: (1) identification of the concrete forms of the linear transform K and the convex functions F and G; and (2) calculations of the proximal mappings of functions F* and G in Lines 6 and 7 of Table 1, where symbol “*” refers to convex conjugate [29].
For discussion convenience, let a and b denote two vectors of sizes kN and N, where k ≥ 1 is a positive integer. Let aj denote the jth entry of a, j = 1, 2,…, kN, and bj the jth entry of b, j = 1, 2,…, N, respectively. Their multiplication and division are defined below as
where j = 1, 2,…, kN, and jm = mod (j, N) indicates the remainder of j dividing by N, and bjm ≠ 0. In particular, when k = 1, a and b are of the same size N, and vectors ab and a/b thus are of size N depicting element-wise multiplication and division. We also use a⊤b to denote their inner product for vectors a and b of an identical dimension.
It can be shown [18, 19] that Eq. (5) can be interpreted as a primal problem with the form in Eq. (7) by using the following assignments:
| (8) |
and
| (9) |
where r = Wcℋf, z = ν∇f, |z|MAG depicts a vector of size N in which entry i is given by , and zi indicates entry i of vector z.
Using F and G are determined Eq. (9), one can analytically derive the proximal mappings of functions F* and G (see Appendix A of Ref. [19]), which are given by
| (10) |
and
| (11) |
where
p and q are vectors of sizes M and 3N, vector Σ1 = 1D//|| Wcℋ|| 1I ) of size M, vectors 1D and 1I of sizes M and N with all components set to 1, vector 1V of size 3N with entries set to 1; vector Σ2 = 1V/2ν of size 3N, vector s = ProjectOntoℓ1Ballνt1(2ν|q|MAG), and operator ProjectOntoℓ1Ballνt1 projects vector 2ν|q|MAG of size N onto the ℓ1-ball of scale νt1 [18, 30], operator pos(f) = 0 and fj for fj ≤ 0 and fj > 0, respectively, enforcing the non-negativity constraint, vector of size N.
Using Eqs. (10) and (11) to replace proxΣ[F*](y) and prox𝒯[G](x) in Lines 6 and 7 of Table 1, the pseudo codes are obtained for the tailored CP algorithm specifically for solving the program in Eq. (5), or equivalently, the program in Eq. (1).
3.3 Practical Convergence Conditions
The tailored CP algorithm summarized above can mathematically converge a convex optimization program. Without loss of generality, we use three quantitative metrics below to define the necessary convergence conditions:
| (12) |
where D̄W (fn) and denote the normalized data divergence and image-TV at iteration n, and the normalized conditional primal-dual gap is defined as [24]
and ||·||∞ denotes the largest entry of the vector. Using the metrics defined, one obtains necessary mathematical convergence conditions, given by
| (13) |
The mathematical convergence conditions can be satisfied by the tailored CP algorithm summarized above. However, it is unlikely that they can be met in numerical studies due to the limited computer precision. Therefore, practical convergence conditions are needed for numerical studies. Based upon the mathematical convergence conditions, we define below practical convergence conditions for specific real-data studies considered:
| (14) |
4 Results
Although the mathematical form of the optimization program is given by Eq. (1), the complete specification of the program depends upon the program parameters involved. For a given set of parameters, without loss of generality, we first performed reconstruction studies to verify that the practical convergence conditions in Sect. 3.3 can be achieved by the tailored CP algorithm. Then, we will illustrate the strategy and scheme to determine the program parameters for each of the studies involving physical phantom and patient subject, followed by presenting the results obtained for the physical phantom and patient subjects considered by applying the tailored CP algorithm to solving the optimization program completely specified by selected parameters.
4.1 Practical Convergence Conditions
Without loss of generality, we first perform a study using the physical head phantom with parameter t1 = 18,000 to demonstrate that the practical convergence conditions in Eq. (14) above can be reached. In Fig. 2, we display metrics , and calculated from reconstructions of the physical phantom as functions of iteration number n, along with the convergence reconstruction of the physical head phantom shown in Fig. 3b. It can be observed that the tailored CP algorithm takes about 900 iterations to satisfy the practical convergence conditions in Eq. (14). This observation can also be made for other subjects and
Fig. 2.
Metrics , and as functions of iteration number n. The values at n = 900 satisfy the practical convergence conditions in Eq. (14) conditions studied in the work. Therefore, the reconstructions at n = 900 is used as the surrogate solution to the convergent solution to the optimization program in Eq. (1).
Fig. 3.
Convergent reconstructions from the head-phantom data within a transverse slice reconstructed by use of the tailored CP algorithm with parameter t1 = 12,000 (a), 18,000 (b), and 25,000 (c), along with the corresponding reference (d). The region enclosed by the circle is the selected ROI for computing the contrast-resolution metric, CNR. Display window: [0, 200] HU
4.2 Determination of Program Parameters
As shown in Eq. (1), there exist several important program parameters for completely specifying the optimization program, including system matrix, image array (i.e., voxel shape and size), modulation parameter c, and TV-constraint parameter t1.
4.2.1 Determination of Program Parameters Other than t1
In our studies, scanning geometry information was incorporated into system matrix ℋ in which each element was defined as the intersection length of X-ray measured and a voxel in the image array. We used detecting-bin size and data size identical to clinical parameters discussed in Sect. 2. For the purpose of comparison with the clinical FDK reconstructions, the image arrays of sizes N = 700 × 560 × 50 and N = 750 × 700 × 50 were used in head-phantom and patient reconstructions, and the voxel sizes are 0.47 × 0.47 × 0.47 mm3 and 0.37 × 0.37 × 0.37 mm3, respectively. With the determination of system matrix ℋ and voxel size, c and t1 are the only two remaining program parameters to be determined. In our previous [19] and current studies, it has been shown empirically that c = 0.05 appears to be effective in reducing image artifacts. With the selection of c = 0.05, parameter t1 remains the only program parameter to be determined.
4.2.2 Determination of Program Parameter t1
Using the program parameters determined above, we performed multiple reconstructions with different values of t1 for each data set of the physical phantom and patient subject, and, based upon visual inspection of the reconstructions, then selected the values of parameter t1 yielding reconstructions with visually least artifacts. For example, we show in Figs. 3 and 4 reconstructions from physical phantom and patient data sets, respectively, for different values of parameter t1. It can be observed that t1 = 18,000 and t1 = 10,000 appear to yield reconstructions of the phantom and patient with visually least truncation artifacts. Additionally, this is a qualitative, subjective scheme for determination of t1, it seems to work effectively in terms of selecting t1 for showing the degree of artifacts reduction. Furthermore, as one leading interest in the clinical procedures considered is in the detection of low-contrast anatomy in the image, we defined a contrast-resolution metric below for guiding the selection of parameter t1 for a given data set:
| (15) |
where fs and σs denote the mean and standard deviation within a region of interest (ROI), and fb and σb denote the mean and standard deviation within a selected background region. CNRs were computed in ROIs containing low-contrast insert in the phantom image and low-contrast structure in the patient image, indicated by the circle in the second panel in Figs. 3 and 4, respectively. We show in Fig. 5 the CNRs calculated from images of the phantom and patient reconstructed with different t1 values. It can be observed that the CNR results corroborate visual inspection results by reaching roughly its maximum around the optimal t1 value determined by use of visual inspection. Therefore, this approach is used for selecting the value of parameter t1 for each of the studies in Sect. 4.
Fig. 4.
Convergent reconstructions from the patient data within a transverse slice reconstructed by use of the tailored CP algorithm with parameter t1 = 6000 (a), 10,000 (b), and 15,000 (c), along with the corresponding reference image (d). The region enclosed by the circle is the selected ROI for computing the contrast-resolution metric, CNR. Display window: [−150, 200] HU
Fig. 5.
CNRs computed within the ROIs enclosed by the circles shown in Figs. 3 and 4 for the head phantom (a) and patient (b), along with the CNRs (dashed lines) of the corresponding reference images, as functions of t1. The values of t1 indicated by the square symbols are selected as the optimal value of t1 for image reconstruction
4.3 Results of the Phantom-Data Study
For the phantom data collected, image array of size N = 700 × 560 × 512 and the voxel size 0.47 × 0.47 × 0.47 mm3 were used in the reconstructions. The modulate parameter c = 0.05 was chosen. By using the approach described in Sect. 4.2.2 with metric CNR, we selected t1 = 70,000 based upon the phantom data. Using these program parameters determined, we then applied the tailored CP algorithm to reconstructing images from the phantom-data set of size 512 × 512 × 247.
In Figs. 6, 7 and 8, we display the images within three transverse, coronal, and sagittal slices of the phantom reconstructed, with a narrow display window for revealing details of both low-contrast structures and artifacts. The images are convergent solutions to the optimization program in Eq. (1) obtained with about 900 iterations in the sense the practical convergence conditions in Eq. (14) are satisfied. As a result of the metal object placed outside the FOV of the system, significant streak artifacts can be observed in the reconstructions obtained with the FDK algorithm. Conversely, the artifacts appear to be considerably suppressed in the reconstructions of the tailored CP algorithm, thus some of the low-contrast structures can be identified more readily than those obscured in the FDK reconstructions. Moreover, it is interesting to observe that some of the cone-beam artifacts near the jaw region, as pointed by the arrows, in the FDK reconstructions appear to be reduced considerably in the reconstructions of the CP algorithm in Figs. 7 and 8.
Fig. 6.
Reconstructed (row 1) and reference (row 2) images of the head phantom within transverse slices specified by z = 37.6 mm (a), 12.2 mm (b), and −41.8 mm (c), respectively. Display window: [0, 200] HU
Fig. 7.
Reconstructed (row 1) and reference (row 2) images of the head phantom within coronal slices specified by x = −12.7 mm (a), 18.8 mm (b), and 44.2 mm (c), respectively. Display window: [0, 200] HU. The arrow in the reference image indicates the cone-beam artifacts.
Fig. 8.
Reconstructed (row 1) and reference (row 2) images of the head phantom within sagittal slices specified by y = −24.9 mm (a), 12.2 mm (b), and −44.2 mm (c), respectively. Display window: [0, 200] HU. The arrow in the reference image indicates the cone-beam artifacts
4.3.1 Impact of Parameter c
As discussed above, program parameter c also plays a role in the complete specification of the optimization program in Eq. (1). The results above was obtained with c = 0.05 based upon our previous experience [19]. In this work, we have also carried out a study on the impact of c on artifact reduction. For example, we show in Fig. 9 images reconstructed with c = 0.05 and c = 1.0 from the same data set. It can be observed that, while c = 1.0 can suppress considerably the streak artifacts, prominent residual artifacts remain, and that c = 0.05 appears effectively to further reduce the residual artifacts. Similar results were obtained for c values that significantly differ than 0.05.
Fig. 9.
Images of the head phantom within slices specified by z = 37.6 mm (a), z = 12.2 mm (b), y = −24.9 mm (c), and x = −12.7 mm (d) reconstructed with c = 0.05 (row 1) and c = 1.0 (row 2). Display window: [0, 200] HU
4.4 Results of the Patient-Data Study
For the patient-data study, we also used the parameters selected in Sect. 4.2.1 and use the scheme described in Sect. 4.2.2 to determine parameter t1. Using these program parameters determined, we then apply the tailored CP algorithm to reconstructing images from the patient data of size 512 × 512 × 247.
In the patient study, image array of size N = 750 × 700 × 612 and the voxel size 0.37 × 0.37 × 0.37 mm3 were used in the reconstructions. By using the approach described in Sect. 4.2.2 with metric CNR, we selected t1 = 120,000 based upon the patient data. Again, the modulate parameter c = 0.05 was chosen.
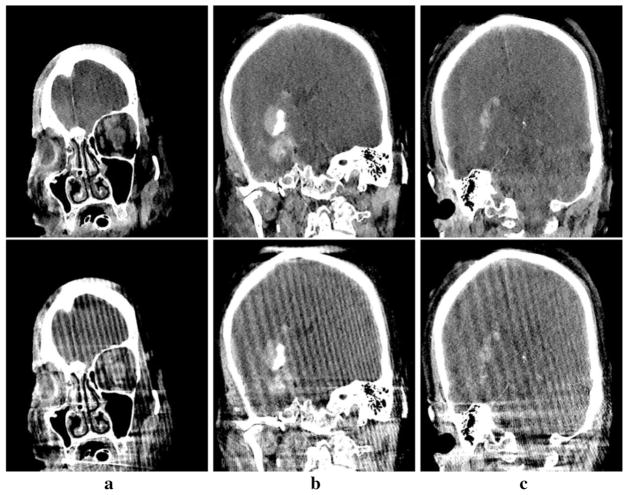
For this study, we display in Figs. 10, 11 and 12 images within three transverse, coronal, and sagittal slices of the patient reconstructed, with a narrow display window for revealing details of both low-contrast structures and artifacts. Again, the images are convergent solutions to the optimization program in Eq. (1) obtained with about 900 iterations in the sense the practical convergence conditions in Eq. (14) are satisfied. The streak artifacts observed in the reference images, caused by the high-contrast interventional devices placed outside of the FOV, are significantly reduced in CP reconstructions. Moreover, the low-contrast intracranial structures in the CP reconstructions, such as hemorrhage and ventricle indicated by the arrow and the arrowhead in bottom panel of Fig. 10a, can be more discernible than those in the clinical FDK reconstruction. Conspicuous streak artifacts in the images obtained with the FDK algorithm are visually distracting and possibly obscure information of clinical significance; whereas the CP reconstructions suppress the artifacts.
Fig. 10.
Reconstructed (row 1) and reference (row 2) images of the patient subject within transverse slices specified by z = 18.5 mm (a), −22.2 mm (b), and −51.1 mm (c), respectively. Display window: [ −150, 200] HU. The arrow and arrowhead in the reference image indicate the hemorrhage and ventricle, respectively
Fig. 11.
Reconstructed (row 1) and reference (row 2) images of the patient subject within sagittal slices specified by y =− 62.9 mm (a), − 2.2 mm (b), and 20.4 mm (c), respectively. Display window: [− 150, 200] HU
Fig. 12.
Reconstructed (row 1) and reference (row 2) images of the patient subject within coronal slices specified by x = 5.6 mm (a), − 2.2 mm (b), and − 46.2 mm (c), respectively. Display window: [− 150, 200] HU
5 Conclusion
In this work, we have investigated an optimization-based image reconstruction in C-arm CBCT used in neurological interventional procedures. In an attempt effectively to suppress streak artifacts as a result of the angularly-varying-data truncation caused by the high contrast devices/tubes placed outside the FOV of the C-arm CBCT system in the clinical procedures, we used a data-derivative fidelity term in the optimization program. The study results of phantom and patient data suggest that the data-derivative term helps the recovery of detailed structures, similar to that observed in Λ- or local-tomography [20–23], more effectively than does the standard optimization-based reconstruction without the data-derivative term, while the regular ℓ-data term in the optimization program ensures the recovery of the image grey levels of various contrast anatomies.
In the study, we have collected data from physical phantom and patient subject by using clinical C-arm CBCT systems. Applying the tailored CP algorithm to the data, we then reconstructed images by solving the optimization program. Results reveal that the optimization program containing a data derivative term, along with the tailored CP algorithm, can yield image reconstructions with substantially reduced artifacts resulted from the angulary-varying-data truncation, thus improving the visualization of low-contrast structures that would otherwise be obscured in the clinical reconstructions.
As we discussed in Sect. 3, the performance of the optimization-based algorithm depends upon a number of parameters and performance metrics used. Therefore, it is necessary and important to discuss the determination of the key parameters that impact significantly image quality. In the study, TV-constraint parameter t1 plays a key role in impacting the visualization of a low-contrast anatomy within a reconstructed image. We have designed contrast metric CNR for determination of parameter t1 because one leading task in the clinical procedure considered is to identify the low-contrast anatomies embedded in the soft-tissue background. When different practical tasks are considered, it is likely that metrics and procedures suited to the tasks should be designed for the determination of the reconstruction parameters.
Finally, we remind that the study is not meant to produce a practical procedure for direct use in clinical applications. In fact, additional issues must be taken into consideration, such as specific clinical tasks to be performed. Instead, our reconstruction investigation entails, in essence, a survey of the multi-dimensional parameter spaces to yield insights into artifact reduction for the scenarios of practical, clinical significance. Knowledge gained in the study, along with other important clinical task-specific considerations, can be exploited for aiding in the design of practical procedures of truly clinical-task utility and be generalized for investigating image reconstruction in other CBCT applications.
Acknowledgments
This work was supported in part by NIH R01 Grants Nos. CA182264, and EB018102. The contents of this article are solely the responsibility of the authors and do not necessarily represent the official NIH views.
References
- 1.Daly MJ, Siewerdsen JH, Moseley DJ, Jaffray DA, Irish JC. Intraoperative cone-beam CT for guidance of head and neck surgery: Assessment of dose and image quality using a C-arm prototype. Medical Physics. 2006;33:3767. doi: 10.1118/1.2349687. [DOI] [PubMed] [Google Scholar]
- 2.Chen GH, Zambelli J, Nett BE, Supanich M, Riddell C, Belanger B, et al. Design and development of C-arm based cone-beam CT for image-guided interventions. SPIE medical imaging. 2006:614210–614210. [Google Scholar]
- 3.Louie JD, Kothary N, Kuo WT, Hwang GL, Hofmann LV, Goris ML, et al. Incorporating cone-beam CT into the treatment planning for yttrium-90 radioembolization. Journal of Vascular and Interventional Radiology. 2009;20:606. doi: 10.1016/j.jvir.2009.01.021. [DOI] [PubMed] [Google Scholar]
- 4.Tognolini A, Louie JD, Hwang GL, Hofmann LV, Sze DY, Kothary N. Utility of C-arm CT in patients with hepatocellular carcinoma undergoing transhepatic arterial chemoembolization. Journal of Vascular and Interventional Radiology. 2010;21:339. doi: 10.1016/j.jvir.2009.11.007. [DOI] [PubMed] [Google Scholar]
- 5.Solomon SB, Silverman SG. Imaging in interventional oncology. Radiology. 2010;257:624. doi: 10.1148/radiol.10081490. [DOI] [PubMed] [Google Scholar]
- 6.Morimoto M, Numata K, Kondo M, Nozaki A, Hamaguchi S, Takebayashi S, et al. C-arm cone beam CT for hepatic tumor ablation under real-time 3D imaging. American Journal of Roentgenology. 2010;194:w452. doi: 10.2214/AJR.09.3514. [DOI] [PubMed] [Google Scholar]
- 7.Schafer S, Nithiananthan S, Mirota DJ, Uneri A, Stayman JW, Zbijewski W, et al. Mobile C-arm cone-beam CT for guidance of spine surgery: Image quality, radiation dose, and integration with interventional guidance. Medical Physics. 2011;38:4563. doi: 10.1118/1.3597566. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Floridi C, Radaelli A, Abi-Jaoudeh N, Grass M, Lin MD, Chiaradia M, et al. C-arm cone-beam computed tomography in interventional oncology: Technical aspects and clinical applications. La Radiologia Medica. 2014;119:521. doi: 10.1007/s11547-014-0429-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Bapst B, Lagadec M, Breguet R, Vilgrain V, Ronot M. Cone beam computed tomography (CBCT) in the field of interventional oncology of the liver. Cardio Vascular and Interventional Radiology. 2015;39:1. doi: 10.1007/s00270-015-1180-6. [DOI] [PubMed] [Google Scholar]
- 10.Kalender WA, Hegel R, Ebersberger J. Reduction of CT artifacts caused by metallic implants. Radiology. 1987;164:576. doi: 10.1148/radiology.164.2.3602406. [DOI] [PubMed] [Google Scholar]
- 11.Xia D, Roeske J, Yu L, Pelizzari C, Pan X. A hybrid approach to reducing CT metal artifact in intracavitary brachytherapy. Brachytherapy. 2005;4:18. doi: 10.1016/j.brachy.2004.11.001. [DOI] [PubMed] [Google Scholar]
- 12.Lemmens C, Faul D, Nuyts J. Suppression of metal artifacts in CT using a reconstruction procedure that combines MAP and projection completion. IEEE Transactions on Medical Imaging. 2009;28:250. doi: 10.1109/TMI.2008.929103. [DOI] [PubMed] [Google Scholar]
- 13.Meyer E, Raupach R, Lell M, Schmidt B, Kachelrieb M. Normalized metal artifact reduction (NMAR) in computed tomography. Medical Physics. 2010;37:5482. doi: 10.1118/1.3484090. [DOI] [PubMed] [Google Scholar]
- 14.Haase C, Schafer D, Kim M, Chen SJ, Carroll J, Eshuis P, et al. Automatic cable artifact removal for cardiac C-arm CT imaging. SPIE medical imaging. 2014:90330K–90330K. doi: 10.1088/0031-9155/59/14/3861. [DOI] [PubMed] [Google Scholar]
- 15.Ohnesorge B, Flohr T, Schwarz K, Heiken JP, Bae KT. Efficient correction for CT image artifacts caused by objects extending outside the scan field of view. Medical Physics. 2000;27:39. doi: 10.1118/1.598855. [DOI] [PubMed] [Google Scholar]
- 16.Borg L, Jørgensen JS, Frikel J, Sporring J. Reduction of variable-truncation artifacts from beam occlusion during in situ X-ray tomography. Measurement Science and Technology. 2017;28:124004. [Google Scholar]
- 17.Borg L, Frikel J, Jørgensen JS, Quinto ET. Full characterization of reconstruction artifacts from arbitrary incomplete X-ray CT data. 2018 arXiv :1707.03055 [math.FA] [Google Scholar]
- 18.Sidky EY, Kraemer DN, Roth EG, Ullberg C, Reiser IS, Pan X. Analysis of iterative region-of-interest image reconstruction for X-ray computed tomography. Journal of Medical Imaging. 2014;1:031007. doi: 10.1117/1.JMI.1.3.031007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Xia D, Langan DA, Solomon SB, Zhang Z, Chen B, Lai H, et al. Optimization-based image reconstruction with artifact reduction in C-arm CBCT. Physics in Medicine & Biology. 2016;61:7300. doi: 10.1088/0031-9155/61/20/7300. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Ramm AG, Katsevich AI. The radon transform and local tomography. London: CRC Press; 1996. [Google Scholar]
- 21.Katsevich AI. Cone beam local tomography. SIAM Journal on Applied Mathematics. 1999;59:2224. [Google Scholar]
- 22.Anastasio MA, Zou Y, Sidky EY, Pan X. Local cone-beam tomography image reconstruction on chords. Journal of the Optical Society of America. 2007;24:1569. doi: 10.1364/josaa.24.001569. [DOI] [PubMed] [Google Scholar]
- 23.Frikel J, Quinto ET. Characterization and reduction of artifacts in limited angle tomography. Inverse Problems. 2013;29:125007. [Google Scholar]
- 24.Chambolle A, Pock T. A first-order primal-dual algorithm for convex problems with applications to imaging. Journal of Mathematical Imaging and Vision. 2011;40:120. [Google Scholar]
- 25.Sidky EY, Jørgensen JH, Pan X. Convex optimization problem prototyping for image reconstruction in computed tomography with the Chambolle–Pock algorithm. Physics in Medicine & Biology. 2012;57:3065. doi: 10.1088/0031-9155/57/10/3065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Zhang Z, Xia D, Han X, Sidky EY, Pelizzari C, Pan X. Impact of image constraints and object structures on optimization-based reconstruction. Proceedings of the 4th international conference on image formation in X-ray computed tomography; 2016. pp. 487–490. [Google Scholar]
- 27.Zhang Z, Han X, Pearson E, Pelizzari C, Sidky EY, Pan X. Artifact reduction in short-scan CBCT by use of optimization-based reconstruction. Physics in Medicine & Biology. 2016;61:3387. doi: 10.1088/0031-9155/61/9/3387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Pock T, Chambolle A. Diagonal preconditioning for first order primal-dual algorithms in convex optimization. International conference on computer vision (ICCV 2011); 2011. pp. 1762–1769. [Google Scholar]
- 29.Rockafellar RT. Convex analysis. Princeton: Princeton University Press; 1970. [Google Scholar]
- 30.Duchi J, Shalev-Shwartz S, Singer Y, Chandra T. Efficient projections onto the ℓ1-ball for learning in high dimensions. Proceedings of the 25th international conference on machine learning; 2008. pp. 272–279. [Google Scholar]