Abstract
Considerable evidence suggests a role of beta-band oscillations in voluntary movements. However, most of the studies linking beta power to motor performance are based on data averaged across trials that ignore the fast dynamics of oscillatory activity and trial-to-trial variations in motor responses. Recently, emphasis has shifted from the functional implications of the mean beta power to the presence and nature of episodic bursts of beta activity. Here we test the hypothesis that beta bursts, though short in duration in more physiological state, may help explain spontaneous variations in motor behavior of human adults at the single-trial level. To this end, we recorded local field potential activity from the subthalamic nucleus of parkinsonian patients of both genders whose motor behavior had been normalized as far as possible through treatment with the dopamine prodrug, levodopa. We found that beta bursts present in a time-limited window well before movement onset in the contralateral subthalamic nucleus reduce the peak velocity of that movement and that this effect is further amplified by the amplitude of the burst. Additionally, prolonged reaction times are observed when bursts occur immediately after the GO cue. Together, these results suggest that the modulation of the timing and amplitude of beta bursts might serve to dynamically adapt motor performance. These results offer new insight in the pathology of Parkinson's disease, and suggest that beta bursts whose presence and nature are modulated by context may have a physiological role in modulating behavior.
SIGNIFICANCE STATEMENT Beta oscillations (∼13–30 Hz) have been increasingly interpreted as transient bursts rather than as rhythmically sustained oscillations (Feingold et al., 2015). Prolonged and increased probability of beta bursts in the subthalamic nucleus correlates with the severity of motor impairment in Parkinson's disease (Tinkhauser et al., 2017a, b). However, it remains unclear whether beta bursts act to modify motor performance on a trial-by-trial basis under more physiological condition. Here, we found that, according to the time window in which they fall, beta bursts reduced the velocity of the forthcoming movement or prolonged the reaction time. These results offer new insight in the pathology of Parkinson's disease and also suggest that the modulation of beta bursts might serve to dynamically adapt motor performance.
Keywords: beta bursts, beta oscillations, motor performance, Parkinson's disease, reaching movement, subthalamic nucleus
Introduction
Neural oscillations in the beta frequency band (∼13–30 Hz) are a prominent feature in the corticobasal ganglia motor network. During motor control, beta oscillations are systematically modulated, showing a marked reduction of mean power before and during voluntary movement, followed by a rebound at the end of movement. This movement-related modulation of beta power has been observed in a multitude of motor tasks and in various cortical regions (Pfurtscheller and Lopes da Silva, 1999; Tan et al., 2014a, 2016; Torrecillos et al., 2015; Fischer et al., 2016; for review, see Kilavik et al., 2013), as well as in different structures of the basal ganglia (Cassidy et al., 2002; Kühn et al., 2004; Doyle et al., 2005; Tan et al., 2014b). Additionally, during tonic holding contractions, cortical beta activity is coherent with the electromyogram of contralateral contracting muscles (Baker et al., 1997). Hence, beta oscillations in the corticobasal ganglia motor circuit are now widely associated with motor control (Jenkinson and Brown, 2011; Singh, 2018).
More recently, it has been realized that beta oscillations in this motor network emerge as brief transient events or bursts (Murthy and Fetz, 1992, 1996; Bartolo and Merchant, 2015; Feingold et al., 2015; Sherman et al., 2016; Shin et al., 2017; Tinkhauser et al., 2017a, b). Recordings in the subthalamic nucleus (STN) of untreated patients with Parkinson's disease (PD) at rest demonstrate that the mean duration of beta bursts is prolonged and that the probability of long beta bursts correlates with the severity of motor impairment (Tinkhauser et al., 2017b). This is likely to be related to the rise in burst amplitude, indicative of an increase in local neural synchronization, which negatively impacts upon the motor system when excessive (Brittain and Brown, 2014).
The change in beta power typically observed around movements has also been suggested to reflect changes in the probability of beta bursts rather than a smooth modulation of sustained beta activity (Feingold et al., 2015). Studies in nonhuman primates have confirmed that beta burst probability changes across trials with motor and cognitive processes (Feingold et al., 2015; Lundqvist et al., 2016). In patients with PD, the movement-related modulation in the beta band is reduced in the basal ganglia (Doyle et al., 2005) and the average beta desynchronization correlates with overall motor performance (Kühn et al., 2004). The reduced modulation in the beta power averaged over multiple trials may reflect impairment in the modulation of the timing of the beta bursts, suggesting that it is not only the duration of beta bursts but also their precise timing that can contribute to the motor impairment evident in PD. A recent study has demonstrated that the probability of cortical beta bursts before a stimulus can predict detection performance and attentional shifts in both animal and human data (Shin et al., 2017). However, it is unknown how changes in the probability and timing of beta bursts around a go cue might affect motor performance.
Here, we test the hypothesis that the timing and amplitude of beta bursts in the basal ganglia modify motor behavior by seeking predictive, within-subject correlations between beta bursts and motor performance in PD patients who have undergone surgery for deep brain stimulation (DBS) and have been treated with the dopamine prodrug levodopa. These patients afford an opportunity to record local field potential (LFP) activity directly from the STN in the awake, behaving human. As patients were on medication, motor performance was optimized as far as possible and was tested in a visually cued joystick task, as measured by reaction time (RT) and movement velocity. We showed that the timing and the amplitude of beta bursts occurring in the contralateral STN before movement are associated with measurable changes in motor performance at the single-trial level. According to the time window in which they fall, beta bursts can reduce the velocity of the forthcoming movement and/or slow down the RT.
Materials and Methods
Subjects.
Twelve patients (5 females) with PD gave their written informed consent to participate in the experiment, which was approved by the local ethics committees. Their mean age at the time of the recording was 63.8 years (range, 56–70 years) with average disease duration of 10.8 years (range, 4–17 years). All subjects were right handed by self-report and had normal or corrected-to-normal vision. Clinical severity was measured by using the Unified Parkinson's Disease Rating Scale, and the mean score was 46.4 ± 4 in the OFF and 21.8 ± 2.7 in the ON medication state. Patients were implanted with DBS electrodes (model 3389, Medtronic Neurological Division) in the left and right STN. The clinical details of the patients and of the surgical intervention are reported in Table 1.
Table 1.
Patients detailsa
| Case no. | Gender, age (yr) | Disease duration (yr) | UPDRS III (OFF) | UPDRS III (ON) | Predominant symptom(s) | Medication (daily doses) |
|---|---|---|---|---|---|---|
| 1 | F, 65 | 5 | 33 | 11 | Bradykinesia, | Levodopa, 300 mg |
| tremor | Amantadine, 200 mg | |||||
| Rasagiline, 1 mg | ||||||
| 2 | F, 68 | 14 | 28 | 15 | Bradykinesia, rigidity | Levodopa, 200 mg |
| Ropinirole, 18 mg | ||||||
| Rasagiline 1 mg | ||||||
| 3 | M, 68 | 13 | 42 | 24 | Bradykinesia, rigidity, freezing | Levodopa, 500 mg |
| Amantadine,100 mg | ||||||
| Ropinirole, 24 mg | ||||||
| 4b | M, 59 | 7 | 61 | 9 | Bradykinesia, rigidity, freezing | Levodopa, 600–1100 mg Ropinirole,12 mg |
| 5 | F, 59 | 14 | 61 | 27 | Dyskinesia, | Levodopa, 750 mg |
| prolonged OFF periods | Selegiline,1.25 mg | |||||
| 6 | M, 59 | 8 | 49 | 25 | Dyskinesia, freezing, | Levodopa, 850 mg |
| prolonged OFF periods | Amantadine,100 mg Entacapone,1000 mg | |||||
| Ropinirole,10 mg | ||||||
| Rasagiline,1 mg | ||||||
| 7 | M, 62 | 11 | 63 | 38 | Tremor, bradykinesia, rigidity | Levodopa, 500 mg |
| Ropinirole 24 mg | ||||||
| 8 | M, 69 | 9 | 53 | 26 | Rigidity, bradykinesia | Levodopa, 375 mg |
| Entacapone, 800 mg | ||||||
| Ropinirole, 2 mg | ||||||
| 9 | F, 66 | 17 | 25 | 14 | Freezing, falls | Levodopa, 375 mg |
| Entacapone, 1000 mg | ||||||
| Amantadine, 200 mg | ||||||
| Ropinirole, 16 mg | ||||||
| 10 | M, 70 | 11 | NA | NA | Tremor | Levodopa, 600 mg |
| Entacapone, 1000 mg | ||||||
| Rotigotine, 4 mg | ||||||
| 11 | F, 56 | 9 | 49 | 29 | Dystonia, bradykinesia, rigidity | Levodopa, 50 mg |
| Apomorphine, 5 mg/h | ||||||
| Rasagiline, 1 mg | ||||||
| 12 | M, 65 | 6 | NA | NA | Tremor | Levodopa, 650 mg |
| Rasagiline, 1 mg | ||||||
| Ropinirole, 21 mg |
aUPDRS (III), Part III motor score of the Unified Parkinson's Disease Rating Scale; NA, missing data. All patients had bilateral implantations.
bIn Subject 4, no signal was recorded for 2 contacts of the right electrode (R3/R4).
Experimental protocol.
Subjects performed a visually cued joystick reaching task as described in Figure 1A. They were seated in front of a computer monitor and held a finger joystick with their right hand, which rested on a padded arm support. The position of the joystick was displayed on the computer monitor as a cursor in the form of a red circle with 6 mm diameter. Subjects were instructed to make rapid out and back movements to move the cursor from the center of the monitor to a target position. The target was a green circle (6 mm diameter, 0.6 visual degrees) displayed on the screen. Each trial started with the red cursor in the center of the monitor. Then a green target appeared at a position randomly selected from three positions equally spaced around an invisible arc with a radius of 7.5 cm (6.1 visual degrees) and central angle of 90°, which acted as the GO cue. The green target remained at its new position for 1 s before it disappeared. Subjects were instructed to respond as fast as possible after the GO cue by moving the cursor toward the green target in a ballistic and straight movement. To minimize any corrective movements, no visual feedback of the cursor position was provided during the movement. The position of the red cursor was presented at rest and disappeared after movement onset, once it had reached 5% of the maximal displacement. It reappeared once it had reached 90% of the maximal displacement to show the endpoint of the reaching movement. Thereafter, the position of the red cursor did not respond to further corrective movements in that trial and returned to its central starting position when participants released the joystick. The cursor remained at the center for 1.5–2 s (uniformly distributed) before the next trial began, making the total intertrial interval between 2.5 and 3 s. In the present study, the data from the three target positions were pooled and analyzed together, as a visual inspection of the hand paths and velocity profiles revealed no systematic difference between the three directions. After familiarization with the apparatus, each subject performed 50 trials that corresponded to the baseline session of a longer experiment (not described here).
Figure 1.
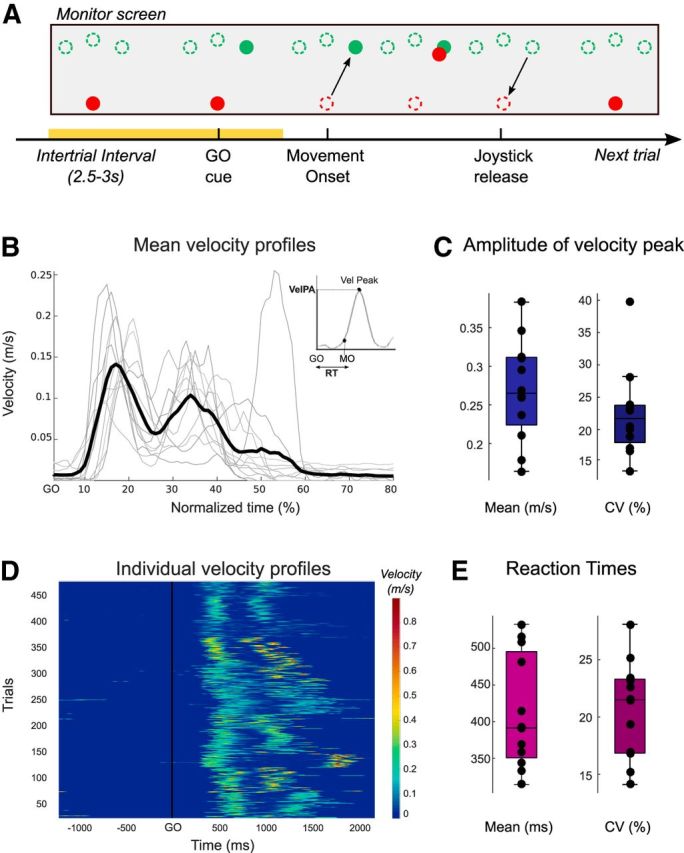
Task and behavioral results. A, Visual stimuli in the joystick task and timeline of each trial. Single-trial beta oscillations were analyzed in the premovement period, from −600 ms before the GO cue to −200 ms before movement onset (yellow shading). The dashed circle outlines were not visible to the subject. During movement, only the endpoint feedback of the red cursor position was shown. B, Velocity profiles averaged across all trials for each subject (gray) and the grand average computed across all subjects (black). The time is normalized between two consecutive GO cues (100%) to average trials of different duration. Inset, How the RT and the amplitude of the velocity peak (VelPA) were defined for each trial. C, Mean peak velocity of each subject and their CV. D, Velocity profiles of all individual trials and all subjects (n = 506 trials, 12 subjects) relative to the GO cue. E, Mean RTs of each subject and their CV.
Data recording.
Recordings were made when the patients were on their usual dopaminergic medication, between 3 and 6 d postoperatively, while electrode leads were still externalized and before implantation of the pulse generator. STN LFPs were recorded from the four different contacts of each implanted electrode (right and left STN) using a 32-channel TMSi-Porti amplifier and its respective software (TMS International). The ground electrode was placed on the left forearm. LFP signals were amplified, low-pass filtered at 550 Hz, sampled at 2048 Hz, and common average referenced. The behavioral task was presented using open-source software (PsychoPy version 1.74). To synchronize the behavioral measurements and the LFP recordings, a trigger signal was generated using PsychoPy software and converted to an analog signal through a digital-to-analog converter (U3; LabJack). This trigger signal changed from 0 to 3 V at the start of each trial and was simultaneously recorded with the monopolar LFPs using the same amplifier (TMSi). The displacement of the joystick in x and y axes and the timing of the target jump were also recorded through the TMSi-Porti amplifier and sampled at 2048 Hz.
Behavioral analysis.
Behavioral data were analyzed off-line using custom-written MATLAB scripts (version R2015b; The MathWorks). The position of the cursor was differentiated to calculate velocity, which was subsequently filtered through a Gaussian kernel with a window duration of 10 ms. As illustrated in Figure 1B, the joystick velocity profiles were characterized by two distinct peaks corresponding to the reaching movement (center-out) followed by the joystick release (center-in), respectively. To assess the motor performance of each subject, we focused our analysis on two main behavioral parameters: the RT and the velocity peak of the outgoing movement. First, we defined the movement onset of each single movement as the time when the joystick velocity crossed the threshold of three times the SD of the signal (and its noise) at rest, and sustained this speed for at least 100 ms. The RT was then computed as the delay between the GO cue and the movement onset (RT; see Fig. 1B, inset). Second, the amplitude of the velocity peak of the out reaching movement was defined for each trial (VelPA; see Fig. 1B, inset). For both, the coefficients of variation were computed for each subject by dividing the SD by the mean and multiplying by 100.
Because of the high kinematic variability between and within subjects (see, e.g., Fig. 1B,D), the velocity profiles of all individual trials were visually inspected to manually correct movement onset and peak velocity when necessary. For further analyses, trials with extra-long RT (mean >2.5 SD) were discarded. Similarly, trials with abnormal hand path trajectories or in which the hand was not maintained stable enough during the intertrial interval were visually identified and excluded.
STN-LFP preprocessing.
All LFP data preprocessing was performed offline using the free and open-source FieldTrip toolbox (Oostenveld et al., 2011). Before any analysis, LFP recordings were downsampled to 1000 Hz and bandpass filtered between 1 and 100 Hz. Continuous time series were segmented into 4 s epochs, from −1.5 s until 2.5 s after the GO cue or the movement onset. Continuous time series were also processed as described below to determine the mean characteristics of bursts (duration and amplitude; see Results). Individual trials were visually inspected, and those with channels containing artifacts were excluded. LFP signals were then converted to bipolar montages between adjacent contact pairs resulting in three bipolar montages per STN to limit the effects of volume conduction from distant sources (Marmor et al., 2017). After behavioral and electrophysiological artifact removal, analyses were based on averages of 42.4 ± 1.5 trials by subject, resulting in a total number of 506 included trials.
LFP analysis: frequency–time decomposition, channels and beta peak selection.
Single-trial LFP signals were transformed in the time-frequency domain by convolution with complex Morlet wavelets characterized by the ratio f0/σf = 7, with f0 ranging from 1 to 45 Hz by steps of 0.25 Hz. Event-related changes in power were calculated by normalizing for each frequency band the value of each time point against the mean power calculated across all trials. For each subject, the normalized power was separately averaged over all trials for each of the three bipolar contacts for each STN. The bipolar contact with the largest movement-related power change in the whole beta band (13–30 Hz), that is, the largest difference between the trough of the event-related desynchronization during movement and the peak of the postmovement synchronization (event-related synchronization) in the beta band, was then selected for further analysis. This was motivated by evidence linking maximal beta band activity to the dorsal (motor) region of the STN (Chen et al., 2006; Zaidel et al., 2010; Horn et al., 2017) and maximal beta band movement-reactivity to the site that offers the most effective DBS (Ince et al., 2010; Zaidel et al., 2010; Tinkhauser et al., 2018a), this site corresponding also to the one with the maximal beta band movement-reactivity (Devos et al., 2006).
For each chosen bipolar contact pair, the beta frequency peaks were individually selected. To this end, the movement-related beta power modulation was computed across all trials for each beta frequency (from 13 to 30 Hz in 1 Hz steps). The frequency with the largest difference between movement-related desynchronization and postmovement-related synchronization was then selected. Time-frequency maps and normalized beta power time courses were also visually inspected to confirm the contact and frequency peak selection. Across all subjects, this selection process results in a mean frequency of 19.6 ± 1.3 Hz for the left STN and 18.7 ± 1.1 Hz for the right STN.
LFP analysis: burst detection.
To explore the trial-by-trial relationship between beta oscillations and motor performance, we used the concept of beta bursts (Tinkhauser et al., 2017a, b). Beta bursts were detected according to the following procedure. First, beta power time courses were computed for each single trial by averaging over a 6-Hz-wide frequency band centered on the contact's beta peak frequency (see Fig. 2A). A threshold was set at the 75th percentile of the mean beta power calculated for each subject and STN over the individualized beta frequency band across the whole session. In contrast to Tinkhauser et al. (2017a, b), the thresholds were defined based on data including cued movements. All time points surpassing the threshold were labeled as “potential bursts,” and only those lasting >2 oscillatory cycles were definitively defined as “beta bursts” (see Fig. 2A). Thus, the minimal beta burst duration depended on the individual frequency band and was different for each subject. Across subjects, the minimum burst duration was on average 111 ± 7 ms for both STNs (range, 73–163 ms). The probability of bursts was computed as the number of burst trials divided by the total number of trials for each subject. The impact of the burst detection threshold was also tested by using eight different thresholds ranging from 50% to 85% in steps of 5% (see Fig. 3B,C). The threshold could not be increased further as too few trials with bursts were detected with a 90% threshold.
Figure 2.
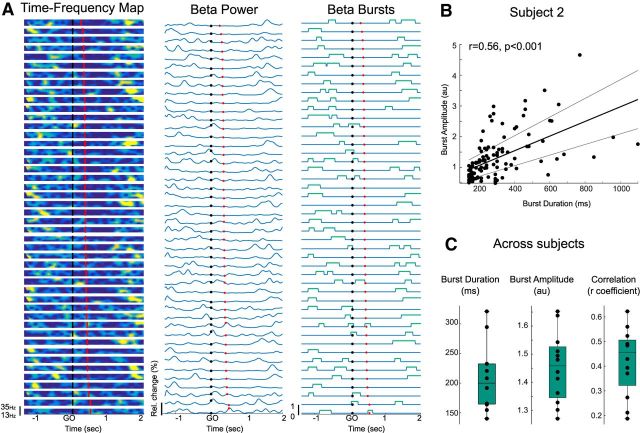
Definition of beta bursts. A, Single-trial data for 1 subject sorted by RTs. The beta power time courses were computed by averaging over a 6 Hz frequency band centered on the individual beta frequency peak. Then bursts were defined as beta amplitude exceeding the 75th percentile threshold with a minimum duration of 2 cycles. Black dots represent GO cue. Red dots represent movement onset. B, Positive correlation between the burst duration and amplitude in 1 example subject (same as for A; r = 0.56, p < 0.001). C, Mean burst duration and amplitude and positive correlations between the 2 for the 12 subjects. For all plots, only the contralateral STN was considered.
Figure 3.
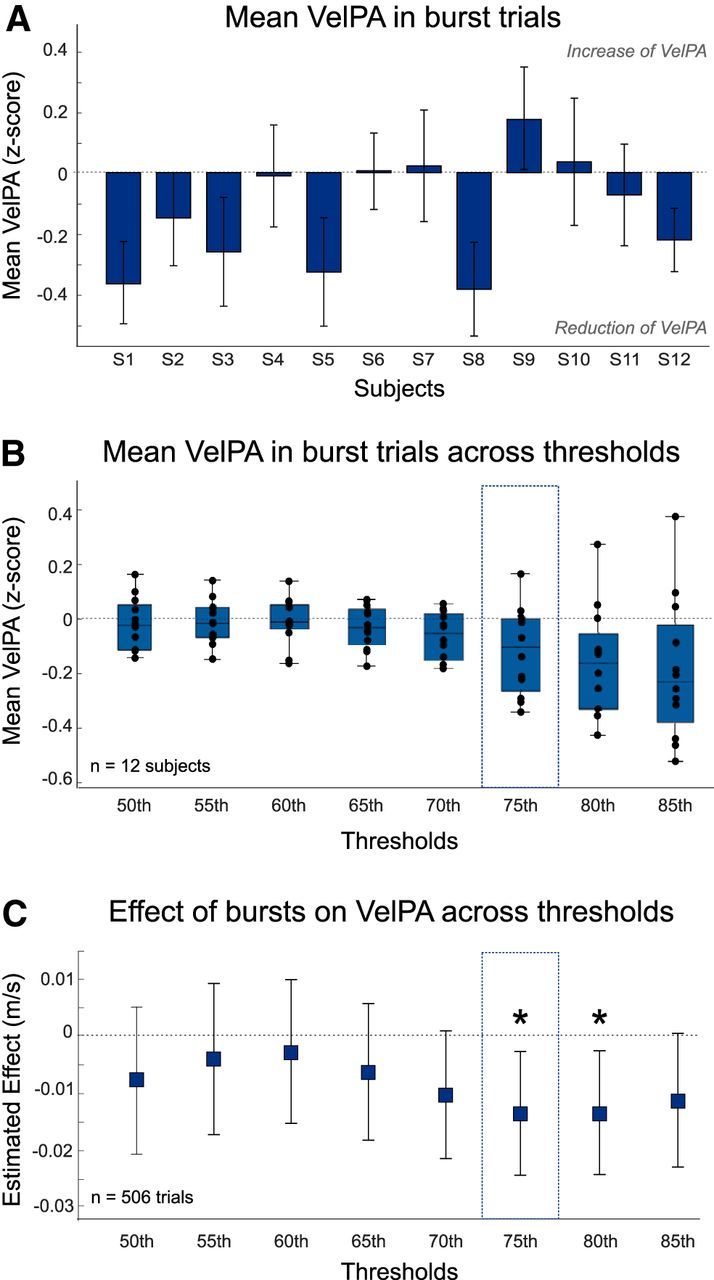
Effect of bursts before and overlapping with the GO cue on the amplitude of the peak velocity and impact of burst detection threshold. A, Mean peak velocity in burst trials normalized (z score) to the mean velocity of all trials for all subjects. A negative value indicates a reduction of peak velocity in burst trials. Trials are divided according to the presence of a burst in a 600 ms window before the GO cue where bursts are only included if more than half of their duration falls in the time window. Bursts were defined with the default threshold of 75th percentile. B, Impact of burst detection threshold on the peak velocity reduction. For each subject, the velocity peak of each trial is normalized (z scores) as described for A. C, Estimated effects and 95% CIs derived from the linear mixed-effects models testing the impact of bursts occurring before or overlapping with the GO cue on peak velocity. Burst detection thresholds stop at 85th as too few trials with bursts were identified for the next 90th threshold. For the modeling, the peak velocities were power transformed (see Materials and Methods). *Significant model (p < 0.05).
LFP analysis: extraction of burst features.
To determine the influence of STN bursting activity on motor performance, we first considered a window from −600 ms to the GO cue (see Fig. 1A). Based on the beta power profiles and the mean intertrial interval, the duration of the window was set to 600 ms to avoid any overlap with the end of the previous trial and ensure that beta rebound of that previous movement was excluded. On average, across subject, the delay between the end of the last movement and the GO cue was 1.88 ± 0.07 s. For each subject and STN, the number of bursts in the window was calculated by keeping only bursts with more than half of their duration in the window. This meant that some bursts could overlap with the presentation of the GO cue. Each trial with at least one burst in the window was labeled as “burst trial.” All other trials were labeled as “no-burst trials.”
To characterize the impact of bursts on the next movement, we then extracted their main features: amplitude, duration, and timing. For trials with more than one burst before and/or overlapping with the GO cue, only the last burst was considered. The burst amplitude was calculated by averaging the power value of each time point exceeding the burst detection threshold of 75th percentile. The burst timing corresponded to the time between the termination point of the beta burst and the GO cue. Importantly, the timing could be negative if the termination point occurred before the GO cue, or positive if it occurred after the GO cue.
The effect of the timing of bursts was further explored by testing the impact of the presence of bursts in short time windows of 50 ms (bins). Based on our results, bins were defined relative to the GO cue from −400 ms to 200 ms. The bin (200 ms:250 ms) was not included due to the small number of bursts observed for some subjects (<3 bursts for 3 subjects) due to the typical premovement beta desynchronization (see Fig. 2). For each bin, each single trial was labeled with a “1” if at least one time point of the bin exceeded the burst detection criteria.
Bursts in lower- and higher-frequency bands.
To confirm the specificity of effects to the beta band, similar analyses were performed in two other frequency ranges: the alpha range and the low gamma range. For both, bursts were defined in a 6 Hz band derived by shifting the individually defined beta peak frequency up or down. The low gamma range was derived in each subject by adding 20 Hz to the frequency of their beta peak. This avoided any overlap with the high beta band (lower limit of the low gamma range >30 Hz in all subjects). Across subjects, the selected mean low gamma frequency band was centered on 39.6 ± 1.3 Hz. For the theta/alpha range, we could not systematically subtract the same number from each individual's beta peak frequency as this resulted in low-frequency peaks ranging from the δ to the low beta range. Thus, to avoid this heterogeneity and constrain all the frequency peaks in the alpha range, the same frequency band was considered for each subject (8–12 Hz). Then all bursts analyses were performed as previously described for the beta band.
Statistical analysis.
Statistical analyses were performed using the free software R (version 3.3.1). We used the nlme package (Pinheiro et al., 2018) to perform linear mixed-effects models of the single-trial relationship between beta oscillations and behavioral performance. To correct the non-normality of the dependent variables, the RTs were log-transformed and the peak velocities were raised by the λ exponents identified by a Box-Cox procedure (power transformation). The normal distribution of each variable was then visually inspected with quantile-quantile plots and histograms of distribution. All models were estimated by the method of maximum likelihood and included random intercept for subjects, to allow different intercepts for each subject capturing individual differences.
To explore the effect of bursts that had more than half of their duration in the 600 ms time window before the GO cue, we first defined the presence of a burst (trials labeled with 1 or 0) as fixed effect and tested its impact on each behavioral parameter separately (RT and VelPA). Second, if the presence of a burst had a significant impact on a motor parameter, we performed a new linear mixed-effects analysis to evaluate the influence of the burst features. To this end, we entered each burst feature separately (burst amplitude, duration, and timing) as individual factors. When multiple features significantly contributed to the prediction but were correlated to each other, the different models were compared based on the Akaike's Information Criterion and the correlation between the predicted and actual measured values (r2). If the predictors were not correlated, a model including all significant factors was compared with the model that included only one factor to assess whether the model's improved fit to the data merited the added complexity associated with the inclusion of that component (likelihood ratio test).
For the binning procedure, linear mixed-effect models were estimated with the presence of a burst in each bin as fixed factor and the velocity peak or the RT as dependent variables. For all models, the residuals plots were visually inspected to control for any obvious deviation from homoscedasticity or normality. Multiple comparisons were corrected for using the false discovery rate procedure (Benjamini and Hochberg, 1995).
Results
In the present study, our principal goal was to explore the within-subject relationship between transient beta oscillations and motor performance in treated PD patients. To do so, we performed single-trial analysis by focusing on the effects of premovement beta bursts on two motor parameters: the RT and the peak velocity.
Behavioral results
Subjects performed 50 reaching movements by controlling a joystick with their right hand to move a red cursor from a starting position in the center of the monitor to one of three green targets displayed on the screen (Fig. 1A). They were instructed to respond as fast as possible after the GO cue (target appearance) and to perform ballistic movements. The velocity profiles were two-peaked with the first peak corresponding to the outgoing movement and the second one to the joystick release, which resulted in the cursor returning to the center (Fig. 1B). For each single trial, the RT and the peak velocity of the outgoing movement were extracted (Fig. 1B, inset). These were averaged across trials for each subject and then averaged across subjects. Mean RT and peak velocity were 413 ± 21 ms (314–533 ms; Fig. 1E) and 0.27 ± 0.02 m/s (0.14–0.4 m/s; Fig. 1C), respectively. These behavioral results based on subject averaged data reflect the intersubject variability but ignore the trial-by-trial variability in behavior that may or may not be linked to the dynamics of beta oscillations in the STN. The within-subject variability is illustrated in Figure 1D and can be quantified by the coefficient of variation (CV), computed for each subject across trials. Across subjects, the CV for the RT was 20.7 ± 1% (14%–28%; Fig. 1E) and 22.4 ± 1.9% for the peak velocity (14%–40%; Fig. 1C).
Beta burst characteristics
As illustrated in Figure 2A, beta bursts were defined as beta amplitude exceeding the 75th percentile threshold of beta power in a 6 Hz frequency band centered on the individual beta frequency peak (see Materials and Methods). Across all subjects, the mean burst frequency was centered on 19.6 ± 1.3 Hz for the left STN and 18.7 ± 1.1 Hz for the right STN. The mean duration of beta bursts across subjects was 207.6 ± 16.2 ms and their mean amplitude was 1.45 ± 0.04 a.u. (Fig. 2C). The mean burst duration is similar to the burst duration previously reported in PD patients ON medication, in contrast to the longer bursts observed OFF medication (274 and 406 ms, respectively, in Tinkhauser et al., 2017b). The slight difference between our results and this previous report might be due to the smoothing of the LFP signals applied in the latter (0.2 s in Tinkhauser et al., 2017b). On average, bursts longer than 600 ms, which have been previously correlated with clinical impairment in PD patients (Tinkhauser et al., 2017a, b), comprised 6.1 ± 3.2% of the total burst time and 2.2 ± 1% of total number of beta bursts. The amplitude of beta bursts increased with burst duration, with a significant positive correlation observed for all the subjects (p < 0.05, r = 0.42 ± 0.04 across subject; for one example subject, see Fig 2B,C).
Presence of beta bursts before and overlapping the GO cue reduces the peak velocity of the following movement
The first question we asked was whether the presence of beta bursts before the GO cue affects the following movement. To this end, bursts were considered in a temporal window beginning 600 ms before the GO cue to avoid inclusion of the beta rebound typically observed at the end of the last movement. Across subjects, the mean delay between the end of the last movement and the GO cue was 1.88 ± 0.07 s. We included bursts with more than half of their duration in the 600 ms time window, which meant that some bursts could overlap the presentation of the GO cue. Across all subjects, at least one burst was observed in the window for 60 ± 4% of all trials. Trials with a burst were labeled with a “1” (300 burst trials across all subjects) and trials without any burst with a “0” (206 no burst trials). To explore the impact of bursts on motor performance within each subject, we performed linear mixed-effects analyses with fixed effects describing the relationship between the presence of a burst and each of the two movement parameters separately (RT and peak velocity).
The presence of a burst in the 600 ms window before the GO cue resulted in a significant difference in the peak velocity of the next movement (b = −0.0135, t(493) = −2.4, p = 0.016; Table 2). The direction of the relationship (b < 0) indicated that trials with bursts in this window were associated with lower velocities. To corroborate and visualize this effect, average peak velocities of trials in which bursts occurred (normalized to all trials) were plotted for each subject (Fig. 3A). The effect with velocity was selective so the presence of a burst in this time window did not affect RT (p = 0.31). Moreover, the relationship between peak velocity and burst occurrence was confined to the STN contralateral to the active limb because the model with ipsilateral beta bursts was not significant (p = 0.75). The relationship with velocity was maintained regardless of whether bursts in the contralateral STN were defined with a 75th or 80th percentile threshold (80th; b = −0.014, t(493) = −2.4, p = 0.02; Fig. 3C). Hereafter, we limit further analysis to bursts determined using our default 75th percentile threshold.
Table 2.
Summary of linear mixed-effects modeling results for peak velocity and RTa
| Dependent variable | Predictors | Estimated effects | t | p | AIC | R2 |
|---|---|---|---|---|---|---|
| Peak velocity | Burst presence | −1.35E-02 | −2.41 | 0.0163* | −1363.4 | 0.56 |
| Power transformed | Burst amplitude | −1.00E-02 | −3.19 | 0.0015* | −1367.7 | 0.57 |
| Burst duration | −5.00E-05 | −2.07 | 0.0394 | −1361.8 | — | |
| Burst timing | −3.12E-05 | −2.76 | 0.0061* | −1365.1 | 0.56 | |
| Mean beta power | −1.28E-02 | −2.16 | 0.0313 | −1362.2 | 0.56 | |
| Burst amplitude (only burst trials) | −1.32E-02 | −2.49 | 0.0135* | −804.2 | 0.60 | |
| RT | Burst presence | 2.07E-02 | 1.03 | 0.3054 | −72.7 | — |
| Log transformed | Burst amplitude | 1.75E-02 | 1.55 | 0.1128 | −74.1 | — |
| Burst duration | 9.00E-05 | 0.99 | 0.3204 | −72.6 | — | |
| Burst timing | 9.80E-05 | 2.34 | 0.0168* | −77.4 | 0.42 |
aThe presence and parameters of beta bursts in the 600 ms time window before the GO cue was used as predictors for the modeling. Bursts were included in the model if more than half of their duration was in the 600 ms time window. When more than one burst was found in the time window, the amplitude, duration, and timing were extracted from the last burst (the burst closest to the GO). If not mentioned, models included all the trials (506 trials). AIC, Akaike's Information Criterion.
*Significant model after FDR correction (p < 0.05).
Amplitude of the burst before or overlapping the GO cue also reduces the velocity of the following movement
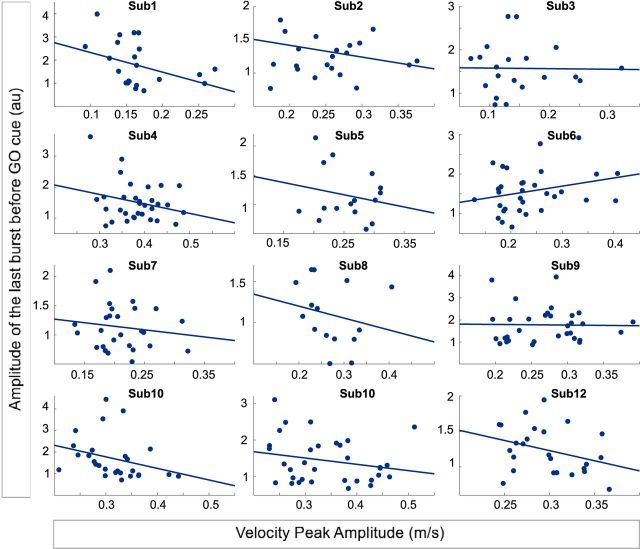
The fact that the peak velocity was slower when preceded by bursts, defined as beta power exceeding a high threshold, raises the possibility that the amplitude of episodes of beta activity matters. This hypothesis was further supported by the greater peak velocity reduction when higher thresholds were used to define bursts (Fig. 3B). Accordingly, we specifically tested whether, when a burst occurs, its amplitude further influences velocity in the following movement. To deal with trials for which more than one burst was found in the pre-GO time window, we only considered the last beta burst in the window (the burst closest to the GO cue). Where more than one burst occurred within the window of interest (29% of trials), the last bursts were no different in amplitude to earlier bursts (t(10) = 0.09, p = 0.9). Our model confirmed that higher-amplitude beta bursts before or overlapping the GO cue were associated with a lower peak velocity in the following movement (b = −0.01, t(493) = −3.2, p = 0.0015). The effect was again specific for the contralateral STN (ipsilateral STN, p = 0.78) and for the velocity peak (RT, p = 0.11). To illustrate the relationship between burst amplitude and peak velocity, Figure 4 shows scatterplots from each subject.
Figure 4.
Single-trial data in individual subjects illustrating the relationship between last burst amplitude and peak velocity. The linear mixed-effects model showed a negative relationship between the amplitude of the last burst before or overlapping the GO cue, and the peak velocity (25 ± 1.8 burst trials per subject; b = −0.013, t(287) = −2.5, p = 0.014). Only the burst trials of the contralateral STN are considered.
Critically, we also confirmed that the effect was specific to burst amplitude, and not secondary to the mean beta power over the same 600 ms window in each trial. Whereas a similar relationship between mean power and velocity could be observed when all trials were included in the model (506 trials, b = −0.013, t(493) = −2.2, p = 0.03), the model was no longer significant after FDR correction (p corrected = 0.06, Table 2). In addition, a model that only considered beta power in no-burst trials was not significant (206 trials, 17 ± 1.7 trials per subject; t(193) = 0.13, p = 0.9). This result suggested that subthreshold beta power (<75th percentile amplitude) does not contribute to the behavioral outcome. In contrast, the last burst amplitude still predicted the velocity when only burst trials were entered in the model (300 trials; 25 ± 1.8 trials per subject; b = −0.013, t(287) = −2.5, p = 0.014, Table 2).
In addition to the burst amplitude, we also extracted the duration of the last burst before the GO cue, which was highly correlated with the burst amplitude (r = 0.77, p < 0.001 across all trials). As an individual factor, the burst duration revealed a weak relationship with the peak velocity (b = −0.005, t(493) = −2.1, p = 0.04), which, however, did not survive multiple-comparisons corrections (corrected p = 0.07). This weaker relationship might be explained by the smaller range of burst duration compared with the range of burst amplitude (Fig. 2C).
When is motor performance most vulnerable to beta bursts?
To explore when precisely velocity was most affected by the occurrence of a beta burst, we next considered their timing. To this end, we defined the timing of the last burst beginning before the GO cue as the delay between its termination point and the GO cue. Importantly, this termination point could occur before (negative delay) or after the GO cue (positive delay). There was a clear relationship between the termination of the last burst before the GO cue and the reduction of velocity peak (b = −0.031, t(493) = −2.8, p = 0.006; Table 2) whereby bursts ending close to or shortly after the GO cue were more likely to slow down movement velocity.
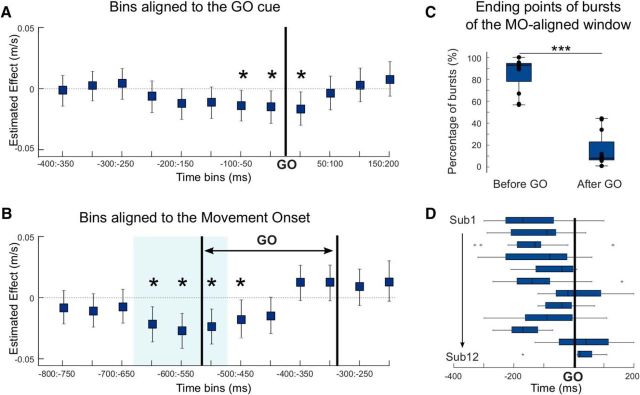
These results suggest a limited window in which bursts affect movement velocity. To test this hypothesis further, we considered the effect of bursts in bins of 50 ms duration around the GO cue. As can be seen in Figure 2, the post-GO cue window corresponds to the time period in which the premovement beta desynchronization is typically observed. Hence, the probability of a burst drops rapidly to reach its minimum around the movement onset. We therefore considered 12 bins from −400 ms to 200 ms around the GO cue and stopped at 200 ms, as this was the end of the last bin (150 ms:200 ms) where bursts were present in at least 3 trials for each subject. The number of burst trials per bin comprised between 83 (150:200 ms; 7 ± 0.8 per subject) and 135 trials (−400:−350 ms, 11.3 ± 1 per subject). The results confirmed the timing effect and revealed three significant bins around the GO cue (b = −0.014, t(493) = −2.2, p = 0.032; b = −0.015, t(493) = −2.1, p = 0.035; b = −0.016, t(493) = −2.4, p = 0.018, for the three bins, respectively), which, however, did not survive multiple-comparisons corrections (Fig. 5A). Yet, these results suggest that bursts had to terminate just before or after the GO cue to have an effect on the peak velocity of the following movement. They also had to occur in the contralateral STN, as the same binning procedure revealed that bursts in the ipsilateral STN failed to correlate with velocity (p > 0.05 for all bins).
Figure 5.
Bursts affect the velocity peak when they are in a critical peri-GO window, with a maximal effect when realigned to movement onset. A, Estimated effects and 95% CIs derived from the linear mixed-effects model testing the impact of bursts in 50 ms bins on peak velocity. Bins are defined relative to the GO cue, which is indicated by the bold vertical line. B, Estimated effects and 95% CIs derived from the same linear mixed-effects model when bins were defined relative to the movement onset. Pair of bold vertical lines indicates the range in which the GO cue would have fallen. For the modeling, the velocity peaks are power transformed (see Materials and Methods). *Significant model (p < 0.05) when bins are considered in isolation. Blue shading represents significant bins after FDR correction. C, D, The majority of the beta bursts occurring in the significant window aligned to movement onset (B, blue shading) end before the GO cue or right after (yet still have more than half of their duration before the GO). C, The percentage of these across subjects is shown (Before GO). D, The timing of the burst termination points for each subject. ***p < 0.001.
Based on these results, however, the lack of effect previously observed for the subthreshold mean beta power over the 600 ms pre-GO window could indeed be due to the size of the time window that excluded power at and just after the GO cue, and did not allow for a differential effect closer to the GO cue. Therefore, to confirm the selective effect of bursting, we also tested the relationship between velocity peak and mean beta power in each of the 12 time bins around the GO cue. When keeping all trials, four significant bins were observed from −200 ms to the GO cue (b = −0.005, t(493) = −2.1, p = 0.037; b = −0.007, t(493) = −2.6, p = 0.009; b = −0.008, t(493) = −2.5, p = 0.014; b = −0.007, t(493) = −2.2, p = 0.032 for the four bins, respectively), but as for the presence of a burst, none was still significant after FDR correction. Moreover, when removing the trials with bursts, the subthreshold mean power failed to predict the velocity peak (p > 0.05 for all bins). It was unlikely that this absence of relationship with beta power was related to small sample size as the number of no burst trials by subject was on average between 32 ± 2 and 35.5 ± 1.8 for each bin (i.e., ≥3 times the number of burst trials).
The same binning procedure was then applied with bins defined relative to the movement onset, and the results revealed a larger critical window with three significant bins after multiple-comparisons corrections (Fig. 5B; b = −0.019, t(493) = −3, p = 0.003; b = −0.024, t(493) = −3.7, p < 0.001; b = −0.02, t(493) = −3.2, p = 0.001; for the three bins, respectively). The bin (−500:−450 ms) was significant when considered in isolation (b = −0.015, t(493) = −2.2, p = 0.03) but not after multiple-comparisons corrections. This result and the bigger estimated effects observed for the movement onset alignment compared with GO cue alignment (Fig. 5A,B) suggest that bursts had to fall at ∼650–500 ms before the movement to impact velocity. Considering the RTs (Fig. 1E), these same bursts might therefore overlap with the GO cue when trials were aligned to the latter, although here the relationship was weaker (Fig. 5A). To clarify this, we determined the endpoints of the beta bursts occurring in the whole significant window aligned to the movement onset (Fig. 5B, blue shading). The results revealed that most of them occurred before the GO (endpoint before the GO or shortly after, sign-rank test, Z = 78, p < 0.001; Fig. 5C,D).
In summary, beta bursts present in the contralateral STN just before or around the time of the GO cue reduced the peak velocity of the subsequent movement. This effect was likely secondary to the timing of these bursts with respect to the movement itself. The biggest effect of beta bursts on velocity was observed when these were aligned to movement onset and not GO cue presentation. Of note, this effect of beta bursts falling at ∼650–500 ms before movement onset was time-limited, and bursts occurring after this, but still before movement onset, had no significant effect on velocity (Fig. 5B).
Bursting after the GO cue affects RT
The binning procedure reported above was repeated for RT and revealed significant effects of the presence of beta bursts upon RTs in all four bins after the GO cue (Fig. 6A; b = 0.06, t(493) = 2.5, p = 0.01; b = 0.09, t(493) = 3.4, p < 0.001; b = 0.08, t(493) = 3.3, p = 0.001; b = 0.07, t(493) = 2.8, p = 0.005 for the four bins, respectively). RTs were longer in trials in which beta bursts were present in the 200 ms after the GO signal (Fig. 6B). These results are in line with the significant relationship observed between the timing of bursts in the pre-GO window and the RT (b = 9.80E-05, t(493) = 2.4, p = 0.02; Table 2), which suggested that bursts had to end after the GO cue to affect the RT. This effect was again confined to the contralateral STN (ipsilateral STN p > 0.05 for all bins). To confirm the selective effect of bursting we also tested the relationship between RT and mean beta power in each bin. When all trials were included, the three bins from 50 ms to 200 ms showed a significant effect (b = 0.03, t(493) = 2.5, p = 0.012; b = 0.03, t(493) = 2.9, p = 0.004; b = 0.02, t(493) = 2.03, p = 0.04, for the 3 bins respectively), which disappeared after multiple-comparison corrections and when only trials without bursts were considered.
Figure 6.
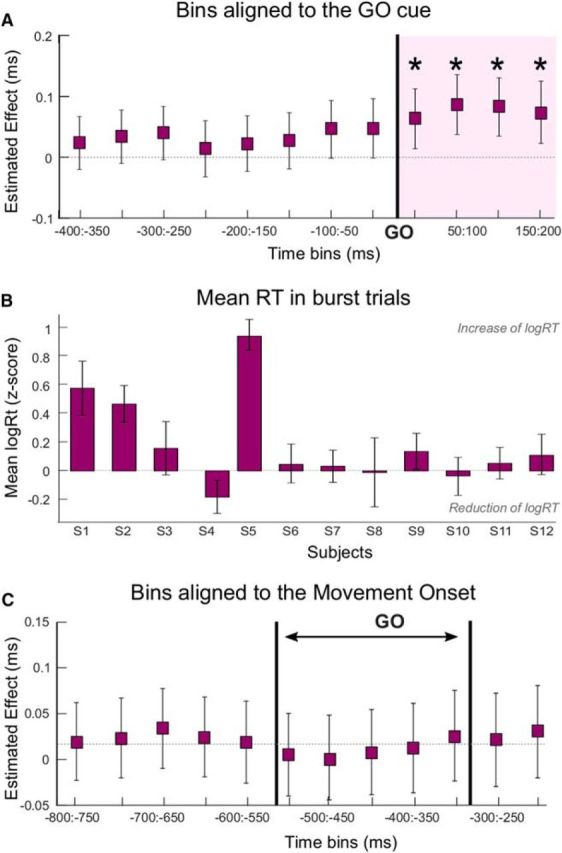
Bursts after the GO cue increase the RT, with a maximal effect when realigned to GO. A, Estimated effects and 95% CIs derived from the linear mixed-effects model testing the impact of bursts in 50 ms bins on RT. Bins were defined relative to the GO cue, which is indicated by the bold vertical line. B, Mean RTs in burst trials normalized (z score) to the mean RT of all trials for all subjects. A positive value indicates an increase in RT in burst trials. Trials are divided according to the presence of a burst in the 200 ms after GO. C, Estimated effects and 95% CIs derived from the linear mixed-effects model when bins were defined relative to the movement onset. Pair of bold vertical lines indicates the range in which the GO cue would have fallen. For the modeling, the RTs were log transformed. *Significant model (p < 0.05) when bins are considered in isolation. Purple shading represents significant bins after FDR correction.
We also tested the effect of bursts when the bins were aligned to the movement onset. In contrast to the bursting effect on velocity, the effect on RT was then no longer observed (Fig. 6C; p > 0.05 for all bins). Thus, the effect of bursts on RT was determined by their precise timing with respect to the GO cue, and not unlike the effect on velocity, on the timing with respect to movement onset. Still, the presence of bursts several 100 milliseconds before movement onset already reflected differences in RT. This effect was also time-limited, as the probability of bursts dramatically reduced soon after the GO cue (Fig. 2A).
Effects of bursts on motor performance are confined to the beta band
To test the specificity of the described effects to the beta band, we tested the impact of bursting activity on motor performance in two other frequency bands. The first was the alpha frequency range with a similar 8–12 Hz frequency band considered for each subject, and therefore sparing the lower beta band. Activity in the alpha band was again thresholded at the 75th percentile. The mean duration of bursts in this band was 342.3 ± 4.8 ms, and as for beta bursts, the amplitude of the alpha bursts increased with the burst duration (p < 0.05 for all subjects, across subject r = 0.37). However, the presence of an alpha burst in the contralateral STN before or overlapping with the GO cue was not significantly related to the motor performance (155 bursts trials, p > 0.05 for both velocity and RT).
The second frequency band was in the low gamma range and was derived by adding 20 Hz to the frequency of the beta peak in each subject. The 6 Hz band was centered on 39.6 ± 1.3 Hz, and again did not overlap with the beta band (>30 Hz for all subjects). The mean duration of low gamma bursts was 86.2 ± 2.4 ms and, as for the alpha and beta bursts, significantly increased with the burst amplitude (p < 0.05 for all subjects, across subject r = 0.3). The linear mixed-effects analysis revealed no significant relationship between the low gamma bursts in the contralateral STN before and overlapping the GO cue and the motor performance (415 bursts trials, p > 0.05 for both the velocity and the RT). Together, these results indicate that the effects of bursts on both the velocity and the RT were specific to the beta frequency band.
Discussion
Our results showed that, in treated PD patients, STN beta bursts occurring before movement are associated with measurable changes in motor performance within subjects. First, beta bursts present in a time-limited window around the GO cue reduce the peak velocity of the subsequent movement, and this effect is further amplified by the amplitude of the burst. Second, beta bursts present immediately after the GO cue increase the RT. Importantly, we confirmed that the variations in motor performance were better explained by the beta bursts than averaged beta power and that the effect of bursts was limited to the STN contralateral to the active limb and confined to the beta frequency band.
Beta bursts ON medication are briefer than OFF medication
The transient nature of beta oscillations is now well established and observed at both the cortical (Feingold et al., 2015; Lundqvist et al., 2016; Sherman et al., 2016; Shin et al., 2017) and subcortical levels (Bartolo and Merchant, 2015; Feingold et al., 2015). The duration of beta bursts may serve to distinguish pathological from physiological beta activity in patients with PD (Tinkhauser et al., 2017a, b). Beta bursts are more often longer in untreated patients compared with ON medication, and the increased probability of bursts longer than 600 ms positively correlates with clinical impairment. For instance, OFF medication, 40% of the total burst duration and 20% of the total number of defined bursts were longer than 600 ms (Tinkhauser et al., 2017a). This compares with 6% of the total burst duration and 2% of the total number of bursts in the present study where patients were ON medication. Our results show that beta bursts, even when of short duration, can also affect motor performance when they happen in a specific time window relative to the movement. These findings lead us to posit that the predominant brevity of beta bursts could be important in normal beta-band function (Feingold et al., 2015; Lundqvist et al., 2016; Shin et al., 2017).
Beta bursts and their timing predict behavioral dynamics
According to the time window in which they fall, beta bursts in the contralateral STN were associated with reduction of movement velocity or prolongation of RTs. These results add to the growing evidence that elevated beta oscillations are linked to slowing of movement.
Clinical observations have related gross movement slowing, termed bradykinesia, to exaggerated oscillatory beta band synchronization (Kühn et al., 2006; Ray et al., 2008) and to longer and higher-amplitude beta bursts (Tinkhauser et al., 2017a, b). In PD patients, STN stimulation at 20 Hz reduced movement velocity in a tapping task (Chen et al., 2007) and contraction velocity in a gripping task (Chen et al., 2011). Similarly, transcranial alternating current stimulation at 20 Hz applied over the motor cortex of healthy participants slowed down the initial and peak velocity of voluntary movements (Pogosyan et al., 2009).
The prolongation of RT associated with beta bursts present just after the GO cue is consistent with previous results showing that short latencies of the premovement desynchronization in STN beta power are associated with short RTs across PD patients (Kühn et al., 2004) and even across single trials within individual subjects, independent of the medication state (Williams et al., 2005). This is in line with the observation that high-amplitude beta activities in motor cortical regions during critical preparatory periods delay movement onset in nonhuman primates performing a neurofeedback reaching task (Khanna and Carmena, 2017) or in healthy participants performing joystick tasks (Boulay et al., 2011; McFarland et al., 2015).
Time-dependent effects of beta bursts
Consistent with previous findings, our results demonstrate that beta bursts relate to differences in motor performance way beyond their termination (Gilbertson et al., 2005; Androulidakis et al., 2008; Herz et al., 2018). For example, Shin et al. (2017) found that beta bursts have an effect on detection/attentional performances that outlasted their duration by ∼200 ms. Our results suggest that the impact of bursts upon function strongly depends on the time window in which they fall relative to the movements, presumably because processing related to different functions dominates in different time windows throughout a task. The effect of beta bursts on RT was observed immediately following the GO cue, which informs the subjects about the direction of the reach. This information may be contrasted with evidence drawn from earlier trials about the probabilities of targets, given only three options were available. Where expectations and instructions do not coincide, it may be advantageous to delay responses to avoid wrong prepotent responses. A time-limited delaying effect of beta bursts has also been reported in the STN of untreated PD patients in a brief post-GO cue time window (∼100 ms) in the setting of more explicitly conflicting information (Herz et al., 2018). The latter, together with the trial-by-trial relationship between cortical beta bursts and detection performance reported by Shin et al. (2017), also suggests that beta synchrony is not exclusively motoric in its consequences (Engel and Fries, 2010).
In contrast to the effect on RT, beta bursts affecting movement velocity were better aligned to movement onset than to the GO cue. Surprisingly, most of these bursts already terminated before the target was specified (GO cue). As response vigor is not necessarily dependent on the response direction, it could be determined before the GO cue, particularly when the little variation in the timing of trials allows temporal expectancy, as in our paradigm. Accordingly, beta bursts before the GO cue may impact the specification of the movement vigor, previously associated with the STN (Turner and Desmurget, 2010). Thus, movement triggered during periods of elevated beta synchrony (i.e., with bursts estimated by finger microtremor) are slowed compared with movements that are randomly triggered, and a negative correlation between bursts of cortical synchrony and response acceleration may similarly occur around or before the cue (Gilbertson et al., 2005).
Here we showed that brief episodes of oversynchronization, as quantified by beta bursts, explained variations in behavior better than averaged beta power before movements. By identifying the precise time window relative to movements in which the presence of beta burst can have a modulatory effect on the motor performance, our results offer new insights on the pathology of PD. The lack of modulation in the timing of beta bursts relative to movement may contribute to reduced movement-related desynchronization previously observed in averaged data (Doyle et al., 2005).
Beta bursts may have functional significance through excessive synchronization
In the above discussion, we have assumed that bursts can be considered discrete events whose impact on motor performance increases with amplitude above a threshold value. The alternative is that instantaneous beta amplitude impacts on motor performance as a continuous, linear variable, with threshold crossings merely representing stochastic deviations in a random signal. The present study alone cannot categorically distinguish between these two possibilities, although the lack of an effect of instantaneous beta amplitude in trials without suprathreshold activity (i.e., bursts) in the critical time windows would be more in favor of the former interpretation. Additionally, the previously reported frequency-selective temporal overlapping of beta bursts and phase synchronization between sites that respectively exceed that expected by chance and that present in nonburst periods also serves to suggest that beta bursts may have a special significance (Tinkhauser et al., 2017a,b, 2018b).
How might a nonlinearity arise to underpin the behavioral associations confined to high-amplitude bursts? Here it should be noted that the amplitude of LFP activity in the beta band is a proxy for the degree of local synchronization of neural elements in this frequency band. Synchronization is often viewed as advantageous as it increases the signal-to-noise ratio of neural communication (Hanslmayr et al., 2012; Brittain and Brown, 2014). However, as synchronization increases, this effect will eventually be offset by the inherent restriction in information coding capacity of the circuit entailed by synchronization across its elements (Mallet et al., 2008; Brittain and Brown, 2014). At that point, ever increasing synchronization may have an increasingly negative effect on the performance of the circuit. We speculate that it is the crossing of this point that leads to the behavioral associations of bursts demonstrated here. This, however, does not necessarily mean that such behavioral effects are uniformly deleterious. Brief increases in beta activity in the STN have been linked to the beneficial delaying of responses in the presence of conflicting information (Herz et al., 2018). Thus, there may be contexts in which the dynamic control of network performance by varying beta synchrony might represent a means of adjusting behavior according to context on a trial-by-trial basis (Feingold et al., 2015; Leventhal et al. 2012). Intriguingly, the impaired event-related desynchronization reported in PD patients OFF medication implies that the occurrence of beta bursts may be less modulated by movements when dopaminergic activity is diminished (Doyle et al., 2005). Taking these observations together, we posit that beta bursts whose presence, size, and duration are modulated by context may have a physiological role, but that this modulation may fail in untreated PD. Further studies are warranted to test and explore this framework.
Limitations
The present study was performed in patients with PD; therefore, it remains uncertain whether our findings apply to healthy participants in whom such intracranial LFPs cannot be recorded. The patients we studied were ON medication and were able to perform the task without any observable impairment. Analysis of group data confirmed that they have similar RTs to healthy volunteers performing the exact same task (sign-rank test, p = 0.38) but did indicate that patients' movements were significantly slower (sign-rank test, p < 0.001). Overall, a key unanswered question remains whether the correlations observed here between STN beta bursts and motor performance reflect a physiological neural correlate of reaching behavior or are linked to the underlying pathology.
Footnotes
This work was supported by Medical Research Council MR/P012272/1 and MC_UU_12024/1, the Rosetrees Trust, and National Institute of Health Research Oxford Biomedical Research Centre. G.T. was also supported by the Swiss Parkinson Association.
The authors declare no competing financial interests.
References
- Androulidakis AG, Brücke C, Kempf F, Kupsch A, Aziz T, Ashkan K, Kühn AA, Brown P (2008) Amplitude modulation of oscillatory activity in the subthalamic nucleus during movement. Eur J Neurosci 27:1277–1284. 10.1111/j.1460-9568.2008.06085.x [DOI] [PubMed] [Google Scholar]
- Baker SN, Olivier E, Lemon RN (1997) Coherent oscillations in monkey motor cortex and hand muscle EMG show task-dependent modulation. J Physiol 501:225–241. 10.1111/j.1469-7793.1997.225bo.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bartolo R, Merchant H (2015) β oscillations are linked to the initiation of sensory-cued movement sequences and the internal guidance of regular tapping in the monkey. J Neurosci 35:4635–4640. 10.1523/JNEUROSCI.4570-14.2015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benjamini Y, Hochberg Y (1995) Controlling the false discovery rate: a practical and powerful approach to multiple testing. J R Stat Soc B 57:289–300. [Google Scholar]
- Boulay CB, Sarnacki WA, Wolpaw JR, McFarland DJ (2011) Trained modulation of sensorimotor rhythms can affect reaction time. Clin Neurophysiol 122:1820–1826. 10.1016/j.clinph.2011.02.016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brittain JS, Brown P (2014) Oscillations and the basal ganglia: motor control and beyond. Neuroimage 85:637–647. 10.1016/j.neuroimage.2013.05.084 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cassidy M, Mazzone P, Oliviero A, Insola A, Tonali P, Di Lazzaro V, Brown P (2002) Movement-related changes in synchronization in the human basal ganglia. Brain 125:1235–1246. 10.1093/brain/awf135 [DOI] [PubMed] [Google Scholar]
- Chen CC, Pogosyan A, Zrinzo LU, Tisch S, Limousin P, Ashkan K, Yousry T, Hariz MI, Brown P (2006) Intra-operative recordings of local field potentials can help localize the subthalamic nucleus in Parkinson's disease surgery. Exp Neurol 198:214–221. 10.1016/j.expneurol.2005.11.019 [DOI] [PubMed] [Google Scholar]
- Chen CC, Litvak V, Gilbertson T, Kühn A, Lu CS, Lee ST, Tsai CH, Tisch S, Limousin P, Hariz M, Brown P (2007) Excessive synchronization of basal ganglia neurons at 20 Hz slows movement in Parkinson's disease. Exp Neurol 205:214–221. 10.1016/j.expneurol.2007.01.027 [DOI] [PubMed] [Google Scholar]
- Chen CC, Lin WY, Chan HL, Hsu YT, Tu PH, Lee ST, Chiou SM, Tsai CH, Lu CS, Brown P (2011) Stimulation of the subthalamic region at 20 Hz slows the development of grip force in Parkinson's disease. Exp Neurol 231:91–96. 10.1016/j.expneurol.2011.05.018 [DOI] [PubMed] [Google Scholar]
- Devos D, Szurhaj W, Reyns N, Labyt E, Houdayer E, Bourriez JL, Cassim F, Krystkowiak P, Blond S, Destée A, Derambure P, Defebvre L (2006) Predominance of the contralateral movement-related activity in the subthalamo-cortical loop. Clin Neurophysiol 117:2315–2327. 10.1016/j.clinph.2006.06.719 [DOI] [PubMed] [Google Scholar]
- Doyle LM, Kühn AA, Hariz M, Kupsch A, Schneider GH, Brown P (2005) Levodopa-induced modulation of subthalamic beta oscillations during self-paced movements in patients with Parkinson's disease. Eur J Neurosci 21:1403–1412. 10.1111/j.1460-9568.2005.03969.x [DOI] [PubMed] [Google Scholar]
- Engel AK, Fries P (2010) Beta-band oscillations: signalling the status quo? Curr Opin Neurobiol 20:156–165. 10.1016/j.conb.2010.02.015 [DOI] [PubMed] [Google Scholar]
- Feingold J, Gibson DJ, DePasquale B, Graybiel AM (2015) Bursts of beta oscillation differentiate postperformance activity in the striatum and motor cortex of monkeys performing movement tasks. Proc Natl Acad Sci U S A 112:13687–13692. 10.1073/pnas.1517629112 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischer P, Tan H, Pogosyan A, Brown P (2016) High post-movement parietal low-beta power during rhythmic tapping facilitates performance in a stop task. Eur J Neurosci 44:2202–2213. 10.1111/ejn.13328 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilbertson T, Lalo E, Doyle L, Di Lazzaro V, Cioni B, Brown P (2005) Existing motor state is favored at the expense of new movement during 13–35 Hz oscillatory synchrony in the human corticospinal system. J Neurosci 25:7771–7779. 10.1523/JNEUROSCI.1762-05.2005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hanslmayr S, Staudigl T, Fellner MC (2012) Oscillatory power decreases and long-term memory: the information via desynchronization hypothesis. Front Hum Neurosci 6:74. 10.3389/fnhum.2012.00074 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Herz DM, Little S, Pedrosa DJ, Tinkhauser G, Cheeran B, Foltynie T, Bogacz R, Brown P (2018) Mechanisms underlying decision-making as revealed by deep-brain stimulation in patients with Parkinson's disease. Curr Biol 28:1169–1178.e6. 10.1016/j.cub.2018.02.057 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Horn A, Neumann WJ, Degen K, Schneider GH, Kühn AA (2017) Toward an electrophysiological “sweet spot” for deep brain stimulation in the subthalamic nucleus. Hum Brain Mapp 38:3377–3390. 10.1002/hbm.23594 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ince NF, Gupte A, Wichmann T, Ashe J, Henry T, Bebler M, Eberly L, Abosch A (2010) Selection of optimal programming contacts based on local field potential recordings from subthalamic nucleus in patients with Parkinson's disease. Neurosurgery 67:390–397. 10.1227/01.NEU.0000372091.64824.63 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jenkinson N, Brown P (2011) New insights into the relationship between dopamine, beta oscillations and motor function. Trends Neurosci 34:611–618. 10.1016/j.tins.2011.09.003 [DOI] [PubMed] [Google Scholar]
- Khanna P, Carmena JM (2017) Beta band oscillations in motor cortex reflect neural population signals that delay movement onset. Elife 6:e24573. 10.7554/eLife.24573 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kilavik BE, Zaepffel M, Brovelli A, MacKay WA, Riehle A (2013) The ups and downs of beta oscillations in sensorimotor cortex. Exp Neurol 245:15–26. 10.1016/j.expneurol.2012.09.014 [DOI] [PubMed] [Google Scholar]
- Kühn AA, Williams D, Kupsch A, Limousin P, Hariz M, Schneider GH, Yarrow K, Brown P (2004) Event-related beta desynchronization in human subthalamic nucleus correlates with motor performance. Brain 127:735–746. 10.1093/brain/awh106 [DOI] [PubMed] [Google Scholar]
- Kühn AA, Kupsch A, Schneider GH, Brown P (2006) Reduction in subthalamic 8–35 Hz oscillatory activity correlates with clinical improvement in Parkinson's disease. Eur J Neurosci 23:1956–1960. 10.1111/j.1460-9568.2006.04717.x [DOI] [PubMed] [Google Scholar]
- Leventhal DK, Gage GJ, Schmidt R, Pettibone JR, Case AC, Berke JD (2012) Basal ganglia beta oscillations accompany cue utilization. Neuron 73:523–536. 10.1016/j.neuron.2011.11.032 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lundqvist M, Rose J, Herman P, Brincat SL, Buschman TJ, Miller EK (2016) Gamma and beta bursts underlie working memory. Neuron 90:152–164. 10.1016/j.neuron.2016.02.028 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mallet N, Pogosyan A, Márton LF, Bolam JP, Brown P, Magill PJ (2008) Parkinsonian beta oscillations in the external globus pallidus and their relationship with subthalamic nucleus activity. J Neurosci 28:14245–14258. 10.1523/JNEUROSCI.4199-08.2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marmor O, Valsky D, Joshua M, Bick AS, Arkadir D, Tamir I, Bergman H, Israel Z, Eitan R (2017) Local vs. volume conductance activity of field potentials in the human subthalamic nucleus. J. Neurophysiol. 117:2140–2151. 10.1152/jn.00756.2016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- McFarland DJ, Sarnacki WA, Wolpaw JR (2015) Effects of training pre-movement sensorimotor rhythms on behavioral performance. J Neural Eng 12:066021. 10.1088/1741-2560/12/6/066021 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murthy VN, Fetz EE (1992) Coherent 25- to 35-Hz oscillations in the sensorimotor cortex of awake behaving monkeys. Proc Natl Acad Sci U S A 89:5670–5674. 10.1073/pnas.89.12.5670 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murthy VN, Fetz EE (1996) Oscillatory activity in sensorimotor cortex of awake monkeys: synchronization of local field potentials and relation to behavior. J Neurophysiol 76:3949–3967. 10.1152/jn.1996.76.6.3949 [DOI] [PubMed] [Google Scholar]
- Oostenveld R, Fries P, Maris E, Schoffelen JM (2011) FieldTrip: open source software for advanced analysis of MEG, EEG, and invasive electrophysiological data. Comput Intell Neurosci 2011:156869. 10.1155/2011/156869 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pfurtscheller G, Lopes da Silva FH (1999) Event-related EEG/MEG synchronization and desynchronization: basic principles. Clin Neurophysiol 110:1842–1857. 10.1016/S1388-2457(99)00141-8 [DOI] [PubMed] [Google Scholar]
- Pinheiro J, Bates D, DebRoy S, Sarkar D (2018) nlme: linear and nonlinear mixed effects models. R package version 3.1–131.1. https://CRAN.R-project.org/package=nlme.
- Pogosyan A, Gaynor LD, Eusebio A, Brown P (2009) Boosting cortical activity at beta-band frequencies slows movement in humans. Curr Biol 19:1637–1641. 10.1016/j.cub.2009.07.074 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ray NJ, Jenkinson N, Wang S, Holland P, Brittain JS, Joint C, Stein JF, Aziz T (2008) Local field potential beta activity in the subthalamic nucleus of patients with Parkinson's disease is associated with improvements in bradykinesia after dopamine and deep brain stimulation. Exp Neurol 213:108–113. 10.1016/j.expneurol.2008.05.008 [DOI] [PubMed] [Google Scholar]
- Sherman MA, Lee S, Law R, Haegens S, Thorn CA, Hämäläinen MS, Moore CI, Jones SR (2016) Neural mechanisms of transient neocortical beta rhythms: converging evidence from humans, computational modeling, monkeys, and mice. Proc Natl Acad Sci U S A 113:E4885–E4894. 10.1073/pnas.1604135113 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shin H, Law R, Tsutsui S, Moore CI, Jones SR (2017) The rate of transient beta frequency events predicts behavior across tasks and species. ELife 6:e29086. 10.7554/eLife.29086 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Singh A. (2018) Oscillatory activity in the cortico-basal ganglia-thalamic neural circuits in Parkinson's disease. Eur J Neurosci. Retrieved Jan. 30, 2018. doi: 10.1111/ejn.13853. 10.1111/ejn.13853 [DOI] [PubMed] [Google Scholar]
- Tan H, Jenkinson N, Brown P (2014a) Dynamic neural correlates of motor error monitoring and adaptation during trial-to-trial learning. J Neurosci 34:5678–5688. 10.1523/JNEUROSCI.4739-13.2014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tan H, Zavala B, Pogosyan A, Ashkan K, Zrinzo L, Foltynie T, Limousin P, Brown P (2014b) Human subthalamic nucleus in movement error detection and its evaluation during visuomotor adaptation. J Neurosci 34:16744–16754. 10.1523/JNEUROSCI.3414-14.2014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tan H, Wade C, Brown P (2016) Post-movement beta activity in sensorimotor cortex indexes confidence in the estimations from internal models. J Neurosci 36:1516–1528. 10.1523/JNEUROSCI.3204-15.2016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tinkhauser G, Pogosyan A, Little S, Beudel M, Herz DM, Tan H, Brown P (2017a) The modulatory effect of adaptive deep brain stimulation on beta bursts in Parkinson's disease. Brain 140:1053–1067. 10.1093/brain/awx010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tinkhauser G, Pogosyan A, Tan H, Herz DM, Kühn AA, Brown P (2017b) Beta burst dynamics in Parkinson's disease OFF and ON dopaminergic medication. Brain 140:2968–2981. 10.1093/brain/awx252 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tinkhauser G, Pogosyan A, Debove I, Nowacki A, Shah SA, Seidel K, Tan H, Brittain JS, Petermann K, di Biase L, Oertel M, Pollo C, Brown P, Schuepbach M (2018a) Directional local field potentials: a tool to optimize deep brain stimulation. Mov Disord 33:159–164. 10.1002/mds.27215 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tinkhauser G, Torrecillos F, Duclos Y, Tan H, Pogosyan A, Fischer P, Carron R, Welter ML, Karachi C, Vandenberghe W, Nuttin B, Witjas T, Régis J, Azulay JP, Eusebio A, Brown P (2018b) Beta burst coupling across the motor circuit in Parkinson's disease. Neurobiol Dis 117:217–225. 10.1016/j.nbd.2018.06.007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Torrecillos F, Alayrangues J, Kilavik BE, Malfait N (2015) Distinct modulations in sensorimotor postmovement and foreperiod: band activities related to error salience processing and sensorimotor adaptation. J Neurosci 35:12753–12765. 10.1523/JNEUROSCI.1090-15.2015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Turner RS, Desmurget M (2010) Basal ganglia contributions to motor control: a vigorous tutor. Curr Opin Neurobiol 20:704–716. 10.1016/j.conb.2010.08.022 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Williams D, Kühn A, Kupsch A, Tijssen M, van Bruggen G, Speelman H, Hotton G, Loukas C, Brown P (2005) The relationship between oscillatory activity and motor reaction time in the parkinsonian subthalamic nucleus. Eur J Neurosci 21:249–258. 10.1111/j.1460-9568.2004.03817.x [DOI] [PubMed] [Google Scholar]
- Zaidel A, Spivak A, Grieb B, Bergman H, Israel Z (2010) Subthalamic span of β oscillations predicts deep brain stimulation efficacy for patients with Parkinson's disease. Brain 133:2007–2021. 10.1093/brain/awq144 [DOI] [PubMed] [Google Scholar]