Network Mapping with GIMME

Abstract

Network science is booming! While the insights and images afforded by network mapping techniques are compelling, implementing the techniques is often daunting to researchers. Thus, the aim of this tutorial is to facilitate implementation in the context of GIMME, or group iterative multiple model estimation. GIMME is an automated network analysis approach for intensive longitudinal data. It creates person-specific networks that explain how variables are related in a system. The relations can signify current or future prediction that is common across people or applicable only to an individual. The tutorial begins with conceptual and mathematical descriptions of GIMME. It proceeds with a practical discussion of analysis steps, including data acquisition, preprocessing, program operation, a posteriori testing of model assumptions, and interpretation of results; throughout, a small empirical data set is analyzed to showcase the GIMME analysis pipeline. The tutorial closes with a brief overview of extensions to GIMME that may interest researchers whose questions and data sets have certain features. By the end of the tutorial, researchers will be equipped to begin analyzing the temporal dynamics of their heterogeneous time series data with GIMME.

People are unique, complex, and ever-changing, despite the assumptions of homogeneity made by many researchers and statistical analyses (Molenaar, 2004). This is seen when experimental manipulations show an overall effect, but closer examinations reveal that the effect was relatively weak for one subset of individuals and particularly strong for another subset. It is also seen when linear regression analyses fail to detect a relationship between two variables, but additional scrutiny divulges that a relationship actually exists with functional forms (e.g., linear, quadratic, logistic) that differ across people. Interest in network analysis, a set of methods for quantifying interconnectedness among variables, is piquing with increasing acknowledgement of this nuanced and knotty nature of psychological data. Consequently, network conceptualizations of human brain function, behavior, and mental and physical health are becoming more and more prevalent (e.g., Bajardi et al., 2011; Borsboom & Cramer, 2013; Smith, 2012).

Networks are particularly powerful when they are used to delineate the temporal dynamics of a unique system, pushing scientific understanding beyond cross-sectional group averages. Consider the following example (Beltz, Beekman, Molenaar, & Buss, 2013). Sex differences in children’s play behavior are established; boys are more active than girls, and girls play more cooperatively than boys (Blakemore, Berenbaum, & Liben, 2009). Relatively little is known, however, about the dynamics underlying these interactions. Is boys’ activity influenced by the activity of their peers, and how do girls’ affective experiences during cooperation unfold over time? To answer these questions, play dynamics were studied in groups of three or four same-sex children during a 15-minute laboratory session. Each child’s positive affect and vigor of activity were rated on a 1 (none) to 5 (intense) scale every 10 seconds, resulting in time series of 90 ratings for each group. When traditional analyses were conducted that collapsed ratings across children and groups, an expected sex difference was found in positive affect, with girls displaying higher levels than boys, with the sex difference in activity level not reaching statistical significance. But, when the same ratings were entered into a time series network analysis (called unified structural equation modeling; Gates, Molenaar, Hillary, Ram, & Rovine, 2010), sex differences in temporal dynamics became apparent. For girls more than boys, positive affect characterized the play of the group – at a time lag: One girl’s positive affect predicted another girl’s positive affect at the next time point (10 seconds later), highlighting a delay in emotion contagion. For boys more than girls, vigor of activity characterized the play of the group – instantaneously: One boy’s vigor predicted another boy’s vigor at the same time point, highlighting an immediacy of activity contagion. Thus, this network mapping approach exposed the temporal dynamics underlying sex differences in play that were missed by traditional analyses.

If networks have the capability of illuminating the dynamics of psychological processes, then why are they only now beginning to be integrated into psychological science? Perhaps researchers are anticipating or experiencing roadblocks in their application. Researchers may wonder what types of questions network models help them ask and answer, if it matters which network analysis technique they use, what type of data they must have, if there are restrictions on the number of participants, variables, or missing cases that can exist in their data set, how they actually run the analysis, what software they need, and if they will be able to interpret results with respect to other data in their sample.

The goal of this tutorial is to answer questions like these with respect to group iterative multiple model estimation (GIMME; Gates & Molenaar, 2012), leaving researchers equipped to conduct state-of-the-art temporal network analyses on their own time series data. To accomplish this, the tutorial is divided into three parts. Part I includes a basic explanation of GIMME and the mathematics underlying it. Part II contains procedures for conducting a GIMME analysis, including data acquisition, preprocessing, general program operation, assumption testing, and results interpretation. Throughout this section, an empirical example is used to illustrate the analysis steps. Part III provides brief overviews of extensions to GIMME, such as exogenous influences on networks, identification of subgroups, and the generation of multiple well-fitting solutions. The tutorial ends with a discussion of limitations.

Part I: Group Iterative Multiple Model Estimation (GIMME)

There are a variety of network analysis approaches for time series data (for examples and reviews, see Bringmann et al., 2016; Bulteel, Tuerlinckx, Brose, & Ceulemans, 2016; Friston, Harrison, & Penny, 2003; Henry & Gates, 2017; Molenaar & Lo, 2016; Ramsey, Hanson, & Glymour, 2011; Smith et al., 2011), and researchers should carefully weigh the pros and cons of each with respect to their scientific aims and characteristics of their data. GIMME has been shown to be valid and reliable, outperforming most competitors in large-scale simulation studies in neuroscience, the field from which it originated (Gates & Molenaar, 2012). GIMME detected more true edges and fewer spurious edges than 38 other undirected and directed functional connectivity approaches, ranging from partial correlations and coherence analyses to Granger causality inferred from autoregressive models and a variety of Bayesian net methods (for details on data simulation, see Smith et al., 2011). Since those simulations, GIMME has provided novel insights into the brain and behavioral processes underlying substance use (Beltz, Gates, et al., 2013; Nichols, Gates, Molenaar, & Wilson, 2014; Zelle, Gates, Fiez, Sayette, & Wilson, 2016), psychopathology (Beltz, Wright, Sprague, & Molenaar, 2016; Gates, Molenaar, Iyer, Nigg, & Fair, 2014; Price et al., 2017), cognition (Grant, Fang, & Li, 2015), language acquisition (Yang, Gates, Molenaar, & Li, 2015), and olfaction (Karunanayaka et al., 2014), among other areas of inquiry. Moreover, GIMME has been fully-automated and boasts multiple features and extensions that make it suitable for a plethora of research questions and data sets (Beltz & Molenaar, 2016; Gates, Lane, Varangis, Giovanello, & Guskiewicz, 2017; Gates & Molenaar, 2012; Lane, Gates, & Molenaar, 2017).

GIMME Networks

GIMME creates networks, or in this context, statistical models that explain patterns of temporal covariation in a system. Networks contain nodes and edges (for a review and discussion, see Sporns, 2011). Nodes are elements in a system, such as kids in a play group, regions of interest (ROIs) in the brain, or variables used to operationalize constructs in a psychological study. With respect to temporal networks, edges are connections, relations, or paths between nodes that signify an association. Like GIMME, many network analysis tools were introduced to the psychological community via the neuroscience literature, but increasingly, researchers are adapting them to enable innovative analyses of a broad range of psychological phenomena (e.g., Borsboom & Cramer, 2013; Bringmann et al., 2016; Bulteel et al., 2016; Molenaar & Lo, 2016).

The particular networks GIMME creates are referred to as directed functional networks (Friston, Moran, & Seth, 2013), especially in the neuroscience literature. They are directed because the edges point from one node to another, signifying statistical prediction. They are functional because they concern statistical dependencies in observed data across time, such as blood oxygen level-dependent (BOLD) signal in functional magnetic resonance imaging (fMRI) data. There is a distinction between the edges in GIMME-created networks. Some edges are lagged, indicating that the relation between the nodes is separated in time, while other edges are contemporaneous, indicating that the relation between the nodes is instantaneous, or occurs at the same point in time. The inclusion of edges that reflect different temporal dimensions helps ensure that all time-based information in dynamic data is reflected in the network.

The networks GIMME creates are person-specific: There is a personalized result for each member of a sample that contains edges common across the sample (i.e., group-level relations) and edges unique to the person (i.e., individual-level relations). The group-level edges reflect pattern homogeneity in network structure and facilitate interpretation and generalization of results, while the individual-level edges reflect heterogeneity and honor the extreme variability in psychological processes present across people and time (see Finn et al., 2015; Molenaar, 2004). Moreover, this combination of group- and individual-level parameters is in large part responsible for GIMME’s outperformance of 38 competing connectivity approaches in simulations (Gates & Molenaar, 2012), as most alternatives only model networks at the group- or the individual-level (e.g., Friston et al., 2003; Ramsey et al., 2011; Smith et al., 2011).

A review of the first empirical application of GIMME elucidates some of the features of the analysis and demonstrates its utility for time-indexed data. This application was to longitudinal functional magnetic resonance imaging (fMRI) data of college students completing a go/no-go task in which pictures of alcoholic or non-alcoholic beverages were the response cues (Beltz, Gates, et al., 2013). Students completed the task three times: during the summer before college, the first semester of college, and the second semester of college. GIMME analyses focused on blood oxygen level-dependent signal from eight ROIs, with four representing an emotion processing network (bilateral amygdala and orbitofrontal cortex) and four representing a cognitive control network (bilateral dorsolateral prefrontal cortex and rostral and dorsal anterior cingulate cortex). Figure 1 shows the resulting network for a single participant completing the task the summer before college. The eight ROIs are nodes, and they are connected by directed edges that either are present for everyone in the sample (thick lines) or present only for the exemplar individual (thin lines), and that either reflect relations at the current time point (solid lines) or relations at a future time point (dashed lines). Edges are statistically significant for the individual or majority of the sample even though they differ in magnitude (evidenced by varying β weights). Standard fit indices (e.g., root mean squared error of approximation) are provided to show that the network model is an excellent reflection of the observed data. Across participants, longitudinal measurements showed a denser cognitive control network (i.e., a network with more edges) in the first semester of college than in the summer before college and the second semester of college. This is consistent with behavioral data, which showed a spike in negative consequences of alcohol use in the first semester of college. Thus, GIMME revealed that there is more cross-talk among cognitive control regions during alcohol-related decision making at a time when students were experiencing increased alcohol exposure.

Figure 1.

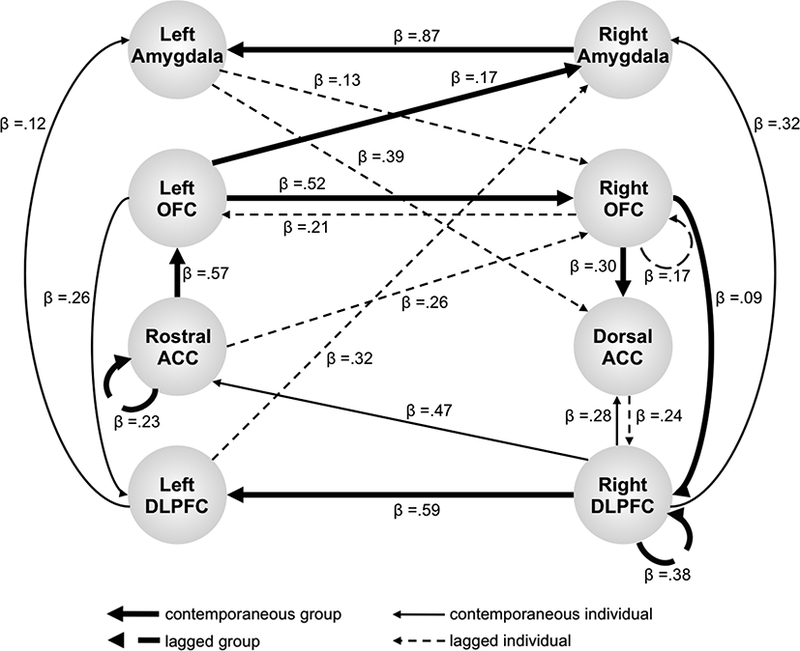
GIMME neural network for a single participant completing a go/no-go task in which images of alcoholic beverages were the response cues (Beltz, Gates, et al., 2013). Data are from the first wave (i.e., summer before college) of a longitudinal fMRI study of neural responses to alcohol during the college transition, and the network fit these data well according to alternative fit indices (CFI = 1.00, NNFI = 1.00, RMSEA = .000, SRMR = .050). Thick lines are group-level edges estimated for all participants (in the first wave of the study), thin lines are individual-level edges estimated for this participant, solid lines are contemporaneous edges, dashed lines are lagged edges, and edge magnitude is shown by β weights. See text for description of fit indices. OFC: orbitofrontal cortex; ACC: anterior cingulate cortex; DLPFC: dorsolateral prefrontal cortex. (Reproduced with permission from Elsevier from Beltz, Gates, et al., 2013.)

Mathematics and Model Fitting

GIMME implements unified structural equation models (uSEMs; Gates et al., 2010; Kim, Zhu, Chang, Bentler, & Ernst, 2007). uSEMs are a type of structural vector autoregressive (VAR) model, which is a class of models that contain both contemporaneous and lagged parameters. uSEMs differ from other structural VARs, however, in the way they are fitted to the data. Typically, structural VARs are estimated by first fitting a standard VAR to identify lagged relations between variables, and then submitting the covariance matrix of the residuals to a Cholesky decomposition to identify contemporaneous relations (Lütkepohl, 2005). But, results obtained in this way are dependent upon the order in which the variables are input (Loehlin, 1996; Lütkepohl, 2005). uSEMs do not do this “step-wise” model fitting, and instead, identify both lagged and contemporaneous relations in the same step, producing results independent of variable input order (Molenaar & Lo, 2016).

GIMME for a mean-centered input p-variate time series η(t) containing measurements from time t = 1, 2, …, T is defined as:

$${\eta }_i\left(t\right)=({\mathrm{A}}_i+{{\mathrm{A}}_i}^g){\eta }_i\left(t\right)+({\Phi }_{1,i}+{{\Phi }_{1,i}}^g){\eta }_i(t-1)+{\zeta }_i\left(t\right).$$ (1)

A is the p × p matrix of contemporaneous edges among the p nodes; the diagonal is zero because nodes cannot predict themselves at the same time point. This matrix can be understood as a SEM within GIMME. Φ₁ is the p × p matrix of first order lagged edges among the p nodes; the diagonal is estimated and contains autoregressive effects, that is, a node’s prediction of itself at the next time point. Because GIMME implements a first order model, estimates are made only for the influence of one time point prior. The Φ₁ matrix can be understood as a standard VAR of order 1 within GIMME. ζ is the p-variate vector of errors assumed to have means of zero with a diagonal covariance matrix and no sequential dependencies, such that all temporal information is explained within A and Φ₁ (see A Posteriori Testing of Assumptions). The subscript i denotes that parameters are uniquely estimated for each individual, and the superscript g denotes patterns that exist for the group (i.e., full sample); matrices with no superscript g indicate individual-level patterns. All parameters are estimated separately for each individual; thus, A_i^g and Φ_1,i^g show the structure of the group-level edges (e.g., a given path φ_mn^g ≠ 0 for all i), with the magnitude of the edges varying across individuals (e.g., φ_mn = .23 for i = 1), where m and n denote different nodes.

GIMME is fit via data-driven forward selection. (Theoretically, it can also be fit via backward selection or in a confirmatory way, but this would require reprogramming and testing to ensure valid and reliable results.) It is fit using the block Toeplitz method (Molenaar, 1985). Although the estimation is pseudomaximum likelihood because the observations (i.e., input time series) contain dependencies, it produces results similar to raw maximum likelihood (Hamaker, Dolan, & Molenaar, 2005; Zhang, Hamaker, & Nesselroade, 2008). Fitting proceeds according to the steps shown in Figure 2. First, a null network model is fit for each individual, that is, a model with no parameters (i.e., edges) in the A or Φ matrices is fit to the data. Second, the group-level model is identified. This is done via Lagrange Multiplier tests (i.e., modification indices; Sörbom, 1989). These tests indicate the extent to which a given parameter – if added to the model – would improve model fit. If there is a parameter that would significantly improve model fit for a researcher-specified criterion for what constitutes the “majority” of the sample (usually 75%), then it is added to the network, and the model is re-estimated. In this way, GIMME begins by only adding effects that are replicated across the sample (i.e., individuals). Prior work that is critical of model searches suggests that the replication of effects is an optimal method for arriving at valid and reliable results, with appropriate caveats for sample size or time series length and model misspecification (MacCallum, Roznowski, & Necowitz, 1992). This search-and-add procedure continues until there is no longer an edge that would significantly improve model fit for the criterion of the sample. If any edges became non-significant for the majority (using the criterion selected) through this iterative process, then they are pruned from the group-level network. Third, individual-level models are identified. Separately for each individual in the sample, the group-level model is fit, and then Lagrange Multiplier tests are used to determine whether additional parameters – if added to the model – would significantly improve model fit. If so, they are added to the network, and the model is re-estimated. This search-and-add procedure continues until a model with excellent fit is obtained, according to two out of four commonly accepted fit indices (Brown, 2006): comparative fit index (CFI) ⩾ .95; non-normed fit index (NNFI; also known as the Tucker-Lewis index) ⩾ .95; root mean squared error of approximation (RMSEA) ⩽ .05; standardized root mean residual (SRMR) ⩽ .05. Due to this iterative procedure, models usually fit well, but this is not always the case, especially for short time series or variables with little covariation. If any edges that are not in the group-level model became non-significant for the individual through this iterative process, they are pruned from the network; within GIMME, results are corrected for the number of individuals and the number of candidate paths being searched. Fourth, a confirmatory model that includes all group- and individual-level edges after trimming is fit.

Figure 2.

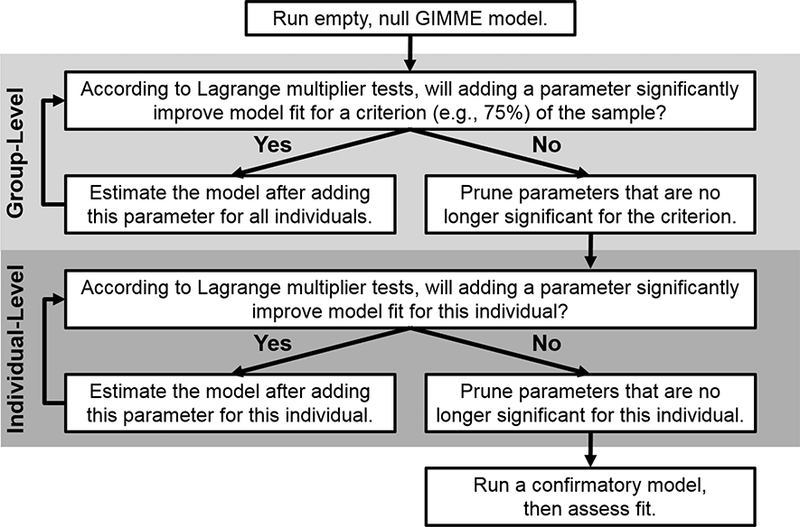
Schematic showing the model fitting steps employed within GIMME (Gates & Molenaar, 2012). Note that the “null” model can be empty or have specified group-level contemporaneous or lagged connections (e.g., the autoregressive effects). Lagrange Multiplier tests (i.e., modification indices) are used to identify optimal parameters (i.e., contemporaneous or lagged edges in the A_i, A_i^g, Φ_1,i, and Φ_1,i^g matrices of equation 1, respectively) to add to the model structure (i.e., network). Models are assessed with alternative fit indices, such as the comparative fit index, non-normed fit index, root mean squared residual, and standardized root mean squared error. (Reproduced with permission from Elsevier from Gates & Molenaar, 2012.)

Part II: Analyzing Data with GIMME

There are several steps in the GIMME analysis pipeline. Although the details of each step vary depending upon study goals and the nature of the data being analyzed, GIMME analyses typically include data acquisition, preprocessing, program operation, testing model assumptions, and results interpretation. These steps are described below, noting special considerations. A small, but novel, daily diary data set from 10 women is analyzed step-by-step to illustrate the GIMME workflow.

Data Acquisition

GIMME creates sparse, directed networks from multivariate time series; these are sets of variables that have been intensively repeatedly measured. Examples include functional neuroimages (e.g., from fMRI or electroencephalography, EEG), ecological momentary assessments (e.g., daily diary reports or actigraphy), coded observations (e.g., videotaped interactions), or biomedical assessments (e.g., heart rate or hormone sampling). Typically, variables are assessed on a continuous interval or ratio scale, and they can reflect a single measure (e.g., BOLD signal from a voxel or ROI) or a composite (e.g., summary score from a questionnaire). Most applications of GIMME have utilized between 4 and 10 variables, but the program generally works well with between 3 and 20 variables. To enter data in the program, researchers must create a data matrix for each participant, in which the columns are the variables (i.e., nodes) and the rows are the repeated measurements. GIMME will create person-specific block Toeplitz matrices. These matrices can be visualized as submatrices (blocks), with each block along descending diagonals (Toeplitz) providing the contemporaneous covariances, while the off-diagonal blocks provide lagged covariances.

Although GIMME is robust, there are several things researchers should consider with respect to variable selection, measurement intervals, and time series length to optimize the analysis and interpretation of results. Concerning variable selection, it is important to remember that GIMME creates networks that show how parts of a dynamic system covary. Thus, variables that have limited variation should not be used. In fact, a variable currently cannot be used if it does not contain sufficient variation across time.

The length of the interval between intensive longitudinal measurements can influence the networks derived by GIMME. Although the length of the interval is sometimes determined by data collection instruments (e.g., the time to repetition in an fMRI study), it often is not. When it is not, it is obviously most important to consider the time course of the biological or psychological process being investigated. Is it thought to unfold over seconds, hours, or days? Data collected with short measurement intervals (e.g., milliseconds in EEG) have high resolution. These data could be downsampled during preprocessing (e.g., using lags detected with auto- or cross-correlation functions) prior to GIMME (see Preprocessing). They could also be used in GIMME with the knowledge that they will increase the number and magnitude of lagged edges and maybe even the temporal order of the model, that is, the estimation of lagged edges in which the variability in one node predicts the variability in another node two, three, four, or more measurements in the future (see Results Validation and Interpretation; Beltz & Molenaar, 2015). Moreover, data collected with long measurement intervals (e.g., 24 hours in daily diaries) are likely to increase the number and magnitude of contemporaneous edges since the rate of measurement occurs at a longer time span than the rate of the process being studied. When autoregressive effects do not exist or are small, the contemporaneous edges increase the likelihood of having multiple solutions that describe the data equally well (see Handling Multiple Solutions; Beltz & Molenaar, 2016). In all cases, GIMME assumes the length between observations is equidistant.

The length of the time series (i.e., the number of repeated measurements) required to estimate a GIMME model depends upon the number of nodes, features of the data, and aspects of the network model being estimated (e.g., with or without external input; see Modeling Exogenous Effects). Of course, longer time series are always better. Most GIMME applications in the literature have had time series that were at least 100 measurements long, but analyses have been done with fewer measurements, including the data example presented below. Time series length can differ across individuals.

In the empirical data illustration, 10 women completed an online set of questionnaires and cognitive tests, including a modified daily version of the NEO Personality Inventory (Costa & McCrae, 1989), at the end of each of 75 days. Participants were asked the extent to which 60 statements described them that day. Responses ranged from 1 (strongly disagree) to 5 (strongly agree). Composite scores were created by averaging 12 items reflecting each of the Big Five personality dimensions. Complementing work on the individualized structure of personality (Molenaar & Campbell, 2009), the aim of this analysis was to explore the interrelations among group- and individual-level personality dimensions. Despite great heterogeneity in the structure of personality, are there commonalities in the temporal interconnectedness among traditional dimensions? Thus, there were five nodes; each showed within-person variation (standard deviations had a mean of .34 and ranged from .09 to .61) across the time series that consisted of 75 measurements with a 24-hour measurement interval.

Preprocessing

Preprocessing should be implemented prior to GIMME analyses. These procedures obviously depend upon the type of time series data being studied and the preferences of researchers. For example, standard preprocessing should be applied to fMRI data before time series are extracted from ROIs for each participant. Behavioral data require special consideration of missing data, temporal trends, and sampling frequency, too. Careful attention should also be paid to the order in which preprocessing steps are conducted; the optimal order may depend on features of the data.

There is little consensus on the best way to handle missing data in person-specific time series (see, e.g., Honaker & King, 2010). GIMME accommodates missing data using full information maximum likelihood (FIML). This approach utilizes all available information and does not conduct listwise deletion, which removes all measurements from a time point in which one or more variables does not have an observed value. Although listwise deletion is standard practice in time series analyses, it may affect network results and substantive inferences, particularly concerning lagged edges when over 20% of the measurements are missing (Rankin & Marsh, 1985). For this reason GIMME utilizes FIML. Researchers simply must indicate missing observations in the input time series; if long periods of time are missing, then one line of missingness is sufficient as a placeholder for the section of missing data. In this way, full rows of data are not deleted, and issues regarding deletion of observations are reduced if data are missing at random.

Researchers might instead choose to handle missing data prior to GIMME analyses, especially if the data require additional preprocessing (e.g., researchers may want to impute raw data before detrending). One option is to restructure the data to avoid missingness. For example, observational data could be coded in 6-second intervals instead of 2-second intervals to increase the possibility that the behaviors of interest occur within the measurement interval. This may have consequences, such as decreasing the time series length or increasing variability for nodes in which variability is limited. Another option is to impute the missing data, with special consideration of the dependencies in time series. Sliding window averages and the individual VAR (iVAR) program are options. Sliding windows replace missing values with the mean of surrounding values, and iVAR imputes time series data and works well when data are missing in the latter half of the time series (Liu & Molenaar, 2014). Neither option should introduce bias if the time series are weakly stationary, that is, have variables with a constant mean and covariance that only depends on the order of the lag.

GIMME analyses assume weak stationarity. GIMME maps the dynamics in a system; it does not necessarily assess gradual change over time as in traditional longitudinal or growth curve analyses. For these reasons, trends in variables (e.g., relatively slow changes in functional form) should be handled prior to GIMME. For instance, a linear trend could be removed by regressing the data against time and then entering residuals into GIMME.

Researchers might also consider downsampling when working with data of a high temporal resolution or when lags greater than one are expected (as mentioned in Data Acquisition). Doing this enables immediate use of GIMME, which currently only models a lag of one, but the pros and cons of downsampling versus explicitly modeling higher order lags after GIMME analyses are still unclear (see A Posteriori Testing of Assumptions); thus, simulations are needed. Downsampling can only be done if the data were collected at a time scale shorter than the process of interest. If so, then standard time series approaches can be used, such as detecting lags with the (partial) auto- and cross-correlation functions, regressing them out, and using residuals in subsequent analyses (much like detrending). Measurements can also be skipped or aggregated (e.g., when working with psychophysiological data). Other approaches, such as basis functions, might be meaningful for detecting cycles (e.g., weekly events in daily diaries).

Once preprocessing is completed, researchers must save the data in the format necessary for GIMME. There must be a separate file for each participant arranged with columns as the nodes and rows as the time points or measurement occasions; several different file formats (e.g., text, comma separated values) are compatible.

In the data illustration, time series from the 75-day self-reports of 10 women were examined for missingness. Missing data ranged from 0% to 16%. Local means were imputed for missing days using sliding windows of width 5 (i.e., two measurements before and two measurements after the missing data point). The time series were then examined for trends, focusing on linear effects. At least one personality factor showed a linear trend for all participants, according to univariate regression analyses with α = .05. Thus, for all participants, time was regressed on personality factor composite scores, and the standardized residuals were saved for GIMME analyses.

Preprocessing results are depicted for three exemplar participants in Figure 3. For each participant, the original time series of all five personality factors are plotted; days with imputed data are indicated by transparent gray bars, and linear trends are indicated by thin lines. The standardized residual time series that were eventually used in GIMME are also plotted for each participant. Participant A had no missing data, but a negative linear trend for agreeableness. Participant B had 12 days missing, with linear trends for neuroticism, extroversion, and agreeableness. Participant C had 3 days missing, with linear trends for neuroticism, openness, and conscientiousness. Time series files for the standardized residualized personality time series for all 10 women were created; for each participant, there was a text file with 5 columns (personality factors) and 75 rows (days).

Figure 3.

Preprocessing results for three exemplar participants illustrating the GIMME work flow. On the left, composite scores from each of the five personality factors are plotted by diary day. Transparent gray bars indicate days with missing data, imputed with the individual’s local average, and thin lines indicate personality factors with significant linear trends (at p < .05). On the right, standardized residuals from the linear regression of time on personality factor plotted by day. These residuals remove the linear trends from the data, and were subsequently entered into GIMME.

Program Operation

GIMME is fully automated and can be used through a graphic user interface (GUI) or command line. It was initially developed in Matlab® (Mathworks, 2015) with a LISREL (Jöreskog & Sörbom, 1992) dependency, but now is available and maintained in R (R Core Team, 2015). All code is freely accessible at https://cran.r-project.org/web/packages/gimme (Lane et al., 2017) and from the authors. The program is under continual development, so GUI images and command line prompts are not included here, but rather in detailed guides (see Lane & Gates, 2017) and user manuals accompanying the program.

After loading the program into their preferred platform, researchers enter some basic information into the GUI or command line. They enter paths to the folder containing the individual time series files created during processing and to the output folder where results files should be written. They also specify some details about the data and desired analysis features. These vary, but can include the number of nodes, measurement interval, analysis type (e.g., with or without an exogenous effect; see Modeling Exogenous Effects), subgrouping option (see Identifying Similar Patterns Among Subsets of Individuals), and equality criteria (see Handling Multiple Solutions).

GIMME provides the option to begin the analysis with the autoregressive terms estimated. The autoregressive terms are lagged edges between each variable and itself; they reflect self-prediction. When this option is used, the autoregressive parameters are added to the group-level model (Φ_1,i^g) before Lagrange Multiplier testing begins. On the one hand, this seems logical. The autoregressive terms statistically control for potential node autocorrelations prior to examining cross-lags, with the goal being to test the temporal relations between nodes from a Granger causality perspective (Granger, 1969). For an edge to satisfy conditions for Granger causality, it must predict the target node above and beyond the extent to which the node predicts itself over time. Procedures like this are common in neuroimaging general linear models (e.g, Friston et al., 2000; Woolrich, Ripley, Brady, & Smith, 2001) and will likely speed up network estimation, since time series with short measurement intervals are likely to have the autoregressive terms estimated in the data-driven search anyway. On the other hand, autoregressive terms may not be significant for all individuals, particularly when samples are heterogeneous or when measurement intervals are long. In these cases, freeing the terms a priori might artificially increase network homogeneity and might influence the order in which parameters are freed in the data-driven search. For example, the parameter with the largest modification index in the null model may not be the first parameter to be freed in a data-driven search with autoregressive terms, and this has consequences for the structure and number of network solutions that GIMME provides (see Handling Multiple Solutions; Beltz & Molenaar, 2016). The conditions under which the a priori estimation of autoregressive terms are optimal or suboptimal still requires extensive simulation studies.

The output provided by GIMME depends upon the version being used, so researchers should refer to user manuals for details. Briefly, a set of information is provided for the network estimated for each participant. This includes fit indices and matrices or lists containing estimates of the lagged and contemporaneous edges organized according to terms of the GIMME model in equation 1. Typically, the presence or absence of edges is of interest as well as the weight of specific edges. Because GIMME contains both contemporaneous and lagged connections (in the p × p A matrix and the p × p Φ₁ matrix, respectively), the full β matrices containing the estimated parameters are 2p × 2p. Within the matrices, the nodes in the rows are explained by the nodes in the columns, both of which are organized such that the nodes at time t – 1 are listed first (top of the rows and left in the columns) followed by the nodes at time t. Because variation in the nodes is explained at time t, all parameters in the top half of the matrix (at time t – 1) are fixed at 0. The nodes at time t are then explained by the nodes at time t – 1 (i.e., entries in the lower left corner of the matrix) and by the nodes at time t (i.e., entries in the lower right corner of the matrix). The entries in the matrix could be depicted with a 0 or 1 indicating whether or not an edge was estimated in the network, or they could be standardized β weights showing the magnitude of an estimated edge; standard errors and significance tests (i.e., t-tests) are provided for each β weight.

Returning to the data illustration, an input folder of the preprocessed time series and an empty output folder were created prior to GIMME analysis. A Matlab® version of GIMME was used for the analysis; the GIMME GUI was activated from the command line. In the GUI, the input and output folder paths were entered, along with the number of nodes (5) and measurement interval (24 hours). A uSEM analysis was run because there was no external input (e.g., task component or moderating variable; see Modeling Exogenous Effects), and the autoregressive terms were not estimated at the outset because the measurement interval was relatively long, and temporal correlations were not expected to be large. Standard group- and individual-level significance criteria were used.

The resulting networks fit the data well for all participants, with average alternative fit indices of RMSEA = .04, SRMR = .09, CFI = .97, and NNFI = .95. One group-level edge was identified by GIMME. It was a contemporaneous connection from neuroticism to agreeableness that (when significant) ranged in magnitude from .31 to .72 and was always negative in direction, indicating an inverse relation between the two personality factors. The edge was not statistically significant for two participants, but it still exceeded the 75% criterion for inclusion in the model as a group-level parameter. The number of individual-level edges ranged from 3 to 12, depending upon the participant, and all were statistically significant.

Modified output matrices and network depictions of the results are displayed for the three exemplar participants in Figure 4. The personality factors in the matrix rows are explained at time t by the personality factors in the columns. Parameters in the A matrix denote β estimates of contemporaneous relations and are shown as solid lines with weights in the networks. Parameters in the Φ matrix denote β estimates of lagged relations and are shown as dashed lines with weights in the networks. The single group-level edge is bold and boxed in the matrix and is shown as a thick solid line with a β weight in the networks. The networks for participants A, B, and C fit the data well: χ²(30) = 41.67, p = .08, RMSEA = .07, SRMR = .16, CFI = .96, NNFI = .95; χ²(28) = 32.79, p = .24, RMSEA = .05, SRMR = .08, CFI = .96, NNFI = .93; and χ²(28) = 27.45, p = .49, RMSEA = .00, SRMR = .07, CFI = .99, NNFI = .98, respectively. The group-level edge was significant for these participants, who had four, six, and six individual-level edges, respectively.

Figure 4.

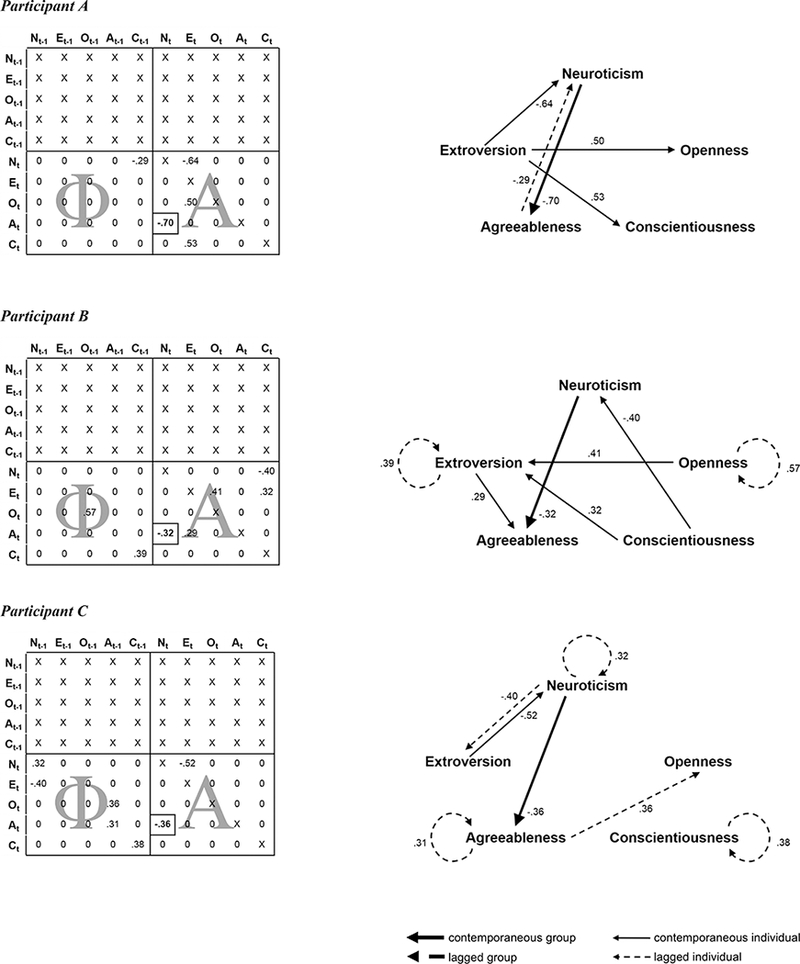
GIMME behavioral network results for three exemplar participants illustrating the GIMME workflow; these are the same participants whose time series are plotted in Figure 3. On the left are output matrices for each participant, modified for illustration purposes. Beta weights show the direction and magnitude of estimated connections, 0’s indicate connections that could have been estimated but were not (e.g., because they did not significantly improve model fit), X’s indicate parameters that were fixed at 0, and thus, could not have been estimated, and the boxed estimate indicates the single group-level connection. The matrices are read with the nodes in the rows being explained at time t by either lagged (t – 1 edges in the Φ matrix) or contemporaneous (t edges in the A matrix) connections with the nodes in the columns. On the right are the network depictions of the results. Contemporaneous connections are shown by directed solid arrows, lagged connections are shown by directed dashed arrows, the single group-level connection is shown by a thick line, and the individual-level connections are shown by thin lines. Beta weights are shown for all connections. N: neuroticism; E: extroversion; O: openness; A: agreeableness; C: conscientiousness.

A Posteriori Testing of Assumptions

A posteriori model validation should be conducted for each person-specific network estimated by GIMME (Beltz & Molenaar, 2015; Box & Jenkins, 1970). In other words, researchers should verify that the generated networks are optimal representations of the data and satisfy model assumptions; this is standard practice in VAR modeling (Box & Jenkins, 1970; Lütkepohl, 2005). In particular, after assessing the fit of each model, such that at least two of the following four fit indices suggest excellent fit (Brown, 2006; Gates & Molenaar, 2012): CFI ⩾ .95; NNFI ⩾ .95; RMSEA ⩽ .05; SRMR ⩽ .05, researchers should verify the white noise assumption for the standardized residuals output for each model (refer to Mathematics and Model Fitting; for details, see Beltz & Molenaar, 2015). If the residuals are white noise (i.e., have no auto- or cross-correlations), then the first order lagged model implemented by GIMME was sufficient for removing all temporal dependencies from the data. If the residuals are not white noise, as is likely in data sets with relatively short measurement intervals or strong sequential correlations (Beltz & Molenaar, 2015), then higher order terms should be considered. Although GIMME can mathematically be extended to higher orders, white noise tests and data-driven searches of higher order uSEMs are not currently implemented in the program because the first order models have been sufficient for most previous applications, many of which had relatively long measurement intervals and strong contemporaneous correlations (e.g., Beltz, Gates, et al., 2013; Grant et al., 2015). In order to maintain the homogeneity of GIMME’s first order group-level structure, it is recommended that researchers add higher order terms (when needed) at the individual-level. Such a model with the mean centered at 0 is defined as:

$${\eta }_i\left(t\right)=\left(A_i+A_i{}^g\right){\eta }_i\left(t\right)+\left({\Phi }_{1,i}+{\Phi }_{1,i}{}^g\right){\eta }_i\left(t-1\right)+{\displaystyle {\sum }_{q=2}^r{\Phi }_{q,i}}{\eta }_i\left(t-q\right)+{\zeta }_i\left(t\right)$$ (2)

where η, t, A, Φ₁, ζ, i, and g are defined as in equation 1, and Φ_q is the p × p matrices of individual lagged edges at order q = 2, 3,…, r.

There are many ways to conduct white noise tests, and there are some study-specific decisions required in the process. Detailed procedures and LISREL sample scripts, however, are available (see Appendix; Beltz & Molenaar, 2015). The general idea is to use the estimated model to generate one-step-ahead prediction errors, and then to examine whether there are distinguishable temporal correlations in those errors when estimated across higher orders. If there are no significant temporal correlations, then the network output from GIMME is sufficient. If there are temporal relations, then higher order terms must be added to the model for that individual. Researchers can use Lagrange Multiplier tests to facilitate identification of specific higher order parameters. After identifying a higher order model, researchers should conduct another white noise test to ensure the residuals are now white noise. If they are not, then an even higher order model is necessary. If researchers wish to sidestep this issue, they could consider regressing out higher orders prior to analysis and using residuals in GIMME (see Preprocessing).

The importance of the a posteriori validation procedure was reported in the analysis of resting state fMRI data from 32 college students (Beltz & Molenaar, 2015). BOLD time series from four ROIs constituting the default mode network were analyzed with GIMME (Biswal et al., 2010; Van Dijk et al., 2010). A prominent group-level network was identified, but a posteriori model validation revealed that residuals were white noise for only 56% of the sample. For the remaining 44%, second order individual-level edges had to be added to their networks in order for residuals to be white noise. There were few patterns among the second order parameters, and thus, there was no indication that a second order group-level edge was necessary.

Regarding the data illustration, network results were subjected to a posteriori model validation. The estimated parameters from each participant’s GIMME network were used to generate prediction errors at each time point: ${\xi }_{\iota }={\eta }_i\left(t\right)=\widehat{A}{\eta }_i\left(t\right)-{\widehat{\Phi }}_1{\eta }_i\left(t-1\right)$. This resulted in a five (factor) by 74 (time points minus 1 degree of freedom) matrix of residuals for each participant. Temporal dependencies in the residual matrices were examined by generating block Toeplitz matrices up to a lag order of 3 and testing the fit of models specifying that there are no temporal relations among any of the variables. Model fitting was conducted in LISREL, and a sample script is provided in the Appendix. The models fit the data well for all participants, with average alternative fit indices of RMSEA = .00, SRMR = .10, CFI = .99, and NNFI = .99. Thus, results suggest that the residuals are white noise, and that a first order model was sufficient for capturing all temporal information in the networks.

Results Interpretation

The GIMME analysis pipeline produces a network for each participant that contains (if they exist) group-level connections and individual-level connections that indicate the magnitude and direction of one node’s contemporaneous or lagged relation to another node. Meaningful person-specific information can be determined from these network features. For example, the presence and magnitude of autoregressions indicate the extent to which a node is self-predictive. In Figure 4, participants B and C have positive autoregressive terms, potentially suggesting that these factors are steady for the two women (after accounting for the removed linear trend, as all edges and estimates must be interpreted in the context of preprocessing). Also, the presence of feedback and feedforward loops indicates a dynamic coupling between sets of nodes. Participants A and C have such loops related to neuroticism. For the former, neuroticism is related to decreases in same-day agreeableness, which, in turn, predicts decreases in next-day neuroticism, while for the latter, same-day extroversion predicts lower neuroticism, which feeds back to reduce next-day extroversion. The discussion of autoregression and feedback temporal loops both concern the interpretation of lagged connections in GIMME-produced networks. The interpretive value of the lagged connections depends upon the research question, nature of the data, length of the measurement interval, and preprocessing steps, among other considerations. For instance, many neuroimaging researchers are primarily interested in contemporaneous, or time-locked connections among brain regions (e.g., Hillary et al., 2011), and so, they model lagged relations to ensure accurate estimation of contemporaneous relations, since simulations show that the failure to account for temporal dependencies in network maps can lead to spurious contemporaneous results (Gates et al., 2010). In other data, however, the lagged connections may have substantive meaning, as in the observational study of children’s positive affect and vigor of activity described above. Results revealed more lagged edges among positive affect in groups of girls than in groups of boys, consistent with data on sex differences in co-rumination, which is a temporal process (Beltz, Beekman, et al., 2013; Rose, 2002).

There are several other ways to extract and synthesize information from GIMME-derived networks; this information can then be used in comparisons of previously-defined subgroups (e.g., determined by task performance, diagnosis, or sex), or they can be linked to individual differences measures (e.g., temperament, substance use, or language ability). Some examples follow. First, the magnitude of group-level edges, which have continuous distributions, could be indexed by their estimated β weights (i.e., the parameter estimates in the A_i^g and Φ_1,i^g matrices). Results from the illustrative GIMME analysis revealed one contemporaneous group-level connection from neuroticism to agreeableness. For participants A, B, and C, whose networks are shown in Figure 4, this connection had a β weight of −.70, −.32, −.36, respectively. These values could be extracted from all 10 participants and related to other variables of interest, such as internalizing and externalizing behavior or performance in an experiment.

It is not meaningful to examine the β weights of individual-level edges because they are not normally distributed. Specifically, individual-level edges are 0 for some participants (because they are not estimated) and statistically significant for others, with the possibility of positive or negative effects for those who have the edge. For example, participants A and C have a contemporaneous connection from extroversion to neuroticism, but participant B does not; participant B cannot simply be assigned a value of 0 for this connection in subsequent analyses because the β weight was not estimated, and it is unlikely that it would be exactly 0 if it were. Should researchers wish to test a specific effect by using the estimated weights as a continuous variable, they could specify that the edge be estimated at the group-level null model when initializing the analysis (see Mathematics and Model Fitting).

The second type of information that can be used in subsequent analyses is the presence or absence of individual-level edges. In these cases, researchers can count the number of specific types of edges that are present (e.g., edges that are interhemispheric in fMRI research) or generate hypotheses related to the presence or absence of particular edges. For instance, perhaps a clinical researcher would like to investigate if the presence of a relation between two symptom variables relates to treatment outcomes. Additionally, the total number of edges present in a network could also be used as an index of network sparsity or density. Of the participants in Figure 4, participant A has the sparsest network, with 5 edges, and participants B and C have equally dense networks with 7 edges. High density can be an indication of maladaptive response cycles in a clinical sample, or in neuroimaging research, of decreased optimization in brain processes that may lead to poor performance (Nichols et al., 2014).

Third, graph theoretical metrics could be calculated, and are especially insightful and reliable for networks with many nodes (i.e., those at the upper limit of what is well-suited for GIMME). Hubs could be identified by examining the in-degree and strength (number and weight of edges predicting a node), out-degree and strength (number and weight of edges a node predicts), and importance of a node in the overall network reflected in its interconnectedness to other nodes (Rubinov & Sporns, 2010; Sporns, 2011). For instance, in Figure 4, extroversion has the greatest out-degree for participant A, and it is a hub for participant B. Neuroticism is the hub for participants A and C. These are just a few ways in which GIMME results can be reduced into measures that describe the nature of nodes or full networks. Though written with fMRI researchers in mind, Rubinov and Sporns (2010) explain some additional options for quantifying network attributes. Regardless of the metrics used, researchers are urged to think critically about the alignment of their hypotheses with GIMME-derived network features. Are they more interested in the weight of an edge that might be a target for treatment, the node that seems to drive the system, or a network-level attribute? These fundamental questions should guide analyses.

Part III: Extensions of GIMME

There are additional features of GIMME targeted to certain research questions and types of data. They are reviewed briefly below, and interested researchers are directed to the cited primary sources for more information.

Modeling Exogenous Effects

GIMME can be applied to data that are influenced by exogenous input. “Exogenous” here refers to a variable that cannot be influenced by other variables in the network; examples include the weather or a set of stimuli presented in an fMRI study to examine the correspondence between brain activity and time-locked psychological stimuli. Clearly, the weather and fMRI stimuli cannot be predicted by a person’s mood or brain activity; the directionality can only occur from the exogenous variable to the variables in the network. The ability to model exogenous influences on individuals’ networks is a unique feature of GIMME, as most network mapping approaches for neuroimaging data do not explicitly model task effects (dynamic causal modeling is one exception, see Friston et al., 2003). GIMME does this by implementing an extended uSEM (euSEM; Gates, Molenaar, Hillary, & Slobounov, 2011). When GIMME is used to estimate euSEMs (instead of uSEMs), not only does it identify group- and individual-level contemporaneous and lagged edges among nodes, but it also identifies group- and individual-level contemporaneous and lagged direct effects of an exogenous influence on a node. It can also model the modulating effects, or how the magnitudes of node connections change depending upon the exogenous input.

The option to conduct euSEMs was originally developed and maintained in the Matlab® version of GIMME, but is now also available in the R version. To conduct an euSEM, researchers must provide the program with a vector (or matrix) of exogenous inputs (e.g., onset times and durations of stimuli presentations). This is similar to task regressors organized by volumes or seconds used in general linear models of fMRI data. For other types of data, researchers must be certain that the input has the same measurement schedule as the nodes (e.g., time series of the same length) and that it contains sufficient variability (e.g., not a dichotomous variable). Up to two inputs can be modeled in GIMME, and they can differ across individuals. For an example, see Hillary and colleagues (2014).

Identifying Similar Patterns Among Subsets of Individuals

Sometimes it can be difficult to tell from individual-level network results what patterns of effects might relate to specific constructs of interest. For instance, while it is possible to test if a specific edge exists for individuals, it is less straightforward to test if combinations or patterns of edges might exist for subsets of individuals in a sample. Further complicating the issue is that oftentimes there are no a priori subgroups, or clusters of individuals that researchers believe to be similar, to help guide the search. This may occur in studies of diagnostic categories where varied biological markers give rise to similar behaviors or symptoms (e.g., equifinality), or anywhere there is heterogeneity within a sample that may, in fact, be systematic. Alternatively, there could be meaningful subsets of individuals with different processes that do help differentiate, for instance, among diagnostic categories. Subgrouping within GIMME can help elucidate situations where researchers wish to identify subsets of individuals who have some similarities in their dynamic processes.

The option of subgrouping individuals based on the temporal models that describe their neural, psychological, or social processes was originally developed in the R version of GIMME. This algorithm, called “subgrouping GIMME” (or S-GIMME; Gates et al., 2017), clusters individuals into subgroups using information available after the group-level search; thus, individuals are clustered based solely on their network patterns. Previous work using this algorithm differentiated clinically depressed individuals from controls based on brain connectivity during an emotion task and also differentiated individuals within the same diagnostic category (Price et al., 2017). Alternatively, researchers can provide a priori subgroups (e.g., determined by task performance, diagnosis, or sex).

Regardless of whether subgroups are data-driven or a priori, GIMME first arrives at group-level edges in the typical way (see Mathematics and Model Fitting). Next, subgroup-level edges are identified similar to the way group-level edges are identified. Finally, individual-level edges are obtained by using group- and subgroup-level edges as a prior. The final solutions provide group-, subgroup-, and individual-level edges, all of which are estimated at the individual-level. The output also indicates the subgroup in which each individual was placed. The “subgroups” that are obtained are best thought of as subsets of individuals that had the most in common. Of course, individuals in one subgroup might have some things in common with individuals in other subgroups in terms of their dynamic processes. Nonetheless, S-GIMME aims to find similarities in patterns of effects that might not exist for all individuals.

Handling Multiple Solutions

After reviewing the results of GIMME analyses (e.g., as depicted in Figures 1 and 4), researchers might wonder about the robustness of the findings, particularly the directionality of the edges. For example, reversing the direction of a contemporaneous edge in a network may not significantly affect model fit or the temporal dependencies in the residuals, even though it drastically alters a researcher’s substantive interpretation.

This issue has been addressed in the context of cross-sectional path models, of which SEMs and the A matrix in GIMME are examples. In these models, it is established that multiple equivalent or plausible alternative solutions – perhaps an infinite number of them – are possible (MacCallum, Wegener, Uchino, & Fabrigar, 1993; Markus, 2002). This is most relevant to GIMME when contemporaneous edges in the A matrix are the first to be added to a network in the data-driven search (Beltz & Molenaar, 2016). In these instances, the contemporaneous edges have equal modification indices (according to Lagrange Multiplier tests); for instance, model improvement for the estimation of the connection from node m to node n is the same as the improvement for the estimation of node n to node m. Researchers can explicitly model and compare multiple solutions arising from equal modification indices such as this using GIMME for multiple solutions (GIMME-MS; Beltz & Molenaar, 2016).

A beta version of GIMME-MS is available from the authors. GIMME-MS maintains many features of GIMME, such as the estimation of euSEMs (see Modeling Exogenous Effects), but also generates multiple solutions when they are present. Researchers activate this feature by indicating the equality criteria, that is, whether modification indices must be equal to 3, 4, or 5 decimal places in order to trigger the creation of multiple solution paths. For an example analysis and a description of ways to select a solution if multiple were estimated, see Beltz and colleagues (2016) and Beltz and Molenaar (2016), respectively.

GIMME Limitations and Considerations

There are some limitations inherent in the GIMME analysis pipeline, many of which are shared with data-driven approaches in general. The primary concern surrounds the possibility of overfitting the data. Overfitting is when the model becomes more complex than necessary, often by attempting to explain variance in the variables by modeling noise. When this occurs, the model may have more parameters than needed to model the data. While this is certainly a possibility with GIMME, attempts have been made to limit this. For instance, the search procedure stops as soon as the model is found to appropriately explain a reasonable amount of variance in the data, according to alternative fit indices. This contrasts an alternative approach where all paths are added if they are significant. By using a stopping mechanism such as fit indices, more parsimonious models are obtained. Other reliable techniques for conducting data-driven models, such as Independent Multiple-Sample Greedy Equivalent Search (IMaGES; Ramsey et al., 2011) also utilize a stopping mechanism based on fit rather than adding all paths that reach significance in their estimates.

This preference for parsimony decreases the likelihood of overfitting but does not remove it. As with any approach, the model will only be as reliable as the data, and it is a common issue in neural, psychological, and social sciences for data to contain noise and measurement error. GIMME is currently unable to directly model the noise in variables. Remedies do exist. Since GIMME estimates models from within an SEM framework, latent variables can be generated (Bollen, 1989). Latent variables arrive at a signal for an unobserved construct using observed variables as indicators. In this way, measurement errors can directly be modeled and would not be included in the search for relations among latent variables. Epskamp and colleagues (2017) have implemented this approach for analysis on individual data sets. Extension to the multiple modeling method within GIMME is rather straightforward, and this work is underway.

A related issue is that GIMME uses a feed-forward approach for model building. This may cause problems if the final models are sensitive to the starting point early on in the data-driven search; hence, an incorrect path or direction added early in the search will change the search space and possibly perpetuate errors. To circumvent this, the option for multiple solutions has been proposed (see Handling Multiple Solutions; Beltz & Molenaar, 2016). Another solution would be to utilize a feature selection approach that simultaneously considers all possible paths.

A few other limitations exist that will cause issues for specific types of data. For one, GIMME assumes the relations among variables are constant across time. This may be an untenable criterion for data in which change across time (e.g., development) occurs. To address this, trends can be removed from the data prior to analyses (as in the data illustration), or the time-varying nature of the data could be explicitly modeled (e.g., by dividing the times series into windows). These solutions may not work for all data sets, though. Two, in the absence of any group-level paths, the directionality of the paths may not be reliably recovered. As noted above, GIMME improves upon the individual-level search approach by utilizing shared information obtained by first identifying effects that are replicated across individuals. Without any shared paths, the final models may be even further from the “true” model (MacCallum et al., 1992). One fix would be to include autoregressive effects for all individuals, as most time series data can be expected to have serial dependencies. This has been found to improve model recovery in some instances. Another option would be to allow for multiple solutions. From this, researchers can look for common themes and converging evidence from which to draw inferences (Beltz & Molenaar, 2016). Finally, GIMME does not model the means (i.e., level) of the variables. While not of interest for network modeling or looking at relations among variables, it might be of interest for some research questions.

Conclusions

GIMME is an accurate, data-driven, and automated approach for the analysis of time series data, including task-based or resting state neuroimaging data, daily diaries, coded observations, and biomedical assessments. It creates person-specific networks that explain covariation in time series via directed edges between nodes (e.g., ROIs or variables). The edges can be contemporaneous (explaining covariation at the current time point) or lagged (explaining covariation at future time points), their direction can be evaluated in multiple solutions, and they can apply to the full sample, a subgroup of the sample, or just to an individual.

This tutorial provided researchers with a step-by-step guide to conducting network analyses with GIMME. It included information about acquiring time series data and preparing them for analysis, running the program, reviewing output, and validating and interpreting results. Researchers are hopefully now prepared to contribute to the ever-growing literature on the application of GIMME to research questions concerning the dynamics of complex brain, behavioral, and psychological systems.

Appendix

White Noise Test

da no=74 ni=20 ma=km

cm sy fi=cov_res.txt

mo ny=20 ne=20 ly=id te=ze ps=sy,fi

fr ps(1,1)

fr ps(2,1) ps(2,2)

fr ps(3,1) ps(3,2) ps(3,3)

fr ps(4,1) ps(4,2) ps(4,3) ps(4,4)

fr ps(5,1) ps(5,2) ps(5,3) ps(5,4) ps(5,5)

eq ps(1,1) ps(6,6) ps(11,11) ps(16,16)

eq ps(2,1) ps(7,6) ps(12,11) ps(17,16)

eq ps(2,2) ps(7,7) ps(12,12) ps(17,17)

eq ps(3,1) ps(8,6) ps(13,11) ps(18,16)

eq ps(3,2) ps(8,7) ps(13,12) ps(18,17)

eq ps(3,3) ps(8,8) ps(13,13) ps(18,18)

eq ps(4,1) ps(9,6) ps(14,11) ps(19,16)

eq ps(4,2) ps(9,7) ps(14,12) ps(19,17)

eq ps(4,3) ps(9,8) ps(14,13) ps(19,18)

eq ps(4,4) ps(9,9) ps(14,14) ps(19,19)

eq ps(5,1) ps(10,6) ps(15,11) ps(20,16)

eq ps(5,2) ps(10,7) ps(15,12) ps(20,17)

eq ps(5,3) ps(10,8) ps(15,13) ps(20,18)

eq ps(5,4) ps(10,9) ps(15,14) ps(20,19)

eq ps(5,5) ps(10,10) ps(15,15) ps(20,20)

ou all