Hierarchical groove discrimination by Class I and II aminoacyl-tRNA synthetases reveals a palimpsest of the operational RNA code in the tRNA acceptor-stem bases

Abstract

Class I and II aaRS recognition of opposite grooves was likely among the earliest determinants fixed in the tRNA acceptor stem bases. A new regression model identifies those determinants in bacterial tRNAs. Integral coefficients relate digital dependent to independent variables with perfect agreement between observed and calculated grooves for all twenty isoaccepting tRNAs. Recognition is mediated by the Discriminator base 73, the first base pair, and base 2 of the acceptor stem. Subsets of these coefficients also identically compute grooves recognized by smaller numbers of aaRS. Thus, the model is hierarchical, suggesting that new rules were added to pre-existing ones as new amino acids joined the coding alphabet. A thermodynamic rationale for the simplest model implies that Class-dependent aaRS secondary structures exploited differential tendencies of the acceptor stem to form the hairpin observed in Class I aaRS•tRNA complexes, enabling the earliest groove discrimination. Curiously, groove recognition also depends explicitly on the identity of base 2 in a manner consistent with the middle bases of the codon table, confirming a hidden ancestry of codon-anticodon pairing in the acceptor stem. That, and the lack of correlation with anticodon bases support prior productive coding interaction of tRNA minihelices with proto-mRNA.

INTRODUCTION

The genetic coding language is implemented by fitting—stereochemical recognition—of the 3D structures of transfer RNAs (tRNAs) specific for each amino acid into complementary pockets in the surfaces of the appropriate one of the 20 aminoacyl-tRNA synthetases (aaRS). Ideally, only a truly complementary tRNA–aaRS pair will attach an amino acid to tRNA, assuring that the correct amino acid forms a chemical bond with the correct tRNA—that which has the corresponding anticodon. Formation of correct amino acid–tRNA bonds therefore translates the genetic code. In reality, mischarging errors resulting from error-prone recognition of both amino acid and tRNA doubtless occurred with higher frequencies as the coding system was forming and progressively drove the selection of higher specificity complexes and error-correcting mechanisms (see Figure 5 of reference 1), reducing mischarging to levels observed today.

Figure 5.

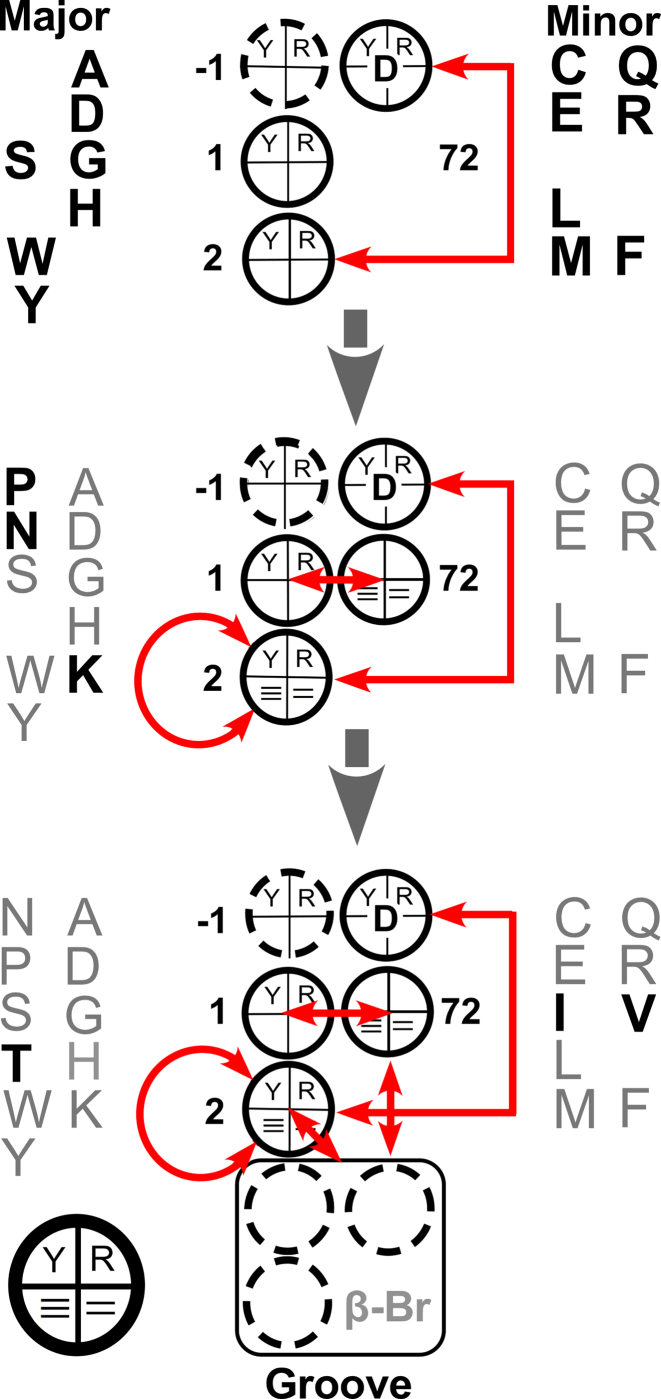
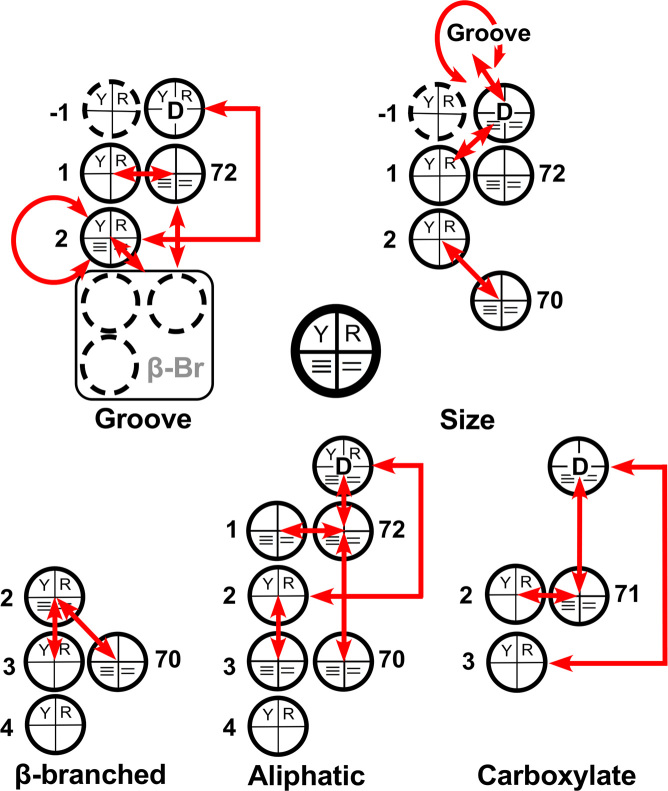
Hierarchy in regression models for groove recognition. Coefficients are diagrammed schematically using a circle to represent each base, as indicated by the key at the bottom left. Each circle is divided into quadrants. The top two quadrants represent the choice between pyrimidine and purine; the bottom the number of hydrogen bonds made when the base pairs. Red arrows indicate two-way interactions. The grooves recognized by fourteen of the twenty aaRS can be predicted (perfectly) using only three coefficients (top). Additional amino acids (bold) require additional coefficients, indicated in the middle and bottom schemes. The hierarchy does not necessarily imply an evolutionary succession.

Division of both tRNA and synthetase structures into complementary domains (2) and the demonstration that fragments of synthetase catalytic domains called Urzymes retain a full functional repertoire (3) despite being too small to interact with both acceptor stem and anticodon strengthened earlier proposals (4) that genetic coding began with an ‘operational RNA code’ embedded in tRNA acceptor stem bases that directed recognition by a cognate aaRS. Further, evidence that the aaRS all diverged from a single bidirectional gene encoding ancestral Class I and II amino acid activating catalysts in-frame on opposite strands (5) strongly suggested that acceptor-stem bases also dictated the initial division of tRNAs into those specific for Class I and Class II aaRS substrates. Because they determine synthetase recognition of tRNA, details of the operational RNA code—how the acceptor-stem bases differentiate between aaRS Classes and more generally how they relate to amino acid physical chemistry and aaRS Class recognition—are thus crucial steps toward understanding the origin of genetic coding.

The operational RNA code was initially a hypothetical proposal, essentially without details (2,6). Several subsequent efforts have failed to provide those details (7–9). An important analysis by Shaul (8) subsequently provided a comprehensive description in the form of complex trees whose branches are regression models that lead to decisions on classification. The actual details, however, remain encrypted by the provenance of the tree branching, and thus are difficult to use in a practical sense.

Our previous work used more explicitly-targeted regression modeling to establish associations between aaRS tRNA base recognition and various properties of the canonical twenty amino acids (10,11) to establish that tRNA bases embed amino acid physical chemistry into tRNA and revealed that amino acid sizes are encoded by bases in the acceptor stem, whereas their polarities are encoded by anticodon bases. Additional distinctions encoded by the tRNA acceptor stem identity-determining bases include the discrimination between β-branched and unbranched, as well as carboxylate and aliphatic side chain functional groups.

Crystal structures of aaRS•tRNA complexes (12) have contributed two essential qualitative aspects of recognition. (i) Class II aaRS bind to the tRNA major groove in a manner that does not distort the 3′ acceptor terminus, whereas Class I aaRS approach via the minor groove and thus must somehow distort the tRNA 3′-terminus into a hairpin, allowing the terminal adenosine to turn back into the aaRS active site, which leads to acylation of the 2′-, rather than the 3′-OH group. (ii) Crystal structures for tRNA complexes of aaRS specific for aromatic amino acids from both Class I (TrpRS; (13,14); TyrRS; (15)) and Class II (PheRS; (16)) show that they recognize grooves opposite to those recognized by the rest of their Class. The groove recognized by each aaRS thus constitutes a dependent variable expected to be related to the independent variables derived from tRNA bases. There is a rich, but somewhat inconclusive literature on the ability of proteins to recognize sequence information from the two grooves of nucleic acids (17–20). Thus, aaRS recognition of cognate tRNA acceptor stems raises fundamental questions. At the time of our previous work (10,11), we tried to identify patterns of bases that discriminated between either Class or Groove recognition. Persistent attempts failed, as noted further in RESULTS.

Our recent in-depth consideration of the key role of ancestral bidirectional aaRS coding (1,21) prompted us to re-visit this question. Those studies emphasized the important possibility that the contemporary genetic code likely arose stepwise from a much simpler code implementing a substantially reduced alphabet by gradually incorporating additional amino acids that may not previously have been distinguishable, and hence would require distinctive modifications of the recognition rules to enable selective recognition by newly differentiated aaRS. Thus, the most recent expansions of the genetic code may have come long after the Class or groove recognition had served its original purpose, and hence may have overwritten the recognition signals for such amino acids while necessarily preserving groove recognition.

For this reason, we re-examined the regression modeling with particular attention to identifying and rejecting outliers among the amino acids. Various modeling attempts were more or less successful in predicting tRNA groove recognition for 12–16 of the amino acids. A breakthrough came when we realized that the same rules might apply differently to different groups of related amino acids, and decided to test combinations of the base-related predictors with descriptors based on selective groups of amino acids. Including a binary descriptor for one such group, those—valine, isoleucine, and threonine—with β-branched side chains, elevated the success dramatically, both in scope and statistical significance. Coefficients for all bases excepting the four topmost bases were identically zero. Our surprising conclusion is that groove recognition elements for all twenty amino acids can be consistently attributed, with high statistical confidence, to the four topmost acceptor stem bases if we simultaneously specify the β-branching.

Curiously, coefficients for base 2 are pivotal to groove definition and implications for each of the four bases relate readily to the first two columns of the codon table, containing codon middle-bases U for minor groove (Class I) recognition and C for major groove (Class II) recognition. Thus, base 2 appears to represent an underlying image of the codon middle base as suggested by published models in which the anticodon triplet immediately precedes the Discriminator base (22,23). The acceptor stem code specifying aaRS groove recognition rounds out a set of models for the ‘operational RNA code’, the details of which have never been articulated. We therefore summarize and update those models here.

MATERIALS AND METHODS

tRNA Sequences, relevant crystal structures and identity elements

Bacterial tRNA sequences

Unpublished studies associated with our previous analysis of the tRNA acceptor stem bases (11) had suggested that bases −1, 1, 2, 72 and 73 might form a complete ‘code’ for the groove recognition by aaRS. That database, however, was restricted to bases that had been previously assigned as identity elements (24), leaving multiple absences that compromised tests for groove specification (in fact, that design matrix was actually quite sparse, as 49% of its cells were empty). Acceptor-stem sequences were therefore collected from all bacterial tRNAs in the 2009 database, ‘tRNAdb 2009: compilation of tRNA sequences and tRNA genes’ (25). tRNAs for each amino acid are represented in our data table by 3–14 sequences, there being more sequences generally for amino acids with multiple isoacceptors. Restriction to bacterial sequences was thus a compromise. It provided multiple sequence alignments in which the Discriminator base (26), the 1–72 bp, and base 2 were almost entirely unambiguous at the expense of reducing the redundancy of the dataset and excluding a significant majority of known tRNA sequences analyzed in (8) and (9).

Further justification for using only bacterial tRNAs came from the fact that ancestral reconstructions of aaRS Urzyme sequences produced a substantially stronger codon middle-base pairing frequency, suggesting that bacterial synthetase sequences retain a clearer signal of their remote ancestry (27). As we hoped to characterize structures and events as close as possible to the earliest genetic coding relationships, the clarity of that signal may be advantageous. The resulting patterns identified from bacterial tRNA sequences lend consistency to that choice. Models described below for recognition patterns for specific types of amino acids (amino acid sidechain size, β-branching, carboxylate, and aliphatic sidechains) were, however, based on the previously published identity elements (24).

X-ray co-crystal structures

Giegé and Springer (12) cite aaRS•tRNA co-crystal structures for 14 of the twenty aaRS of bacterial origin. Although aaRS•tRNA co-crystal structures should provide complementary information, not all complexed aaRS crystal structures provide relevant data. A fair percentage show the tRNA interacting via the anticodon loop without an interpretable configuration for the entire acceptor stem (e.g. 1H3E, 1H4Q, 1J1U, 1QU3, 2AKE, 2XSL, 2CSX, 4KR3, 4QEI, 4RQF, 4RQE, 1SET, 4YYE) or show the acceptor stem interacting with an editing domain (e.g. 1GAX, 5AH5) and hence are not useful for our purposes. Co-crystal structures did, however, emphasize a key unanswered question quite central to the origin of genetic coding: what factors underlie the discrimination between the faces of the tRNA acceptor stem recognized by each aaRS Class?

Identity elements

Considerable effort has been devoted to estimating the relative strengths of the tRNA ID elements summarized in Table 1 (12,24). One might expect, a priori, that this database too might complement the tRNA sequence alignments when addressing the question of groove recognition. However, quite surprisingly as outlined below, the tRNA sequences and especially the topmost four bases in the acceptor stem contain sufficient information to account completely for the correct groove recognition by all 20 bacterial aaRS, independently of either the structural data or the experimental data on relative strengths of ID elements.

Table 1.

Comparison of ID elements identified by Giegé (24) with those identified by Rodin (9) and Shaul (8). Although Giegé’s compilation is more detailed, the more recent analyses show essentially no discordances with that list.

Amino acid	Class	Giegé	Rodin	Shaul	Discordancea
Val	I	A73; G3:C70; U4:A69	A73; 3:70; 4:69	A73	—
Ile	I	A73; C4:G69	A73; C4:G69;	A73, C4:G69	—
Leu	I	A73; C 3:G70; A4:U69	A73	A 73	—
Met	I	A73; G2:C71; C3:G70; U4:A69	A73; U4:A69	A73; C2:G71; U4:A69	—
Cys	I	U73; G2:C7I; C3:G70	U73; G2:C71; C:G70	U73	—
Tyr	I	A73; C1:G72	A73; C1:G72	C1:G72	—
Trp	I	G73; A1:U72; G2:C71; G3:C70	G73; A1:U72; G2:C71; G3:C70	G73, G2:C71	—
Glu	I	G1:C72; U2:A71	G1:C72	A73; G1:C72; U2:A71, C4:G69	—
Gln	I	G73; U1:A72; G2:C71; G3:C70	G73; U1:A72; G2:C71; G3:C70	G73, G2:C71, G3:C70; G4:C69	—
Arg	I	A/G73	A/G73	A/G73	—
Ser	II	G73; C72; G2:C71; A3:U70	G73; C72; G2:C71; A3:U70; G4:C69	G73; C72; G2:C71; A3:U70; G4:C69	—
Thr	II	U73; G1:C72; C2:G71; G3:C70	U73; G1:C72; C2:G71; G3:C70	U73; G1:C72; C2:G71; G3:C70	—
Pro	II	A3; G72	A3; G72	A3; G72	—
Gly	II	U73; G1:C72; C2:G71; G3:C70	U73; G1:C72; C2:G71; G3:C70	U73; G1:C72; C2:G71; G3:C70	—
His	II	C73; G-1	C73; G-1	C73; G(-1	—
Asp	II	G73; G2:C71	G73; G2:C71	G73	—
Asn	II	G73	G73	G73; U1:A72	(?)b
Lys	II	A 73	A 73	A 73	—
Phe	II	A73	A73	A73	—
Ala	II	A73; G2:C71; G3•U70; G4:C69	A73; G2:C71; G3•U70; G4:C69	A73, G2:C71, G3:U70	—

^aThis column identifies possible discrepancies between the three authors.

^bThe U1:A72 base pair is identified only by Shaul, and thus could represent a discordance and thus is indicated by a (?).

Regression modeling

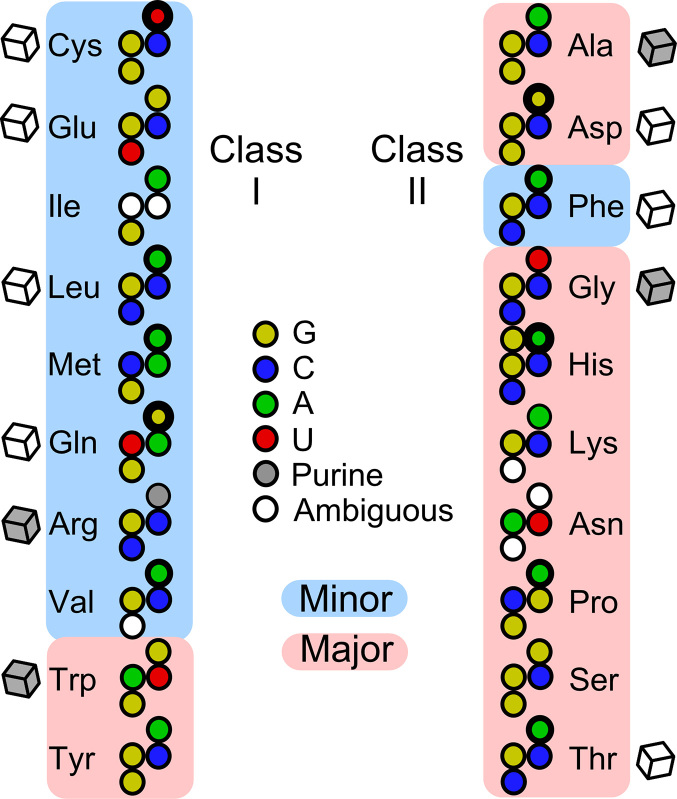
As in our previous study (11), each base was represented by two binary flags, derived from whether base N was a pyrimidine (1) or a purine (–1), i.e. (N,Y/R), and whether it could form three (1) or two (–1) hydrogen bonds in a base pair, i.e. (N,≡/=). Columns of these predictors, together with the Class, and groove recognized by the cognate aaRS form the design matrix in Supplementary Table S1, in which each row corresponds to a different amino acid. No differentiation is made between isoacceptors. Both groove definition and the binary predictor columns were treated as continuous variables in the statistical analysis. There is, in principle, nothing wrong with this procedure, although logistic regression is often preferred. Our case differs from others because ambiguous indications for a small number of the bases (i.e. the 1–72 bp in isoleucyl-tRNAs; Figure 1) require a third value in the design matrix, which in this case is 0.

Figure 1.

tRNA acceptor-stem bases considered in the analysis of aaRS groove recognition. Pyrimidines are colored with primary colors, purines with their respective complements. Cubes adjacent to each tRNA represent the availability of aaRS•tRNA co-crystals showing productive acceptor-stem interactions in prokaryotes (open) or other (gray) organisms. The width of the circle for each discriminator base indicates its strength as compiled by Giegé and Eriani (50). Note the following idiosyncratic features: (i) tRNA^Leu, tRNA^Phe, tRNA^Thr and tRNA^His have identical bases in all four positions; (ii) tRNA^Asp and tRNA^Ser similarly share identical signatures; (iii) tRNA^His has a unique extra G at position –1; (iv) tRNA^Ile has a completely ambiguous first base pair.

A comprehensive set of regression models was generated and assessed using the JMP (28) stepwise regression module, together with the design matrix in Supplementary Table S1, testing possible predictors and their two-way interactions. As we had previously observed, our first attempts to identify coefficients that correctly predicted the groove recognized by cognate tRNAs revealed a small number of outliers leading to a poor fit between actual and observed recognition groove. The outliers prominently included isoleucine, valine, and threonine, the three with branched amino acid side chains. Thus, a new binary column was added to the design matrix to identify branched (1) or unbranched (0) side chains. As a control, we also included a column defining amino acids with carboxylate side chains. No significance was ever detected for that column in any of our stepwise searches.

A well-known hazard of using stepwise regression to select models from a larger number of predictors than dependent variables—as is the case if we consider all two-way interactions—is that there will always be a very large number of models that fit the smaller number of dependent variables exactly, so there is no way to ensure that any model is unique. We believe this problem is unavoidable in our case, because the main effects themselves cannot achieve an R² value greater than 0.22. Furthermore, as the canonical amino acids necessarily limit us to twenty simultaneous equations, many of the higher-order effects are necessarily collinear with (i.e. aliased to) the main effects and two-way interactions.

To avoid this problem to the extent possible, we paid particular attention to selecting, from among the models (all highly similar) that gave the best fit between observed and calculated values of the dependent variable, that model with the highest proportion of main effects (6/11 of predictors for our model for the groove recognized) and the fewest adjustable parameters (here, 12). Thus, while we cannot rigorously exclude the possibility that there exists a superior model, we have conducted a wide and comprehensive search to ensure that the one described here is most probably the best. We reinforced that conclusion by prying apart the hierarchical nature of the groove recognition model.

Cross-validation

We previously used the two non-canonical amino acids selenocysteine and pyrrolysine for cross-validation. The 2009 database (25) lacks any bacterial tRNA^Pyl sequences, leaving just a single tRNA outside the training set, making it impossible to use the prediction R² as a metric. An analogous reason makes the Jackknife procedure (29) problematic. For that reason, we elected instead to use a conventional resampling method of iteratively leaving out a selected percentage of the amino acids randomly chosen to serve retroactively as the test set. Cross-validating models identified by stepwise regression in this way also presents subtle difficulties because the network of connections between acceptor stem bases and synthetase groove recognition is initially (i) unknown and (ii) idiosyncratic because the same acceptor stem bases are also used to form codes for amino acid physical properties and hence for recognition by specific aaRS (11).

For these reasons, omitting some amino acids from the training set may remove crucial information about the pattern of aaRS groove recognition without reducing the ability of the model to correctly predict the training set. Our choice, facilitated by the ability in JMP to select random partitions of the data, was therefore to construct 101 partitions between training (17 amino acids) and test (3 amino acids) sets. As the regression coefficients are estimated by inverting the matrix describing the simultaneous equations, one for each amino acid (tRNA type) in the training set, the process is sensitive to collinearities among the coefficients, a condition referred to as a singularity. Such singularities are especially likely if the training set is depleted of a particular type of amino acid. For this reason, we saved the predicted values, test set amino acids, and the R² value for each test set in a separate JMP database. Then, using this secondary database, we could examine the dependence of the test set R² metric on its components. That dependence provided an indication of how critical each of the twenty canonical amino acids was to the training set, from which a rational cross-validation emerged for the optimal regression model.

RESULTS

AARS groove recognition appears to reside in the uppermost bases of the tRNA acceptor stem

We previously (10,11) described regression models for four properties of the amino acid side chains—(i) their size and whether or not they have (ii) carboxylate, (iii) aliphatic or (iv) β-branched side chains—based on consensus ID elements in the tRNA acceptor stem. Repeated efforts to find satisfactory regression models relating the groove recognized to the multiple descriptors for each ID element failed to account satisfactorily for any reasonable subset of the tRNAs. Nevertheless, we obtained crucial information by deleting the outliers—tRNAs for those amino acids that were uncorrelated by the various unsuccessful models. Successively eliminating outliers produced models dominated by the topmost four unique bases of the acceptor stem, and without significant contributions from bases lower down the acceptor stem.

As discussed in METHODS, the sparseness of the design matrix drawn from the consensus ID elements appeared to have eliminated information necessary to reproduce the correct groove recognized by the corresponding synthetases. For that reason, we chose to look for groove-recognition rules using a more complete design matrix based on bacterial tRNA multiple sequence alignments to fill in missing specifiers for all of the topmost four bases from the tRNA sequence database (25).

The resulting database is usefully presented graphically (Figure 1). It has never been obvious that the limited information in Figure 1 should suffice to differentiate recognition mechanisms for Class I and II aaRS. In particular, there are multiple redundancies such that only 14 of the 20 isoaccepting tRNAs have distinct patterns and several of the redundancies entail recognition from opposite grooves. In fact, the base compositions of the patterns recognized by the major and minor grooves are nearly indistinguishable (supplementary §A; Supplementary Figure S1). We nevertheless develop evidence that there is a hidden and statistically significant pattern that discriminates absolutely between the grooves recognized by the twenty aaRS when coupled to the identification of the three amino acids valine, isoleucine and threonine, having β-branched side chains.

Patterns illustrated in Figure 1 can be represented by a design matrix with twenty rows, one for each amino acid, and 13 columns. Each base from Figure 1 is represented in Supplementary Table S1 by two columns as described in METHODS. These independent variables are supplemented by one additional column containing a binary code designating whether (1) or not (0) the side chain is branched at the β-carbon. The final column is the variable, G_i,_obs, that designates the groove recognized by the cognate aaRS (Figure 2). With the exception of tRNAs for aromatic amino acids, Class I aaRS recognize the minor groove (1) and Class II aaRS recognize the major groove (–1).

Figure 2.

Superposition of the acceptor stems available from co-crystals containing relevant configurations of the 3′-CCA terminus. The 3′-terminal adenosine is shown as colored spheres; Class I tRNAs are colored different shades of green; Class II different shades of blue. Those for aromatic amino acids (Phe, Trp) are colored shades of red as they penetrate the population of the opposite class.

That design matrix defines a set of simultaneous linear equations, expressing the equality between the cognate groove, G_i, and linear combinations of the independent variables, or predictors, P_i:

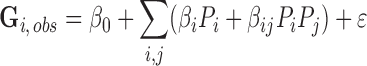(1)

where ϵ is the residual error to be minimized. As can be seen in the design matrix (Supplementary Table S1) independent parameters, P_i, are all either –1, 0 or 1. Their contributions to the dependent variable G_i,obs, differ, depending on their coefficient, β_i. The cross terms, indicated by β_ij, imply that the contribution factor j makes depends on the value of factor i.

The highly multivariate Equation (1) has a very large number of possible solutions, of which the (unknown) optimal subsets include those that: (i) use a minimum number of coefficients, β_i, β_ij, in order to (ii) minimize the sum of squares of the differences between predicted and observed G_i values: Σ_i(G_i,pred – G_i,obs)², and (iii) do so with the most statistically significant coefficients, i.e. those with the smallest overall P-values of their Student t-tests. Criterion (i) is inversely related to the number of degrees of freedom, DFE, remaining to estimate the statistical error. The squared correlation coefficient, R² must improve as additional degrees of freedom are used to estimate additional coefficients. Criteria (ii) and (iii) often improve together, but just as often behave in contradictory ways requiring a trade-off. Thus, the choice of an optimum model involves elaborating and testing amongst many models that differ in the number and combination of independent variables and deciding which of these best satisfies criteria (i)-(iii).

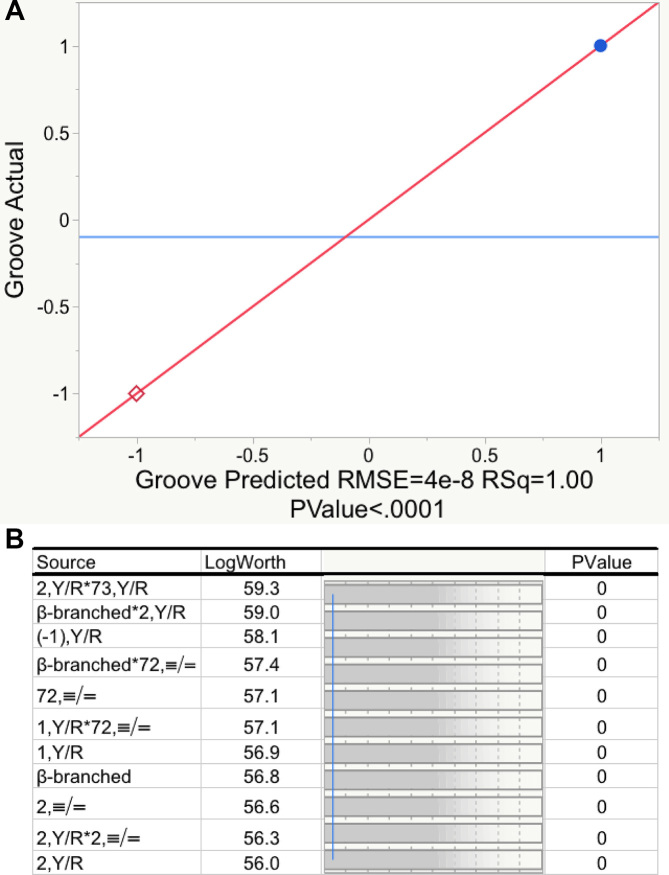
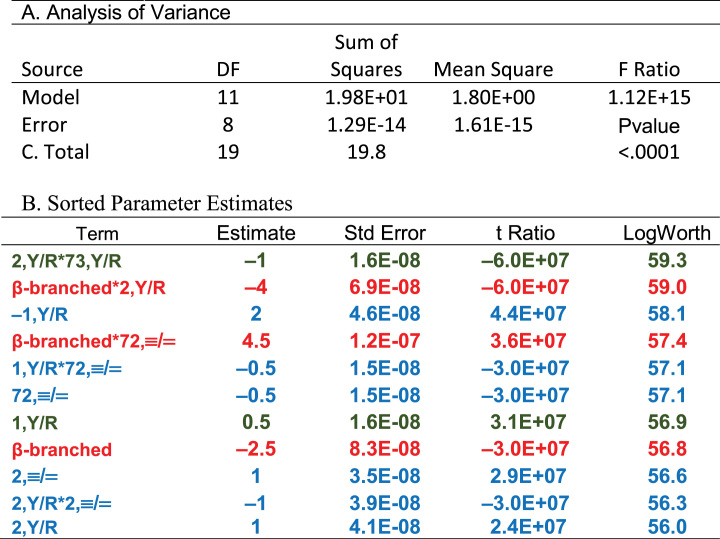
JMP (28) provides an excellent interactive stepwise multiple regression search procedure. Multiple alternative pathways through this algorithm—the automatic search driven by JMP itself; manually stepping through the selection of descriptors; and specifying first the two descriptors defining base 2 and their interaction, followed by manual identification of additional descriptors in order of descending estimated P-values—produced the model summarized in Figure 3 and Tables 2 and 6. The model satisfies all three of the aforementioned criteria: (i) the model requires only 11 of the total degrees of freedom; (ii) the predictors explain all of the variation in observed groove recognition and (iii) all 11 coefficients have Student's t-test P-values with log(Worth) values between ∼56 and 60, far greater than those (log(Worth) = 2 ≥ P = 0.01) required for reasonable statistical significance (Figure 3B). Another way to consider the last point is that the coefficients are defined with standard errors <10⁻⁷ of their magnitude (Table 2B); i.e. the fit is perfect, as can be verified by referring to Supplementary Table S2. The high number of degrees of freedom (8) and the fact that a major fraction of the coefficients are main effects greatly reduce the likelihood that there are other models superior to the one in Table 2B.

Figure 3.

Regression model relating tRNA groove recognition to tRNA acceptor-stem bases. (A) Actual versus Predicted Groove values for the twenty amino acids. Blue dots designate minor groove (1), red diamonds designate major groove (–1) interaction. (B) Log(worth) values plotted for each predictor. Worth is equal to the negative log of the P-value. The blue vertical line indicates a probability of 0.01 of observing a Student's t-test as large as that actually found for the model.

Table 2.

Statistics for the regression model in Figure 2. A. Analysis of variance. B. Coefficients of the regression model and their statistical significance. The logWorth is equal to the negative base10 logarithm of the P value. Colors in Table 2B highlight a hierarchical partition of coefficients. Green entries are presumably the oldest and account for 14 of the 20 canonical amino acids; red and blue entries came later to encode distinctions between β-branched amino acids (red) and asn, pro, and lys (blue), as discussed in the section on hierarchies.

Table 6.

Regression models for amino acid size and explicit side chain properties. All three models had R² = 1.0; none had non-zero intercepts. Data from these tables are compared schematically in Figure 9. The logWorth is equal to the negative logarithm of the P value.

Term	Estimate	Std Error	t Ratio	LogWorth
Size
73,≡/=1,Y/R	3.42	0.17	20.51	8.1
2,Y/R*70,≡/=	1.56	0.13	12.3	6.2
Groove	–0.79	0.11	–7.48	4.4
–1,Y/R	–1.97	0.34	–5.82	3.6
72,≡/=	0.99	0.18	5.57	3.5
70,≡/=	0.65	0.13	5.08	3.2
73,≡/=*2,Y/R	0.73	0.17	4.39	2.8
2,Y/R	–0.59	0.15	–3.9	2.4
73,≡/=*Groove	–0.34	0.10	–3.38	2.1
73,≡/=	–0.25	0.13	–1.99	1.1
β-Branched
4,Y/R	0.85	0.040	21.34	10.2
3,Y/R	–0.50	0.040	–12.6	7.6
70,≡/=	–0.28	0.023	–12.03	7.3
2,Y/R	0.25	0.023	10.72	6.8
2,≡/=*3,Y/R	0.49	0.048	10.24	6.6
2,≡/=	0.25	0.027	9.12	6.0
2,Y/R*70,≡/=	–0.27	0.030	–8.89	5.9
Carboxylate
2,Y/R*71,≡/=	–0.75	3.1E-09	–2.0E+08	94.8
2Y/R	0.75	3.4E-09	2.2E+08	94.2
73,≡/=*3,Y/R	0.5	2.6E-09	1.9E+08	93.5
3,Y/R	0.5	2.6E-09	1.9E+08	93.5
71,≡/=	0.5	3.2E-09	1.6E+08	92.5
73,≡/=*71,≡/=	0.5	3.2E-09	1.5E+08	92.4
Aliphatic
1,≡/=	–1	9.9E-09	–1.0E+08	78.6
2,Y/R	0.125	4.5E-09	2.8E+07	76.3
4,Y/R	1	5.0E-09	2.0E+08	75.6
72,≡/=	0.875	8.7E-09	1.0E+08	75.6
73,Y/R*2,Y/R	0.5	4.3E-09	1.2E+08	73.5
70,≡/=*72,≡/=	0.5	8.1E-09	6.2E+07	73.2
73,≡/=*2Y/R	0.375	6.6E-09	5.7E+07	70.3
2,Y/R*3,≡/=	–0.25	8.6E-09	–3.0E+07	70.0
73,≡/=**72,≡/=	–0.125	5.6E-09	–2.0E+07	69.1

The model depends critically on including a variable separating branched from unbranched sidechains and its interactions with 2(Y/R) and 72(≡/=). Without these terms, which have among the largest log(Worth) values, the overall R²-value for a comparable model was ∼0.62 and no t-test probabilities were significant.

Cross-validation analysis identifies several idiosyncratic tRNAs

We used a conventional 85%/15% resampling algorithm to test the robustness of predictions based on the regression model in Figure 3 and Table 2. The 85% partition of the data (i.e. 17 amino acids) was used to train the regression model—that is, to determine the best fit values of coefficients—and then evaluated the squared correlation coefficients for both the training set and the 15% test partition not used to estimate coefficients. Even this procedure was not without some complications, arising from idiosyncrasies, some of which are identified in the Figure 1 legend. As a consequence, many randomly selected training sets exhibited singularities, arising from algebraic equivalence of linear combinations of multiple predictors that allow the training set to be fitted without generating information necessary to fit the test set. Thus, they compromise the evaluation of the corresponding test sets.

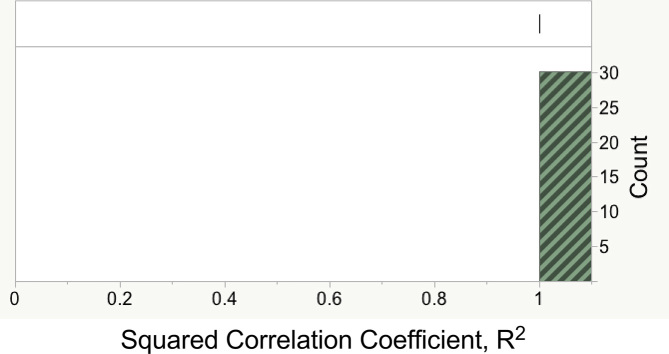
Values estimated for coefficients in Table 2B by fitting to 101 randomly selected 85% training subsets gave R² values identically equal to 1, convincingly demonstrating the internal consistency of the coefficients. Of these partitions, 71 led to singularities. R² values for the remaining 30 test sets, shown in Figure 4, were also identically 1, confirming the robust predictive power of coefficients estimated for training sets without singularities.

Figure 4.

Distribution of R² for 24 random 30% subsets of amino acids based on coefficients estimated for the complementary training set. All values were identically 1.0.

All 101 training set compositions were analyzed by a secondary regression analysis of the R² metric as a function of the training set compositions to identify significant sources of singularities (Table 3). From this table we can infer that the dominant predictor of singularities is the absence of β-branched side chains from the training set. Other predictors include the absence of amino acids proline, histidine and glutamate, from the training set.

Table 3.

Regression model identifying significant contributors to singularities in randomly selected training subsets containing ∼15% of the 20 canonical amino acids. The R² value for this model is 0.56; the logWorth is the negative logarithm of the P-value.

Term	Estimate	Std Error	t Ratio	LogWorth
Branch	–0.57	0.06	–8.96	13.5
Pro	–0.59	0.10	–5.77	7.0
His	–0.44	0.10	–4.51	4.7
Glu	–0.42	0.10	–4.10	4.1
Pro*Branch	0.52	0.14	3.77	3.5

The model for groove recognition is hierarchical, suggesting that ancestral patterns were overlaid as new amino acids were added to the coding alphabet

The idiosyncratic tRNAs—Pro, His, Glu, Val, Ile, Thr—suggest that incorporating their cognate amino acids into the code required some ‘overwriting’ of the earliest ‘rules’ by which their aaRS recognized cognate tRNAs. This possibility is elaborated further in the Discussion, and thus merits support. To develop such support, we examined the structure of the regression model to identify whether hierarchical subsets using fewer coefficients could predict the groove recognized for smaller subsets of amino acids (Supplementary §B). We systematically eliminated predictors from the full model to identify outlying amino acids that could no longer be fitted. This procedure produced two notable results.

First, removing the distinction of β-branched side chains eliminated three coefficients from Table 2B, leaving a model with 8 coefficients that correctly predicted the groove recognized by 17 of the 20 aaRS. Notably, the coefficients for that model had values identical to those in the full model. Thus, although the major subset of 17 and the three β-branched amino acids obey different rules, the underlying structure of the model was the same. The three new coefficients required to correctly predict the groove(s) recognized by aaRS for β-branched side chains, red in Table 2B, did not alter the remaining coefficients. The interactions of β-branching with 2,Y/R and 72,≡/=, together with an offset to the constant term, simply changed the manner in which the existing rules were applied to tRNAs for β-branched amino acids. Thus, those three coefficients are independent of the remaining 8 and could have been accumulated at any point—even quite early—in the evolution of the code.

Second (Supplementary §C; Supplementary Table S3), a subset of 2 coefficients correctly predicts the grooves for 13 of the remaining aaRS. Those two coefficients, {1(Y/R) and 2(Y/R)*73(Y/R)}, green in Table 2B, imply the same rules in the entire hierarchical set of rules. Supplementary Table S3 provides details of this model. tRNA^His uniquely has a Guanosine in the –1 position at the 5′-terminus. A third coefficient allows calculation of the groove recognized by HisRS by similarly providing an offset to the intercept. The outlying amino acids for this model are Asn, Pro and Lys, in addition to the β-branched amino acids.

Figure 5 summarizes the hierarchy embedded in the regression model for groove recognition. This nesting, and the fact that most numerical values for coefficients do not change as new predictors are incorporated to predict grooves recognized by AsnRS, ProRS, LysRS and the aaRS for amino acids with branched side chains, argue that regression modeling has uncovered significant aspects of the ancestral division of tRNAs cognate to the two aaRS Classes. Note, however, that the hierarchical nesting of regression models may not necessarily indicate the order in which amino acids were incorporated into the coding alphabet.

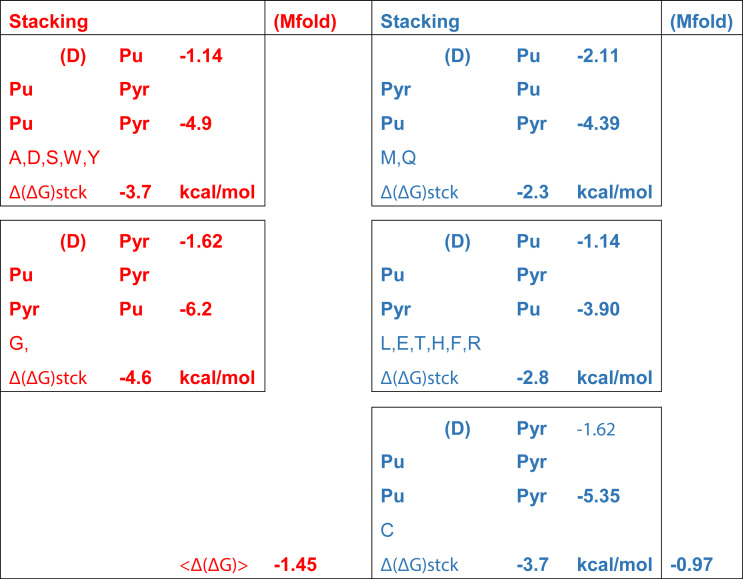
Rules arising from the (1(Y/R) = 1) and (2(Y/R)*73(YR) = –1) coefficients are summarized in Table 4. That these rules entail only whether the four topmost bases are pyrimidines or purines, choices that can be distinguished from both grooves (17,19,30), together with the fact that the Class I hairpin determines whether a tRNA will bind via the minor groove, suggest that these rules arise from thermodynamic effects of base stacking on RNA helical stability (31–33), which destabilize the helical path of the 3′-terminal extension relative to the hairpin, thus favoring the hairpin recognized by aaRS that interact via the minor groove. This question is developed further in supplementary §D. Table 5 summarizes two different estimates consistent with the hypothesis that the rules in Table 4 reflect a slightly increased thermodynamic tendency of tRNA substrates recognized via the minor groove to form the characteristic 3′-terminal hairpin. Further work is certainly required to confirm and further delineate the thermodynamic implications of the rules in Table 4.

Table 4.

Rules for groove recognition according to two coefficients (1(Y/R) and 2(Y/R)*73(Y/R)

Minor Groove (1)	Major Groove (–1)
Base 1 is pyrimidine	Base 1 is a purine
Base 2 is a pyrimidine and Base 73 is a purine	Base 2 and 73 are both pyrimidines
Base 2 is a purine and Base 73 is a pyrimidine	Base 2 and 73 are both purines

Table 5.

Stabilities in free energy estimated for the acceptor stems of 14 isoacceptors that obey rules in Table 4. Of eight possible configurations consistent with these rules, five are observed among known bacterial tRNA isoacceptors and are boxed. Configurations predicted to bind aaRS via the major groove are colored RED; those predicted to bind via the minor groove by forming a 3′-terminal hairpin are colored BLUE. Stabilities of double-helical configurations are estimated from averaged stacking energies compiled in (31), scaled separately for (A,C,G) and (U) to computational estimates for RNA (33). Δ(ΔG)_stck energies are the difference between the total stacking energies of the five bases implicated by the rules in Table 4 and that contributed only by the discriminator base (D), which are the two entries in the third column of each box. Estimates are confirmed qualitatively by the average values for minihelices estimated using Mfold (71) as described in the text.

We next develop the notion that contrasting secondary structural elements in ancestral Class I and II aaRS would have reinforced the slightly different thermodynamic tendencies of the acceptor-stem bases to form the hairpin.

The structural biology of aaRS•tRNA complexes yields insights into the Class-dependent bifurcation of tRNA acceptor-stem structures

The hierarchical rules predicting the groove recognized by aaRS for cognate tRNAs suggest that the initial separation between ancestral tRNA substrates of Class I and II aaRS may have had a thermodynamic basis that distinguished tRNAs with a smaller free energy difference, Δ(ΔG_3′conf), between the extended and hairpin conformations of the 3′ CCA terminus. The partial structural database tends to support this hypothesis, as the differences between major and minor groove recognition can be linked to gross structural differences, rather than to detailed interactions. Thus, the partial structural database reinforces the thermodynamic hypothesis.

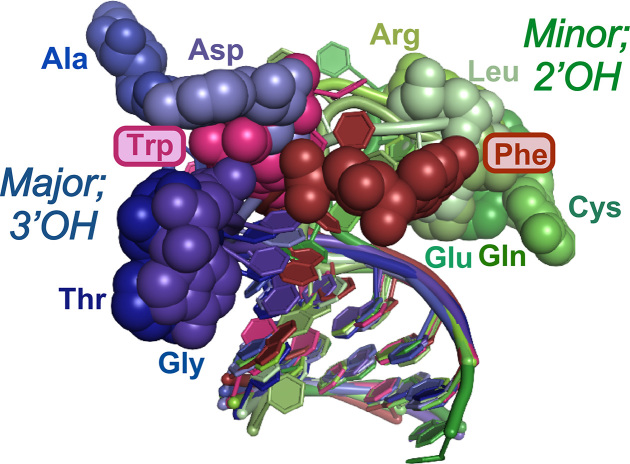
We have already noted that despite the abundance of synthetase•tRNA co-crystals, the structural database is nevertheless inadequate for our purposes because only eleven complexes (Supplementary Table S4) show the 3′-CCA terminus interacting with the catalytic apparatus. Of those, only seven have been co-crystallized with aminoacyl-5′AMP or an analog. The available structures suggest few details that could explain how the topmost acceptor-stem bases lend themselves to the observed conformational differences. Nevertheless, comparison of Figures 6–7 with Figure 8 confirms that specific secondary structures in the two aaRS Classes provide complementary surfaces that may exploit the small thermodynamic differences between cognate tRNA 3′-terminal conformations.

Figure 6.

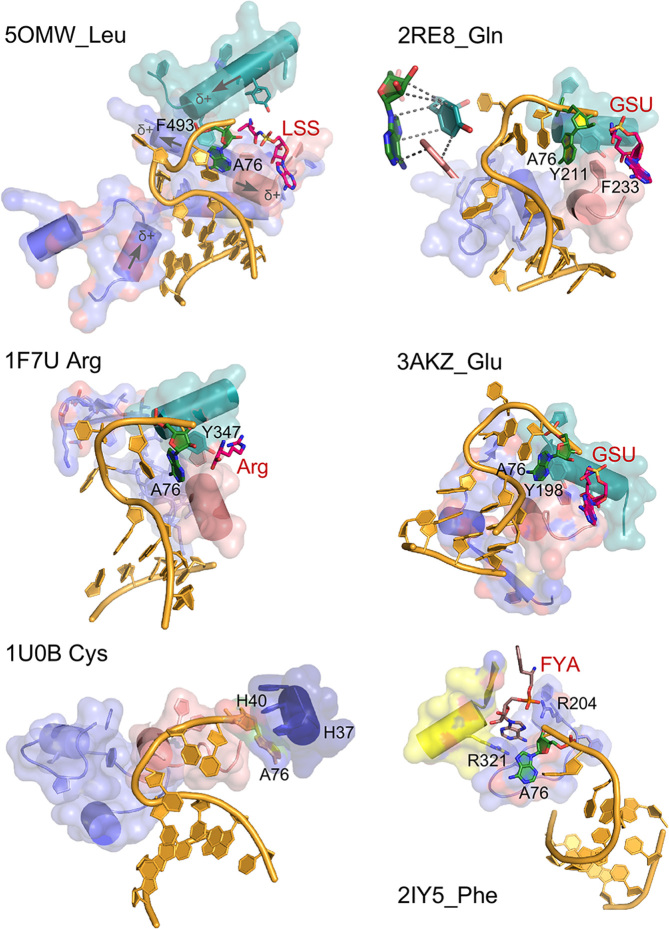
AARS•tRNA complexes interacting from the minor groove side. PDB IDs and amino acids are as indicated. Active-site ligands are abbreviated as follows: LSS, 5′-O-(l-leucylsulfamoyl)adenosine; Arg, arginine; GSU, O5′-(l-glutamyl-sulfamoyl)-adenosine; FYA, adenosine-5′-[phenylalaninol-phosphate]. Class I secondary structures depicted by color include a homologous section of connecting peptide 1 (CP1), slate; the ‘specificity-determining helix’ teal; and the base of the helix from the second crossover of the Rossmann fold, containing the signature GxDQ, salmon), and in the case of PheRS the Motif-2 loop (slate) and Motif-3 (yellow). Electrostatic influences of the dipole moments of various helices are indicated on the helices of 5OMW_Leu. Side chains that interact with the tRNA 3′-terminal adenosine (A76) are indicated by number. Note that in the 1U0B (CysRS) complex the 3′-terminal adenosine occupies an unproductive position close to the HIGH catalytic signature, suggesting that in the absence of aminoacyl-5′-adenylate, the adenine ring finds a site similar to that normally occupied by the adenine ring of the adenylate, underscoring its potential binding affinity for the heterocycle. Inset in 2ER8_Gln shows the interaction between A76 and a conserved aromatic side chain at the N-terminus of the specificity-determining helix.

Figure 7.

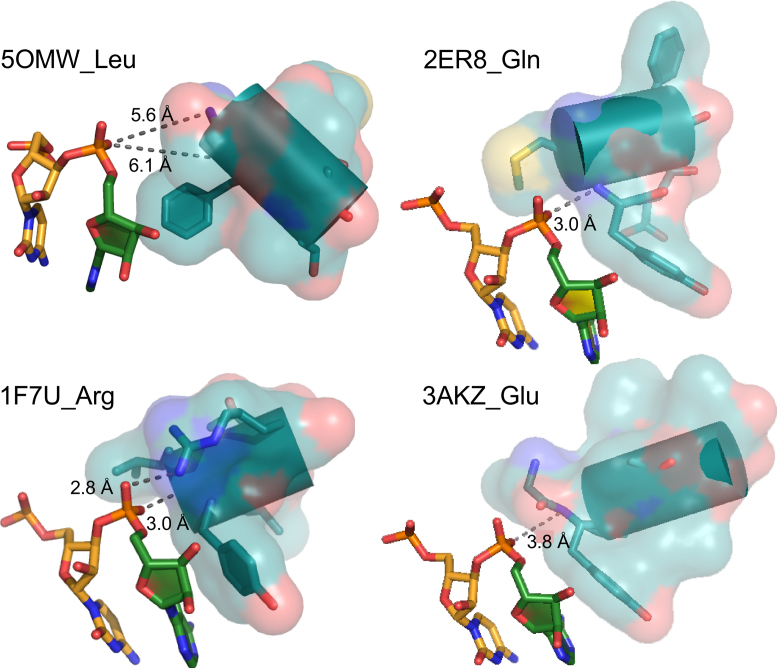
Interactions of Class I aaRS with the phosphate group of the 3′-terminal adenosine. The hairpin structure orients this phosphate group so that it points toward the N-terminus of the specificity-determining helix. Hydrogen bond distances shown suggest that, except in the case of 5OMW_Leu, these interactions may be strong. In 1F7U_Arg, the interaction is reinforced by a salt bridge between the phosphate group and R350.

Figure 8.

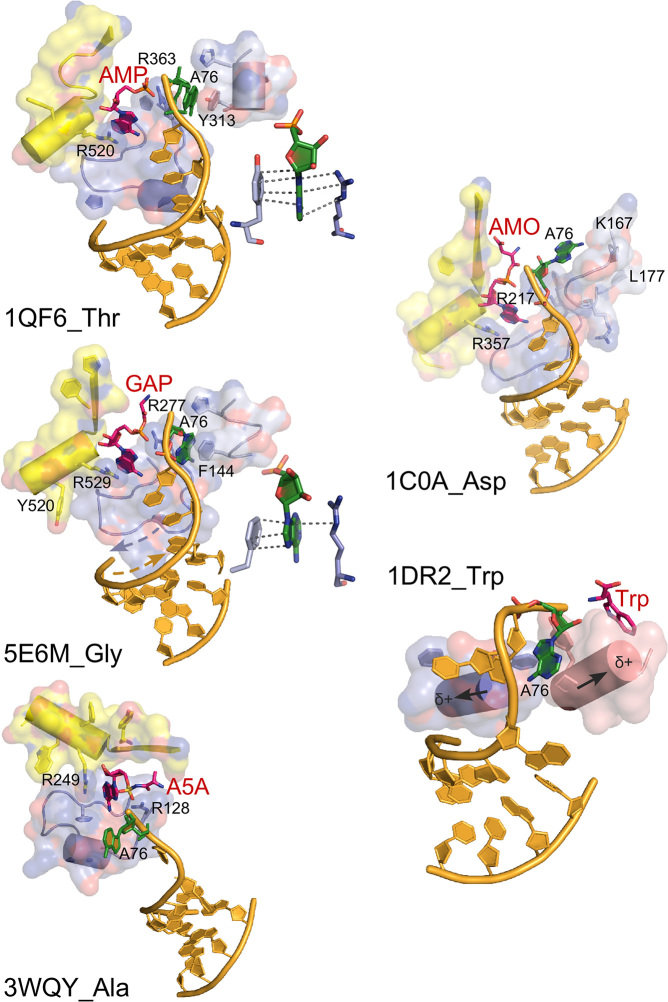
AARS•tRNA complexes interacting from the major groove side. PDB IDs and amino acids are as indicated. Active-site ligands are abbreviated as follows: AMP, adenosine 5′ monophosphate; GAP, glycyl-adenosine-5′-phosphate; AMO, aspartyl-adenosine-5′-monophosphate; Trp, l-tryptophan. Class II secondary structures depicted by color include the Motif-2 loop (slate), Motif-3 (yellow), and a loop that occurs prior to Motif-2 (salmon), and in the case of TrpRS, the base of the helix from the second crossover of the Rossmann fold (salmon) and a segment of CP1 (slate). Side chains that interact with the tRNA 3′-terminal adenosine (A76) are indicated by number. Antiparallel helix directions of the Motif 2 loop and the 3′-CCA terminus are shown as dashed arrows on 5EM6_Gly. Helix dipoles indicated for 2DR2_Trp suggest that the reorientation of the tRNA^Trp acceptor stem has moved it to a position that minimizes electrostatic disruption of the RNA double helix. Insets in 1QF6_Thr and 5E6M_Gly show interactions of A76 with a conserved aromatic side chain N-terminal to the Motif 2 loop and a conserved arginine from Motif 3.

There is considerable variation in the detailed configurations of the induced hairpin necessary for productive interaction with the minor groove (Figure 6). In all cases, base C74 is flipped out of the way of the 3′-terminal C75-A76, which are stacked in all cases. In the two Class IA complexes (5OMW_Leu and 1F7U_Arg) however, the discriminator base faces away from the active site, whereas in the two Class IB complexes (3AKZ_Glu and 2RE8_Gln) it is stacked on bases C75 and A76. Stacking on C75 in the latter cases introduces a C2′-endo configuration of the Discriminator base 73 ribose.

Despite these variations, however, all 3′ terminal hairpins entail proximity of the unpaired 3′-terminus to the N-termini of multiple α-helices (Figure 6). Two of these—those referred to elsewhere (34) as the specificity-determining and second-crossover helices (Figure 7)—arise from within the Class I Urzymes, and are thus likely more ancestral. The electrostatic potential field from the unpaired peptide NH groups (35) may facilitate formation of the hairpin by destabilizing the extended helical path of the 3′ CCA extension. The most distinctive and reproducible of such interactions is that between the specificity-determining helix, and the A76 phosphate group (36). This interaction orients the phosphate oxygen atom toward the N-terminus of that helix in four of the five Class I complexes (Figure 7), but is missing in the CysRS complex, in which the 3′-terminal adenosine interacts with the HIGH sequence which, for that reason, is likely artefactual.

On the other hand, the Motif-2 loop in each of the Class II complexes (Figure 8) covers and protects the 5′-terminal base-pair with the N-to-C polypeptide chain direction running antiparallel to the 5′-3′ direction of the 3′-terminal RNA strand in a manner anticipated by ((37); see 5E6M in Figure 8). The net dipole moment of the loop is expected to be relatively small, as that of an antiparallel β-hairpin is negligible (38). Its electrostatic properties should thus not perturb the tRNA acceptor stem appreciably. Notably, this structural motif coincides with the Class II Protozyme (5), and hence is also the oldest structural motif in Class II aaRS.

Side-chain interactions in the aaRS•tRNA complexes are, for the most part, idiosyncratic excepting a small number of possibly conserved interactions with the 3′-terminal A76. The latter are expanded in schematics associated with 2RE8_Gln (Figure 6), 1QF6_Thr, and 5E6M_Gly (Figure 8). In each case, the base associates with a conserved aromatic side chain, which, in the case of Class I association, is also associated with the non-polar face of the ribose (39).

Class II active sites use a pair of conserved arginine side chains to ‘clamp’ the adenosine of ATP in place (40). The two arginine residues appear also to interact with the 3′-terminal adenosine (Figure 8). In two cases (5E6M_Gly, 1FQ6_Thr) this adenosine fits between the Motif 2 arginine and an aromatic side chain conserved in a position N-terminal to the Motif 2 loop.

Interactions with the Discriminator base 73 divide into two groups, one (Leu, Arg, Trp, Ala, Asp and Gly) for which nearest approach distances average 3.9 ±0.7 Å for multiple distances, some of which make arguably specific interactions with the C6 substituent of the base, and another (Gln, Cys, Glu, Thr, Phe) for which the closest approach averages 10.3 ±1.1 Å. Notably, these groups do not correlate with experimental determinations of the strengths of the Discriminator base (24), agreeing in only 3 of 11 cases. Such poor correlation may arise either from inappropriate interpretations of experimental data or from the fact that static X-ray crystal structures sampled inappropriate configurations, so little can be concluded from the comparisons.

DISCUSSION

We highlight here the combinatorial power of three acceptor stem bases: 1, 2 and 73. The notion that these bases play such a central role in determining which groove is recognized by cognate aaRS has an interesting antecedent in studies of single mutations near the CCA terminus of the su⁺_III tyrosine suppressor tRNA (41). Both in vivo suppression and in vitro aminoacylation with TyrRS and GlnRS were used to assay the effects of mutating those bases. Some, but not all mutations to bases 1, 2, 72 and 73 changed the aminoacylation specificity from TyrRS (major groove) to GlnRS (minor groove), in keeping with what we report.

Whence the ‘Operational RNA Code’?

Primordial differentiation of the aaRS into Classes was likely a precondition for symbolic coding (1,21)

In turn, recognition elements differentiating tRNAs cognate to ancestral Class I and II aaRS must therefore also have been among the earliest informational signals to be embedded into tRNA acceptor-stem sequences. Groove recognition elements in Table 2B and the resulting rules in Table 4 therefore appear to be a sine qua non for the emergence of genetic coding via an operational RNA code. The fundamental solution to this problem appears to be that tRNA acceptor-stem sequences fall into two sets, one of which has a slightly greater thermodynamic tendency than the other to form the 3′-terminal hairpin enabling recognition of the CCA terminus from the minor groove. Ancestral aaRS Urzymes were then able to provide secondary structural elements that reinforced that distinction, giving rise to primordial, simultaneous, differentiation of amino acid types, aaRS and cognate tRNAs. That simultaneity is a non-trivial requirement for the emergence of symbolic coding. It reinforces the centrally important conclusion that the evolution of aaRSs was necessary and sufficient to embed protein folding rules (1,10,11,42) into the tRNA acceptor stem bases.

The 3′-terminal CCA tag on each tRNA must interact productively with each synthetase. Thus, bases that could function in aaRS Class differentiation begin with the Discriminator base (26) and the first base-pair of the stem. The patterns illustrated in Figure 1 belong to a broader set of coding relationships whose existence was proposed by Giegé (4) and re-iterated in (2). The latter authors coined the phrase ‘Operational RNA code’ to describe the putative acceptor stem recognition by cognate aaRS, without, however, specifying any relationships between acceptor stem base configurations and specific groups of amino acids. We previously reported (10,11) the identification of statistically significant relationships between identity elements for aaRS recognition and the sizes and particular subsets (β-branched, aliphatic, carboxylate) of amino acids.

It was not possible in that previous study to identify patterns anywhere in the tRNA sequences that partitioned the amino acids correctly into substrates for the two aaRS Classes. That frustrating failure left a substantial gap in how we consider the operational RNA code. Filling that gap is more pressing in light of the accumulated evidence (1,3,27,43,44) that the two aaRS Classes co-evolved from a single, bidirectional ancestral gene (5) that encoded a Class I precursor on one strand, and a Class II precursor, in frame, on the opposite strand.

An important implication of that simple, binary ancestry is that the earliest genetic coding consisted of just two amino acid type-to-codon assignments. The fact that amino acid size correlates so closely to patterns of acceptor stem bases (11) raised the obvious possibility that the two codewords were used operationally by ancestral aaRS to distinguish between large and small side chains, in keeping with a decisive primordial differentiation of the synthetases into Classes (45).

From another perspective, however, the functional recognition of any code embedded in tRNA bases reflects a one-way transfer of information from the tRNA, ultimately to the synthesis of aminoacylated tRNA. Thus, it is possible that the apparently complementary nature of tRNA recognition by aaRS is incomplete, and that the operational code can be extracted only from the tRNA bases themselves. Even if that is true from a contemporary perspective, however, the complementarity of tRNA•aaRS complexes themselves implies a detailed co-evolution of both polymeric forms over the entire duration of their co-existence.

Thus, specific recognition between elements of two sets necessarily implicates members of both sets (7). The hypothesis that the aaRS co-evolved with their cognate tRNAs, has been articulated in detail for the more recent co-evolution of several synthetase tRNA complexes (36,46,47) and remains an article of faith for earlier evolution. Reconstructing the remotely coupled ancestries of aaRS and cognate tRNAs during the expansion of the genetic code has, however, seemed inaccessible, especially absent details of the operational RNA code.

The unusually strong statistical significances reported here for coefficients in Tables 2, 4, and 6, together with the extensive cross-validation of Table 3 (Figure 4) imply that the relationships implicit in these tables are meaningful

It also is quite unusual that a solution of twenty simultaneous equations relating a binary-valued dependent variable exists that requires only 12 discrete-valued independent variables. Moreover, the coefficients in Table 2B are themselves discrete-valued as they all have either integer or half-integer values. These are properties of a system of digital equations. We note that this result is consistent with the fact that the system we have analyzed is fundamental to biology's computational code operating system (1,48). These features of the regression analysis and their resonance with structural and thermodynamic analysis compose persuasive evidence that the hierarchical groove-recognition model does represent important components of the operational RNA code.

The operational RNA code is a palimpsest, helping to elude previous attempts to define it

Evidence summarized in (1) that genetic coding began with a binary code that differentiated only between amino acids from Class I vs those from Class II implies that the sine qua non of the operational code lay in the discrimination by Class I and II aaRS of acceptor-stem base patterns that dictated recognition of the minor and major acceptor-stem grooves. Tables 2B, 5, and 7 appear to furnish those details, rounding out an earlier description of the operational code summarized in Table 6 (10,11).

Table 7.

AARS groove recognition rules implied by the topmost four acceptor-stem bases

Term	Estimate		Implications
Intercept	–0.5
β-branched	–2.5	Coeff > 0;	β-branched = > minor groove
			Unbranched = > major groove
–1,Y/R	2	Coeff >0;	Base −1 purine = > major groove
			Base −1 pyrimidine = > minor groove
1,Y/R	0.5	Coeff > 0;	Base 1 pyrimidine = > minor groove
			Base 1 purine = > major groove
2,Y/R	1	Coeff > 0;	Base 2 pyrimidine = > minor groove
			Base 2 purine = > major groove
2,≡/=	1	Coeff > 0;	Base 2 G,C = > minor groove
			Base 2 A U = > major groove
72,≡/=	–0.5	Coeff < 0;	Base 72 G/C = > major groove
			Base 72 A/U = > minor groove
β-branched*2,Y/R	–4	Coeff < 0;	Branched sc with Base 2 = C,U = > major groove
			Branched sc with Base 2 = G,A = > minor groove
1,Y/R*72,≡/=	–0.5	Coeff < 0;	C = G = > major groove;
			G = C = > minor groove
			A = U = > major groove
			U = A = > minor groove
2,Y/R*73,Y/R	–1	Coeff < 0;	Base 2 = C,U and Base 73 = C,U = > major groove
			Base 2 = C,U Base 73 = G,A = > minor groove
			Base 2 = G,A Base 73 = C,U = > minor groove
			Base 2 = G,A Base 73 = G,A = > major groove
2,Y/R*2,≡/=	–1	Coeff < 0;	C = > major groove
			U = > minor groove
			G = > minor groove
			A = > major groove
β-branched*72,≡/=	4.5	Coeff > 0;	Branched sc with Base 72 G, C = > minor Groove
			Branched sc with Base 72 A, U = > major Groove

Since the codon/amino acid assignment table was worked out (49), the essential puzzle has been the ‘operational code’ by which the aaRS recognize cognate tRNAs. For this reason, transfer RNA has remained the subject of substantial experimental and bioinformatic analysis, culminating in comprehensive Classification and Regression Tree (8) and Bayesian network (9) analyses. However, direct relationships between the recognition elements used by aaRS and the twenty canonical amino acids remain somewhat encrypted within those network treatments. They must be teased out in more detail (11) in order to fully understand the operational code. Pal and others (7) concluded that Class-specific tRNA sequence features do exist, although not in terms of strictly conserved nucleotides as had been anticipated. Thus, important information about aaRS Class-specific recognition was somehow hidden in tRNA sequences and thus inaccessible to traditional statistical methods.

Previous analyses differed from ours fundamentally in three respects. First, they sought Class-specific determinants, whereas we sought groove-specific elements. Second, they examined the entire sequence of tRNAs from all three domains, whereas we examined only a small portion of the acceptor stem of bacterial tRNAs. Finally, they implemented a classification algorithm, whereas we used multiple regression models that included up to two-way coupled interactions. A key decision that enabled the present analysis was to use groove recognition, rather than Class, as the dependent variable in the regression. It appears significant that when considered together with the distinction between amino acids with β-branched side chains, the small set of acceptor-stem bases illustrated in Figure 1 are necessary and sufficient to define without ambiguity the groove recognized by all 20 canonical aaRS. Similarly, the sparse matrix of identity elements compiled by Giegé is also necessary and sufficient to define four binary partitions of the canonical amino acids with similar precision (Table 6).

Our methods appear to have uncovered layers of meaning that accrued as the genetic code—and the number of distinct isoaccepting tRNA genes—expanded (Figure 5). Thus, like a rubbed-out medieval manuscript that was overwritten, it appears to be a palimpsest, making it harder to decode it. The operational RNA code is defined by coefficients in Tables 2 and 6

The operational RNA code emerges from this work as a set of five overlapping distinctions between groups of amino acids that can each be identified, statistically, with rules arising from specific patterns of acceptor stem bases

As noted in Materials and Methods, coefficients in Table 2 derive from a full experimental matrix involving the topmost four acceptor-stem bases from all twenty tRNAs, whereas those in Table 6 were estimated from a sparse matrix representing identity elements identified throughout the topmost five base pairs in the acceptor stem together with the Discriminator base 73 (10,11). Regression models in Table 6 have been updated from those described previously (11) to correct inadvertent errors in the design matrices identified during the extensive cross-referencing that accompanied creation of Supplementary Table S1 and Table 2B. No substantive changes have arisen, although the model for size in Table 5 differs slightly from that in (11). Coefficients for all models are summarized visually in Figure 9, in the manner of Figure 5, to illustrate their location within the acceptor stem, and how they define the operational code. Details of this work (Figures 5 and 9, supplementary §B and §C, Supplementary Tables S2–S3) reinforce our previous discussion of the coding properties of acceptor stem bases (10,11).

Figure 9.

Elements of the ‘Operational RNA Code’ (10,11). Coding properties of the tRNA acceptor stem are represented schematically, to illustrate graphically relationships from each regression model in Tables 2B and 6. Bases that do not contribute to the respective regression model are omitted. Interpretation of the schematic key is given in Figure 5.

The presumptive acceptor-stem coding elements in Tables 2,5,6 and Figure 9 differentiate both cognate aaRS and the corresponding amino acids according to different characteristics—the groove recognized by the aaRS, the size of the side chain, and whether or not it is β-branched, carboxylate, or aliphatic. Their idiosyncrasy, together with the hierarchy illustrated in Figure 5 strongly suggest that tRNA acceptor stem bases form a palimpsest in which ID elements have been successively overwritten to accommodate new amino acids to the alphabet.

The operational RNA code is fully-defined by acceptor-stem bases

One might have expected that 3D structural data from the tRNA•aaRS co-crystals structures would be necessary to elucidate these tRNA coding properties. It is possible that such 3D data could be used to build a complementary analysis to that of the bases, but that possibility appears to remain beyond our current resources as the structural database remains too small to support statistically rigorous identification of the complementarity-determining amino acid side chains at aaRS–tRNA interfaces. The present work began with the summary data provided by Geigé (25). Updates (12,50) represent primarily expansions of the idiosyncratic variation observed in archaea and eukarya and thus are not expected to alter our conclusions (see Table 1).

Several considerations make us confident that conclusions presented here merit consideration in their own right. (i) The substantially higher residual signal of ancestral middle-codon base pairing in bacterial aaRS sequences (27) implies that the translation systems in Eubacteria lie closer to the root than those in Archaea and Eukarya. (ii) The comprehensiveness, high internal consistency (Figure 3), and robust cross-validation (Figure 4) of our regression modeling of groove recognition signals in bacterial tRNA acceptor stems furnish exceptionally strong statistical support. (iii) The resonance of our conclusions with previously described models for the origin of tRNAs from molecular fusion events (22,23,51–54) provides mutually reinforcing support for both types of modeling.

Testing the Operational RNA codes can clarify the origins of translation

Further validation of these codes can be sought by (i) establishing their generality, (ii) testing them using designed experiments and (iii) using them to constrain joint sequence reconstruction of aaRS•tRNA pairs from both aaRS Classes in search of evidence for simpler ancestral coding alphabets.

How well do the codes in Figure 9 generalize to archaeal and eukaryotic tRNAs?

The extensive consistency of three previous compilations of tRNA identity elements across domains (Table 1) is important evidence for the generality of models derived from them. Testing the model for groove recognition with a broader sequence database is, however, problematic because the additional sequence ambiguities across domains will deplete the design matrix (Supplementary Table S1), but would nevertheless be worthwhile to highlight interesting outliers.

Digital aspects of the operational codes suggest testing them with designed experiments using incomplete factorial sampling

Mutagenesis and commercial RNA synthesis have both made combinatorial experimental design (55) a practical option. We have shown that aaRS Urzymes will aminoacylate full-length tRNAS (3) and are currently investigating the extent to which they aminoacylate minihelices (56,57). The activity with which Urzymes acylate minihelices may be sufficient to permit high-throughput analysis of combinatorial designs to test specific predictions of these codes.

Patterns identified in this work should constrain multiple sequence alignments in the reconstruction of ancestral tRNA sequences

Although derived from contemporary multiple sequence alignments, they furnish constraints that may help resolve ambiguities, particularly as reconstructed sequences approach ancestral nodes where two related amino acids fuse into a single precursory amino acid type. In this way, they may help map out plausible joint ancestries of the Class I and II aaRS tRNA substrates. Such work will, however, require enhancing computer algorithms used for sequence reconstruction (58).

Rules arising from interaction between the two bits of base 2 (i.e. 2,Y/R*2,≡/=) are closely related to contemporary codon middle bases, identifying an early image of the codon-anticodon interaction in the acceptor stem

An important thread in the literature on the origin of the tRNA molecule entails the notion that the operational RNA code first began coding as ancestral minihelices, and later duplicated and fused in some fashion to produce full-length, mature tRNAs (2). A recurrent element of that thread (22,23,51–54) is the persistent evidence that the 3′ end of the acceptor stem, just 5′ to the Discriminator base, often contains three bases similar to the anticodon (54). Among the predictors in Tables 2 and 7 only the interaction between the two bits for base 2 (2,Y/R*2,≡/=) uniquely associates each individual base with a specific groove (Table 7).

This unique specification of the bold-faced entries in Table 7 is evidently related to the middle codon bases. Amino acids with U as the codon middle base are recognized by PheRS, LeuRS, ValRS, IleRS, and MetRS via the minor groove of their cognate tRNAs; those with a C are recognized by SerRS, ProRS, ThrRS, and AlaRS via the major groove; codons with middle base A are recognized by TyrRS, HisRS, AsnRS, LysRS, and AspRS via the major groove; and those with middle base G are recognize by CysRS and ArgRS via the minor groove. Thus, groove recognition by 16 of the 20 aaRS occurs consistently with the rule implied by the bold-faced coding elements in Table 7. Thus, the relative importance of base 2 in the tRNA acceptor stem is conspicuously consistent with both aaRS:tRNA pairing and the codon table!

It is noteworthy that the logWorth values for base 2-related coefficients in Tale 2 are statistically highly significant despite the fact that the actual bases that those rules imply cannot be identified directly by inspection of Figure 1. For example, only two of the twenty amino acids have codon middle bases consistent with rules adduced in the previous paragraph. Of those tRNAs that code for second-column amino acids, only tRNA^Thr actually has C as base 2; similarly, tRNA^Cys is the only tRNA from the fourth column that actually has G as base 2. None of the first-column tRNAs have U, and none of the third-column tRNAs have A as base 2.

Regression analysis appears to have uncovered another underlying correlation distinct from the rules in Table 5, that also has been overwritten by other rules implicit in Table 2B that modify significantly the meaning of base 2 in contemporary sequences. It is tempting to suggest that rules that overrode base 2-dependent rules occurred sequentially, after the rules implied by the (2,Y/R*2,≡/=) interaction had functioned at an earlier stage. This result unexpectedly confirms previous work of Di Giulio (22,23) and Rodin and Ohno (53,54) by suggesting that the tRNA acceptor stem retains a palimpsest of the anticodon. The image of the codon-anticodon interaction in the tRNA acceptor stem raises the key question of whether or not ancestral tRNA minihelices interacted with proto-mRNAs.

Did minihelices interact with proto-mRNAs?

Could tRNA minihelices once have been capable of symbolic information transfer from RNA sequences into rudimentary coded polypeptides according to codon sequences in proto-mRNAs and hence been important evolutionary intermediates in the transition from primordial stereochemically-based information transfer into computationally-based genetic coding (1)? Others (59) have postulated alignment of minihelix pairs via complementary hydrogen bonding between bases in exposed minihelix loops. That ingenious idea was supported by experimental data on complex formation. However, without a mechanism to transfer information from proto-mRNA to an anticodon present in the minihelix, it could not have functioned, via ancestral aaRS selection, to embed the information now evident in Tables 2B and 6 into the tRNA acceptor stem. Moreover, if the operational ‘code’ contained no image of the anticodon, one would then need to postulate a hidden level of coding communicating acceptor stem sequences and the anticodon, thereby violating a parsimony principle.

Two additional requirements would have to have been met in order for the anticodon image in tRNA minihelices to interact specifically and productively with potential codon sequences in proto-mRNA.

• The minihelix would have to form a triple helix with the proto-mRNA such that the major groove of the minihelix 3′-terminus ran antiparallel to the codon. The minor groove of RNA double helices is notably ambiguous, as it is used to validate formation of Watson-Crick base pairs in the 30S ribosomal decoding mechanism (17,60) via formation of the A-minor motif. However, unique information can be read from the DNA and conceivably also from the RNA major groove (19,30). Sequence-specific triple helical configurations were studied by Roberts and Crothers (61), who noted marked compositional effects ranging over ∼10 kcal/mole for formation of 12-base DNA and RNA polypyrimidine strands binding to 28-base hairpins constructed with 12-base polypurines at the 5′-terminus. More recent NMR experiments characterized the structures and stability of a triple-helical RNA in which Watson-Crick base pairs formed between two antiparallel strands connected by a tetraloop formed sequence-specific Hoogstein pairs with a designed sequence 3′ to the double stranded region (62). Complementary base pairing of the third strand occurred over 7 bases in that structure, albeit between parallel strands, which makes it a poor model for codon–anticodon interaction. Comparable experiments might be done using antiparallel arrangements of complementary sequences. Roles for triplex RNA helices in contemporary organisms have also been recently reviewed (63).

• Codon-dependent polymerization of amino acids would also require that successive minihelices aligned in sequence be capable of juxtaposing their 3′-aminoacylated terminal adenosines appropriately to permit reaction between them. Class I aaRS:cognate tRNA complexes have shown that the 3′-CCA terminus is conformationally flexible, making an abrupt hairpin to embed the terminal adenosine into the active site, despite primary interactions with the minor groove (12). The added length of the DCCA terminus would appear twice in such complexes, and would need to span only the length of a codon. It may therefore have served to juxtapose the 3′-acyl-adenosine moieties of successive minihelices, giving rise to a codon-informed sequence of polyaminoacids at a stage of molecular evolution prior to the displacement of coding function from the acceptor stem by the advent of the ribosomal 30S subunit.

Thus, neither of these requirements is entirely implausible, in light of published work.

This discussion poses many new questions—e.g. (i) What is the origin of the DCCA 3′-terminal extension of tRNA acceptor stems? (ii) Was it present at the time synthetases began to acylate minihelices? (iii) Did codewords using the two purines as middle bases accompany those with pyrimidines as middle bases or did these two events occur sequentially? (iv) Was the original readout confined to a single strand, or was bidirectional coding used in some way from the beginning? Reading of putative messages by acylated minihelices also is equally suited to either strand of a double-helical RNA molecule. Thus, it is consistent with bidirectional coding as outlined by Rodin and Rodin (53,64) and implied by the evidence that the first aaRS were produced from bidirectional genes (5). Despite the need to answer these questions, the additional validation of an image of the codon-anticodon interaction in the tRNA acceptor stem given here strengthens previous suggestions that the transfer RNA molecule evolved in at least two stages, both of which may have functioned in codon-directed protein synthesis with or without participation of proto-ribosomes (65,66).

Moreover, we emphasize that the remote ancestry of genetic coding in a peptide/RNA cooperation that implemented a reduced 2- or 4-letter alphabet (1) mandates that the operational code in the tRNA acceptor stem co-evolved with the aaRS. The consistency of the full set of rules in Table 2B with the reduced set in Table 4 therefore reinforces our conclusion that the acceptor stem must have contained an image of the anticodon from the very beginning of codon-directed protein synthesis.

Expansion of the simple operational code, the advent of the anticodon, and stages of protein evolution

As the code expanded from a binary code to the contemporary universal code specifying 20+ amino acids new additions to the alphabet appear to have made it necessary to modify the simplest rules summarized in Table 4. Changes necessary to enhance discrimination between variant synthetases that assumed specificity for new amino acids also eventually created the conflicting rules evident in the contrasts between Table 7 and Figure 1. These changes to the operational code also may have overwritten the original meaning of base 2 as the middle codon base.

Figure 5 might be seen as a putative model for successive incorporation of new amino acids into the genetic code. Six of the first eight amino acids on the list suggested as the earliest amino acids by the multivariate analysis of Trifonov (67) are included in the set of 14 amino acids. However, the aromatic amino acids, plus histidine and methionine are also included in our smallest subset, but are the most recent additions to the code according to Trifonov. Notably, the branched amino acids all appear early in Trifonov's lists, but require a different set of rules for groove recognition. Thus, although aspects of the evolution of the code may be revealed by the succession in Figure 5, there are alternative explanations for the separation of the 20 amino acids into successive subsets. For example, the code may actually have accumulated aromatic amino acids late, but rotation of the subclass C aaRS about the acceptor stem to approach cognate tRNA acceptor stems via opposite grooves (68) may have allowed them to obey the simplest rules (i.e. 2 coefficients) without ambiguity.

More likely in our view, increasing ambiguity of the anticodon image in the acceptor stem enhanced the selective advantage of exporting the anticodon itself to a separate location in a larger tRNA molecule, so that the operational code could continue to assume enhanced precision without interfering with the anticodon itself and inadvertently corrupting the coding table. Moreover, anticodon bases significantly influence recognition by many of the aaRS in the contemporary ‘operational code’ by encoding the polarity of amino acid side-chains (10,11).

The simplicity of the four choices of amino acid types enabled by the operational code (Figure 9) and the fact that some of the rules evident from the analysis are actually buried in contemporary acceptor-stem sequences suggest an alternative temporal order to the appearance and evolution of protein secondary and tertiary structures. The initial two codewords for large and small amino acid side chains enabled the search for proto-mRNAs with binary patterns (69), which may already have begun to discriminate between extended β- and α-helical structures. That distinction would have been reinforced by adding selections for β-branched and aliphatic versus polar side chains, leading to a finer distinction between the two types of chain segments. Adding the anticodon, with its new precision for side-chain polarity would then have enabled a tuning of differences between core and surface residues (10,11), stabilizing and continuing to shape the evolution of protein tertiary structures.

There is an appealing continuity in this model for codon development, arising initially from aaRS groove discrimination in the acceptor stem. Thus, characteristics of the operational code are consistent with recent suggestions that protein structures evolved coordinately with the alphabet size and that the evolution of the genetic code also traces the discovery of protein folding rules (1). Correlations between secondary and tertiary structures of ribosomal proteins and the estimated order of rRNA additions motivated a similar hypothesis from an entirely different direction (70). Those authors postulated staged protein evolution, earlier stages marked initially by the absence of secondary structures, followed by the presence of β-, then α-structures, and then only after a prolonged development of secondary structures, by the emergence of tertiary structures. Their hypothesis, assumes co-evolution of protein folding with the genetic code, but makes no reference to how properties of the genetic code might have undergone comparable development. Thus, the present work furnishes a necessary complement to their observations.

Watson–Crick base-pairing swept aside the conceptual mystery of genetic inheritance in a single stroke, leaving codon-dependent translation as arguably the quintessential remaining mystery of evolutionary molecular biology. Because it entails such numerous, diverse, and non-trivial problems—the need to (i) mobilize ATP to activate amino acid carboxylate group for protein synthesis; (ii) protect activated amino acids until they could acylate tRNA; (iii) establish specific recognition of transfer RNAs by aaRS, i.e. from complementary polymer families, and (iv) differentiate them simultaneously into cognate pairs; (v) build the codon table by adaptive radiation of cognate aaRS/tRNA pairs; (vi) rapidly stabilize an optimal coding table and (vii) make the codon table consistent with protein folding rules—the origin of genetic coding and protein synthesis cannot be described with anything like the elegant precision and finality of the origins of inheritance. In this work, we have tightly constrained the manner in which the operational code came into being, by identifying relationships between acceptor stem bases and cognate aaRS, rationalizing their effects in structural and thermodynamic terms, and relating them to the universal code.

In summary, the regression analyses presented here suggest that detectable patterns from the operational RNA code have survived in today's tRNA/aaRS recognition complexes, supporting the inference that the distinct acceptor stem conformations leading to major or minor groove recognition are largely determined by thermodynamic differences in base stacking free energies. It also confirms a hidden ancestry of codon-anticodon pairing in the acceptor stem. That ancestry implies that the earliest synthetase recognition identity elements in acceptor-stem minihelices also could have participated in codon-dependent polymerization of amino acids employing a code similar to the universal genetic code, establishing a basis for continuity between that code and much simpler ancestors, for whose participation we argued previously (1).

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

National Institute of General Medical Sciences [R01-78227 to C.W.C. Jr]. This publication was made possible also through the support of a grant from the John Templeton Foundation. The opinions expressed in this publication are those of the author(s) and do not necessarily reflect the views of the John Templeton Foundation. Funding for open access charge: Center for Scientific Review [GM78227].

Conflict of interest statement. None declared.