Abstract
Introduction
Within the field of Pharmacovigilance, the most common approaches for assessing causality between a report of a drug and a corresponding adverse event are clinical judgment, probabilistic methods and algorithms. Although multiple methods using these three approaches have been proposed, there is currently no universally accepted method for assessing drug-event causality in ICSRs and variability in drug-event causality assessments is well documented.
Objective
This study describes the development and validation of an Individual Case Safety Report (ICSR) Causality Decision Support Tool to assist Safety Professionals (SPs) performing causality assessments.
Methods
Roche developed this model with nine drug-event pair features capturing important aspects of Naranjo’s scoring system, selected Bradford–Hill criteria, and internal Roche safety practices. Each of the features was weighted based on individual safety professional (n = 65) assessments of the importance of that feature when assessing causality, using an ordinal weighting scale (0 = no importance, 4 = very high importance). The mean and associated standard deviation for each feature weight was calculated and were used as inputs to a fitted logistic equation, which calculated the probability of a causal relationship between the drug and adverse event. Model training, validation, and testing were conducted by comparing MONARCSi causality classifications to previous company causality assessments for 978 randomly selected, clinical trial drug-event pairs based on their respective features and weights.
Results
The final model test, a two-by-two comparison of the results, showed substantial agreement (Gwet Kappa = 0.77) between MONARCSi and Roche safety professionals’ assessments of causality, using global introspection. The model exhibited moderate sensitivity (65%) and high specificity (93%), high positive and negative predictive values (79 and 88%, respectively), and an F1 score of 71%.
Conclusion
Analysis suggests that the MONARCSi model could potentially be a useful decision support tool to assist pharmacovigilance safety professionals when evaluating drug-event causality in a consistent and documentable manner.
Electronic supplementary material
The online version of this article (10.1007/s40264-018-0690-y) contains supplementary material, which is available to authorized users.
Key Points
| The MONARCSi exploratory causality decision support tool is a novel drug-event pair causality assessment method that combines selected parts of Naranjo’s original score with aggregate feature weights determined by safety professionals and a logistic function. |
| The MONARCSi model could potentially be a useful decision support tool to assist safety professionals in evaluating causality when conducting medical reviews of potential drug-related safety events. |
Introduction
Within the field of pharmacovigilance, the three most common approaches for assessing causality between a report of a drug and a corresponding adverse event (i.e., drug-event pair) are clinical judgment, probabilistic methods, and algorithms [1, 2]. Clinical judgment or global introspection uses subjective individual assessments by clinical experts based on their knowledge and experience in the field to assess causality. Probabilistic methods use specific ‘features’ of each drug-event pair within the individual case safety report (ICSR) to transform a prior estimate of probability calculated from existing epidemiologic information into an estimate of probability of drug causation. Algorithms typically use a set of specific ‘yes/no’ questions regarding ‘features’ of a drug-event pair that have associated scores for calculating a potential cause–effect relationship.
Although multiple methods using these three approaches have been proposed, there is currently no universally accepted method for assessing drug-event causality in ICSRs [1]. Publications within the field of pharmacovigilance since the 1980s have evaluated the performance of these approaches with varying results for reproducibility and validity. In general, agreement between methods is poor [1, 3–6].
Overall, algorithms demonstrate relatively high agreement with other algorithms [7, 8]. When compared to global introspection, algorithms demonstrate high sensitivity but low specificity [9]. Probability or Bayesian approaches are difficult to use because they require precise quantified information for each parameter or drug-event feature, to model the probability of causation [1, 2]. Consequently, global introspection is the most commonly used approach to determining drug-event causality [1, 2]. However, global introspection as a method has its own deficiencies. Low inter-rater agreement between clinical experts when evaluating the same drug-event ICSR cases has been well documented in the medical literature [10–13]. This phenomenon is part of a larger finding that clinical judgment is often inferior to, or no better than, more structured methods of decision making that use simple algorithms for tasks such as disease diagnosis, prognosis, and treatment selection [14–16].
One of the challenges in determining drug-event causality is that there is no objective ‘ground truth’ (i.e., gold standard) to compare the relative performance of either an algorithmic or human expert’s assessment [5, 13, 17]. Given this lack of ground truth, known benefits of using algorithms, and the variability in drug-event causality assessments by safety professionals, we aimed to develop a hybrid decision support tool that would combine a clinical assessment of the presence or absence of specific drug-event ICSR features with an algorithm to arrive at a ‘weight of evidence’ score for the probability of drug-event causality.
One commonly used algorithm is the Adverse Drug Reaction Probability Scale developed in 1981 by Naranjo and colleagues to standardize causality assessments [18]. The key advantage of the Naranjo score is its simplicity of use and clarity [2]. Additionally, the Naranjo score results in a significant increase in inter- and intra-rater agreement compared with global introspection alone [18]. However, algorithms alone lack the ability to accurately provide a quantitative assessment of the probability of the causal relationships [17].
In contrast to the pure algorithmic approach, Theophile and colleagues have explored the utility of using a ‘logistic approach’, which takes a summary score from the French Pharmacovigilance Algorithm (similar to Naranjo) and fits this to a logistic function to estimate the probability of drug-event causality [3, 19]. This approach has demonstrated high sensitivity at the expense of poor specificity, compared to expert consensual judgment for drug-event pairs. In contrast, the French Pharmacovigilance Algorithm alone showed poor sensitivity but good specificity, relative to human judgment [3]. The comparatively good sensitivity and positive predictive values of the logistic method suggest that it may be a useful tool in combination with algorithms in the routine assessment of drug-event pairs.
The key requirements for a combined algorithmic approach are simplicity, transparency, and validity. The resulting tool (i.e., model) must be simple enough for safety professionals to use intuitively by answering simple yes/no questions about the features of a drug-event narrative. The underlying algorithm should be transparent and understandable such that a user with a minimal quantitative/computational background can walk through the underlying calculations for a specific drug-event pair and obtain the same results as the model. Finally, the tool should demonstrate validity with a relatively high degree of agreement with human expert judgment using global introspection.
This study describes the development and validation of an exploratory individual case safety report (ICSR) causality decision support tool based on aspects of the well-known Naranjo causality score, modified to incorporate aggregated feature weights. This tool then uses a fitted logistic transformation of the final scores similar to Theophile and colleagues, to estimate the probability or confidence level for causality between a drug and event. The final result is a binary classifier for determining if a drug event is ‘related’ or ‘not related’ to potentially assist safety professionals in evaluating potential safety events.
Methods
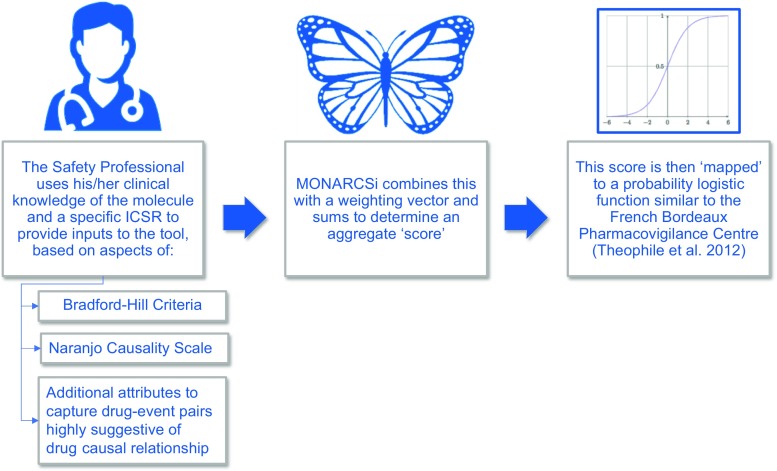
From 2016 to 2017, Roche scientists developed the MOdified NARanjo Causality Scale for ICSRs (MONARCSi) exploratory causality decision support tool. The approach uses a feature matrix and feature weights determined by aggregating how important the presence or absence of a specific drug-event feature is to safety professionals. Final scores, obtained by using the feature matrix for a specific drug-event pair, are then logistically transformed to estimate the probability or confidence level in the ‘relatedness’ or ‘unrelatedness’ for drug-event causality. Finally, based on the logistic probability level for a given drug-event pair, the model then assigns a ‘binary’ classification label: related vs. unrelated. Validation of the new tool was assessed against a database of completed clinical trial drug-event pairs with final company causality determinations and by comparing MONARCSi and Naranjo raw scores to assess concurrent validity. Figure 1 illustrates the process flow for the MONARCSi causality decision support tool. In this section, we describe the technical details in each step of the development process.
Fig. 1.
MOdified NARanjo Causality Scale for ICSRs (MONARCSi) causality decision support tool process flow. ICSR individual case safety report
Drug-Event Pair Feature Matrix
Using the basic framework and scoring approach of the Naranjo score, Bradford–Hill criteria for causality, [18, 20] and internal Roche practices in pharmacovigilance, we developed a nine-row by three-column matrix with the drug-event pair features (Table 1). Features are noted as being present (+ 1), absent (− 1), or unknown/not applicable (0) based on the safety professional’s assessment of a specific drug-event pair narrative.
Table 1.
Nine-row by three-column MONARCSi drug-event pair feature matrix (); each feature is noted as present (yes), absent (no), or unknown/not applicable (UNK/NA) by a safety professional evaluating a drug-event pair
| Feature(Row i,Column j) | Yes(1) | No(2) | UNK/NA(3) |
|---|---|---|---|
| Significant safety event(1) | F1,1 = + 1 | F1,2 = − 1 | F1,3 = 0 |
| Previous association(2) | F2,1 = + 1 | F2,2 = − 1 | F2,3 = 0 |
| Temporality(3) | F3,1 = + 1 | F3,2 = − 1 | F3,3 = 0 |
| Mechanism of action(4) | F4,1 = + 1 | F4,2 = − 1 | F4,3 = 0 |
| De-challenge(5) | F5,1 = + 1 | F5,2 = − 1 | F5,3 = 0 |
| Re-challenge(6) | F6,1 = + 1 | F6,2 = − 1 | F6,3 = 0 |
| Dose response(7) | F7,1 = + 1 | F7,2 = − 1 | F7,3 = 0 |
| Experimental data(8) | F8,1 = + 1 | F8,2 = − 1 | F8,3 = 0 |
| Confounding factors(9) | F9,1 = − 1 | F9,2 = + 1 | F9,3 = 0 |
Each feature is assigned a value for being present (+ 1), absent (− 1), or UNK/NA (0) based on the safety professional’s assessment of a specific drug-event pair narrative. Each feature element is multiplied by its corresponding element in the weighting matrix () and summed to create the aggregate score (see Table 3 and Eq. 1)
Development of Weighting Scale for MONARCSi Drug-Event Features
To determine a causality score based on the presence of absence of drug-event features, each item in the feature matrix is multiplied by corresponding weights. The original adverse drug reaction score by Naranjo used pre-specified weights (e.g., 0, ± 1, ± 2) [18]. In contrast, we wanted to use the judgment and experience of individuals that perform causality judgments regularly, to best determine the feature weights for MONARCSi. The MONARCSi team used an independent blinded survey (Google forms) to collect individual feature weights from safety professionals across Roche safety science work areas.
Safety Professional Feature Weighting Survey
Participating Roche safety professionals (n = 65; approximately 86% response rate) from three distinct geographic regions (North America, Europe, Asia Pacific) and four of the most common Roche safety science work areas [oncology (40%), immunology (29%), mature products (14%), and early development (17%)] were polled for their assessment of the importance of each feature’s presence (or absence) when assessing causality (Table 2). The experience level among the safety professionals varied with approximately 50% of the group having greater than 250 case evaluations of causality (during medical reviews of clinical trial cases) and approximately 25% having evaluated fewer than 50 ICSRs. The remaining proportion of the safety professional sample ranged between 50 and 250 cases. For each of the nine features, the safety professionals rated the importance of the feature to causality, using a five-point ordinal weighting scale (0 = no importance, 1 = low importance, 2 = medium importance, 3 = high importance, 4 = very high importance).
Table 2.
Roche safety professionals participating in the feature weight survey by geographic region, safety science work area, and individual case safety report (ICSR) causality assessment experience
| Safety professional category | Label | Count | %Total |
|---|---|---|---|
| Geographic region | Asia Pacific | 6 | 9 |
| Europe | 22 | 34 | |
| North America | 37 | 57 | |
| Total | 65 | 100 | |
| Safety science work area | Immunologya | 19 | 29 |
| Early development | 11 | 17 | |
| Mature products | 9 | 14 | |
| Oncologyb | 26 | 40 | |
| Total | 65 | 100 | |
| Causality assessment experience (total no. of ICSRs) | < 50 | 14 | 24 |
| > 50–100 | 4 | 7 | |
| > 100–150 | 7 | 12 | |
| > 150–200 | 2 | 3 | |
| > 200–250 | 3 | 5 | |
| > 250 | 29 | 49 | |
| Totalc | 59 | 91 |
aA single individual from the central nervous system group was combined into the immunology safety science work area
bOne individual in both early development and oncology was combined into the oncology safety science work area
cSix individuals did not specify an experience level
Assessment of Variability in Weights Assigned to Each Feature by Safety Professionals
Variability in safety professionals’ judgment of a feature’s importance across safety science work areas and geographic regions was assessed descriptively. Additionally, we performed an ad-hoc analysis of the means and standard deviations for each feature’s confirmatory drug-event pair weights and dis-confirmatory weights across all of the geographic and safety science work area categories (separately) using a one-way analysis of variance. For these tests, we used alpha = 0.05 with the following null hypotheses:
- H01
no difference in confirmatory (or dis-confirmatory) drug-event pair feature means across the geographic regions;
- H02
no difference in confirmatory (or dis-confirmatory) drug-event pair feature means across the safety science work areas
Weighting Matrix
A weighting matrix () was created by aggregating individual weights from the safety professional survey results. The resulting was populated with the mean weights across the sample of safety professionals for both presence (i.e., confirmatory) and absence (i.e., dis-confirmatory) of features where 0 = no importance, 1 = low importance, 2 = medium importance, 3 = high importance, and 4 = very high importance (Table 3).
Table 3.
Nine-row by three-column MOdified NARanjo Causality Scale for ICSRs (MONARCSi) drug-event pair feature weighting matrix (); populated with mean weights for importance of presence or absence of each feature in determining causality
| Feature(Row i, Column j) | Yes(1) | No(2) | UNK/NA(3) |
|---|---|---|---|
| Significant safety event(1) | W 1,1 | W 1,2 | W 1,3 |
| Previous association(2) | W 2,1 | W 2,2 | W 2,3 |
| Temporality(3) | W 3,1 | W 3,2 | W 3,3 |
| Mechanism of action(4) | W 4,1 | W 4,2 | W 4,3 |
| De-challenge(5) | W 5,1 | W 5,2 | W 5,3 |
| Re-challenge(6) | W 6,1 | W 6,2 | W 6,3 |
| Dose response(7) | W 7,1 | W 7,2 | W 7,3 |
| Experimental data(8) | W 8,1 | W 8,2 | W 8,3 |
| Confounding factors(9) | W 9,1 | W 9,2 | W 9,3 |
Each feature in the weighting matrix () is assigned a mean weight from the sample of safety professionals for both presence (i.e., confirmatory) and absence (i.e., dis-confirmatory) of features where 0 = no importance, 1 = low importance, 2 = medium importance, 3 = high importance, and 4 = very high importance. Mean feature weights are multiplied by the corresponding element in the feature matrix () and summed to create the aggregate score (see Table 1 and Eq. 1)
UNK/NA unknown/not applicable
A similar matrix (), was created that contains the standard deviations of the feature weights across the sample of safety professionals polled. This allowed an estimate of the uncertainty in the final MONARCSi score based on the safety professional sample, using the mathematic rule of combining variances for a summed quantity [21].
Creation of the Causal Probability Score
To estimate the causal probability for a drug-event pair, the first step is to calculate the MONARCSi score (SM) based on the presence or absence of features. Based on the inputs from the safety professional, each element in the feature matrix () is multiplied by its corresponding element in the and summed across all nine features, yielding a final MONARCSi score as shown in Eq. (1).
| 1 |
In addition to the mean feature weights, the associated standard deviation for each feature weight was also calculated from the safety professional survey to allow estimation of the uncertainty associated with the final probability of a causal relationship (Eq. 2) [21]:
| 2 |
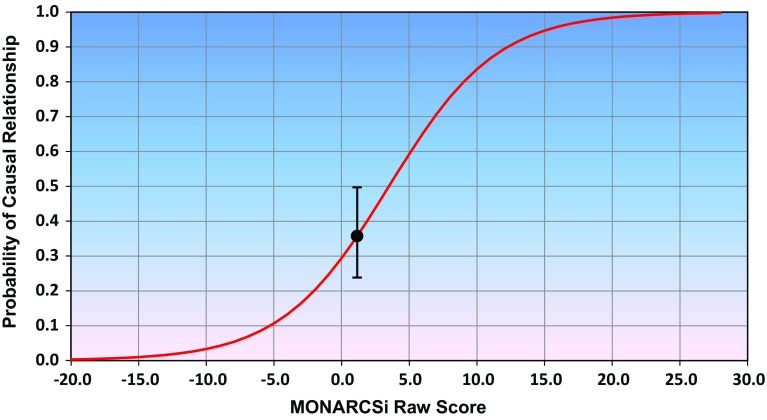
The final step is to use the resulting MONARCSi score (SM) and the associated standard deviation as inputs to a fitted logistic equation, (Eq. 3) where the parameters α and β are estimated using logistic regression. The resulting equation calculates the probability or confidence level for a causal relationship between the drug and adverse event (Fig. 2). Note that the probabilities are calculated using three separate MONARCSi raw score inputs:
SM (mean score);
SM + SdM (mean score + 1 standard deviation); and
SM − SdM (mean score − 1 standard deviation).
Fig. 2.
Sample MOdified NARanjo Causality Scale for ICSRs (MONARCSi) probability or confidence level for a causal relationship between the drug and adverse event for a drug-event pair. The MONARCSi scores and associated standard deviations are used in a fitted logistic equation (Eq. 3), which calculates the probability of a causal relationship between a drug and an adverse event. The MONARCSi raw scores range between approximately − 20 and 27. The MONARCSi probability scores can range between 0.00 and 1.00 (see Table 4)
These inputs estimate the values for plotting the mean and variability of the causal probability. This is illustrated in Fig. 2 with the error bars representing the ± 1 sample standard deviation from the mean. The MONARCSi raw score is plotted along the x-axis in Fig. 2 with − 20 being the approximate minimum and 27 the approximate maximum possible sum of scores. The logistic transformed MONARCSi probability scores can range between 0.00 and 1.00, and are plotted along the y-axis.
| 3 |
MONARCSi Causal Probability Interpretation
The final step in the development of the model is the interpretation of the causal probability or confidence score. For this purpose, two complementary approaches are used to create interpretation labels: binary and discrete level classification. The primary approach used for medical review at Roche is binary classification into the categories of ‘related’ and ‘not related’.
For MONARCSi, we made this decision based on a threshold probability where ≤ 0.45 was determined to be ‘not related’, corresponding to the lower bound of ‘indeterminate’ classification in Arimone et al.’s 2005 paper [11]. This threshold was chosen as a general conservative preference for ‘false positives’ over ‘false negatives’ and to match the binary and discrete levels based on a series of probability thresholds published by Arimone et al. [11] (Table 4). It should be noted though that this threshold is not fixed and could be modified, if warranted. The inclusion of the Arimone et al.’s discrete labels was to allow safety professionals in different geographic and regulatory areas to provide a more granular assessment of the assessed drug-event causality, if desired. Note that Arimone et al.’s levels also show some correspondence to the World Health Organization causality categories [22–24].
Table 4.
Discrete and binary classification labels for drug-event causality
aDiscrete causality levels based on Arimone et al. [11]
In addition to binary classification, MONARCSi provides a mechanism to assess how certain the assessment of related/not related is. The underlying calculated probability of causal relationship ranges from 0 to 1. The closer this value is to 0 or 1, the more certain the determination of not related or related. To simplify the understanding of the calculated probability of a causal relationship, the range of values has been mapped into a discrete list of ‘causality level classifications’ that indicates the likelihood of the drug-event pair being related. Currently, we have used the values: certain, likely, plausible, indeterminate, doubtful, unlikely, and excluded [11].
Model Training and Performance Assessment
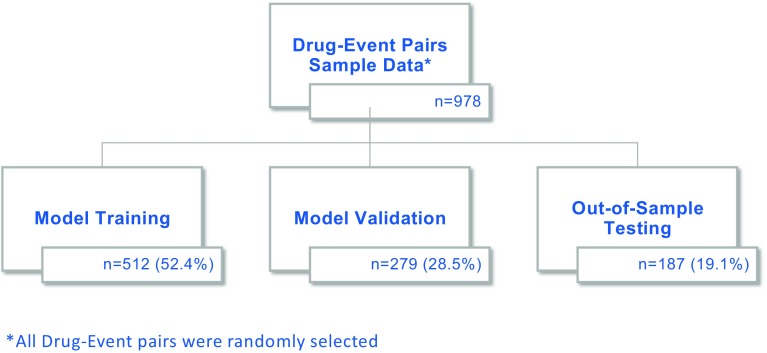
Evaluation of the model performance was conducted by comparing the MONARCSi binary causality classification labels to the preexisting company causality labels for the same drug-event pair. These reports were randomly selected from past or ongoing clinical trial drug-event pairs that had undergone medical reviews and had a final company causality determination. The disposition of drug-event pairs is shown in Fig. 3 and the Electronic Supplementary Material (ESM) 1. Using the Roche safety database, over a 9-month period, 978 drug-event pairs were randomly selected as a convenience sample for MONARCSi validation testing. These 978 drug-event pairs were randomly split into three separate data groups: 512 for ‘Training’, 279 for model ‘Validation’, and 187 for final ‘Testing’. The training dataset was used to fit logistic regression models for the MONARCSi raw scores (Sm) across the corresponding company causality classification of ‘Related’ or ‘Not Related. The validation dataset (n = 279) was used to determine the best fitting model, and finally an assessment of the model’s likely realistic performance was conducted by comparing the MONARCSi binary classification labels against the company causality, using the final testing dataset. This final performance was evaluated using confusion matrices, Gwet Kappa (gKappa), sensitivity, specificity, positive predictive value, negative predictive value, F1 measure, and other standard classification metrics.
Fig. 3.
Disposition of drug-event pairs
In addition, we wanted to compare the MONARCSi and Naranjo scores to assess the concurrent validity (see ESM 2–6). Because the features included in MONARCSi and Naranjo do not fully overlap, a direct comparison of the two instruments was not possible. However, we were able to compare the raw scores from the full MONARCSi classification of causality to a restricted Naranjo score using the seven features in Naranjo that are included in both instruments. This was performed using the final MONARCSi test dataset of 187 ICSRs. The results of this testing can be found in ESM 4–6.
Currently, evaluations of drug-event pairs are still performed using global introspection without additional formal algorithms or techniques, which is a common practice across the industry. For this reason, specific drug-event pair features (e.g., whether a drug-event pair is temporally plausible) are not made explicit in the case narratives. Instead, these aspects are evaluated subjectively by the company safety professional. To use MONARCSi, we had to extract the explicit drug-event pair features from each case so that these could be used as inputs for the model. To accomplish this, we partnered with an outside vendor, PAREXEL-Quantum Solutions Incorporated (Parexel-QSI), to create a team of four pharmacovigilance experts (one medical professional lead and three pharmacovigilance scientists) that reviewed each selected drug-event pair to extract the nine MONARCSi features and determine whether they were present or absent. To minimize discrepancies during feature extraction, the QSI team rotated completed cases so that each case was reviewed by three pharmacovigilance specialists who then met to adjudicate any disagreements. In addition, the MONARCSi and PAREXEL-QSI teams held regular meetings to adjudicate complicated cases requiring additional discussion.
To train and test the MONARCSi causality classifications, the comparative ‘ground truth’ was taken to be the official company causality determination. As discussed previously, these determinations were based on global introspection performed by the specific safety professionals during medical review. Thirty-seven Roche safety science professionals performed the medical review of clinical cases in this study. Of these individuals, 11 (or 30%) also participated in the weighting survey for the MONARCSi score.
Results
Drug-Event Pair Feature Matrix
The nine drug-event pair features included in the current MONARCSi model are shown in Table 5, along with brief descriptions. Many of these features are similar to the Naranjo score although several have different phrasing, to fit with terminology currently used within Roche Pharmacovigilance (e.g., temporality). One additional feature describing Significant Safety Events was added based on routine safety professional practice. The intent is to specifically identify and weight ICSRs that are frequently associated with drug effects (see ESM 7 for the list of Significant Safety Events). In short, the Significant Safety Event feature is a subset of the Designated Medical Events listings described by the US Food and Drug Administration. Finally, not all features from Naranjo’s score are part of the MONARCSi drug-event pair feature matrix. We did not include features assessing whether the same reaction occurred with placebo, if the drug was detected in the blood (or other fluids) at concentrations known to be toxic, or whether there were previous similar reactions to the drug because in our experience these aspects of a drug-event pair are infrequently known in the clinical trial setting. For a more detailed comparison of the MONARCSi and Naranjo features, see ESM 2 and 3.
Table 5.
Nine drug-event pair features of the MOdified NARanjo causality scale for ICSRs (MONARCSi) causality scale
| Feature | Description |
|---|---|
| F1: Significant safety event | Is this adverse event consistent with a significant safety event associated with drug/molecule use? |
| F2: Previous association | Are there previous reports on this adverse reaction with this drug/class that support a causal relationship? |
| F3: Temporality | Is the adverse event onset temporarily associated with drug/molecule use? |
| F4: Mechanism of action | Is the adverse event consistent with drug/molecule mechanism of action? |
| F5: De-challenge | Did the adverse event resolve or improve when the drug/molecule was discontinued, or a specific antagonist was administered? |
| F6: Re-challenge | Did the adverse event recur when the drug/molecule was re-administered? |
| F7: Dose response | Was the adverse event affected by dosing changes, either increase or decrease? |
| F8: Experimental data | Are other data present that support a causal relationship? |
| F9: Confounding factors | Are there alternative explanatory causes or confounding factors for the adverse event present? |
Feature Weighting
The mean feature weights and associated standard deviations corresponding to the nine drug-event pair features were derived from the safety professional survey and are shown in Table 6. Confirmatory features weighted near the upper end of the five-point ordinal scale and therefore reflecting their higher value in determining potential causality for drug-event pairs include: consistency with mechanism of action, presence of significant safety event, and previous association. The corresponding absence of these features was not as heavily weighted by the surveyed safety professionals. In general, the confirmatory features tend to be weighted higher than their corresponding absence. Additional information comparing the MONARCSi scale and Naranjo score, including weighting differences, are available in ESM 2–9.
Table 6.
MOdified NARanjo Causality Scale for ICSRs (MONARCSi) aggregate feature weightinga by safety professionals using an ordinal weighting scale (0 = no importance, 4 = very high importance) [n = 65, mean ± standard deviation]
| Feature | Present (confirmatory) | Not present (dis-confirmatory) |
|---|---|---|
| F1: Significant safety event | 3.58 ± 0.75 | 1.23 ± 1.25 |
| F2: Previous association | 3.42 ± 0.56 | 2.14 ± 0.95 |
| F3: Temporality | 2.42 ± 0.90 | 2.00 ± 1.09 |
| F4: Mechanism of action | 3.66 ± 0.57 | 2.95 ± 1.14 |
| F5: De-challenge | 2.77 ± 0.90 | 2.92 ± 1.12 |
| F6: Re-challenge | 2.86 ± 0.68 | 1.80 ± 0.94 |
| F7: Dose response | 2.63 ± 0.86 | 1.89 ± 0.97 |
| F8: Experimental data | 2.89 ± 0.89 | 1.72 ± 0.88 |
| F9: Confounding factors | 2.69 ± 0.95 | 2.95 ± 0.87 |
aDrug-event pair features that are unknown or missing are assigned a magnitude of 0.00
Variability in Aggregate Weights Determined by Safety Professionals Across Safety Science Work Areas and Geography
A descriptive assessment of the mean feature weights assigned by the safety professionals for the Mechanism of Action feature shows that the means and standard deviations appear similar across geography and safety science work areas (ESM 10). In addition to the descriptive assessment of variability, an ad-hoc analysis was performed to evaluate whether there were obvious differences across the four broad safety science work area categories and three geographic regions. The results of an exploratory analysis of variance of the means and standard deviations for the confirmatory drug-event pair feature weights and dis-confirmatory weights for both the geographic and safety science work categories are shown in ESM 11a–d. The null hypothesis (i.e., ‘no difference’) was not rejected for any of the comparisons. Thus, there appears to be no statistically significant difference between the mean aggregate weights of confirmatory features by individual safety science work area or geographic region. Likewise, for the dis-confirmatory features, there were no statistically significant differences by individual safety science work area or geographic region. Based on this analysis, there does not appear to be an obvious difference in the weightings based on either geographic region or safety science work area.
Model Training and Performance Assessment Results: Agreement with Prior Drug-Event Pair Final Causality Determination Using Global Introspection
The results of the fitted logistic function (Eq. 3) on the training dataset (n = 512) were statistically significant (p > χ2 < 0.0001). Validation results (n = 279) showed that the model achieved 65% sensitivity, 93% specificity, an inter-rater agreement of 0.74, and an area under the receiver operating characteristic (ROC) curve of 0.85 with the Roche company causality. Complete tables of the training and validation results are available online (ESM 12–15).
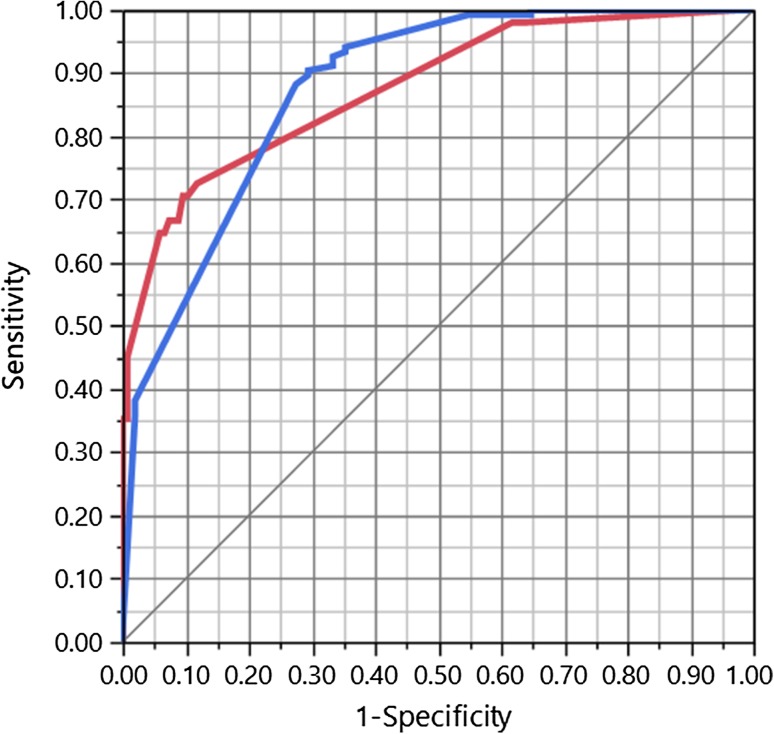
The final out-of-sample MONARCSi causality determinations were compared to the company causality determinations by safety professionals using a two-by-two matrix (see Table 7) for the 187 testing drug-event pairs. Two-by-two comparison of these results showed substantial inter-rater agreement between MONARCSi and Roche safety professionals’ assessments of causality using global introspection (gKappa = 0.77). In addition, this performance is shown graphically as a ROC curve with an area of 0.88, considered a ‘very good’ classification performance as shown in Fig. 4. The area under the ROC curve depicts the probability that MONARCSi detects a true causal relationship between a drug and an adverse event. The model exhibited moderate sensitivity (65%) and high specificity (93%), as well as high positive (79%) and excellent negative (88%) predictive values, and a high F1 score of 71% (Table 8).
Table 7.
Test dataset results for the MOdified NARanjo causality scale for ICSRs (MONARCSi) model compared to company causality ratings (n = 187 drug-event pairs)
| MONARCSi causality determination | |||
|---|---|---|---|
| Yes | No | Total | |
| Company causality determination Using global introspection | |||
| Yes | 33 | 18 | 51 |
| No | 9 | 127 | 136 |
| Total | 42 | 145 | 187 |
Fig. 4.
MOdified NARanjo causality scale for ICSRs (MONARCSi) receiver operating characteristic (ROC) curve for the test dataset, illustrating the diagnostic ability of MONARCSi; a plot of the true positive rate against the false-positive rate. Area under the ROC curve = 0.88
Table 8.
Test dataset performance metrics for MOdified NARanjo causality scale for ICSRs (MONARCSi) compared with clinical judgment using global introspection as the reference
| Performance metric | Value (%) |
|---|---|
| Sensitivity % Positive agreement |
64.7 |
| Specificity % Negative agreement |
93.4 |
| Positive predictive value (precision) Proportion of true ‘related’ out of all classified ‘related’ |
78.6 |
| Negative predictive value Proportion of true ‘unrelated’ out of all classified ‘unrelated’ |
87.6 |
| gKappa score Inter-rater agreement with ‘ground truth’ |
76.9 |
|
F score (F1) Harmonic mean between precision and recall |
71.0 |
Note that in addition to the 2 × 2 validation and testing comparisons of MONARCSi and the prior safety professional causality assessments, we also performed a comparison of MONARCSi vs. Naranjo for the final test data. Results from the comparison using the seven features included in both Naranjo and the full MONARCSi showed a high correlation (r = 0.88), which supports the concurrent validity of MONARCSi and are included in ESM 6.
Discussion
The results of this project describe the development of MONARCSi, an exploratory novel ICSR drug-event pair decision support tool that combines selected aspects of Naranjo’s original score with aggregate feature weights determined by safety professionals and a logistic function similar to Theophile et al. to produce a probability of drug causality [19]. The resulting MONARCSi nine-row by three-column feature matrix includes nine features consistent with many of the Bradford–Hill criteria for determining causality [20] and the Naranjo scale [18]. One additional feature describing a significant safety event was added and three features present in the Naranjo scale were not included as they were aspects that were deemed irrelevant or rarely known in the clinical trial setting.
The feature weighting results indicated generally higher weightings for the presence of features (e.g. confounders) than the absence of features. Our hypothesis is that this illustrates a general conservatism on the part of safety professionals that seems reasonable. For example, the presence of a significant safety event often associated with drug exposure (e.g., acute liver abnormality) could strongly suggest a causal relationship. However, the absence of such a feature does not necessarily indicate that there is no causal relationship between a drug-event pair. Finally, descriptive analysis and an ad-hoc comparison both suggest that the feature weightings are consistent across geographic regions and Roche safety science work areas. This observation was surprising in that the population of safety professionals was diverse with members having different languages, cultures, and educational backgrounds. We hypothesize that the lack of obvious difference may reflect a commonality of thinking about drug-event pair causality, common training, or possibly a result of the relatively small sample size. This could be tested by repeating this feature-weighting exercise with a larger sample population of safety professionals.
The training and validation results for the logistic transformation function showed moderate sensitivity and high specificity, as well as good agreement with the company causality for the training dataset. The final testing results on the hold-out (‘out of sample’) dataset show similar results to the training and validation, with a slightly greater area under the ROC curve. Typically, the training results show the best possible ‘fit’, and the more ‘realistic’ results obtained with the validation and hold-out testing sample are slightly lower. However, here the results across all three datasets are generally close and suggest that the model is robust and has not ‘over learned’ from the training data.
The results using the final hold-out test data show good performance on the majority of typical classification metrics including inter-rater agreement, sensitivity, and specificity. In addition, the area under the curve for the ROC curve (0.88) shows very good discrimination ability. Similarly, the F ratio (i.e., harmonic mean of precision and recall) indicated good binary classification performance. In addition, we undertook a separate concurrent validation analysis of the MONARCSi vs. Naranjo (restricted to the seven common features in both scores) raw scores for the same final test data and obtained high correlation. Although not all of these metrics may be familiar to the pharmacovigilance audience, we believe it is important to include multiple measures of validity, as they each reflect different attributes of the model that can guide assessment of the performance and may suggest ways to improve classification with future modifications.
It is important to place our results into context with other previously published algorithms. The results presented here, comparing MONARCSi and Roche safety professionals’ causality classifications using global introspection differ from previous published algorithmic models for drug-event pair causality. Specifically, the MONARCSi model shows a stronger inter-rater agreement with global introspection, with an area under the curve for the ROC considered ‘good’ discrimination with moderate sensitivity and high specificity [25]. In contrast, some previous algorithms tended to have high sensitivity but lower specificity, although this varies by study and clinical context [9]. The MONARCSi model also estimates the uncertainty in the causal probability assessment. This uncertainty (sample deviation) is derived from the variability of feature weights across individual safety professionals participating in this effort.
Decades of research documenting inconsistent human assessments of drug-event causality support the premise that individual assessments are often unreliable [10, 12, 13]. For this project, we relied upon the individual safety professional’s company causality assessment as our comparator ‘ground truth’ for both training and validation. We realize that this is, at best, an ‘imperfect’ gold standard for comparison. For future efforts, we hope to follow Forster et al.’s suggestion to aggregate multiple opinions from drug-safety experts, for example, using a ‘two out of three’ rule for expert adjudication [26, 27] to create a more robust ‘ground truth’ database of drug-event pairs. If this approach were taken to an extreme, it is clear that performing a triple review of all drug-event pairs for all organizations collecting and reporting on safety data would be infeasible. Another potential approach could be to create a large public training and testing dataset of redacted drug-event pairs with appropriate expert adjudication, for the development of algorithms like MONARCSi as well as other more sophisticated machine learning models.
Limitations
Like all models, MONARCSi has limitations. A specific limitation noted by the authors is that MONARCSi, like many other algorithms we have examined, is not able to classify complex cases involving more than one specific causative drug such as with drug–drug interactions. Incorporating the ability to classify drug–drug causal interactions is an area that we hope to explore in future versions of the model. Much of MONARCSi, like Naranjo, uses the Bradford–Hill criteria including aspects of pharmacology with features such as mechanism of action and temporality. However, it is well known that for some drugs there can be unusual events that show up later in the post-marketing stage that may not easily fit into a Bradford–Hill type classification. For this reason, we hypothesize that adding another feature that allows safety professionals to note whether a drug-event pair is unusual or extremely uncommon may increase the generality of MONARCSi to capture causality for these types of cases.
The current version of the model also shows a lower sensitivity than we would prefer. We hypothesize that this may be owing to cases within the ‘Indeterminate’ classification range, where the model as well as Roche safety professionals is more likely to disagree on causation. In an earlier version of the model, we excluded cases in this probability zone to observe the effect and found a marked increase in sensitivity as well as the other performance metrics, suggesting that drug-event pairs in this ‘doubtful’ zone may be causing our lower sensitivity and be responsible for many of the model-safety professional disagreements in causality attribution. This may be investigated further in future iterations of the model with additional drug-event pair data. Finally, MONARCSi was developed for use in the clinical trial setting where the ICSR data are relatively complete and therefore the tool is most applicable to that setting.
Conclusions
The MONARCSi model is a novel approach to pharmacovigilance that combines aspects of the Naranjo scale with a logistic transformation model similar to Theophile et al. to provide the probability of drug causality along with an estimate of its uncertainty [19]. It also uses the collective judgment of safety professionals to assign weights to the underlying drug-event pair features. The goal of the MONARCSi model is to function as a decision support tool to assist safety professionals in evaluating drug-event pair causality. Thus, this approach may enhance consistency and allow for easier tracking and recording of causality decisions and the rationale behind them. Future work is planned to modify the MONARCSi model to incorporate additional drug-event pair features and to perform periodic re-training using machine-learning algorithms with the addition of more adjudicated drug-event pairs.
We recognize that we are in the early stages of developing machine-based learning tools that can augment human expertise in the field of drug safety. Although MONARCSi was developed by Roche as an internal exercise, one purpose of this article is to provide enough detail regarding the design, development approach, and validation results so that others can easily reproduce our model. Ultimately, our hope is that by sharing this approach, improved models with higher performance can be created with input from across the pharmacovigilance community. As more safety professionals and researchers develop similar tools and share their results, we hope to see new levels of performance in human plus machine causality assessments promoting superior evaluation and adjudication of safety events.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Acknowledgements
The authors thank the following team members at PAREXEL-QSI for their assistance in creating the drug-event pair datasets for training and validation of the MONARCSi model. Project Manager: Paramdeep Singh; Team Lead: Anmol Toor; Team Members: Aneesh Sharma, Priyanka Bhandari. Medical writing and editorial support funded by Roche were provided by Chantal Dolan PhD, Kathryn Fisher MPH, and Michelle Hansen of CMD Consulting Inc. based on detailed discussion and feedback from all authors.
Funding
Funding for this study was supplied by Genentech, a Member of the Roche Group.
Conflict of interest
Shaun Comfort, Darren Dorrell, Shawman Meireis, and Jennifer Fine were employed by Roche at the time this research was completed.
Ethics approval
All human subject data used in this analysis were used in a de-identified format.
References
- 1.Agbabiaka TB, Savovic J, Ernst E. Methods for causality assessment of adverse drug reactions. Drug Saf. 2008;31(1):21–37. doi: 10.2165/00002018-200831010-00003. [DOI] [PubMed] [Google Scholar]
- 2.Kahn LM, Al-Harthi SE, Osman AM, Sattar MA, Ali AS. Dilemmas of the causality assessment tools in the diagnosis of adverse drug reactions. Saudi Pharm J. 2016;24:485–492. doi: 10.1016/j.jsps.2015.01.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Théophile H, Arimone Y, Miremont-Salamé G, Moore N, Fourrier-Réglat A, Haramburu F, et al. Comparison of three methods (consensual expert judgment, algorithmic and probabilistic approaches) of causality assessment of adverse drug reactions: an assessment using reports made to a French pharmacovigilance center. Drug Saf. 2010;33(11):1045–1054. doi: 10.2165/11537780-000000000-00000. [DOI] [PubMed] [Google Scholar]
- 4.Miremont G, Haramburu F, Bégaud B, Péré JC, Dangoumau J. Adverse drug reactions: physicians’ opinions versus a causality assessment method. Eur J Clin Pharmacol. 1994;46(4):285–289. doi: 10.1007/BF00194392. [DOI] [PubMed] [Google Scholar]
- 5.Macedo AF, Marques FB, Ribeiro CF, Teixeira F. Causality assessment of adverse drug reactions: comparison of the results obtained from published decisional algorithms and from the evaluations of an expert panel, according to different levels of imputability. J Clin Pharm Ther. 2003;28:137–143. doi: 10.1046/j.1365-2710.2003.00475.x. [DOI] [PubMed] [Google Scholar]
- 6.Macedo AF, Marques FB, Ribeiro CF, Teixeira F. Causality assessment of adverse drug reactions: comparison of the results obtained from published decisional algorithms and from the evaluations of an expert panel. Pharmacoepidemiol Drug Saf. 2005;14(12):885–890. doi: 10.1002/pds.1138. [DOI] [PubMed] [Google Scholar]
- 7.Michel DJ, Knodel LC. Comparison of three algorithms used to evaluate adverse drug reactions. Am J Hosp Pharm. 1986;43(7):1709–1714. [PubMed] [Google Scholar]
- 8.Kane-Gill SL, Forsberg EA, Verrico MM, Handler SM. Comparison of three pharmacovigilance algorithms in the ICU setting: a retrospective and prospective evaluation of ADRs. Drug Saf. 2012;35(8):645–653. doi: 10.1007/BF03261961. [DOI] [PubMed] [Google Scholar]
- 9.Macedo AF, Marques FB, Ribeiro CF. Can decisional algorithms replace global introspection in the individual causality assessment of spontaneously reported ADRs? Drug Saf. 2006;29(8):697–702. doi: 10.2165/00002018-200629080-00006. [DOI] [PubMed] [Google Scholar]
- 10.Koch-Weser J, Sellers EM, Zacest R. The ambiguity of adverse drug reactions. Eur J Clin Pharmacol. 1977;11:75–78. doi: 10.1007/BF00562895. [DOI] [PubMed] [Google Scholar]
- 11.Arimone Y, Bégaud B, Miremont-Salamé G, Fourrier-Réglat A, Moore N, Molimard M, et al. Agreement of expert judgement in causality assessment of adverse drug reactions. Eur J Clin Pharmacol. 2005;61:169–173. doi: 10.1007/s00228-004-0869-2. [DOI] [PubMed] [Google Scholar]
- 12.Arimone Y, Miremont-Salamé G, Haramburu F, Molimard M, Moore N, Fourrier-Réglat A, et al. Inter-expert agreement of seven criteria in causality assessment of adverse drug reactions. Br J Clin Pharmacol. 2007;64(4):482–488. doi: 10.1111/j.1365-2125.2007.02937.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Kosov M, Maximovich A, Riefler J, Dignani MC, Belotserkovskiy M, Batson E. Interexpert agreement on adverse events’ evaluation. Applied Clinical Trials Online. 2016 Apr 21. http://www.appliedclinicaltrialsonline.com/interexpert-agreement-adverse-events-evaluation. Accessed 21 Jun 2017.
- 14.Meehl PE. Clinical versus statistical prediction: a theoretical analysis and a review of the evidence. Minneapolis: University of Minnesota Press; 1954. [Google Scholar]
- 15.Grove WM, Zald DH, Lebow BS, Snitz BE, Nelson C. Clinical versus mechanical prediction: a meta-analysis. Psychol Assess. 2000;2(12):19–30. doi: 10.1037/1040-3590.12.1.19. [DOI] [PubMed] [Google Scholar]
- 16.Grove WM, Lloyd M. Meehl’s contributions to clinical versus statistical prediction. J Abnorm Psychol. 2006;115(2):192–194. doi: 10.1037/0021-843X.115.2.192. [DOI] [PubMed] [Google Scholar]
- 17.Doherty MJ. Algorithms for assessing the probability of an adverse drug reaction. Respir Med CME. 2009;2:63–67. doi: 10.1016/j.rmedc.2009.01.004. [DOI] [Google Scholar]
- 18.Naranjo CA, Busto U, Sellers EM, Sandor P, Ruiz I, Roberts EA, et al. A method for estimating the probability of adverse drug reactions. Clin Pharmacol Ther. 1981;30(2):239–245. doi: 10.1038/clpt.1981.154. [DOI] [PubMed] [Google Scholar]
- 19.Theophile H, André M, Arimone Y, Haramburu F, Miremont-Salamé G, Bégaud B. An updated method improved the assessment of adverse drug reaction in routine pharmacovigilance. J Clin Epidemiol. 2012;65:1069–1077. doi: 10.1016/j.jclinepi.2012.04.015. [DOI] [PubMed] [Google Scholar]
- 20.Hill AB. The environment and disease: association or causation? Proc R Soc Med. 1965;58(5):295–300. doi: 10.1177/003591576505800503. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Taylor JR. An introduction to error analysis. 2. Herndon: University Science Books; 1997. [Google Scholar]
- 22.Edwards IR, Biriell C. Harmonization in pharmacovigilance. Drug Saf. 1994;10:93–102. doi: 10.2165/00002018-199410020-00001. [DOI] [PubMed] [Google Scholar]
- 23.Meyboom RHB, Hekster YA, Egberts ACG, Gribnau FWJ, Edwards IR. Causal or casual? The role of causality assessment in pharmacovigilance. Drug Saf. 1997;17(6):374–389. doi: 10.2165/00002018-199717060-00004. [DOI] [PubMed] [Google Scholar]
- 24.Arimone Y, Bégaud B, Miremont-Salamé G, Fourrier-Réglat A, Molimard M, Moore N, et al. A new method for assessing drug causation provided agreement with experts’ judgement. J Clin Epidemiol. 2006;59:308–314. doi: 10.1016/j.jclinepi.2005.08.012. [DOI] [PubMed] [Google Scholar]
- 25.Safari S, Baratloo A, Elfil M, Negida A. Evidence based emergency medicine; part 5 receiver operating curve and area under the curve. Emergency (Tehran). 2016;4(2):111–113. [PMC free article] [PubMed] [Google Scholar]
- 26.Forster AJ, Taljaard M, Bennett C, van Walraven C. Reliability of the peer-review process for adverse event rating. PLoS One. 2012;7(7):e41239. doi: 10.1371/journal.pone.0041239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Coeytaux RR, Leisy PJ, Wagner GS, McBroom AJ, Green CL, Wing L, et al. Systematic review of ECG-based signal analysis technologies for evaluating patients with acute coronary syndrome. Rockville (MD): Agency for Healthcare Research and Quality; 2012 Jun. https://www.ncbi.nlm.nih.gov/books/NBK280225/. Accessed 28 May 2018. [PubMed]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.