Evaluation of Computer-Based Training to Teach Adults Visual Analysis Skills of Baseline-Treatment Graphs

Abstract

The primary method of data analysis in applied behavior analysis is visual analysis. However, few investigations to date have taught the skills necessary for accurate visual analysis. The purpose of the present study was to evaluate computer-based training on the visual analysis skills of adults with no prior experience. Visual analysis was taught with interactive computer-based training that included written instructions and opportunities for practice with textual feedback. Generalization of participant skills from simulated to handwritten and authentic data graphs was programmed for and assessed during the study. A multiple-baseline design was used across visual analysis properties (i.e., variability, level, and trend), with continuous overall intervention effect generalization probes, replicated across 4 participants to evaluate computer-based training for accurate visual analysis of A-B graphs. The results showed that all participants accurately visually analyzed A-B graphs following the computer-based training for variability, level, trend, and overall intervention effect. These visual analysis skills generalized to handwritten and authentic data graphs and maintained approximately 1 day, 1 week, 2 weeks, and 1 month following mastery of each property for all participants. Implications of the results suggest that computer-based training improved accurate visual analysis skills for adults with no prior experience.

The field of applied behavior analysis (ABA) relies heavily on single-subject research designs, and the primary method of data analysis is visual analysis (Baer, 1977). Visual analysis is based on examining graphed data to reach a decision about the consistency and reliability of intervention effects (Baer, 1977; Cooper, Heron, & Heward, 2007). This method of analysis depicts intervention effects powerful enough to produce clinically, socially, and educationally meaningful results (Baer, 1977; Parsonson & Baer, 1992). Specifically, Parsonson and Baer (1992) indicate that visual analysis of graphs is based on the inspection of data paths, estimation of the stability of the data, and direction of the data-path changes, within and between conditions over time. The visual analysis properties that are systematically examined are changes in level, trend, and variability (Cooper et al., 2007; Parsonson, 1999). Collectively, these visual analysis properties determine overall treatment effect (Cooper et al., 2007).

Visual analysis and interpretation of single-subject designs are vital skills for staff and critical to the successful evaluation of interventions based on the principles of ABA (Fisher, Kelley, & Lomas, 2003). Although visual analysis of data is a cornerstone of ABA, previous literature has demonstrated low agreement across raters when visually analyzing graphed data presented in single-subject designs (e.g., Wolfe, Seaman, & Drasgow, 2016). Wolfe et al. (2016) evaluated visual analysis agreement of 52 behavior-analytic experts on 31 multiple-baseline graphs at the individual-tier and functional-relation levels. They found that overall agreement between raters was minimally acceptable at the individual-tier level and below minimally acceptable at the functional-relation level. However, few investigations to date have targeted approaches to teach individuals to accurately analyze and interpret single-subject graphs, especially A-B graphs. For instance, Fisher et al. (2003) taught participants to identify a reliable change in behavior in A-B graphs. They sought to increase both the reliability and validity of visual analysis by creating a refinement of the split-middle method that is used to estimate trend lines. Drawing split-middle lines is accomplished by superimposing criterion lines from the baseline phase mean into the treatment phase (Cooper et al., 2007). However, Fisher et al. (2003) found that the split-middle method resulted in unacceptably high type I errors. Thus, the dual-criteria (DC) method was created by adding a second criterion line superimposed from the baseline mean onto the treatment phase along with the split-middle line. The participants, who were experienced clinicians, were also given a visual aid in the form of a data sheet with a table indicating the number of data points required to be above both criterion lines to conclude that a treatment effect was present. Although participants’ correct interpretations increased from baseline to treatment using the DC lines, the participants were not directly educated on the visual analysis properties of variability, level, and trend. Instead, the participants learned to visually analyze A-B graphs through the use of a visual aid.

Stewart, Carr, Brandt, and McHenry (2007) expanded on this potential limitation and included a 12-min visual analysis video lecture on the components of visual analysis to teach inexperienced college students the properties of level, trend, and variability. After the students correctly answered a minimum of 8 out of 10 questions on the video lecture material, they were asked to determine whether A-B graphs (without superimposed criteria lines) demonstrated a behavior change. Accurate interpretations did not increase following the lecture, as compared to baseline responding. Therefore, Stewart et al. (2007) taught students to interpret graphs based on the conservative-dual criteria (CDC; Fisher et al., 2003) method, a variation of the DC method used by Fisher et al. (2003). In the CDC method, the positions of the mean and split-middle lines were raised by 0.25 standard deviations from the mean baseline data (Fisher et al., 2003; Stewart et al., 2007). Although these procedures resulted in successfully training students to analyze A-B graphs in the presence of the CDC method, the students did not maintain accurate visual analysis skills after the mean and split-middle lines were removed (Fisher et al., 2003; Stewart et al., 2007). Therefore, it is necessary to evaluate procedures for interpreting A-B graphs that produce skills that are resistant to extinction and that maintain in the absence of visual aids.

Recent evaluations have examined methods to train inexperienced university students to visually analyze and interpret A-B graphs. Notably, Jostad (2011) examined the effectiveness of a visual aid paired with a teaching condition compared to a video traditional lecture condition. The visual aid included four parts: (a) instructions to evaluate trend, level, and variability; (b) sample graphs depicting trend, level, and variability; (c) exceptions to be noted; and (d) information to make a final decision on overall intervention effect. Participants in the visual aid condition experienced an experimenter-led session enriched with a Microsoft PowerPoint® presentation in which they followed along with sample graphs by writing on worksheets and drawing on sample graphs as the experimenter provided instructions and answered questions. An experimenter administered the Microsoft PowerPoint® presentation in the traditional lecture condition that included basic information on visual analysis from Cooper et al. (2007) and simulated data graphs depicting variations in variability, level, and trend within and across phases. In both conditions, participants were taught to draw split-middle lines to estimate trend. Prior to and following the intervention, participants were asked to interpret five effect and noneffect graphs across 10 different graph types. Participants were asked to determine whether each graph demonstrated an observable effect by checking “yes” or “no” at the bottom of the graph. The accuracy of visual analysis improved significantly from pre- to posttest in both the visual aid and lecture conditions. Although 55% of participants in the visual aid condition met 80% accuracy on the first posttest compared with 35% in the lecture group, there was no statistically significant difference between conditions. Additionally, as the visual aid was developed and validated, correct responding did not maintain once the visual aid was faded.

Wolfe and Slocum (2015) compared computer-based training, a video lecture, and a control condition on the accurate visual analysis of A-B graphs across trend and level changes. Although variability was not targeted, instruction on how variability influences level and trend was provided. In the computer-based training, visual analysis was segmented into three module subcomponents of level, trend, and level and trend change. Each module assessed participant response through a pretest of each specific property. Then participants were provided with multiple self-paced opportunities to practice visual analysis regarding the presence or absence of level and trend change. Feedback was included for correct and incorrect responses within each module. Correct responses resulted in immediate textual praise (e.g., “That’s right.”), and incorrect responses resulted in error correction and remedial loops that provided extra practice. Participants were required to meet a 90% or higher mastery criterion at the end of each module to advance to the next module. In the lecture condition, participants were required to read a textbook chapter on visual analysis and view a recorded lecture of the computer-based content. The control condition consisted of no treatment. A pre- and posttest measure was used, which contained 40 A-B graphs with questions on level and trend for which participants were required to circle “yes” or “no” to property-change questions. Results indicated that both interventions improved student accuracy of visual analysis compared to the control condition. However, the computer-based training did not result in significantly higher accurate responding compared with the traditional lecture group.

Furthermore, Wolfe and Slocum’s (2015) study was the first to use expert consensus on A-B graphs as the measure to evaluate participant responses, whereas Jostad (2011) and past investigations used mathematically generated comparison measures. Expert ratings for participant responses may serve as an additional measure of accuracy because visual analysis of graphs is common in clinical practice. Also, Wolfe and Slocum were the first to teach and measure visual analysis properties separately (i.e., trend, level, and trend and level) through mastery-based computer software, whereas in past studies participants were taught global interpretation of effect or noneffect. However, there are several limitations in the Wolfe and Slocum (2015) study: (a) although separate properties (i.e., trend and level) were taught, participants were not taught to identify an overall intervention effect; (b) two separate visual analysis properties were targeted (i.e., trend and level), whereas the third property of visual analysis (i.e., variability) was omitted; and (c) following any incorrect response within a module, participants engaged in the same remedial loops of practice graphs before returning to the original practice graph without additional instruction specific to the nature of the error.

Although past studies targeted accurate visual analysis of A-B graphs, no study to date has evaluated generalized visual analysis skills from targeted and/or simulated graphs to handwritten and/or authentic data graphs. Additionally, no visual analysis training study to date has programmed for or assessed maintenance of accurate visual analysis following mastery. Furthermore, past studies in which visual analysis skills were taught omitted a thorough evaluation of social validity (Fisher et al., 2003; Jostad, 2011; Wolfe & Slocum, 2015) and procedural integrity analyses (Fisher et al., 2003; Jostad, 2011).

Thus, an evaluation of computer-based training with feedback on visual analysis of A-B graphs in terms of variability, level, trend, and overall intervention effect is necessary (with the understanding that experimental control of intervention effects cannot be concluded from A-B graphs).

The purpose of the current study was to extend the work of Jostad (2011) and Wolfe and Slocum (2015). Specifically, Jostad’s (2011) visual aid was modified to an interactive computer-based training program. The training included three visual analysis properties (i.e., variability, level, and trend), taught separately until mastery while assessing and/or teaching overall intervention effect across simulated A-B graphs, which were validated using expert consensus and mathematically derived comparison measures. The computerized software allowed participants to progress through the training at their own pace, engage in several opportunities to practice visual analysis, and receive textual feedback with specific remediation loops exclusive to the nature of the error. The present study further contributes to the literature by measuring generalization of visual analysis skills from assessment graphs to authentic (rather than simulated) data and handwritten graphs, maintenance of visual analysis skills over time, social validity, and procedural integrity. This structured, objective, and consistent method decreased the need for a trainer and facilitated generalization and maintenance of skills in the absence of contrived training tools.

Method

Participants

Twenty participants (undergraduate, graduate, and postgraduate students) were selected for this study. Exclusion criteria included adults that have completed a research methods course or worked as a research assistant during which extensive exposure to A-B graphs was obtained. Their average age was 25.42 (range 19–58 years). Thirteen were female (62%), and of the 17 adults that reported their GPA, the average was 3.46 (range 3–3.91). Various majors were reported, spanning from psychology, music therapy, and education to chemical engineering, digital media technology, and environmental business. Fifteen participants who scored greater than 70% accuracy on level, trend, variability, or overall intervention effect were excluded from the study. One participant, who met inclusion, left the study following baseline sessions.

Four participants who did not have experience in ABA, psychology, or special education completed the training. Of these participants, all were male. Cody was 30 years old and received a bachelor’s degree in accounting with a 3.0 GPA. Herbie was 22 years old and received a bachelor’s degree in criminal justice with a 3.49 GPA. Kasey was 23 years old and received a bachelor’s degree in music education with a 3.5 GPA. Finally, Oliver was 58 years old and received a master’s in business administration.

Setting

The study was conducted in living rooms and a kitchen of residential homes and in a private classroom of a university. The living rooms and kitchen all had a large table, several chairs, and at least two laptop computers. The classroom had three personal desktop computers and several chairs.

Materials

Graphs

A subset of graphs created by Jostad (2011) were used in the current study. Jostad created 500 various A-B graphs using simulated data in Microsoft Excel® and the Resampling Stats® plug-in. These graphs contained simulated data, varying possibilities of data in clinical and research settings across level, trend, and variability properties, with half demonstrating an intervention effect and the other half demonstrating a noneffect. All graphs had the same number of data points (i.e., 10 data points) in the baseline and treatment conditions. To create these graphs, Jostad first programmed effect sizes into the computer program, specifically 0 for noneffect graphs and 0.25–1.0 for effect graphs. Second, the CDC method (Fisher et al., 2003) was applied to the graphs to indicate an effect or noneffect graph. Ten types of graphs were created. Specifically, (a) no effect with increasing trends in baseline and treatment; (b) no effect with zero trend, no observable change in level, and low variability; (c) no effect with zero trend, no observable change in level, and high variability; (d) no effect with zero trend, no observable change in level, and moderate variability; (e) no effect with decreasing trends in baseline and treatment; (f) effect with changes in direction of trend (e.g., zero trend to increasing) and level; (g) effect with changes in steepness of slope (e.g., descending with steeper slope to descending with flatter slope); (h) effect with changes in variability; (i) effect with moderate change in level between baseline and treatment; and (j) effect with changes in level, trend, and variability (for a detailed description of graph creation, see Jostad, 2011). The accuracy of these graphs was assessed with experienced raters (i.e., faculty and graduate students in behavior analysis) to determine whether they depicted the qualities they were created to exhibit, with a mean agreement of 91.4% (range 75%–100%) for each graph type.

In the current study, graphs across the 10 types (i.e., 8 graphs from each type) were selected from Jostad’s (2011) 500 graphs such that various exemplars within each graph type were represented. This increased the external validity of the selected graphs. Each graph packet to be rated contained an equal number of effect and noneffect graphs (i.e., five each) that were arbitrarily ordered within each packet. Each graph was presented as a hard copy (i.e., on paper) and included questions on variability, level, trend, and overall intervention effect at the bottom of the graph. The questions per property were “Is there a convincing and overall change in [visual analysis property] between baseline and treatment conditions?” and the overall intervention effect question was “Did behavior change from baseline to treatment?” Next to each question, a “yes” and “no” was included. Additionally, 20 graphs presented in ABA journal articles (i.e., the Journal of Applied Behavior Analysis, summer 2014) and from learners’ programs (i.e., learners’ skill acquisition and behavior reduction graphs obtained from a university-based autism center) were used. These graphs displayed various level, trend, and variability properties. Half of the graphs displayed an overall intervention effect and half did not. Authentic data graphs had varying numbers of data points in the baseline and treatment conditions, with a minimum of three data points in the baseline condition. For example, one graph may have had five data points in baseline and nine data points in the treatment condition, whereas another graph may have had four data points in baseline and eight data points in the treatment condition.

After the graphs were obtained, a group of nine BCBA-Ds (Board Certified Behavior Analyst-Doctoral) and one BCBA (Board Certified Behavior Analyst), who were productive researchers, editorial review board members, and/or clinicians, aided in the selection of graphs used in the study. Each rater received 100 graphs presented on the computer, to mimic the format of the computer-based training. Graphs included 80 simulated data graphs (i.e., 60 graphs presented on computer paper and 20 graphs presented on graph paper) from Jostad (2011) and 20 authentic data graphs with the questions “Is there a convincing and overall change in [visual analysis property] between baseline and treatment conditions?” and “Did behavior change from baseline to treatment?” Graphs that had the highest agreement across raters, relative to Jostad’s (2011) parameters, were retained. Specifically, the final graphs with the highest agreement across graph categories (i.e., simulated data graphs, handwritten graphs, and authentic data graphs) were selected. These graphs were arbitrarily selected across graph types and made into graph packets (i.e., preexperimental assessment graphs, assessment graphs, handwritten graphs, and authentic data graphs; more details to follow).

Preexperimental Assessment Graphs

The preexperimental assessment graphs were composed of Jostad’s (2011) simulated data graphs and were presented on computer paper. To select the simulated data graphs (i.e., preexperimental assessment graphs and assessment graphs), two graphs, out of the six graphs in each graph type, with the lowest agreement were discarded; if there was a tie, a graph was selected arbitrarily. Ten types of A-B graphs (Jostad, 2011) with different level, trend, variability, and effect size characteristics (across the 10 graph types) were selected and made into one graph packet.

Assessment Graphs

The assessment graphs were also composed of Jostad’s simulated data graphs presented on computer paper. Thirty graphs from Jostad (2011) were retained and arbitrarily selected into three packets of 10 A-B graphs (see Appendix for a sample graph). As in Jostad, each packet contained different graphs; however, the makeup of the packets was consistent in the 10 types of A-B graphs included (Jostad, 2011).

Handwritten Graphs

The handwritten graphs were composed of simulated data graphs from Jostad (2011) and were transcribed by hand onto graph paper. To select the handwritten graphs, one graph out of the two graphs in each graph type with the lowest means was discarded; if there was a tie, a graph was selected arbitrarily. Ten A-B graphs were retained and made into one graph packet.

Authentic Data Graphs

The authentic data graphs were composed of A-B graphs selected from ABA journal articles (i.e., the Journal of Applied Behavior Analysis, summer 2014) and from learners’ programs and were presented on computer paper. To select the authentic data graphs, multiple exemplars of effect and noneffect graphs, with varying examples and nonexamples of properties, were selected; when possible, the graphs with the lowest means were discarded. The packet comprised 10 various types of graphs, with an equal number of effect and noneffect graphs, which are representative of skill acquisition and behavior reduction programs in clinical settings. Ten A-B graphs were retained and made into one graph packet.

Computer-Based Training

The computer-based training was created using the Adobe Captivate 8® software program (http://www.adobe.com/products/captivate.html). This interactive software allowed the experimenter to supplement Microsoft PowerPoint® slides with written instructions, interactivity, quizzes, and textual feedback. Once the modules were finalized, they were uploaded from the Adobe Captivate® files to the online course-management system, Blackboard®. The Adobe Captivate® and Blackboard® programs recorded data on participant responses. The content for the modules was based on chapters of a textbook on ABA describing visual analysis of graphs (i.e., Cooper et al., 2007) and the lectures of Jostad (2011). Specifically, Module 1 included basic information on single-subject designs, visual analysis, and graph analysis and pretraining on the skills necessary for the training. Each visual analysis property (i.e., variability, level, and trend) training module (Modules 2, 3, and 4) included written instructions providing information on the properties and changes from baseline to treatment responses. Multiple exemplars of A-B graphs and property effects with necessary steps to visually analyze the graphs were provided. Participants followed along with (i.e., clicked to the next slides) and engaged in embedded sample practice graphs based on the information presented in the module until correct responding occurred. Each training module progressed the participant through four levels of prompting (full to no prompting), adapted from Ray and Ray (2008), and varying textual feedback.

Prompts were systematically faded contingent on participant performance. In Level 1, the answers were bolded to increase the salience of the important information without requiring a response to specific questions. In Level 2, the answers were bolded and the participant was required to emit a response by selecting the bolded answer. In Level 3, the answers were not bolded and the participant was required to independently select an answer. Finally, in Level 4, participants were required to independently emit a response across two questions depicting an effect and noneffect graph per property and overall intervention effect. Immediate text-based feedback (i.e., within Adobe Captivate®) was provided for accurate and inaccurate visual analysis for Levels 2 through 4. Specifically, for Levels 2 and 3, praise was provided for correct responses and another opportunity was provided for incorrect responses (e.g., “Try again.”). For Level 4, contingent on correct responses, praise was provided (e.g., “That’s right! There is an observable change in level!”) and, contingent on incorrect responses, corrective feedback was provided (e.g., “The level of the treatment phase is the same as the level of the baseline phase. Here’s some more information.”) with remedial loops, additional information (i.e., examples of property changes or a stepwise guideline for determining overall change from baseline to treatment), and extra practice.

The remedial loops in Level 4 were exclusive to the nature of the error. Specifically, each remediation loop included feedback on the correct answer, why the participant’s response was incorrect, additional information, and a single practice graph (contingent on accurate response; from Jostad’s, 2011 graphs) before the participant was presented with a graph similar to the original question (from Jostad’s [2011] graphs). For example, if the original graph depicted a level change between baseline and treatment, the participant was directed to non-level-change graphs until an accurate response was obtained, then was presented with a similar graph that depicted a level change. Each time a participant entered into a module, the content was identical except for the two original questions in prompt Level 4. This was accomplished by creating three different modules per property; this allowed for a manual arbitrary rotation of original questions, as a random draw from a question pool of graphs was not available in the Adobe Captivate® software. If a participant entered the module a fourth time, the first file would again be presented. Memorization of graphs and answers was minimized by including three module files with different original questions, an average of eight remedial loop questions, and questions that were similar to original questions per question type (i.e., Original Question #1 and Original Question #2) in each module.

If participants successfully completed all modules but did not accurately interpret overall intervention effects, measured through continuous probes, Module 5 was introduced to teach interpreting an intervention effect. Module 5 contained the same components as training Modules 2, 3, and 4. However, Module 5 taught participants to make a decision regarding the presence of an intervention effect per graph, using a summary of all three properties.

After the computer-based training was created, the training content was emailed to a group of 10 BCBAs to score for content validity. Refer to the social validity section for more information. Feedback from the BCBAs led to the finalization of the computer-based training content. After the training content was inserted into Adobe Captivate® and made into the five modules, one advanced PhD student in ABA and one BCBA-D reviewed the modules to ensure the accuracy of the material presented.

Experimenter and Assistants

The experimenter was a graduate student in the master of arts program in ABA. At the start of the study, the primary experimenter had worked in the field of ABA for 4 years. The assistants were also graduate students in the master of arts program in ABA. Assistants collected interobserver agreement (IOA) and procedural integrity data.

Dependent Variables and Response Definitions

Percentage of Accurate Visual Analysis

The primary dependent variable was the percentage of accurate visual analysis responses across three visual analysis properties (i.e., variability, level, and trend). Participants answered the question “Is there a convincing and overall change in [visual analysis property] between baseline and treatment conditions?” with a “yes” or “no.” The accuracy of visual analysis was analyzed based on the number of correct responses to the question about the specific property (i.e., level, variability, trend) out of the total number of response opportunities per packet (i.e., 10 graphs per packet). A response was scored as correct if the participant’s response matched the expert raters’ responses. A response was scored as incorrect if the participant answered the question differently than expert raters did or did not answer the question. Data were summarized as the percentage of accurate visual analysis per graph packet.

Total Training Time

Total training time was defined as the total duration of training time in minutes across all visual analysis property modules per participant and, if applicable, the overall intervention effect module. The Blackboard® software captured and analyzed the duration of each participant’s training time per module. A session began when the participant opened the computer-based training file and ended when the participant completed the module.

Total Testing Time

Total testing time was defined as the total duration of testing time in minutes across all assessment graphs. At the beginning of each assessment (following completion of a training module session), a timer was started. An assessment began when the participant turned over the first graph. An assessment ended when the participant turned over the last graph.

Assignment of Stimuli

Graph Presentation

The order of the assessment graphs (i.e., three-graph packets) following each module presentation was created using a computer-based random-sequence generator to create a unique running order for each participant. This was done to decrease the possibility that the order of graph presentations may have differently affected the results. The experimenter assigned each graph packet a number and put the numbers into the random number generator until the order for 45 graph packets was determined. If a participant required more than 45 graph packets, additional graph packet running orders would have been obtained.

Training Assignment

All participants were trained across three visual analysis properties. Training modules consisting of variability, level, and trend were counterbalanced across and within participants to decrease the possibility that the order of training may have differently affected the results. A modified Latin square was used.

Experimental Design

A multiple-baseline design across visual analysis properties (i.e., variability, level, and trend), with continuous overall intervention effect generalization probes, replicated across four participants, was used. Participants were required to score 90% or higher on three out of four consecutive assessment graph packets (i.e., three different A-B graph packets) to complete each visual analysis property and advance to the next property. The mastery criterion was determined following a pilot of the procedures.

Procedure

General Format

Participants were given one graph packet (10 A-B graphs per packet) and were told, “Analyze the data as best you can and please flip the packet over when you are done,” by answering questions on the visual analysis properties (i.e., trend, level, and variability) and overall intervention effect (i.e., behavior change from baseline to treatment). Specifically, participants were asked to determine whether each graph depicted a convincing and overall change between the visual analysis properties from baseline to treatment and whether an overall intervention effect or noneffect occurred by indicating “yes” or “no” for each question. Participants were not provided with guidance or feedback. At the completion of the assessment, the experimenter thanked the participants.

Preexperimental Assessments

Prior to conducting the procedure, all participants were given a packet of 10 graphs. Any participants scoring higher than 70% on any property or overall intervention effect were excluded from the study.

Baseline

Participants independently completed graph packets until stable responding was observed.

Computer-Based Training

Participants were given paper and pen to use if needed throughout the training and asked to sit in front of a computer to start the computer-based training on Module 1 (i.e., basic visual analysis). After one completion of Module 1, all participants began Module 2 (i.e., first specific-property module). Participants followed along with the computer training and answered the sample practice-graph questions. Immediately following the completion of a module (except Module 1), an assessment session was conducted that consisted of one of three packets of 10 various A-B graphs from Jostad’s (2011) simulated data. If a participant scored above 90% on the specific property, then another assessment graph was presented. However, if a participant scored below 90%, then the participant was required to repeat the module. This continued until the mastery criterion (i.e., three out of four consecutive sessions at 90%) was met on the assessment graphs per property. After a participant met the mastery criterion on the assessment graphs, the participant advanced to the next module until he or she met the criterion across all visual analysis properties. If a participant successfully completed Modules 2–4 but did not accurately interpret overall intervention effect, the participant completed Module 5 (i.e., overall intervention effect) until the mastery criterion was met on the assessment graphs.

Ongoing Generalization Probes

Ongoing generalization probes of overall treatment effect were programmed through the use of multiple exemplars of A-B graphs. Ongoing generalization probes assessed participant responding to overall intervention effect. Participants indicated whether an overall intervention effect was demonstrated in the graph by answering the question, “Did behavior change from baseline to treatment?” with a “yes” or “no.” If participant responding did not meet the criterion for ongoing generalization probes following mastery of all visual analysis properties, then overall intervention effect was taught. The same data-collection procedures used during assessment graphs were used during ongoing generalization probes. Data were summarized as the percentage of accurate visual analysis.

Pre- and Posttest Generalization Probes

Generalization of simulated data on computer paper was programmed and assessed during two pre- and posttest generalization probes. Responding to simulated data on handwritten graphs and to actual data on computer paper was assessed during two sessions prior to the intervention and two sessions following mastery. The same data-collection procedures used during assessment graphs was used during generalization probes. Data were summarized as the percentage of accurate visual analysis.

Maintenance

Maintenance of visual analysis skills was assessed at approximately one day, one week, two weeks, and one month following mastery. Maintenance sessions were conducted across all properties taught and overall intervention effect using the same packets of 10 A-B graphs as in baseline conditions. The same data-collection procedures and data summary used during assessment graphs were used during maintenance sessions.

Social Validity Measures

The acceptability of the study’s goals (i.e., to train adults to visually analyze A-B graphs), procedures (i.e., computer-based training with feedback), and outcomes (i.e., accurate visual analysis of A-B graphs following training) was assessed in different ways. To assess the study’s goals, a group of 10 BCBAs (i.e., two doctoral-level and eight master’s-level BCBAs) were surveyed prior to the study. Each BCBA was provided with the computer-based training instructional content through e-mail. They were given a 6-item questionnaire using a 5-point Likert rating scale of 1 (strongly disagree) to 5 (strongly agree) to rate the clarity and importance of the computer-based training. These data were summarized as means and ranges per question. Results suggested that the BCBAs strongly agreed that training adults to visually analyze A-B graphs is an important instructional area (mean 5) and that the computer-based training is an acceptable method (mean 4.1, range 4–5) that is clear (mean 4.6, range 4–6) and easy to follow (mean 4.6, range 4–6). In addition, the BCBAs strongly agreed or agreed that they would use this procedure to train individuals (mean 4.5, range 4–5). To further assess the study’s goals, the same group of BCBAs scored the computer-based training on the validity of the content using the Fidelity Checklist modified from Jostad (2011). The computer-based training was modified based on these assessments. These data were summarized as the percentage of included components per question. Results indicated that most of the components were included in the training at 100% agreement, with minimum mean agreement of 90% and 95% across two questions. Additionally, 100 hard copies of A-B graphs were analyzed by raters to ensure the accuracy of the mathematically generated graphs, specifically, to determine whether the graphs depicted property and overall effect or noneffect across baseline to treatment conditions they were chosen to exhibit. As previously noted, 60 graphs with the highest mean agreement were retained.

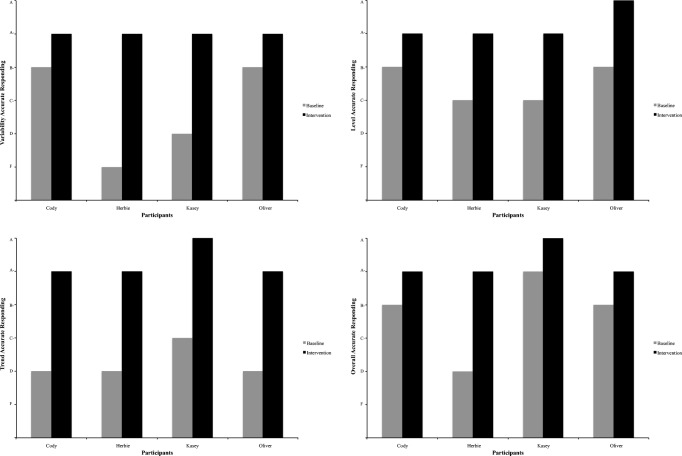
To assess the acceptability of the procedures, each participant completed a modified version of the Treatment Acceptability Rating Form-Revised (Reimers & Wacker, 1988). Participants were given a 5-item questionnaire using a 5-point Likert rating scale of 1 (strongly disagree) to 5 (strongly agree) to rate the acceptability of the procedures. These data were summarized as means and ranges per question. The results of the survey indicate that most participants enjoyed the training (mean 4, range 2–5) and the training had a positive impact on performance (mean 4, range 2–5). Additionally, all participants agreed or strongly agreed that the training was clear to them (mean 4.5, range 4–5) and that it was easy to visually analyze graphs following training (mean 4.25, range 4–5). To assess the outcomes, participant scores on the first baseline measure and last intervention measure, across all measures, were converted to relevant letter grades used in university courses by using the following conversion: 100% = A, 90% = A−, 80% = B−, 70% = C−, 60% = D, and below 60% = F (Fienup & Critchfield, 2010; Schnell, Sidener, DeBar, Vladescu, & Kahng, 2014). These data were summarized as the percentage of letter grades per measure. All participants increased at least one letter grade for each visual analysis property (see Fig. 1).

Fig. 1.

Letter-grade conversion of baseline and intervention scores across variability (top left), level (top right), trend (bottom left), and overall (bottom right) for all participants

Interobserver Agreement

Point-by-point agreement was used to determine the interobserver agreement score. This was calculated by dividing the number of agreements by the number of agreements and disagreements and multiplying by 100. The IOA mean across all participants was 100% across all phases of the study.

Procedural Integrity

Two procedural integrity measures were conducted. First, one of the research assistants scored the functioning of the computer-based training software to ensure that the program opened, presented the correct module, and delivered appropriate feedback. Data were scored in vivo one time during the study and scoring was completed with 100% accuracy. Data were summarized as the percentage of correctly implemented components. Second, the assistants scored the experimenter’s implementation of the procedures during sessions (i.e., preexperimental assessment, baseline, assessment, pre- and postgeneralization probes, and maintenance). Procedural integrity was collected for 88.5% across all assessments, specifically 100% for Cody, 60% for Herbie, 97% for Kasey, and 97% for Oliver across all sessions. Data were summarized as the percentage of correctly implemented components. The implementation of the procedures by the experimenter was completed with 100% integrity. IOA data were also collected on procedural integrity for all sessions in which procedural integrity data were videotaped (86%). IOA data for procedural integrity were also 100%.

Results

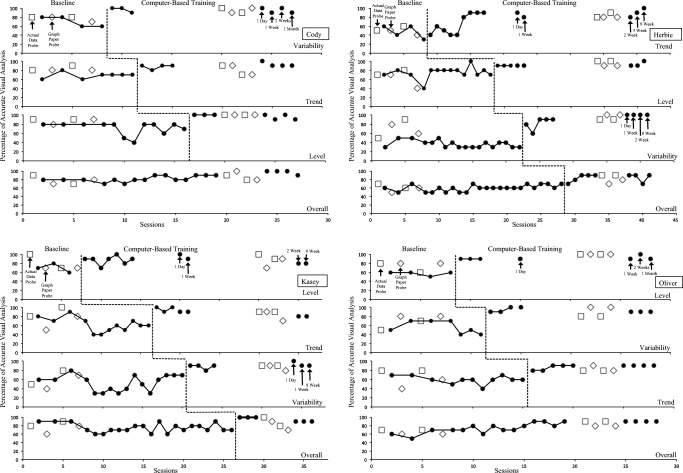
Figure 2 shows the percentage of accurate visual analysis properties for all participants. For Cody (top-left panel), responding remained stable and between 40% and 80% in baseline for all visual analysis properties. Following the introduction of the computer-based training on all properties, an immediate increase in percentage of accurate visual analysis occurred for Cody, whereas the subsequent properties remained stable and below criterion. Specifically, once computer-based training was implemented on variability, responding increased to a mean of 97% (range 90%–100%); on trend, responding increased to a mean of 87.5% (range 80%–90%); and finally, on level, responding increased to 100%. For Herbie (top-right panel), baseline responding remained stable and below criterion for all visual analysis properties. After computer-based training was introduced on trend, accurate responding increased from a mean of 47.5% (range 30%–60%) to 64% (range 40%–90%); on level, responding increased to 90%; and on variability, responding increased to a mean of 82% (range 60%–90%). For Kasey (bottom-left panel), responding remained stable in baseline for all visual analysis properties. Following the introduction of training on all properties, an immediate increase in percentage of accurate visual analysis occurred for Kasey, whereas the other properties remained stable and below criterion. Once training was implemented on level, accurate responding increased to a mean of 87% (range 70%–100%); on trend, responding increased to a mean of 97% (range 90%–100%); and on variability, responding increased to a mean of 87.5% (range 80%–90%). Finally, for Oliver (bottom-right panel), baseline responding remained stable and between 40% and 70% for all visual analysis properties. After the introduction of the computer-based training on all properties, an immediate increase in percentage of accurate visual analysis occurred for Oliver, whereas successive properties remained stable and below criterion. Once computer-based training was implemented on level, accurate responding increased to a mean of 90%; on variability, responding increased to a mean of 93% (range 90%–100%); and on trend, responding increased to a mean of 86% (range 80%–90%).

Fig. 2.

Data for percentage of accurate visual analysis for Cody (top left), Herbie (top right), Kasey (bottom left), and Oliver (bottom right) during computer-based training across visual analysis properties of variability, level, and trend and overall intervention effect

Furthermore, total training time was approximately 20 min for Cody, 1 h 5 min for Herbie, 33 min for Kasey, and 52 min for Oliver. The average training time was 42 min 25 s (range 20 min 3 s–1 h 4 min 57 s). The total testing time was approximately 40 min for Cody with a mean time per graph packet of 4 min (range 3–6 min), 2 h 29 min for Herbie with a mean of 6 min (range 4–8 min), 1 h 24 min for Kasey with a mean of 4 min (range 3–7 min), and 1 h 9 min for Oliver with a mean of 6 min (range 5–8 min). The average testing time per graph packet was 5 min 12 s (range 3 min 57 s–6 min 15 s).

Figure 2 depicts the percentage of accurate responding for all participants on overall intervention effect, demonstrated at the bottom of each panel. Responding remained stable for all participants prior to training. For Cody (top-left panel) and Oliver (bottom-right panel), as each property’s training was introduced, accurate responding to these probes increased and the mastery criterion was met. However, for Herbie (top-right panel) and Kasey (bottom-left panel), as each property’s training was introduced, accurate responding remained constant; therefore, overall intervention effect had to be trained, and they quickly mastered this. Additionally, Fig. 2 depicts the results for the pre- and posttest generalization probes of handwritten and authentic data graphs during two sessions prior to intervention and two sessions following mastery. Before training, participants did not meet criterion on the handwritten graphs; however, following the intervention, average responding increased for all but one measure, in which Cody’s average responding remained constant at 80% for trend. For the authentic graphs, before training, participants did not meet the mastery criterion. Following training, average responding to authentic data graphs increased for most measures.

Figure 2 depicts the results for maintenance probes for each participant following mastery of each property and overall intervention effect. All skills maintained at 90% or higher for Cody and Oliver at approximately one day, one week, two weeks, and one month following mastery. For Herbie, skills maintained at 90% or higher for level and variability; however, trend responding decreased to 80% at 1-week and 2-week probes and increased to 100% at 9-week probe. Similarly, overall responding decreased to 70% at 2-week probe but increased to 90% at 8-week probe. For Kasey, skills maintained at 90% or higher for variability and overall; however, level and trend responding deceased to 80% at 2-week and 9-week probes.

Discussion

Prior to receiving training, participants’ percentage of accurate visual analysis was below criterion. With the introduction of the computer-based training, each participant accurately visually analyzed A-B graphs on the three main visual analysis properties (i.e., variability, level, and trend) and overall intervention effect. This procedure allowed for exclusive reliance on computer-based training and, therefore, may potentially reduce the cost and time associated with hiring clinicians while simultaneously promoting accurate and consistent training on visual analysis. Furthermore, accurate visual analysis of A-B graphs is necessary for the successful implementation of ABA (Fisher et al., 2003) and client outcomes (Cooper et al., 2007).

This study was the first, to the authors’ knowledge, to use computer-based training to teach individuals accurate visual analysis of A-B graphs on all visual analysis properties, sequentially to mastery, while assessing overall intervention effect responding. This study contributes to previous research that successfully used a mastery-based computer software program to teach adults to accurately visually analyze graphs on two properties (i.e., trend and level; Wolfe & Slocum, 2015) and that taught students to interpret intervention effect or noneffect based on visual analysis properties (i.e., level, trend, and variability; Jostad, 2011) simultaneously. It was hypothesized that the mastery-based design of the computer-based training was successful in increasing individuals’ accurate visual analysis of A-B graphs because this training incorporated most of the components typical of behavioral skills training (i.e., written instructions, behavior rehearsal, and feedback; Nosik & Williams, 2011; Sarokoff & Sturmey, 2004). All of these components have been found to be effective individually and in combination. Furthermore, past studies used either mathematically generated comparison measures (Jostad, 2011) or expert consensus (Wolfe & Slocum, 2015) as the measure to evaluate participant responses. This study combined these methods by using expert responses as they compared to Jostad’s (2011) statistical parameters per graph. This allowed for an additional way of measuring participant responses compared to using one method alone. Additionally, as in Wolfe and Slocum (2015), feedback was provided for correct and incorrect responses during training. However, in the current study, remediation loops were specific to the nature of the error. Particularly, each remediation loop included feedback on the correct answer, an explanation why the participant’s response was incorrect, and a single additional practice graph before the participant was presented with a similar graph (contingent on accurate response). This format may have decreased the redundancy of the repetitive practice graphs, increased effectiveness of the computer-based training, and led to maintenance of visual analysis skills.

Wolfe and Slocum (2015) used a successive (i.e., level then trend until mastery) and simultaneous (i.e., level and trend until mastery) training approach; however, they did not assess overall intervention effect responding. The current study expanded on this potential limitation by using successive training to evaluate effectiveness while assessing generalization probes of overall intervention effect to observe if and when overall intervention effect was learned. Moreover, this allowed determination if one property exerted more control on overall effect responding. In the current study, two out of four participants’ responding generalized to analysis of overall intervention effect. It is hypothesized that order of training may have influenced responding. Specifically, both participants received training on their final property of trend or level (not variability) when overall intervention effect responding generalized. Interestingly, Cody received training on trend (second property) and level (third property) and mastery criterion was missed by one session during training on trend. Future studies may evaluate which order of training leads to rapid generalization of overall responding, as trend and level seemed to influence overall intervention effect responding the most. Additionally, while piloting the study, carry-over effect was noted and addressed by varying the order in which the participants received the training and editing the content within the modules to ensure there was no overlap across properties. Although these efforts were made to prevent carry-over effect, for Herbie, when training began on trend, level responding remained stable at 80%. This could be corrected by teaching the properties simultaneously. Future studies may evaluate simultaneous training compared to successive training, as simultaneous may be more efficient and likely to obtain generalization (Saunders & Green, 1999).

Moreover, no study to date has programmed or assessed generalization of accurate visual analysis skills. Therefore, this study further extended previous research by demonstrating that individuals’ visual analysis skills generalized from simulated data to handwritten and authentic data graphs (as evidenced by the pre- and posttest generalization probes). Furthermore, studies that taught visual analysis and interpretation of A-B graphs either did not target teaching directly (Fisher et al., 2003) or did not assess maintenance of intervention effects following the removal of the teaching aid and over time (Fisher et al., 2003; Jostad, 2011; Stewart et al., 2007; Wolfe & Slocum, 2015). During the current study, two participants (i.e., Cody and Oliver) maintained gains at 90% or higher at approximately one day, one week, two weeks, and one month following mastery. Because of scheduling conflicts, two participants were assessed closer to a two-month probe (in place of a one-month probe). For Herbie, gains maintained at 90% or higher for all four properties, and for Kasey, gains maintained at 90% for two properties. Therefore, the current study directly contributes to the existing literature by demonstrating that computer-based training led to accurate visual analysis of A-B graphs that maintained up to 2 months following mastery. Additionally, this study was the first to assess full social validity of the goals, procedures, and outcomes, which validated the importance and effectiveness of this training to trainers and consumers.

While conducting the current study, feedback was obtained from several of the raters that assessed the A-B graphs. The overwhelming concern was with the last question (i.e., “Did behavior change from baseline to treatment?”). Teaching visual analysis skills on A-B graphs is the simplest way to train the type of graph that most clinicians will likely come into contact with; however, experimental control cannot be determined from A-B graphs (Cooper et al., 2007). Although it was expected that the raters would use the combined principles of visual analysis to answer this question, many of the raters took the question literally, at face value, which yielded a different answer. Suggestions were shared from BCBA-Ds as to how to make this last question clearer. Several included rephrasing the question to one of the following: (a) “Using visual analysis only, does the behavior appear to have changed from baseline to treatment?” (b) “Although no conclusions can be drawn from an A-B design, does the behavior appear to have changed from baseline to treatment?” or (c) “Before possibly testing for functional control, did the behavior change from baseline to treatment?” Future investigations may take this information into consideration when formulating questions targeted to evaluate overall intervention effect when training on A-B graphs. Additionally, several raters expressed concern with some of the graphs created by Jostad (2011), which did not have stable baselines prior to implementing treatment. Pluchino (1998) indicated that when teaching visual analysis skills, graphs should not have a slope in baseline. Future research may take this feedback into consideration when obtaining graphs.

Interestingly, while developing materials used in the current study, it was found that many of the participants who pretested out of the study (n = 15; i.e., obtained 70% or higher on any of the measures) scored higher on graphs than the expert raters (i.e., nine BCBA-Ds and one BCBA). The average age of the participants that did not meet inclusion criteria was 23.73 (range 19–56 years) and average reported GPA from 12 participants was 3.56 (range 3–3.91). Most of these participants reported psychology (n = 7) or education (n = 2) as their majors. Because naïve participants (i.e., adults that did not have extensive experience in ABA or special education) were used in the study, it is hypothesized that individuals with advanced experience in the field of ABA may view the graphs in terms of learner behavior whereas naïve individuals may view graphs in terms of data points. Additionally, most participants that pretested out developed rules for themselves that influenced responding; for example, one participant stated her rule for evaluating trend as similar to “trending” on Twitter, which means you are going up. Another participant indicated that for level, he thought of people being tall or short in stature.

Furthermore, the software developed included written instructions, interactivity, quizzes, and textual feedback. The written instructions may have caused an increase in accurate responding as this component was similar to a lecture, and past research found lecture conditions alone increase accurate responding (Jostad, 2011; Wolfe & Slocum, 2015). Future research may conduct a component analysis to determine which components of the training procedure lead to accurate responding. Other avenues for future research include assessing generalization to non- A-B graphs, such as reversal and multiple-baseline designs. Future research could also include development of a fully automated computer-based training program leading to a streamlined training that may reduce total testing time. This could allow for learner-paced instruction (Skinner, 1958), especially as online ABA programs continue to increase (Lee, 2017). Also, future studies may evaluate if brief written instructions in baseline influence responding of individuals without prior experience in visual analysis. Furthermore, this study was conducted in an academic setting; perhaps future research could investigate conditions in which experimenters could simulate a clinical setting by evaluating training in a more generic way. For example, participants could be asked to describe a novel graph in vivo (e.g., “Tell me about this graph.”), to vocally state the rules they were taught while visually analyzing a novel graph, or to analyze actual unfinished data from a learner’s programming binder. This would provide meaningful information on participants’ actual performance in a natural context, rather than a training context.

Overall, the present study taught adults with no prior experience to visually analyze A-B graphs on the visual analysis properties of variability, level, and trend and overall intervention effect. The training was expedited in nature as it took 20 min for Cody to learn all visual analysis components and under one hour for 75% of the participants. This was the first known study to demonstrate generalization and maintenance of visual analysis skills. Therefore, a computer-based training approach that leads to accurate visual analysis, while simultaneously expediting the training process, may be of great value to clinicians, staff, and organizations.

Implications for Practice

• This extends previous research on training individuals to analyze baseline-treatment graphs.

• This research is the first investigation to evaluate the effects of computer-based training on the visual analysis skills of variability, level, and trend while assessing generalization to overall intervention effect.

• Computer-based training led to successful analysis of baseline-treatment graphs.

• Visual analysis skills generalized to untrained graph formats and maintained up to 2 months following the conclusion of the training.

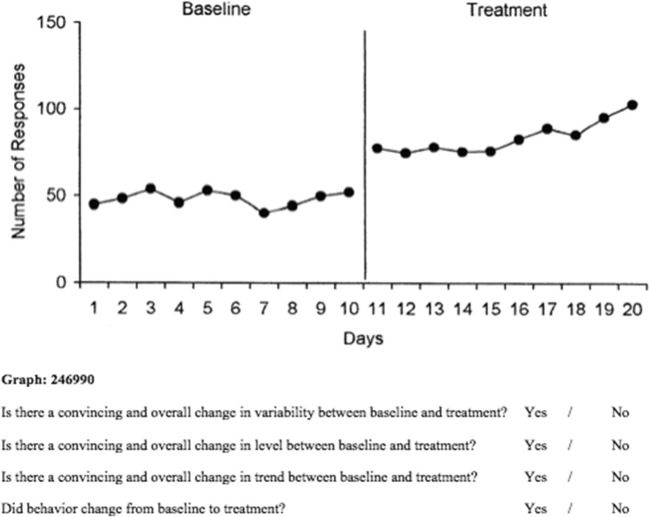
Appendix

A sample of an assessment graph presented to participants. This graph demonstrates a baseline-to-treatment change in level, trend, and overall intervention effect, but no change in variability.

Funding

No funding was used for this research.

Compliance with Ethical Standards

Conflicts of Interest

All authors declare that they have no conflicts of interest.

Ethical Approval

All procedures performed in studies involving human participants were in accordance with the ethical standards of the institutional and/or national research committee and with the 1964 Helsinki declaration and its later amendments or comparable ethical standards.

Informed Consent

Informed consent was obtained from all individual participants included in the study.