Fully Automated Tissue Classifier for Contrast-enhanced CT Scans of Adult and Pediatric Patients

Abstract

Purpose:

To develop a consistent, fully-automated classifier for all tissues within the trunk and to more accurately discriminate between tissues (such as bone) and contrast medium with overlapping high CT numbers

Methods:

Twenty-eight contrast enhanced NCAP (neck-chest-abdomen-pelvis) CT scans (4 adult and 3 pediatric patients) were used to train and test a tissue classification pipeline. The classifier output consisted of 6 tissue classes: lung, fat, muscle, solid organ, blood/bowel contrast and bone. The input features for training were selected from 28 2D image filters and 12 3D filters, and one hand crafted spatial feature. To improve differentiation between tissue and blood/bowel contrast classification, 70 additional CT images were manually classified. Two different training data sets consisting of manually classified tissues from different locations in body were used to train the models. Training used the random forest algorithm in WEKA (Waikato Environment for Knowledge Analysis); the number of trees was optimized for best out-of-bag error. Automated classification accuracy was compared with manual classification by calculating Dice Similarity Coefficient (DSC).

Results:

Model performance was tested on 21 manually classified slices (2 adult and 1 pediatric patient). The overall DSC at image locations represented in the training dataset were - lung: 0.98, fat: 0.90, muscle: 0.85, solid organ: 0.75, blood/contrast: 0.82, and bone: 0.90. The overall DSC for slice locations that were not represented in the training dataset were - lung: 0.97, fat: 0.89, muscle: 0.76, solid organ: 0.79, blood: 0.56, and bone: 0.74. Analyzing the classification maps for the entire scan volume revealed that except for misclassifications in the trabecular bone region of the spinal column, and solid organ and blood/contrast interfaces within the abdomen, the results were acceptable.

Conclusions:

A fully-automated whole-body tissue classifier for adult and pediatric contrast-enhanced CT using random forest algorithm and intensity-based image filters was developed.

1. INTRODUCTION

Implementing a fully automated organ and tissue classification algorithm for reconstructed CT images is an important step towards quantitative diagnostic analyses including patient specific CT dose calculations, robust analysis of image quality using iterative image reconstruction techniques, and applications of radiomics. Modern CT scanners can create hundreds of slices for each examination, and with multiple examinations performed on a wide variety of patient sizes each day, manual or even semi-automated segmentation for all patients is impractical. Many existing organ and tissue segmentation algorithms for CT are based on traditional approaches such as shape analysis, atlas based localization, thresholding, edge detection, voxel-based texture analysis, region growing, deformable models, Markov random field models, morphological operations, etc. (Pham et al., 2000); these segmentation algorithms may be specific to certain regions of the body or application-specific, and often combine multiple strategies to achieve their end result (Sharma and Aggarwal, 2010). Furthermore, for pediatric populations, the variation of body habitus limits approaches using shape analysis, atlas based segmentation, and algorithms that require organ dependent or tissue dependent parameter tuning. Currently, no fully-automated CT classifier has been created to classify tissues throughout the body for the large range of patient sizes found in children and adults.

Creating a full-body, fully-automated tissue segmentation algorithm for CT is a complex task due to multiple factors: overlapping CT Hounsfield numbers (HU) between tissues and organs (i.e., intravenous/oral contrast and bone); tissue texture variability due to quantum noise; variability in scan parameters such as reconstruction kernels and tube potential (kV) that affect the presentation of the image; partial volume artifacts; and organ shape, size, and location variability between patients. With advancements in machine learning tools for computer vision problems (Nitze et al., 2012), it has become feasible to develop tissue classification pipelines using general algorithms that can be trained for complex classification tasks such as segmentation of CT images. Neural network based machine learning algorithms have been used with satisfactory results when segmenting high-contrast regions such as lung tissue from the thorax (Karthikeyan and Ramadoss, 2011); however, neural networks have multiple hyper-parameters, and determining the optimal parameters can be tedious for whole body segmentation of subtly varying tissue contrasts typical of soft tissue organs. Multiple organ segmentation has been explored using advanced decision trees (Montillo et al., 2011) and active learning concepts to maximize the training performance (Iglesias et al., 2011), but the reported performances were not satisfactory.

More recently, a new class of algorithms called deep learning have proven very successful for various computer vision problems. These algorithms are based on advanced machine learning concepts known as convolutional neural networks (CNNs) that perform well for complex tasks. A recent study used deep learning for automatic bone segmentation of whole body CT. The study used a data-set of 6000 images for training. When applied to 15 whole-body CT scans, the CNN model achieved an accuracy >0.91 on cross-validation. The major bottleneck in using deep learning for medical image segmentation is the need for large dataset of manually contoured slices for training and validation. The bone segmentation study used a simpler thresholding based algorithm to generate the bone segments which were then corrected manually by an expert (Klein et al., 2018).

For a whole-body CT tissue segmentation task, a traditional machine learning algorithm has shown promising results with a smaller dataset (Polan et al., 2016). In that study, a random forest classifier was trained and tested on contrast-enhanced neck-chest-abdomen-pelvis (NCAP) CT scans of adult and pediatric patients. The random forest algorithm was selected as an appropriate candidate for that study due to its robust nature and fewer hyper-parameters (Caruana and Niculescu-Mizil, 2006). The random forest algorithm also was desirable for its computational efficiency, probabilistic output, ability to handle varied image input features, and iterative improvement based on error handling (Breiman, 2001). Additionally, a random forest algorithm prevents over-fitting of the data by building decision trees using randomly selected features at each node and combining the output of multiple random trees into a final classifier. The classifier model was trained using a Trainable WEKA (Waikato Environment for Knowledge Analysis; University of Waikato, Hamilton, New Zealand) Segmentation (TWS) plugin for FIJI (Fiji, NIH, Bethesda, MD) (Arganda-Carreras et al., 2014) (Schindelin et al., 2012) . The results were reasonable for distinct-contrast tissue regions such as lungs, fat, and muscle with average Dice Similarity Coefficient’s (DSC’s) of 0.91, 0.81 and 0.82, respectively. But classification of tissues with overlapping or similar CT intensity values such as bone, blood/bowel opacified with contrast media, and solid organs perfused with contrast medium (e.g., the liver) was poor, with average DSC’s of 0.70, 0.18 and 0.77, respectively.

The goal of this study is to (1) implement advanced 2D and 3D image feature extraction and analysis methodologies towards developing a more robust classifier model to improve the discrimination of our previously validated random forest classifier model (Somasundaram et al., 2017; Polan et al., 2016), (2) to study the dependence of classifier performance on the axial location of the training slices, and (3) to improve discrimination and segmentation in the regions where intravenous and oral contrast agents overlap in CT number intensity with tissues such as bone and solid organs infused with contrast (e.g., kidneys, spleen, liver, etc.). To this end, the capabilities of the TWS plugin to generate advanced 2D and 3D image features, and provisions within WEKA for data sampling, feature selection, and classifier optimizations (Hall et al., 2009), are investigated.

2. METHODS

The classifier model development presented in this work was performed in two stages, [Figure 1]. In the first stage, the classifier was developed using two sets of training data for six tissue classes and one background class. The training pixels were selected using random sampling across all the training image slices. Feature selection algorithms were investigated to determine the best image features for the classifying task from all 2D image filters supported in the FIJI-TWS framework. The effect of the training data set on the classification of inter-patient and intra-patient image slices also was studied to better understand the training data requirements for a comprehensive automated classification pipeline for NCAP CT scans.

Figure 1:

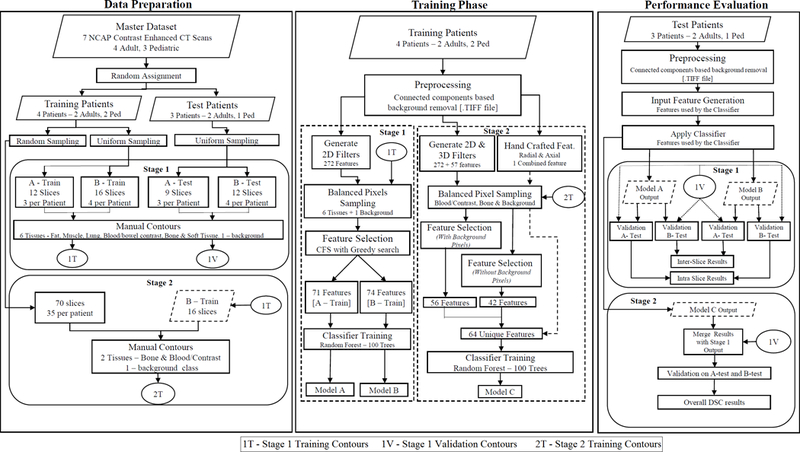
Flowchart detailing the data preparation, training and validation phases for developing the random forests based tissue classifier in this study.

In the second stage, based on knowledge gained in the first stage, a more rigorous training data sampling and feature selection including 3D image filters was performed to specifically target two tissues with overlapping CT number intensities: contrast opacified blood/bowel and bone. Novel spatial features developed using MATLAB (Mathworks, Natick, MA) were included in the training process, and provided shape information from the patient images in addition to the intensity information provided by the image filters.

2.1. Datasets

The input dataset for the classification algorithm consisted of axial reconstructed images from contrast-enhanced (both intravenous and oral) NCAP CT scans of 4 adult and 3 pediatric patients. Intravenous contrast used was iodixanol 270 administered via power injector at 2 ml/kg, and oral contrast was administered as a 1.5% solution of iohexol 300 contrast mixed in sugar-free liquid diluent, administered by volume based on age. The training input for the classifier had 4 patients (2 adult and 2 pediatric). The test set for evaluating the model performance consisted the remaining 3 patients (2 adult and 1 pediatric).

2.1.1. Stage 1 – Data for all tissue classification

The manually classified input dataset used in the previous feasibility study consisted of image slices at 3 fixed locations in the scan volume that were manually classified by an experienced radiologist into 6 tissue classes – muscle, fat, lung/air, solid organ, bone and blood/bowel contrast and 1 background class (Polan et al., 2016). In the feasibility study, the classifier was validated on test slices that were at the same axial location as the training slices. In this study, a goal was to analyze the dependence of the classifier performance on the axial location of the training slices when applied to the entire scan volume. Hence, for the first stage of this study, slices at 4 additional locations in the scan volume were manually classified as shown in Table 1. This resulted in two independent sets of training and test datasets, one containing 3 slices per patient (A-train, A-test) and another containing 4 slices per patient (B-train, B-test). Consequently, two classifier models were trained, one using pixel samples from A-train dataset containing a total of 12 slices from four patients and another using pixel samples from B-train dataset containing a total of 16 slices from the same four patients. The two classifier models were then tested on both A-test and B-test datasets to investigate the performance of the models on slices that were present (intra-slice) and on slices that were not present (inter-slice) in the training set.

Table 1:

Description of the training and test datasets for Stage 1 and Stage 2 (Somasundaram et al., 2017)

Dataset	Slices	Patients	Slice Locations
A-train	12	4	At the aortic arch, upper liver, and directly above the iliac crests
A-test	9	3	At the aortic arch, upper liver, and directly above the iliac crests
B-train	16	4	Above the aortic arch, below the left atrium, mid kidney, and mid             pelvis
B-test	12	3	Above the aortic arch, below the left atrium, mid kidney, and mid             pelvis
C-Train	70	2	35 slices sampled across the scan volume between aortic arch and         femoral head in the pelvis

2.1.2. Stage 2 – Data for high contrast tissue classification

To improve the discrimination between bone and contrast opacified blood/bowel, 70 additional training slices randomly sampled across the scan volume of 2 training patients (see Table 1) were manually classified for training the second stage classifier. Image pixels within the 70 slices (C-Train) were classified into 2 tissue classes, bone and contrast opacified blood/bowel. All the remaining pixels were assigned to a background class. The final training set consisted of 86 slices which included 16 slices (B-train) from stage 1 and 70 slices (C-train) classified exclusively for stage 2. The performance evaluation of the stage 2 classifier was performed on the same test slices used for stage 1 (A-test, B-test) by keeping the bone and blood/bowel segments and assigning the other tissue classes to background.

2.2. Image preprocessing

All models were trained with preprocessed image data with background homogenized by removing the scan table and other miscellaneous external objects near the patient (e.g., wires, lead cords, blankets, etc). The preprocessing step included thresholding and removing smaller connected components in the image with MATLAB routines, which removed noise in the tissue classification due to background.

2.3. Image features generation

2.3.1. Feature selection

Due to the large number of image features available through FIJI and complex nature of the classification task at hand, feature selection algorithm was used to eliminate redundant features that led to over-fitting, and to discard misleading features that were not correlated to the classifier output. The Correlation-based Feature Selection (CFS) filter implemented in WEKA was used; it searched the input feature space using the Best First Search (BFS) algorithm. The BFS algorithm used greedy hill climbing and backtracking to scan the input feature space (Rich et al., 2008). When a bi-directional search was initiated, the algorithm started with a random subset in feature space and searched both directions by adding and eliminating features until there was no improvement in the evaluation metric for a fixed number of additional features (or nodes). The number of nodes for convergence was set to a default value of 5. The evaluation metric used by the CFS algorithm to measure the merit of a feature subset took into account the usefulness of individual features in predicting the class label along with the level of inter-correlation between them. The overall score ($G_s$) of the subset was calculated using a formula that was directly proportional to the correlation measure between the features and the class$\left(\stackrel{-}{r_{cƖ}}\right)$ and inversely proportional to the square root of the correlation measure between the different features in the subset $\left(\stackrel{-}{r_{ƖƖ}}\right)$ (Hall and Smith, 1998).

$$G_s= \frac{k \overline{r_{cƖ}}}{\sqrt{k+k\left(k-1\right) \overline{r_{ƖƖ}}}},$$

where $k$ was the number of features in the input. The evaluation metric used by the CFS algorithm ensured selection of a subset of features that were highly correlated with the predicted class, yet uncorrelated with each other and not redundant.

Further, to study the effect of the number of features in the training input on the performance of the random forest classifier, classifier models are trained using feature subsets of reduced sizes by ranking the features based on their overall correlation to the output and removing them in blocks from the original subset generated by the feature selection algorithm (Hall et al., 2009; Hall and Smith, 1998). Features with lower correlation ranks were removed in blocks of 10 and classifier models were evaluated when trained with as few as 20 features.

2.3.2. Stage 1 – 2D image filters

To remove selection-bias when selecting the training features for the classifier model, all available 2D image filters in the TWS platform (Arganda-Carreras et al., 2014) were evaluated using the CFS algorithm. Twenty-seven 2D image filters along with the original HU value of each pixel resulted in a total of 272 features. A complete list of the features (Somasundaram et al., 2017) along with a description of filter implementation and image processing effect (Arganda-Carreras et al., 2014) has been published previously

The CFS algorithm resulted in a reduced subset of 74 and 71 features for the A-train and B-train datasets, respectively. The classifier trained on A-train will be referred to as classifier A, and the one trained on B-train will be referred to as classifier B. The features selected by the CFS algorithm consisted of the following 2D image filters: Anisotropic diffusion, Lipschitz, Gabor, Sobel, Hessian orientation, Hessian Eigenvalue difference (squared and normalized), Kuwahara, Gaussian blur, maximum, derivatives, structure smallest, structure largest, entropy, Laplacian, median, membrane projections and neighbor filters. Approximately half the features in the subset selected for the 2 datasets consisted of neighbor filters.

2.3.3. Stage 2 – 2D, 3D image filters and spatial features

Twelve 3D image filters with 86 features [Table 2] were investigated to provide more spatial information, and to better discriminate between the distribution of bone and contrast opacified blood/bowel. The 3D features were implemented independent of the TWS plugin using bean shell scripting to access the underlying Java classes directly, as in its current form TWS does not support the use of 2D and 3D image filters simultaneously.

Table 2:

Feature set generated using FIJI’s 3D image filters in TWS

3D Filter name	Number of Features
Derivatives	20
Difference of Gaussians	6
Edges	4
Gaussian blur	4
Hessian_largest	4
Hessian_middle	4
Hessian_smallest	4
Laplacian	4
Maximum	4
Mean	4
Median	4
Minimum	4
Structure_largest	8
Structure_smallest	8
Variance	4
Total 3D	86

Except for the Edges filter, all 3D filters performed similarly to their 2D counterparts, but included pixels from adjacent slices in the z-direction. The Edges filter calculated edges in the image by applying a combination of Canny edge detection using gradients and non-maximum suppression along with thresholding. All the isotropic filters used a radius of 16 pixels for the 2D calculation, while a radius of 8 was used for the 3D calculations. Since the slices used in training were axially spaced across the scan volume and are not necessarily adjacent to each other, the entire scan volume for each patient is provided to generate the 3D features. The final training pixels were sampled from the training slices (slices that had been manually contoured).

The CFS algorithm for 2 classes (bone, contrast opacified blood/bowel) resulted in a subset of 63 features, reduced from the original feature set consisting of 357 2D and 3D features. An additional hand crafted spatial feature (see section 2.3.4) was added to the feature set resulting in 64 features, and was used to train classifier C; classifier C was classified both with and without the spatial feature in order to validate the effectiveness of the novel feature. The 2D features selected for stage 2 consisted of: Anisotropic diffusion, Lipschitz, Gabor, Hessian Eigenvalue, Hessian orientation, Gaussian blur, Entropy, Maximum, Laplacian, Structure smallest, Structure largest, Membrane projections, and Neighbors. The 3D features selected consisted of the following filters: Gaussian blur, Hessian largest, Hessian smallest, Edges, Structure smallest, Maximum, Variance, and Difference of Gaussian.

2.3.4. Features selected for stage 2

In addition to the intensity based 2D and 3D image filters available in FIJI, a novel feature developed in house that provided spatial information of the patient anatomy was investigated. The distribution of most contrast opacified blood/bowel and bone pixels in an axial reconstructed image varied based on the axial location along the scan volume, e.g., in the chest, blood/contrast pixels were centrally located due to the position of the heart and great vessels, whereas bone pixels were distributed peripherally due to the location of the rib cage and spine. Spatial dependence along the AP (Anteroposterior) direction and the LAT (Lateral) direction was calculated by: (1) measuring radial distances for each pixel in the transaxial slice from the center of image space by determining the Euclidean distance between each pixel and the center of the patient volume in the scan. (2) A measure of the axial distance (z-distance) of the slice in the patient volume was calculated as the slice number multiplied by slice thickness and normalized for patient height and scan length. The steps involved in computing the spatial feature are summarized below:

1. Center of the body identified as the average of the x and y coordinates of all body pixels:

   $$r=(x_r,y_r)=\left(\frac{{\displaystyle {\sum }_i^{n_x}xi}}{n_x}\right),\left(\frac{{\displaystyle {\sum }_i^{n_y}{y}_i}}{n_y}\right),$$ (Eq.1)

   where $n_x$and $n_y$ were the total number of body pixels in the $x$ and $y$ directions after thresholding the background.
2. Radial distance of each pixel ($p_{radial}$) from center was calculated as:

   $$p_{radial=\sqrt{{(x-x_r)}^2+{(y-y_r)}^2.}}$$ (Eq.2)
3. The axial distance ($p_z)$ was calculated as the slice number ($Z_n$) multiplied by the distance between slices (T):

   $$p_z=z_n\ast T.$$ (Eq.3)
4. The axial distance was normalized by the median height ($H_a)$ for the patient’s age ($a$) from the CDC charts (2017) to obtain an axial measure (${\widehat{p}}_z)$ that accounted for the patient height:

   $${\widehat{p}}_z=\frac{p_z}{H_a}.$$ (Eq.4)
5. The axial distance was normalized for scan length by transforming ${\widehat{p}}_z$ to a discrete scale with a maximum value of 200 by using a nearest integer function

   $${\widehat{p}}_{z\_discrete}=nearest\_integer({\widehat{p}}_z\ast 200).$$ (Eq.5)
6. The discrete axial location values were scaled by the image width ($w)$ and radial distances were added to yield the final feature value for each pixel ($p_f)$:

   $$p_f=p_{radial}+{\widehat{p}}_{z\_discrete}\ast w.$$ (Eq.6)

   Scaling by image width was performed to ensure that the spatial feature remained unique to the normalized axial location.

2.4. Automated pixel sampling for training

The six tissue classes (lung/internal gas, fat, muscle, solid organ, contrast opacified blood/bowel, and bone), and one background class were highly unbalanced due to the large numbers of pixels belonging to fat, lung, and muscle while the number of pixels belonging to contrast opacified blood/bowel and bone were an order of magnitude smaller. To prevent pixel sample bias leading to unbalanced training datasets, WEKA’s balanced sampling filter was applied to generate a sample size for each class that was 12% of all the pixels in the training slices without replacement for stage 1. The 12% sample size was chosen based on the total number of pixels belonging to contrast opacified blood/bowel, which had the lowest number of pixels among the 7 classes (including background) in the training datasets. The final training sample for the A-train dataset had approximately 54,000 pixels sampled uniformly across the 7 classes and the B-train dataset had approximately 72,000 pixels. For stage 2, training pixels were sampled for bone and contrast opacified blood/bowel from a combined B-train and C-train dataset. Since the pelvic and shoulder regions contained far less blood/contrast than bone, performing a balanced random sampling could fail to include bone pixels from this region. Therefore, the number of pixels in each class was optimized by resampling datasets in different proportions. The optimized dataset had 825,698 pixels for bone and background, and 567,818 pixels for contrast opacified blood/bowel.

2.4.1. Model training and validation

The Fast Random Forest classifier option in WEKA was used to train the model. The training was performed on an Intel core-i7 6850K 3.5 GHz CPU with 6 physical cores and 12 threads. The Fast Random Forest classifier supported multithreading during training and prediction. The training of the classifiers, including feature generation, took approximately one hour; prediction of tissue classes for all images in the patient scan volume took approximately 20 minutes depending on the patient size.

To find the optimal number of trees for the random forest algorithm, the classifier models were trained using varying numbers of trees in the forest, and the optimal number of trees was found using cross-validation. Cross-validation error during the training phase was calculated using out-of-bag (OOB) error (Breiman, 2001). The OOB error was computed by testing each tree on bootstrapped samples from the training input that were not used to train that particular tree. The average error in predicting each sample from all the trees that did not contain the sample during training is the OOB error.

The classifier model published previously (Polan et al., 2016) is referred to as classifier P. Classifier P was trained on data sampled from the same set of 3 slices present in the A-train dataset, but pixels were sampled manually from only one adult patient among the two adult and two pediatric patients present in the A-train dataset. The classifiers A, B and P were validated for intra-slice and inter-slice performance on A-test and B-test datasets. For stage 2, the classifier C was tested on the B-test dataset. Since the stage 2 classifier was trained on the B-train and C-train datasets combined, the B-test dataset can be treated as an intra-slice test data for the stage 2 classifier. The results of the best performing models from stage 1 and stage 2 were merged to create the final classification.

To evaluate the performance of the classifier, the DSC was used as the evaluation metric (Dice, 1945). DSC is a measure of the spatial overlap in the classified image with the reference standard (manually segmented image) for each tissue class. A value of unity for the DSC indicates complete overlap while zero indicates no overlap:

$$DSC=\frac{2h}{a+b},$$ (Eq.1)

where, $h$ = number of pixels classified as a certain class in both manual and automated classifications; $a$ = number of pixels belonging to the class in manual classification; $b$ = number of pixels classified as the same class in automated classification. The sensitivity and specificity values of the automatic segmentation also were calculated to evaluate the classifier performance:

$$sensitivity=\frac{{\displaystyle \sum TP}}{{\displaystyle \sum (TP+FN)}},$$ (Eq.2)

$$sensitivity=\frac{{\displaystyle \sum TN}}{{\displaystyle \sum (TN+FP)}},$$ (Eq.3)

where, for a given tissue class, True Positive (TP) refers to all pixels that belong to the same class in manual and automatic classification; True Negative (TN) refers to classified pixels that do not belong to that class in both automatic and manual classification; False Positive (FP) refers to pixels that belong to the class in the automatic classification but not in the manual classification; False Negative (FN) refers to pixels that belong to the class in manual classification but incorrectly classified as a different class in the automatic classification.

3. RESULTS

3.1. Stage 1 – Results

3.1.1. Performance evaluation of the number of input features

The DSC values obtained when classifiers A and B were applied to their corresponding intra-slice test datasets are shown in Figure 2(a). For classifier A, there is a small dip in the DSC values for bone and blood from 20 to 30 input features after which adding more features resulted in a gradual increase in the DSC values until all the features in the feature subset are added. For classifier B, the solid organ DSC values on the test set decreased when the number of input features were increased from 20 to 30. However, the DSC values for the solid organ gradually increases after 40 features until all the features in the subset are added. On the other hand, the blood DSC values increase rapidly and saturated around 40 features. The results show that subset of features selected by the CFS algorithm (74 and 71 for A and B, respectively) provide the best performance on the test set.

Figure 2:

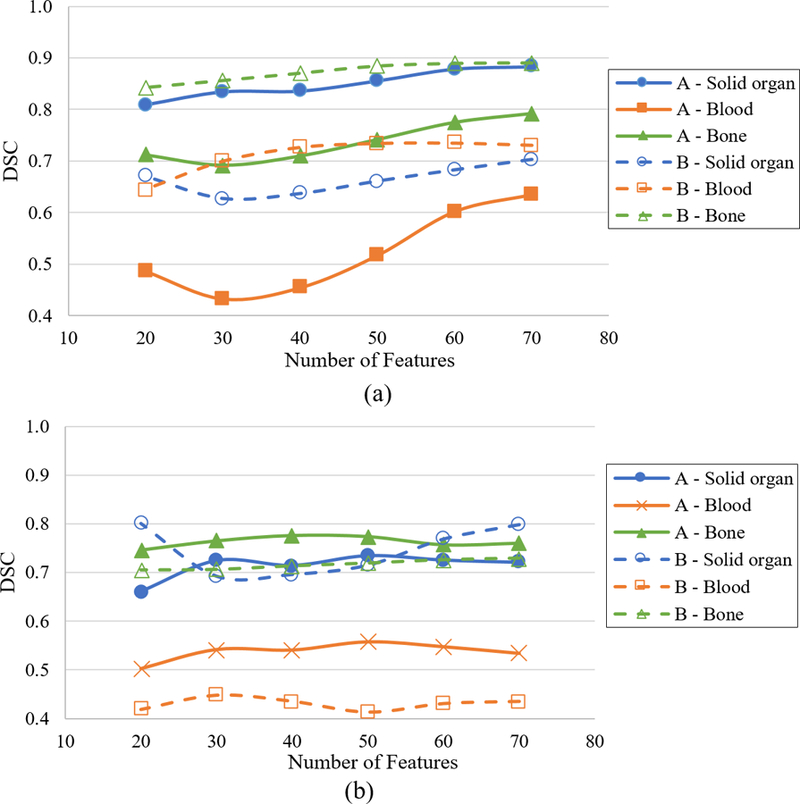
Dice Similarity Coefficient (DSC) for classifiers A and B on (a) intra-slice and (b) inter-slice test dataset as a function of number of training features. (Somasundaram et al., 2017)

The DSC values of A and B classifiers, when applied to inter-slice test data, are shown in Figure 2(b) as a function of the number of features in the training input. The results for both models on the inter-slice test data show no clear trend of increasing DSC values with increased number of features as observed in the intra-slice test results. In fact, for classifier B, the DSC values for solid organ falls sharply when features are added and the best DSC is achieved at 20 features, although the performance with 71 features is only slightly lower. The trends in the DSC values with respect to the number of input features in the training set for intra-slice and inter-slice test data reveal that model parameters are tuned for slices in the training set and may not provide optimal performance for slices not in the training data, especially in the overlapping tissue regions containing blood/bowel contrast.

3.1.2. Classifier optimization

Figure 2 demonstrates no significant improvement in OOB (Out-of-Bag) error for both classifier models A and B for more than 100 trees. All the random forest models used in this study are trained using 100 trees and 7 random features per node. In comparison, Classifier P from the previous study had 200 trees in its random forest model.

3.1.3. Classifier performance on intra-slice test data

The performance of the classifiers on intra-slice test data is shown in Figure 3(a). Classifier A from this study and classifier P from the previous study were trained on slices from the same transaxial locations and when tested on the intra-slice test set, the DSC values for contrast opacified blood/bowel class improved by more than 3 times (0.17 for P vs 0.64 for A) in this study while also improving the DSC values for all the other classes. Classifier B, which was trained on a different set of transaxial slices, also exhibits similar performance on its intra-slice test set. For lung/air, fat and muscle segments, the DSC values agree to better than 1% for both models on their respective intra-slice test data (A-test and B-test for model A and B, respectively) indicating that the classification pipeline is robust in predicting these 3 classes irrespective of the slice locations. For contrast enhanced blood/bowel and bone segments, the DSC values for classifier B are higher by 0.1. For solid organs, the DSC values for classifier A are higher by ~0.2. Table 3 shows the sensitivity values for the classifiers on intra-slice test data. The specificity values for all classifiers were ≥ 0.98 for all classes.

Figure 3:

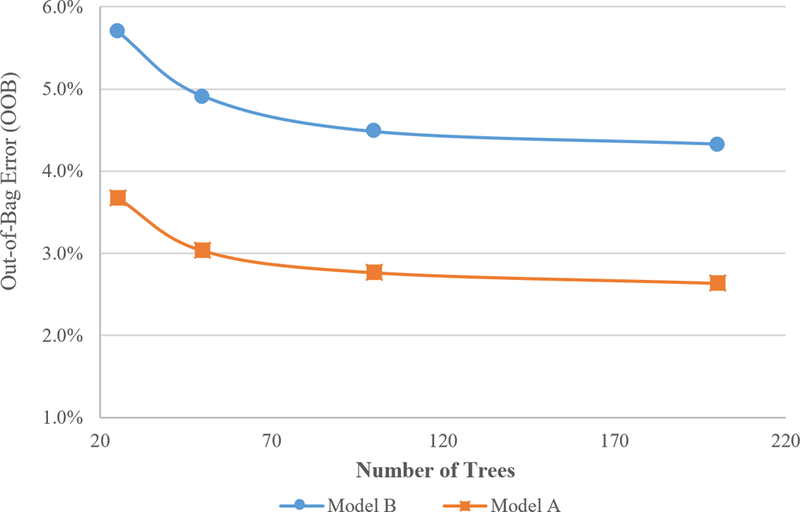
OOB as a function of number of trees in the random forest algorithm (Somasundaram et al., 2017)

Table 3:

Sensitivity values for intra-slice test

Classifier	Sensitivity
	Lung	Fat	Muscle	Solid organ	Blood/Contrast	Bone
P	0.96	0.73	0.79	0.71	0.58	0.70
A	0.97	0.85	0.86	0.96	0.64	0.72
B	0.97	0.88	0.87	0.65	0.81	0.89
C					0.80	0.95

3.1.4. Classifier performance on inter-slice test data

DSC values for classifier A on inter-slice test sets, [Figure 3(b)], remained high (0.72–0.98) for lung, fat, muscle, solid organ and bone, but the classifier performed poorly for blood/bowel contrast (0.52). Similarly, the DSC values of classifier B for lung, fat, muscle, solid organ and bone remained high (0.73– 0.98) while the DSC value for blood/bowel contrast was low (0.44). When compared to the intra-slice test result, inter-slice DSC values were lower by ~0.10 for lung, fat, and muscle, by 0.20 for solid organ, and by < 0.05 for bone and blood/bowel contrast. Inter-slice testing with classifiers A and B demonstrated better performance than P classifier. Table 4 shows the sensitivity values for the inter-slice test data. The specificity values remained ≥ 0.98 for all the classifiers.

Table 4:

Sensitivity values for inter-slice test

Classifier	Sensitivity
	Lung	Fat	Muscle	Solid organ	Blood/Contrast	Bone
P	0.95	0.77	0.84	0.42	0.64	0.92
A	0.97	0.84	0.83	0.69	0.53	0.81
B	0.95	0.87	0.73	0.93	0.58	0.61
C					0.46	0.97

3.2. Stage 2 – Results

3.2.1. Classifier performance

Figure 5 shows the DSC comparison for stage 1 and stage 2 classifiers on the B-test dataset. Classifier C shows the highest DSC values for bone and blood. The additional hand crafted spatial location feature used to train classifier C minimally improved the classifier performance (0.01 DSC) for blood/contrast with no improvement for bone. For blood/bowel contrast, the 2^nd stage classifier performed better by more than 9% over stage 1 classifiers on B-test dataset.

Figure 5:

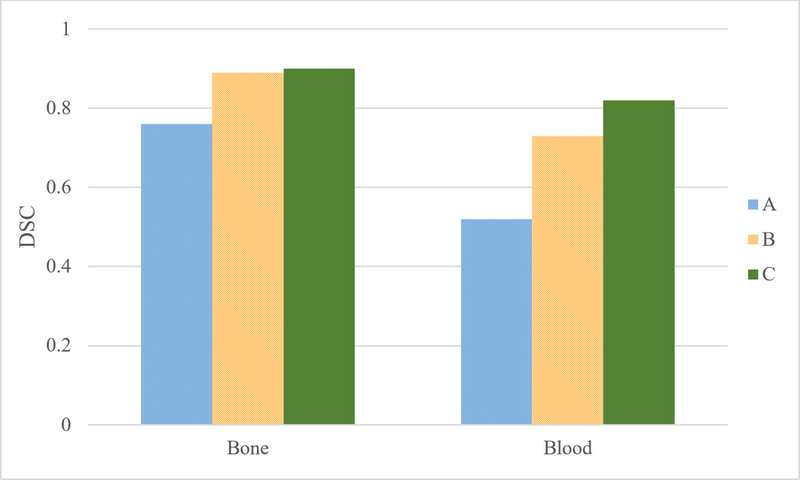
Bone and Blood DSC for stage 1 and stage 2 classifiers on B-test dataset

Table 4 provides the sensitivity values for the stage-2 classifiers on B-test dataset. For bone the sensitivity values are greater than 0.94 which is better than the 0.89 sensitivity value from stage 1 classifiers. For contrast opacified blood/bowel, the sensitivity values remained similar when compared to stage 1.

Figure 6 shows the performance of stage 2 classifiers on slice locations that were not in the training set (inter-slice test), the A-test dataset was used. Classifier C shows a 2% improvement in the DSC for bone and a 12% improvement in the DSC for blood/bowel contrast. However, classifier A, which was trained on A-train dataset, still performed better than classifier C (0.62 for B vs 0.56 for C).

Figure 6:

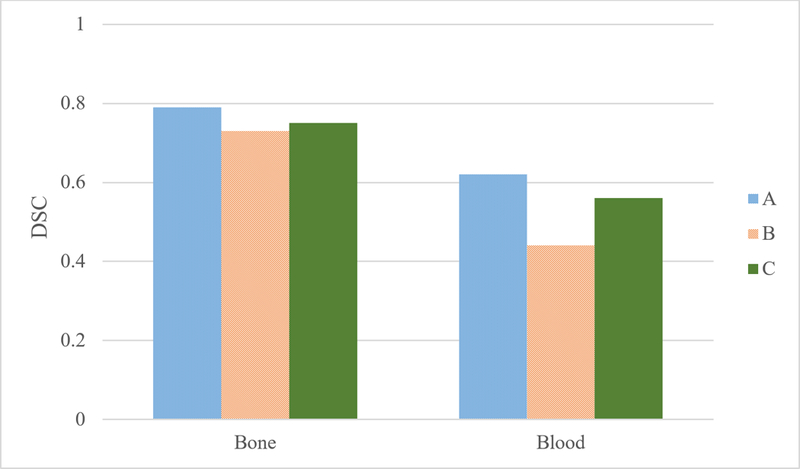
Bone and Blood DSC for stage 1 and stage 2 classifiers on A-Test dataset

3.2.2. Effect of individual image filters on the classifier performance

To evaluate if there is a particular image filter that is most significant for the classifier performance in stage 2, multiple classifiers were trained and tested by excluding specific image filter groups in the training feature set. Table 5 shows the DSC values for the different classifiers, which were all within 1% of each other except for the classifier with the maximum filter removed which had a blood DSC 5% lower than that of the classifier C. This indicates that except for the maximum filter, the other image filters compared equally and the performance of the classifier is uniquely determined by the combination of these filters and not by a single filter group.

Table 5:

Removal of Filter Groups from classifier

Classifier	DSC
	Bone	Blood
C (all features)	0.90	0.82
No Anisotropic Diffusion	0.90	0.82
No Difference of Gaussian	0.90	0.82
No Entropy	0.90	0.81
No Gaussian Blur	0.90	0.82
No Gabor	0.90	0.82
No Hessian	0.90	0.82
No Location	0.90	0.81
No Maximum	0.89	0.77
No Neighbors	0.90	0.80

3.3. Overall performance:

To assess the overall performance of the classifiers in providing tissue-wise classification for contrast enhanced CT scans, a final classification map was created by overlaying the bone and blood/contrast classification from stage 2 over the classification masks from stage 1. Table 6 shows the combined DSC and sensitivity values by applying classifiers B and C on intra-slice (B-test) and inter-slice (A-test) test data.

Table 6:

DSC and sensitivity values after applying stage 1 and stage 2 classifiers

Class	DSC		Sensitivity
	Intra Slice	Inter Slice	Intra Slice	Inter Slice
Lung	0.98	0.97	0.97	0.95
Fat	0.90	0.89	0.88	0.87
Muscle	0.85	0.76	0.88	0.73
Solid organ	0.75	0.79	0.74	0.95
Blood/Contrast	0.82	0.56	0.82	0.67
Bone	0.90	0.74	0.84	0.60

When the combined results were compared to stage 1 classifier results for intra-slice test set, an improvement in DSC of 0.09 and 0.05 was achieved for blood/contrast and solid organ classes. The sensitivity for solid organ also increased by 0.10 when compared to the stage 1 classifier. There was also a decrease in the sensitivity for bone by 0.04, however, the DSC value increased by 0.01. For inter-slice test set, the combined classifier results improved the blood DSC by 0.12 and bone DSC by 0.01, while the sensitivity increased by 0.10 for blood and decreased by 0.01 for bone. Remaining classes were not affected significantly by applying the stage 2 classifier.

Figure 6 shows the final classification across the entire scan volume for a test patient using classifiers B and C. The figure also shows the coronal and sagittal views of the patient scan along with their classification maps. Overall, except for the bowel components of the scan volume containing segments of irregular blood/bowel contrast opacification, and the spongy (trabecular) region of the spinal column, the tissue classification demonstrates good agreement with the CT images.

4. DISCUSSION

Overall performance improvement was observed for classifiers A, B, and C developed in this study when compared to classifier P from the previous study. The improved DSC values for classifier A over classifier P across all the tissue classes demonstrate the performance benefits of (1) a balanced uniform sampling of training pixels for all the tissues from multiple patient scans, and (2) using robust feature selection algorithms. The comparison of DSC values of classifier A and classifier B demonstrated the robustness of the CT classification pipeline for two independent sets of slices in a patient image volume. For lung/air, fat, and muscle classes, the reason for this performance difference between the two models can be understood from the average Hounsfield (HU) values for the tissue classes. The smaller difference in mean HU values [Table 7] between blood and solid organ in the B-test data, along with the larger deviation in the HU values for muscle when compared to A-test data, caused the relatively poor performance of classifier B for solid organ in its intra-slice test data.

Table 7:

Mean HU values for A-test and B-test datasets

Tissue	Mean HU
	A – Test	B – Test
Muscle	1067 ± 56	991± 259
Solid organ	1119 ± 43	1123 ± 34
Blood/contrast	1240 ± 173	1158 ± 190
Bone	1354 ± 193	1264 ± 320

The sensitivity values for lung, fat, and muscle remain consistent for the classifier A and B. However, classifier A had high sensitivity for solid organ and relatively poor sensitivity for blood/bowel contrast and bone, whereas classifier B had poor sensitivity for solid organ and relatively better sensitivity values for blood/bowel contrast and bone. The specificity values for all the classifiers remained greater than 0.98 for all classes and although this indicates that the classifiers are largely successful in avoiding type 2 error, the large differences in the numbers of pixels belonging to the different tissue classes means that even with a high specificity value, the number of pixels that are misclassified can be significant, as was evident in the blood/bowel contrast DSC values shown in Figure 2.

The inter-slice results indicate that although there is a slight drop in DSC values for regions like fat, lungs, and muscle when compared to the intra-slice test results, they retain good performance on inter-slice test slices. The DSC values for bone also exhibits a similar trend. However, for contrast opacified blood/bowel, there was a drop in performance (> 0.1 DSC) on inter-slice test data for both classifiers indicating a dependence on the training samples. This could be due to the fact that the contrast enhanced blood/bowel tissue area is smaller compared with other tissues, and during the training phase all blood/bowel contrast pixels in the training images are used possibly leading to over-fitting. For solid organs, the performance of classifier B is better for inter-slice test data (A-test) than for intra-slice test data (B-test). This demonstrates that for slices with tissues whose mean HU values fall closely within the HU range of other tissues, the classifier can perform poorly irrespective of the training data used.

For muscle, classifier A has similar sensitivity values for both intra-slice and inter-slice results while the sensitivity drops by 0.14 for classifier B on inter-slice results. For solid organ, the sensitivity values are reversed for classifier A and B when compared to the intra-slice results, confirming that for solid organ, the performance of the classifiers is dictated by the nature of the test slice. For bone and blood/bowel contrast the sensitivity values for classifier P are higher than those of classifiers A and B, however the DSC values demonstrated that classifiers A and B had better performance. This is because classifier P misclassifies the majority of blood and bone pixels as solid organ resulting in poor sensitivity values for solid organ.

Although the segmentation pipeline developed in this work improved the DSC values for the bone and contrast opacified blood/bowel, visual inspection of the classified images revealed that there is still minor misclassification of bone and blood/bowel contrast in slices that show prominent trabecular bone regions and high intensity blood/bowel contrast regions. Figure 7 demonstrates misclassifications observed in the sternum and thymus in a) - row 1. The second row showed some misclassified pixels in the bowel region, in the kidneys and the vertebral body.

Figure 7:

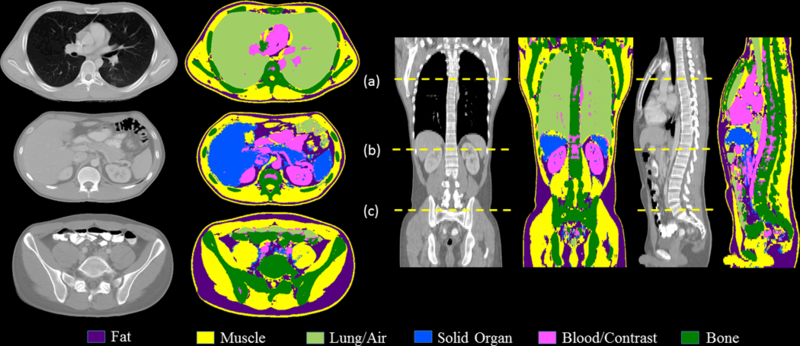
Tissue classification results of the entire scan volume of a test patient after applying classifier B (stage 1) and C (stage 2) with axial slices at: (a) mid-lung, thorax (b) upper abdomen at pancreas and upper pole of kidneys, and (c) at the pelvic inlet, upper sacrum.

The segmentation performed in this work is unique in segmenting all tissues in the scan volume into 6 broad tissue groups, whereas previous studies have focused on specific organs or tissue types, only. Our work is developing a cascade of classifiers that can take the broadly segmented tissues and classify individual organs. When compared to previous multi-organ segmentation studies, the results of this study are comparable or better. A multi-organ segmentation study using statistical region merging method reported DSC values of 0.95 for lungs, 0.93 for heart and kidneys, an average of 0.90 for liver and spleen, and an average of 0.86 for spinal cord and bones for a single adult test patient (Bajger et al., 2013). A study using entangled decision trees reported an overall Jaccard overlapping index of 56% for 8 organs from 50 patient scans from various CT vendors (Montillo et al., 2011). A work investigating active learning methods used a random forest classifier to classify 6 organs using a database of 196 patient scans from various CT vendors, and reported mean DSC values of 0.90, 0.70, 0.47, 0.76, 0.57, and 0.60 for lungs, heart, kidneys, liver, spleen and pelvis (left and right pelvis), respectively (Iglesias et al., 2011). In comparison, the mean DSC values in this study were 0.98, 0.90, 0.81, 0.77, 0.69, and 0.82 for lungs, fat, muscle, solid organ, blood/contrast and bone, respectively.

A limitation of this study is the generation of manual classification maps of the entire scan volume for a large number of patients. To generate the 7 manual contours per patient in this study, required an average of 8 – 9 hours. However, as demonstrated in the stage 2 training which included pixels sampled from 70 training slices to better differentiate between tissues with high CT numbers and blood/bowel contrast, it is essential to have manual contours spanning the entire volume of the scan to minimize overfitting and to achieve consistent classification performance for all slices in the scan volume. Further work is needed to generate more manual classifications; the classifiers developed in this study can be used to generate an initial classification mask and a user can correct the misclassified pixels such that time to create manual classifications can be greatly reduced. As the number of manual classifications increases, the classifier model can be retrained to improve its performance. To facilitate this recursive process, the classifications pipeline developed using TWS and WEKA can be integrated into a sophisticated classification program like seg3D which allows easy manipulation of the classification masks.

5. CONCLUSION

A random forest based tissue classifications pipeline for contrast-enhanced neck-chest-abdomen-pelvis CT scans for adult and pediatric patients was developed. By adopting automated sample generation techniques and automated feature selection algorithms along with a heterogeneous training dataset comprised of 2 adult and 2 pediatric patients, a classifier model with improved performance across all the tissue classes was developed. The classification performance, when tested on intra-slice test data, revealed that for high-contrasting regions, i.e., lung, fat, and muscle, both models performed consistently and provided DSC values greater than 0.80. Tissue classes with overlapping CT number intensities, i.e., contrast enhanced solid organs, contrast opacified blood/bowel, and bone, have slightly lower DSC values (0.70 – 0.90) and variability in their values is observed between the two models considered. The inter-slice test data demonstrated that for high-contrast regions, all classifier models resulted in DSC values similar to the intra-slice classification. However, the high-contrast regions had poor DSC values when compared to the intra-slice DSC for contrast enhanced blood/bowel and bone. A study of the number of features in the training input showed that the model parameters are tuned for the slices present in the training set and therefore do not generalize well for slices outside the training data.

To improve the differentiation and classification of tissues with high CT numbers from blood/bowel contrast, and to achieve consistent performance of the classifier across the scan volume, a set of classifiers that classified only bone and blood/bowel contrast was developed. These classifiers were trained using 3D image filters and additional training samples from randomly sampled slices across the patient volume. The 2^nd stage classifiers improved the DSC values for blood/bowel contrast tissue by up to 12% for inter-slice testing and up to 9% on intra-slice testing. For bone the 2^nd stage classifiers improved the performance by 2%.

Figure 4:

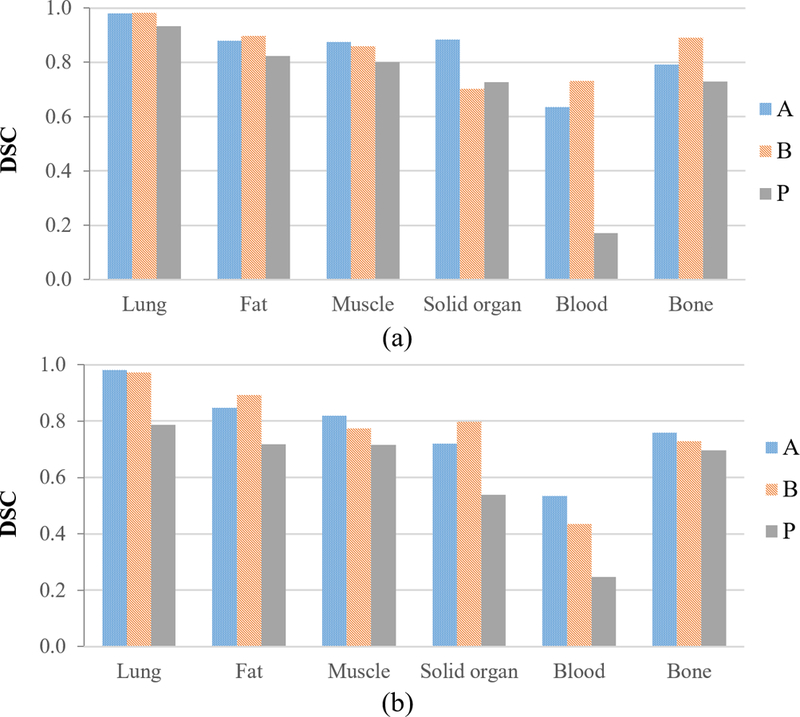
Tissue-wise DSC for classifiers A, B and P on their respective (a) intra-slice test data, and (b) inter-slice test data. (Somasundaram et al., 2017)

Figure 8:

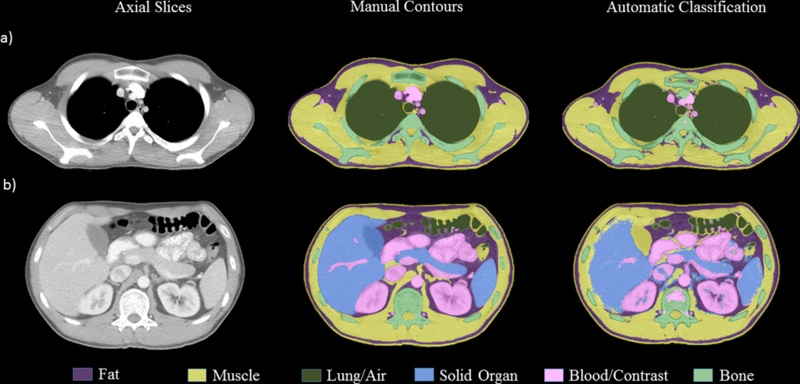
Comparison of manual and automatic classification by classifier B and C for a test patient at a) chest at top of aortic arch, b) at lower liver/spleen and mid-pancreas/gallbladder level.

6. ONLINE.1 APPENDIX

The following is a brief description of filter implementation and image processing effects utilized in this study (Arganda-Carreras et al., 2014). The most common image filters that achieve various levels of image smoothing such as the mean, median, variance, minimum, and maximum are calculated for regions of interest (ROIs) varying in radius as 2n with n ranging from 0 to 16; Additionally, sophisticated filters that provide shape, texture and gradient information of the image are also calculated; the Gaussian blur used Gaussian kernels with different sizes (n=16) to convolve the image pixels resulting in a blurred image. The Difference of Gaussians filter takes the difference of two Gaussian blurred images computed using 2 different sized kernels. The Sobel filter calculates the gradient of the image intensity across each pixel and applied it with and without Gaussian blurring. The Hessian filters were based on the Hessian matrix calculated for each pixel after applying Gaussian blur of various sizes. The Hessian matrix was calculated by taking second-order partial derivatives of the pixel intensity to give a measure of curvature in the image. Moduli, trace, determinant, first eigenvalue, second eigenvalue, orientation, eigenvalue difference, and squared eigenvalue difference of the Hessian matrix were calculated and applied as separate filters. The Membrane Projections filter produced images with enhanced membrane-like structures by convolving the image with a kernel that was rotated at different angles to produce 30 images. Sum, mean, standard deviation, maximum, and minimum of the 30 images were used to produce six final features. The Kuwahara filter enhanced edges within the image while reducing the noise by using linear smoothing kernels. For the Kuwahara filter, a kernel size of 16 was used and rotated with 30 different angles. The resulting images were then grouped by 3 different criteria: Variance, Variance / Mean and Variance / Mean^2 to yield the final features. The Anisotropic Diffusion filter reduced noise in the image without eroding image detail; this filter was applied with an edge threshold of 5, and convolved using a Gaussian square filter (of size 3×3) for 20 iterations. The Bilateral filter reduced noise while preserving the edges within the image by performing a weighted average of surrounding pixels that have intensity values within a specified threshold. The Lipschitz filter used the Lipschitz bounds to generate a mask of the image which is equivalent to a grayscale opening by a cone, a morphological operation that can highlight finer details in the image. The mask was then used to eliminate slowly varying background detail in the image. The Gabor filters were a family of kernels to achieve edge detection and texture filtering. They acted as band-pass filters, and were implemented after a frequency transformation of the image. The Derivatives and Laplacian filters computed the first and second order derivatives of the input image. The Structure filter calculated the smallest and largest eigenvalues (smallest and largest) of the so-called structure tensor of each pixel. The Entropy filter drew a circle of multiple radii and measured the entropy using a histogram calculation. The Neighbors filter shifted the image in 8 directions by n number of pixels and created 8n features (Arganda-Carreras et al., 2014).