polymapR—linkage analysis and genetic map construction from F₁ populations of outcrossing polyploids

Abstract

Motivation

Polyploid species carry more than two copies of each chromosome, a condition found in many of the world’s most important crops. Genetic mapping in polyploids is more complex than in diploid species, resulting in a lack of available software tools. These are needed if we are to realize all the opportunities offered by modern genotyping platforms for genetic research and breeding in polyploid crops.

Results

polymapR is an R package for genetic linkage analysis and integrated genetic map construction from bi-parental populations of outcrossing autopolyploids. It can currently analyse triploid, tetraploid and hexaploid marker datasets and is applicable to various crops including potato, leek, alfalfa, blueberry, chrysanthemum, sweet potato or kiwifruit. It can detect, estimate and correct for preferential chromosome pairing, and has been tested on high-density marker datasets from potato, rose and chrysanthemum, generating high-density integrated linkage maps in all of these crops.

Availability and implementation

polymapR is freely available under the general public license from the Comprehensive R Archive Network (CRAN) at http://cran.r-project.org/package=polymapR.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

In recent years there has been an acceleration of progress in the understanding of the genetics underlying important traits in autopolyploid species. This has been to a large extent due to developments in high-density genotyping platforms for single nucleotide polymorphism (SNP) markers, which have found increasing application in polyploids. For example, high-density SNP arrays have been developed in potato (Felcher et al., 2012; Vos et al., 2015), rose (Koning-Boucoiran et al., 2015), alfalfa (Li et al., 2014) and chrysanthemum (van Geest et al., 2017a), enhancing the scope for genetic studies in these species.

In polyploid species, as opposed to diploids, co-dominantly scored markers can possess multiple classes in the heterozygous condition, usually termed marker ‘dosage’. In a tetraploid there are five possible dosage classes of a bi-allelic SNP marker, namely nulliplex with a dosage 0 for one of the alleles, simplex with dosage 1, duplex with dosage 2, triplex with dosage 3, and quadruplex with dosage 4. In a hexaploid, the number of dosage classes at a bi-allelic locus rises to seven. Various software have been developed to convert the signal from SNP arrays into these discrete dosage calls for polyploids, such as fitTetra (Voorrips et al., 2011) or ClusterCall (Schmitz Carley et al., 2017). Dosage estimation from read-counts of sequencing data will also in time likely become available.

Genetic linkage maps have traditionally been used for both exploratory trait mapping (often termed quantitative trait locus (QTL) analysis) and the subsequent fine mapping of traits, as well as for assisting genome assembly efforts by guiding the integration and orientation of contigs. High-density linkage maps may also improve our understanding of the chromosomal composition and genetics of polyploid species, uncovering such phenomena as double reduction or partially-preferential chromosome pairing. In many polyploid species which lack reference genome sequences, linkage maps are also a (vital) first genomic description of that species.

Despite the importance of both linkage maps and polyploid species, there are still relatively few software tools available for polyploid linkage map construction. Allopolyploid species showing disomic inheritance can be treated (genetically speaking) as diploids, with a wide range of software options available. In the case of polysomic polyploids (autopolyploids and segmental allopolyploids), the options available to the research community are limited. Probably the most well-known autopolyploid mapping software is TetraploidMap (Hackett and Luo, 2003; Hackett et al., 2007), which has been used in studies of various autotetraploid species such as potato, alfalfa, rose and blueberry (e.g. Bradshaw et al., 2008; Gar et al., 2011; McCallum et al., 2016; Robins et al., 2008). Recently, its successor TetraploidSNPMap (TSNPM) has been released to accommodate high-density marker data from SNP arrays (Hackett et al., 2017). However, it can only handle autotetraploid datasets and provides a graphical user interface for the Windows platform only. Linkage studies in species exhibiting strong preferential chromosomal pairing or other ploidy levels are not currently possible using this software. An alternative polyploid mapping software is the PERGOLA package in R (Grandke et al., 2017). However, this software has been developed for use with F₂ or backcross populations from homozygous parents only. In many cases, either due to inbreeding depression or the difficulties imposed by polysomic inheritance, F₁ populations from two heterozygous parents are typically used instead.

In short, there is currently no software which can perform linkage mapping at various ploidy levels under a variety of inheritance models for outcrossing species using dosage-scored marker data. Here we present polymapR, an R package (R Core Team, 2016) for linkage mapping in outcrossing polyploid species which can generate linkage maps for polysomic triploids, tetraploids and hexaploids, accommodating either fully tetrasomic or mixed meiotic pairing behaviour (segmental allopolyploidy) at the tetraploid level. Its modularity will facilitate its adaption to other marker genotyping technologies or ploidy levels in the future.

2 Materials and methods

The polymapR pipeline consists of four parts—data inspection, linkage analysis, linkage group assignment and marker ordering, which are detailed below. A description of the functions within polymapR is described in the vignette which accompanies the package, going through all the steps in a typical mapping project. For consistency and simplicity, all examples mentioned here describe a tetraploid cross.

2.1 Data inspection, filtering and preparation for linkage analysis

The input data for polymapR is dosage-scored marker data, available from a number of packages such as fitTetra (Voorrips et al., 2011) or ClusterCall (Schmitz Carley et al., 2017). Both fitTetra and ClusterCall are limited to tetraploid data; fitTetra has recently been upgraded to fitPoly (https://CRAN.R-project.org/package=fitPoly) and can accommodate any ploidy level. Regardless of how it is generated, the input dosage-scored marker data should consist of a column of marker dosages for the mother, one for the father followed by a column for each of the offspring of the F₁ cross. Checks for marker skewness (segregation distortion) and shifted markers (when dosage scores are shifted by a fixed amount) are currently provided in polymapR from a suite of tools developed for the fitPoly package (Voorrips et al., 2011).

The next step in data preparation is the conversion of marker dosages to their simplest form, such that the sum of the parental dosage scores is minimized (e.g. 3×0, 3×4 and 1×4 markers can be recoded as 1×0 in a tetraploid). There are two possible conversions—a relabelling of the reference and alternative allele in both parents and a single-parent relabelling if the other parent is homozygous. Marker conversions are performed to reduce the number of marker segregation classes for the linkage analysis (which is directed according to the parental dosages), but have no effect on the pairwise results. In a tetraploid there are nine fundamental segregation types (i.e. 1×0, 0×1, 2×0, 0×2, 1×1, 1×2, 2×1, 1×3 and 2×2), rising to nineteen for a hexaploid. Identifiable double reduction scores are preserved during conversion [e.g. a dosage of 0 from a triplex × nulliplex (3×0) marker becomes a dosage of 2 in its converted form as a simplex × nulliplex (1×0) marker], allowing an investigation of double reduction post-mapping. Any impossible scores (like a dosage of 3 or 4 from a 1×0 marker) are made missing.

High-quality data facilitates the generation of high-quality maps. polymapR assumes the dosage scores are accurate and error-free, but incorporates some controls to screen out problematic markers. One indication of poor data quality is a high proportion of missing values. The user may choose to screen out markers or individuals with more than a desired rate of missing values (by default up to 10% is tolerated), or duplicate individuals. Identical markers, which often occur in high-density marker datasets with limited population sizes and hence a limited number of recombination events, can be identified and reduced to one representative marker for the mapping steps, and reintegrated later. A principal component analysis can also be performed and visualized, which may highlight some unwanted structure in the population (for example due to pollination from an unknown external pollen parent or from self-pollination) or outlying individuals (for example because of admixture).

2.2 Linkage analysis

2.2.1 Linkage analysis under a polysomic model

In autopolyploid species with polysomic inheritance, it is possible to model meiotic pairing structures as random bivalents or multivalents. In practice, both pairing structures tend to occur, with a relatively low frequency of multivalents in stable autopolyploids (Bomblies et al., 2016; Santos et al., 2003). The main consequence of multivalent formation from a genetic perspective is the phenomenon of double reduction, where two segments of a particular homologue can end up in the same gamete and become transmitted together to F₁ offspring. It has been demonstrated that double reduction introduces some bias in recombination frequency estimates under a random bivalent model. This can be safely ignored if the rate of quadrivalent pairing is low (Bourke et al., 2015, 2016).

Under a random bivalent model, there are three possible bivalent pairing conformations in a tetraploid. In general, for any even ploidy p = 2n there are $c=\frac{\left(2n\right)!}{\left(2^n\right).n!}$ possible bivalent pairing conformations to be considered. Given any pair of marker loci with unknown recombination frequency r, we consider the contribution of recombinant homologues with a within-bivalent probability of $\frac{1}{2}r$ and non-recombinant homologues with a within-bivalent probability of $\frac{1}{2}(1-r)$. In cases where recombinants and non-recombinations cannot be distinguished, both are assigned a probability of $\frac{1}{2}$. Assuming random pairing, the probability of any particular pairing configuration is 1/c (in the case of preferential pairing, we introduce a preferential pairing factor to model deviations from randomness here).

The expected frequency of each offspring class $n$ ($0\le i,j\le 2n$) is first summed over all c bivalent conformations:

$$E\left(n_{ij}\right)=\sum _{k=1}^c\frac{1}{c}{f}_k(r,1-r)$$

where $f_k(r,\mathrm{ }1-r)$ denotes a function of $r$ and $1-r$, dependant on the marker combination considered. Given these expected frequencies, we relate them to the observed counts of individuals in each class $O\left(n_{ij}\right)$ to yield the likelihood function $\mathcal{L}\left(r\right)$:

$$\mathcal{L}\left(r\right)\propto \mathrm{ }\prod _{i,j=0}^{2n}{E\left(n_{ij}\right)}^{O\left(n_{ij}\right)}$$

The likelihood equation is found by equating the first derivative of the log of the likelihood function (differentiated with respect to r) with zero:

$$\sum _{i,j=0}^{2n}\left(O\left(n_{ij}\right)\mathrm{ }.\mathrm{ }\sum _{k=1}^c\frac{1}{c}\frac{d}{dr}\mathrm{l}\mathrm{n}\left(f_k\left(r,1-r\right)\right)\right)=0$$

In cases where no analytical solution exists, we use Brent’s algorithm (Brent, 1973) to numerically maximize the log likelihood function in the bounded interval $0\le r<0.5$. For any pair of markers there are a number of possible phases between these markers to consider, which describe the physical linkage between marker alleles. In the case of a pair of duplex × nulliplex (2×0) markers, these phases are termed ‘coupling’, ‘mixed’ and ‘repulsion’ (Fig. 1a). As the phase between markers is initially unknown, we must compute expressions for each of the possible phases, and select the most likely as the phase for which $0\le r<0.5$ and which maximizes the log of the likelihood (Hackett et al., 2013).

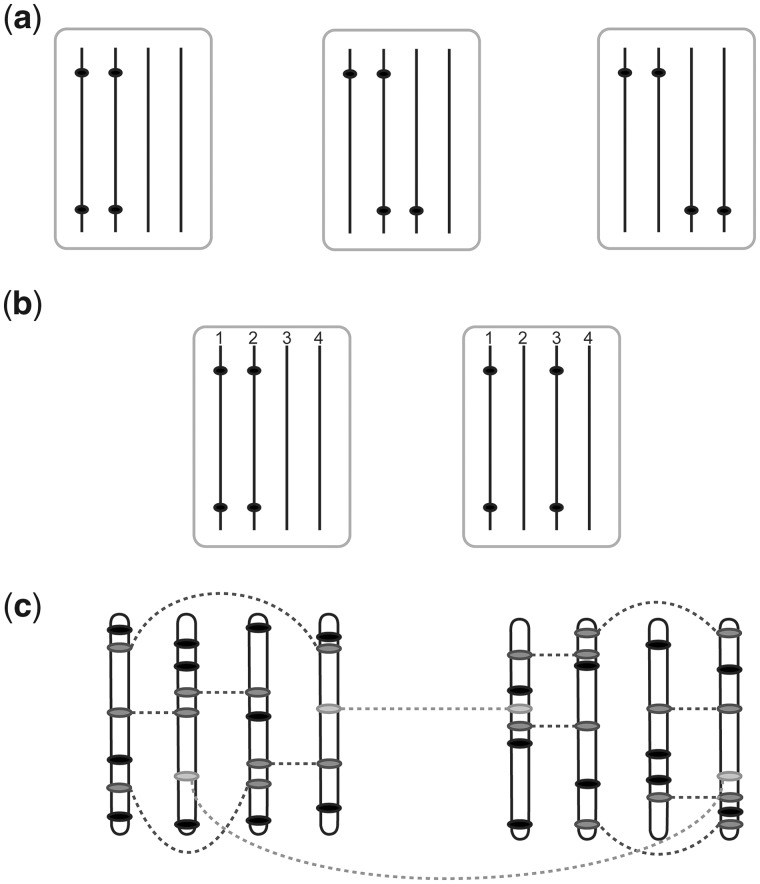
Fig. 1.

Phase considerations and clustering strategy in a tetraploid. (a) The three phases considered for a pair of 2 × 0 markers, from left to right, ‘coupling’, ‘mixed’ and ‘repulsion’; (b) In the case of preferential pairing between homologues 1–2 and 3–4, we must consider two separate types of coupling phase, either coupling within preferential bivalents (left) or coupling between preferential bivalents (right). In the extreme case of an allotetraploid, this distinction could also be termed ‘subgenome-specific’ versus ‘subgenome-straddling’; (c) Simplex × nulliplex (1 × 0) markers (solid black dots) uniquely define homologous chromosomes and are initially clustered together. Higher-dosage marker types such as duplex × nulliplex (2 × 0) markers (dark grey) provide linkage associations between simplex × nulliplex homologues, helping to identify chromosomal linkage groups. Cross-parental markers such as simplex × simplex (1 × 1, light grey) can also link these groups together, leading to consistent linkage group numbering across parents

Finally, we also compute the logarithm of odds (LOD) score, which provides a useful measure of the confidence in the estimate and is used for both marker clustering and marker ordering:

$$\mathrm{L}\mathrm{O}\mathrm{D}={\mathrm{l}\mathrm{o}\mathrm{g}}_{10}\left(\frac{\mathcal{L}\left(r=\mathrm{ }\widehat{r}\right)}{\mathcal{L}\left(r=\mathrm{ }0.5\right)}\right)$$

where $\widehat{r}$ is the maximum likelihood estimate of r.

2.2.2 Linkage analysis in the presence of preferential chromosomal pairing

In certain polyploid species the meiotic pairing is neither fully random nor fully partitioned into exclusively pairing subgenomes, a situation described as segmental allopolyploidy (Stebbins, 1947). Regardless of the underlying mechanism, the result of preferential pairing is that both the segregation ratios and the co-inheritance of marker alleles are affected. In the example of a 2×0 marker introduced earlier, the expected segregation ratio in a polysomic autotetraploid is 1:4:1. With increasing preferential pairing, this ratio will approach 1:2:1 in the case of subgenome-straddling markers (Fig. 1b, right), or approach non-segregation in the case of subgenome-specific markers (Fig. 1b, left).

In order to model this behaviour, we introduce a preferential pairing parameter ρ, such that (in the case of a tetraploid) the probability of the chromosome pairing configuration 1–2/3–4 is $\frac{1}{3}+\rho$ and the probability of pairing configurations 1–3/2–4 and 1–4/2–3 is $\frac{1}{3}-\frac{\rho }{2}$. Attempting to model preferential pairing at higher ploidy levels introduces further complications; Zhu et al. (2016) have proposed a solution for hexaploids by introducing three preferential pairing parameters θ₁, θ₂ and θ₃ to model deviations in bivalent configuration 1–2, 3–4 and 5–6, respectively, with all other configurations having a probability of $\frac{1}{15}-\hspace{1em} \frac{1}{12}({\theta }_1+{\theta }_2+{\theta }_3)$. In our software, we have not yet attempted to model segmental allohexaploidy, and confine our attention to the tetraploid level for now.

We do not simultaneously estimate ρ and r, which can lead to an over-estimation of the preferential pairing parameter (Wu et al., 2002). Instead, we estimate the chromosome-wide strength of preferential pairing after map construction and thereafter include it as a (parent and chromosome-specific) constant in the likelihood framework to correct the pairwise recombination frequency estimates. A robust method of preferential pairing detection and estimation is to use inheritance probability estimates such as those provided by TetraOrigin (Zheng et al., 2016); in polymapR we offer a simpler likelihood-based approach which uses closely-linked repulsion marker pairs to test for deviations from random pairing and simultaneously estimate the strength of this deviation. As described in Bourke et al. (2017), tightly-linked pairs of SxN markers in repulsion phase identified as being on preferentially-pairing homologues can be used to estimate ρ. The expected frequency of offspring classes n₀₀, n₀₁, n₁₀ and n₁₁ (where n₀₁ is the number of offspring with a dosage of 0 at marker A and 1 at marker B etc.) are given by $\frac{1}{6}-\frac{\rho }{4}$, $\frac{1}{3}+\frac{\rho }{4}$, $\frac{1}{3}+\frac{\rho }{4}$ and $\frac{1}{6}-\frac{\rho }{4}$, respectively. This gives rise to the likelihood function $\mathcal{L}(\rho )\propto {\left(\frac{1}{6}-\frac{\rho }{4}\right)}^{n_{00}+n_{11}}.{\left(\frac{1}{3}+\frac{\rho }{4}\right)}^{n_{01}+n_{10}}$, which when solved leads to the following maximum-likelihood estimate for $\rho$:

$$\rho =\mathrm{ }\frac{2\left(n_{01}+n_{10}\right)-4\left(n_{00}+n_{11}\right)\mathrm{ }}{3(n_{00}+n_{01}+n_{10}+n_{11})}$$

Given a parent- and chromosome-specific estimate for the preferential pairing factor ρ, we modify the expression for the expected frequency of individuals in marker class $n$ of a tetraploid as follows:

$$E\left(n_{ij}\right)=\left(\frac{1}{3}+\rho \right)f_1\left(r,1-r\right)+\left(\frac{1}{3}-\frac{\rho }{2}\right)f_2\left(r,1-r\right)+\mathrm{ }\left(\frac{1}{3}-\frac{\rho }{2}\right)f_3\left(r,1-r\right)$$

Due to the lack of symmetry, we must consider all possible conformations within each phase, an example of which is shown in Figure 1b. The procedure for estimating r and LOD remain otherwise the same. The inclusion of preferential pairing imposes an extra computational burden as each phase can have up to four sub-phase conformations, all of which are calculated prior to selection of the most likely phase and its associated r and LOD score.

Finally, in both the case of random and preferential pairing, linkage calculations can be run in parallel using doParallel (Microsoft Corporation and Weston, 2017) on any Windows or Unix-like multi-core desktop computer, resulting in significant time-savings. High-density marker datasets with tens of thousands of markers can be processed in a few hours.

2.3 Linkage group assignment

In diploid studies, the term linkage group is loosely synonymous with the term chromosome. In autopolyploids two levels of linkage group exist—homologue groups and integrated chromosomal groups. The first step in linkage group assignment is to cluster the 1×0 linkage data into homologue groups, for which we currently use the R package igraph (Csardi and Nepusz, 2006). Clustering is performed using the pairwise linkage LOD scores, although the LOD for independence can be used if desired, which may be more robust with skewed marker data (Van Ooijen and Jansen, 2013).

A number of visual aids are provided to assist in clustering (Fig. 2). In general, clustering should be performed over a suitable range of LOD thresholds (e.g. from LOD 3–10) in order to inform the choice of LOD score to partition the data into both homologues and chromosomes (Fig. 2a and b). If chromosome and homologue clusters cannot be readily identified using 1×0 markers alone, coupling-phase homologue clusters are first identified at a high LOD and later re-connected into chromosomal clusters using a higher-dose marker type (Fig. 1c). Visualizations help display the strength of associations between homologues (Fig. 2c). Occasionally complete homologue clusters might be broken up in the clustering step (perhaps due to uneven marker distribution or noisy data); various approaches to merge these fragments into complete homologues are provided (Fig. 2d–f).

Fig. 2.

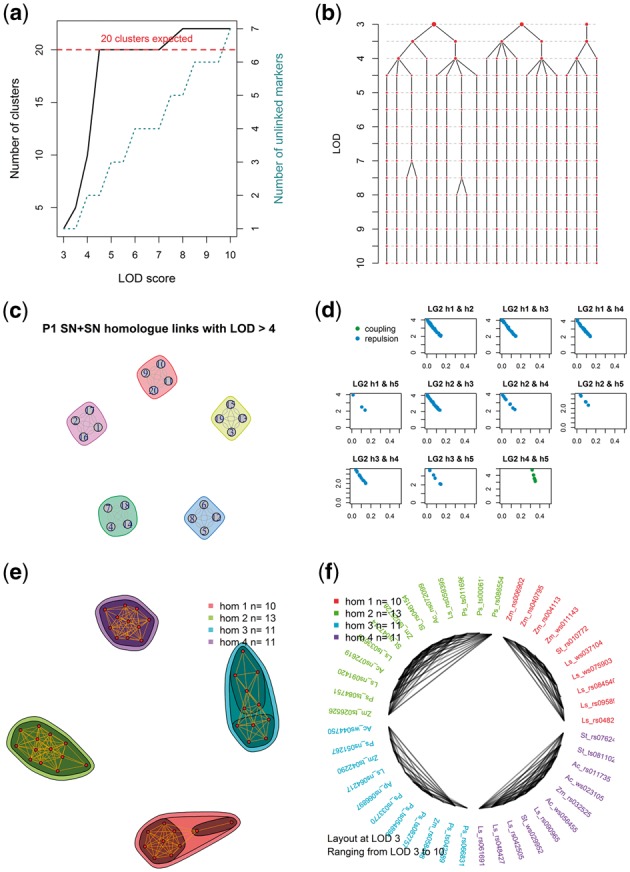
Example visualizations produced by polymapR to facilitate linkage group identification and marker clustering. (a) As LOD score is increased, the number of 1 × 0 clusters increases, as does the number of single-marker clusters (unlinked markers). For a given ploidy and chromosome base number, the expected number of (homologue) clusters is also shown; (b) Alternative representation of (a) which shows the splitting of each cluster as the LOD score is increased. In this example, five chromosomal clusters are identified at LOD 3.5, which split into four homologue clusters between LOD 4.5 and 7; (c) Using linkage to other marker segregation types such as 2 × 0 markers, homologue clusters can be associated into chromosomal clusters, if this was not achieved using 1 × 0 data alone. Here, five chromosomes are represented; (d) If homologues fragment, cross-homologue phase information can help determine which fragments to merge. Here, homologues 4 and 5 show only coupling-phase linkage and should therefore be joined as a single homologue; (e) Alternative approach to merge fragments showing network of linkages over a range of LOD scores. Here, four homologues were successfully identified and merged directly; (f) Alternative representation of (e), showing these connections in a circular format instead

In the case of triploid populations, the phasing approach differs between the diploid and tetraploid parents: for the diploid parent, phasing can be achieved directly using the phase assignment from the linkage analysis. Following the definition of the chromosome and homologue structure using the 1×0 markers, all other marker segregation classes are assigned to both homologues and chromosomes using their linkage to these markers, generating the final phase assignment of all marker types.

2.4 Marker ordering

One of the challenges of marker ordering and map construction in autopolyploid species using marker dosages is the variable accuracy of recombination frequency estimates which must be integrated somehow. Ordering algorithms which only use unweighted recombination frequency estimates are unlikely to find an optimal map order, as there is no distinction between equal estimates of r from situations with vastly different information contents and variances. A thorough description of this issue is provided in Preedy and Hackett (2016). Within the polymapR package, marker ordering can be achieved in two ways—either using the weighted regression algorithm as originally developed by Stam (1993) and implemented in JoinMap (Van Ooijen, 2006) and now also in polymapR, or to use the multi-dimensional scaling algorithm as implemented in the MDSMap package (Preedy and Hackett, 2016). Given the computation efficiency of the MDS algorithm, in almost all circumstances this will be the preferred choice. Identical markers that were originally set aside can be added back to the final maps after marker ordering is complete. Marker positions (in centiMorgans) are also calculated by MDSMap, by default using the projected positions of markers on a fitted Principal Curve (more details are provided by the authors Preedy and Hackett, 2016).

3 Results

3.1 Software output—final linkage maps

The final output of the polymapR package is a phased integrated map. Maps can either be generated per homologue or per chromosome, facilitating the definition of haplotypes within a population. A record is kept in a log file of any markers that were removed at any stage during the procedure, as well as logging the function calls that generated each step, improving project reproducibility and later reporting. Visualizations are provided throughout the mapping procedure, facilitating the diagnosis of issues as well as summarizing the results. An example of an integrated map with five chromosomes, generated using the sample data provided with the package, is shown in Figure 3a. Phased linkage maps, giving the position of the SNP alleles on each parental homologue are also generated, as visualized in Figure 3b for a triploid species. For tetraploid datasets polymapR can generate input files for TetraOrigin (Zheng et al., 2016) which can calculate IBD probabilities for the population, useful for QTL analysis. Alternatively, input files for TetraploidSNPMap (Hackett et al., 2017) can be generated with which QTL analysis can be directly performed.

Fig. 3.

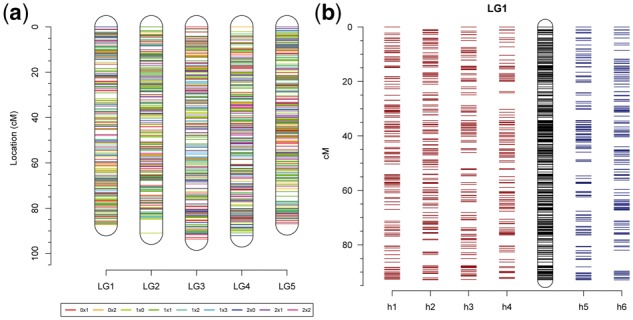
Linkage map visualizations of polymapR. (a) Integrated chromosomal linkage maps generated using the sample tetraploid dataset provided with the package, with each marker segregation type highlighted; (b) Phased homologue-specific maps of a single chromosomal linkage group from a triploid dataset (simulated with PedigreeSim; Voorrips and Maliepaard, 2012). Maternal homologue maps (h1–h4) from the tetraploid parent are shown on the left, and paternal homologue maps (h5–h6) from the diploid parent are shown on the right, with the integrated chromosomal map in the middle

3.2 Application of polymapR to real data

Various developmental versions of the polymapR package have been used for linkage map construction in potato, rose and chrysanthemum (Bourke et al., 2016, 2017; Vukosavljev et al., 2016; van Geest et al., 2017b). The current version brings together all the capacities developed previously, while extending the algorithm to triploid populations as well (produced in a tetraploid × diploid cross). Cross-ploidy hybrids are commonly produced in ornamental breeding, as well as in certain fruit species such as banana (Musa spp.), watermelon (Citrullus lanatus var. lanatus) or grape (Vitis vinifera) to generate seedless fruit (Acquaah, 2012). polymapR is applicable to a wide range of commercially-important crop species such as potato, leek, alfalfa, blueberry, chrysanthemum, sweet potato and kiwifruit, as well as the myriad of cross-ploidy populations developed in ornamental and fruit breeding programmes.

4 Discussion

4.1 Comparison with other polyploid mapping software

The range of options for linkage mapping in autopolyploid species is quite limited. We compared the performance and applicability of polymapR with two alternative softwares (TetraploidSNPMap (TSNPM) and PERGOLA).

4.1.1 TetraploidSNPMap

TSNPM possesses a graphical user interface for Windows, uses optimized routines for marker clustering and offers interactive cluster plots for linkage group assignment. It goes beyond linkage map construction to compute IBD probabilities and perform QTL interval mapping as well. Given that polymapR uses the same random bivalent pairing assumption and the same ordering algorithm (MDSMap; Preedy and Hackett, 2016), we did not expect much difference in output. Using the sample tetraploid dataset provided with polymapR (with 3000 markers over five chromosomes and 207 F₁ individuals, including seven pairs of duplicate individuals), polymapR produced phased maps within 24 min on an Intel i7 desktop with 16 Gb RAM; TSNPM took 5 min, but took another 10 minutes to phase (so a total of 15 min were needed). However, the phased output of TSNPM is more difficult to interpret than that of polymapR and would likely require extra time for curation. The maps themselves were remarkably similar in terms of numbers of mapped markers map length and marker order (Supplementary Fig. S1).

Marker phasing in polymapR is automatic, by selecting phase based on the counts of significant linkages to 1×0 homologue clusters and ignoring any spurious linkages that go against the general trend. On the other hand, phase assignment seems to (generally) require manual intervention in the TSNPM pipeline. Despite its computational efficiency, TSNPM has also set an upper limit of 8000 SNP markers, and the maximum mapping population size is currently 300 F₁ individuals. polymapR sets no limits on marker numbers or population sizes, employing parallel processing to help speed up calculations for large datasets. Duplicated markers are initially binned (also possible in TSNPM) and identical individuals are merged (this feature was missing from TSNPM) to avoid needless calculations. Overall, the main difference between TSNPM and polymapR appears to be in applicability: polymapR can analyse autotriploid, autotetraploid, autohexaploid as well as segmental allotetraploid data, whereas TSNPM is currently confined to autotetraploid data. polymapR is also cross-platform given that it is written in R (R Core Team, 2016).

4.1.2 PERGOLA

The PERGOLA package in R has been developed for F₂ or backcross populations from an initial cross between homozygous parents. Such a situation is highly unusual for most polysomic polyploids, since inbreeding requires many more generations before homozygosity is reached compared to a diploid or disomic polyploid. In a polysomic hexaploid for example, it would take 25 generations of selfing an F₁ individual before 90% homozygosity is reached (ignoring the effects of double reduction; Haldane, 1930). The applicability of the PERGOLA software to real populations in polysomic polyploids is therefore limited.

Despite the highly unusual type of population, we simulated a small F₂ dataset of selfed F₁ individuals randomly chosen from a cross between two inbred parental lines using PedigreeSim (Voorrips and Maliepaard, 2012), leading to a marker dataset of 500 duplex × duplex markers over five chromosomes. The calculation of recombination frequencies took a mere 3.54 s in PERGOLA, in comparison to 28 min using polymapR (on a single core; using 6 cores this step took 8 min). However, for polymapR this particular marker combination is complex, with nine possible phase combinations in the parents to be separately calculated per marker pair, and with extremely complicated likelihood functions for each phase (all 25 dosage combinations are possible in a tetraploid, from n₀₀ to n₄₄). It is therefore a somewhat unfair comparison, as PERGOLA labours under no such ‘generalist’ difficulties. Phase considerations are trivial and therefore ignored by PERGOLA because of their simplistic population assumptions. If such populations could be generated, PERGOLA would produce excellent maps. In our test, PERGOLA identified all five chromosomes, with near perfect marker order in each, although the map lengths were inflated—from 200 cm using the Kosambi mapping function to 400 cm using Haldane’s (when 100 cm was expected). polymapR also produced near-perfect maps with map-lengths of ∼90 cm using Haldane’s mapping function. The polymapR package can handle data from both cross-pollinating and inbred populations whereas PERGOLA cannot, but given the performance difference, PERGOLA would appear to be the software of choice for inbred polyploid populations, should they be developed.

4.2 Robustness against genotyping errors

Of potential concern is the effect of genotyping errors on the mapping pipeline. We ran a small simulation study using the previously-mapped potato chromosome 10 (Bourke et al., 2016) and five F₁ populations (n = 200) simulated in PedigreeSim (Voorrips and Maliepaard, 2012) with randomized errors in the offspring dosages (error rates of 0, 2, 5, 10, 20 and 50%). At the higher rates of error (>20%) many markers would (by default) be filtered out due to skewness or poor concordance between parents and offspring scores (Supplementary Fig. S2). In general, error rates of up to 10% appear to be acceptable in terms of marker order, while higher rates will likely lead to map inflation and poorer marker orders.

4.3 Concluding remarks

The development and release of polymapR comes at a time when there is increasing need for tools to perform genetic analysis in polyploids. Understanding the genetic control of important biological traits in polyploid species will have a large impact on plant breeding (or in the case of certain salmonid fish, animal breeding as well), facilitating the adoption of genomics-driven breeding decisions such as marker-assisted selection or genomic prediction into breeding programmes. For these advances to take place, high-density and accurate maps showing the relative position of markers on chromosomal groups are needed—which is precisely what polymapR delivers.