Optically transparent, high-toughness elastomer using a polyrotaxane cross-linker as a molecular pulley

We prepared a mechanically tough, highly transparent elastomer by using a polyrotaxane cross-linker acting as a molecular pulley.

Abstract

An elastomer is a three-dimensional network with a cross-linked polymer chain that undergoes large deformation with a small external force and returns to its original state when the external force is removed. Because of this hyperelasticity, elastomers are regarded as one of the best candidates for the matrix material of soft robots. However, the comprehensive performance required of matrix materials is a special challenge because improvement of some matrix properties often causes the deterioration of others. For example, an improvement in toughness can be realized by adding a large amount of filler to an elastomer, but to the impairment of optical transparency. Therefore, to produce an elastomer exhibiting optimum properties suitable for the desired purpose, very elaborate, complicated materials are often devised. Here, we have succeeded in creating an optically transparent, easily fabricated elastomer with good extensibility and high toughness by using a polyrotaxane (PR) composed of cyclic molecules and a linear polymer as a cross-linking agent. In general, elastomers having conventional cross-linked structures are susceptible to breakage as a result of loss of extensibility at high cross-linking density. We found that the toughness of the transparent elastomer prepared using the PR cross-linking agent is enhanced along with its Young’s modulus as cross-linking density is increased.

Elastomers are used in automobiles, aircraft, buildings, and sporting goods because they flexibly deform under an applied load and further exhibit elastic recovery, such as reversible restoration. Elastomers are also indispensable for the development of future products (1–4), such as medical products that improve the quality of life (5, 6), flexible displays that can be used for wearable devices (7), and soft robots that can coexist with people (8). In addition to the flexibility and elasticity, toughness is another physical property of elastomers that is required to meet the needs of these products (9–15). To develop elastomers suitable for the intended use, in addition to selecting appropriate materials, a new mechanism is needed to realize the required physical properties.

For a polymeric material to be used as an elastomer, it must be flexible. Even a cross-linked hard polymeric material will become supple with the addition of a plasticizer. However, over time, bleeding occurs in which the plasticizer melts, resulting in deterioration of the elastomer and contamination of the surface (16). Some plasticizers have adverse human health effects, and when elastomers containing these plasticizers are used in applications that require direct contact with people, the safety of the elastomers must be considered (17). A polymer having a glass transition temperature sufficiently lower than the operation temperature of the elastomer may be used to obtain an elastomer that does not suffer from bleeding. Such an elastomer can be prepared without a plasticizer in these polymer chains with low glass transition temperature. Furthermore, the mechanical properties of the elastomer can be adjusted by changing its cross-linking density. As the cross-linking density increases, the stiffness (Young’s modulus) of the elastomer increases, whereas the elongation at break (λ_max) and toughness decreases because the polymer strand length between the cross-linking points becomes shorter (18). Generally, a simultaneous increase in the extensibility and elasticity of an elastomer having a conventional cross-linked structure requires a trade-off with other properties; thus, improving the toughness of the elastomer is difficult. Introducing a large amount of a filler such as carbon black or fine silica particles into an elastomer is known to be effective for creating an elastomer with a conventional cross-linked structure that has a high toughness (19). However, for the large required amount of filler to be incorporated into an elastomer, the filler must be dispersible in the polymer material constituting the elastomer, and an appropriate kneading method must be applied (20), yet these methods are not easily applied to all polymeric materials. Moreover, the addition of a filler to an elastomer often impairs the transparency of the material, which may limit the use of the material in flexible displays and soft robotics. Various methods have been developed to improve the toughness while simultaneously increasing the extensibility and elasticity. By introducing sacrificial interpenetrated networks (11), a significantly toughened triple-network elastomer is realized. However, irreversible breakage of sacrificial networks results in permanent damage after the first stretch. On the other hand, many of the recoverable tough elastomers require the construction of a very complicated structure by a challenging preparation method (10, 21).

In this study, to prepare transparent and tough elastomers more easily, we developed a method for introducing a new cross-linking mode different from that of the conventional cross-linking approach into the elastomer structure by using a polyrotaxane (PR) as a cross-linking agent. The PR formed from polyethylene glycol (PEG) and α-cyclodextrin (α-CD) is known to exhibit free movement of the cyclic α-CD along the linear PEG (22–24). By modifying α-CD with a vinyl group capable of reacting with various vinyl monomers, a large number of vinyl groups could be attached to the PR (25). As a result, a three-dimensional (3D) network composed of various polymers could be easily prepared with the PR as a cross-linking agent (PR cross-linker) (26). For a hydrogel synthesized with this PR, the cross-linking points can move freely over a wide range, and hydrogels can exhibit significant deformability rise and unusual stiffness-toughness independence compared with that obtained by a conventional cross-linking agent (27). Some studies also reported enhanced mechanical properties in rotaxane– and PR–cross-linked elastomers (28–31). However, the opposing relationship between stiffness and toughness can still be observed (29, 30), suggesting that the PR–cross-linked elastomeric system is completely different considering that the PR in the hydrogel system fabricated in solution phase is usually more flexible. Here, we polymerized the PR cross-linker with a methacrylate-based monomer and successfully prepared a transparent elastomer showing simultaneously enhanced stiffness and toughness. A severe conformational change of the PR cross-linker due to sliding motion was observed for the first time via in situ small-angle x-ray scattering (SAXS).

Figure 1A shows the stress (σ)–extension (λ) ratio curves of dumbbell-shaped specimens of the two different elastomers (scheme S1): One is the target elastomer prepared from a hydroxypropyl-modified PR cross-linking agent (HPR-C) with improved dispersibility and 2-(2-methoxyethoxy) ethyl methacrylate (MEO₂MA) as the main monomer, and the other is the comparative elastomer prepared from ethylene glycol dimethacrylate (EGDMA), which is a traditional cross-linking agent, and MEO₂MA. As will be described later, the glass transition temperature of the MEO₂MA polymer is sufficiently below room temperature, and the uncross-linked MEO₂MA polymer is in the rubber state at room temperature. The mass concentration of EGDMA was intentionally fixed at 1.0 weight % (wt %) to obtain comparative elastomer having similar Young’s modulus—in other words, similar effective cross-linking density—with 1.0 HPR-C elastomer, which is nominated on the basis of the mass concentration of 1.0 wt % of HPR-C against the amount of the monomer. In the case of uniaxial elongation, the extension ratio λ = L/L₀, where L₀ is the length before stretching and L is the length after stretching. Young’s modulus (E) obtained from the slope of the initial proportional section of the stress-extension ratio curve is approximately the same for both elastomers with a value of 0.27 MPa. The relationship between stress and extension ratio in uniaxial stretching can be expressed by classical Neo-Hookean model with the assumption that the polymer chains constituting the elastomer are Gaussian chains and that the microscopic deformation of the polymer chain constituting the elastomer is proportional to the macroscopic deformation of the elastomer (32, 33)

Fig. 1. Comparison of mechanical properties of elastomers prepared using polyrotaxane cross-linking agent and general cross-linking agent.

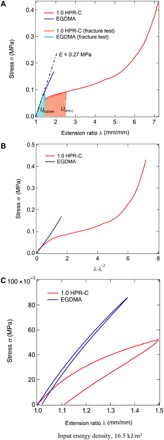
(A) Stress-extension ratio curves of the MEO₂MA elastomers prepared with HPR-C and EGDMA as cross-linkers. (B) The horizontal axis of (A) was converted to λ-λ⁻² to analyze the results of (A). On the basis of the linear relationship observed in (B), the polymer between the cross-linking points behaves as a Gaussian chain. (C) Hysteresis loops of the stress-extension ratio curves of the MEO₂MA elastomers prepared with HPR-C and EGDMA as cross-linkers.

$$\mathrm{\sigma }=\frac{\mathrm{\rho }\mathrm{R}\mathit{T}}{\overline{{\mathit{M}}_{\mathrm{c}}}}(\mathrm{\lambda }-\frac{1}{{\mathrm{\lambda }}^2})$$ (1)

Here, ρ is the material density, R is the ideal gas constant, T is the temperature, and $\overline{{\mathit{M}}_{\mathrm{c}}}$ is the average molecular weight between the cross-linking points of the polymer chains constituting the elastomer. On the basis of the results shown in Fig. 1A, we plotted the stress σ against λ-λ⁻², and the results are shown in Fig. 1B. We observed a behavior consistent with the relation described above in Eq. 1 for the system with EGDMA, as the plot indicates a constant linear relationship. Here, the slope = ρRT/$\overline{{\mathit{M}}_{\mathit{c}}}$ = G = 0.1 MPa, and G is the shear modulus. Assuming that Poisson’s ratio ν = 0.5, the values of Young’s modulus (E) obtained from the relation E = 2G (1 + ν) = 3G and from the λ-σ curve (0.27 MPa) are similar. Therefore, the uniaxial tensile behavior of the elastomer using EGDMA is consistent with an elastomer network according to the Neo-Hookean theory. On the other hand, the elastomer containing HPR-C shows softening compared with stress-extension ratio relation based on the Neo-Hookean model.

In the system with EGDMA, the extension ratio at break is 1.75 (±0.15), whereas for the system with HPR-C, the extension ratio at break is 7.20 (Fig. 1A). In other words, using HPR-C as the cross-linking agent increases the elongation of the elastomer remarkably. To quantitatively evaluate the mechanical toughness of the elastomers with different cross-linking modes, we conducted a tear test. The theory of fracture energy determined by Rivlin-Thomas’ tear test is effective for discussing the rupture of the rubbery polymers (28). In the tear test, it is possible to estimate the fracture energy, which indicates how much energy is needed to create a unit area of new crack surface. For a strip specimen with a notch of length c on its side, the fracture energy Γ can be expressed as follows

$$\mathrm{\Gamma }=2\mathit{k}\mathit{U}\mathit{c}$$ (2)

Here, k is a constant related to the extension ratio (λ) as follows (34)

$$\mathit{k}=\frac{3}{\sqrt{\mathrm{\lambda }}}$$ (3)

In addition, U is the energy density function, which represents the free energy per unit volume accumulated inside the specimen by deformation in the extension ratio range of 1 ≦ λ ≦ λ_max.

Note that λ_max is the value of the critical extension at the beginning of crack advancement in the sample during the tear test. Therefore, based on the results of the uniaxial tensile tests shown in Fig. 1A, U was obtained from Eq. 4 using λ_max

$$\mathit{U}={\displaystyle {\int }_1^{{\mathrm{\lambda }}_{\text{max}}}}\mathrm{\sigma }(\mathrm{\lambda })\mathit{d}\mathrm{\lambda }$$ (4)

The shaded area in ​​Fig. 1A is the energy density function (U). On the basis of the single-edge notch tension (SENT) test (scheme S1) with a strip of elastomer with a cut of 2 mm in length, λ_max was 1.42 in the system with EGDMA, whereas in the system with HPR-C, λ_max was 2.50. Table 1 shows the energy density function (U) and the fracture energy (Γ) calculated from the experiments. The fracture energy of the system with HPR-C is approximately five times that of the system with EGDMA, suggesting that a larger amount of energy is required to generate a unit area of crack surface by HPR-C. In other words, when we used HPR-C as a cross-linking agent, the resistance of the material to static fracture increased relative to that of the system with EGDMA. The energy required to generate a crack of one unit area on the surface is larger in the system with HPR-C than in the system with EGDMA possibly because the energy dissipation and homogenization of the stress concentration at the crack increase in the former.

Table 1. Fracture energy (Γ) of 1.0 wt % HPR-C and EGDMA elastomers.

	EGDMA	1.0 wt % HPR-C
Strain energy density U (kPa)	20.2	102.2
Fracture energy Γ (J/m2)	147.8	703.1

The hysteresis loops for both elastomers are shown in Fig. 1C. The input energy density calculated from the area under the loading curve was similar (16.5 kJ/m²) for the HPR-C and EGDMA elastomers. However, a larger percentage of the input energy was dissipated in the HPR-C–cross-linked system during the deformation than in the EGDMA-MEO₂MA system. In the system with HPR-C, we spent the added energy on plastic flow.

To investigate the thermal properties of both elastomers, we performed differential scanning calorimetry (DSC) and thermogravimetric analysis (TGA) measurements. On the basis of the DSC results (Fig. 2A), the HPR-C– and EGDMA–cross-linked elastomers showed similar thermal behavior. The glass transition occurred at −45°C, and no other changes were observed during the heating process. On the basis of a combination of the DSC and TGA results (Fig. 2B), the elastomers started to degrade and caused a change in the DSC curve at approximately 100°C. Therefore, to avoid deterioration of the elastomers, we set the temperature range of the dynamic viscoelasticity measurements to −80° to 80°C.

Fig. 2. Comparison of thermophysical properties of elastomers prepared using polyrotaxane cross-linking agent and general cross-linking agent.

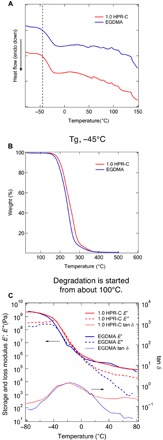
(A) DSC results of the MEO₂MA elastomers prepared with HPR-C and EGDMA as cross-linkers. (B) TGA of the MEO₂MA elastomers prepared with HPR-C and EGDMA as cross-linkers. (C) Temperature dependence of the storage modulus, loss elastic modulus, and tan δ obtained from the dynamic viscoelasticity measurements of the MEO₂MA elastomers prepared with HPR-C and EGDMA as cross-linkers.

The results of the dynamic viscoelasticity measurements are shown in Fig. 2C. The ratio of the loss modulus to the storage modulus (i.e., the tan δ value) of the HPR-C elastomer is considerably larger than that of the EGDMA elastomer; this result suggests that the larger energy hysteresis is due to the far-field dissipation of the HPR-C system. As the value of tan δ increases, the dissipative component of the energy becomes larger than the stored component, and the energy consumption is high. In other words, based on the dynamic viscoelasticity measurements, when HPR-C was used as the cross-linking agent, the added energy was more extensively dissipated than when EGDMA was used as the cross-linking agent.

On the basis of the above results, higher energy dissipation at both small and large deformations is exhibited by the elastomer composed of MEO₂MA and HPR-C because of the higher fluidity inside the elastomer compared to that of the elastomer prepared with the conventional cross-linking agent, EGDMA. This can be attributed to the sliding movement of cyclic cross-links along the linear polymer chain. The cross-linking point sliding effect of HPR-C seems to work effectively.

To investigate the cause of the large fluidity in the elastomer containing HPR-C, we carried out an analysis by SAXS. SAXS can detect the structure of PR in the samples since the scattering length density (SLD) of cyclodextrin in the PR (13.6 × 10⁻⁶ Ų) is larger than the SLD of the MEO₂MA matrix (9.5 × 10⁻⁶ Ų). Figure 3A shows the scattering profiles, I(Q), of the EGDMA and HPR-C elastomers. We analyzed HPR-C elastomers with various amounts of HPR-C (1.0, 2.0, and 4.0 wt %). The scattering intensities of the HPR-C elastomers are larger than that of the EGDMA elastomer and increase with increasing PR concentration. As shown in Fig. 3B, the I(Q) plots normalized to the PR concentration ϕ overlap for the elastomers with different PR concentrations. This result suggests that the PR units do not overlap but instead distribute randomly in the HPR-C samples. The I(Q) plots of these samples reflect the conformation of PR in the elastomers, and the I(Q) plot of 1.0 HPR-C is fitted well by the Debye function representing coil conformation of polymer

$$\mathit{I}(\mathit{Q})=2{\left({\mathit{Q}}^2{{\mathit{R}}_{\mathrm{g}}}^2\right)}^{-2}\left\{\text{exp}\right(-{\mathit{Q}}^2{{\mathit{R}}_{\mathrm{g}}}^2)+({\mathit{Q}}^2{{\mathit{R}}_{\mathrm{g}}}^2)-1\}$$ (5)

where R_g is the radius of gyration. In the undeformed state, the PR has a random coil conformation, and the R_g of PR is estimated to be 3.1 nm.

Fig. 3. SAXS analysis of the behavior of polyrotaxane in elastomers.

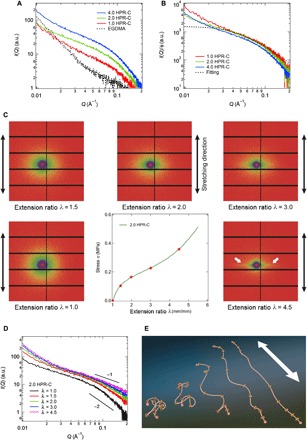
Scattering profiles obtained by SAXS measurements of the MEO₂MA elastomers prepared with HPR-C and EGDMA as cross-linkers: (A) Elastomers prepared with different amounts of HPR-C or with EGDMA. (B) The scattering profiles of the elastomers containing different amounts of HPR-C in (A) were normalized to the concentration of HPR-C. (C) 2D SAXS pattern obtained during uniaxial stretching of the MEO₂MA elastomer prepared with 2 wt % HPR-C as a cross-linker. (D) Sector-averaged scattering profiles, I(Q), for the direction parallel to the deformation of the MEO₂MA elastomer prepared with 2 wt % HPR-C. (E) Schematic diagram of the change in the conformation of PR due to elongation of the elastomer. The arrow in the figure indicates the elongation direction of the elastomer.

The conformation of PR changes severely with macroscopic deformation. As shown in Fig. 3C, the 2D scattering patterns of 2.0 HPR-C under uniaxial deformation become anisotropic as the extension ratio λ increases, and streak-like patterns appear at λ above 3.0, at which point the stress starts to increase markedly because of the fully extended and highly oriented chains. Figure 3D shows the sector-averaged scattering profiles, I(Q), for the direction parallel to deformation. The slope in the high-Q regime changes from −2 to −1 with increasing extension, which suggests that the coil-like conformation of PR becomes a rod-like structure at higher deformations (Fig. 3E). This drastic conformational change provides evidence that the sliding movement of the cross-links contributes to the fluidity of the PR in the elastomers. For conventional elastomers, chain conformation in a deformed network has been studied by small-angle neutron scattering (SANS) on partially deuterated samples. Beltzung et al. (35) performed SANS experiments on polydimethylsiloxane (PDMS) elastomers containing 20% deuterated chains. The confirmation of the deuterated chains changes with macroscopic deformation and follows the phantom chain model

$$\frac{{\mathit{R}}_{\mathrm{g},//}}{{\mathit{R}}_{\mathrm{g},0}}={\left(\frac{\mathit{f}+2+(\mathit{f}-2){\mathrm{\lambda }}^2}{2\mathit{f}}\right)}^{1/2}$$ (6)

where R_g,// and R_g,0 are the deformed and initial gyration radius, respectively, f is the functionality (f = 4 in their case), and λ is the macroscopic extension. When λ = 3.0, the PDMS chain deformation is calculated to be only 70%, suggesting that the PDMS conformation is still an anisotropic coil at high extensions. On the other hand, for our PR–cross-linked elastomers, the conformation of PR changes markedly from coil to rod when λ reaches 3.0. The significant conformational change may be caused by the sliding of rings toward the end of the axial chain so that the shortest part between cross-linking points within the axis, due to random cross-linking reaction, can be avoided from rupture. The higher fluidity of polymer chains surrounding these movable cross-links thus contributes to the large deformability and energy dissipation of the elastomer.

In elastomers prepared with conventional cross-linking agents, an increase in the cross-linking density impairs the extensibility of the elastomer, and as a result, the toughness of the elastomers decreases as well (18). However, in the case of the elastomer with HPR-C, the length of the polymer chain present between the cross-linking points is modulated as the elastomer is elongated, in contrast to the behavior of the conventional elastomers. Therefore, even if the cross-linking density is increased, the mechanical properties of the elastomer, such as the extensibility and toughness, are not expected to be greatly impaired as they are in the conventional system. Therefore, we performed uniaxial tensile tests, tear tests, and dynamic viscoelasticity measurements on HPR-C elastomers cross-linked by varying concentrations of HPR-C. The results of the uniaxial tensile tests performed on dumbbell-shaped elastomer specimens are shown in Fig. 4A as solid lines. Stress-extension ratio curves of strip-shaped HPR-C elastomers with initial cracks are also shown as dotted lines. The Young’s modulus value obtained from this stress-extension ratio curve and the extension at break are shown in Table 2. Table 2 also shows the energy density function (U) and the fracture energy (Γ) of the HPR-C elastomers calculated on the basis of Eqs. 1 to 4. Young’s modulus increased from 125 to 400 kPa as the concentration of HPR-C increased. On the other hand, the maximum extension decreased from 8.6 to 5.8 as the concentration of the cross-linking agent increased from 0.5 to 4.0 wt %. However, when HPR-C was used as the cross-linking agent (Fig. 5), the fracture energy (Γ) increased with increasing amount of cross-linking agent. The dynamic viscoelastic properties of the HPR-C elastomers with various cross-linker concentrations are shown in Fig. 4 (B to D). The storage modulus (Fig. 4B) and the loss modulus (Fig. 4C) increased with increasing HPR-C concentration in the temperature range tested, whereas similar tan δ values ​​were observed for the four samples (Fig. 4D). However, above approximately 20°C, the tan δ value of the HPR-C elastomer is considerably larger than that of the EGDMA elastomer, suggesting a larger energy hysteresis due to the far-field dissipation of the HPR-C specimen. In other words, the large hysteresis obtained from dynamic viscoelastic measurements at temperatures above 20°C suggested that the improvement in the toughness of HPR-C elastomer is due to the increasing energy dissipation within the system.

Fig. 4. Mechanical properties of polyrotaxane cross-linked elastomers at various polyrotaxane concentrations.

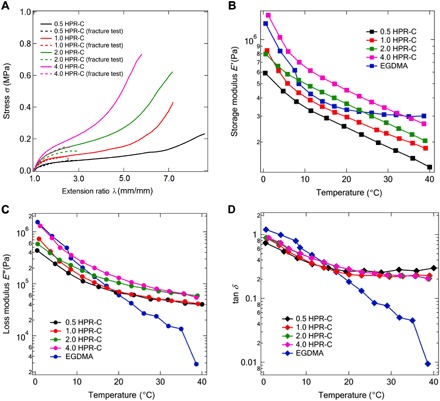
(A) Results of the uniaxial tensile tests and tear tests of the MEO₂MA elastomers prepared with different amounts of HPR-C as a cross-linker. (B) Temperature dependence of the storage modulus of the MEO₂MA elastomers prepared with different amounts of HPR-C or with EGDMA. (C) Temperature dependence of the loss modulus of the MEO₂MA elastomers prepared with different amounts of HPR-C or with EGDMA. (D) Temperature dependence of tan δ of the MEO₂MA elastomers prepared with different amounts of HPR-C or with EGDMA.

Table 2. Mechanical properties obtained from the uniaxial tests of the MEO₂MA elastomers prepared with different amounts of HPR-C as a cross-linker.

	0.5 wt % HPR-C	1.0 wt % HPR-C	2.0 wt % HPR-C	4.0 wt % HPR-C
Young’s modulus E (kPa)	125	280	349	400
Extension at break λ (mm/mm)	760	620	615	481
U (kPa)	70.8	102.2	138.3	145.9
Γ (J/m2)	415.9	703.1	1019.1	1320.2

Fig. 5. Chemical structure of the cross-linkers (HPR-C and EGDMA) and monomer (MEO₂MA) used in this study.

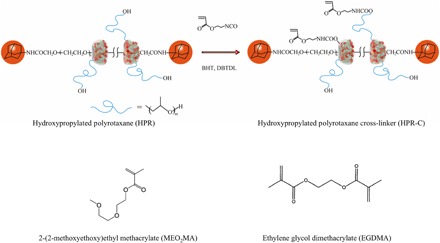
Here, only two cyclic cyclodextrin molecules are shown, in order to simplify the diagram.

In this study, we succeeded in developing an optically transparent, high-toughness elastomer by using PR as a cross-linker. Severe conformation transformation of PR was observed for the first time via in situ SAXS analysis during large deformation test, suggesting the sliding motion of cyclic molecules in PR cross-linker in the elastomeric system. Because of the movable PR cross-links, the polymer chains in the elastomer were more mobile, and a larger proportion of energy added to the elastomer was spent on plastic flow. As a result, fracture toughness of PR–cross-linked MEO₂MA elastomer was simultaneously enhanced with its stiffness by increasing PR cross-linker concentration. A transparent, high-strength elastomer is very important in research on bionics and soft robotics, which is becoming increasingly important. This elastomer is easy to synthesize, so it can be used in many fields. This research is very unique in the sense that soft material of high mechanical properties can be constructed with PR, which acts as a molecular pulley.

Methods

Experimental

Materials

HPR (M_n = 136,978; polyethylene oxide chain length, 35,000 g/mol; propylene oxide substitution, 50%; and CD inclusion ratio, 25%) was obtained from Advanced Softmaterials Inc. (Kashiwa, Japan) and used without further purification. MEO₂MA was purchased from Sigma-Aldrich (Tokyo, Japan) and used as received. 2-Acryloyloxyethyl isocyanate from Showa Denko K.K. (Tokyo, Japan), EGDMA from Wako Pure Chemical Industries Ltd. (Osaka, Japan), α,α′-azoisobutyronitrile (AIBN) from Kanto Chemical Co. (Tokyo, Japan), dibutylenetindilaurate (DBTDL) from Tokyo Kasei Kogyo Co. (Tokyo, Japan), and butyl hydroxyl toluene (BHT) from Tokyo Kasei Kogyo Co., Ltd. (Tokyo, Japan) were used as received. Spectra/Por 2 dialysis membrane (pre-wetted regenerated cellulose tubing) with a molecular weight cutoff value of 12,000 to 14,000 was purchased from Spectrum Laboratories Inc. (CA, USA). Ultrapure Millipore deionized water obtained from the Millipore Milli-Q Lab System (Kobayashi Shokai) was used throughout the experiment.

Preparation of HPR-C

HPR (1 g), DBTDL (catalyst, two or three drops), and BHT (inhibitor, 1.56 mg) were dissolved in dehydrated dimethyl sulfoxide (DMSO; 60 ml) in a three-neck flask. 2-Acryloyloxyethyl isocyanate (156 mg) dissolved in dehydrated DMSO (20 ml) was then added dropwise to the mixture under continuous stirring in the dark. The reaction was carried out overnight at 40°C to ensure completion. The reaction mixture was then first dialyzed with DMSO for 1 week and then with water for another week. The dialysis medium was changed twice a day. The product was then collected by freeze-drying with a freeze dryer (Eyela FDU-1200, Tokyo Rikakikai Co. Ltd., Tokyo, Japan). Finally, the product was stored in a refrigerator. The percent yield of HPR-C was approximately 80%. Detailed information is shown in our previous paper (27).

Preparation of MEO₂MA elastomers

The slide-ring elastomer was prepared by conventional free radical polymerization of the MEO₂MA monomer in the presence of HPR-C. Varying amounts of MEO₂MA, HPR-C, and AIBN (1.3 mg) were dissolved in anhydrous DMSO (tables S1 and S2). N₂ was then bubbled through the solutions to remove any dissolved O₂, which may act as a polymerization scavenger, and fused to glass slides separated by Teflon spacers (1 mm thick) inside an acrylic type B glove box (AS ONE Co.). The polymerizations were carried out at 75°C in a drying oven (DO-300A, AS ONE Co.) for 15 hours to prepare gel slabs. The polymer gel was washed by immersion in methanol for 1 week and then stored in an open environment at room temperature to allow the gradual evaporation of methanol. Finally, vacuum drying was performed to obtain a colorless, highly transparent and mechanically strong slide-ring elastomer. The conventional chemical elastomers were prepared by following the identical procedure mentioned above with 1.0 wt % EGDMA as a cross-linker instead of HPR-C (table S3).

Tensile analysis

We conducted uniaxial tensile tests on dumbbell-shaped specimens and fracture tests on SENT specimens for both the EDGMA–cross-linked (1.0 wt %) MEO₂MA and HPR-C–cross-linked (1.0 wt %) MEO₂MA elastomers. For the stress-extension ratio curves, 1-mm-thick slab elastomer samples were prepared and cut into dumbbell shapes (length, 50 mm; width, 4 mm) by the Super Dumbbell Cutter SDMK-1000 (JIS K6251-8; Kawagoe-Shi, Japan). The samples were placed between two fixtures, and the screws of the sample loading bolts on either end were tightened. The sample was ensured to be aligned in the fixtures, and neither wrinkles nor kinks were present in the elastomer samples before the measurements. The total analyzing length was 10 mm. The transient deformation-controlled multiple extension mode was used as the test setup. Throughout the entire experiment, an extension rate of 0.1 mm/min was applied by an EZ-S 500 table-top universal tester (Shimadzu Corporation). The load and displacement were recorded, and the tensile processes were recorded on video. The measurements were carried out in air at room temperature (22°C). After successive measurements, the most representative stress-extension ratio curve was taken for each elastomer. The reproducibility of the stress-extension ratio curves was checked through successive measurements. For the fracture tests, the SENT specimen shown in scheme S1 was stretched at a speed of 0.1 mm/min on the EZ-S 500 table-top universal tester (Shimadzu Corporation). The hysteresis pattern was also recorded. Dumbbell-shaped specimens of the HPR-C–cross-linked MEO₂MA elastomer were uniaxially stretched to the extension ratio of 1.50 at a crosshead speed of 0.1 mm/min and then returned to their origin length. The EGDMA–cross-linked elastomer was stretched to the extension ratio of 1.37 to achieve the same amount of energy input. The stress-extension ratio curves were recorded by a universal test machine.

Differential scanning calorimetry

DSC measurements were carried out with a DSC Q200 (TA Instruments, Tokyo, Japan). From room temperature, 0.5-mg specimens were (i) heated to 100°C at a rate of 10°C/min and then held for 5 min, (ii) cooled to −80°C at a rate of −10°C/min and then held for 5 min, and (iii) heated to 150°C at a rate of 2°C/min. The DSC spectra were recorded in the third step.

Thermogravimetric analysis

TGA was performed with a Thermo plus EVO2 TG8120 (Rigaku, Tokyo, Japan) to determine a suitable temperature sweep range for the dynamic mechanical analysis (DMA) test.

Dynamic mechanical analysis

DMA tests were performed with the RSA III Solids Analyzer (TA Instruments, New Castle, DE, USA) to observe the hysteresis effects caused by agglomerates and their temperature dependencies from −80° to 80°C. To obtain a similar strain rate as that in the tensile tests, a frequency of 0.021 rad/s was chosen. The static and dynamic strain was 3% and ±0.5%, respectively. The specimen geometry was 10 mm × 3 mm × 0.7 mm.

SAXS experiments measurement

SAXS experiments conducted at BL05SS at SPring-8 (Hyogo, Japan) and at BL-6A at the Photon Factory, High Energy Accelerator Research Organization, KEK (Ibaraki, Japan). The wavelength λ of the incident x-ray beam was 1 Å, and the beam size was 0.1 mm (vertical) × 0.2 mm (horizontal). The sample-to-detector distance was 4 m, and the 2D detector was PILATUS 1M (DECTRIS). The elastomer films were cut into 25 mm × 3 mm rectangular specimens, and the initial sample thickness was approximately 0.7 mm. The specimens were stretched uniaxially at a constant velocity of 50 mm/min using a LINKAM TST350 tensile stage. The initial gap between the clamps was 15 mm. 2D SAXS patterns were recorded every 2 s during uniaxial deformation until the sample fractured. The exposure time for obtaining an image was 1 s. The transmittance was calculated from the ratio between the incident beam intensity measured by an ionization chamber and the transmitted beam intensity measured by a PIN diode embedded in the beam stopper. The 2D SAXS patterns were converted to 1D intensity profiles for the direction parallel to stretching by sector-averaging over azimuthal angles of 0° ± 10°. The averaged scattering intensity normalized by the transmission and sample thickness were plotted against the amplitude of the scattering vector Q, defined as

$$\mathit{Q}=\frac{4\mathrm{\pi }}{\mathrm{\lambda }}\text{sin}\left(\frac{\mathrm{\theta }}{2}\right)$$

where θ is the scattering angle calibrated to the diffraction pattern of dried chicken collagen.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/4/10/eaat7629/DC1

Table S1. Preparation of MEO₂MA elastomer with HPR-C with varying amounts of monomer-to-solvent ratio.

Table S2. Preparation of MEO₂MA elastomer with HPR-C with varying amounts of HPR-C concentration.

Table S3. Preparation of MEO₂MA elastomer with EGDMA with varying amounts of monomer to solvent ratio.

Scheme S1. Elastomer shapes used for the mechanical tests.

Fig. S1. Viscoelasticity dynamics of polyrotaxane cross-linked elastomers at various polyrotaxane concentrations.

Fig. S2. Stress-extension ratio curves of PR–cross-linked elastomer (PR concentration, 1 wt %) under loading-unloading process at various strain rates.

Fig. S3. Young’s moduli of elastomers with various HPR-C cross-linker concentrations.

Fig. S4. Photos of the HPR-C–cross-linked MEO₂MA elastomer exhibiting a reversible extensibility change.