Inter-subject Similarity Guided Brain Network Modeling for MCI Diagnosis

Abstract

Sparse representation-based brain network modeling, although popular, often results in relatively large inter-subject variability in network structures. This inevitably makes it difficult for inter-subject comparison, thus eventually deteriorating the generalization capability of personalized disease diagnosis. Accordingly, group sparse representation has been proposed to alleviate such limitation by jointly estimating connectivity weights for all subjects. However, the constructed brain networks based on this method often fail in providing satisfactory separability between the subjects from different groups (e.g., patients vs. normal controls), which will also affect the performance of computer-aided disease diagnosis. Based on the hypothesis that subjects from the same group should have larger similarity in their functional connectivity (FC) patterns than subjects from other groups, we propose an “inter-subject FC similarity-guided” group sparse network modeling method. In this method, we explicitly include the inter-subject FC similarity as a constraint to conduct group-wise FC network modeling, while retaining sufficient between-group differences in the resultant FC networks. This improves the separability of brain functional networks between different groups, thus facilitating better personalized brain disease diagnosis. Specifically, the inter-subject FC similarity is roughly estimated by comparing the Pearson’s correlation based FC patterns of each brain region to other regions for each pair of the subjects. Then, this is implemented as an additional weighting term to ensure the adequate inter-subject FC differences between the subjects from different groups. Of note, our method retains the group sparsity constraint to ensure the overall consistency of the resultant individual brain networks. Experimental results show that our method achieves a balanced trade-off by not only generating the individually consistent FC networks, but also effectively maintaining the necessary group difference, thereby significantly improving connectomics-based diagnosis for mild cognitive impairment (MCI).

1 Introduction

Characterized by progressive perceptive and cognitive deficits, Alzheimer’s disease (AD) is an irreversible neurological disease with no cure [1]. Mild cognitive impairment (MCI) is known as a prodromal stage of AD, and individuals with MCI tend to progress to AD at a rate of about 10–15% per year [2]. Early detection of MCI is of great clinical significance, thus imaging-based diagnosis has attracted much attention in the past few years [3]. However, accurate MCI diagnosis is considerably challenging due to subtle brain anatomical and functional changes during this early stage [4, 5].

As an in vivo brain functional imaging technique, the resting-state functional magnetic resonance imaging (rs-fMRI) measures blood oxygenation level-dependent (BOLD) signals related to spontaneous neural activity when subject is in the natural rest. In recent years, rs-fMRI has been successfully applied to abnormality detection of various neurological diseases and psychiatric disorders, including schizophrenia, autism spectrum disorder, and AD/MCI [6]. The most-widely used methods with rs-fMRI are based on functional connectivity (FC), which measures temporal correlation of BOLD signals between any pair of brain regions. Based on FC between each pair of brain regions, the brain FC network can be constructed for characterizing the intrinsic functional architecture of the human brain and its abnormality caused by the possible pathological attack [7, 8]. Accurate construction of the brain FC network based on rs-fMRI is one of the most essential problems for more reliable early detection of MCI and also better understanding of potential biomarkers at the whole-brain systematical level [9].

Of various brain FC network modeling methods, the most widely-used one is Pearson’s correlation (PC). Despite of its simplicity and biological intuitiveness, this method also suffers drawbacks that only pair-wise linear interactions are revealed without accounting for more complex influences from other brain regions. To solve this problem, sparse representation (SR) has been adopted for constructing sparse brain FC networks based on the observations that the brain network is largely sparse and the wiring is efficient and cost-effective [10]. Based on SR, the BOLD signals of a brain region can be represented by a linear combination of the signals from a small number of other brain regions, under a sparsity constraint by forcing insignificant connections to be zero. However, because of the data-driven nature, a potential issue of the SR is that it often results in brain networks with a relatively large inter-subject variability due to unpredicted interferences of rs-fMRI noise and artifact. This often leads to a consequence of poor generalization ability of a trained classifier for brain disease diagnosis and, more problematically, for MCI diagnosis because the subtle pathological changes in MCI could be overwhelmed by the large inter-subject variability [11]. Targeting at increasing inter-subject comparability, group sparse representation (GSR) has been proposed by jointly estimating the FC weights for all subjects using a group lasso constraint with l_2,1-norm [12]. This will make certain connectivity links in all subjects being zero or non-zero jointly, which alleviates inter-subject variability, but potentially sacrificing inter-subject separability especially for the subjects from different (e.g., patient and control) groups. Therefore, it will yield suboptimal classification performance when applied to brain disease diagnosis [3].

More recently, connectivity strength-weighted SR method was proposed for individual brain network construction by exploiting FC connectivity prior [13]. With guidance from connectivity strength of PC, the network modeled at the individual level achieved better biological meaning and yielded improved classification accuracy of MCI. One previous study about unsupervised cluster analysis on major depression [14] suggested that subjects from the same group often have larger FC similarity than those from different groups. Accordingly, in this study, we introduce such a prior into GSR-based brain FC network modeling to preserve systematical group difference, without losing the merit of inter-subject consistency in sparse learning framework. Specifically, we propose an “inter-subject FC similarity-guided group sparse” brain network modeling method to increase the between-group separability of FC networks, thus facilitating personalized brain disease diagnosis. In particular, the inter-subject similarity of FC networks is estimated by comparing the PC-based FC pattern of each brain region (i.e., the one-to-all FC pattern) between each pair of subjects. This inter-subject PC-based FC-pattern resemblance is then used as a weighting to form an additional constraint that could penalize those excessive “inter-subject differences in SR-weights” for subjects from the same group, while retaining the sufficient SR-weight differences between subjects from different groups. Next, we will show how this idea can be seamlessly integrated into the GSR-based brain network modeling. To validate the effectiveness of our proposed method, we carry out experiments by applying the new network modeling method to MCI patient identification, a challenging problem due to subtle pathological changes in MCI compared with large inter-subject variability. Results show that our method can not only effectively detect group difference, but also significantly improve the brain functional connectomics-based MCI diagnosis.

2 Methods

2.1 GSR for Brain Network Modeling

Suppose that ${\mathbf{X}}_i=[{\mathbf{x}}_i^1,{\mathbf{x}}_i^2,\dots ,{\mathbf{x}}_i^K]$ contains the mean time series of a total of K regions-of-interest (ROIs) for the i-th subject. Without loss of generality, let us assume that ${\mathbf{x}}_i^k$ has been de-meaned and variance-standardized (i.e., divided by the standard deviation). With PC, the brain FC network of each subject i can be roughly estimated by calculating the full correlation ${\mathbf{C}}_i={\mathbf{X}}_i^T{\mathbf{X}}_i$, such that the k-th column ${\mathbf{c}}_i^k$ in C_i characterizes the functional interactions between the k-th ROI and all other ROIs (i.e., one-to-all FC-pattern of the k-th ROI for the i-th subject). Different from PC, SR estimates such a one-to-all FC-pattern ${\mathbf{w}}_i^k$ through linearly regressing BOLD signals from the k-th ROI ${\mathbf{x}}_i^k$ by BOLD signals of all other regions ${\mathbf{X}}_i^k$ using a l₁-norm sparse regularization:

$${\mathbf{w}}_i^k=\arg {min}_{{\mathbf{w}}_i^k}\frac{1}{2}{\Vert {\mathbf{x}}_i^k-{\mathbf{X}}_i^k{\mathbf{w}}_i^k\Vert }_2^2+\lambda {\Vert {\mathbf{w}}_i^k\Vert }_1,$$ (1)

where λ is a regularization parameter controlling the sparsity of ${\mathbf{w}}_i^k$. SR models a brain network for each subject separately; such an independent modeling strategy may easily lead to relatively large inter-subject variability in ${\mathbf{w}}_i^k$. GSR-based FC network modeling can alleviate such a problem by jointly estimating non-zero connections across subjects via l_2,1-norm regularization-based group lasso:

$${\mathbf{W}}^k=\arg {min}_{{\mathbf{W}}^k}{\displaystyle {\sum }_{i=1}^N\frac{1}{2}{\Vert {\mathbf{x}}_i^k-{\mathbf{X}}_i^k{\mathbf{w}}_i^k\Vert }_2^2}+\lambda {\Vert {\mathbf{W}}^k\Vert }_{2,1},$$ (2)

where ${\mathbf{W}}^k=[{\mathbf{w}}_1^k,{\mathbf{w}}_2^k,\dots ,{\mathbf{w}}_N^k]$ consists of the one-to-all FC-patterns of the k-th ROI for all N subjects, and λ controls the amount of group sparsity. The brain networks modeled by GSR will share similar topological structures (by enforcing similar nonzero or zero connectivities for all subjects) to reduce inter-subject variability. However, an inherent problem of the GSR-based network modeling roots in the group lasso constrain term, which also sacrifices the potentially important between-group differences that often benefit the disease diagnosis. Thus, the suboptimal classification performance is achieved when applied to computer-aided disease diagnosis.

2.2 Inter-subject Similarity-Guided GSR for Brain Network Modeling

We propose to estimate inter-subject FC similarity based on PC values of the same FC-patterns between different subjects, and then use this as a prior to control the inter-subject similarity/difference in the final estimated FC. In the following, we explain how the constraint can be integrated into the GSR-based method for guiding the construction of better brain networks. Let ${\mathbf{c}}_i^k$ and ${\mathbf{c}}_j^k$ denote the regional FC-patterns (estimated by PC) of the k-th ROI for the i-th and the j-th subjects, respectively. A graph Laplacian [15, 16] is constructed with a similarity matrix ${\mathbf{S}}^k=[s_{ij}^k]\in {\mathrm{ℝ}}^{N\times N}$ with $s_{ij}^k=\exp (-{\Vert {\mathbf{c}}_i^k-{\mathbf{c}}_j^k\Vert }_2^2/\sigma )$ defining the pairwise similarity of subjects in terms of their FC patterns for the k-th ROI. For simplicity, we set the kernel width σ = 1 in our experiments. Then, a similarity-preserving regularization term can be defined to control the inter-subject similarity/difference as follows:

$$\mathbf{\Theta }={\displaystyle {\sum }_{i,i=1}^N{s}_{ij}^k{\Vert {\mathbf{w}}_i^k-{\mathbf{w}}_j^k\Vert }_2^2=tr({\mathbf{W}}^k{\mathbf{L}}^k{({\mathbf{W}}^k)}^T)},$$ (3)

where L^k = D^k − S^k, and D^k ∈ ℝ^N×N is a diagonal matrix with its diagonal elements defined as $d_{ii}^k={\displaystyle {\sum }_j{s}_{ij}^k}$. By integrating the regularization term Θ into GSR, a new model for constructing brain network is derived as:

$${\mathbf{W}}^k=\arg {min}_{{\mathbf{W}}^k}{{\displaystyle {\sum }_{i=1}^N\frac{1}{2}\Vert {\mathbf{x}}_i^k-{\mathbf{X}}_i^k{\mathbf{w}}_i^k\Vert }}_2^2+\lambda {\Vert {\mathbf{W}}^k\Vert }_{2,1}+tr({\mathbf{W}}^k{\mathbf{L}}^k{({\mathbf{W}}^k)}^T),$$ (4)

where λ₁ and λ₂ denote the regularization parameters for group sparsity and inter-subject FC-pattern similarity, respectively. In Eq. (4), by further adding the second regularization term Θ, we encourage inter-subject FC-pattern resemblance if their PC-based FC patterns are similar, and penalize inter-subject FC-pattern resemblance if their PC-based FC patterns are quite distinct. This will suppress within-group FC difference while retaining sufficient group differences. That is, the proposed new model will allow us to both achieve the good separability without losing the merit of group sparsity and promote the brain connectomics-based diagnosis. The optimization problem in Eq. (4) can be solved by an iterative approach, based on the accelerated proximal gradient algorithm [17]. Figure 1 illustrates the framework of our proposed inter-subject FC similarity constraint based GSR modeling. Specifically, for the i-th subject, the constructed brain network is formed as ${\mathbf{G}}_i=[{\mathbf{w}}_i^1,{\mathbf{w}}_i^2,\dots ,{\mathbf{w}}_i^K]$. Note that, the network matrix G_i is typically asymmetric. Thus, a symmetry operation ${\mathbf{G}}_i=({\mathbf{G}}_i+{\mathbf{G}}_i^T)/2$ is further carried out to achieve the symmetric network.

Fig. 1.

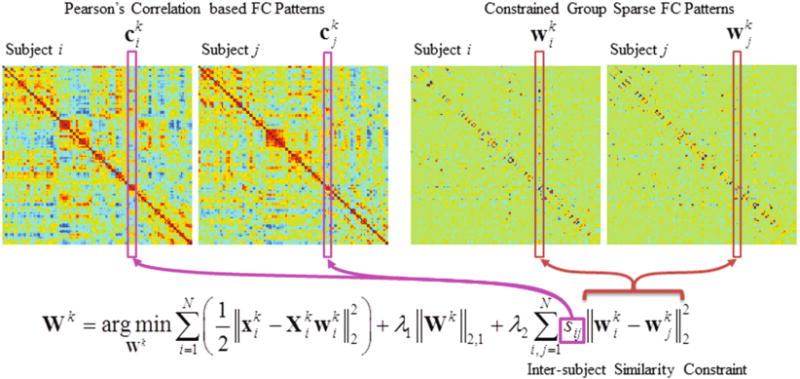
Framework of our proposed brain network modeling method.

3 Experiments

3.1 Data Preprocessing

We use a publicly available Alzheimer’s Disease Neuroimaging Initiative (ADNI) phase-2 dataset (http://adni.loni.usc.edu/) to evaluate our proposed brain FC network modeling method. Specifically, 52 normal control (NC) subjects and 52 MCI subjects with rs-fMRI data are selected. These selected subjects are age- and gender-matched, and were all scanned using 3.0T Philips scanners with the same imaging parameters. The rs-fMRI data of these subjects are preprocessed using SPM8 toolbox (http://www.fil.ion.ucl.ac.uk/spm/software/spm8/). In particular, the first three volumes of each rs-fMRI data are discarded for magnetization equilibrium. After head motion correction, the remaining rs-fMRI data are nonlinearly registered into Montreal Neurological Institute (MNI) space and further spatially smoothed by an isotropic Gaussian kernel with full-width-at-half-maximum (FWHM) of 6 mm. Of note, we do not perform data scrubbing (i.e., removing the rs-fMRI frames with larger than 0.5-mm frame-wise displacement), since this would introduce additional artifacts. However, the subjects with large frame-wise displacement for 2.5-min data are excluded in data screening. The rs-fMRI data are then parcellated into 116 ROIs based on the Automatic Anatomical Labeling (AAL) template. In each ROI, the mean time series is extracted and band-pass filtered (0.015–0.15 Hz); also, head motion parameters and the mean BOLD time series of both white matter and cerebrospinal fluid are regressed out for reducing the potential interference to the subsequent FC estimation.

3.2 Performance Evaluation

The upper triangle elements of the constructed brain network of each subject are concatenated to form a feature vector. The dimensionality of this feature vector is 116 × (116 – 1)/2 = 6670. Then, we carry out two-sample t-tests with a significance level of p < 0.05 to reduce the redundant features. Lasso [18] is further employed to select a small number of features with better discriminative ability. Finally, a support vector machine (SVM) with a linear kernel is trained on the selected features for MCI classification. The leave-one-out cross-validation (LOOCV) scheme is adopted for evaluation of diagnosis performance. In each fold of LOOCV procedure, an additional inner LOOCV is also carried out on the training data to determine the optimal hyper-parameters for the sparse regression (λ₁ and λ₂) as well as for the SVM. Classification performance is evaluated based on classification accuracy (ACC), area under ROC curve (AUC), sensitivity (SEN), and specificity (SPE). To further evaluate the effectiveness of our proposed framework, we have made extensive comparisons with the brain networks constructed by Pearson’s correlation (PC), sparse representation (SR), group sparse representation (GSR), and our method, using the same dataset.

3.3 Experimental Results

Table 1 summarizes the classification results by different brain network modeling methods. Compared with PC, all of other sparse representation-based methods improved the classification accuracy. Among them, GSR performed better than SR, and our proposed method performed better than GSR. In particular, our proposed method produced the highest accuracy of 85.6%, with improvements of 21.2%, 15.4% and 7.7% compared with PC, SR, and GSR, respectively.

Table 1.

Performance comparison of different network construction methods in MCI classification.

Method	ACC (%)	AUC	SEN (%)	SPE (%)
PC	64.4	0.709	61.5	67.3
SR	70.2	0.750	69.2	71.2
GSR	77.9	0.835	76.9	78.9
Proposed	85.6	0.927	82.7	88.5

To intuitively illustrate the superiority of our proposed network modeling method, we also present the separability values (r² value, with larger value indicating higher separability [19, 20]) between two groups, for each connection of the brain FC networks modeled using GSR (Fig. 2a) and our proposed method (Fig. 2b). Our method reveals larger and more group differences compared to the GSR-based method. Moreover, the potential biomarkers detected by our method are largely non-overlapped with those detected by GSR, indicating that including an additional constraint term has resulted in systematical changes of the constructed brain network. Our newly identified connectivities with large MCI/NC separability (r² > 0.07) mainly include three sets of connections: (1) within-hemisphere connections that specifically located in the left hemisphere (Fig. 2c), (2) inter-hemisphere connections (Fig. 2c), and (3) cerebro-cerebellar connections (Fig. 2d). Most of these connections involve brain regions at the frontal lobe, which indicates that the pathological changes of AD start from the frontal area.

Fig. 2.

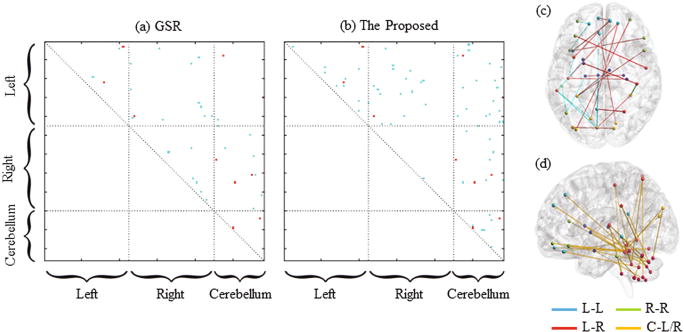
Illustration of the separability matrices measured by r² values between the MCI and NC groups for the brain FC networks modeled by (a) GSR and (b) our proposed method, respectively. Here, only the r² values at the upper triangle are shown, since the matrices are symmetric. The blue points denote different biomarkers suggested by the two methods, while the red points denote the shared biomarkers by the two methods. Subfigures (c) and (d) depict the FC connectivities detected by our proposed method, where the connections of left-hemisphere (L-L), right hemisphere (R-R), and inter-hemisphere (L-R) are shown in (c) and the cerebro-cerebellar (C-L/R) connections are shown in (d).

4 Conclusion

In this paper, we propose a group-level brain network modeling method (i.e., with inter-subject similarity-guided group sparse representation) for better brain functional network construction. Experimental results show that our method is capable of improving network separability between different groups, which facilitates brain disease diagnosis. The effectiveness of our method has also been proven by significantly improving MCI classification, compared with the traditional Pearson’s correlation or sparse representation based brain network modeling methods. All these suggest the promise of our method for future clinical brain imaging studies, especially for biomarker detection and personalized brain connectomics-based disease diagnosis.