Minimal number of gradient directions for robust measurement of spherical mean diffusion weighted signal

Abstract

Purpose:

Determination of the minimum number of gradient directions (N_min) for robust measurement of spherical mean diffusion weighted signal ($\overline{\mathrm{S}}$).

Methods:

Computer simulations were employed to characterize the relative standard deviation (RSD) of the measured spherical mean signal as a function of the number of gradient directions (N). The effects of diffusion weighting b-value and signal-to-noise ratio (SNR) were investigated. Multi-shell high angular resolution Human Connectome Project diffusion data were analyzed to support the simulation results.

Results:

RSD decreases with increasing N, and the minimum number of N needed for RSD ≤ 5% is referred to as N_min. At high SNRs, N_min increases with increasing b-value to achieve sufficient sampling. Simulations showed that N_min is linearly dependent on the b-value. At low SNRs, N_min increases with increasing b-value to reduce the noise. RSD can be estimated as $\frac{\sigma }{\overline{\mathrm{S}}\sqrt{\mathrm{N}}}$, where σ = 1/SNR is the noise level. The experimental results were in good agreement with the simulation results. The spherical mean signal can be measured accurately with a subset of gradient directions.

Conclusion:

As N_min is affected by b-value and SNR, we recommend using 10×b/b₁ (b₁ = 1 ms/μm²) uniformly distributed gradient directions for typical human diffusion studies with SNR ~ 20 for robust spherical mean signal measurement.

Introduction

Diffusion MRI is a non-invasive tool to detect tissue microstructural information based on restricted water Brownian motion within tissues. The conventional technique measuring tissue microstructure is diffusion tensor imaging (DTI), a technique that models water diffusion in each voxel as a symmetric tensor [1]. The DTI derived mean diffusivity (MD) and fractional anisotropy (FA), measures widely used to quantify tissue microstructure, are rotationally invariant. However, for two voxels with different fiber directions, the measured FAvoxel1 and FAvoxel2 cannot be simply averaged to obtain the entire voxel FA. In other words, the single tensor model is inappropriate for quantifying tissue microstructure in situations with complex fiber orientation distribution (FOD). Another diffusion-based approach to quantify tissue microstructure is direct measurement of tissue properties, such as axon size and intra-axonal volume fraction (V_in) [2–5]. V_in is rotationally invariant, independent of FOD, and can be averaged. The crossing fiber problem still needs to be considered in order to measure V_in accurately. Simultaneous fitting of FOD and V_in is challenging as the number of unknown parameters increases with increasing the complexity of FOD [6–9]. Recently, it was demonstrated that the FOD information can be factored out by analyzing the spherical mean diffusion weighted signal ($\overline{\mathrm{S}}$) averaged over all gradient directions [10–12]. A simple linear relation between V_in and $\overline{\mathrm{S}}$ was further derived analytically [12]. $\overline{\mathrm{S}}$-based analysis has been applied in various recent works, such as apparent fiber density [13–15], spherical mean technique [11,16,17], fiber ball imaging [12,18], power-law scaling [19,20], and rotationally-invariant framework [21–23].

Previous $\overline{\mathrm{S}}$-based studies employed a large number of gradient directions, but subsequent sparse sampling analysis demonstrated that the number of gradient directions could be reduced without significant effect on accuracy [16–18]. Clinical diffusion scan protocols are typically less than 5 min, which only allows acquiring ~ 30 different directions. It is undetermined as whether 30 directions is enough for accurate $\overline{\mathrm{S}}$ measurement, especially at high b-values (b ≥ 3 ms/μm²). Multi-shell acquisition schemes are able to obtain a more comprehensive diffusion dataset, and hence, provide greater sensitivity in detecting tissue microstructure than single-shell schemes [11,16,24]. The increased scanning time requires optimal design of number of directions for each shell.

Given the substantial recent interest in using $\overline{\mathrm{S}}$ to quantify tissue microstructure, it is worthwhile to determine the minimum number of gradient directions for robust measurement of $\overline{\mathrm{S}}$. The current study aims to determine the minimum number of gradient directions for robust measurement of spherical mean signals at different b-values. Similar to previous DTI and spherical deconvolution studies [25–27], we employed computer simulations to investigate the effect of signal-to-noise ratio (SNR) on the required number of gradient directions. Multi-shell Human Connectome Project (HCP) diffusion datasets were used to support the simulation results.

Materials and methods

Theory

The results of single fiber analysis can be generalized to crossing fibers as illustrated by Tournier et al. [27] in the determination of the minimum number of directions for spherical deconvolution. The problem of determining the minimum number of directions for spherical mean signal can also be restricted to single fiber analysis. The total spherical mean signal in each voxel is simply the sum of each single fiber’s spherical mean signal, and the spherical mean signal of a single fiber is independent of the fiber orientation [10,11]. For this reason, we focus on the analysis of a single fiber pointing in the direction n. Based on the widely used two-compartment model of intra- and extra-axonal spaces, the diffusion weighted signal (S) along gradient direction g can be expressed as

$$S(b,\mathbf{g})=S_0\cdot [V_{\mathit{in}}\cdot e^{-{\mathit{bD}}_{\mathit{in}}^{\perp }-b(D_{\mathit{in}}^{\parallel }-D_{\mathit{in}}^{\perp })\cdot {(\mathbf{n}\cdot \mathbf{g})}^2}+(1-V_{\mathit{in}})\cdot e^{-{\mathit{bD}}_{\mathit{ex}}^{\perp }-b(D_{\mathit{ex}}^{\parallel }-D_{\mathit{ex}}^{\perp })\cdot {(\mathbf{n}\cdot \mathbf{g})}^2}]$$ (1)

where S₀ is the signal for b=0, and $D_{\mathit{in}}^{\parallel }$, $D_{\mathit{in}}^{\perp }$, $D_{\mathit{ex}}^{\parallel }$, $D_{\mathit{ex}}^{\perp }$ are intra-axonal axial diffusivity, intra-axonal radial diffusivity, extra-axonal axial diffusivity, and extra-axonal radial diffusivity, respectively. Following previous multi-compartment modeling studies, we assume $D_{\mathit{in}}^{\perp }=0$ [16,18,23], $D_{\mathit{ex}}^{\perp }=(1-{\mathrm{V}}_{\text{in}})\cdot D_{\mathit{ex}}^{\parallel }$ [16,28], and $D_{\mathit{ex}}^{\parallel }=D_{\mathit{in}}^{\parallel }=$ the intrinsic diffusivity λ [16]. The ground truth $\overline{\mathrm{S}}$ is the signal averaged over all gradient directions, and it can be expressed as

$$\overline{S}(b)=S_0\cdot [\frac{V_{\mathit{in}}\cdot \sqrt{\pi }\cdot \text{erf}(\sqrt{b\lambda })}{2\sqrt{b\lambda }}+\frac{(1-V_{\mathit{in}})\cdot \sqrt{\pi }\cdot \text{erf}(\sqrt{b\lambda V_{\mathit{in}}})}{2\sqrt{b\lambda V_{\mathit{in}}}}\cdot e^{-b\lambda (1-V_{\mathit{in}})}]$$ (2)

where erf is the error function. Due to the exponential decay term, the extra-axonal water contribution can be neglected with sufficiently large b-values. In that case, a simple linear relation between $\overline{\mathrm{S}}$ and V_in can be derived as $\overline{\mathrm{S}}={\mathrm{S}}_0\cdot {\mathrm{V}}_{\text{in}}\cdot \frac{\sqrt{\pi }}{2\sqrt{b\lambda }}$ [12,13]. Note that erf $(\sqrt{b\lambda })\ge 0.98$ when bλ ≥ 3.

Simulations

Diffusion-weighted signals were simulated with gradient directions approximately evenly distributed on a unit sphere as proposed by Jones et al. [29]. The number N of gradient directions varied from 6 to 100, and the spherical mean signal $\overline{\mathrm{S}}$ was calculated as the signal averaged over N directions. For each value of N, 10,000 different directions of the single fiber n (uniformly sampled on a sphere) were simulated, from which the mean and standard deviation of $\overline{\mathrm{S}}$ were calculated. The relative standard deviation (RSD), defined as the ratio of the standard deviation to the mean, was used to indicate the precision of $\overline{\mathrm{S}}$ measurement. N_min was determined as the minimum number of gradient directions for RSD($\overline{\mathrm{S}}$) ≤ 5%. N_min is the number of gradient directions needed to achieve sufficient sampling.

Computer simulations were performed in MATLAB with S₀ = 1, V_in = 0.6, and λ = 2 μm²/ms to mimic typical brain white matter parameters [16,18,23]. The diffusion weighting b-value varied from 1 to 10 ms/μm². To investigate the effect of SNR on N_min, complex Gaussian noise was added to the simulated signal S(b,g), and the magnitude of the noisy signal was then taken as the measured signal M(b,g). To correct for Rician bias in the measured signal, here we used the corrected amplitude signal $\mathrm{A}(b,\mathbf{g})=\sqrt{{\mathrm{M}}^2(b,\mathbf{g})-2{\sigma }^2}$, where σ = 1/SNR is the noise level. The corresponding $\overline{\mathrm{M}}$, $\overline{\mathrm{A}}$, RSD($\overline{\mathrm{M}}$), and RSD($\overline{\mathrm{A}}$) were calculated accordingly. Two typical SNRs in the b=0 image of 20 and 40 were used for current study. Two factors are expected to affect RSD($\overline{\mathrm{M}}$) or RSD($\overline{\mathrm{A}}$). The first is the noiseless RSD($\overline{\mathrm{S}}$), and the second is the impact of noise. Since the standard deviation of the mean of N normally distributed random variables is $\frac{\sigma }{\sqrt{\mathrm{N}}}$, the noise related RSD is estimated as $\frac{\sigma }{\overline{\mathrm{S}}\sqrt{\mathrm{N}}}$. Therefore, we used the maximum of RSD($\overline{\mathrm{S}}$) and $\frac{\sigma }{\overline{\mathrm{S}}\sqrt{\mathrm{N}}}$ to approximate RSD($\overline{\mathrm{M}}$) or RSD($\overline{\mathrm{A}}$).

$${\text{RSD}}_{\text{app}}=\text{max}\{\text{RSD}(\overline{S}),\frac{\sigma }{\overline{S}\sqrt{N}}\}$$ (3)

N_min was determined as the minimum number of gradient directions for RSD_app ≤ 5%.

Human data

High-quality HCP data from 3 healthy adults, as part of the MGH-USC Adult Diffusion Dataset, were downloaded from ConnectomeDB (http://db.humanconnectome.org). Diffusion data were acquired with 4 different b-values (i.e., 4 shells): 1 ms/μm² (64 directions), 3 ms/μm² (64 directions), 5 ms/μm² (128 directions), and 10 ms/μm² (256 directions). The gradient direction sets were specifically designed so that a lower shell set is a subset of higher shell set. At each shell, the gradient directions were approximately uniformly distributed [29–31]. One non-diffusion weighted b=0 image was collected for every 13 diffusion weighted images. The signal-to-noise ratio (SNR) was about 20 for white matter in the b=0 image, which was estimated with a maximum-likelihood approach [32].

To demonstrate the accuracy of subsampling for $\overline{\mathrm{M}}$ measurement, a subset of gradient directions at each shell were selected: 10 directions for b = 1 ms/μm², 30 directions for b = 3 ms/μm², 50 directions for b = 5 ms/μm², and 100 directions for b = 10 ms/μm². Those subsets were determined with the incremental sampling scheme to guarantee reasonably uniform coverage [31]. The numbers of gradient directions in subsets were guided by the simulation results. The relative differences of $\overline{\mathrm{M}}$ between full data sets and subsets were calculated.

Results

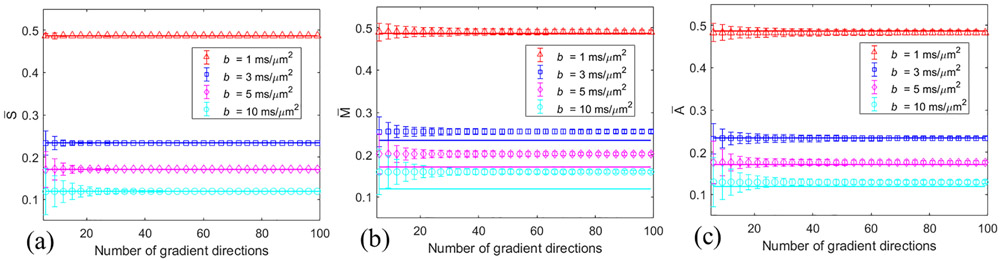
The simulated signal $\overline{\mathrm{S}}$, measured magnitude $\overline{\mathrm{M}}$, and corrected amplitude $\overline{\mathrm{A}}$ were dependent on the number N of gradient directions (Figure 1). The markers represent the mean values over 10,000 different directions of the single fiber n, and the error-bars represent the standard deviations. The solid lines are the ground truth spherical mean signals based on Eq. (2). As shown in Figure 1(a), the mean $\overline{\mathrm{S}}$ is consistent with the ground truth at each b-value and the standard deviation decreases with increasing N. The Rician bias is evident in Figure 1(b), especially at high b-values. Increasing N did not help reduce the Rician bias. The corrected amplitude $\overline{\mathrm{A}}$ is closer to the ground truth than $\overline{\mathrm{M}}$.

Figure 1.

Dependence of the calculated $\overline{\mathrm{S}}$ (a), $\overline{\mathrm{M}}$ (b), and $\overline{\mathrm{A}}$ (c) on the number N of gradient directions. The markers represent the mean values, and the error-bars represent the standard deviations. The solid lines are the ground truth spherical mean signals based on Eq. (2). SNR = 20 for (b) and (c).

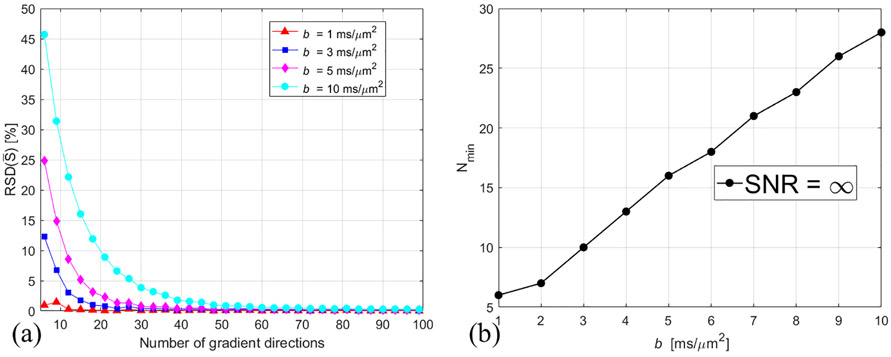
RSD($\overline{\mathrm{S}}$) decreases with increasing N, and the minimum number of N needed for RSD($\overline{\mathrm{S}}$) ≤ 5% is referred to as N_min. Figure 2(a) shows the calculated RSD($\overline{\mathrm{S}}$) as a function of the number of gradient directions. As expected from previous spherical deconvolution work [27], the diffusion signal profile becomes sharp with increasing b-value and more gradient directions are needed for accurate measurements of $\overline{\mathrm{S}}$. Figure 2(b) shows the linear dependence of N_min on b-value.

Figure 2.

Dependence of the calculated RSD($\overline{\mathrm{S}}$) on N for different b-values (a), and dependence of N_min on b-value (b). SNR = ∞ for the simulated $\overline{\mathrm{S}}$.

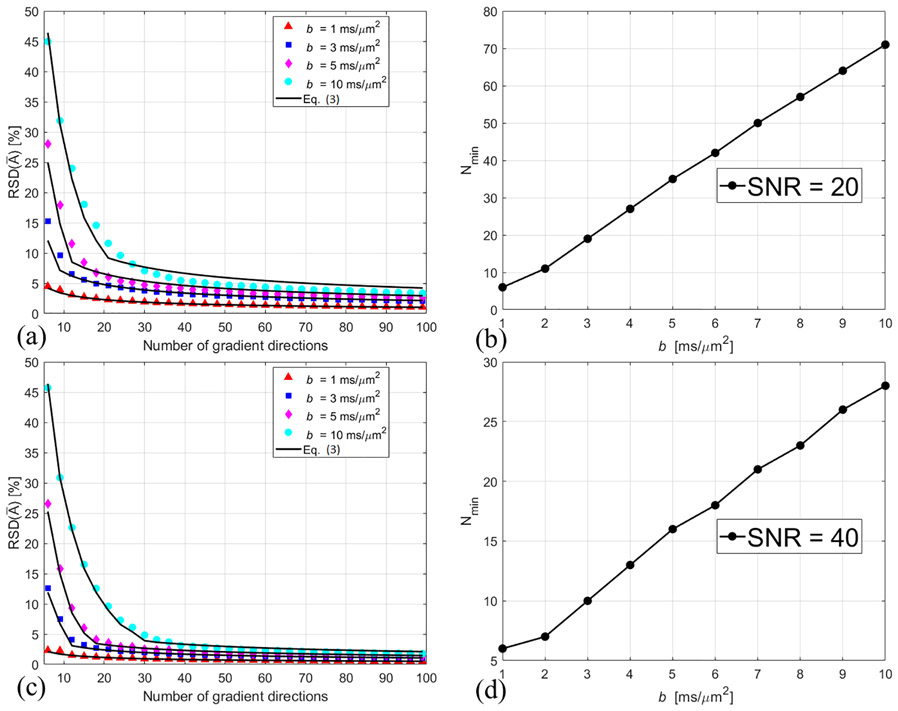
Our simulations showed that RSD($\overline{\mathrm{A}}$) can be properly fit by Eq. (3). Figures 3 (a) and (c) show the calculated RSD($\overline{\mathrm{A}}$) at SNR = 20 and 40, respectively. The solid curves represent the approximated RSD_app based on Eq. (3). Here the minimum number of N needed for RSD_app ≤ 5% is referred to as N_min. The lower the SNR, the higher the number of gradient directions needed for accurate measurement. At SNR = 40, N_min is the same with that of SNR = ∞. At SNR = 20, RSD($\overline{\mathrm{A}}$) is dominated by $\frac{\sigma }{\overline{\mathrm{S}}\sqrt{\mathrm{N}}}$. N_min is still linearly dependent on b-value.

Figure 3.

The markers are the calculated values of RSD($\overline{\mathrm{A}}$) at SNR = 20 (a) and 40 (c). The solid curves in (a) and (c) represent the approximated RSD_app based on Eq. (3). N_min is the minimum number of gradient directions for RSD_app ≤ 5%. Figure 3 (b) and (d) show the b-value dependent N_min at SNR = 20 and 40, respectively.

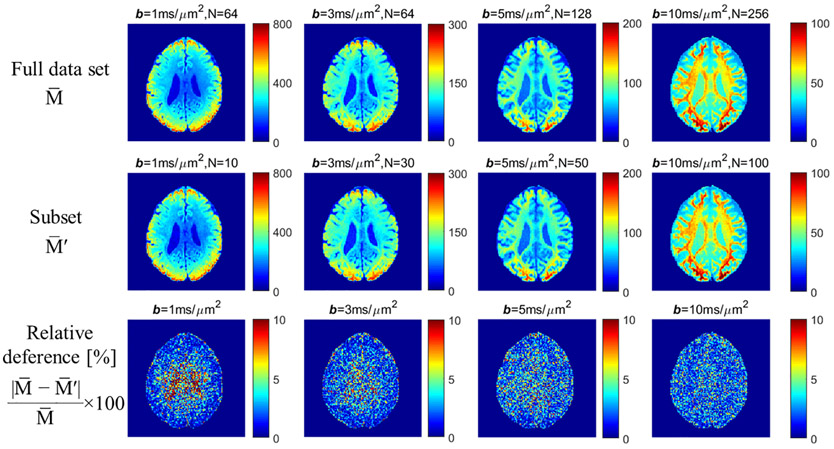
Multi-shell high angular resolution HCP diffusion data were analyzed to support the simulation results. SNR was ~ 20 for white matter in the b=0 image, suggesting that Figure 3 (b) can be used to determine the number of gradient directions for each subset. Since the subset is not fully uniformly distributed, it is better to use a slightly larger N than N_min in Figure 3(b) to guarantee reasonably uniform coverage, which could also help reduce the noise. Here we used 10 directions for b = 1 ms/μm², 30 directions for b = 3 ms/μm², 50 directions for b = 5 ms/μm², and 100 directions for b = 10 ms/μm². Figure 4 shows the comparison between full data sets and subsets for $\overline{\mathrm{M}}$ measurements at different b-values. The relative differences were shown in the last row. The high relative difference in cerebrospinal fluid (CSF) at b = 1 ms/μm² is due to the low signal in CSF and small number of gradient directions in subset. Overall, the whole brain relative differences are 3.14 ± 0.26%, 2.56 ± 0.17%, 2.77 ± 0.10%, and 2.34 ± 0.07% for b = 1, 3, 5, and 10 ms/μm², respectively. Thus, the experimental results were in good agreeement with the simulation results. The spherical mean signal can be measured accurately with a subset of gradient directions.

Figure 4.

Comparison between full data sets and subsets for $\overline{\mathrm{M}}$ measurements from a representative subject. The relative differences were shown in the last row. The low relative differences demonstrate that $\overline{\mathrm{M}}$ can be measured accurately with a subset of gradient directions.

Discussion

The conventional DTI method is significantly limited by the crossing fiber problem for accurate quantification of tissue microstructure. To factor out the complex fiber orientation distribution, the spherical mean technique was proposed to analyze the spherical mean signal instead of the individual signal along each gradient direction [11,16]. The current study investigated the minimum number of gradient directions for robust measurement of spherical mean signals at different b-values. In the case of SNR = ∞, N_min is the number of gradient directions needed to achieve sufficient sampling. Computer simulations were employed to characterize the dependence of RSD($\overline{\mathrm{S}}$) on N and b-value (see Figure 2). In the case of limited SNR, RSD can be estimated by the maximum of the noiseless RSD($\overline{\mathrm{S}}$) and noise-dependent $\frac{\sigma }{\overline{\mathrm{S}}\sqrt{\mathrm{N}}}$. For typical human diffusion studies with SNR ~ 20, we recommend using 10×b/b₁ (b₁ = 1 ms/μm²) uniformly distributed gradient directions for robust $\overline{\mathrm{S}}$ measurement. For example, 30 gradient directions is sufficient for robust $\overline{\mathrm{S}}$ measurement at b = 3 ms/μm², which is achievable within 5 min.

Although our simulations were based on a simplified two-compartment model with predefined λ and V_in, the conclusion can be generalized to other situations. The assumption of $D_{\mathit{ex}}^{\perp }=(1-{\mathrm{V}}_{\text{in}})\cdot D_{\mathit{ex}}^{\parallel }$ is based on the first-order tortuosity approximation for a system of randomly placed parallel cylinders [28]. Several studies have proposed to estimate $D_{\mathit{ex}}^{\parallel }$ and $D_{\mathit{ex}}^{\perp }$ using more comprehensive diffusion datasets [18,21,23]. The choice of an extra-axonal model is insignificant to our study as the extra-axonal water contribution is negligible with sufficiently large b-values [12,13]. Due to the small axon size in brain white matter, the intra-axonal transverse diffusion is highly restricted, and it is commonly assumed that $D_{\mathit{in}}^{\perp }=0$ [12,16,23,33]. Recent power-law scaling studies supported that the approximation is reasonable for white matter [19,20]. This approximation is also insignificant to our study as a larger $D_{\mathit{in}}^{\perp }=0$ is expected to make the diffusion profile more isotropic, which in turn requires less number of gradient directions for sufficient sampling. The intrinsic diffusivity λ was fixed in our simulations. Recent studies demonstrated that λ varies substantially in the brain and that the variation may provide information about the underlying cellular milieu [16,18,23]. However, according to Eq. (2), changing λ is equivalent to changing b-value. The extra simulation with varying λ is unnecessary. Similarly, changing V_in is equivalent to changing SNR. Eq. (3) is always valid for determination of the minimum number of gradient directions for robust measurement of spherical mean signal.

The Rician bias correction was not implemented on the HCP data. Our simulations suggest that $\mathrm{A}(b,\mathbf{g})=\sqrt{{\mathrm{M}}^2(b,\mathbf{g})-2{\sigma }^2}$ is better than the standard $\mathrm{A}(b,\mathbf{g})=\sqrt{{\mathrm{M}}^2(b,\mathbf{g})-{\sigma }^2}$ [34] for $\overline{\mathrm{S}}$ measurement in white matter. For repeated measurements along a single gradient direction or isotropic diffusion measurements along different directions, $\mathrm{A}(b,\mathbf{g})=\sqrt{{\mathrm{M}}^2(b,\mathbf{g})-{\sigma }^2}$ is preferable [34]. However, for anisotropic diffusion in white matter, the measured signals along different directions are different and $\overline{\mathrm{S}}$ is the mean of the signals from N different Rician distributions. In that case, simulations suggest that $\mathrm{A}(b,\mathbf{g})=\sqrt{{\mathrm{M}}^2(b,\mathbf{g})-2{\sigma }^2}$ is better. Note that the reconstruction method and data preprocessing may alter the noise properties [16,35]. The Rician bias correction will need to be investigated further in future studies.

Conclusion

In this study we characterized the relative standard deviation of the spherical mean signal as a function of the number of gradient directions. The minimum number of gradient directions for robust spherical mean signal measurement was then determined. At high SNRs, N_min increases with increasing b-value to achieve sufficient sampling. At low SNRs, N_min increases with increasing b-value to reduce the noise. We recommend using 10×b/b₁ uniformly distributed gradient directions for typical human diffusion studies with SNR ~ 20 for robust spherical mean signal measurement.